Знак множества – Таблица научных, математических, физических символов и сокращений. Сокращённая и символьная запись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический алфавит. Математическая скоропись.
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | ||
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
dic.academic.ru
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| $ \Rightarrow\, $ | ⇒ | Импликация, следование | $ A \Rightarrow B\, $ означает «если $ A $ верно, то $ B $ также верно». Иногда вместо него используют $ \rightarrow\, $. | $ x = 2 \Rightarrow x^2 = 4\, $ верно, но $ x^2 = 4 \Rightarrow x = 2\, $ неверно (так как $ x=-2 $ также является решением). |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| $ \Leftrightarrow $ | ⇔ | Равносильность | $ A \Leftrightarrow B $ означает «$ A $ верно тогда и только тогда, когда $ B $ верно». | $ x + 5 = y + 2 \Leftrightarrow x + 3 = y\, $ |
| «если и только если» или «равносильно | ||||
| везде | ||||
| $ \wedge $ | ∧ | Конъюнкция | $ A \wedge B $ истинно тогда и только тогда, когда $ A $ и $ B $ оба истинны. | $ (n>2)\wedge (n<4)\Leftrightarrow (n=3) $, если $ n $ — натуральное число. |
| «и» | ||||
| Математическая логика | ||||
| $ \vee $ | ∨ | Дизъюнкция | $ A\vee B $ истинно, когда хотя бы одно из условий $ A $ и $ B $ истинно. | $ (n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\ne 3 $, если $ n $ — натуральное число. |
| «или» | ||||
| Математическая логика | ||||
| $ \neg $ | ¬ | Отрицание | $ \neg A $ истинно тогда и только тогда, когда ложно $ A $. | $ \neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B) $ $ x\notin S\Leftrightarrow \neg(x\in S) $ |
| «не» | ||||
| Математическая логика | ||||
| $ \forall $ | ∀ | Квантор всеобщности | $ \forall x, P(x) $ обозначает «$ P(x) $ верно для всех $ x $». | $ \forall n\in \mathbb N,\;n^2\geqslant n $ |
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| $ \exists $ | ∃ | Квантор существования | $ \exists x,\;P(x) $ означает «существует хотя бы один $ x $ такой, что верно $ P(x) $» | $ \exists n\in \mathbb N,\;n+5=2n $ (подходит число 5) |
| «существует» | ||||
| Математическая логика | ||||
| $ =\, $ | = | Равенство | $ x=y $ обозначает «$ x $ и $ y $ обозначают один и тот же объект». | 1 + 2 = 6 − 3 |
| «равно» | ||||
| везде | ||||
| $ := $ $ :\Leftrightarrow $ $ \stackrel{\rm{def}}{=} $ | := :⇔ | Определение | $ x := y $ означает «$ x $ по определению равен $ y $». $ P :\Leftrightarrow Q $ означает «$ P $ по определению равносильно $ Q $» | $ {\rm ch} (x) := {1\over 2}\left(e^x+e^{-x}\right) $ (Гиперболический косинус) $ A \oplus B :\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B) $ (Исключающее или) |
| «равно/равносильно по определению» | ||||
| везде | ||||
| $ \{ ,\} $ | { , } | Множество элементов | $ \{a,\;b,\;c\} $ означает множество, элементами которого являются $ a $, $ b $ и $ c $. | $ \mathbb N = \{0,\;1,\;2,\;\ldots \} $ (множество натуральных чисел) |
| «Множество…» | ||||
| Теория множеств | ||||
| $ \{ | \} $ $ \{ : \} $ | { | } { : } | Множество элементов, удовлетворяющих условию | $ \{x\,|\,P(x)\} $ означает множество всех $ x $ таких, что верно $ P(x) $. | $ \{n\in \mathbb N\,|\,n^2<20\} = \{0,\;1,\;2,\;3,\;4\} $ |
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| $ \varnothing $ $ \{\} $ | ∅ {} | Пустое множество | $ \{\} $ и $ \varnothing $ означают множество, не содержащее ни одного элемента. | $ \{n\in \mathbb N\,|\,1<n^2<4\} = \varnothing $ |
| «Пустое множество» | ||||
| Теория множеств | ||||
| $ \in $ $ \notin $ | ∈ ∉ | Принадлежность/непринадлежность к множеству | $ a\in S $ означает «$ a $ является элементом множества $ S $» $ a\notin S $ означает «$ a $ не является элементом $ S $» | $ 2\in \mathbb N $ $ {1\over 2}\notin \mathbb N $ |
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| $ \subseteq $ $ \subset $ | ⊆ ⊂ | Подмножество | $ A\subseteq B $ означает «каждый элемент из $ A $ также являестя элементом из $ B $». $ A\subset B $ обычно означает то же, что и $ A\subseteq B $. Однако некоторые авторы используют $ \subset $, чтобы показать строгое включение (то есть $ \subsetneq $). | $ (A\cap B) \subseteq A $ $ \mathbb Q\subseteq \mathbb R $ |
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| $ \subsetneq $ | ⫋ | Собственное подмножество | $ A\subsetneq B $ означает $ A\subseteq B $ и $ A\ne B $. | $ \mathbb N\subsetneq \mathbb Q $ |
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| $ \cup $ | ∪ | Объединение | $ A\cup B $ означает множество элементов, принадлежащих $ A $ или $ B $ (или обоим сразу). | $ A\subseteq B\Leftrightarrow A\cup B=B $ |
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| $ \cap $ | ⋂ | Пересечение | $ A\cap B $ означает множество элементов, принадлежащих и $ A $, и $ B $. | $ \{x\in \R\,|\,x^2=1\}\cap \mathbb N = \{1\} $ |
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| $ \setminus $ | \ | Разность множеств | $ A\setminus B $ означает множество элементов, принадлежащих $ A $, но не принадлежащих $ B $. | $ \{1,\;2,\;3,\;4\}\setminus \{3,\;4,\;5,\;6\} = \{1,\;2\} $ |
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| $ \to $ | → | Функция | $ f\!\!:X\to Y $ означает функцию $ f $ с областью определения $ X $ и областью прибытия $ Y $. | Функция $ f\!\!:\mathbb Z\to \mathbb Z $, определённая как $ f(x)=x^2 $ |
| «из … в», | ||||
| везде | ||||
| $ \mapsto $ | ↦ | Отображение | $ x \mapsto f(x) $ означает, что образом $ x $ после применения функции $ f $ будет $ f(x) $. | Функцию, определённую как $ f(x)=x^2 $, можно записать так: $ f\colon x \mapsto x^2 $ |
| «отображается в» | ||||
| везде | ||||
| $ \mathbb N $ | N или ℕ | Натуральные числа | $ \mathbb N $ означает множество $ \{1,\;2,\;3,\;\ldots\} $ или $ \{0,\;1,\;2,\;3,\;\ldots\} $ (в зависимости от ситуации). | $ \{\left|a\right|\,|\,a\in \mathbb Z\}=\mathbb N $ |
| «Эн» | ||||
| Числа | ||||
| $ \mathbb Z $ | Z или ℤ | Целые числа | $ \mathbb Z $ означает множество $ \{\ldots,\;-3,\;-2,\;-1,\;0,\;1,\;2,\;3,\;\ldots\} $ | $ \{a,\;-a\,|\,a\in\mathbb N\}=\mathbb Z $ |
| «Зед» | ||||
| Числа | ||||
| $ \mathbb Q $ | Q или ℚ | Рациональные числа | $ \mathbb Q $ означает $ \left\{\left.{p\over q} \right| p\in \mathbb Z \wedge q\in \mathbb Z\wedge q\ne 0\right\} $ | $ 3,\!14\in \mathbb Q $ $ \pi \notin \mathbb Q $ |
| «Ку» | ||||
| Числа | ||||
| $ \mathbb R $ | R или ℝ | Вещественные числа, или действительные числа | $ \R $ означает множество всех пределов последовательностей из $ \mathbb Q $ | $ \pi \in \R $ $ i \notin \R $ ($ i $ — комплексное число: $ i^2=-1 $) |
| «Эр» | ||||
| Числа | ||||
| $ \mathbb C $ | C или ℂ | Комплексные числа | $ \mathbb C $ означает множество $ \{a+b\cdot i\,|\,a\in \R \wedge b\in \R\} $ | $ i\in \mathbb C $ |
| «Це» | ||||
| Числа | ||||
| $ <\, $ $ >\, $ | < > | Сравнение | $ x<y $ обозначает, что $ x $ строго меньше $ y $. $ x>y $ означает, что $ x $ строго больше $ y $. | $ x<y\Leftrightarrow y>x $ |
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| $ \leqslant $ $ \geqslant $ | ≤ или ⩽ ≥ или ⩾ | Сравнение | $ x\leqslant y $ означает, что $ x $ меньше или равен $ y $. $ x\geqslant y $ означает, что $ x $ больше или равен $ y $. | $ x\geqslant 1\Rightarrow x^2\geqslant x $ |
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| $ \approx $ | ≈ | Приблизительное равенство | $ e\approx 2,\!718 $ с точностью до $ 10^{-3} $ означает, что 2,718 отличается от $ e $ не больше чем на $ 10^{-3} $. | $ \pi \approx 3,\!1415926 $ с точностью до $ 10^{-7} $. |
| «приблизительно равно» | ||||
| Числа | ||||
| $ \sqrt{ } $ | √ | Арифметический квадратный корень | $ \sqrt x $ означает положительное действительное число, которое в квадрате даёт $ x $. | $ \sqrt 4=2 $ $ \sqrt {x^2}= \left|x\right| $ |
| «Корень квадратный из …» | ||||
| Числа | ||||
| $ \infty $ | ∞ | Бесконечность | $ +\infty $ и $ -\infty $ суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | $ \lim\limits_{x\to 0} {1\over \left|x\right|}= \infty $ |
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| $ \left|\;\right| $ | | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | $ \left|x\right| $ обозначает абсолютную величину $ x $. $ |A| $ обозначает мощность множества $ A $ и равняется, если $ A $ конечно, числу элементов $ A $. | $ \left|a+b\cdot i\right|=\sqrt {a^2+b^2} $ |
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| $ \sum $ | ∑ | Сумма, сумма ряда | $ \sum_{k=1}^n a_k $ означает «сумма $ a_k $, где $ k $ принимает значения от 1 до $ n $», то есть $ a_1+a_2+\ldots+a_n $. $ \sum_{k=1}^{\infty} a_k $ означает сумму ряда, состоящего из $ a_k $. | $ \sum_{k=1}^4 k^2= $ $ = 1^2 + 2^2 + 3^2 + 4^2 $ $ = 30 $ |
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| $ \prod $ | ∏ | Произведение | $ \prod_{k=1}^n a_k $ означает «произведение $ a_k $ для всех $ k $ от 1 до $ n $», то есть $ a_1\cdot a_2\cdot\ldots\cdot a_n $ | $ \prod_{k=1}^4 (k+2)= $ $ =3\cdot 4\cdot 5\cdot 6=360 $ |
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| $ \int dx $ | ∫ | Интеграл | $ \int\limits_a^b f(x)\, dx $ означает «интеграл от $ a $ до $ b $ функции $ f $ от $ x $ по переменной $ x $». | $ \int\limits_0^b x^2\, dx = b^3/3 $ $ \int x^2\, dx = x^3/3 $ |
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| $ \frac{df}{dx} $ $ f'(x) $ | df/dx f'(x) | Производная | $ \frac{df}{dx} $ или $ f'(x) $ означает «(первая) производная функции $ f $ от $ x $ по переменной $ x $». | $ \frac{d \cos x}{dx} = -\sin x $ |
| «Производная … по …» | ||||
| Математический анализ | ||||
| $ \frac{d^n f}{dx^n} $ $ f^{(n)} (x) $ | $ d^n f/dx^n $ $ f^{(n)}(x) $ | Производная $ n $-го порядка | $ \frac{d^n f}{dx^n} $ или $ f^{(n)} (x) $ (во втором случае если $ n $ — фиксированное число, то оно пишется римскими цифрами) означает «$ n $-я производная функции $ f $ от $ x $ по переменной $ x $». | $ \frac{d^4 \cos x}{dx^4} = \cos x $ |
| «$ n $-я производная … по …» | ||||
| Математический анализ |
ru.vlab.wikia.com
Элементы теории множеств
1. Логические символы
Квантор — заменяет выражение «для любого», «для произвольного», «для какого бы ни было».
Квантор — заменяет выражение «существует», «найдется».
Запись (импликация) означает, что из справедливости высказывания A вытекает справедливость высказывания B. Если, кроме того, из справедливости высказывания B вытекает справедливость A, то записываем . Если , то высказывание B является необходимым и достаточным условием для того, чтобы выполнялось высказывание A.
Если предложения A и B справедливы одновременно, то записываем . Если же справедливо хотя бы одно из предложений A или B, то записываем .
2. Операции над множествами
Математическое понятие множества элементов принимается в качестве интуитивного. Множество задается правилом или признаком, согласно которому определяем, принадлежит ли данный элемент множеству или не принадлежит.
Множество обозначают символом A = {x}, где x — общее наименование элементов множества A. Часто множество записывают в виде A = {a, b,c, …}, где в фигурных скобках указаны элементы множества A. Будем пользоваться обозначениями:
N — множество всех натуральных чисел; Z — множество всех целых чисел; Q — множество всех рациональных чисел; R — множество всех действительных чисел; C — множество всех комплексных чисел; Z0 — множество всех неотрицательных целых чисел.
Запись (или ) означает, что элемент a принадлежит множеству A.
Запись (или ) означает, что элемент a не принадлежит множеству A.
Множество B, все элементы которого принадлежат множеству A, называется подмножеством множества A, и при этом записывают (или ) (см. рис. 1).
Всегда , так как каждый элемент множества, естественно, принадлежит A. Пустое множество, т. е. множество, не содержащее ни одного элемента, обозначим символом . Любое множество содержит пустое множество в качестве своего подмножества.
Если , то A и B называются равными множествами, при этом записывают A = B.
Если , то множество элементов множества , не принадлежащих A, называется дополнением множества A к множеству (см. рис. 2).
Дополнение множества A к множеству обозначают символом ; или просто CA, если известно, к какому множеству берется дополнение. Таким образом,
Если , то иногда дополнение множества B к множеству A называют разностью множеств A и B и обозначают A\B (см. рис. 3), т. е.
Пусть A и B — подмножества множества .
Объединением множеств A и B называется множество (см. рис. 4)
Аналогично, если , подмножества множества , то их объединением будет множество
Пересечением подмножеств A и B называется множество (см. рис. 5)
Аналогично, символом обозначают пересечение подмножеств , множества , т. е. множество
Если каждому сопоставлено некоторое множество , то говорят, что задано семейство множеств . В этом случае множество называют объединением семейства множеств , а множество — пересечением этого семейства.
Симметрической разностью двух множеств A и B называется множество, определяемое объединением разностей A\B и B\A (см. рис. 6).
Симметрическую разность обозначают символом .
Два элемента a и b называются упорядоченной парой, если указано, какой из этих элементов первый, какой второй, при этом .
Упорядоченную пару элементов a и b обозначают символом (a, b).
Аналогично определяется упорядоченная система из n элементов a1, a2, …, an, которую обозначают символом (a1, a2, …, an). Элементы a1, a2, …, an называются координатами упорядоченной системы (a1, a2, …, an).
Совокупность всевозможных упорядоченных пар (a, b), где , называется произведением множеств A и B и обозначается символом .
Аналогично, символом обозначают произведение множеств , т. е. совокупность всевозможных упорядоченных систем (a1, a2, …, an), где .
studfiles.net
Основные математические знаки и символы :: SYL.ru
Как известно, математика любит точность и краткость – недаром одна-единственная формула может в словесной форме занимать абзац, а порой и целую страницу текста. Таким образом, графические элементы, используемые во всем мире в науке, призваны увеличить скорость написания и компактность представления данных. Кроме того, стандартизованные графические изображения может распознать носитель любого языка, имеющий базовые знания в соответствующей сфере.
История математических знаков и символов насчитывает много столетий – некоторые из них были придуманы случайным образом и предназначались для обозначения иных явлений; другие же стали продуктом деятельности ученых, целенаправленно формирующих искусственный язык и руководствующихся исключительно практическими соображениями.
Плюс и минус
История происхождения символов, обозначающих простейшие арифметические операции, доподлинно неизвестна. Однако существует достаточно вероятная гипотеза происхождения знака «плюс», имеющего вид перекрещенных горизонтальной и вертикальной черт. В соответствии с ней символ сложения берет начало в латинском союзе et, который переводится на русский язык как «и». Постепенно, с целью ускорения процесса записи, слово было сокращено до вертикально ориентированного креста, напоминающего букву t. Самый ранний достоверный пример подобного сокращения датируется XIV веком.
 Общепринятый знак «минус» появился, по всей видимости, позже. В XIV и даже XV веке в научной литературе использовался целый ряд символов, обозначающих операцию вычитания, и лишь к XVI веку «плюс» и «минус» в их современном виде стали встречаться в математических трудах вместе.
Общепринятый знак «минус» появился, по всей видимости, позже. В XIV и даже XV веке в научной литературе использовался целый ряд символов, обозначающих операцию вычитания, и лишь к XVI веку «плюс» и «минус» в их современном виде стали встречаться в математических трудах вместе.
Умножение и деление
Как ни странно, математические знаки и символы для этих двух арифметических действий не полностью стандартизованы и сегодня. Популярным обозначением умножения является предложенный математиком Отредом в XVII веке диагональный крестик, который можно увидеть, например, на калькуляторах. На уроках математики в школе ту же операцию обычно представляют в виде точки – данный способ предложил в том же веке Лейбниц. Ещё один способ представления – звёздочка, которая наиболее часто используется при компьютерном представлении различных расчётов. Использовать её предложил всё в том же XVII веке Иоганн Ран.
Для операции деления предусмотрены знак наклонной черты (предложен Отредом) и горизонтальная линия с точками сверху и снизу (символ ввел Иоганн Ран). Первый вариант обозначения является более популярным, однако второй также достаточно распространен.
Математические знаки и символы и их значения порой изменяются во времени. Однако все три способа графического представления умножения, а также оба способа для деления являются в той или иной степени состоятельными и актуальными на сегодняшний день.
Равенство, тождество, эквивалентность
Как и в случае многих других математических знаков и символов, обозначение равенства изначально было словесным. Достаточно продолжительное время общепринятым обозначением служило сокращение ae от латинского aequalis («равны»). Однако в XVI веке математик из Уэльса по имени Роберт Рекорд предложил в качестве символа две горизонтальные прямые, расположенные друг под другом. Как утверждал ученый, нельзя придумать ничего более равного между собой, чем два параллельных отрезка.
 Несмотря на то что аналогичный знак использовался для обозначения параллельности прямых, новый символ равенства постепенно получил распространение. К слову, такие знаки как «больше» и «меньше», изображающие развернутые в разные стороны галочки, появились лишь в XVII-XVIII веке. Сегодня же они кажутся интуитивно понятными любому школьнику.
Несмотря на то что аналогичный знак использовался для обозначения параллельности прямых, новый символ равенства постепенно получил распространение. К слову, такие знаки как «больше» и «меньше», изображающие развернутые в разные стороны галочки, появились лишь в XVII-XVIII веке. Сегодня же они кажутся интуитивно понятными любому школьнику.
Несколько более сложные знаки эквивалентности (две волнистые линии) и тождества (три горизонтальные параллельные прямые) вошли в обиход лишь во второй половине XIX века.
Знак неизвестного – «Икс»
История возникновения математических знаков и символов знает и весьма интересные случаи переосмысления графики по мере развития науки. Знак обозначения неизвестного, именуемый сегодня «иксом», берет своё начало на Ближнем Востоке на заре прошлого тысячелетия.
Ещё в X веке в арабском мире, славящемся в тот исторический период своими учеными, понятие неизвестного обозначалось словом, буквально переводящимся как «нечто» и начинающимся со звука «Ш». С целью экономии материалов и времени слово в трактатах стало сокращаться до первой буквы.
 Спустя многие десятилетия письменные труды арабских ученых оказались в городах Пиренейского полуострова, на территории современной Испании. Научные трактаты стали переводиться на национальный язык, но возникла трудность — в испанском отсутствует фонема «Ш». Заимствованные арабские слова, начинающиеся с неё, записывались по особому правилу и предварялись буквой X. Научным языком того времени была латынь, в которой соответствующий знак имеет название «Икс».
Спустя многие десятилетия письменные труды арабских ученых оказались в городах Пиренейского полуострова, на территории современной Испании. Научные трактаты стали переводиться на национальный язык, но возникла трудность — в испанском отсутствует фонема «Ш». Заимствованные арабские слова, начинающиеся с неё, записывались по особому правилу и предварялись буквой X. Научным языком того времени была латынь, в которой соответствующий знак имеет название «Икс».
Таким образом, знак, на первый взгляд являющийся лишь случайно выбранным символом, имеет глубокую историю и изначально является сокращением арабского слова «нечто».
Обозначение других неизвестных
В отличие от «Икса», знакомые нам со школьной скамьи Y и Z, а также a, b, c имеют гораздо более прозаичную историю происхождения.
В XVII веке была издана книга Декарта под названием «Геометрия». В этой книге автор предлагал стандартизировать символы в уравнениях: в соответствии с его идеей, последние три буквы латинского алфавита (начиная от «Икса») стали обозначать неизвестные, а три первые – известные значения.
Тригонометрические термины
По-настоящему необычна история такого слова, как «синус».
Первоначально соответствующие тригонометрические функции получили название в Индии. Слово, соответствующее понятию синуса, буквально означало «тетива». В эпоху расцвета арабской науки индийские трактаты были переведены, а понятие, аналога которому не оказалось в арабском языке, транскрибировано. По стечению обстоятельств, то, что получилось на письме, напоминало реально существующее слово «впадина», семантика которого не имела никакого отношения к исходному термину. В результате, когда в 12 веке арабские тексты были переведены на латынь, возникло слово «синус», означающее «впадина» и закрепившееся в качестве нового математического понятия.
 А вот математические знаки и символы для тангенса и котангенса до сих пор не стандартизованы – в одних странах их принято писать как tg, а в других – как tan.
А вот математические знаки и символы для тангенса и котангенса до сих пор не стандартизованы – в одних странах их принято писать как tg, а в других – как tan.
Некоторые другие знаки
Как видно из примеров, описанных выше, возникновение математических знаков и символов в значительной мере пришлось на XVI-XVII века. На этот же период пришлось возникновение привычных сегодня форм записи таких понятий, как процент, квадратный корень, степень.
Процент, т. е. сотая доля, долгое время обозначался как cto (сокращение от лат. cento). Считается, что общепринятый на сегодняшний день знак появился в результате опечатки около четырехсот лет назад. Получившееся изображение было воспринято как удачный способ сокращения и прижилось.
 Знак корня изначально представлял собой стилизованную букву R (сокращение от латинского слова radix — «корень»). Верхняя черта, под которую сегодня записывается выражение, выполняла функцию скобок и являлась отдельным символом, обособленным от корня. Круглые скобки были придуманы позже — в повсеместное обращение они вошли благодаря деятельности Лейбница (1646-1716). Благодаря его же трудам был введен в науку и символ интеграла, выглядящий как вытянутая буква S — сокращение от слова «сумма».
Знак корня изначально представлял собой стилизованную букву R (сокращение от латинского слова radix — «корень»). Верхняя черта, под которую сегодня записывается выражение, выполняла функцию скобок и являлась отдельным символом, обособленным от корня. Круглые скобки были придуманы позже — в повсеместное обращение они вошли благодаря деятельности Лейбница (1646-1716). Благодаря его же трудам был введен в науку и символ интеграла, выглядящий как вытянутая буква S — сокращение от слова «сумма».
Наконец, знак операции возведения в степень был придуман Декартом и доработан Ньютоном во второй половине XVII века.
Более поздние обозначения
Учитывая, что знакомые нам графические изображения «плюса» и «минуса» были введены в обращение всего несколько столетий назад, не кажется удивительным, что математические знаки и символы, обозначающие сложные явления, стали использоваться лишь в позапрошлом веке.
Так, факториал, имеющий вид восклицательного знака после числа или переменной, появился лишь в начале XIX века. Приблизительно тогда же появились заглавная «П» для обозначения произведения и символ предела.
Несколько странно, что знаки для числа Пи и алгебраической суммы появились лишь в XVIII веке – позже, чем, например, символ интеграла, хотя интуитивно кажется, что они являются более употребительными. Графическое изображение отношения длины окружности к диаметру происходит от первой буквы греческих слов, означающих «окружность» и «периметр». А знак «сигма» для алгебраической суммы был предложен Эйлером в последней четверти XVIII столетия.
Названия символов на разных языках
Как известно, языком науки в Европе на протяжении многих веков была латынь. Физические, медицинские и многие другие термины часто заимствовались в виде транскрипций, значительно реже – в виде кальки. Таким образом, многие математические знаки и символы на английском называются почти так же, как на русском, французском или немецком. Чем сложнее суть явления, тем выше вероятность, что в разных языках оно будет иметь одинаковое название.
Компьютерная запись математических знаков
Простейшие математические знаки и символы в «Ворде» обозначаются обычной комбинацией клавиш Shift+цифра от 0 до 9 в русской или английской раскладке. Отдельные клавиши отведены под некоторые широкоупотребительные знаки: плюс, минус, равенство, наклонная черта.
 Если же требуется использовать графические изображения интеграла, алгебраической суммы или произведения, числа Пи и т. д., требуется открыть в «Ворде» вкладку «Вставка» и найти одну из двух кнопок: «Формула» или «Символ». В первом случае откроется конструктор, позволяющий выстроить целую формулу в рамках одного поля, а во втором – таблица символов, где можно найти любые математические знаки.
Если же требуется использовать графические изображения интеграла, алгебраической суммы или произведения, числа Пи и т. д., требуется открыть в «Ворде» вкладку «Вставка» и найти одну из двух кнопок: «Формула» или «Символ». В первом случае откроется конструктор, позволяющий выстроить целую формулу в рамках одного поля, а во втором – таблица символов, где можно найти любые математические знаки.
Как запомнить математические символы
В отличие от химии и физики, где количество символов для запоминания может превосходить сотню единиц, математика оперирует относительно небольшим числом знаков. Простейшие из них мы усваиваем ещё в глубоком детстве, учась складывать и вычитать, и только в университете на определенных специальностях знакомимся с немногочисленными сложными математическими знаками и символами. Картинки для детей помогают за считанные недели достичь мгновенного узнавания графического изображения требуемой операции, гораздо больше времени может понадобиться для овладения навыком самого осуществления этих операций и понимания их сущности.
Таким образом, процесс запоминания знаков происходит автоматически и не требует особых усилий.
В заключение
Ценность математических знаков и символов заключается в том, что их без труда понимают люди, говорящие на разных языках и являющиеся носителями различных культур. По этой причине крайне полезно понимать и уметь воспроизводить графические изображения различных явлений и операций.
Высокий уровень стандартизации этих знаков обуславливает их использование в самых различных сферах: в области финансов, информационных технологий, инженерном деле и др. Для каждого, кто хочет заниматься делом, связанным с числами и расчетами, знание математических знаков и символов и их значений становится жизненной необходимостью.
www.syl.ru
Операции над множествами. Обозначение множеств и их элементов — Мегаобучалка
Обозначение множеств и их элементов. Равенство множеств.
Подмножество ( включение ). Сумма ( объединение ) множеств.
Произведение ( пересечение ) множеств. Разность ( дополнение )
множеств.Симметричная разность множеств. Свойства
операций над множествами.
Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись a R означает, что элемент а принадлежит множеству R , то есть а является элементом множества R . В противном случае, когда а не принадлежит множеству R , пишут a R .
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
Говорят, что множество А содержится в множестве В ( рис.1 ) или множество А является подмножеством множества В ( в этом случае пишут А В), если каждый элемент множества А одновременно является элементом множества В . Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: А и А А .
Сумма ( объединение ) множеств А и В ( пишется А В ) есть множество элементов, каждый из которых принадлежит либо А , либо В. Таким образом, е А В тогда и только тогда, когда либо е А ,либо е В .
Произведение ( пересечение ) множеств А и В ( пишется А В , рис.2 ) есть множествоэлементов, каждый из которых принадлежит и А , и В. Таким образом, е А В тогда и только тогда, когда е А и е В .
Разность множеств А и В ( пишется А – В , рис.3 ) есть множествоэлементов, которые принадлежат множеству А , но не принадлежат множеству В.Это множество называется также дополнением множества В относительно множества А.
Симметричная разность множеств А и В ( пишется А \ В ) есть множество:
А \ В = ( А – В ) ( В – А ).
Свойства операций над множествами:

П р и м е р ы. 1. Множество детей является подмножеством всего населения.
2. Пересечением множества целых чисел с множеством поло-
жительных чисел является множество натуральных чисел.
3. Объединением множества рациональных чисел с множест-
вом иррациональных чисел является множество действи-
тельных чисел.
4. Нуль является дополнением множества натуральных чисел
относительно множества неотрицательных целых чисел.
Множество содержится во множестве (множество включает множество ), если каждый элемент есть элемент :
В этом случае называется подмножеством , — надмножеством . Если и , то называется собственным подмножеством . Заметим, что . По определению .
Два множества называются равными, если они являются подмножествами друг друга:
Иногда для того, чтобы подчеркнуть, что множества могут быть равны, используется запись:
Бинарные операции
Ниже перечислены основные операции над множествами:
· пересечение:
· объединение:
Если множества и не пересекаются: , то их объединение обозначают также: .
· разность (дополнение):
· симметрическая разность:
· Декартово или прямое произведение:
Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Билет 2.
Правило вида f: A->B, ставящее в соответствие каждому элементу множества A какой-либо элемент (или элементы) множества B, называется отображением из A в B. Пример: A — множество футбольных команд, B — множество населённых пунктов; каждой футбольной команде ставится в соответствие пункт, где находится её родной стадион (ну или стадион, где она официально играет «на своём поле», если нет собственного стадиона).
Если какому-либо элементу множества A соответствует более одного элемента множества B, то отображение многозначное. Пример многозначного изображения можно привести следующий. Пусть A — множество олигархов, B — множество особняков. Есть олигархи, владеющие несколькими особняками. Тогда отображение, ставящее в соответствие каждому олигарху его особняки, является многозначным.
В дискретной математике, как правило, рассматриваются однозначные отображения. Отображение из A в B однозначное, если всякому элементу из A поставлен в соответствие только один элемент из B. Пример однозначного отображения: пусть есть воинская часть, в ней множество солдат и множество батальонов. Отображение, ставящее в соответствие солдату батальон, в котором он числится, однозначное, если только в списках составов не допущено ошибок. Заметим, что определение однозначного отображения из A в B не запрещает ситуаций, когда двум разным элементам множества A соответствует один и тот же элемент из B. Ярко видно это по примеру с солдатами.
Далее мы рассмотрим некоторые виды однозначных отображений, для простоты понятие «однозначное» иногда будем опускать.
megaobuchalka.ru
Математические знаки и символы: список, таблица, история возникновения
Когда люди долгое время взаимодействуют в рамках определенной сферы деятельности, они начинают искать способ оптимизировать процесс коммуникации. Система математических знаков и символов представляет собой искусственный язык, который был разработан, чтобы уменьшить объем графически передаваемой информации и при этом полностью сохранить заложенный в сообщение смысл.
Любой язык требует изучения, и язык математики в этом плане – не исключение. Чтобы понимать значение формул, уравнений и графиков, требуется заранее владеть определенной информацией, разбираться в терминах, системе обозначений и т. д. При отсутствии такого знания текст будет восприниматься как написанный на незнакомом иностранном языке.
В соответствии с запросами общества графические символы для более простых математических операций (например, обозначение сложения и вычитания) были выработаны раньше, чем для сложных понятий наподобие интеграла или дифференциала. Чем сложнее понятие, тем более сложным знаком оно обычно обозначается.
Модели образования графических обозначений
На ранних этапах развития цивилизации люди связывали простейшие математические операции с привычными для них понятиями на основе ассоциаций. Например, в Древнем Египте сложение и вычитание обозначались рисунком идущих ног: направленные по направлению чтения строки они обозначали «плюс», а в обратную сторону – «минус».
Цифры, пожалуй, во всех культурах изначально обозначались соответствующим количеством черточек. Позже для записи стали использоваться условные обозначения — это экономило время, а также место на материальных носителях. Часто в качестве символов использовались буквы: такая стратегия получила распространение в греческом, латинском и многих других языках мира.
 История возникновения математических символов и знаков знает два наиболее продуктивных способа образования графических элементов.
История возникновения математических символов и знаков знает два наиболее продуктивных способа образования графических элементов.
Преобразование словесного представления
Изначально любое математическое понятие выражается некоторым словом или словосочетанием и не имеет собственного графического представления (помимо лексического). Однако выполнение расчетов и написание формул словами – процедура длительная и занимающая неоправданно много места на материальном носителе.
Распространенный способ создания математических символов – трансформация лексического представления понятия в графический элемент. Иначе говоря, слово, обозначающее понятие, с течением времени сокращается или преобразуется каким-либо другим способом.
 Например, основной гипотезой происхождения знака «плюс» является его сокращение от латинского et, аналогом которого в русском языке является союз «и». Постепенно в скорописи первая буква перестала писаться, а t сократилась до креста.
Например, основной гипотезой происхождения знака «плюс» является его сокращение от латинского et, аналогом которого в русском языке является союз «и». Постепенно в скорописи первая буква перестала писаться, а t сократилась до креста.
Другой пример – знак «икс», обозначающий неизвестное, который изначально представлял собой сокращение от арабского слова «нечто». Сходным образом произошли знаки для обозначения квадратного корня, процента, интеграла, логарифма и др. В таблице математических символов и знаков можно встретить более десятка графических элементов, появившихся таким образом.
Назначение произвольного символа
Второй распространенный вариант образования математических знаков и символов – назначение символа произвольным образом. В этом случае слово и графическое обозначение между собой не связаны — знак обычно утверждается в результате рекомендации одного из членов научного сообщества.
Например, знаки умножения, деления, равенства были предложены математиками Уильямом Отредом, Иоганном Раном и Робертом Рекордом. В некоторых случаях несколько математических знаков могли быть введены в науку одним ученым. В частности, Готфрид Вильгельм Лейбниц предложил целый ряд символов, в том числе интеграла, дифференциала, производной.
Простейшие операции
Такие знаки, как «плюс» и «минус», а также символы, обозначающие умножение и деление, знает каждый школьник, несмотря на то, что для последних двух упомянутых операций существует несколько возможных графических знаков.
Можно с уверенностью говорить, что складывать и вычитать люди умели ещё за много тысячелетий до нашей эры, а вот стандартизованные математические знаки и символы, обозначающие данные действия и известные нам сегодня, появились лишь к XIV-XV столетию.
 Впрочем, несмотря на установление определенной договоренности в научном сообществе, умножение и в наше время может изображаться тремя различными знаками (диагональный крестик, точка, звёздочка), а деление – двумя (горизонтальная черта с точками сверху и снизу или наклонная черта).
Впрочем, несмотря на установление определенной договоренности в научном сообществе, умножение и в наше время может изображаться тремя различными знаками (диагональный крестик, точка, звёздочка), а деление – двумя (горизонтальная черта с точками сверху и снизу или наклонная черта).
Латинские буквы
На протяжении многих столетий научное сообщество использовало для обмена информацией исключительно латынь, и многие математические термины и знаки обнаруживают свои истоки именно в этом языке. В некоторых случаях графические элементы стали результатом сокращения слов, реже – их намеренного или случайного преобразования (например, вследствие описки).
Обозначение процента («%»), вероятнее всего, происходит от ошибочного написания сокращения cto (cento, т. е. «сотая доля»). Сходным образом произошёл знак «плюс», история которого описана выше.
Гораздо большее количество символов было образовано путём намеренного сокращения слова, хотя это не всегда очевидно. Далеко не каждый человек узнает в знаке квадратного корня букву R, т. е. первый знак в слове Radix («корень»). Символ интеграла также представляет собой первую букву слова Summa, однако интуитивно она похожа на прописную f без горизонтальной черты. К слову, в первой публикации издатели совершили именно такую ошибку, напечатав f вместо данного символа.
Греческие буквы
В качестве графических обозначений для различных понятий используются не только латинские, но и греческие буквы. В таблице математических символов можно найти целый ряд примеров такого наименования.
Число Пи, представляющее собой отношение длины окружности к её диаметру, произошло от первой буквы греческого слова, обозначающего окружность. Существует ещё несколько менее известных иррациональных чисел, обозначаемых буквами греческого алфавита.
 Крайне распространенным знаком в математике является «дельта», отражающая величину изменения значения переменных. Ещё одним употребительным знаком является «сигма», выполняющая функцию знака суммы.
Крайне распространенным знаком в математике является «дельта», отражающая величину изменения значения переменных. Ещё одним употребительным знаком является «сигма», выполняющая функцию знака суммы.
Более того, практически все греческие буквы так или иначе используются в математике. Однако данные математические знаки и символы и их значение знают только люди, занимающиеся наукой профессионально. В быту и повседневной жизни эти знания человеку не требуются.
Знаки логики
Как ни странно, многие интуитивно понятные символы были придуманы совсем недавно.
В частности, горизонтальная стрелка, заменяющая слово «следовательно», была предложена лишь в 1922 года Давидом Гильбертом. Кванторы существования и всеобщности, т. е. знаки, читающиеся как: «существует…» и «для любого…», были введены в 1897 и 1935 году соответственно.
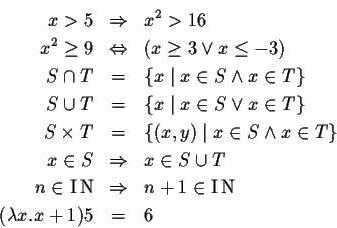 Символы из области теории множеств были придуманы в 1888-1889 гг. А перечеркнутый круг, который сегодня известен любому учащемуся средней школы как знак пустого множества, появился в 1939 году.
Символы из области теории множеств были придуманы в 1888-1889 гг. А перечеркнутый круг, который сегодня известен любому учащемуся средней школы как знак пустого множества, появился в 1939 году.
Таким образом, знаки для столь непростых понятий, как интеграл или логарифм, были придуманы на столетия раньше, чем некоторые интуитивно понятные символы, легко воспринимаемые и усваиваемые даже без предварительной подготовки.
Математические символы на английском
Ввиду того, что значительная часть понятий была описана в научных трудах на латыни, ряд названий математических знаков и символов на английском и русском языке одинаковы. Например: Plus («плюс»), Integral («интеграл»), Delta function («дельта-функция»), Perpendicular («перпендикулярный»), Parallel («параллельный»), Null («нуль»).
Часть понятий в двух языках называются различным образом: так, деление – это Division, умножение – Multiplication. В редких случаях английское название для математического знака получает некоторое распространение в русском языке: например, косая черта в последние годы нередко именуется «слешем» (англ. Slash).
Таблица символов
Самый простой и удобный способ ознакомиться с перечнем математических знаков – посмотреть специальную таблицу, в которой содержатся знаки операций, символы математической логики, теории множеств, геометрии, комбинаторики, математического анализа, линейной алгебры. В данной таблице представлены основные математические знаки на английском языке.

Математические знаки в текстовом редакторе
При выполнении различного рода работ зачастую требуется использовать формулы, где употребляются знаки, отсутствующие на клавиатуре компьютера.
Как и графические элементы из практически любой области знаний, математические знаки и символы в «Ворде» можно найти во вкладке «Вставка». В версиях программы 2003 или 2007 года существует опция «Вставка символа»: при нажатии на кнопку в правой части панели пользователь увидит таблицу, в которой представлены все необходимые математические знаки, греческие строчные и прописные буквы, различные виды скобок и многое другое.
В версиях программы, вышедших после 2010 года, разработана более удобная опция. При нажатии на кнопку «Формула» происходит переход в конструктор формул, где предусмотрено использование дробей, занесения данных под корень, смена регистра (для обозначения степеней или порядковых номеров переменных). Здесь же могут быть найдены все знаки из таблицы, представленной выше.
Стоит ли учить математические символы
Система математических обозначений представляет собой искусственный язык, который лишь упрощает процесс записи, но не может принести понимание предмета стороннему наблюдателю. Таким образом, запоминание знаков без изучения терминов, правил, логических связей между понятиями не приведет к овладению данной областью знаний.
 Человеческий мозг легко усваивает знаки, буквы и сокращения – математические обозначения запоминаются сами при изучении предмета. Понимание смысла каждого конкретного действия создает настолько прочные ассоциативные связи, что знаки, обозначающие термины, а зачастую и формулы, связанные с ними, остаются в памяти на многие годы и даже десятилетия.
Человеческий мозг легко усваивает знаки, буквы и сокращения – математические обозначения запоминаются сами при изучении предмета. Понимание смысла каждого конкретного действия создает настолько прочные ассоциативные связи, что знаки, обозначающие термины, а зачастую и формулы, связанные с ними, остаются в памяти на многие годы и даже десятилетия.
В заключение
Поскольку любой язык, в том числе искусственный, является открытым к изменениям и дополнениям, число математических знаков и символов непременно будет расти с течением времени. Не исключено, что какие-то элементы будут заменены или скорректированы, а другие – стандартизованы в единственно возможном виде, что актуально, например, для знаков умножения или деления.
Умение пользоваться математическими символами на уровне полного школьного курса является в современном мире практически необходимым. В условиях бурного развития информационных технологий и науки, повсеместной алгоритмизации и автоматизации владение математическим аппаратом следует воспринимать как данность, а освоение математических символов – как неотъемлемую его часть.
Поскольку расчеты используются и в гуманитарной сфере, и в экономике, и в естественных науках, и, разумеется, в области техники и высоких технологий, понимание математических понятий и знание символов станет полезным для любого специалиста.
fb.ru
Основные математические понятия и обозначения
44
Одним из основных математических понятий является понятие множества.
Определение: Множеством называют совокупность каких-то объектов, объединенных по некоторому правилу или признаку.
Примерымножеств: — натуральные числа, целые числа, действительные числа.
Определение: Объекты, которые входят в состав множества, называют элементами данного множества.
Обычно множества обозначаются большими латинскими буквами (A, B, C), а их элементы – малыми (a, b, c).
Определение: Множество, которое имеет конечное число элементов – именуется конечным множеством; бесконечное — бесконечным.
Обычно любое множество задается некоторым свойством, т.е. таким свойством, которым обладают только элементы данного множества, например: M=a,b,c,d- некоторое множество.
Множество натуральных четных чисел: N2={2*n, где nN}
Определение:Множество, которое не содержит ни одного элемента, называется пустым множеством и обозначается 0
Множества чисел и их обозначения
N — множество натуральных чисел- {1,2,3,…, n,….}
Z — множество целых чисел {…-3,-2,-1,0,1,2,……….}
Q — множество рациональных чисел – это те числа, которые можно представить в виде дроби m/n, где m -принадлежит множеству целых чисел, а n — множеству натуральных чисел
Q={m/n, mZ, nN}
Иррациональные числа: J={ 2, 3, , e, …..}
Множество действительных чисел: R=Q U J
Множество комплексных чисел:
C={a+i*b; i=-1, a, bR}
Любое множество графически можно изобразить в виде круга (диаграммы Эйлера-Венна):
А
Определение: Множество В называется подмножеством множества А , (В А), если любой элемент множества В, является элементом множества А.
A
B В А
Основные операции над множествами
1. Сумма (Объединение) двух множеств А и В называется такое множество, которое состоит только из тех элементов, которые принадлежат хотя бы одному из множеств А или В.
В виде характеристического свойства — А U В={x, xA или xB}
Если изображают
ввиде круговA B А U В
Пример:
А={1,2,3} B={2,4,5} А U В={1,2,3,4,5}
2. Произведение (Пересечение) двух множеств А и В состоит из тех элементов, которые одновременно принадлежат и множеству А и множеству В: А В={x, xA и xB}
для рассмотренного
выше примера:A B А В
А В={2}
3. Разность двух множеств А и В (обозначается А\В) – называется множество, состоящее из элементов, которые принадлежат множеству А и не принадлежат множеству В
А\В={x, xA и x B} A B А\В
Для рассмотренного выше
примера:
А\В={1,3}
Логические символы
Для краткости записи, вместо слов: существует, найдется, будет использован символ ,
вместо слов любой, каждый, всякий .
Примеры: x, x+1N ; xX,X:2
Специальные математические символы
Для краткости записи произведения первых n-натуральных чисел вводят:
1*2*3*4*……..* n = n! , n –факториал.
1!=1 , 2!=1*2=2 , 5!=1*2*3*4*5=120,
0!=1 0-факториал.
Для краткости записи суммы и произведения будем использовать символы:
n
сумма ai = a1+a2+a3+….+an ; ai = a1+a2+…+an +…;
i=1 i=1
n
Произведение ai = a1*a2*a3*….*an
i=1
studfiles.net
