Вычислить логарифмы – Как считать логарифм с калькулятором 🚩 как считать на инженерном калькуляторе 🚩 Математика

Логарифм. Как вычислить логарифм?

Логарифмом положительного числа \(c\) по основанию \(a\) \((a>0, a\neq1)\) называется показатель степени \(b\), в которую надо возвести основание \(a\), чтобы получить число \(c\) \((c>0)\), т.е.

\(a^{b}=c\)       \(\Leftrightarrow\)       \(\log_{a}{c}=b\)

Объясним проще. Например, \(\log_{2}{8}\) равен степени, в которую надо возвести \(2\), чтоб получить \(8\). Отсюда понятно, что \(\log_{2}{8}=3\).

Примеры:		\(\log_{5}{25}=2\)		т.к. \(5^{2}=25\)
		\(\log_{3}{81}=4\)		т.к. \(3^{4}=81\)
		\(\log_{2}\)\(\frac{1}{32}\)\(=-5\)		т.к. \(2^{-5}=\)\(\frac{1}{32}\)

Аргумент и основание логарифма

Любой логарифм имеет следующую «анатомию»:

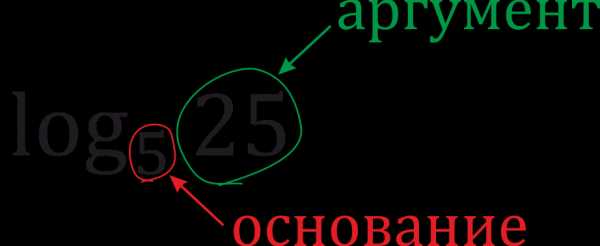
Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».

Как вычислить логарифм?

Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?

Например, вычислите логарифм:  а) \(\log_{4}{16}\)     б) \(\log_{3}\)\(\frac{1}{3}\)     в) \(\log_{\sqrt{5}}{1}\)     г) \(\log_{\sqrt{7}}{\sqrt{7}}\)      д) \(\log_{3}{\sqrt{3}}\)

а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому: 

\(\log_{4}{16}=2\)

б) В какую степень надо возвести \(3\), чтобы получить \(\frac{1}{3}\)? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами

степени).

\(\log_{3}\)\(\frac{1}{3}\)\(=-1\)

в) В какую степень надо возвести \(\sqrt{5}\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!

\(\log_{\sqrt{5}}{1}=0\)

г) В какую степень надо возвести \(\sqrt{7}\), чтобы получить \(\sqrt{7}\)? В первую – любое число в первой степени равно самому себе.

\(\log_{\sqrt{7}}{\sqrt{7}}=1\)

д) В какую степень надо возвести \(3\), чтобы получить \(\sqrt{3}\)? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень — это степень \(\frac{1}{2}\).

\(\log_{3}{\sqrt{3}}=\)\(\frac{1}{2}\)

Пример: Вычислить логарифм \(\log_{4\sqrt{2}}{8}\)

Решение:

\(\log_{4\sqrt{2}}{8}=x\)		Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма: \(\log_{a}{c}=b\)       \(\Leftrightarrow\)       \(a^{b}=c\)
\((4\sqrt{2})^{x}=8\)		Что связывает \(4\sqrt{2}\) и \(8\)? Двойка, потому что и то, и другое число можно представить степенью двойки: \(4=2^{2}\)         \(\sqrt{2}=2^{\frac{1}{2}}\)         \(8=2^{3}\)
\({(2^{2}\cdot2^{\frac{1}{2}})}^{x}=2^{3}\)		Слева воспользуемся свойствами степени: \(a^{m}\cdot a^{n}=a^{m+n}\) и \((a^{m})^{n}=a^{m\cdot n}\)
\(2^{\frac{5}{2}x}=2^{3}\)		Основания равны, переходим к равенству показателей
\(\frac{5x}{2}\)\(=3\)		Умножим обе части уравнения на \(\frac{2}{5}\)
\(x=1,2\)		Получившийся корень и есть значение логарифма

Ответ: \(\log_{4\sqrt{2}}{8}=1,2\)

Зачем придумали логарифм?

Чтобы это понять, давайте решим уравнение: \(3^{x}=9\). Просто подберите \(x\), чтобы равенство сработало. Конечно, \(x=2\).

А теперь решите уравнение: \(3^{x}=8\).Чему равен икс? Вот в том-то и дело.

Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как \(x=\log_{3}{8}\).

Хочу подчеркнуть, что \(\log_{3}{8}\), как и любой логарифм — это просто число. Да, выглядит непривычно, но зато коротко. Потому что, если бы мы захотели записать его в виде десятичной дроби, то оно выглядело бы вот так: \(1,892789260714…..\)

Пример: Решите уравнение \(4^{5x-4}=10\)

Решение:

\(4^{5x-4}=10\)		\(4^{5x-4}\) и \(10\) никак к одному основанию не привести. Значит тут не обойтись без логарифма. Воспользуемся определением логарифма: \(a^{b}=c\)       \(\Leftrightarrow\)       \(\log_{a}{c}=b\)
\(\log_{4}{10}=5x-4\)		Зеркально перевернем уравнение, чтобы икс был слева
\(5x-4=\log_{4}{10}\)		Перед нами линейное уравнение. Перенесем \(4\) вправо. И не пугайтесь логарифма, относитесь к нему как к обычному числу.
\(5x=\log_{4}{10}+4\)		Поделим уравнение на 5
\(x=\)\(\frac{\log_{4}{10}+4}{5}\)		Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.

Ответ: \(\frac{\log_{4}{10}+4}{5}\)

Десятичный и натуральный логарифмы

Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:

Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\).

То есть, \(\ln{a}\) это то же самое, что и \(\log_{e}{a}\), где \(a\) — некоторое число.

Десятичный логарифм: логарифм, у которого основание равно 10, записывается \(\lg{a}\).

То есть, \(\lg{a}\) это то же самое, что и \(\log_{10}{a}\), где \(a\) — некоторое число.

Основное логарифмическое тождество

У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:

\(a^{\log_{a}{c}}=c\)

Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.

Вспомним краткую запись определения логарифма:

если     \(a^{b}=c\),    то   \(\log_{a}{c}=b\)

То есть, \(b\) – это тоже самое, что \(\log_{a}{c}\). Тогда мы можем в формуле \(a^{b}=c\) написать \(\log_{a}{c}\) вместо \(b\). Получилось \(a^{\log_{a}{c}}=c\) – основное логарифмическое тождество.

Остальные свойства логарифмов вы можете найти здесь. С их помощью можно упрощать и вычислять значения выражений с логарифмами, которые «в лоб» посчитать сложно.

Пример: Найдите значение выражения \(36^{\log_{6}{5}}\)

Решение:

\(36^{\log_{6}{5}}=\)		Сразу пользоваться свойством \(a^{\log_{a}{c}}=c\) мы не можем, так как в основании степени и в основании логарифма – разные числа. Однако мы знаем, что \(36=6^{2}\)
\(=(6^{2})^{\log_{6}{5}}=\)		Зная формулу \((a^{m})^{n}=a^{m\cdot n}\), а так же то, что множители можно менять местами, преобразовываем выражение
\(=6^{2\cdot\log_{6}{5}}=6^{log_{6}{5}\cdot2}=(6^{log_{6}{5}})^{2}=\)		Вот теперь спокойно пользуемся основным логарифмическим тождеством.
\(=5^{2}=25\)		Ответ готов.

Ответ: \(25\)

Как число записать в виде логарифма?

Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_{2}{4}\) равен двум. Тогда можно вместо двойки писать \(\log_{2}{4}\). 

Но \(\log_{3}{9}\) тоже равен \(2\), значит, также можно записать \(2=\log_{3}{9}\)  . Аналогично и с \(\log_{5}{25}\), и с \(\log_{9}{81}\), и т.д. То есть, получается  

\(2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…\)

Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.

Точно также и с тройкой – ее можно записать как \(\log_{2}{8}\), или как \(\log_{3}{27}\), или как \(\log_{4}{64}\)… Здесь мы как аргумент пишем основание в кубе:

\(3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}…\)

И с четверкой:

\(4=\log_{2}{16}=\log_{3}{81}=\log_{4}{256}=\log_{5}{625}=\log_{6}{1296}=\log_{7}{2401}…\)

И с минус единицей:

\(-1=\) \(\log_{2}\)\(\frac{1}{2}\)\(=\) \(\log_{3}\)\(\frac{1}{3}\)\(=\) \(\log_{4}\)\(\frac{1}{4}\)\(=\) \(\log_{5}\)\(\frac{1}{5}\)\(=\) \(\log_{6}\)\(\frac{1}{6}\)\(=\) \(\log_{7}\)\(\frac{1}{7}\)\(…\)

И с одной третьей:

\(\frac{1}{3}\)\(=\log_{2}{\sqrt[3]{2}}=\log_{3}{\sqrt[3]{3}}=\log_{4}{\sqrt[3]{4}}=\log_{5}{\sqrt[3]{5}}=\log_{6}{\sqrt[3]{6}}=\log_{7}{\sqrt[3]{7}}…\)

И так далее.

Любое число \(a\) может быть представлено как логарифм с основанием \(b\):       \(a=\log_{b}{b^{a}}\)

Пример: Найдите значение выражения \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)

Решение:

\(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)\(=\)		Превращаем единицу в логарифм с основанием \(2\): \(1=\log_{2}{2}\)
\(=\)\(\frac{\log_{2}{14}}{\log_{2}{2}+\log_{2}{7}}\)\(=\)		Теперь пользуемся свойством логарифмов: \(\log_{a}{b}+\log_{a}{c}=\log_{a}{(bc)}\)
\(=\)\(\frac{\log_{2}{14}}{\log_{2}{(2\cdot7)}}\)\(=\)\(\frac{\log_{2}{14}}{\log_{2}{14}}\)\(=\)		В числителе и знаменателе одинаковые числа – их можно сократить.
\(=1\)		Ответ готов.

Ответ: \(1\)

Смотрите также:
Логарифмические уравнения
Логарифмические неравенства

cos-cos.ru

Вычисление логарифма числа онлайн | umath.ru

Онлайн калькулятор логарифмов

Калькулятор вычисляет логарифм числа онлайн. Можно вводить как десятичные дроби (в качестве разделителя для десятичных дробей можно использовать как точку, так и запятую), так и обычные (например, если нужно вычислить логарифм то в поле «число» можете смело писать 1/9).

Помните, что операция взятия логарифма определена только для положительных чисел, а основание логарифма должно быть положительным и не должно равняться единице.

Что такое логарифм числа?

Примеры

Пример 2. Вычислить
Решение. Воспользуемся следующим свойством логарифмов:

   

Получаем:

   

Так как то

Как видите, всё очень просто!

Логарифм числа по основанию 10 называют десятичным и обозначают , а логарифм числа по основанию называют

натуральным и обозначают .

Про свойства логарифмов читайте здесь.

umath.ru

Калькулятор логарифма и антилогарифма онлайн

Логарифмирование — это операция, обратная возведению в степень. Если вы задаетесь вопросом, в какую степень нужно возвести 2, чтобы получить 10, то вам на помощь придет логарифм.

Обратная операция для возведения в степень

Возведение в степень — это повторяющееся умножение. Для возведения двойки в третью степень нам потребуется вычислить выражение 2 × 2 × 2. Обратная операция для умножения — это деление. Если верно выражение, что a × b = c, то обратное выражение b = a / c так же верно. Но как обратить возведение в степень? Задача обращения умножения имеет элегантное решение благодаря простому свойству, что a × b = b × a. Однако a

b не равно b^a, за исключением единственного случая, когда 2² = 4². В выражении a^b = с, мы можем выразить a как корень b-ой степени из c, но как выразить b? Вот тут на сцене и появляются логарифмы.

Понятие логарифма

Давайте попробуем решить простое уравнение вида 2^x = 16. Это показательное уравнение, так как нам требуется отыскать показатель степени. Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку на саму себя, чтобы в результате получить 16? Очевидно, что 4, поэтому корень данного уравнения x = 4.

Теперь попробуем решить 2^x

 = 20. Сколько раз нужно умножить двойку на саму себя, что бы получить 20? Это сложно, ведь 2⁴ = 16, а 2⁵ = 32. Рассуждая логически, корень этого уравнения располагается между 4 и 5, причем ближе к 4, возможно 4,3? Математики не терпят приблизительных вычислений и хотят знать точный ответ. Для этого они и используют логарифмы, а корнем этого уравнения будет x = log2 20.

Выражение log2 20 читается как логарифм 20 по основанию 2. Это и есть ответ, которого строгим математикам достаточно. Если вы хотите выразить это число точно, то вычислите его при помощи инженерного калькулятора. В этом случае log2 20 = 4,32192809489. Это иррациональное бесконечное число, а log2 20 — его компактная запись.

Таким элегантным способом вы можете решить любое простое показательное уравнение. Например, для уравнений:

• 4^x = 125, x = log4 125;
• 12^x = 432, x = log12 432;
• 5^x = 25, x = log5 25.

Последний ответ x = log5 25 математикам не понравится. Все потому, что log5 25 легко вычисляется и является целым числом, поэтому вы обязаны его определить. Сколько раз требуется умножить 5 на само себя, чтобы получить 25? Элементарно, два раза. 5 × 5 = 5² = 25. Поэтому для уравнения вида 5^x = 25, x = 2.

Десятичный логарифм

Десятичный логарифм — это функция по основанию 10. Это популярный математический инструмент, поэтому он записывается иначе. К примеру, в какую степень нужно возвести 10, чтобы получить 30? Ответом был бы log10 30, однако математики сокращают запись десятичных логарифмов и записывают его как lg30. Точно также log10 50 и log10 360 записываются как lg50 и lg360 соответственно.

Натуральный логарифм

Натуральный логарифм — это функция по основанию e. В нем нет ничего натурального, и многих неофитов такая функция попросту пугает. Число e = 2,718281828 представляет собой константу, которая естественным образом возникает при описании процессов непрерывного роста. Как важно число Пи для геометрии, число e играет важную роль в моделировании временных процессов.

В какую степень нужно возвести число e, чтобы получить 10? Ответом был бы loge 10, но математики обозначают натуральный логарифм как ln, поэтому ответ будет записан как ln10. Тоже самое с выражениями loge 35 и loge 40, верная форма записи которых – ln34 и ln40.

Антилогарифм

Антилогарифм — это число, которому соответствует значение выбранного логарифма. Простыми словами, в выражении loga b антилогарифмом считается число b^a. Для десятичного логарифма lga, антилогарифм равен 10^a, а для натурального lna антилогарифм равняется e^a. По сути, это тоже возведение в степень и обратная операция для логарифмирования.

Физический смысл логарифма

Нахождение степеней — чисто математическая задача, но для чего нужны логарифмы в реальной жизни? В начале развития идеи логарифмирования данный математический инструмент использовался для сокращения объемных вычислений. Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило труд астронома и удвоило его жизнь». С развитием математического инструмента были созданы целые логарифмические таблицы, при помощи которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовать выражения, оперирующие иррациональным числами в целочисленные выражения. Также логарифмическая запись позволяет представить слишком маленькие и слишком большие числа в компактном виде.

Логарифмы нашли применение и в сфере изображения графических процессов. Если требуется нарисовать график функции, которая принимает значения 1, 10, 1 000 и 100 000, то маленькие значения будут невидны и визуально они сольются в точку около нуля. Для решения подобной проблемы используются десятичный логарифм, которой позволяет построить график функции, адекватно отображающий все ее значения.

Физический же смысл логарифмирования — это описание временных процессов и изменений. Так, логарифм по основанию 2 позволяет определить, сколько требуется удвоений начального значения для достижения определенного результата. Десятичная функция используется для поиска количества необходимых удесятирений, а натуральная представляет собой время, которое необходимо для достижения заданного уровня.

Наша программа представляет собой сборник из четырех онлайн-калькуляторов, которые позволяют вычислить логарифм по любому основанию, десятичную и натуральную логарифмическую функцию, а также десятичный антилогарифм. Для проведения вычислений вам потребуется ввести основание и число, или только число для десятичного и натурального логарифма.

Примеры из реальной жизни

Школьная задача

Как было сказано выше, иррациональные значения по типу log2 345 не требуют дополнительных преобразований, и такой ответ полностью удовлетворит учителя математики. Однако если логарифм вычисляется, вы обязаны представить его в виде целого числа. Пусть вы решили 5 примеров по алгебре, и вам требуется проверить результаты на возможность целочисленного представления. Давайте проверим их при помощи калькулятора логарифма по любому основанию:

• log7 65 — иррациональное число;
• log3 243 — целое число 5;
• log5 95 — иррациональное;
• log8 512 — целое число 3;
• log2 2046 — иррациональное.

Таким образом, значения log3 243 и log8 512 вам потребуется переписать как 5 и 3 соответственно.

Потенцирование

Потенцирование — это нахождение антилогарифма числа. Наш калькулятор позволяет найти антилогарифмы по десятичному основанию, что по смыслу означает возведение десятки в степень n. Давайте вычислим антилогарифмы для следующих значений n:

• для n = 1 antlog = 10;
• для n = 1,5 antlog = 31,623;
• для n = 2,71 antlog = 512,861.

Непрерывный рост

Натуральный логарифм позволяет описывать процессы непрерывного роста. Представим, что ВВП страны Кракожия увеличилось с 5,5 миллиардов долларов до 7,8 за 10 лет. Давайте определим ежегодный прирост ВВП в процентах при помощи калькулятора натурального логарифма. Для этого нам надо подсчитать натуральный логарифм ln(7,8/5,5), что равнозначно ln(1,418). Введем это значение в ячейку калькулятора и получим результат 0,882 или 88,2% за все время. Так как ВВП рос в течение 10 лет, то ежегодный его прирост составит 88,2 / 10 = 8,82%.

Поиск количества удесятирений

Допустим, за 30 лет количество персональных компьютеров увеличилось с 250 000 до 1 миллиарда. Сколько раз количество ПК увеличивалось в 10 раз за все это время? Для подсчета такого интересного параметра нам потребуется вычислить десятичный логарифм lg(1 000 000 000 / 250 000) или lg(4 000). Выберем калькулятор десятичного логарифма и посчитаем его значение lg(4 000) = 3,60. Получается, что с течением времени количество персональных компьютеров возрастало в 10 раз каждые 8 лет и 4 месяца.

Заключение

Несмотря на сложность логарифмов и нелюбовь детей к ним в школьные годы, этот математический инструмент находит широкое применение в науке и статистике. Используйте наш сборник онлайн-калькуляторов для решения школьных заданий, а также задач из разных научных сфер.

bbf.ru

Калькулятор онлайн — Решение логарифмических уравнений

Этот математический калькулятор онлайн поможет вам решить логарифмическое уравнение. Программа для решения логарифмического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Вы можете посмотреть теорию о логарифмической функции и логарифмах и некоторые методы решения логарифмических уравнений.

Примеры подробного решения >>

ln(b) или log(b) или log(e,b)- натуральный логарифм числа b
log(10,b) — десятичный логарифм числа b
log(a,b) — логарифм b по основанию a

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Логарифмическая функция. Логарифмы

Задача 1. Найти положительный корень уравнения x⁴ = 81
По определению арифметического корня имеем \( x = \sqrt[4]{81} = 3 \)

Задача 2. Решить уравнение 3^x = 81
Запишем данное уравнение так: 3^x = 3⁴, откуда x = 4

В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. Способ решения задачи 2 состоял в том, что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 3. Но уже, например, уравнение 3^x = 80 таким способом решить не удаётся. Однако это уравнение имеет корень. Чтобы уметь решать такие уравнения, вводится понятие логарифма числа.
Уравнение a^x = b, где a > 0, \( a \neq 1 \), b > 0, имеет единственный корень. Этот корень называют логарифмом числа b no основанию a и обозначают log_ab
Например, корнем уравнения 3^x = 81 является число 4, т.е. log₃81 = 4.

Определение. Логарифмом положительного числа b по основанию a, где a > 0, \( a \neq 1 \), называется показатель степени, в которую надо возвести число a, чтобы получить b

Например:

log₂8 = 3, так как 2³ = 8
\( \log_3 \frac{1}{9} = -2 \), так как \( 3^{-2} = \frac{1}{9} \)
log₇7 = 1, так как 7¹ = 7

Определение логарифма можно записать так:

$$ a^{\log_a b} = b $$ Это равенство справедливо при b > 0, b > 0, \( a \neq 1 \). Его обычно называют основным логарифмическим тождеством.

Действие нахождения логарифма числа называют логарифмированием.
Действие нахождения числа по его логарифму называют потенцированием.

Вычислить log₆₄128
Обозначим log₆₄128 = х. По определению логарифма 64^x = 128. Так как 64 = 2⁶, 128 = 2⁷, то 2 ^6x = 2⁷, откуда 6x = 7, х = 7/6.
Ответ log₆₄128 = 7/6

Вычислить \( 3^{-2\log_3 5} \)
Используя свойства степени и основное логарифмическое тождество, находим

$$ 3^{-2\log_3 5} = \left( 3^{\log_3 5} \right)^{-2} = 5^{-2} = \frac{1}{25}$$

Решить уравнение log₃(1-x) = 2
По определению логарифма 3² = 1 — x, откуда x = -8

Свойства логарифмов

При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.

Пусть а > 0, \( a \neq 1 \), b > 0, c > 0, r — любое действительное число. Тогда справедливы формулы:

1) log_a(bc) = log_ab + log_ac

2) \( \log_a \frac{b}{c} = \log_a b — \log_a c \)
3) log_ab^r = r log_ab

Десятичные и натуральные логарифмы

Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора. И в том и в другом случае находятся только десятичные или натуральные логарифмы.

Определение. Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут
lg b вместо log₁₀b

Определение. Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e — иррациональное число, приближённо равное 2,7. При этом пишут ln b вместо log_eb

Иррациональное число e играет важную роль в математике и её приложениях. Число e можно представить как сумму:
$$ e = 1 + \frac{1}{1} + \frac{1}{1 \cdot 2} + \frac{1}{1 \cdot 2 \cdot 3} + \dots + \frac{1}{1 \cdot 2 \cdot 3 \cdot \dots \cdot n} + \dots $$

или $$ e = \sum_{n=0}^{\infty} \frac{1}{n!} $$ $$ e \approx 2,7182818284 $$

Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы чисел по любому основанию.
Для этого используется формула замены основания логарифма:

$$ \log_a b = \frac{\log_c b}{\log_c a} $$ где b > 0, a > 0, \( a \neq 1 \), c > 0, \( c \neq 1 \)

Следствия из формулы замены основания логарифма.
При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:
$$ \log_a b = \frac{\lg b}{\lg a} , \;\; \log_a b = \frac{\ln b}{\ln a} $$

Логарифмическая функция, её свойства и график

В математике и её приложениях часто встречается логарифмическая функция
y = log_ax
где а — заданное число, a > 0, \( a \neq 1 \)

Логарифмическая функция обладает свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.

2) Множество значений логарифмической функции — множество всех действительных чисел.

3) Логарифмическая функция не является ограниченной.

4) Логарифмическая функция y = log_ax является возрастающей на промежутке \( (0; +\infty) \), если a > 1,
и убывающей, если 0

5) Если a > 1, то функция y = log_ax принимает положительные значения при х > 1,
отрицательные при 0 Если 0 ax принимает положительные значения при 0 отрицательные при х > 1.

Ось Oy является вертикальной асимптотой графика функции y = log_ax

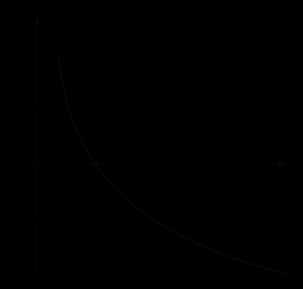
Отметим, что график любой логарифмической функции y = log_ax проходит через точку (1; 0).
При решении уравнений часто используется следующая теорема:

Теорема. Если log_ax₁ = log_ax₂ где a > 0, \( a \neq 1 \), x₁ > 0, x₂ > 0, то x₁ = x₂

Логарифмическая функция y = log_ax и показательная функция y = a^x, где a > 0, \( a \neq 1 \), взаимно обратны.

Логарифмические уравнения

Решить уравнение log₂(x+1) + log₂(x+3) = 3
Предположим, что х — такое число, при котором равенство является верным, т.е. х — корень уравнения. Тогда по свойству логарифма верно равенство
log₂((x+1)(x+3)) = 3
Из этого равенства по определению логарифма получаем
(x+1)(x+3) = 8
х² + 4х + 3 = 8, т.е. х² + 4x — 5 = 0, откуда x₁ = 1, х₂ = -5
Так как квадратное уравнение является следствием исходного уравнения, то необходима проверка.
Проверим, являются ли числа 1 и -5 корнями исходного уравнения.
Подставляя в левую часть исходного уравнения х = 1, получаем
log₂(1+1) + log₂(1+3) = log₂2 + log₂4 = 1 + 2 = 3, т.е. х = 1 — корень уравнения.
При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения не имеет смысла, т.е. х = -5 не является корнем этого уравнения.
Ответ x = 1

Решить уравнение lg(2x² — 4x + 12) = lg x + lg(x+3)
По свойству логарифмов
lg(2x² — 4x + 12) = lg(x² + 3x)
откуда
2x² — 4x + 12 = x² + 3x
x² — 7x + 12 = 0
x₁ = 3, х₂ = 4
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x₁ = 3, х₂ = 4

Решить уравнение log₄(2x — 1) • log₄x = 2 log₄(2x — 1)
Преобразуем данное уравнение:
log₄(2x — 1) • log₄x — 2 log₄(2x — 1) = 0
log₄(2х — 1) • (log₄ x — 2) = 0
Приравнивая каждый из множителей левой части уравнения к нулю, получаем:
1) log₄ (2х — 1) = 0, откуда 2х — 1 = 1, х₁ = 1
2) log₄ х — 2 = 0, откуда log₄ = 2, х₂ = 16
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x₁ = 1, х₂ = 16

www.mathsolution.ru

Расчет логарифмов

Простой математический калькулятор для вычисления логарифмов чисел с указанным основанием. Данный калькулятор способен посчитать как десятичный логарифм, так и натуральный.

Теперь вы можете без всяких формул быстро зайти на наш сайт и посчитать то или иное число, узнать его логарифм.

Также на нашем сайте вы можете посчитать и обратный логарифм числа, антилогарифм, просто нужно зайти на данную страницу:

The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 .. %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

Su

Mo

Tu

We

Th

Fr

Sa

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v.d.

z.d.

yes

no

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

hostciti.net

Решение логарифмов в онлайн калькуляторе

Данная страница рассматривает способы решения логарифмов, как еще одну функцию в богатом арсенале, которым располагает бесплатный калькулятор на нашем сайте. Калькулятор, считающий логарифмы онлайн, станет незаменимым помощником для тех, кому нужно простое решение математических выражений. В нашем калькуляторе любой может легко и быстро посчитать логарифм, не зная логарифмических формул, и даже не представляя суть логарифма.

Буквально 20-30 лет назад решение логарифмов требовало серьезных знаний в математике и как минимум умения пользоваться таблицей логарифмов или логарифмической линейкой. Чтобы привести к табличному виду исходное выражение, часто приходилось осуществлять сложные преобразования, учитывая свойства логарифмов и их функций.

Сегодня же достаточно иметь доступ в интернет, чтобы без труда вычислять всевозможные логарифмические уравнения и неравенства любой сложности. Размещенный на нашем сайте онлайн калькулятор может любой логарифм вычислить за одно мгновение!

Решение логарифма log_yx сводится к нахождению ответа на вопрос, в какую степень требуется возвести основание логарифма y, чтобы получилось значение равное x. Онлайн калькулятор логарифмов поможет рассчитать все виды логарифмов: двоичные, десятичные и натуральные логарифмы, а также логарифм комплексного числа и логарифм отрицательного числа и др.

Вычисление логарифмов в online калькуляторе записывается как log и выполняется с помощью четырех кнопок: нахождение двоичного логарифма, решение десятичных логарифмов, с произвольным основанием и вычисление натурального логарифма.

Некоторые кнопки могут использоваться для записи одного и того же действия. Возьмем, к примеру, расчет логарифмов с произвольным основанием. Понятно что, если указать основание 10, то рассчитается десятичный логарифм, а если 2, то двоичный. Учитывая, что математическое выражение можно и вручную набрать, тогда тот же самый десятичный логарифм посчитать можно тремя способами (точнее записать эту операцию в калькуляторе):

1. используя кнопку log, тогда нужно указать только число,
2. с помощью кнопки log_yx, через запятую указываются число и основание логарифма,
3. внести обозначение логарифма вручную.

Подробную информацию о том, как работать с клавиатурой калькулятора, а также обзор всех его возможностей, можно найти на страницах кнопки калькулятора и функции калькулятора.

Логарифм по основанию 2

Используйте эту кнопку, чтобы рассчитать логарифм, основание которого равно двум (его также называют двоичный логарифм).

В строке ввода отобразится запись log₂(x), соответственно, вам остается внести число, без указания основания, и произвести расчет. В примере найден ответ, чему равен логарифм 8 по основанию 2.

Логарифм по основанию 2:

Десятичный логарифм

Эта кнопка поможет найти логарифм числа по основанию 10.

Логарифм десятичный онлайн калькулятор обозначает записью log(x x,y). На рисунке рассчитано, чему равен десятичный логарифм числа 10000.

Логарифм по основанию 10:

Натуральный логарифм

Клавишей ln выполняется решение натуральных логарифмов, основанием которых является число е. Основание натурального логарифма е — число Эйлера — равно 2.71828182845905.

Онлайн калькулятор может определить, чему равен натуральный логарифм любого числа. На рисунках в качестве примера найдены значения натурального логарифма: слева — ln логарифм числа 8, справа — натуральный логарифм от числа 50.

Натуральные логарифмы, примеры решения:

Как решать логарифмы с произвольным основанием?

Конечно, калькулятор, позволяет решить логарифм онлайн не только по определенному, но по любому основанию. Чтобы найти значение логарифмов с произвольным основанием для любого числа, используйте предназначенную для этого кнопочку log_yx, она подставляет в строке ввода запись log(x x,y).

Определение логарифма числа:

Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>

Решение логарифмов в онлайн калькуляторе was last modified: Март 3rd, 2016 by Admin

compuzilla.ru