Всемирного тяготения – Всемирное тяготение. Всемирное тяготение определение. Закон всемирного тяготения. Формула всемирного тяготения. Всемирная гравитационная постоянная

Содержание

Закон всемирного тяготения и сила тяжести

Описание закона всемирного тяготения

Коэффициент — это гравитационная постоянная. В системе СИ гравитационная постоянная имеет значение:

Эта постоянная, как видно, очень мала, поэтому силы тяготения между телами, имеющими небольшие массы, тоже малы и практически не ощущаются. Однако движение космических тел полностью определяется гравитацией. Наличие всемирного тяготения или, другими словами, гравитационного взаимодействия объясняет, на чем «держатся» Земля и планеты, и почему они двигаются вокруг Солнца по определенным траекториям, а не улетают от него прочь. Закон всемирного тяготения позволяет определить многие характеристики небесных тел – массы планет, звезд, галактик и даже черных дыр. Этот закон позволяет с большой точностью рассчитать орбиты планет и создать математическую модель Вселенной.

С помощью закона всемирного тяготения также можно рассчитать космические скорости. Например, минимальная скорость, при которой тело, движущееся горизонтально над поверхностью Земли, не упадёт на неё, а будет двигаться по круговой орбите – 7,9 км/с (первая космическая скорость). Для того, чтобы покинуть Землю, т.е. преодолеть ее гравитационное притяжение, тело должно иметь скорость 11,2 км/с, (вторая космическая скорость).

Гравитация является одним из самых удивительных феноменов природы. В отсутствии сил гравитации существование Вселенной было бы невозможно, Вселенная не могла бы даже возникнуть. Гравитация ответственна за многие процессы во Вселенной – ее рождение, существование порядка вместо хаоса. Природа гравитации до сих пор до конца неразгаданна. До настоящего времени никто не смог разработать достойный механизм и модель гравитационного взаимодействия.

Сила тяжести

Частным случаем проявления гравитационных сил является сила тяжести.

Сила тяжести всегда направлена вертикально вниз (по направлению к центру Земли).

Если на тело действует сила тяжести, то тело совершает свободное падение. Вид траектории движения зависит от направления и модуля начальной скорости.

С действием силы тяжести мы сталкиваемся каждый день. Камень, брошенный в горизонтальном направлении, через некоторое время оказывается на земле. Книга, выпущенная из рук, падает вниз. Подпрыгнув, человек не улетает в открытый космос, а опускается вниз, на землю.

Рассматривая свободное падение тела вблизи поверхности Земли как результат гравитационного взаимодействия этого тела с Землей, можно записать:

откуда ускорение свободного падения:

Ускорение свободного падения не зависит от массы тела, а зависит от высоты тела над Землей. Земной шар немного сплюснут у полюсов, поэтому тела, находящиеся около полюсов, расположены немного ближе к центру Земли. В связи с этим ускорение свободного падения зависит от широты местности: на полюсе оно немного больше, чем на экваторе и других широтах (на экваторе м/с , на Северном полюсе экваторе м/с .

Эта же формула позволяет найти ускорение свободного падения на поверхности любой планеты массой и радиусом .

Примеры решения задач

ru.solverbook.com

точная формула силы всемирного притяжения, определение гравитации

Самым главным явлением, постоянно изучаемым физиками, является движение. Электромагнитные явления, законы механики, термодинамические и квантовые процессы – все это широкий спектр изучаемых физикой фрагментов мироздания. И все эти процессы сводятся, так или иначе, к одному – к движению тел.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Все во Вселенной движется. Гравитация – привычное явление для всех людей с самого детства, мы родились в гравитационном поле нашей планеты, это физическое явление воспринимается нами на самом глубоком интуитивном уровне и, казалось бы, даже не требует изучения.

Но, увы, вопрос, почему и каким образом все тела притягиваются друг к другу, остается и на сегодняшний день не до конца раскрытым, хотя и изучен вдоль и поперек.

В этой статье мы рассмотрим, что такое всемирное притяжение по Ньютону – классическую теорию гравитации. Однако прежде чем перейти к формулам и примерам, расскажем о сути проблемы притяжения и дадим ему определение.

Быть может, изучение гравитации стало началом натуральной философии (науки о понимании сути вещей), быть может, натуральная философия породила вопрос о сущности гравитации, но, так или иначе, вопросом тяготения тел

заинтересовались еще в Древней Греции.

Движение понималось как суть чувственной характеристики тела, а точнее, тело двигалось, пока наблюдатель это видит. Если мы не можем явление измерить, взвесить, ощутить, значит ли это, что этого явления не существует? Естественно, не значит. И с тех пор, как Аристотель понял это, начались размышления о сути гравитации.

Как оказалось в наши дни, спустя многие десятки веков, гравитация является основой не только земного притяжения и притяжения нашей планеты к Солнцу, но и основой зарождения Вселенной и почти всех имеющихся элементарных частиц.

Задача движения

Проведем мысленный эксперимент. Возьмем в левую руку небольшой шарик. В правую возьмем такой же. Отпустим правый шарик, и он начнет падать вниз. Левый при этом остается в руке, он по-прежнему недвижим.

Остановим мысленно ход времени. Падающий правый шарик «зависает» в воздухе, левый все также остается в руке. Правый шарик наделен «энергией» движения, левый – нет. Но в чем глубокая, осмысленная разница между ними?

Где, в какой части падающего шарика прописано, что он должен двигаться? У него такая же масса, такой же объем. Он обладает такими же атомами, и они ничем не отличаются от атомов покоящегося шарика. Шарик обладает потенциальной энергией? Да, это правильный ответ, но откуда шарику известно, что обладает потенциальной энергией, где это зафиксировано в нем?

Именно эту задачу ставили перед собой Аристотель, Ньютон и Альберт Эйнштейн. И все три гениальных мыслителя отчасти решили для себя эту проблему, но на сегодняшний день существует ряд вопросов, требующих разрешения.

Гравитация Ньютона

В 1666 году величайшим английским физиком и механиком И. Ньютоном открыт закон, способный количественно посчитать силу, благодаря которой вся материя во Вселенной стремится друг к другу. Это явление получило название всемирное тяготение. Когда вас просят: «Сформулируйте закон всемирного тяготения», ваш ответ должен звучать так:

Сила гравитационного взаимодействия, способствующая притяжению двух тел, находится в прямой пропорциональной связи с массами этих тел и в обратной пропорциональной связи с расстоянием между ними.

Важно! В законе притяжения Ньютона используется термин «расстояние». Под этим термином следует понимать не дистанцию между поверхностями тел, а расстояние между их центрами тяжести. К примеру, если два шара радиусами r1 и r2 лежат друг на друге, то дистанция между их поверхностями равна нулю, однако сила притяжения есть. Все дело в том, что расстояние между их центрами r1+r2 отлично от нуля. В космических масштабах это уточнение не суть важно, но для спутника на орбите данная дистанция равна высоте над поверхностью плюс радиус нашей планеты. Расстояние между Землей и Луной также измеряется как расстояние между их центрами, а не поверхностями.

Для закона тяготения формула выглядит следующим образом:

где:

F – сила притяжения,
– массы,
r – расстояние,
G – гравитационная постоянная, равная 6,67·10−11 м³/(кг·с²).

Что же представляет собой вес, если только что мы рассмотрели силу притяжения?

Сила является векторной величиной, однако в законе всемирного тяготения она традиционно записана как скаляр. В векторной картине закон будет выглядеть таким образом:

Но это не означает, что сила обратно пропорциональна кубу дистанции между центрами. Отношение следует воспринимать как единичный вектор, направленный от одного центра к другому:

Закон гравитационного взаимодействия

Вес и гравитация

Рассмотрев закон гравитации, можно понять, что нет ничего удивительного в том, что лично мы ощущаем притяжение Солнца намного слабее, чем земное. Массивное Солнце хоть и имеет большую массу, однако оно очень далеко от нас. Земля тоже далеко от Солнца, однако она притягивается к нему, так как обладает большой массой. Каким образом найти силу притяжения двух тел, а именно как вычислить силу тяготения Солнца, Земли и нас с вами – с этим вопросом мы разберемся чуть позже.

Насколько нам известно, сила тяжести равна:

P = mg,

где m – наша масса, а g – ускорение свободного падения Земли (9,81 м/с²).

Важно! Не бывает двух, трех, десяти видов сил притяжения. Гравитация – единственная сила, дающая количественную характеристику притяжения. Вес (P = mg) и сила гравитации – одно и то же.

Если m – наша масса, M – масса земного шара, R – его радиус, то гравитационная сила, действующая на нас, равна:

Таким образом, поскольку F = mg:

Массы m сокращаются, и остается выражение для ускорения свободного падения:

Как видим, ускорение свободного падения – действительно постоянная величина, поскольку в ее формулу входят величины постоянные — радиус, масса Земли и гравитационная постоянная. Подставив значения этих констант, мы убедимся, что ускорение свободного падения равно 9,81 м/с².

На разных широтах радиус планеты несколько отличается, поскольку Земля все-таки не идеальный шар. Из-за этого ускорение свободного падения в отдельных точках земного шара разное.

Вернемся к притяжению Земли и Солнца. Постараемся на примере доказать, что земной шар притягивает нас с вами сильнее, чем Солнце.

Примем для удобства массу человека: m = 100 кг. Тогда:

Расстояние между человеком и земным шаром равно радиусу планеты: R = 6,4∙10⁶ м.
Масса Земли равна: M ≈ 6∙10²⁴ кг.
Масса Солнца равна: Mc ≈ 2∙10³⁰ кг.
Дистанция между нашей планетой и Солнцем (между Солнцем и человеком): r=15∙10¹⁰ м.

Гравитационное притяжение между человеком и Землей:

Данный результат довольно очевиден из более простого выражения для веса (P = mg).

Сила гравитационного притяжения между человеком и Солнцем:

Как видим, наша планета притягивает нас почти в 2000 раз сильнее.

Как найти силу притяжения между Землей и Солнцем? Следующим образом:

Теперь мы видим, что Солнце притягивает нашу планету более чем в миллиард миллиардов раз сильнее, чем планета притягивает нас с вами.

Первая космическая скорость

После того как Исаак Ньютон открыл закон всемирного тяготения, ему стало интересно, с какой скоростью нужно бросить тело, чтобы оно, преодолев гравитационное поле, навсегда покинуло земной шар.

Правда, он представлял себе это несколько иначе, в его понимании была не вертикально стоящая ракета, устремленная в небо, а тело, которое горизонтально совершает прыжок с вершины горы. Это была логичная иллюстрация, поскольку на вершине горы сила притяжения немного меньше.

Так, на вершине Эвереста ускорение свободного падения будет равно не привычные 9,8 м/с², а почти м/с². Именно по этой причине там настолько разряженный воздух, частицы воздуха уже не так привязаны к гравитации, как те, которые «упали» к поверхности.

Постараемся узнать, что такое космическая скорость.

Первая космическая скорость v1 – это такая скорость, при которой тело покинет поверхность Земли (или другой планеты) и перейдет на круговую орбиту.

Постараемся узнать численной значение этой величины для нашей планеты.

Запишем второй закон Ньютона для тела, которое вращается вокруг планеты по круговой орбите:

где h — высота тела над поверхностью, R — радиус Земли.

На орбите на тело действует центробежное ускорение , таким образом:

Массы сокращаются, получаем:

Данная скорость называется первой космической скоростью:

Как можно заметить, космическая скорость абсолютно не зависит от массы тела. Таким образом, любой предмет, разогнанный до скорости 7,9 км/с, покинет нашу планету и перейдет на ее орбиту.

Первая космическая скорость

Вторая космическая скорость

Однако, даже разогнав тело до первой космической скорости, нам не удастся полностью разорвать его гравитационную связь с Землей. Для этого и нужна вторая космическая скорость. При достижении этой скорости тело покидает гравитационное поле планеты и все возможные замкнутые орбиты.

Важно! По ошибке часто считается, что для того чтобы попасть на Луну, космонавтам приходилось достигать второй космической скорости, ведь нужно было сперва «разъединиться» с гравитационным полем планеты. Это не так: пара «Земля — Луна» находятся в гравитационном поле Земли. Их общий центр тяжести находится внутри земного шара.

Для того чтобы найти эту скорость, поставим задачу немного иначе. Допустим, тело летит из бесконечности на планету. Вопрос: какая скорость будет достигнута на поверхности при приземлении (без учета атмосферы, разумеется)? Именно такая скорость и потребуется телу, чтобы покинуть планету.

Вторая космическая скорость

Запишем закон сохранения энергии:

где в правой части равенства стоит работа силы тяжести: A = Fs.

Отсюда получаем, что вторая космическая скорость равна:

Таким образом, вторая космическая скорость в раз больше первой:

Закон всемирного тяготения. Физика 9 класс

Закон Всемирного тяготения.

Вывод

Мы с вами узнали, что хотя гравитация является основной силой во Вселенной, многие причины этого явления до сих пор остались загадкой. Мы узнали, что такое сила всемирного тяготения Ньютона, научились считать ее для различных тел, а также изучили некоторые полезные следствия, которые вытекают из такого явления, как всемирный закон тяготения.

uchim.guru

Всемирное тяготение — это… Что такое Всемирное тяготение?

Гравита́ция (всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — дальнодействующее фундаментальное взаимодействие в природе, которому подвержены все материальные тела. По современным данным, является универсальным взаимодействием в том смысле, что, в отличие от любых других сил, всем без исключения телам независимо от их массы придаёт одинаковое ускорение. Главным образом гравитация играет определяющую роль в космических масштабах. Термин гравитация используется также как название раздела физики, изучающего гравитационное взаимодействие. Наиболее успешной современной физической теорией в классической физике, описывающей гравитацию, является общая теория относительности, квантовая теория гравитационного взаимодействия пока не построена.

Гравитационное взаимодействие

Гравитационное взаимодействие — одно из четырёх фундаментальных взаимодействий в нашем мире. В рамках классической механики, гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния — то есть

Здесь G — гравитационная постоянная, равная примерно м³/(кг•с²). Знак минус означает, что сила, действующая на тело, всегда равна по направлению радиус-вектору, направленному на тело, то есть гравитационное взаимодействие приводит всегда к притяжению любых тел.

Закон всемирного тяготения — одно из приложений закона обратных квадратов, встречающегося так же и при изучении излучений (см. например, Давление света), и являющимся прямым следствием квадратичного увеличения площади сферы при увеличении радиуса, что приводит к квадратичному же уменьшению вклада любой единичной площади в площадь всей сферы.

Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии и при изучении движения тел в поле тяжести часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал зависит только от положения тела в данный момент времени.

Большие космические объекты — планеты, звезды и галактики имеют огромную массу и, следовательно, создают значительные гравитационные поля.

Гравитация — слабейшее взаимодействие. Однако, поскольку оно действует на любых расстояниях и все массы положительны, это тем не менее очень важная сила во Вселенной. Для сравнения: полный электрический заряд этих тел ноль, так как вещество в целом электрически нейтрально.

Также гравитация, в отличие от других взаимодействий, универсальна в действии на всю материю и энергию. Не обнаружены объекты, у которых вообще отсутствовало бы гравитационное взаимодействие.

Из-за глобального характера гравитация ответственна и за такие крупномасштабные эффекты, как структура галактик, черные дыры и расширение Вселенной, и за элементарные астрономические явления — орбиты планет, и за простое притяжение к поверхности Земли и падения тел.

Гравитация была первым взаимодействием, описанным математической теорией. В античные времена Аристотель считал, что объекты с разной массой падают с разной скоростью. Только много позже Галилео Галилей экспериментально определил, что это не так — если сопротивление воздуха устраняется, все тела ускоряются одинаково. Закон всеобщего тяготения Исаака Ньютона (1687) хорошо описывал общее поведение гравитации. В 1915 году Альберт Эйнштейн создал Общую теорию относительности, более точно описывающую гравитацию в терминах геометрии пространства-времени.

Небесная механика и некоторые её задачи

Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации называется небесной механикой.

Наиболее простой задачей небесной механики является гравитационное взаимодействие двух тел в пустом пространстве. Эта задача решается аналитически до конца; результат её решения часто формулируют в виде трёх законов Кеплера.

При увеличении количества взаимодействующих тел задача резко усложняется. Так, уже знаменитая задача трёх тел (то есть движение трёх тел с ненулевыми массами) не может быть решена аналитически в общем виде. При численном же решении, достаточно быстро наступает неустойчивость решений относительно начальных условий. В применении к Солнечной системе, эта неустойчивость не позволяет предсказать движение планет на масштабах, превышающих сотню миллионов лет.

В некоторых частных случаях удаётся найти приближённое решение. Наиболее важным является случай, когда масса одного тела существенно больше массы других тел (примеры: солнечная система и динамика колец Сатурна). В этом случае в первом приближении можно считать, что лёгкие тела не взаимодействуют друг с другом и движутся по кеплеровым траекториям вокруг массивного тела. Взаимодействия же между ними можно учитывать в рамках теории возмущений, и усреднять по времени. При этом могут возникать нетривиальные явления, такие как резонансы, аттракторы, хаотичность и т. д. Наглядный пример таких явлений — нетривиальная структура колец Сатурна.

Несмотря на попытки описать поведение системы из большого числа притягивающихся тел примерно одинаковой массы, сделать этого не удаётся из-за явления динамического хаоса.

Сильные гравитационные поля

В сильных гравитационных полях, при движении с релятивистскими скоростями, начинают проявляться эффекты общей теории относительности:

Гравитационное излучение

Одним из важных предсказаний ОТО является гравитационное излучение, наличие которого до сих пор не подтверждено прямыми наблюдениями. Однако, имеются косвенные наблюдательные свидетельства в пользу его существования, а именно: потери энергии в двойной системе с пульсаром PSR B1913+16 — пульсаром Халса-Тейлора — хорошо согласуются с моделью, в которой эта энергия уносится гравитационным излучением.

Гравитационное излучение могут генерировать только системы с переменным квадрупольным или более высокими мультипольными моментами, этот факт говорит о том, что гравитационное излучение большинства природных источников направленное, что существенно усложняет его обнаружение. Мощность гравитационного l-польного источника пропорциональна (v / c)^{2l + 2}, если мультиполь имеет электрический тип, и (v / c)^{2l + 4} — если мультиполь магнитного типа ^[1], где v — характерная скорость движения источников в излучающей системе, а c — скорость света. Таким образом, доминирующим моментом будет квадрупольный момент электрического типа, а мощность соответствующего излучения равна:

где Q_ij — тензор квадрупольного момента распределения масс излучающей системы. Константа (1/Вт) позволяет оценить порядок величины мощности излучения.

Начиная с 1969 года (эксперименты Вебера (англ.)) и до настоящего времени (февраль 2007) предпринимаются попытки прямого обнаружения гравитационного излучения. В США, Европе и Японии в настоящий момент существует несколько действующих наземных детекторов (GEO 600), а также проект космического гравитационного детектора [2] республики Татарстан.

Тонкие эффекты гравитации

Помимо классических эффектов гравитационного притяжения и замедления времени, общая теория относительности предсказывает существование других проявлений гравитации, которые в земных условиях весьма слабы и их обнаружение и экспериментальная проверка поэтому весьма затруднительны. До последнего времени преодоление этих трудностей представлялось за пределами возможностей экспериментаторов.

Среди них, в частности, можно назвать увлечение инерциальных систем отсчета (или эффект Лензе-Тирринга) и гравитомагнитное поле. В 2005 году автоматический аппарат НАСА Gravity Probe B провёл беспрецедентный по точности эксперимент по измерению этих эффектов вблизи Земли, но его полные результаты пока не опубликованы.

Квантовая теория гравитации

Несмотря на более чем полувековую историю попыток, гравитация — единственное из фундаментальных взаимодействий, для которого пока ещё не построена непротиворечивая перенормируемая квантовая теория. Впрочем, при низких энергиях, в духе квантовой теории поля, гравитационное взаимодействие можно представить как обмен гравитонами — калибровочными бозонами со спином 2.

Стандартные теории гравитации

Подробней см. статью Теории гравитации

В связи с тем, что квантовые эффекты гравитации чрезвычайно малы даже в самых экстремальных экспериментальных и наблюдательных условиях, до сих пор не существует их надёжных наблюдений. Теоретические оценки показывают, что в подавляющем большинстве случаев можно ограничиться классическим описанием гравитационного взаимодействия.

Существует современная каноническая^[3] классическая теория гравитации — общая теория относительности, и множество уточняющих её гипотез и теорий различной степени разработанности, конкурирующих между собой (см. статью Альтернативные теории гравитации). Все эти теории дают очень похожие предсказания в рамках того приближения, в котором в настоящее время осуществляются экспериментальные тесты. Далее описаны несколько основных, наиболее хорошо разработанных или известных теорий гравитации.

Общая теория относительности

В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причём пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала) иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем или метрикой четырехмерного пространства-времени, а напряженность гравитационного поля — с аффинной связностью пространства-времени, определяемой метрикой. Стандартной задачей ОТО является определение компонент метрического тензора, в совокупности задающих метрику пространства-времени, по известному распределению источников энергии-импульса в рассматриваемой системе четырехмерных координат. В свою очередь знание метрики позволяет рассчитывать движение пробных частиц, что эквивалентно знанию свойств поля тяготения в данной системе. В связи с тензорным характером уравнений ОТО, а также со стандартным фундаментальным обоснованием ее формулировки, считается, что гравитация также носит тензорный характер. Одним из следствий является то, что гравитационное излучение должно быть не ниже квадрупольного порядка. Известно, что в ОТО имеются затруднения с объяснением факта неинвариантности энергии гравитационного поля, поскольку данная энергия не описывается тензором. В классической ОТО также возникает проблема описания спин-орбитального взаимодействия. Считается, что существуют определенные проблемы с однозначностью результатов и обоснованием непротиворечивости. Однако экспериментально ОТО считается подтверждающейся до самого последнего времени. Кроме того, многие альтернативные эйнштейновскому, но стандартные для современной физики, подходы к формулировке теории гравитации приводят к результату, совпадающему с ОТО в низкоэнергетическом приближении, которое в основном и доступно экспериментальной проверке.

Теория Эйнштейна-Картана

Теория Эйнштейна-Картана (ЭК) была разработана как расширение ОТО, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина объектов.^[4] В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана-Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен ОТО, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к ОТО настолько малы, что пока не видно даже гипотетических путей для их измерения.

Релятивистская теория гравитации

Релятивистская теория гравитации (РТГ) разрабатывается академиком Логуновым А. А. с группой сотрудников. ^[5] В ряде работ они утверждают, что РТГ имеет следующие отличия от ОТО^[6] :

Гравитация есть не геометрическое поле, а реальное физическое силовое поле, описываемое тензором.

Гравитационные явления следует рассматривать в рамках плоского пространства Минковского, в котором однозначно выполняются законы сохранения энергии-импульса и момента количества движения. Тогда движение тел в пространстве Минковского эквивалентно движению этих тел в эффективном римановом пространстве.

В тензорных уравнениях для определения метрики следует учитывать массу гравитона, а также использовать калибровочные условия, связанные с метрикой пространства Минковского. Это не позволяет уничтожить гравитационное поле даже локально выбором какой-то подходящей системы отсчёта.

Как и в ОТО, в РТГ под веществом понимаются все формы материи (включая и электромагнитное поле), за исключением самого гравитационного поля. Следствия из теории РТГ таковы: чёрных дыр как физических объектов, предсказываемых в ОТО, не существует; Вселенная плоская, однородная, изотропная, неподвижная и евклидовая.

C другой стороны, существуют не менее убедительные аргументы противников РТГ, сводящиеся к следующим положениям:

РТГ есть биметрическая теория, в случае безмассового гравитона эквивалентная так называемой полевой трактовке ОТО как надстройке над ненаблюдаемым пространством Минковского: «В релятивистской теории гравитации… фигурируют в точности те же лагранжианы…, которые приводят к уравнениям гравитационного поля»^[7], «математическое содержание РТГ сводится к математическому содержанию ОТО (в полевой формулировке)» ^[8]. Этот аргумент в таком изложении, правда, по-видимому не учитывает возможных топологических различий между обычной моделью ОТО и такой моделью, или же, по крайней мере, маскирует их.
Случай массивного гравитона в РТГ не даёт правильного ньютоновского предела при переходе к массе равной 0, и, следовательно, бессмыслен.
Дополнительные уравнения РТГ представляют собой всего лишь координатные условия: «Весь набор уравнений РТГ в терминах метрики искривленного пространства-времени можно свести к уравнениям Эйнштейна плюс гармоническое координатное условие, столь успешно использовавшееся Фоком» ^[8].
Вышеприведённые следствия из РТГ являются лишь следствием неточностей: несуществование чёрных дыр — следствием невозможности покрыть одной координатной картой, эквивалентной пространству-времени Минковского, пространство-время сколлапсировавшего в чёрную дыру объекта; космологических предсказаний — следствием принятых координатных условий в сочетании с совершенно произвольным дополнительным допущением о вложенности световых конусов реального пространства в конусы пространства Минковского. (Как видим, этот аргумент явно противоречит первому, показывая расхождение РТГ и ОТО, которые вполне ощутимы; и, если оставить соображения, очевидно исходящие просто изнутри обычной логики ОТО, или суждения о произвольности постулатов, то решение о верности одного из этих подходов остается за экспериментом, если конечно не будет всё же доказана достаточно неочевидная их полная эквивалентность в области наблюдаемого).

Теория Бранса — Дикке

В скалярно-тензорных теориях, самой известной из которых является теория Бранса — Дикке (или Йордана — Бранса — Дикке), гравитационное поле как эффективная метрика пространства-времени определяется воздействием не только тензора энергии-импульса материи, как в ОТО, но и дополнительного гравитационного скалярного поля. Источником скалярного поля считается свёрнутый тензор энергии-импульса материи. Следовательно, скалярно-тензорные теории, как ОТО и РТГ, относятся к метрическим теориям, дающим объяснение гравитации, используя только геометрию пространства-времени и его метрические свойства. Наличие скалярного поля приводит к двум тензорным уравнениям для метрики. Теория Бранса — Дикке вследствие наличия скалярного поля может рассматриваться также как действующая в пятимерном многообразии, состоящем из пространства-времени и скалярного поля.^[9]

Подобное имеет место и в РТГ, где второе тензорное уравнение вводится для учёта связи между неевклидовым пространством и пространством Минковского^[10]. Благодаря наличию безразмерного подгоночного параметра в теории Йордана — Бранса — Дикке, появляется возможность выбрать его так, чтобы результаты теории совпадали с результатами гравитационных экспериментов.

Теории гравитации

Источники и примечания

↑ См. аналогии между слабым гравитационным полем и электромагнитным полем в статье гравитомагнетизм
↑ http://dulkyn.org.ru/ru/about.html
↑ Канонической эта теория является в том смысле, что она наиболее хорошо разработана и широко используется в современной небесной механике, астрофизике и космологии, причём количество надёжно установленных противоречащих ей экспериментальных результатов практически равно нулю.
↑ Иваненко Д. Д., Пронин П. И., Сарданашвили Г. А., Калибровочная теория гравитации. — М., Изд. МГУ, 1985.
↑ Логунов А. А., Мествиришвили М. А. Релятивистская теория гравитации. — М: Наука, 1989.
↑ Логунов А. А., Мествиришвили М. А. Тензор энергии-импульса материи как источник гравитационного поля. — Теоретическая и математическая физика, 1997, Т. 110, Вып. 1, Стр. 5 — 24.
↑ Зельдович Я. Б., Грищук Л. П. ТЯГОТЕНИЕ, ОБЩАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И АЛЬТЕРНАТИВНЫЕ ТЕОРИИ. УФН, 1986, Т. 149, № 4, с. 695—707. С. 704.
↑ ¹ ² Зельдович Я. Б., Грищук Л. П. Общая теория относительности верна! УФН, 1988, Т. 155, № 3, с. 517—527. С. 521, 524.
↑ Brans, C. H.; Dicke, R. H. (November 1 1961). «Mach’s Principle and a Relativistic Theory of Gravitation». Physical Review 124 (3): 925—935. DOI:10.1103/PhysRev.124.925. Retrieved on 2006-09-23.
↑ С ортодоксальной точки зрения это уравение представляет собой координатное условие, см. выше.

Литература

Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). М.: Наука, 1981. — 352c.
Визгин В. П. Единые теории в 1-й трети ХХ в. М.: Наука, 1985. — 304c.
Иваненко Д. Д., Сарданашвили Г. А. Гравитация, 3-е изд. М.:УРСС, 2008. — 200с.

См. также

Ссылки

Wikimedia Foundation. 2010.

dic.academic.ru

История открытия закона всемирного тяготения

Эта статья уделит внимание истории открытия закона всемирного тяготения. Здесь мы ознакомимся с биографическими сведениями из жизни ученого, открывшего эту физическую догму, рассмотрим ее основные положения, взаимосвязь с квантовой гравитацией, ход развития и многое другое.

Гений

Сэр Исаак Ньютон – ученый родом из Англии. В свое время много внимания и сил уделил таким науками, как физика и математика, а также привнес немало нового в механику и астрономию. По праву считается одним из первых основоположников физики в ее классической модели. Является автором фундаментального труда «Математические начала натуральной философии», где изложил информацию о трех законах механики и законе всемирного тяготения. Исаак Ньютон заложил этими работами основы классической механики. Им было разработано исчисление дифференциального и интегрального типа, световая теория. Он также внес большой вклад в физическую оптику и разработал множество других теорий в области физики и математики.

Закон

Закон всемирного тяготения и история его открытия уходят своим началом в далекий 1666 год. Его классическая форма – это закон, при помощи которого описывается взаимодействие гравитационного типа, не выходящее за пределы рамок механики.

Его суть заключалась в том, что показатель силы F гравитационной тяги, возникающей между 2 телами или точками материи m1 и m2, отделенными друг от друга определенным расстоянием r, соблюдает пропорциональность по отношению к обоим показателям массы и имеет обратную пропорциональность квадрату расстояния между телами:

F = G, где символом G мы обозначаем постоянную гравитации, равную 6,67408(31)•10^-11 м³/кгс².

Тяготение Ньютона

Прежде чем рассмотреть историю открытия закона всемирного тяготения, ознакомимся более детально с его общей характеристикой.

В теории, созданной Ньютоном, все тела с большой массой должны порождать вокруг себя особое поле, которое притягивает другие объекты к себе. Его называют гравитационным полем, и оно имеет потенциал.

Тело, обладающее сферической симметрией, образует за пределом самого себя поле, аналогичное тому, которое создает материальная точка той же массы, расположенная в центре тела.

Направление траектории такой точки в поле гравитации, созданным телом с гораздо более большой массой, подчиняется закону Кеплера. Объекты вселенной, такие как, например, планета или комета, также подчиняются ему, двигаясь по эллипсу или гиперболе. Учет искажения, которое создают другие массивные тела, учитывается с помощью положений теории возмущения.

Анализируя точность

После того, как Ньютон открыл закон всемирного тяготения, его необходимо было проверить и доказать множество раз. Для этого совершались ряды расчетов и наблюдений. Придя к согласию с его положениями и исходя из точности его показателя, экспериментальная форма оценивания служит ярким подтверждением ОТО. Измерение квадрупольных взаимодействий тела, что вращается, но антенны его остаются неподвижными, показывают нам, что процесс наращивания δ зависит от потенциала r ^-(1+δ), на расстоянии в несколько метров и находится в пределе (2,1±6,2)•10^-3. Ряд других практических подтверждений позволили этому закону утвердиться и принять единую форму, без наличия модификаций. В 2007 г. данную догму перепроверили на расстоянии, меньшем сантиметра (55 мкм-9,59 мм). Учитывая погрешности эксперимента, ученые исследовали диапазон расстояния и не обнаружили явных отклонений в этом законе.

Наблюдение за орбитой Луны по отношению к Земле также подтвердило его состоятельность.

Евклидово пространство

Классическая теория тяготения Ньютона связана с евклидовым пространством. Фактическое равенство с достаточно большой точностью (10^-9) показателей меры расстояния в знаменателе равенства, рассмотренного выше, показывает нам эвклидову основу пространства Ньютоновской механики, с трехмерной физической формой. В такой точке материи площадь сферической поверхности имеет точную пропорциональность по отношению к величине квадрата ее радиуса.

Данные из истории

Рассмотрим краткое содержание истории открытия закона всемирного тяготения.

Идеи выдвигались и другими учеными, живших перед Ньютоном. Размышления о ней посещали Эпикура, Кеплера, Декарта, Роберваля, Гассенди, Гюйгенса и других. Кеплер выдвигал предположение о том, что сила тяготения имеет обратную пропорцию расстоянию от звезды Солнца и распространение имеет лишь в эклиптических плоскостях; по мнению Декарта, она была последствием деятельности вихрей в толще эфира. Существовал ряд догадок, который содержал в себе отражение правильных догадок о зависимости от расстояния.

Письмо от Ньютона Галлею содержало информацию о том, что предшественниками самого сэра Исаака были Гук, Рен и Буйо Исмаэль. Однако до него никому не удалось четко, при помощи математических методов, связать закон тяготения и планетарное движение.

История открытия закона всемирного тяготения тесно связанна с трудом «Математические начала натуральной философии» (1687). В этой работе Ньютон смог вывести рассматриваемый закон благодаря эмпирическому закону Кеплера, уже бывшему к тому времени известным. Он нам показывает, что:

форма движения любой видимой планеты свидетельствует о наличичи центральной силы;
сила притяжения центрального типа образует эллиптические или гиперболические орбиты.

О теории Ньютона

Осмотр краткой истории открытия закона всемирного тяготения также может указать нам на ряд отличий, которые выделяли ее на фоне предшествующих гипотез. Ньютон занимался не только публикацией предлагаемой формулы рассматриваемого явления, но и предлагал модель математического типа в целостном виде:

положение о законе тяготения;
положение о законе движения;
систематика методов математических исследований.

Данная триада могла в достаточно точной мере исследовать даже самые сложные движения небесных объектов, таким образом создавая основу для небесной механики. Вплоть до начала деятельности Эйнштейна в данной модели наличие принципиального набора поправок не требовалось. Лишь математические аппараты пришлось значительно улучшить.

Объект для обсуждений

Обнаруженный и доказанный закон в течение всего восемнадцатого века стал известным предметом активных споров и скрупулезных проверок. Однако век завершился общим согласием с его постулатами и утверждениям. Пользуясь расчетами закона, можно было точно определить пути движения тел на небесах. Прямая проверка была совершена Генри Кавендишем в 1798 году. Он сделал это, используя весы крутильного типа с большой чувствительностью. В истории открытия всемирного закона тяготения необходимо выделить особое место толкованиям, введенным Пуассоном. Он разработал понятие потенциала гравитации и Пуассоново уравнение, при помощи которого можно было исчислять данный потенциал. Такой тип модели позволял заниматься исследованием гравитационного поля в условиях наличия произвольного распределения материи.

В теории Ньютона было немало трудностей. Главной из них можно было считать необъяснимость дальнодействия. Нельзя было точно ответить на вопрос о том, как силы притяжения пересылаются сквозь вакуумное пространство с бесконечной скоростью.

«Эволюция» закона

Последующие двести лет, и даже больше, множеством ученых-физиков были предприняты попытки предложить разнообразные способы по усовершенствованию теории Ньютона. Данные усилия окончились триумфом, совершенным в 1915 году, а именно сотворением Общей теории относительности, которую создал Эйнштейн. Он смог преодолеть весь набор трудностей. В согласии с принципом соответствия теория Ньютона оказалась приближением к началу работы над теорией в более общем виде, которое можно применять при наличии определенных условий:

Потенциал гравитационной природы не может быть слишком большим в исследуемых системах. Солнечная система является примером соблюдения всех правил по движению небесного типа тел. Релятивистское явление находит себя в заметном проявлении смещения перигелия.
Показатель скорости движения в данной группе систем является незначительным в сравнении со световой скоростью.

Доказательством того, что в слабом стационарном поле гравитации расчеты ОТО принимают форму ньютоновых, служит наличие скалярного потенциала гравитации в стационарном поле со слабо выраженными характеристиками сил, который способен удовлетворить условия уравнения Пуассона.

Масштаб квантов

Однако в истории ни научное открытие закона всемирного тяготения, ни Общая теория относительности не могли служить окончательной гравитационной теорией, поскольку обе недостаточно удовлетворительно описывают процессы гравитационного типа в масштабах квантов. Попытка создания квантово-гравитационной теории является одной из самых главных задач физики современности.

Со точки зрения квантовой гравитации взаимодействие между объектами создается при помощи взаимообмена виртуальными гравитонами. В соответствии с принципом неопределенности, энергетический потенциал виртуальных гравитонов имеет обратную пропорциональность промежутку времени, в котором он существовал, от точки излучения одним объектом до момента времени, в котором его поглотила другая точка.

Ввиду этого получается, что в малом масштабе расстояний взаимодействие тел влечет за собой и обмен гравитонами виртуального типа. Благодаря данным соображениям можно заключить положение о законе потенциала Ньютона и его зависимости в соответствии обратному показателю пропорциональности по отношению к расстоянию. Наличие аналогии между законами Кулона и Ньютона объясняется тем, что вес гравитонов равняется нулю. Это же значение имеет и вес фотонов.

Заблуждение

В школьной программе ответом на вопрос из истории, как Ньютон открыл закон всемирного тяготения, служит история о падающем плоде яблока. Согласно этой легенде, оно свалилось на голову ученому. Однако это — массово распространенное заблуждение, и в действительности все смогло обойтись без подобного случая возможной травмы головы. Сам Ньютон иногда подтверждал данный миф, но в действительности закон не был спонтанным открытием и не пришел в порыве сиюминутного озарения. Как было написано выше, он разрабатывался долгое время и был представлен впервые в трудах о «Математических началах», вышедших на обозрение публике в 1687 году.

fb.ru

Закон всемирного тяготения: простое пояснение

Содержание:

Кто открыл закон всемирного тяготения

Определение закона всемирного тяготения

Формула закона всемирного тяготения

Закон всемирного тяготения и невесомость тел

Закон всемирного тяготения, видео

Кто открыл закон всемирного тяготения

Ни для кого не секрет, что закон всемирного тяготения был открыт великим английским ученым Исааком Ньютоном, по легенде гуляющим в вечернем саду и раздумывающем над проблемами физики. В этот момент с дерева упало яблоко (по одной версии прямо на голову физику, по другой просто упало), ставшее впоследствии знаменитым яблоком Ньютона, так как привело ученого к озарению, эврике. Яблоко, упавшее на голову Ньютону и вдохновило того к открытию закона всемирного тяготения, ведь Луна в ночном небе оставалась не подвижной, яблоко же упало, возможно, подумал ученый, что какая-то сила воздействует как на Луну (заставляя ее вращаться по орбите), так и на яблоко, заставляя его падать на землю.

Сейчас по заверениям некоторых историков науки вся эта история про яблоко лишь красивая выдумка. На самом деле падало яблоко или нет, не столь уж важно, важно, что ученый таки действительно открыл и сформулировал закон всемирного тяготения, который ныне является одним из краеугольных камней, как физики, так и астрономии.

Разумеется, и задолго до Ньютона люди наблюдали, как падающие на землю вещи, так и звезды в небе, но до него они полагали, что существует два типа гравитации: земная (действующая исключительно в пределах Земли, заставляющая тела падать) и небесная (действующая на звезды и Луну). Ньютон же был первым, кто объединил эти два типа гравитации в своей голове, первым кто понял, что гравитация есть только одна и ее действие можно описать универсальным физическим законом.

Определение закона всемирного тяготения

Согласно этому закону, все материальные тела притягивают друг друга, при этом сила притяжения не зависит от физических или химических свойств тел. Зависит она, если все максимально упростить, лишь от веса тел и расстояния между ними. Также дополнительно нужно принять во внимание тот факт, что на все тела находящиеся на Земле действует сила притяжения самой нашей планеты, получившая название – гравитация (с латыни слово «gravitas» переводиться как тяжесть).

Попробуем же теперь сформулировать и записать закон всемирного тяготения максимально кратко: сила притяжения между двумя телами с массами m1 и m2 и разделенными расстоянием R прямо пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними.

Формула закона всемирного тяготения

Ниже представляем вашему вниманию формулу закона всемирного тяготения.

G в этой формуле это гравитационная постоянная, равная 6,67408(31)•10⁻¹¹ эта величина воздействия на любой материальный объект силы гравитации нашей планеты.

Закон всемирного тяготения и невесомость тел

Открытый Ньютоном закон всемирного тяготения, а также сопутствующий математический аппарат позже легли в основу небесной механики и астрономии, ведь с помощью него можно объяснить природу движения небесных тел, равно как и явление невесомости. Находясь в космическом пространстве на значительном удалении от силы притяжения-гравитации такого большого тела как планета, любой материальный объект (например, космический корабль с астронавтами на борту) окажется в состоянии невесомости, так как сила гравитационного воздействия Земли (G в формуле закона тяготения) или какой-нибудь другой планеты, больше не будет на него влиять.

Закон всемирного тяготения, видео

И в завершение поучительное видео об открытии закона всемирного тяготения.

www.poznavayka.org

Закон всемирного тяготения

Исаак Ньютон выдвинул предположение, что между любыми телами в природе существуют силы взаимного притяжения. Эти силы называют силами гравитации или силами всемирного тяготения. Сила несмирного тяготения проявляется в космосе, Солнечной системе и на Земле.

Закон всемирного тяготения между любыми материальными точками существует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки

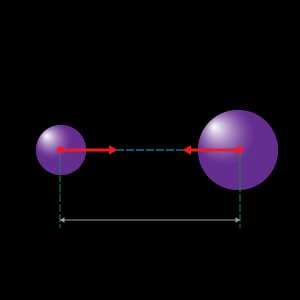
Ньютон обобщил законы движения небесных тел и выяснил, что сила \( F \) равна:

\[ F = G \dfrac{m_1 m_2}{R^2} \]

где \( m_1 \) и \( m_2 \) — массы взаимодействующих тел, \( R \) — расстояние между ними, \( G \) — коэффициент пропорциональности, который называется гравитационной постоянной. Численное значение гравитационной постоянной опытным путем определил Кавендиш, измеряя силу взаимодействия между свинцовыми шарами.

Физический смысл гравитационной постоянной вытекает из закона всемирного тяготения. Если \(m_1 = m_2 = 1 \text{кг} \), \( R = 1 \text{м} \), то \( G = F \), т. е. гравитационная постоянная равна силе, с которой притягиваются два тела по 1 кг на расстоянии 1 м.

Численное значение:

\( G = 6,67 \cdot{} 10^{-11} Н \cdot{} м^2/ кг^2 \) .

Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах (или если хотя бы масса одного из тел велика). Закон же всемирного тяготения выполняется только для материальных точек и шаров (в этом случае за расстояние принимается расстояние между центрами шаров).

Сила тяжести

Частным видом силы всемирного тяготения является сила притяжения тел к Земле (или к другой планете). Эту силу называют силой тяжести. Под действием этой силы все тела приобретают ускорение свбодного падения.

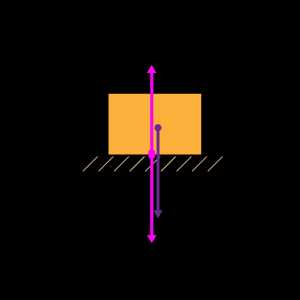
Сила тяжести – это сила, с которой Земля притягивает тело, находящееся на её поверхности или вблизи этой поверхности.

В соответствии со вторым законом Ньютона \( g = F_Т /m \) , следовательно, \( F_T = mg \) .

Если M – масса Земли, R – ее радиус, m – масса данного тела, то сила тяжести равна

\( F = G \dfrac{M}{R^2}m = mg \) .

Сила тяжести всегда направлена к центру Земли. В зависимости от высоты \( h \) над поверхностью Земли и географической широты положения тела ускорение свободного падения приобретает различные значения. На поверхности Земли и в средних широтах ускорение свободного падения равно 9,831 м/с₂.

Вес тела

В технике и быту широко используется понятие веса тела.

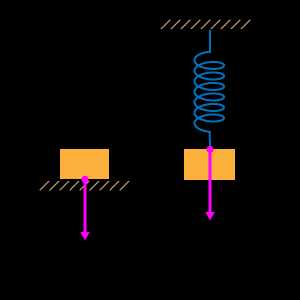
Весом тела называют силу, с которой тело давит на опору или подвес в результате гравитационного притяжения к планете.

Вес тела обозначается \( P \). Единица веса — ньютон (Н). Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо определить, чему равна сила реакции опоры.

При этом предполагается, что тело неподвижно относительно опоры или подвеса.

Вес тела и сила тяжести отличаются по своей природе: вес тела является проявлением действия межмолекулярных сил, а сила тяжести имеет гравитационную природу.

Состояние тела, в котором его вес равен нулю, называют невесомостью. Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением, по¬этому в корабле наблюдается состояние невесомости.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

calcsbox.com

Сила всемирного тяготения: характеристика и практическая значимость

XVI – XVII века многие по праву называют одним из самых славных периодов в истории физики. Именно в это время были во многом заложены те основы, без которых дальнейшее развитие этой науки было бы попросту немыслимым. Коперник, Галилей, Кеплер проделали огромную работу, чтобы заявить о физике как о науке, которая может дать ответ практически на любой вопрос. Особняком в целой череде открытий стоит закон всемирного тяготения, окончательная формулировка которого принадлежит выдающемуся английскому ученому Исааку Ньютону.

Основное значение работ этого ученого заключалось не в открытии им силы всемирного тяготения – о наличии этой величины еще до Ньютона говорил и Галилей, и Кеплер, а в том, что он первым доказал, что и на Земле, и в космическом пространстве действуют одни и те же силы взаимодействия между телами.

Ньютон на практике подтвердил и теоретически обосновал тот факт, что абсолютно все тела во Вселенной, в том числе и те, которые располагаются на Земле, взаимодействуют друг с другом. Это взаимодействие получило название гравитационного, в то время как сам процесс всемирного тяготения – гравитации.
Данное взаимодействие возникает между телами потому, что существует особый, непохожий на другие, вид материи, который в науке получил название гравитационного поля. Это поле существует и действует вокруг абсолютно любого предмета, при этом никакой защиты от него не существует, так как он обладает ни на что не похожей способностью проникать в любые материалы.

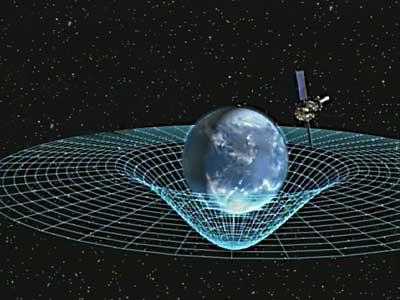
Сила всемирного тяготения, определение и формулировку которой дал Исаак Ньютон, находится в прямой зависимости от произведения масс взаимодействующих тел, и в обратной зависимости от квадрата расстояния междуэтими объектами. Согласно мнению Ньютона, неопровержимо подтвержденного практическими изысканиями, сила всемирного тяготения находится по следующей формуле:

F = Mm/r2.

В ней особое значение принадлежит гравитационной постоянной G, которая приблизительно равна 6,67*10-11(Н*м2)/кг2.

Сила всемирного тяготения, с которой тела притягиваются к Земле, представляет собой частный случай закона Ньютона и называется силой тяжести. В данном случае гравитационной постоянной и массой самой Земли можно пренебречь, поэтому формула нахождения силы тяжести будет выглядеть так:

F=mg.

Здесь g – не что иное, как ускорение свободного падения, числовое значение которого примерно равно 9,8 м/с2.

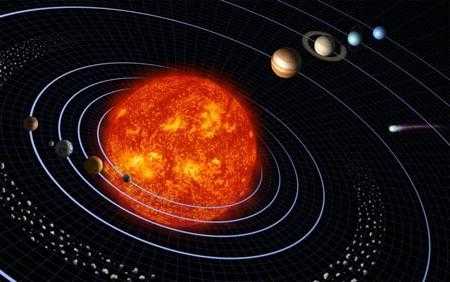
Закон Ньютона объясняет не только процессы, происходящие непосредственно на Земле, он дает ответ на множество вопросов, связанных с устройством всей Солнечной системы. В частности, сила всемирного тяготения между небесными телами оказывает решающее влияние на движение планет по своим орбитам. Теоретическое описание этого движения было дано еще Кеплером, однако обоснование его стало возможно только после того, как Ньютон сформулировал свой знаменитый закон.

Сам Ньютон связывал явления земной и внеземной гравитации на простом примере: при выстреле из пушки ядро летит не прямо, а по дугообразной траектории. При этом при увеличении заряда пороха и массы ядра последнее будет улетать все дальше и дальше. Наконец, если предположить, что возможно достать столько пороха и сконструировать такую пушку, чтобы ядро облетело вокруг Земного шара, то, проделав это движение, оно не остановится, а будет продолжать свое круговое (эллипсовидное) движение, превратившись в искусственный спутник Земли. Как следствие, сила всемирного тяготения одинакова по своей природе и на Земле, и в космическом пространстве.

fb.ru