Все о производной – Производная функции. Подробная теория с примерами

1. Понятие производной

  При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом

  Тот процесс, с помощью которого из данной функции f(x) получают новую функцию f ‘ (x), называют дифференцированием и состоит он из следующих трех шагов:   1) даем аргументу x приращение x и определяем соответствующее приращение функции y = f(x+x) -f(x);   2) составляем отношение

  3) считая x постоянным, а x 0, находим, который обозначаем черезf ‘ (x), как бы подчеркивая тем самым, что полученная функция зависит лишь от того значения

x, при котором мы переходим к пределу.   Определение: Производной y ‘ =f ‘ (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т.е. конечен.   Таким образом, , или

  Заметим, что если при некотором значении x, например при x=a, отношение приx0 не стремится к конечному пределу, то в этом случае говорят, что функция

f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a.

2. Геометрический смысл производной.

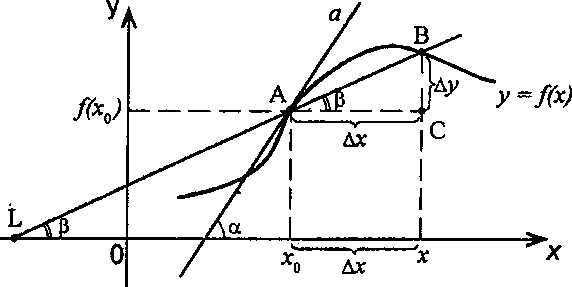
Рассмотрим график функции у = f (х), дифференцируемой в окрест­ностях точки x₀

f(x)

Рассмотрим произвольную прямую, проходящую через точку гра­фика функции — точку А(x₀, f (х₀)) и пересекающую график в некоторой точке B(x;f(x)). Такая прямая (АВ) называется секущей. Из ∆АВС: АС = ∆x; ВС =∆у; tgβ=∆y/∆x .

Так как АС || Ox, то ALO = BAC = β (как соответственные при параллельных). Но ALO — это угол наклона секущей АВ к положи­тельному направлению оси Ох. Значит, tgβ = k — угловой коэффициент прямой АВ.

Теперь будем уменьшать ∆х, т.е. ∆х→ 0. При этом точка В будет прибли­жаться к точке А по графику, а секущая АВ будет поворачиваться. Пре­дельным положением секущей АВ при ∆х→ 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А.

Если перейти к пределу при ∆х → 0 в равенстве tgβ =∆y/∆x, то получимилиtg =f ‘(x₀), так как -угол накло­на касательной к положительному направлению оси Ох , по определению производной. Но tg = k — угловой коэффициент каса­тельной, значит, k = tg = f ‘(x

0).

Итак, геометрический смысл производной заключается в следую­щем:

Производная функции в точке x₀ равна угловому коэффициенту ка­сательной к графику функции, проведенной в точке с абсциссой x₀.

3. Физический смысл производной.

Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени [t₀; t₀+ ∆t] равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е.

Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0.

lim Vср (t) = (t

0) — мгновенная скорость в момент времени t₀, ∆t → 0.

а lim = ∆x/∆t = x'(t₀) (по определению производной).

Итак, (t) =x'(t).

Физический смысл производной заключается в следующем: произ­водная функции y = f(x) в точке x₀ — это скорость изменения функции f (х) в точке x₀

Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.

(t) = x'(t) — скорость,

a(f) = '(t) — ускорение, или

a(t) = x»(t).

Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращатель­ном движении:

φ = φ(t) — изменение угла от времени,

ω = φ'(t) — угловая скорость,

ε = φ'(t) — угловое ускорение, или ε = φ»(t).

Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:

m = m(х) — масса,

x  [0; l], l — длина стержня,

р = m'(х) — линейная плотность.

С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука

F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω² =k/m, получим дифференциальное уравнение пружинного маятника х»(t) + ω

2x(t) = 0,

где ω = √k/√m частота колебаний (l/c), k — жесткость пружины (H/m).

Уравнение вида у» + ω²y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решени­ем таких уравнений является функция

у = Asin(ωt + φ₀) или у = Acos(ωt + φ₀), где

А — амплитуда колебаний, ω — циклическая частота,

φ₀ — начальная фаза.

studfiles.net

Производная

II.Производная

1.Определение производной. Производной функции в точке называется предел отношения приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю, и при условии, что этот предел существует.

2.Дифференцируемая функция. Если в опр.1 — конечная, то функция называется дифференцируемой от .

3.Функция дифференцируема на интервале, если она дифференцируема в каждой его точке.

Теорема о непрерывности дифференцируемой функции.

Теорема.

Если — дифференцируема в точке , то она является непрерывной в этой точке.

Доказательство.

По лемме о функции, имеющий конечный предел:

Тогда:

По второму определению единственности предела функция непрерывна в точке .

Пример:

В силу единственности предела в точке 0

предела нет (рисунок справа).

Дифференциал функции 1-го порядка.

Определение. Дифференциалом функции называется величина, пропорциональная бесконечно малому приращению аргумента

и отличающаяся от соответсвующего приращения функции на бесконечно малую величину более высокого порялка, чем .

Если , то дифференциал 1-го порядка составляет главную часть функции.

Правила дифференцирования.

Пусть функции и дифференцируемы в точке .

Тогда:

4. если — постоянная;

Доказательства.

Посчитаем предел:

Так как функция дифференцирцема в точке , то она непрерывна, то есть ее приращение равно нулю.

Переходим к пределу:

4. если — постоянная;

Таблица элементарных производных

Вывод производных.

Теорема о производной обратной функции

Пусть — дифференцируема в точке , и

— монотонная функция в достаточно малой окрестности точки . Тогда имеет обратную функцию , которая также является непрерывной и монотонной по , дифференцируемой по , и ее производная находится по формуле:

Доказательство:

Выведем все оставшиеся производные обратных функций через эту формулу.

10. Используем тождество:

Гиперболические функции и их производные.

Теорема о производной сложной функции.

Пусть функция дифференцируема в точке , , а функция дифференцируема в точке .

Тогда, если то ;

Доказательство:

Если в данной формуле .

Поделим обе части формулы на , и перейдем к пределу при , т.е. устремим к нулю.

;

Производная показательно-степенной функции.

Тогда:

Вывод формулы:

Логарифмируем:

Что и требовалось доказать.

Геометрический смысл производной и дифференциала.

– дуга графика

Рассмотрим треугольник :

Если , то ,

Если дифференцируема в точке , то

т.е. производная функции равна тангенсу угла наклона касательной.

Уравнения касательной и нормальной прямой.

– прямая, проходящая через точку ;

;

Тогда уравнение касательной к этой прямой записывается следующим образом:

– уравнение касательной;

Нормальная прямая (нормаль) в точке — это прямая, проходящая через эту точку перпендикулярно касательной.

Найти коэффициент можно и другим способом:

Тогда уравнение нормали к этой прямой записывается следующим образом:

— уравнение нормальной прямой;

Дифференциал функции и его свойства.

Пусть дифференцируемы по при некотором

Справедливы свойства:

1. ;

Для независимой переменной ее приращение равно дифференциалу;

3. – некоторая постоянная;

Арифметические свойства:

Инвариантность дифференциала 1-го порядка.

Дифференциал сложной функции записывается так же, как дифференциал внешней функции.

– внутренняя функция;

– внешняя функция;

Пусть эти функции дифференцируемы, тогда

1. ;

Дифференциалы более высоких порядков этим свойством не обладают.

Производная функции, заданной параметрически.

задана параметрически, если ее можно записать в виде:

При этом, функция — монотонная, и — обратная функция.

Доказательство:

Функция – монотонная, следовательно:

По теореме о производной сложной функции, получим:

Пример:

Параметрическое задание:

Это окружность с радиусом .

Покажем, что

Параметрическое задание эллипса

– полуоси эллипса,

Циклоида.

Уравнение циклоиды:

Вывод параметрического задания циклоиды:

Из треугольника :

Найдем угловой коэффициент в точке циклоиды:

Производная функции, заданной неявно.

Пример 1.

— задана неявно,

Продифференцируем левую и правую части уравнения:

Выразим

Пример 2.

Выразим

Основные теоремы дифференциального исчисления:

Теоремы Ролля, Лагранжа, Коши и Ферма.

Понятие локального максимума и локального минимума.

Точка — точка локального максимума, если:

Точка — точка локального минимума, если :

Точки локального минимума и локального максимума называются точками экстремума.

Критическими точками функции называются внутренние точки области определения этой функции, в которых производная равна нулю, или не существует.

Малая теорема Ферма (1601-1665)

Пусть — экстремальная точка функции , и в этой точке функция дифференцируема, тогда производная в этой точке равна нулю.

Пусть — точка локального максимума,

Рассмотрим левостороннюю производную:

studfiles.net

4.1.1 Понятие о производной функции, геометрический смысл производной

Видеоурок: Производная и ее геометрический смысл

Лекция: Понятие о производной функции, геометрический смысл производной

Понятие о производной функции

Рассмотрим некоторую функцию f(x), которая будет непрерывной на всем промежутке рассмотрения. На рассматриваемом промежутке выберем точку х₀, а также величину функции в данной точке.

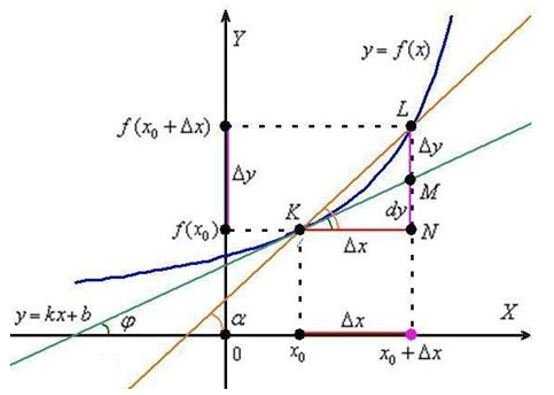
Итак, давайте рассмотрим график, на котором отметим нашу точку х₀, а также точку (х₀ + ∆х). Напомним, что ∆х – это расстояние (разница) между двумя выбранными точками.

Так же стоит понимать, что каждому х соответствует собственное значение функции у. 

Разница значений функции в точке х₀ и (х₀ + ∆х) называется приращением данной функции: ∆у = f(х₀ + ∆х) — f(х₀).

Давайте обратим внимание на дополнительную информацию, которая имеется на графике – это секущая, которая названа КL, а также треугольник, который она образует с интервалами KN и LN.

Угол, под которым находится секущая, называется её углом наклона и обозначается α. Легко можно определить, что градусная мера угла LKN так же равна α.

А теперь давайте вспомним соотношения в прямоугольном треугольнике tgα = LN / KN = ∆у / ∆х.

То есть тангенс угла наклона секущей равен отношению приращения функции к приращению аргумента.

В свое время, производная – это предел отношения приращения функции к приращению аргумента на бесконечно малых интервалах.

 

Производная определяет скорость, с которой происходит изменение функции на некотором участке.

Геометрический смысл производной

Если найти производную любой функции в некоторой точке, то можно определить угол, под которым будет находится касательная к графику в данной токе, относительно оси ОХ. Обратите внимание на график – угол наклона касательно обозначается буквой φ и определяется коэффициентом k в уравнении прямой: y = kx + b.

То есть можно сделать вывод, что геометрическим смыслом производной является тангенс угла наклона касательной в некоторой точке функции.

Для нахождения производных необходимо пользоваться основными формулами, которые можно найти в таблице производных:

cknow.ru

Производная функции — это… Что такое Производная функции?

У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.

История

В классическом дифференциальном исчислении производная чаще всего определяется через понятия теории пределов, однако исторически теория пределов появилась позже дифференциального исчисления.

Русский термин «производная функции» впервые употребил В. И. Висковатов.^[1]

Определение

Пусть в некоторой окрестности точки определена функция Производной функции называется такое число , что функцию в окрестности можно представить в виде

если существует.

Определение производной функции через предел

Пусть в некоторой окрестности точки определена функция Производной функции в точке называется предел, если он существует,

Общепринятые обозначения производной функции в точке

Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).

Дифференцируемость

Производная функции в точке , будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция является дифференцируемой в точке тогда и только тогда, когда её производная в этой точке существует и конечна:

Для дифференцируемой в функции в окрестности справедливо представление

при

Замечания

Геометрический и физический смысл производной

Тангенс угла наклона касательной прямой

Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Если функция имеет конечную производную в точке то в окрестности её можно приблизить линейной функцией

Функция называется касательной к в точке Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть  — закон прямолинейного движения. Тогда выражает мгновенную скорость движения в момент времени Вторая производная выражает мгновенное ускорение в момент времени

Вообще производная функции в точке выражает скорость изменения функции в точке , то есть скорость протекания процесса, описанного зависимостью

Производные высших порядков

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

Если функция дифференцируема в , то производная первого порядка определяется соотношением

Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда

Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от   может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).

  или  

  или  

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

Способы записи производных

В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:

• Лагранжа , при этом для малых n часто используют штрихи и римские цифры:

и т. д.

Такая запись удобна своей краткостью и широко распространена; однако штрихами разрешается обозначать не выше третьей производной.

• Лейбница, удобная наглядной записью отношения бесконечно малых (только в случае, если  — независимая переменная; в противном случае обозначение верно лишь для производной первого порядка):

• Ньютона, которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например:

 — производная первого порядка по при , или  — вторая производная по в точке и т. д.

, или иногда .

• В вариационном исчислении и математической физике часто применяется обозначение , ; для значения производной в точке — . Для частных производных обозначение то же, поэтому смысл обозначения определяют из контекста.

Конечно, при этом необходимо не забывать, что служат все они для обозначения одних и тех же объектов:

Примеры

• Пусть . Тогда

• Пусть . Тогда если то

где обозначает функцию знака. Если то а следовательно не существует.

Правила дифференцирования

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

, то

• Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):

где  — биномиальные коэффициенты.

Следующие свойства производной служат дополнением к правилам дифференцирования:

Доказательство  

Таблица производных некоторых функций

Производная вектор-функции по параметру

Определим производную вектор-функции по параметру:

.

Если производная в точке существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут .

Свойства производной вектор-функции (всюду предполагается, что производные существуют):

См. также

Примечания

Литература

• В. Г. Болтянский, Что такое дифференцирование?, «Популярные лекции по математике», Выпуск 17, Гостехиздат 1955 г., 64 стр.
• В. А. Гусев, А. Г. Мордкович «Математика»
• Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
• В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1

med.academic.ru

Производная функции | Математика | FANDOM powered by Wikia

Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференци́рованием.

Производная как тангенс угла a и отношение приращения функции к приращению аргумента

1. Пусть в некоторой окрестности точки $ x_0 \in \mathbb{R} $ определена функция $ f:U(x_0) \subset \mathbb{R} \to \mathbb{R}. $ Производной функции $ f $ в точке $ x_0 $ называется предел, если он существует,

$ \lim\limits_{x \to x_0} \frac{f(x) — f(x_0)}{x — x_0}. $

• Производная функции в точке $ x_0 $ обозначается символами

$ f'(x_0) = \mathrm{D}f(x_0) = \frac{df(x_0)}{dx} = \left.\frac{dy}{dx}\right\vert_{x = x_0} = \dot{y}(x_0). $

Дифференцируемость Править

Производная $ f'(x_0) $ функции $ f $ в точке $ x_0 $, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция $ f $ является дифференцируемой в точке $ x_0 $ тогда и только тогда, когда её производная в этой точке существует и конечна:

$ \bigl( f \in \mathcal{D}(x_0) \bigr) \Leftrightarrow \bigl( \exists f'(x_0) < \infty\bigr). $

Для дифференцируемой в $ x_0 $ функции $ f $ в окрестности $ U(x_0) $ справедливо представление

$ f(x) = f(x_0) + f'(x_0) (x-x_0) + o(x-x_0) $

• Назовём $ \Delta x = x — x_0 $ приращением аргумента функции, а $ \Delta y = f(x_0+\Delta x) — f(x_0) $ приращением значения функции в точке $ x_0. $ Тогда

  $ f'(x_0) = \lim\limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x}. $

• Пусть функция $ f:(a,b) \to \mathbb{R} $ имеет конечную производную в каждой точке $ x_0 \in (a,b). $ Тогда определена произво́дная фу́нкция

  $ f’:(a,b) \to \mathbb{R}. $

• Функция, имеющая конечную производную в точке, непрерывна в ней. Обратно, вообще говоря, неверно.
• Если производная функция сама является непрерывной, то функцию $ f $ называют непреры́вно дифференци́руемой и пишут: $ f \in C^{(1)}\bigl((a,b)\bigr). $

Геометрический и физический смысл производной Править

Тангенс угла наклона касательной прямой Править

Если функция $ f:U(x_0) \to \mathbb{R} $ имеет конечную производную в точке$ x_0, $ то в окрестности $ U(x_0) $ её можно приблизить линейной функцией

$ f_l(x) = f_(x_0) + f'(x_0)(x-x_0). $

Функция $ f_l $ называется касательной к $ f $ в точке $ x_0. $ Число $ f'(x_0) $ является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции Править

Пусть $ s=s(t) $ — закон прямолинейного движения. Тогда $ v(t_0)=s'(t_0) $ выражает мгновенную скорость движения в момент времени $ t_0. $ Вторая производная $ a(t_0) = s»(t_0) $ выражает мгновенное ускорение в момент времени $ t_0. $

Вообще производная функции $ y=f(x) $ в точке $ x_0 $ выражает скорость изменения функции в точке $ x_0 $, то есть скорость протекания процесса, описанного зависимостью $ y=f(x). $

Производные высших порядков Править

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

$ f^{(0)}(x_0) \equiv f(x_0). $

Если функция $ f $ дифференцируема в $ x_0 $, то производная первого порядка определяется соотношением

$ f^{(1)}(x_0) \equiv f'(x_0). $

Пусть теперь производная $ n $-го порядка $ f^{(n)} $ определена в некоторой окрестности точки $ x_0 $ и дифференцируема. Тогда

$ f^{(n+1)}(x_0) = \left(f^{(n)}\right)'(x_0). $

Производные высших порядков обозначаются символами:

$ f^{(n)}(x_0) = \mathrm{D}^nf(x_0) = \frac{d^nf(x_0)}{dx^n}. $

Когда $ n $ мало, используются штрихи, римские цифры или точки:

$ f^{(1)}(x_0) = f'(x_0) = f^I(x) = \dot{f}(x_0),\; f^{(2)}(x_0) = f»(x_0) = f^{II}(x) = \ddot{f}(x_0),\; f^{(3)}(x_0) = f»'(x_0) = f^{III}(x), $ etc.

• Пусть $ f(x) = x^2. $ Тогда

$ f'(x_0) = \lim\limits_{x \to x_0}\frac{x^2 — x_0^2}{x-x_0} = \lim\limits_{x \to x_0}(x+x_0) = 2x_0. $

• Пусть $ f(x) = |x|. $ Тогда если $ x_0 \neq 0, $ то

$ f'(x_0) = \operatorname{sgn} x_0, $

где $ \operatorname{sgn} $ обозначает функцию знака. Если $ x_0 = 0, $ то $ f’_+(x_0) = 1,\; f’_-(x_0) = -1, $ а следовательно $ f'(x_0) $ не существует.

Эта статья содержит материал из статьи Производная функции русской Википедии.

ru.math.wikia.com

ПРОИЗВОДНАЯ | Энциклопедия Кругосвет

Содержание статьи

ПРОИЗВОДНАЯ – производной функции y = f(x), заданной на некотором интервале (a, b) в точке x этого интервала, называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.

Производную принято обозначать так:

.

Широко употребляются и другие обозначения:

Предел , где рассматривается только Dx > 0 или только Dx f в точке x. О функции f, заданной на отрезке [a, b] принято говорить, что она имеет на этом отрезке производную, если она имеет производную в любой точке интервала (a, b) и, кроме того, правую производную в точке a и левую в точке b.

Понятие производной возникло как результат многовековых усилий, направленных на решение таких задач, как задача о проведении касательной к кривой, о вычислении скорости неравномерного движения, задачи о вычислении площади криволинейной фигуры. В работах Исаака Ньютона и Готфрида Вильгельма Лейбница эта деятельность получила определенное теоретическое завершение. Ньютон и Лейбниц создали общие методы дифференцирования и интегрирования функций и доказали важную теорему, носящую их имя, устанавливающую тесную связь между операциями дифференцирования и интегрирования. Однако современное изложение этих вопросов существенно отличается от того, как они излагались во времена Ньютона и Лейбница. Современный математический анализ базируется на понятии предела, которое было дано (наряду с другими важнейшими понятиями – непрерывность, интеграл и т.д.) в работах французского математика Огюстена Луи Коши.

Мгновенная скорость.

Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M0 , зависит от времени t , т.е. s есть функция времени t: s = f(t). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M0, а в некоторый следующий момент t + Dt оказалась в положении M1 – на расстоянии s + Ds от начального положения (см. рис.).

Таким образом, за промежуток времени Dt расстояние s изменилось на величину Ds. В этом случае говорят, что за промежуток времени Dt величина s получила приращение Ds.

Отношение представляет собой среднюю скорость движения точки за время Dt:

.

Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t. Если, например, тело в начале промежутка Dt перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t. Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени Dt. Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:

.

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути Ds к приращению времени Dt, когда приращение времени стремится к нулю. Так как

,

то.

Геометрическое значение производной. Касательная к графику функции.

Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления.

Пусть кривая есть график функции y = f(x) в прямоугольной системе координат (см. рис.).

При некотором значении x функция имеет значение y = f(x). Этим значениям x и y на кривой соответствует точка M0(x, y). Если аргументу x дать приращение Dx, то новому значению аргумента x + Dx соответствует новое значение функции y+Dy = f(x + Dx). Соответствующей ему точкой кривой будет точка M1(x + Dx, y + Dy). Если провести секущую M0M1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox, из рисунка непосредственно видно, что .

Если теперь Dx стремится к нулю, то точка M1 перемещается вдоль кривой, приближаясь к точке M0, и угол j изменяется с изменением Dx. При Dx ® 0 угол j стремится к некоторому пределу a и прямая, проходящая через точку M0 и составляющая с положительным направлением оси абсцисс угол a, будет искомой касательной. Ее угловой коэффициент:

.

Следовательно, f´(x) = tga

т.е. значение производной f´(x) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке M0(x,y) с положительным направлением оси Ox.

Дифференцируемость функций.

Определение. Если функция y = f(x) имеет производную в точке x = x0, то функция дифференцируема в этой точке.

Непрерывность функции, имеющей производную. Теорема.

Если функция y = f(x) дифференцируема в некоторой точке x = x0, то она в этой точке непрерывна.

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x0 функция y = f(x) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x| непрерывна для всех x (–Ґ х x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.

Некоторые теоремы о дифференцируемых функциях. Теорема о корнях производной (теорема Ролля). Если функция f(x) непрерывна на отрезке [a,b], дифференцируема во всех внутренних точках этого отрезка и на концах x = a и x = b обращается в нуль (f(a) = f(b) = 0), то внутри отрезка [a,b] существует, по крайней мере одна, точка x = с, a c b, в которой производная fў(x) обращается в нуль, т.е. fў(c) = 0.

Теорема о конечных приращениях (теорема Лагранжа). Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a, b] найдется по крайней мере одна точка с, a c b, что

f(b) – f(a) = f ў(c)(b – a).

Теорема об отношении приращений двух функций (теорема Коши). Если f(x) и g(x) – две функции, непрерывные на отрезке [a, b] и дифференцируемые во всех внутренних точках этого отрезка, причем gў(x) нигде внутри этого отрезка не обращается в нуль, то внутри отрезка [a, b] найдется такая точка x = с, a c b, что

.

Производные различных порядков.

Пусть функция y = f(x) дифференцируема на некотором отрезке [a, b]. Значения производной f ў(x), вообще говоря, зависят от x, т.е. производная f ў(x) представляет собой тоже функцию от x. При дифференцировании этой функции получается так называемая вторая производная от функции f(x), которая обозначается f ўў (x).

Производной n-го порядка от функции f(x) называется производная (первого порядка) от производной n-1—го и обозначается символом y(n) = (y(n – 1))ў.

Дифференциалы различных порядков.

Дифференциал функции y = f(x), где x – независимая переменная, есть dy = f ў(x)dx, некоторая функция от x, но от x может зависеть только первый сомножитель f ў(x), второй же сомножитель (dx) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x, то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y:

d(dx) = d2y = f ўў(x)(dx)².

Дифференциалом n-го порядка называется первый дифференциал от дифференциала n-1—го порядка:

dⁿy = d(dⁿ–1 y) = f(n)(x)dx(n).

Частная производная.

Если функция зависит не от одного, а от нескольких аргументов x_i (i изменяется от 1 до n, i = 1, 2,… n), f(x1, x2,… x_n), то в дифференциальном исчислении вводится понятие частной производной, которая характеризует скорость изменения функции нескольких переменных, когда изменяется только один аргумент, например, x_i . Частная производная 1-ого порядка по x_i определяется как обычная производная, при этом предполагается, что все аргументы, кроме x_i, сохраняют постоянные значения. Для частных производных вводятся обозначения

f_xn, или

Определенные таким образом частные производные 1-ого порядка (как функции тех же аргументов) могут, в свою очередь, также иметь частные производные, это частные производные второго порядка и т.д. Взятые по разным аргументам такие производные называются смешанными. Непрерывные смешанные производные одного порядка не зависят от порядка дифференцирования и равны между собой.

Анна Чугайнова

www.krugosvet.ru