Величины какие есть – Список физических величин — Википедия
Список физических величин — Википедия
В метрологии различают понятия размерность физической величины и единица физической величины. Размерность физической величины определяется используемой системой физических величин, которая представляет собой совокупность физических величин, связанных между собой зависимостями, и в которой несколько величин выбраны в качестве основных. Единица физической величины — это такая физическая величина, которой по соглашению присвоено числовое значение, равное единице[1]. Системой единиц физических величин называют совокупность основных и производных единиц, основанную на некоторой системе величин[2]. В расположенных ниже таблицах приведены физические величины и их единицы, принятые в Международной системе единиц (СИ), основанной на Международной системе величин[3][4].
| Основные величины | Размерность | Символ | Описание | Единица СИ | Примечания |
|---|---|---|---|---|---|
| Длина | L | l | Протяжённость объекта в одном измерении. | метр (м) | |
| Масса | M | m | Величина, определяющая инерционные и гравитационные свойства тел. | килограмм (кг) | Экстенсивная величина |
| Время | T | t | Продолжительность события. | секунда (с) | |
| Сила тока | I | I | Протекающий в единицу времени заряд. | ампер (А) | |
| Температура | Θ | T | Средняя кинетическая энергия частиц объекта. | кельвин (К) | Интенсивная величина |
| Количество вещества | N | n | Количество однотипных структурных единиц, из которых состоит вещество. | моль (моль) | Экстенсивная величина |
| Сила света | J | Iv | Количество |
ru.wikipedia.org
| Производные величины | Описание | Единица СИ | Примечания | |
|---|---|---|---|---|
| Площадь | S | Протяженность объекта в двух измерениях. | м2 | |
| Объём | V | Протяжённость объекта в трёх измерениях. | м3 | экстенсивная величина |
| Скорость | v | Быстрота изменения координат тела. | м/с | вектор |
| Ускорение | a | Быстрота изменения скорости объекта. | м/с² | вектор |
| Импульс | p | кг·м/с | экстенсивная, сохраняющаяся величина | |
| Сила | F | Действующая на объект внешняя причина ускорения. | кг·м/с2 (ньютон, Н) | вектор |
| Механическая работа | A | Скалярное произведение силы и перемещения. | кг·м2/с2 (джоуль, Дж) | скаляр |
| Энергия | E | Способность тела или системы совершать работу. | кг·м2/с2 (джоуль, Дж) | экстенсивная, сохраняющаяся величина, скаляр |
| Мощность | P | Скорость изменения энергии. | кг·м2/с3 (ватт, Вт) | |
| Давление | p | Сила, приходящаяся на единицу площади. | кг/(м·с2) (паскаль, Па) | интенсивная величина |
| Плотность | ρ | Масса на единицу объёма. | кг/м3 | интенсивная величина |
| Поверхностная плотность | ρA | Масса на единицу площади. | кг/м2 | |
| Линейная плотность | ρl | Масса на единицу длины. | кг/м | |
| Количество теплоты | Q | Энергия, передаваемая от одного тела к другому немеханическим путём | кг·м2/с2 (джоуль, Дж) | скаляр |
| Электрический заряд | q | А·с (кулон, Кл) | экстенсивная, сохраняющаяся величина | |
| Напряжение | U | Изменение потенциальной энергии, приходящееся на единицу заряда. | м2·кг/(с3·А) (вольт, В) | скаляр |
| Электрическое сопротивление | R | сопротивление объекта прохождению электрического тока | м2·кг/(с3·А2) (ом, Ом) | скаляр |
| Магнитный поток | Φ | Величина, учитывающая интенсивность магнитного поля и занимаемую им область. | кг/(с2·А) (вебер, Вб) | |
| Частота | ν | Число повторений события за единицу времени. | с−1 (герц, Гц) | |
| Угол | α | Величина изменения направления. | радиан (рад) | |
| Угловая скорость | ω | Скорость изменения угла. | с−1 (радиан в секунду) | |
| Угловое ускорение | ε | Быстрота изменения угловой скорости | с−2 (радиан на секунду в квадрате) | |
| Момент инерции | I | Мера инертности объекта при вращении. | кг·м2 | тензорная величина |
| Момент импульса | L | Мера вращения объекта. | кг·м2/c | сохраняющаяся величина |
| Момент силы | M | Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы. | кг·м2/с2 | вектор |
| Телесный угол | Ω | стерадиан (ср) |
dic.academic.ru
Что такое величина?
Безусловно, каждый из нас на уровне самого общего представления прекрасно понимает, что такое величина. Величина — это длина, объем, масса или какая-нибудь другая количественная характеристика предмета или явления. Что значит величина? Если мы слышим, что выпавший град был величиною с грецкий орех, то это значит, что объем одной градины был примерно равен объему грецкого ореха.
Но если нас спросить, что такое скалярная величина, случайная величина, относительная величина, сможем ли мы так же легко ответить и на этот вопрос?
Давайте попробуем разобраться во всем по порядку.
Что такое физическая величина
Физическая величина — это свойство объекта, явления или процесса, которое может быть охарактеризовано количественно. Например, вода, налитая в графин, будет характеризоваться определенным объемом, массой, плотностью и так далее.
Физическая величина всегда имеет числовое значение с указанием единиц, в которых производилось ее измерение. Например, на железнодорожную станцию прибыли два контейнера. Масса одного из них составляет 1,5 тонны, а масса другого — 1 500 кг. Какой из них тяжелее? Как вы уже догадались, на самом деле масса обоих контейнеров одинакова. Просто с изменением единиц измерения изменилось числовое значение массы.
Случайная величина
Случайная величина — это термин математической теории вероятности. Случайная величина принимает в ходе какого-либо опыта конкретное значение. Но это значение не может быть точно известно заранее. Примеры случайных величин:
- количество попаданий из 5 выстрелов;
- количество точек на верхней грани игральной кости, которое выпадет после подбрасывания ее вверх;
- температура воздуха на завтра.
Скалярные и векторные величины
Скалярная величина — это величина, которая имеет только числовое значение. Примерны скалярных величин — время, масса, температура и т. д.
Однако некоторые физические величины (скорость, сила, ускорение), кроме числовой характеристики, имеют еще и направление. Такие величины называются векторными. Векторную величину, например, ту же скорость,
elhow.ru
Величина в математике — это что такое
Величина рассматривается как одна из основ математики, в частности одного из ее разделов — геометрии. Это понятие уходит глубоко в прошлое. Оно было описано в III веке до н. э. древнегреческим математиком Евклидом в его труде «Начала». Люди применяли величины на протяжении более двух тысяч лет, пока они не подверглись ряду обобщений.
Величина в математике — это очень важная тема для изучения в школе. Фактически из понимания детьми величины строится дальнейшее обучение от простого к все более сложному. Измеряя линейкой различные отрезки и площадь, взвешивая на весах массу, определяя скорость, исходя из расстояния и времени, ребенок постепенно учится постигать материальный мир и строит свою картину восприятия, а также определяет для себя роль математики в окружающем мире.
Понятие величины в математике
Величина в математике — это свойство объектов, которое поддается измерению путем сопоставления с единицей измерения, относящейся к величине этого рода. Выделяют длину, массу, объем, скорость, площадь и время. Говоря простым языком, это то, что можно измерить и выразить числом.

Данный раздел математики ученики проходят еще в начальной школе, и все измерения на этом этапе производятся натуральными числами величины. В математике младших классов такой числовой ряд представляет собой последовательность чисел от 1 и до бесконечности. В старших классах для расчетов величины используются также числа и с отрицательным значением.
Исторический очерк
В древних цивилизациях, в основном в связи с обширным развитием торговли, возникла потребность в измерениях товаров, определении расстояния, времени, расчете посевных площадей и прочего. Сначала люди измеряли предметы при помощи сравнения их с человеком или животным. Но все эти меры были довольно относительными, ведь у каждого свои пропорции тела, а величина в математике — это в первую очередь точность. Поэтому со временем возникла необходимость в создании единого эталона системы величин.
Так, во Франции в 1791 году во время Великой революции единицей измерения длины было принято считать метр, который составлял одну сорокамиллионную часть земного меридиана, пересекающего Париж. Кроме метра была установлена такая величина, как килограмм. Он был равен одному кубическому дециметру воды при температуре 4 °С. А также ар как мера площади, литр и грамм.
Так как в основе новых величин был метр, то и система измерения стала называться метрической. В Национальном архиве Франции до сих пор лежат платиновые эталоны метра в виде линейки со штрихами на концах и килограмма в виде цилиндрической гири.
Русская система измерения
С Древней Руси до принятия в Российской империи метрической системы мер принято было производить замеры с помощью длины локтя, ширины ладони, длины стопы — фут. Расстояние от кончика вытянутой вверх руки до пятки противоположной ноги называлось сажень, расстояние между вытянутыми руками — маховая сажень и т. д. Для измерения расстояния брали, например, слышимость петушиного крика или способность лошади без отдыха добраться из пункта А в пункт Б. Так люди измеряли дальность проложенного маршрута.
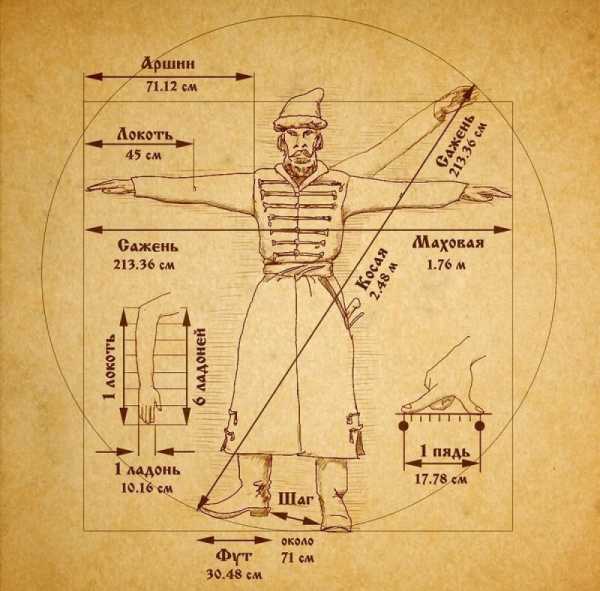
Даже сейчас в пословицах и поговорках мы можем встретить напоминания о существовании старинных величин. Об этом свидетельствую такие выражения, как «слышать за версту», «косая сажень в плечах», «мерить на свой аршин» и другие крылатые фразы.
В 1899 году, 4 июня была принята единая метрическая система, которая являлась необязательной. Обязательной она стала 14 сентября 1918 года уже при советской власти, практически сразу после Великой октябрьской революции.
Основные математические величины
Дети в школе, изучая величины в математике, к 4 классу уже имеют широкое представление о таких значениях, как длина, масса, объем, площадь, скорость и время.
- Под длиной предмета принято понимать характеристику линейного размера. Ее измеряют в миллиметрах, сантиметрах, дециметрах, метрах и километрах. Эту тему в школе дети проходят, начиная с первого класса.

- Масса предмета — еще одна физическая величина, измеряемая в основном граммами и килограммами. А также объем тел, который исчисляется литрами и миллилитрами. Однако не стоит вводить ребенка в заблуждение и считать массу и вес равными понятиями. Масса — это постоянная величина в математике, в то время как вес зависит от силы и скорости притяжения объекта к земле.
- Под площадью геометрической фигуры принято понимать занимаемое ею пространство на плоскости, которое исчисляется в мм2, см2, дм2, м2 и км2.
- Время — понятие довольно относительное и для человека связано с его ощущениями, его нельзя увидеть, но можно почувствовать в смене дня, ночи и времен года. Поэтому для знакомства детей с понятием времени используют точные приборы, такие как песочные часы и часы со стрелкой. Время исчисляется секундами, минутами, часами, днями, годами и так далее.

- На основании пройденной темы о времени и длине дети изучают понятие скорости. По сути, скорость — это отрезок пути, пройденный за некоторое время.
Бесконечная величина измерения в математике
В старших классах школьниками изучается тема бесконечно малых и больших чисел. Это те числовые значения, которые либо стремятся к нулю, либо к бесконечности. Масса дрейфующей льдины в океане, которая находится в процессе таяния, будет относиться к бесконечной малой величине. Ведь под воздействием беспрерывного тепла лед растает, и масса глыбы будет равна нулю. Противоположным процессом с точки зрения физики является расширение Вселенной. Она стремится к бесконечно большой величине, расширяя свои пределы.
Постоянная и переменная величина
В процессе развития математики величины были разделены на два класса: постоянные и переменные.
Постоянная величина, или так называемая научным языком константа, остается неизменной, то есть при любых условиях она сохраняет свое значение. Например, для расчета длины окружности используется постоянная величина «Пи» = 3,14. Константа Пифагора √2=1,41, используемая в математике, также неизменна. Постоянная величина является частным случаем и рассматривается как переменная величина с одинаковым значением.

Переменная величина в математике — это обратный процесс, который по различным причинам меняет свое числовое значение.
fb.ru
Основные физические величины [wiki.eduVdom.com]
Основные величины международной системы единиц (СИ)
| Величина | Обозначение | Единица | |
|---|---|---|---|
| Длина | $l$ | метр | м |
| Масса | $m$ | килограмм | кг |
| Время | $t$ | секунда | с |
| Сила тока | $I$ | ампер | А |
| Температура термодинамическая | $\Theta$ | кельвин | К |
| Сила света | $J$ | кандела | кд |
| Количество вещества | $N$ | моль | моль |
Другие физические величины
| Величина | Обозначение | Единица | |
|---|---|---|---|
| Перемещение | $s$ | м | |
| Пройденный путь | $l$ | м | |
| Скорость | $v$ | м/с | |
| Угловая скорость | $\omega$ | рад/с | |
| Частота вращения | $\nu$ | Гц | |
| Период вращения | $T$ | с | |
| Длина волны | $\lambda$ | м | |
| Ускорение | $a$ | м/с2 | |
| Угловое ускорение | $\alpha$ | рад/с2 | |
| Сила | $F$ | Н | |
| Работа | $A$ | Дж | |
| Энергия | $E$ | Дж | |
| Мощность | $N$ | Вт | |
| Момент силы | $M$ | Н•м | |
| Плотность | $\rho$ | кг/м3 | |
| Молярная масса | $M$ | кг/моль | |
| Давление | $p$ | Па | |
| Объём | $V$ | м3 | |
| Количество теплоты | $Q$ | Дж | |
| Внутренняя энергия | $U$ | Дж | |
| Теплоёмкость | $C$ | Дж/К | |
| Электрический заряд | $q$ | Кл | |
| Напряжённость электрического поля | $E$ | Н/Кл | |
| Потенциал электрического поля | $\varphi$ | В | |
| Электрическая ёмкость | $C$ | Ф | |
| Электрическое напряжение | $U$ | В | |
| Сопротивление | $R$ | Ом | |
| Мощность тока | $P$ | Вт | |
| Магнитная индукция | $B$ | Тл | |
| Магнитный поток | $\Phi$ | Вб | |
| Индуктивность | $L$ | Гн | |
Производные единицы системы СИ
| Обозначение | Название | расшифровка | |
|---|---|---|---|
| Гц | герц | с-1 | $$\frac{1}{с}$$ |
| Н | ньютон | кг•м•с-2 | $$\frac{кг\cdot м}{с^2}$$ |
| Дж | джоуль | кг•м2с-2 | $$\frac{кг\cdot м^2}{с^2}$$ |
| Вт | ватт | кг•м2•с-3 | $$\frac{кг\cdot м^2}{с^3}$$ |
| Па | паскаль | кг•м-1•с-2 | $$\frac{кг}{м\cdot с^2}\;=\;\frac{Н}{м^2}$$ |
| Кл | кулон | А•с | $$А\cdot с$$ |
| В | вольт | кг•м2•с-3•А-1 | $$\frac{кг\cdot м^2}{с^3\cdot А}$$ |
| Ф | фарад | кг-1•м-2•с4•А2 | $$\frac{с^4\cdot А^2}{кг\cdot м^2}$$ |
| Ом | ом | кг•м2•с-3•А-2 | $$\frac{кг\cdot м^2}{с^3\cdot А^2}$$ |
| Тл | тесла | кг•с-2•А-1 | $$\frac{кг}{с^2\cdot А}$$ |
| Вб | вебер | кг•м2•с-2•А-1 | $$\frac{кг\cdot м^2}{с^2\cdot А}$$ |
| Ги | генри | кг•м2•с-2•А-2 | $$\frac{кг\cdot м^2}{с^2\cdot А^2}$$ |
Рекомендуем
subjects/physics/основные_физические_величины.txt · Последние изменения: 2016/09/03 14:02 — ¶
wiki.eduvdom.com
Системы единиц физических величин: понятие
В мире существовало и существует до сих пор множество различных систем измерения величин. Они служат для того, чтобы люди могли обмениваться различной информацией, например, при совершении сделок, назначении препаратов или разработке руководств к использованию техники. Для того чтобы не возникало путаницы, была разработана Интернациональная система измерения физических величин.
Что такое система измерения физических величин?
Такое понятие, как система единиц физических величин, или просто система СИ, часто может встретиться не только на школьных уроках физики и химии, но и в повседневной жизни. В современном мире люди как никогда нуждаются в том, чтобы определенная информация – например, время, вес, объем – была выражена наиболее объективно и структурировано. Именно для этого и была создана единая система измерений – совокупность официально принятых единиц измерений, рекомендуемых для использования в быту и науке.
Какие системы измерения существовали до появления системы СИ
Конечно, потребность в мерах существовала у человека всегда, однако, как правило, эти меры не были официальными, определялись через подручные материалы. А значит, не имели эталона и могли различаться от случая к случаю.

Ярким примером может служить принятая на Руси система мер длины. Пядь, локоть, аршин, сажень – все эти единицы изначально были привязаны к частям тела – ладони, предплечью, расстоянию между раскинутыми руками. Конечно, в результате конечные измерения были неточными. Впоследствии государство прилагало усилия, чтобы стандартизировать эту систему измерения величин, но она все равно оставалась неидеальной.
В других странах существовали свои системы измерения физических величин. Например, в Европе была распространена английская система мер – футы, дюймы, мили и др.
Зачем нужна система СИ?
В XVIII-XIX веках процесс глобализации стал активным. Все больше стран начали устанавливать международные контакты. Кроме того, своего апогея достигла научно-техническая революция. Ученые по всему миру не могли эффективно обмениваться результатами своих научных изысканий из-за того, что они пользовались разными системами измерения физических величин. Во многом из-за таких нарушений связей внутри мирового научного сообщества многие физические и химические законы «открывались» несколько раз разными учеными, что сильно тормозило развитие науки и техники.
Таким образом, сформировалась потребность в единой системе измерения физических единиц, которая бы не только позволила ученым по всему миру сверять результаты своих трудов, но и оптимизировала процесс мировой торговли.
История возникновения Международной системы измерения
Для того чтобы структурировать физические величины и измерение физических величин, система единиц, единая для всего мирового сообщества, стала необходима. Однако создать такую систему, которая бы отвечала всем требованиям и была наиболее объективной, – это действительно трудная задача. Основой будущей системы СИ стала метрическая система, которая получила свое распространение в XVIII веке после Великой французской революции.
Точкой отсчета, с которой началось развитие и совершенствование Интернациональной системы измерения физических величин, можно считать 22 июня 1799 года. Именно в этот день были утверждены первые эталоны – метр и килограмм. Они были выполнены из платины.

Несмотря на это, официально Международная система единиц была принята только в 1960 году на 1-й генеральной конференции по мерам и весам. В нее были включены 6 основных единиц измерения физических величин: секунда (время), метр (длина), килограмм (масса), кельвин (термодинамическая температура), ампер (сила тока), кандела (сила света).
В 1964 году к ним была добавлена седьмая величина – моль, которой измеряется количество вещества в химии.
Кроме того, существуют также производные единицы, которые могут быть выражены через основные с помощью простейших алгебраических действий.
Основные единицы измерения в системе СИ
Так как основные единицы системы физических величин должны были быть максимально объективными и не зависеть от внешних условий, таких как давление, температура, расстояние от экватора и другие, то к формулированию их определений и эталонов нужно было отнестись фундаментально.
Рассмотрим каждую из основных единиц системы измерения физических величин подробнее.
- Секунда. Единица измерения времени. Это относительно легкая для выражения величина, так как она напрямую связана с периодом обращения Земли вокруг Солнца. Секунда – это 1/31536000 года. Существуют, однако, и более сложные способы замерить эталон секунды, связанные с периодами излучения атома цезия. Этот способ сводит погрешность к минимуму, чего требует современный уровень развития науки и технологий.
- Метр. Единица измерения длины и расстояний. В разное время метр пытались выразить как часть экватора или с помощью математического маятника, но все эти способы были недостаточно точными, так что конечное значение могло варьироваться в пределах миллиметров. Такая погрешность является критической, поэтому долгое время ученые искали более точные способы определения эталона метра. На данный момент за один метр принята длина пути, проходимого светом за (1/299 792 458) секунды.
- Килограмм. Единица измерения массы. На сегодняшний день килограмм является единственной величиной, определяемой через вещественный эталон, который хранится в штаб-квартире Международного бюро мер и весов. Со временем эталон немного изменяет свою массу из-за процессов коррозии, а также скопления пыли и других мелких частиц на его поверхности. Именно поэтому планируется и его величину в скором времени выразить через фундаментальные физические свойства.

- Кельвин. Единица измерения термодинамической температуры. Кельвин равен 1/273,16 части термодинамической температуры тройной точки воды. Это такая температура, при которой вода находится сразу в трех состояниях — жидком, твердом и газообразном. Градусы Цельсия переводятся в Кельвины по формуле: t К = t C° + 273
- Ампер. Единица измерения силы тока. Неизменяющийся ток, при прохождении которого по двум параллельным прямым проводникам с минимальной площадью сечения и бесконечной длиной, находящимся на расстоянии 1 метра друг от друга (на каждом участке этих проводников возникает сила, равная 2·10-7Н), равен 1 амперу.
- Кандела. Единица измерения силы света – светимости источника в определенном направлении. Специфическая величина, которая крайне редко используется на практике. Значение единицы выводится через частоту излучения и энергетическую силу света.
- Моль. Единица количества вещества. На данный момент моль – это единица, являющаяся разной для разных химических элементов. Она численно равна массе мельчайшей частицы этого вещества. В будущем планируется точно выразить один моль, используя число Авогадро. Для этого, однако, требуется уточнить значение самого числа Авогадро.
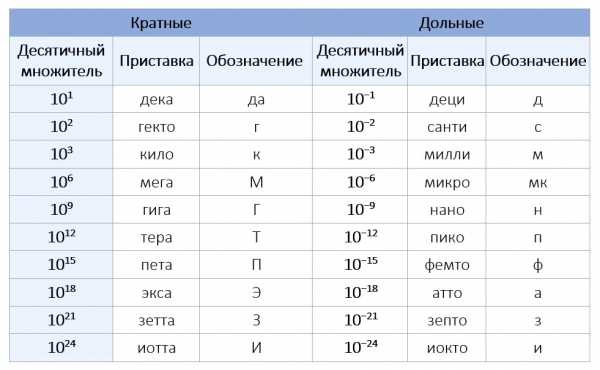
Приставки, принятые в системе СИ и что они означают
Для удобства использования основных единиц физических величин в системе СИ на практике был принят перечень универсальных приставок, с помощью которых образуются дробные и кратные единицы.
Производные единицы
Очевидно, что существует намного больше семи физических величин, а значит, нужны и единицы, в которых эти величины должны измеряться. Для каждой новой величины выводится новая единица, которая может быть выражена через основные с помощью простейших алгебраических действий, например деления или умножения.
Интересно, что, как правило, производные единицы называются в честь великих ученых или исторических лиц. К примеру, единица измерения работы – Джоуль или единица измерения индуктивности – Генри. Существует множество производных единиц – всего более двадцати.
Внесистемные единицы
Несмотря на широкое распространение и повсеместное применение единиц системы физических величин СИ, во многих отраслях все еще применяются на практике внесистемные единицы измерения. Например, в судоходстве – морская миля, в ювелирном деле – карат. В повседневной жизни нам известны такие внесистемные единицы, как сутки, процент, диоптрия, литр и многие другие.
Нужно помнить, что, несмотря на их привычность, при решении физических или химических задач внесистемные единицы нужно обязательно переводить в единицы измерения физических величин в системе СИ.
fb.ru
Единицы физических величин — Википедия
Материал из Википедии — свободной энциклопедии
Едини́ца физи́ческой величи́ны (едини́ца величи́ны, едини́ца, едини́ца измере́ния) (англ. Measurement unit, unit of measurement, unit; фр. Unité de mesure, unité) — физическая величина фиксированного размера, которой условно по соглашению присвоено числовое значение, равное 1{\displaystyle 1}. С единицей физической величины можно сравнить любую другую величину того же рода и выразить их отношение в виде числа. Применяется для количественного выражения однородных с ней физических величин. Единицы измерения имеют присвоенные им по соглашению наименования и обозначения[1][2][3].
Число с указанием единицы измерения называется именованным.
Различают основные и производные единицы. Основные единицы в данной системе единиц устанавливаются для тех физических величин, которые выбраны в качестве основных в соответствующей системе физических величин. Так, Международная система единиц (СИ) основана на Международной системе величин (англ. International System of Quantities, ISQ), в которой основными являются семь величин: длина, масса, время, электрический ток, термодинамическая температура, количество вещества и сила света. Соответственно, в СИ основными единицами являются единицы указанных величин.
Размеры основных единиц устанавливаются по соглашению в рамках соответствующей системы единиц и фиксируются либо с помощью эталонов (прототипов), либо путём фиксации численных значений фундаментальных физических постоянных.
Производные единицы определяются через основные путём использования тех связей между физическими величинами, которые установлены в системе физических величин.
Существует большое количество различных систем единиц, которые различаются как системами величин, на которых они основаны, так и выбором основных единиц.
ru.wikipedia.org
