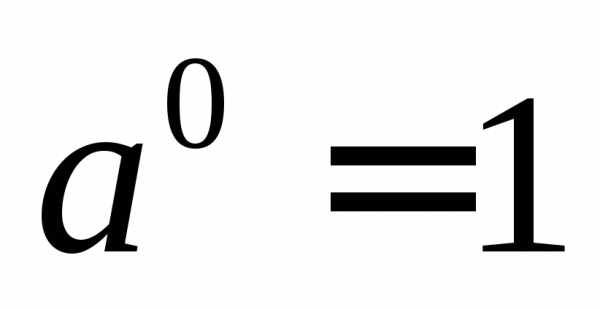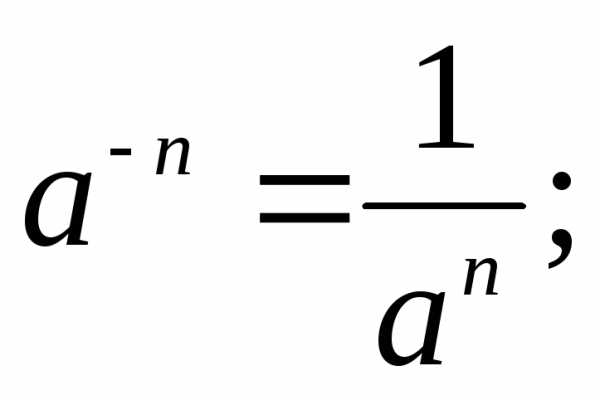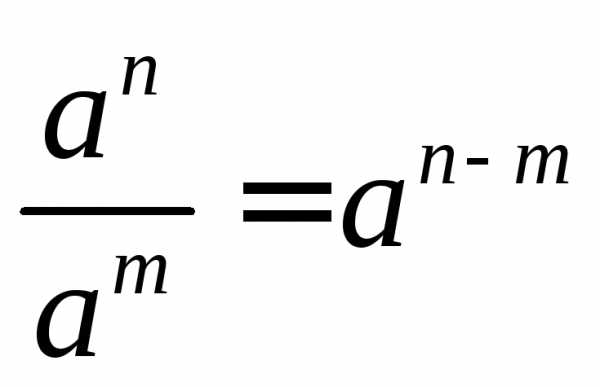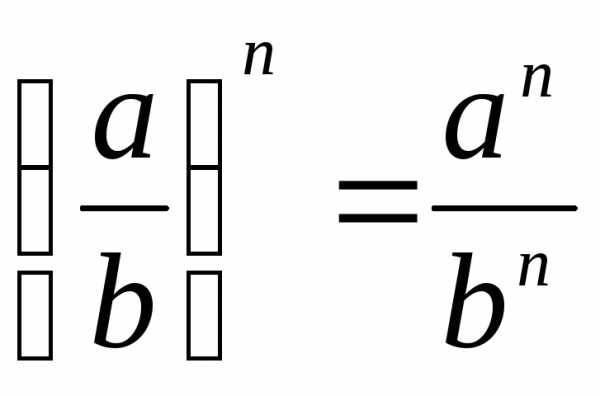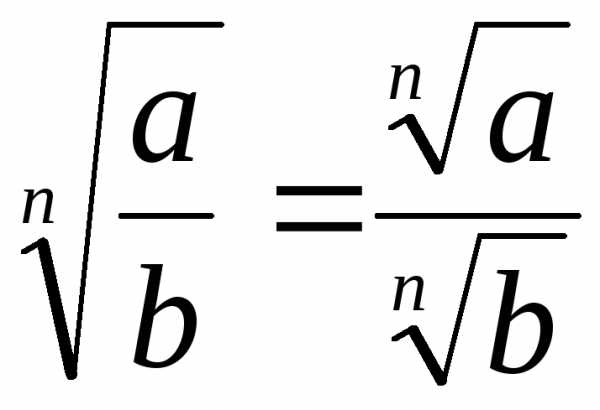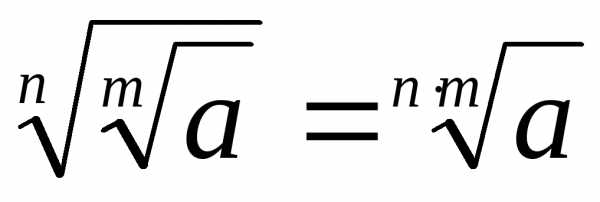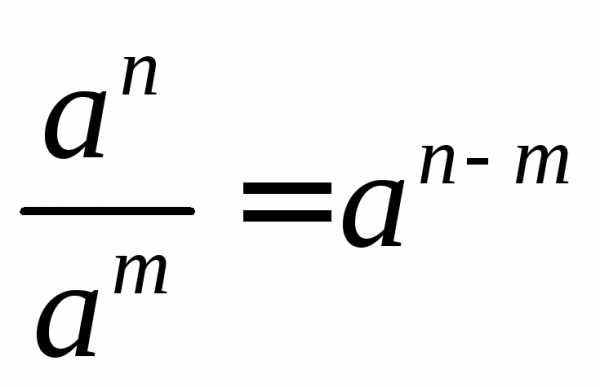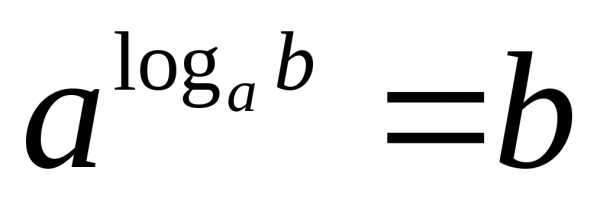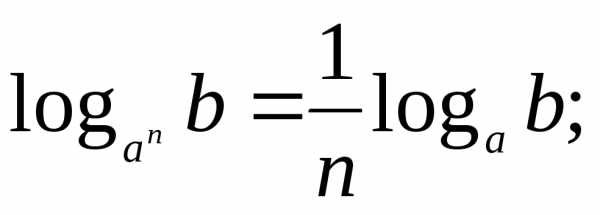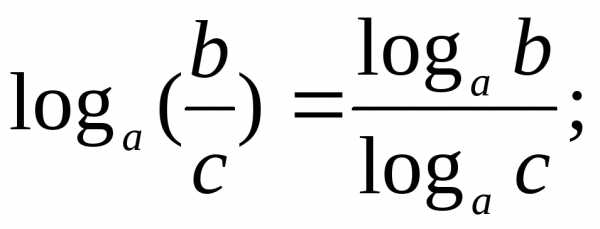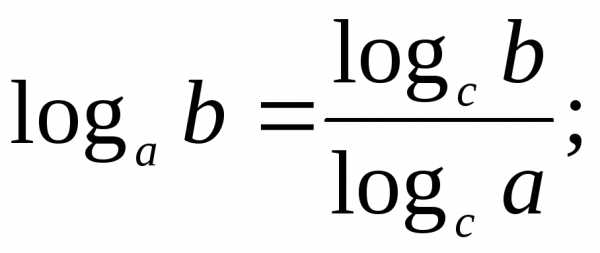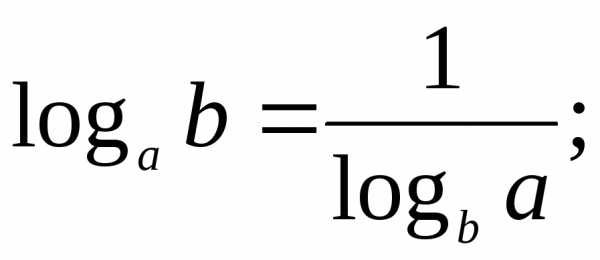В геометрической прогрессии сумма – Формула суммы первых n членов геометрической прогрессии — Геометрическая прогрессия — Арифметическая и геометрическая прогрессии — ПОУРОЧНЫЕ РАЗРАБОТКИ ПО АЛГЕБРЕ 9 КЛАСС — Поурочные планы — разработки уроков — авторские уроки — план-конспект урока
Геометрическая прогрессия | umath.ru
Определение геометрической прогрессии
Определение. Последовательность, каждый член которой, начиная со второго, получается из предыдущего умножением на одно и то же число , называется геометрической прогрессией. Число называется знаменателем прогрессии.То есть геометрическая прогрессия определяется рекуррентным соотношением
Итак, для n-го члена геометрической прогрессии справедлива формула
Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:
Доказательство. Из определения геометрической прогрессии
Следовательно,
откуда
Обратное утверждение тоже верно. Если для всех членов последовательности начиная со второго, выполняется равенство то эта последовательность — геометрическая прогрессия.
Сумма первых n членов геометрической прогрессии
Вычислим сумму первых n членов геометрической прогрессии знаменатель которой :
(1)
Умножим это равенство на :
или
(2)
Вычтем из равенства (2) равенство (1), и приведя подобные члены, получим Отсюда, так как имеем
или
(3)
Так как то формулу (3) можно переписать в виде
(4)
Пример 2. Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.
Мудрец попросил короля за первую клетку шахматной доски дать ему одно зерно пшеницы, за вторую — два, за третью — четыре, и так далее, удваивая количество зёрен за каждую клетку. Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?
Давайте подсчитаем величину награды, то есть найдём сумму геометрической прогрессии
По формуле (3) получаем
Именно столько зёрен должен был выдать король. Это примерно 1200 триллионов тонн или 1500 куб. км. пшеницы, что эквивалентно амбару размерами 10х10х15 км. Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.
Примерно такие расчёты и показали королю, когда тот поинтересовался, почему зерно всё ещё не выдано.
Наверное, вы спросите, чем же всё закончилось. Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.
Сумма бесконечно убывающей геометрической прогрессии
Рассмотрим геометрическую прогрессию Если её знаменатель то эта последовательность называется бесконечно убывающей геометрической прогрессией.
Сумма бесконечно убывающей геометрической прогресcии выражается формулой
(5)
umath.ru
Формула суммы n первых членов геометрической прогрессии + примеры
Геометрическая прогрессия — это числовая последовательность, первый член которой отличен от нуля, а каждый следующий член равен предыдущему члену, умноженному на одно и то же не равное нулю число.
Геометрическая прогрессия обозначается b1,b2,b3, …, bn, … .
Отношение любого члена геометрической погрешности к её предыдущему члену равно одному и тому же числу, то есть b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+1)/bn = … . Это следует непосредственно из определения арифметической прогрессии. Это число называют знаменателем геометрической прогрессии. Обычно знаменатель геометрической прогрессии обозначают буквой q.
Монотонная и постоянная последовательность
Одним из способов задания геометрической прогрессии является задание её первого члена b1 и знаменателя геометрической погрешности q. Например, b1=4, q=-2. Эти два условия задают геометрическую прогрессию 4, -8, 16, -32, … .
Если q>0 (q не равно 1), то прогрессия является монотонной последовательностью. Например, последовательность, 2, 4,8,16,32, … является монотонно возрастающей последовательностью (b1=2, q=2).
Если в геометрической погрешности знаменатель q=1, то все члены геометрической прогрессии будут равны между собой. В таких случаях говорят, что прогрессия является постоянной последовательностью.
Формула n-ого члена геометрической прогрессии
Для того, чтобы числовая последовательность (bn) являлась геометрической прогрессией необходимо, чтобы каждый её член, начиная со второго, являлся средним геометрическим соседних членов. То есть необходимо выполнение следующего уравнения
(b(n+1))^2 = bn * b(n+2),для любого n>0, где n принадлежит множеству натуральных чисел N.
Формула n-ого члена геометрической прогрессии имеет вид:
bn=b1*q^(n-1),
где n принадлежит множеству натуральных чисел N.
Формула суммы n первых членов геометрической прогрессии
Формула суммы n первых членов геометрической прогрессии имеет вид:
Sn = (bn*q – b1)/(q-1), где q не равно 1.
Рассмотрим простой пример:
В геометрической прогрессии b1=6, q=3, n=8 найти Sn.
Для нахождения S8 воспользуемся формулой суммы n первых членов геометрической прогрессии.
S8= (6*(3^8 -1))/(3-1) = 19 680.
Нужна помощь в учебе?
Предыдущая тема: Определение геометрической прогрессии: формула n-го члена прогрессии
Следующая тема:   Сумма бесконечной геометрической прогрессии при |q|
Все неприличные комментарии будут удаляться.
www.nado5.ru
Геометрическая прогрессия | Формулы с примерами
ОпределениеГеометрическая прогрессия — это числовая последовательность (bn), в
которой для любого натурального n, bn ? 0, q ? 0.
q — знаменатель геометрической прогрессии (заданное число).
Пример| Дано | Геометрическая прогрессия | |
| 1. | b1 = 0,5; q = 2 | 0,5; 1; 2; 4; 8; 16; … |
| 2. | b1 = 7; q = -1 | 7; -7; 7; -7; 7; -7; … |
| 3. | b1 = 100; q = 0,2 | 100; 20; 4; 0,8; 0,16; 0,032; … |
Формула общего (n-го) члена геометрической прогрессии: Формулы
Формулы суммы Sn n первых членов геометрической прогрессии:
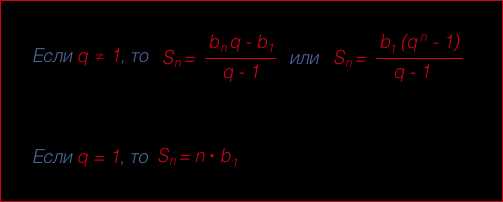
Где: S1 = b1. Sn = b1 + b2 + … + bn.
Пример решенияb1 = 12, b2 = -6. Найти b7 и сумму S8.
Знаменатель q = b2b1 = — 12.
Тогда b7 = b1 • q6 = 12 • (- 12)6 = 3 16 • S8 = b1(q8 — 1)q — 1 = 7 3132.
Характеристическое свойство геометрической прогрессии
Правилоformula-xyz.ru
Геометрическая прогрессия. Формулы п-го члена и суммы п первых членов геометрической прогрессии. Характеристическое свойство геометрической прогрессии.
О.Геометрической прогрессией называется последовательность, в которой первый член отличен от нуля, а каждый из последующих равен предыдущему, умноженному на некоторое постоянное для данной последовательности число, отличное от нуля.
Геометрическая
прогрессия задаётся своим первым членом
и знаменателем. Из определения
геометрической прогрессии следует,
что отношение любого её члена, начиная
со второго, к предыдущему члену равно q, т.е. при любом
натуральномnверно
равенство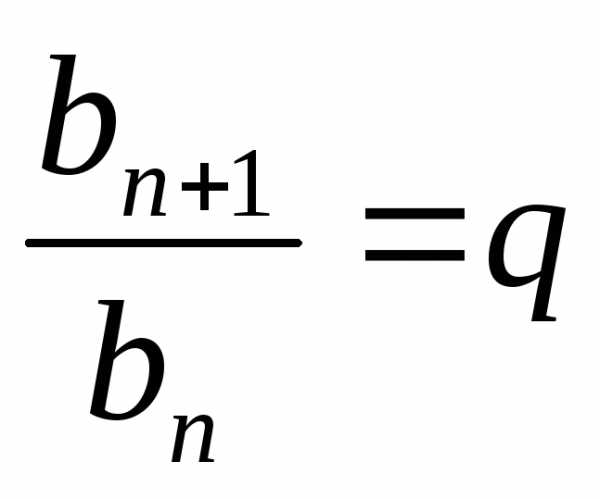 .
.
Формула n-го члена геометрической прогрессии.
Любой член
геометрической прогрессии можно
вычислить по формуле 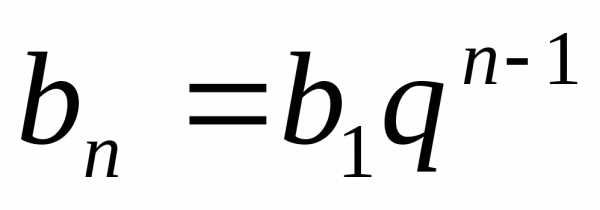 ,где
,где —
член прогрессии с номеромn,
—
член прогрессии с номеромn,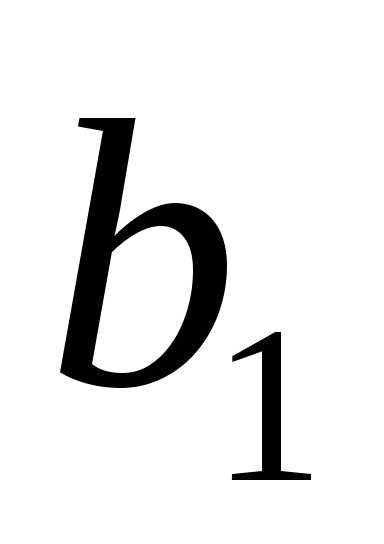 —
первый член иq– её
знаменатель.
—
первый член иq– её
знаменатель.
Возьмём произвольное натуральное n.Из определения геометрической прогрессии следует.
Эта цепочка состоит из nравенств, поэтому для любого конечногоnона может быть выписана. Следовательно, любой член геометрической прогрессии можно вычислить, зная его номер, первый член прогрессии и её знаменатель.
Характеристическое свойство геометрической прогрессии с положительными членами.
Если последовательность положительных чисел является геометрической прогрессией, то все её члены, начиная со второго, являются средним геометрическим предшествующего и последующего членов.
Доказательство.
Из определения
геометрической прогрессии следует,
что 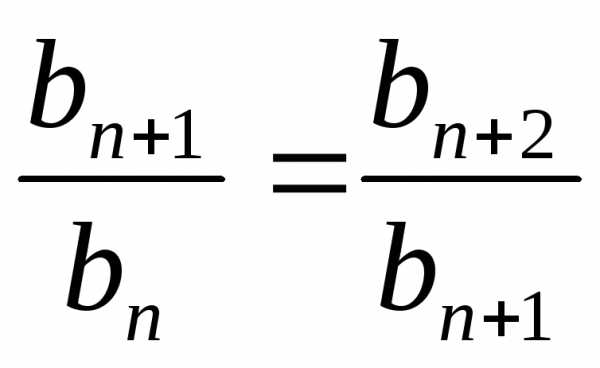 .
.
Выразив из этого
равенства 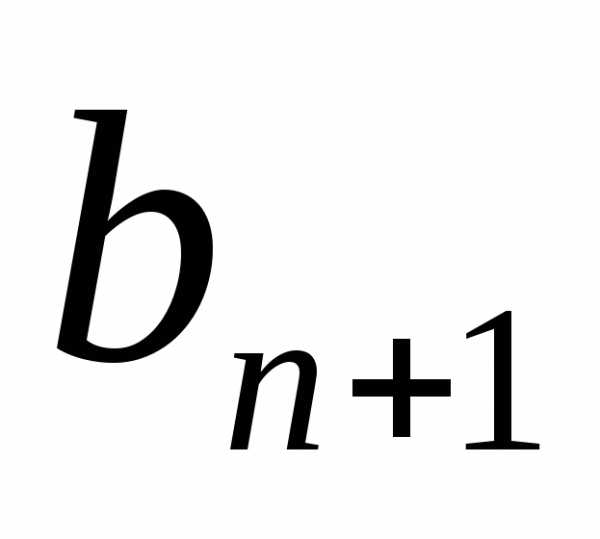
Так как все члены прогрессии положительны, то последнее равенство равносильно следующему .
Теорема. (формула суммы n первых членов геометрической прогрессии).
Сумма n первых членов геометрической
прогрессии равна 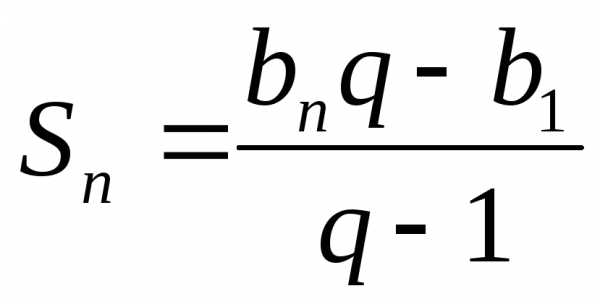 ,при
,при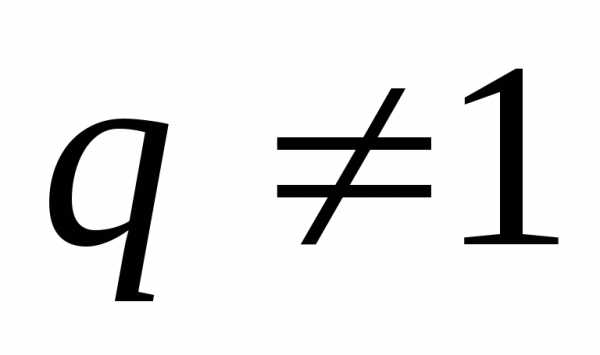 .
.
Доказательство.
Сумма nпервых членов геометрической прогрессии равна
. 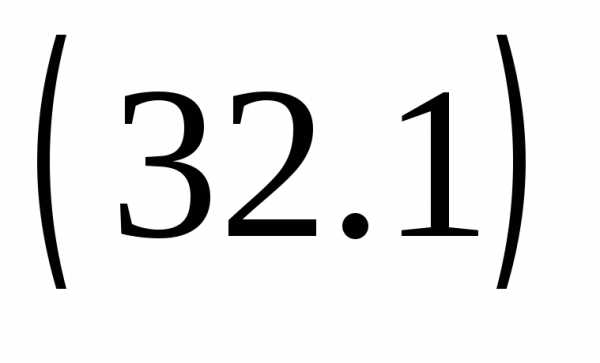
Домножим обе части этого равенства на знаменатель геометрической прогрессии .
Следовательно,
.
Вычтем полученное равенство из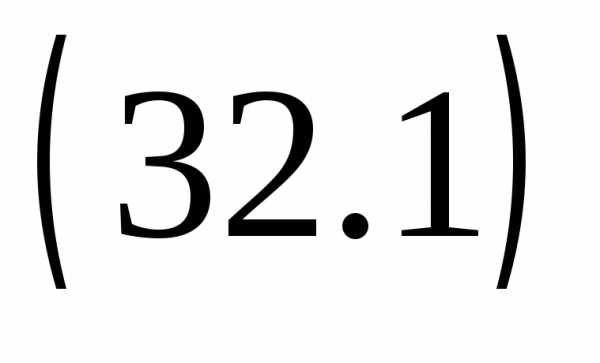 .
Получим:
.
Получим: .
.
Отсюда следует,
что
.
При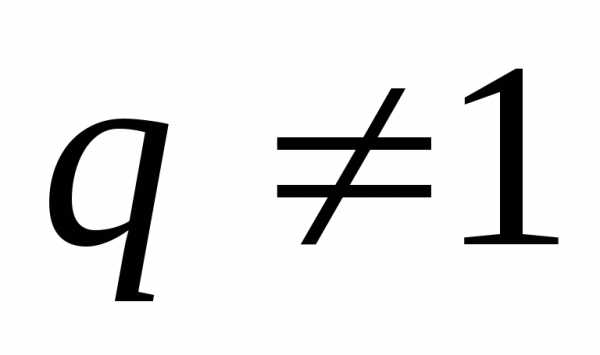 это равенство равносильно доказываемому.
Теорема доказана.
это равенство равносильно доказываемому.
Теорема доказана.
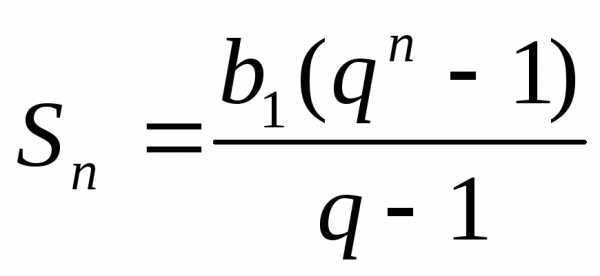 ,при
,при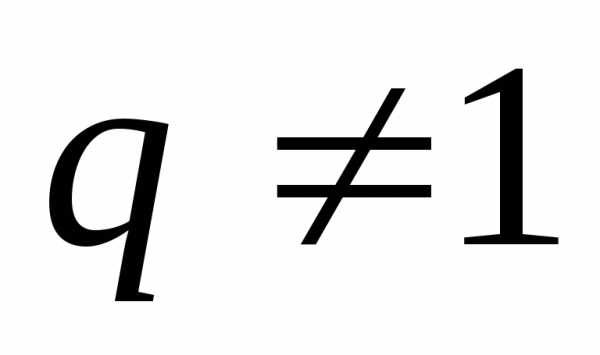 .
.Доказательство.
Выразим 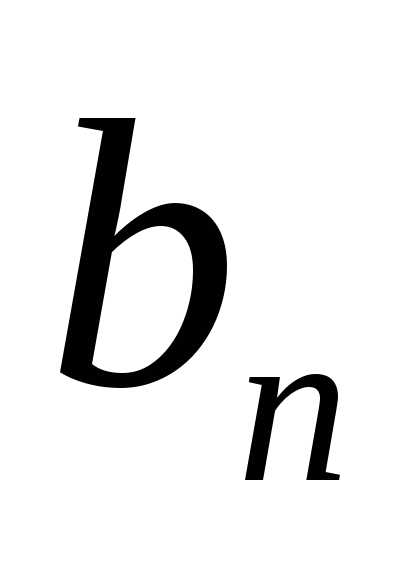 по формулеn-го члена
геометрической прогрессии и подставим
в формулу (1).
по формулеn-го члена
геометрической прогрессии и подставим
в формулу (1).
Геометрическая
прогрессия называется бесконечно
убывающей, если её знаменательq по абсолютной величине меньше
единицы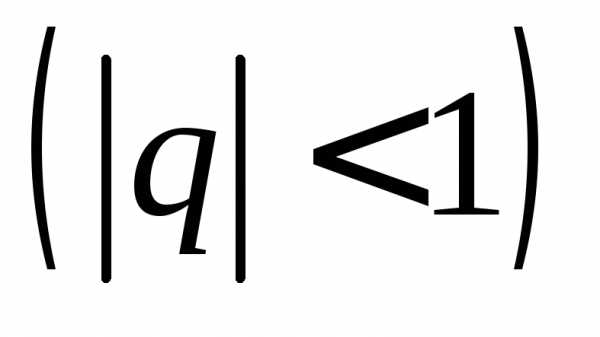
О.Суммой бесконечно убывающей геометрической прогрессииназывается число, к которому неограниченно приближается суммаnпервых членов бесконечно убывающей геометрической прогрессии при неограниченном увеличенииn.
Сумма
бесконечно убывающей геометрической
прогрессии равна 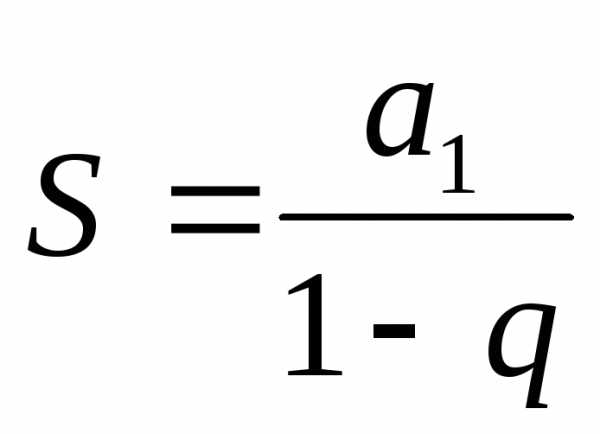 .
.
Приложение
Тригонометрическая окружность

Сборник формул
ТРИГОНОМЕТРИЯ Основные тригонометрические тождества Знаки тригонометрических функций по четвертям   Тригонометрические функции отрицательного аргумента Выражение одной функции через другую Обратные функции отрицательного аргумента Решение простейших тригонометрических уравнений Функция алгебраической суммы двух аргументов Преобразование Преобразование суммы функций в произведение произведения функций в сумму Функции половинного аргумента | АЛГЕБРА Корни квадратных уравнений Теорема Виета Разложение квадратного трехчлена на множители Логарифмы Степень двучлена Извлечение квадратного корня из квадрата. Определение модуля числа. |
studfiles.net
Геометрическая прогрессия на примерах
Геометрическая прогрессия не менее важная в математике по сравнению с арифметической. Геометрической прогрессией называют такую последовательность чисел b1, b2,…, b[n] каждый следующий член которой, получается умножением предыдущего на постоянное число. Это число, которое также характеризует скорость роста или убывания прогрессии называют знаменателем геометрической прогрессии и обозначают
Для полного задания геометрической прогрессии кроме знаменателя необходимо знать или определить первый ее член. Для положительного значения знаменателя прогрессия является монотонной последовательностью, причем если это последовательность чисел является монотонно убывающей и при монотонно возрастающей. Случай, когда знаменатель равен единице на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса
Общий член геометрической прогрессии вычисляют по формуле
Сумма n первых членов геометрической прогрессии определяют по формуле
Рассмотрим решения классических задач на геометрическую прогрессию. Начнем для понимания с простейших.
Пример 1. Первый член геометрической прогрессии равен 27, а ее знаменатель равен 1/3. Найти шесть первых членов геометрической прогрессии.
Решение: Запишем условие задачи в виде
Для вычислений используем формулу n-го члена геометрической прогрессии
На ее основе находим неизвестные члены прогрессии
Как можно убедиться, вычисления членов геометрической прогрессии несложные. Сама прогрессия будет выглядеть следующим образом
Пример 2. Даны три первых члена геометрической прогрессии : 6; -12; 24. Найти знаменатель и седьмой ее член.
Решение: Вычисляем знаменатель геомитрической прогрессии исходя из его определения
Получили знакопеременную геометрическую прогрессию знаменатель которой равен -2. Седьмой член вычисляем по формуле
На этом задача решена.
Пример 3. Геометрическая прогрессия задана двумя ее членами . Найти десятый член прогрессии.
Решение:
Запишем заданные значения через формулы
По правилам нужно было бы найти знаменатель, а затем искать нужное значение, но для десятого члена имеем
Такую же формулу можно получить на основе нехитрых манипуляций с входными данными. Разделим шестой член ряда на другой, в результате получим
Если полученное значение умножить на шестой член, получим десятый
Таким образом, для подобных задач с помощью несложных преобразований в быстрый способ можно отыскать правильное решение.
Пример 4. Геометрическая прогрессия задано рекуррентными формулами
Найти знаменатель геометрической прогрессии и сумму первых шести членов.
Решение:
Запишем заданные данные в виде системы уравнений
Выразим знаменатель разделив второе уравнение на первое
Найдем первый член прогрессии из первого уравнения
Вычислим следующие пять членов для нахождения суммы геометрической прогрессии
Поскольку найти сумму в данном случае не составляет большого труда, то обходя простые выкладки сводим все слагаемые под общий знаменатель
В общем случае, при нахождении суммы знакопеременных рядов следует выделять их положительную часть и отрицательную и найти отдельно их суммы по приведенным выше формулам. Наконец найденные значения добавить.
Примеры на геометрическую прогрессию не так сложны если знать несколько базовых формул. Все остальное сводится к простым математическим манипуляциям. Практикуйте с примерами самостоятельно и подобные задания будут для Вас несложными.
Похожие материалы:
yukhym.com
Сумма бесконечной геометрической прогрессии при |q|
 > Сумма бесконечной геометрической прогрессии при |q|
Геометрическая прогрессия — это числовая последовательность, первый член которой отличен от нуля, а каждый следующий член, равен предыдущему члену, умноженному на одно и то же не равное нулю число.
Понятие геометрической прогрессии
Геометрическая прогрессия обозначается b1,b2,b3, …, bn, … .
Отношение любого члена геометрической погрешности к её предыдущему члену равно одному и тому же числу, то есть b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+1)/bn = … . Это следует непосредственно из определения арифметической прогрессии. Это число называют знаменателем геометрической прогрессии. Обычно знаменатель геометрической прогрессии обозначают буквой q.
Сумма бесконечной геометрической прогрессии при |q|<1
Одним из способов задания геометрической прогрессии является задание её первого члена b1 и знаменателя геометрической погрешности q. Например, b1=4, q=-2. Эти два условия задают геометрическую прогрессию 4, -8, 16, -32, … .
Если q>0 (q не равно 1), то прогрессия является монотонной последовательностью. Например, последовательность, 2, 4,8,16,32, … является монотонно возрастающей последовательностью (b1=2, q=2).
Если в геометрической погрешности знаменатель q=1, то все члены геометрической прогрессии будут равны между собой. В таких случаях говорят, что прогрессия является постоянной последовательностью.
Для того, чтобы числовая последовательность (bn) являлась геометрической прогрессией необходимо, чтобы каждый её член, начиная со второго, являлся средним геометрическим соседних членов. То есть необходимо выполнение следующего уравнения
(b(n+1))^2 = bn * b(n+2),для любого n>0, где n принадлежит множеству натуральных чисел N.
Теперь положим (Xn) – геометрическая прогрессия. Знаменатель геометрической прогрессии q, причем |q|∞).
Если теперь за S обозначить сумму бесконечно геометрической прогрессии, тогда будет иметь место следующая формула:
S=x1/(1-q).
Рассмотрим простой пример:
Найти сумму бесконечной геометрической прогрессии 2, -2/3, 2/9, — 2/27, … .
Для нахождения S воспользуемся формулой суммы бесконечно арифметической прогрессии. |-1/3| < 1. x1 = 2. S=2/(1-(-1/3)) = 3/2.
Нужна помощь в учебе?
Предыдущая тема: Формула суммы n первых членов геометрической прогрессии + примеры
Следующая тема:   Четные и нечетные функции: графики и свойства
Все неприличные комментарии будут удаляться.
www.nado5.ru
Геометрическая прогрессия, сумма геометрической прогрессии
Определение: Геометрическая прогрессия — числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему члену, умноженному на одно и то же число, не равное нулю.
Определения: Знаменатель геометрической прогрессии — постоянное для последовательности число , которое умножают на каждый член.
— геометрическая прогрессия,
— геометрическая прогрессия,
— геометрическая прогрессия
— знаменатель геометрической прогрессии
Характеристические свойства геометрической прогрессии
Свойством: Квадрат любого члена геометрической прогрессии (начиная со второго члена) равен произведению предыдущего и последующего членов и наоборот, если выполняется указанное властивіть, то последовательность будет геометрической прогрессией.
Формулы n-ого члена геометрической прогрессии
Формулы суммы n первых членов геометрической прогрессии
План решению задач на геометрические прогрессии
- Все, о чем говорится в речи задачи (члены прогрессе, их суммы и т. д), выражаем через первый член и разность прогрессии.
- Составляем уравнение (или систему уравнений) по условию задачи. В случае, когда в задачи происходит переход от геометрической прогрессии к арифметической прогрессии и наоборот, для составления уравнений обычно используют характеристические свойства прогрессий.
Бесконечно убывающая геометрическая прогрессия
Определение: Бесконечно убывающая геометрическая прогрессия — это бесконечная геометрическая прогрессия, знаменатель которой по модулю меньше единицы .
Пример
Определение: Сумма бесконечно убывающей геометрической прогрессии — предел, к которому стремится сумма ее первых членов, при бесконечном росте .
.
Формула для вычисления суммы бесконечно убывающей геометрической прогрессии
Пример нахождения суммы бесконечно убывающей геометрической прогрессии
Преобразование периодической десятичной дроби в обычный
Пример
(как сумма бесконечно убывающей геометрической прогрессии с первым членом и знаменателем )
cubens.com

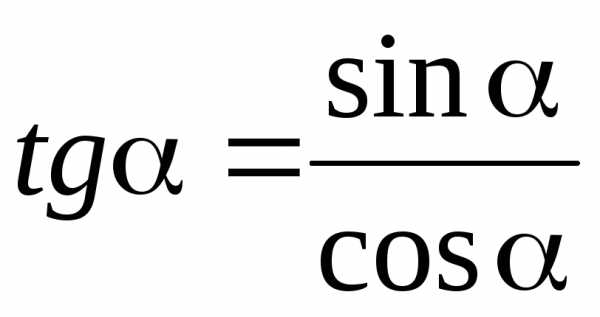
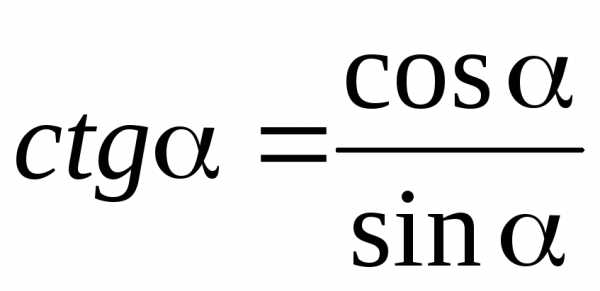
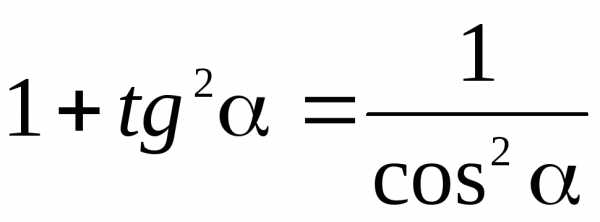
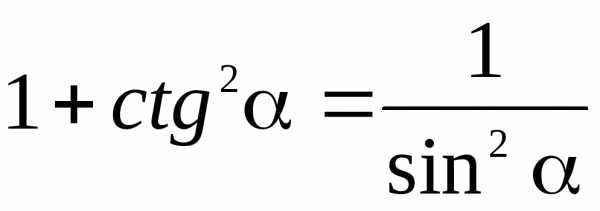




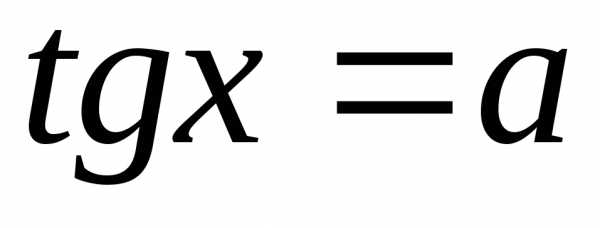
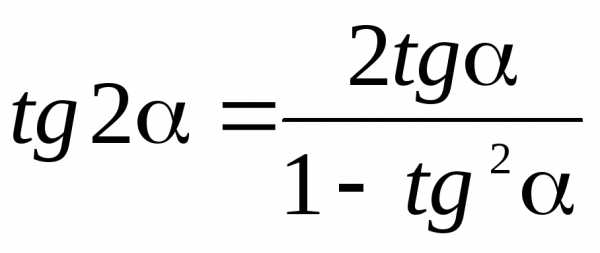 Функции
двойного аргумента
Функции
двойного аргумента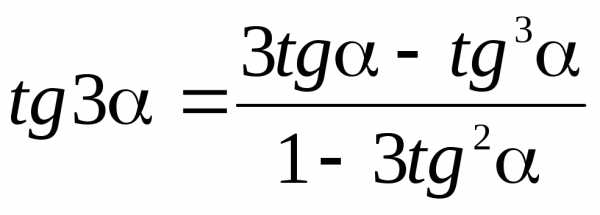 Функции
тройного аргумента
Функции
тройного аргумента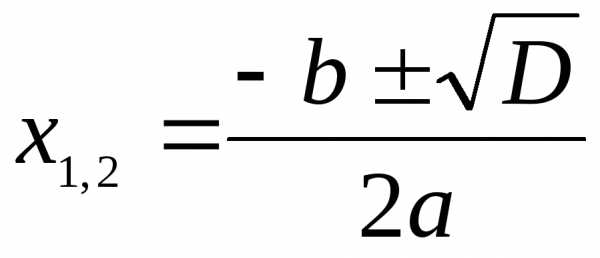
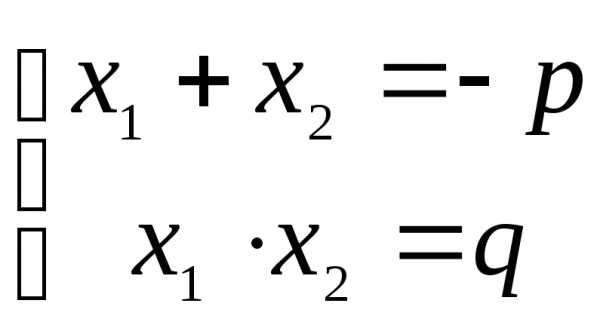
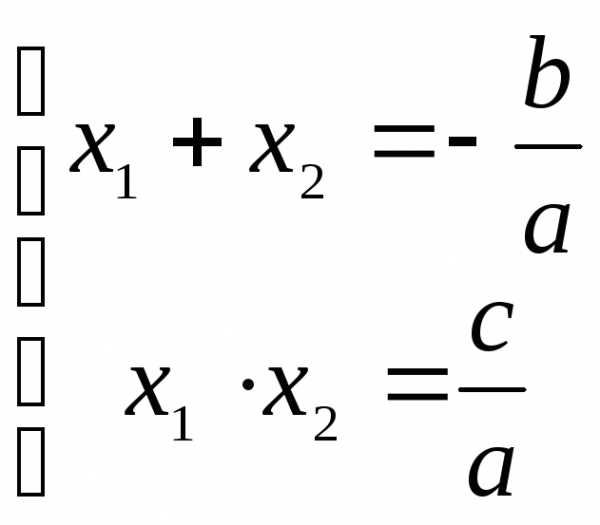
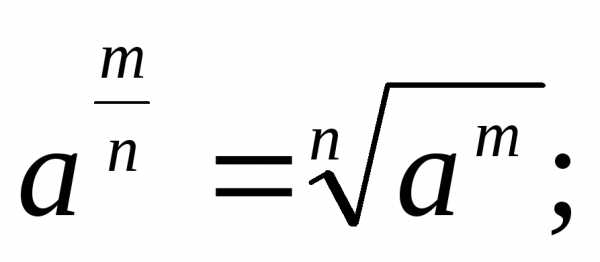 Степени
и корни
Степени
и корни