Уравнения со степенями примеры решения – Обобщающий урок по теме «Показательные уравнения и методы их решения с применением компьютерных технологий», 11-й класс

Примечание:

Если одна часть уравнения содержит убывающую функцию f(x) , а другая часть -возрастающую функцию g(x), и уравнение имеет корень х=, то он -единственный.

В примере 2. : f(x) = убывающая на R функция, а g(x = - возрастающая на R функция, х=1- корень уравнения и он единственный.

Ответ: 1.

Приложение к статье «Методы решения показательных уравнений»

xn--i1abbnckbmcl9fb.xn--p1ai

Показательные уравнения, формулы и примеры

Простейшие показательные уравнения

В зависимости от знака такое уравнение имеет различное количество корней:

1. если , то уравнение (1) решений не имеет, то есть

      

2. если , то

      

1. Если .
2. Если .

Уравнения такого типа равносильны уравнению

1. Если , то обе части такого уравнения равны для любых .
2. Если , то уравнение эквивалентно уравнению .
3. В случае, если , то уравнение эквивалентно системе

Решение показательных уравнений сведением к общему основанию

Если левая и правая части заданного показательного уравнения содержат только произведения, частные, корни или степени, то рациональнее при помощи основных формул для степеней привести обе части равенства к одному основанию, то есть к уравнению вида (2).

Решение показательных уравнений вынесением общего множителя

Если показательное уравнение содержит выражение вида , причем показатели степени отличаются только свободным коэффициентом, то для решения необходимо вынести за скобки наименьшую степень .

Приведение показательных уравнений к квадратным

К показательным уравнениям, которые можно привести к квадратным, относятся следующие уравнения.

где — некоторые числа, .

В этом случае выполняется замена

где — некоторые ненулевые числа, причем , — произвольное действительное число. Для сведения к квадратному обе части уравнения необходимо умножить на :

Далее заменой получаем квадратное уравнение

Однородные показательные уравнения

Делением обеих его частей на (или ), сводим уравнение к показательному вида :

Схема решения таких уравнений следующая:

1) Делим обе части уравнения или на , или на , в результате получаем:

или

2) заменой последнее уравнение сводится к квадратному:

ru.solverbook.com

Показательные уравнения. Решения

Решение множества показательных уравнений не обходится без замен, квадратных уравнений и сложных преобразований. Приведенные ниже примеры помогут Вам в этом быстро разобраться и научат решать самые сложные из них. Также Вы сможете выучить некоторые свойства логарифмов без которых показательные уравнения в простой способ не решить. Начнем с самых азов — теоретического материала об уравнениях.
Показательными называют уравнения в которых неизвестная величина содержится в показателе степени, при этом основа степени не содержит неизвестной величины. Самое простое показательных уравнения a^x=b решают логарифмированием x=log[a](b).

При решении показательных уравнений используют свойство показателей: если в уравнение степени с одной и той же основой то равные показатели степени или основание равно единице.
Из равенства следует или .

Некоторые уравнения требуют замены переменной и сводится к решению степенного уравнения. Например уравнения
легко сводится к квадратному если сделать замену
При этом исходное уравнение примет вид
После его решения нужно вернуться к замене и решить полученное уравнение.
Если показательной уравнение содержит две различные показательные функции ( основы не сводятся к одной) , то выполняют деления уравнения на одну из основ в соответствующей степени и переход до показательного уравнения которое содержит функцию с дробной основой.
Находя решения показательных уравнений следует помнить что показательная функция принимает только положительные значения. Отрицательные значения или нули замененной переменной не принимаются к рассмотрению.

На этом необходимый теоретический материал заканчивается и переходим к рассмотрению распространенных примеров.

Пример 1.Решить показательное уравнение

Решение. Перепишем уравнение к следующему виду

Второе слагаемое распишем как произведение

и сделаем замену в уравнении

Исходное уравнение преобразуем к следующему

Областью допустимых значений будет действительная ось за исключением точки y=0.
Умножим его на y и переносим все в левую сторону

Получили квадратное уравнение корни которого находим по теореме Виета. Нетрудно убедиться что они принимают значения

Возвращаемся к замене и находим решения


Выполняем проверку


Итак оба решения удовлетворяют уравнению.

Пример 2. Решить показательное уравнение

Решение. Используя одну из свойств логарифма записываем правую сторону уравнения в виде

Приравнивая показатели находим

Пример 3. Решить уравнение

Решение. Такого сорта примеры решают логарифмированием обеих сторон что приводит к сведению показательного уравнения к простому виду.


Полученное уравнение относительно переменной решаем через дискриминант

Корни уравнения приобретут значения



Другого метода позволяющего аналитически получить решения Вы не найдете ни в интернете, ни на форумах.

Пример 4. Решить уравнение

Решение. Выполним некоторые преобразования с показателями чтобы упростить уравнение

Эквивалентные значения подставим в уравнение, в результате получим

Выполняем замену

Уравнение превратится к квадратному


Вычисляем дискриминант

Найденное значение подставляем в формулу корней


Возвращаемся к замене и находим


Задача решена.

Пример 5.Решить уравнение

Решение. Такого типа уравнения решают с постоянной основой . За основу классически берут 10 , однако , если взять другую (для данного примера 5 или 9 ) то решение примет компактный вид
Рассмотрим оба метода.
1. Прологарифмируем обе части равенства

Раскрываем скобки и группируем слагаемые при неизвестных


Такой интересный результат.

2. Прологарифмируем обе части равенства по основанию 9

Группируя слагаемые содержащие переменную получим


Оба метода достаточно быстрые и эффективные, для себя выбирайте который Вам больше подходит.

Пример 6.Решить уравнение

Решение.Такого рода задачи решают по следующей схеме. Показательное уравнения превращают к виду

Все слагаемые разделяем на величину чтобы свести к дробному виду

После этого выполняем замену

Уравнение переписываем в виде

Умножаем на переменную и решаем квадратное уравнение


Дискриминант принимает нулевое значение, при етом корни уравнения совпадают

Возвращаемся к замене и решаем


Итак x=2 — единственное решение.
Используйте приведенную схему в подобных задач и гарантированно получите верный результат.

Пример 7. Решить уравнение

Решение. На первый взгляд уравнения достаточно сложное и неизвестно как его упрощать, однако схема решения данного примера и подобных довольно проста и интересна. Выполним над уравнением преобразования

Нужно это уравнение преобразовать к квадратному



Выполним замену

и перепишем уравнение в виде следуещого

Вычисляем дискриминант

и корни уравнения

Возвращаемся к совершенной замене

Такое уравнение сводим к квадратному, выполнив замену

В результате получим

Решаем через дискриминант


Возвращаемся к замене и определяем переменную x

Второе значение рассматривать не будем, поскольку оно отрицательное, а показательная функция всюду положительная.
Решаем вторую половину задачи

Используя предыдущую замену получим

Дискриминант примет значение

Находим корни уравнения

Первый корень имеет место бить, второй — отрицательный и не подходит.

Получили два решения показательного уравнения

Хорошо разберитесь с приведенными методами решения показательных уравнений, возможно некоторые из них пригодятся при прохождении ВНО, экзамене или контрольной работе. Будьте внимательны при упрощении, первое время используйте подстановку для проверки результатов.

Похожие материалы:

yukhym.com

Методы решения уравнений высших степеней

Методы решения уравнений высших степеней.

I) Решение уравнений с помощью деления в столбик.

Очевидно 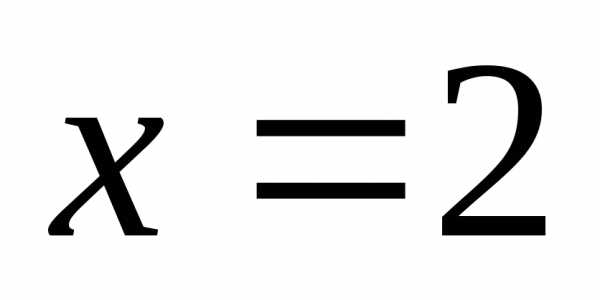— корень уравнения

Очевидно 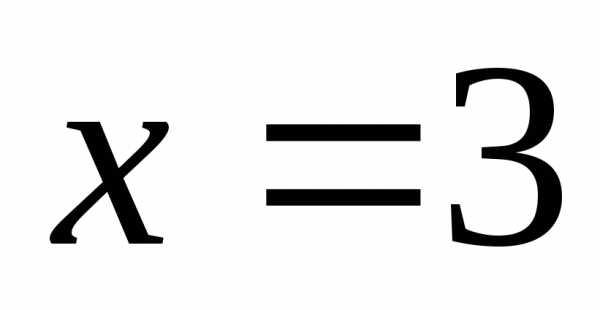— корень уравнения

Ответ: -5;2;3;4

II) Возвратные уравнения и к ним сводящиеся.

Уравнение называется возвратным, если в нем коэффициенты равноудаленные от концов совпадают, т.е. ,,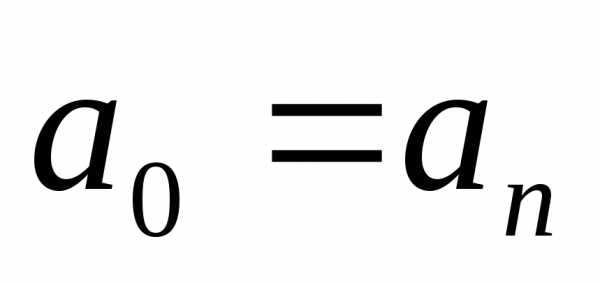

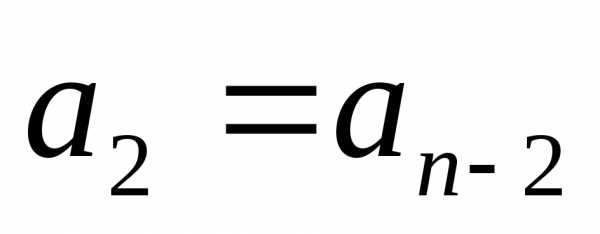
1) Возвратные уравнения четной степени.

т.к. 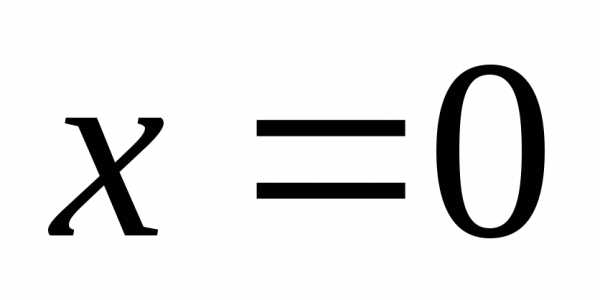— не является корнем уравнения, то разделим обе части уравнения на.

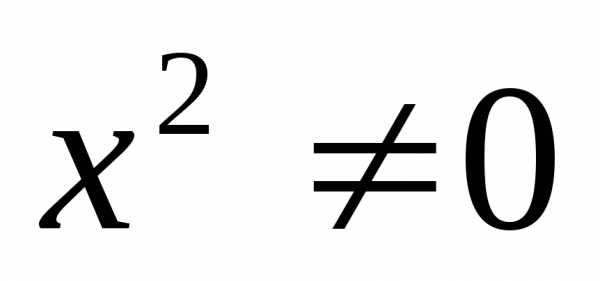Введем замену.

Пусть ,, получим

;

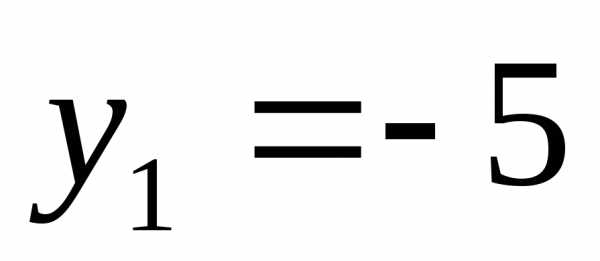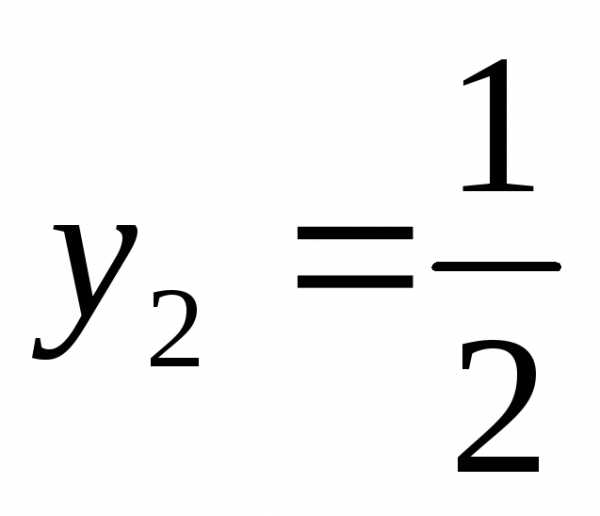
Вернемся к замене.

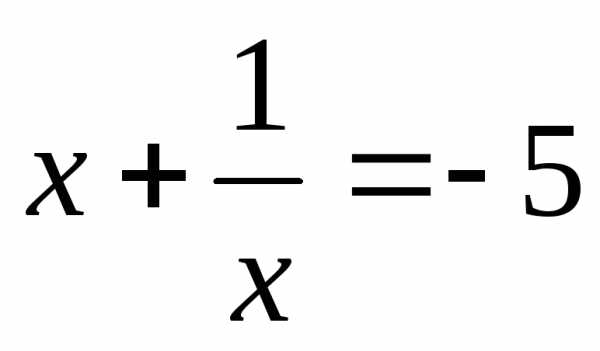или

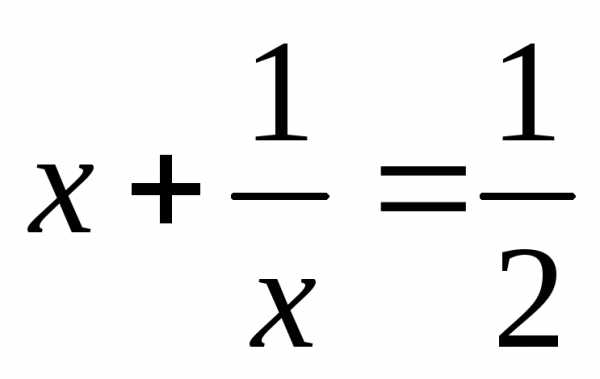
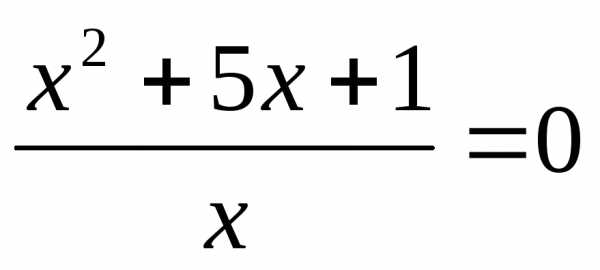
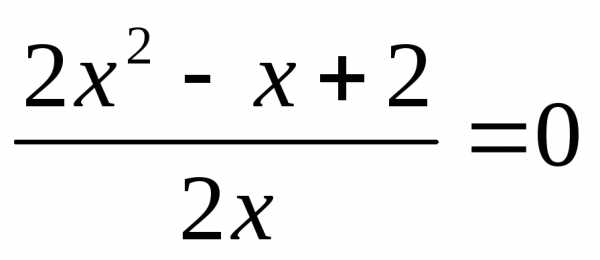
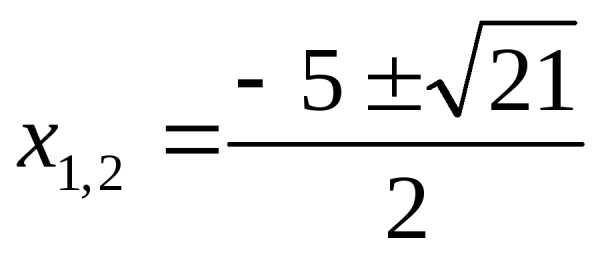корней нет

Ответ: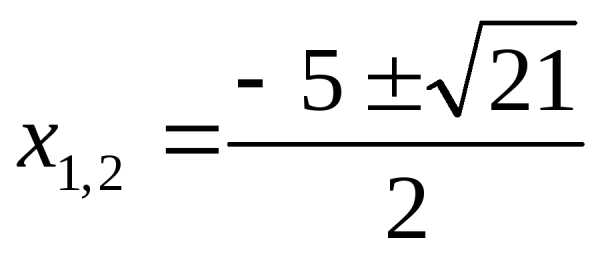

2) Возвратные уравнения нечетной степени.

Любое возвратное уравнение нечетной степени сводится к квадратному уравнению четной степени, т.к у любого возвратного ур–ия нечетной степени один из корней всегда равен –1

Очевидно 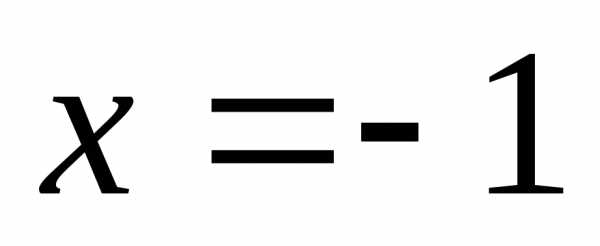— корень уравнения.

или

т.к 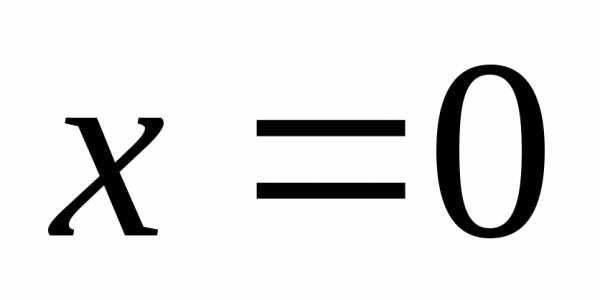— не является корнем уравнения, то разделим обе части

уравнения на

Введем замену.

Пусть 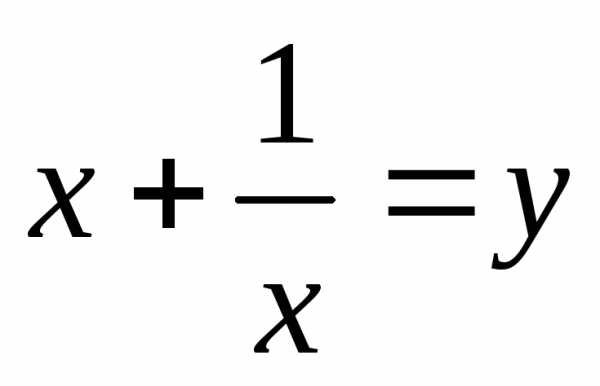,,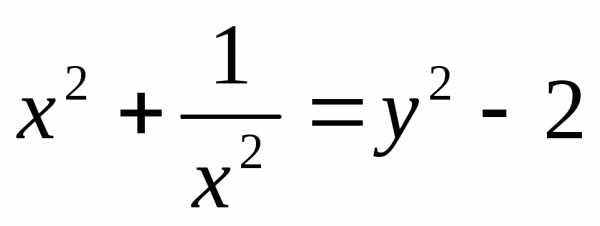, 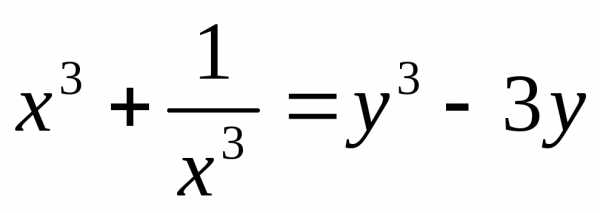получим

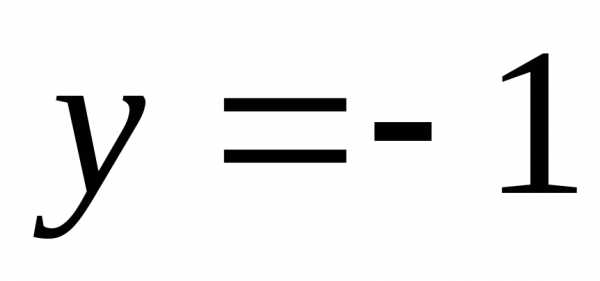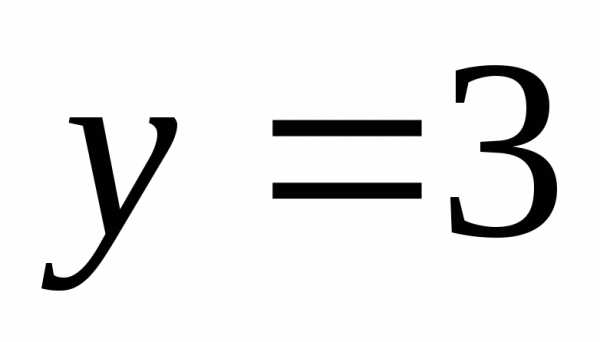илиили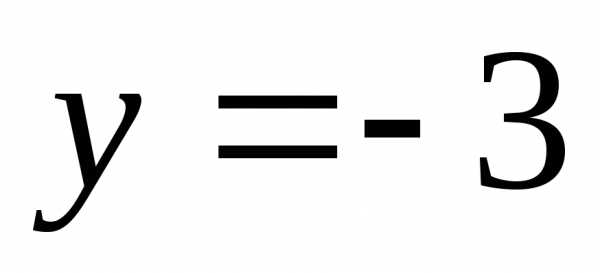

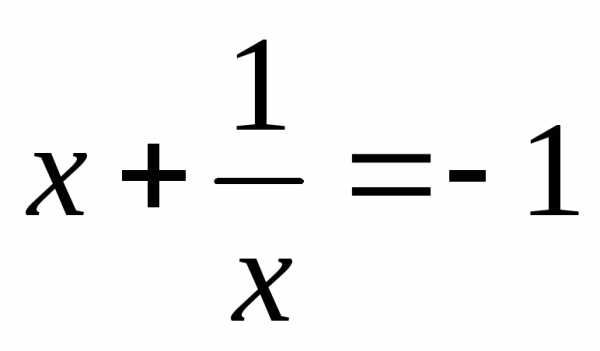
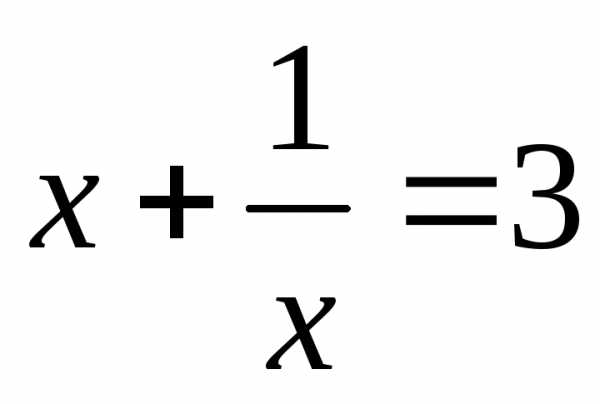
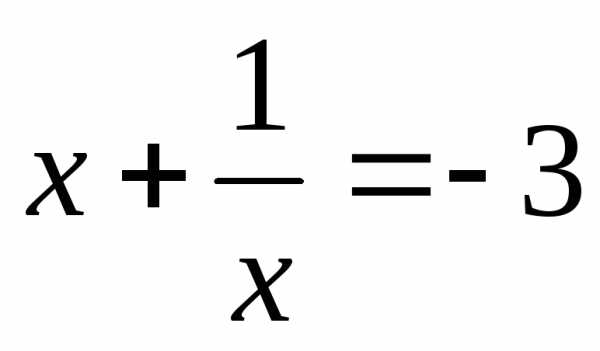
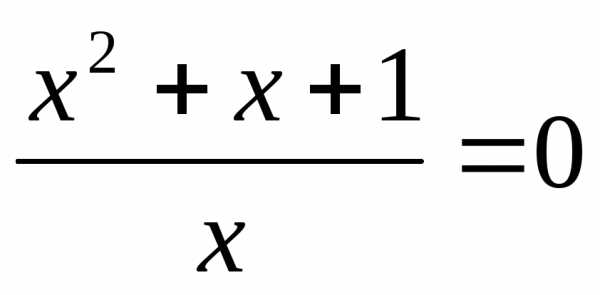
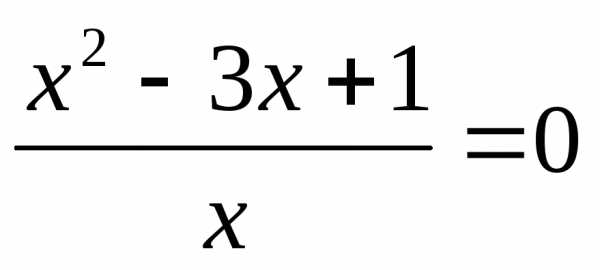
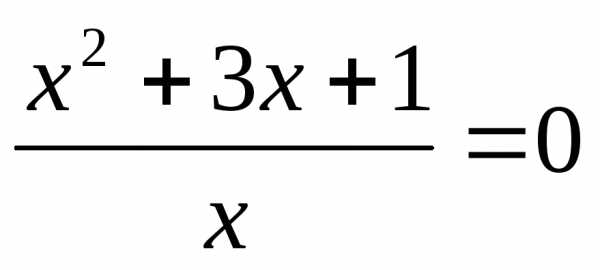
корней нет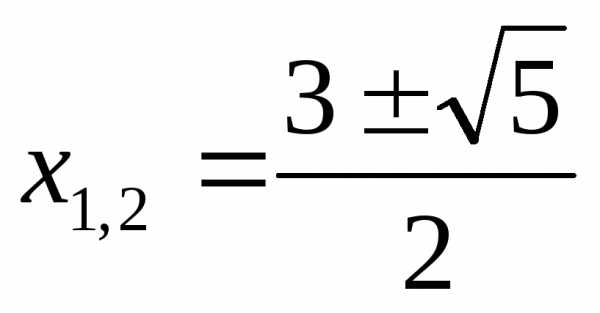

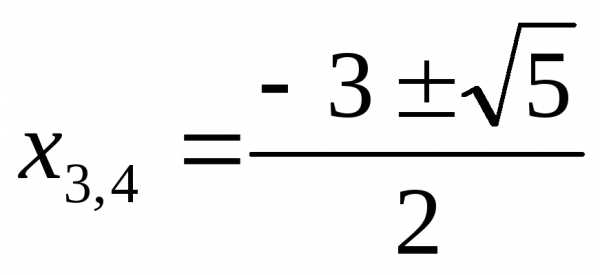
Ответ: ,,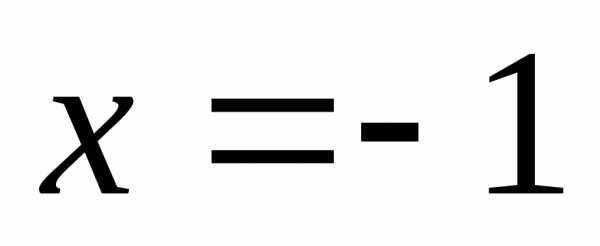

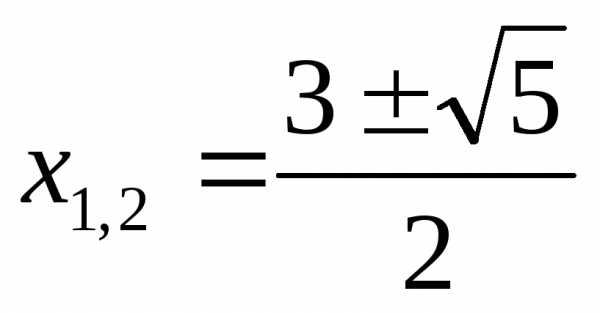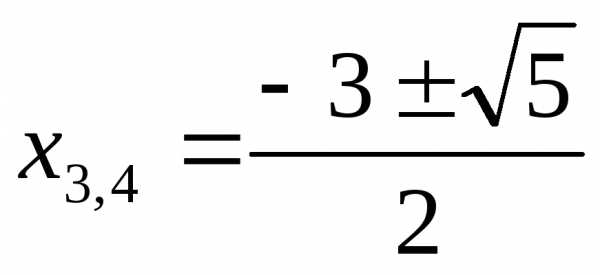
III) Уравнения вида, где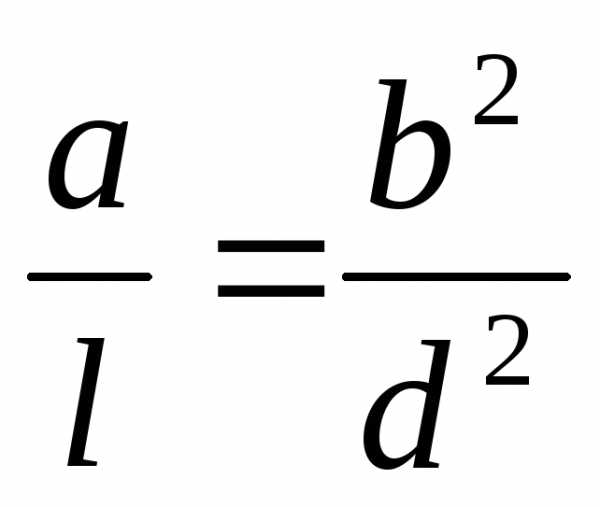решаются как возвратные.

IV) Замена переменных по явным признакам.

V) В следующих уравнениях используется “идея однородности”.

Пример №1

Введем замену.

Пусть 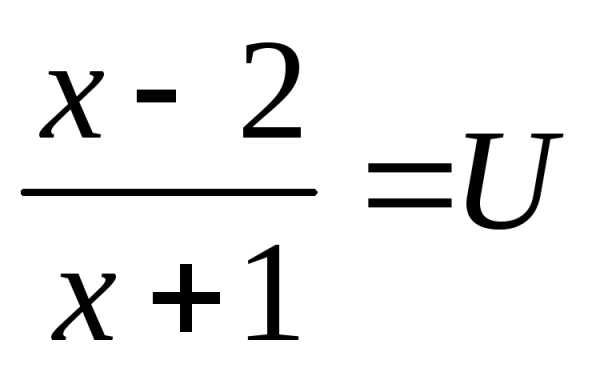,,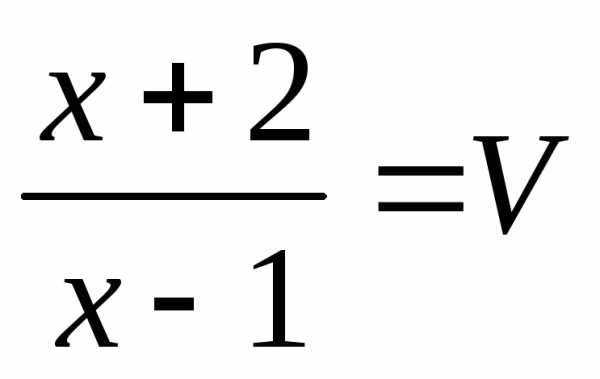 тогда

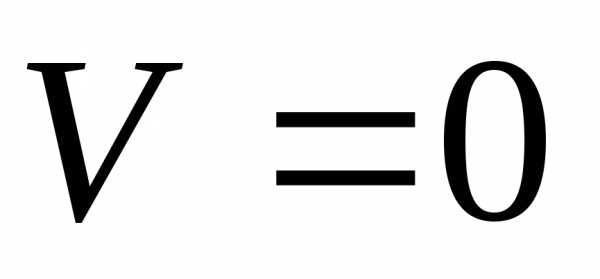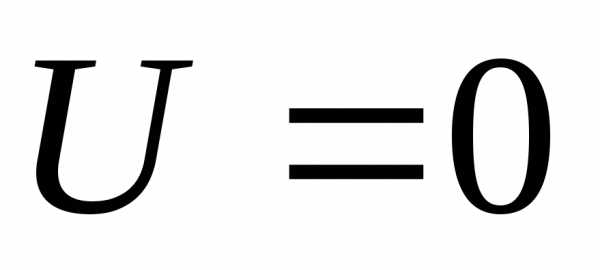1) если , тогда, тогда

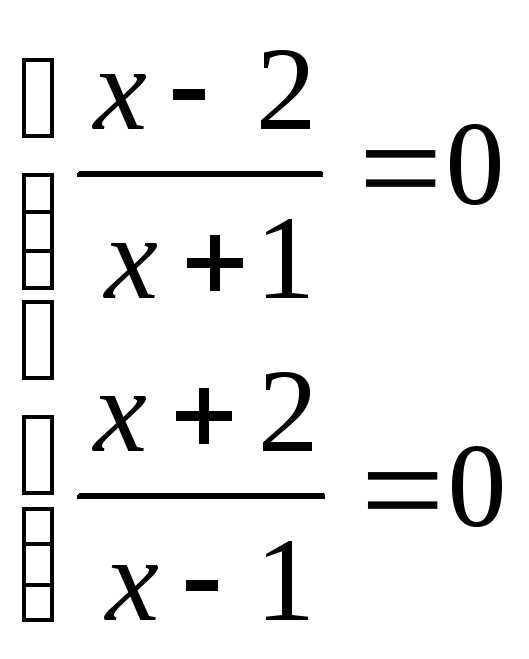
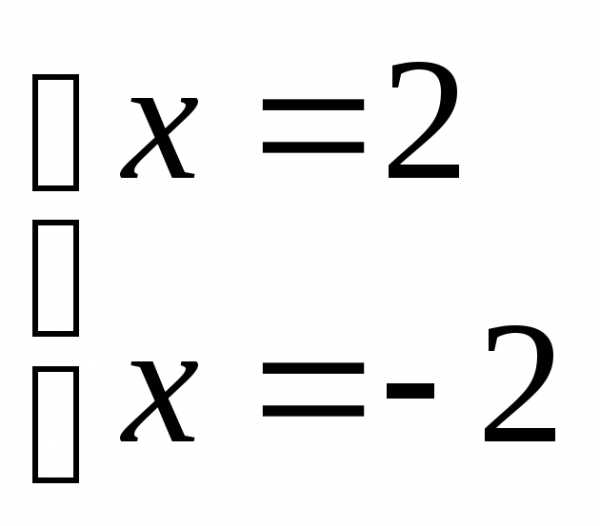решений нет

2) Разделим обе части уравнения на 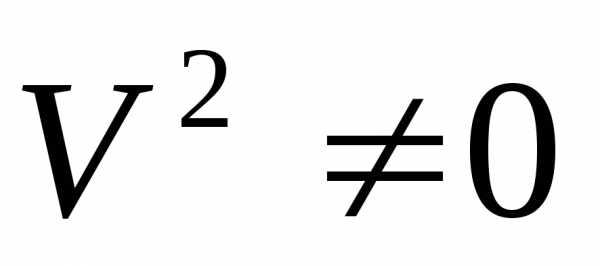, получим

Решим последнее уравнение, как квадратное относительно 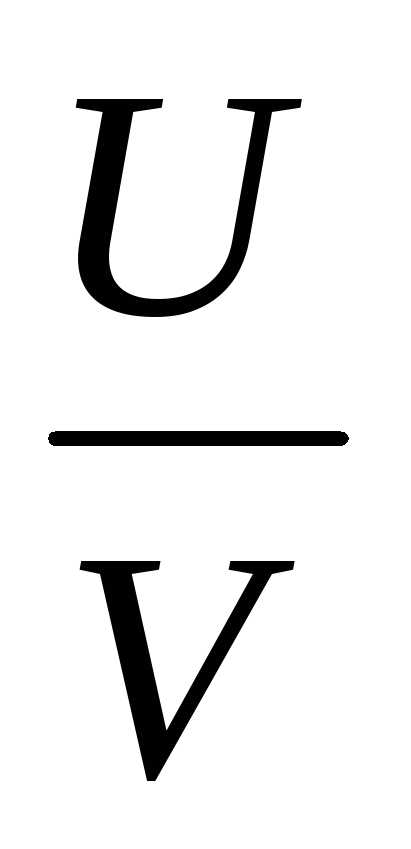, получим

;

;

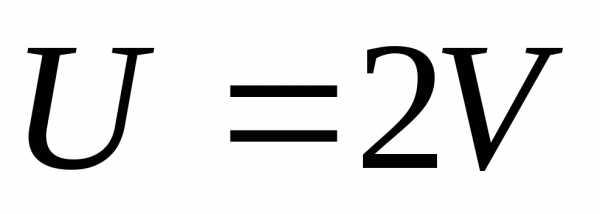Вернемся к замене.

или

корней нет

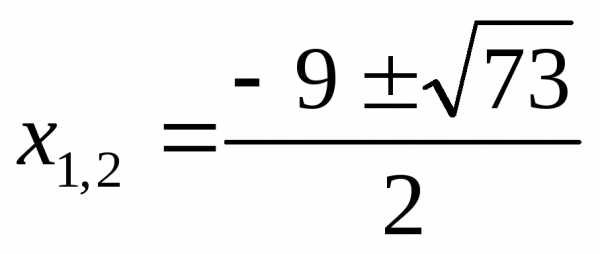
Ответ: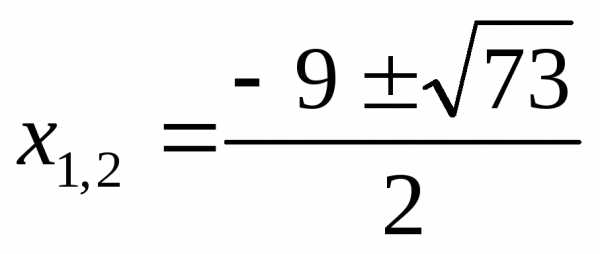

Пример №2.

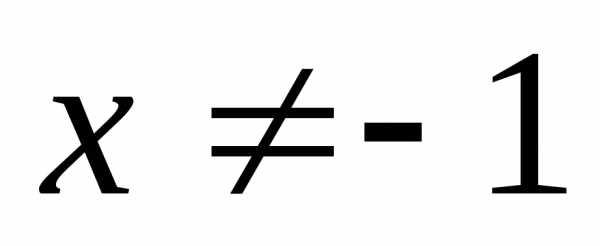
Пусть 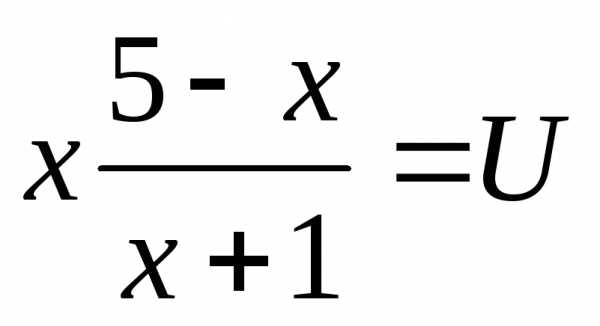,,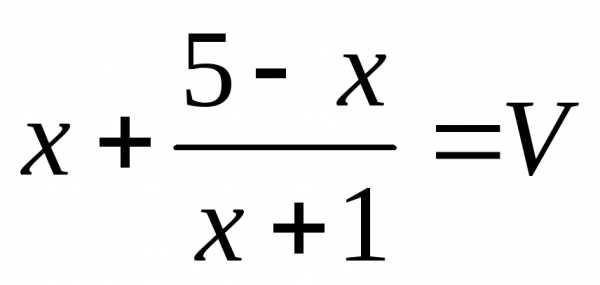 тогда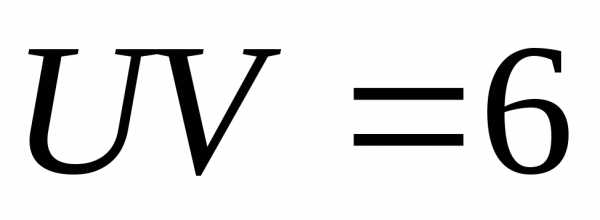

Найдем

Составим систему:

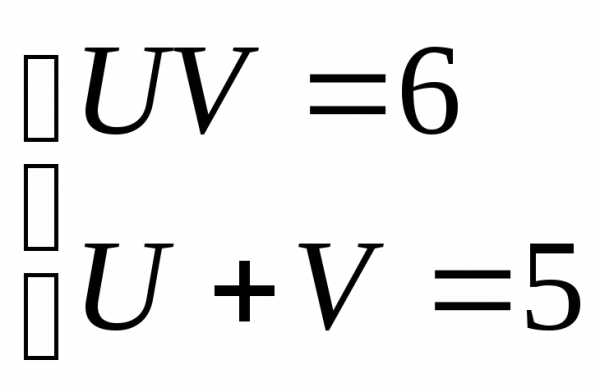
Решая систему подстановкой, получим

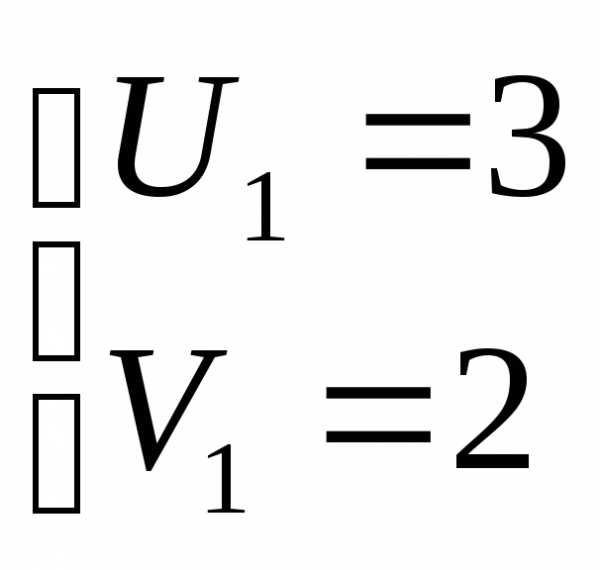или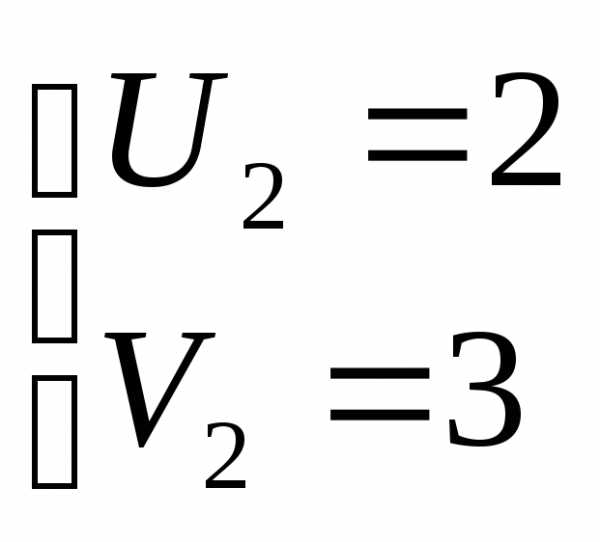

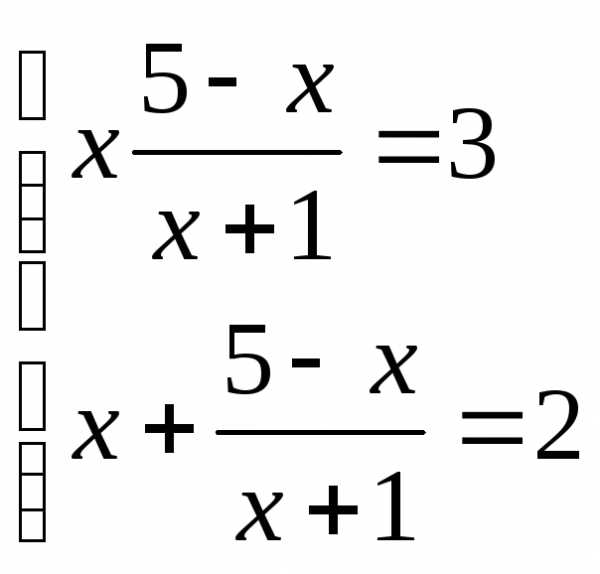
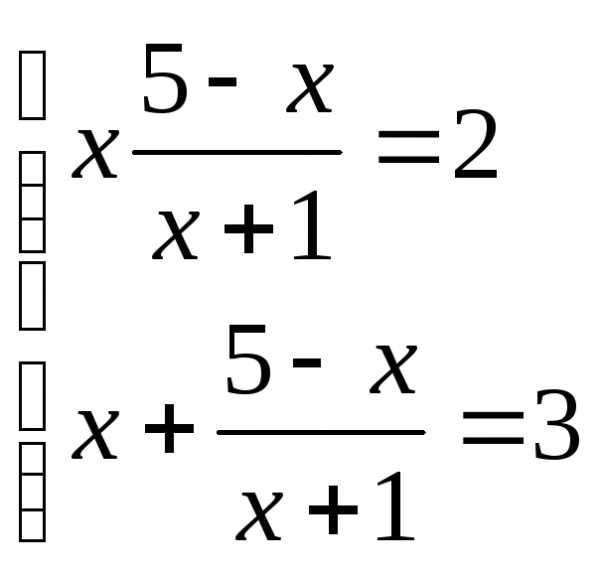
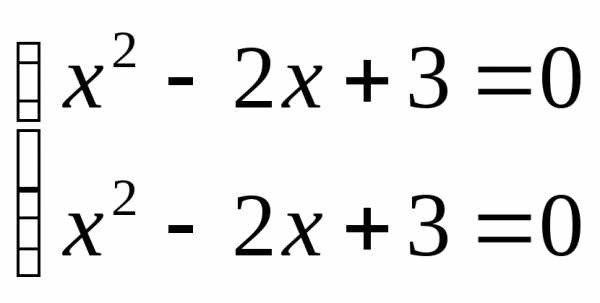
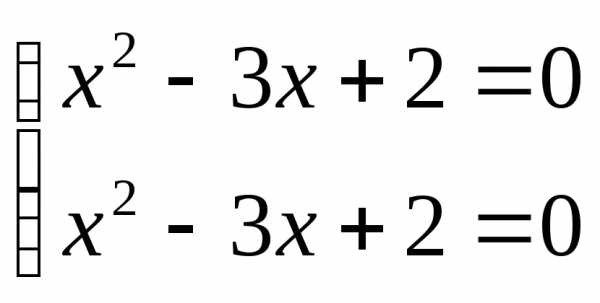
корней нет ;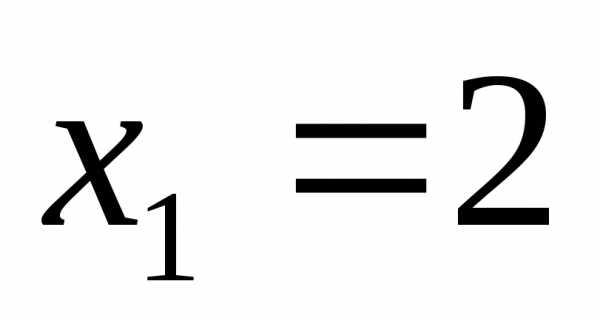

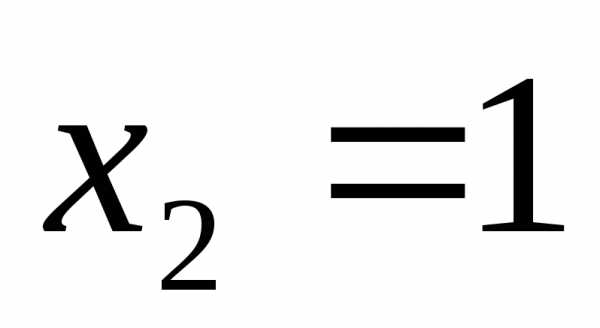
Ответ: ;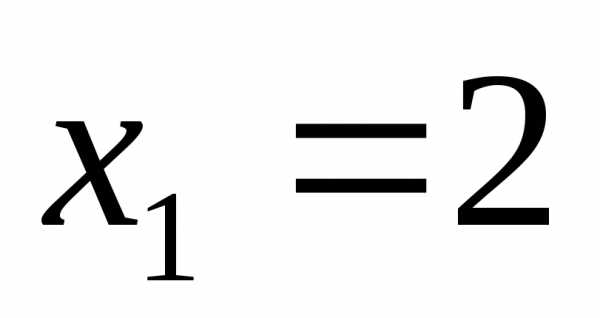

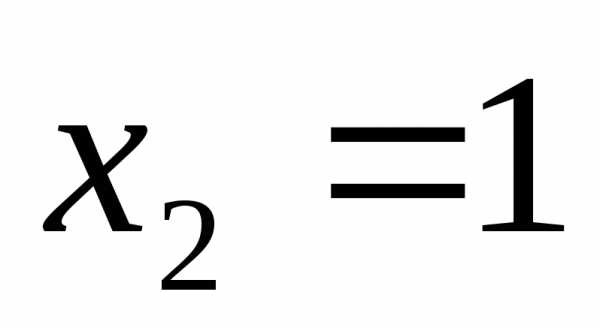
Пример №3.

— не является корнем уравнения

Разделим обе части уравнения на , получим

Введем замену.

Пусть 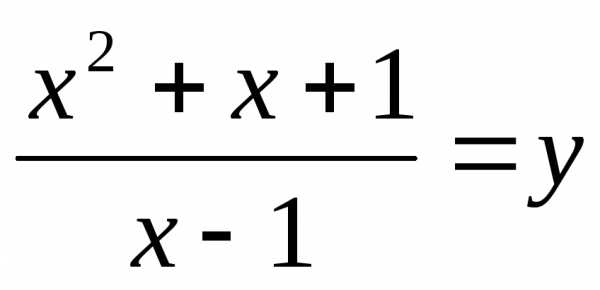, тогда

;

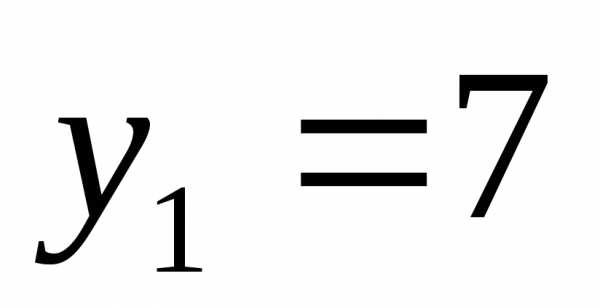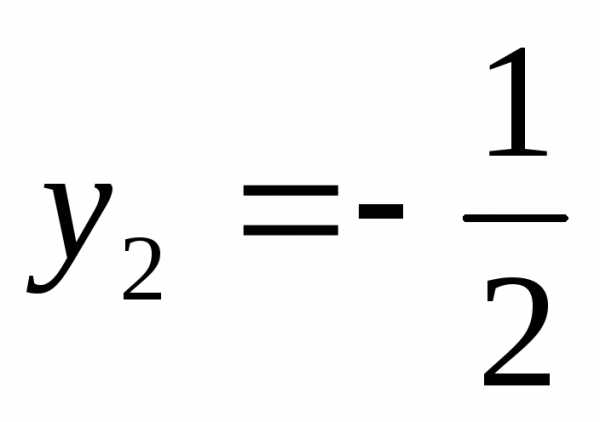
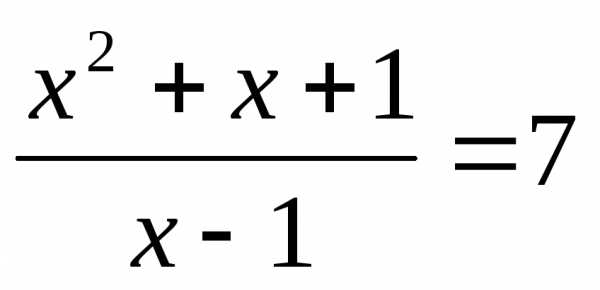или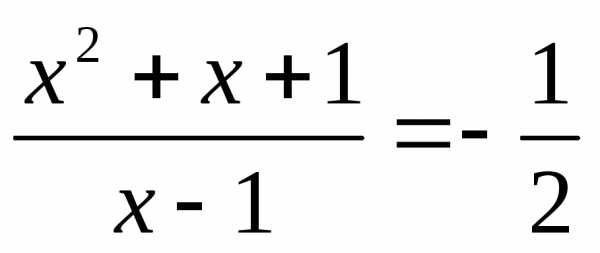

;;

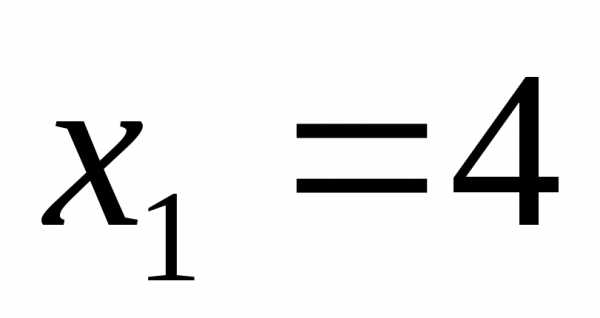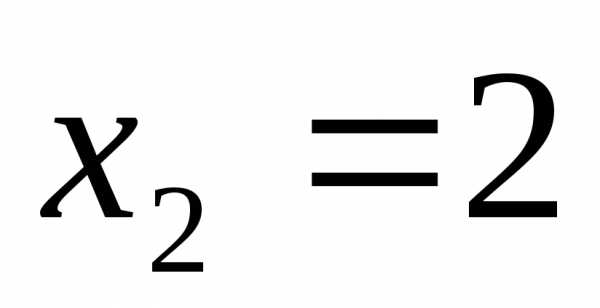
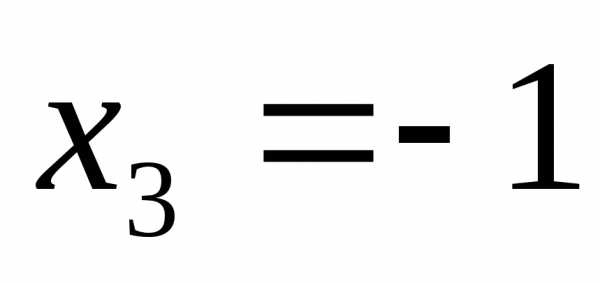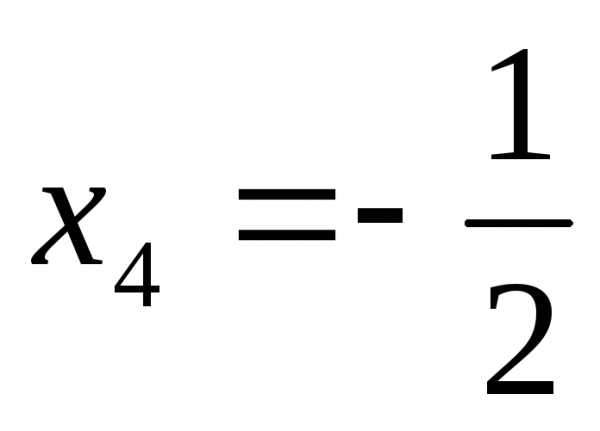
Ответ: ;;;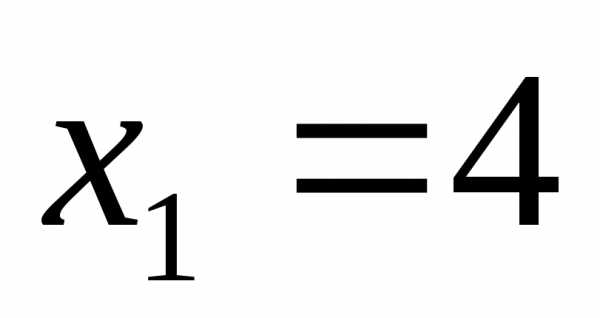

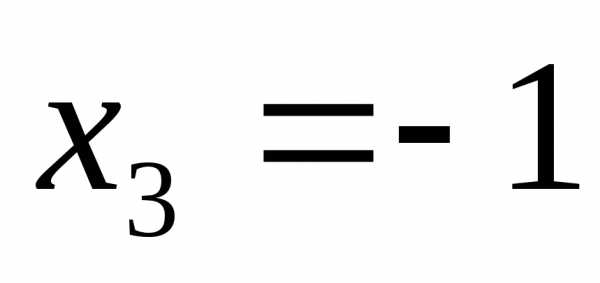VI) Уравнения вида, гдеэффективно решать перемножениеми, а затем делать замену.

VII) В уравнениях вида и в уравнениях к ним сводящимся, в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.

(1)

(2)

При переходе 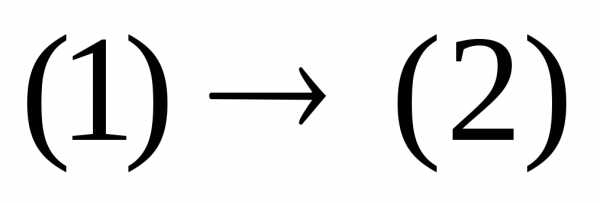область определения уравнения сузилась на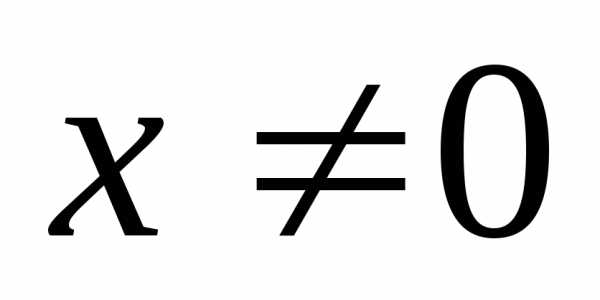. Проверим, является ликорнем уравнения. Не является.

Введем замену.

Пусть ,,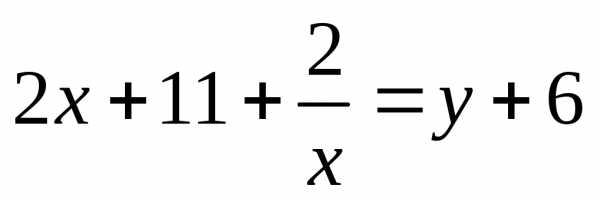 тогда

;

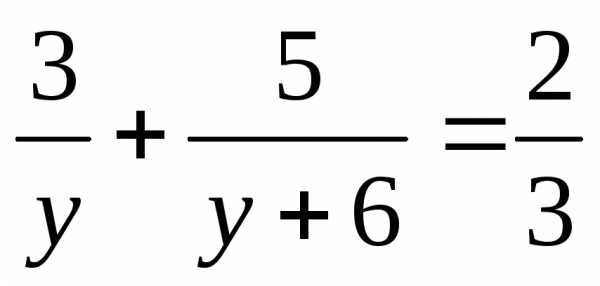
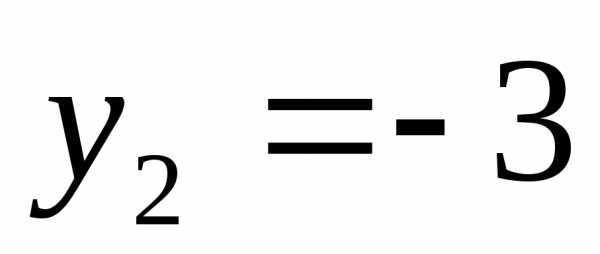
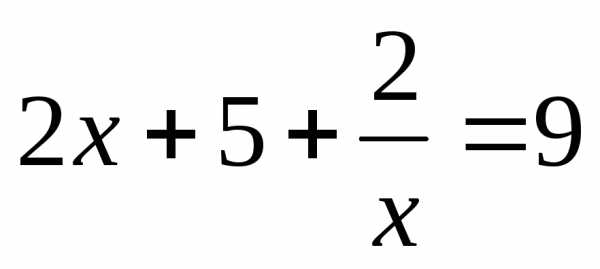или

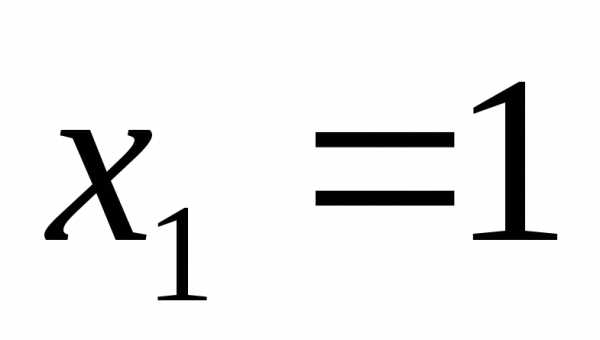
Ответ: ;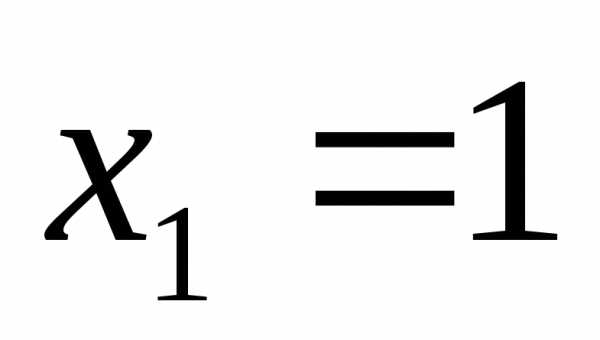

VIII) В уравнениях вида обе части уравнения делятся на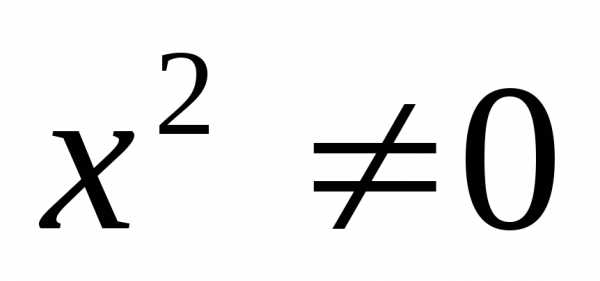

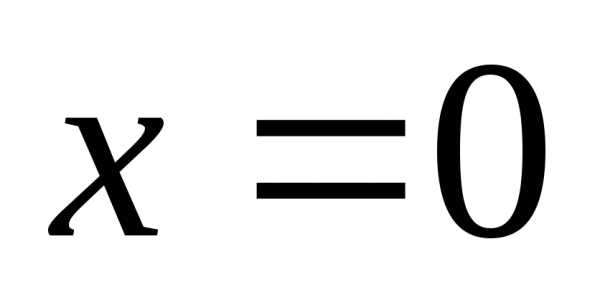— не является корнем уравнения. Разделим на, получим

Введем замену.

Пусть 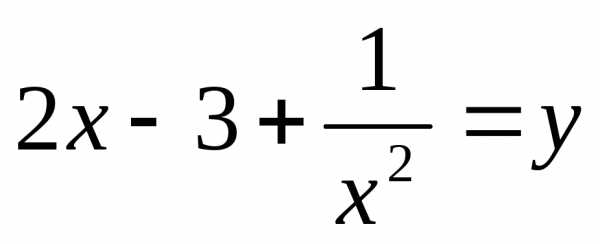;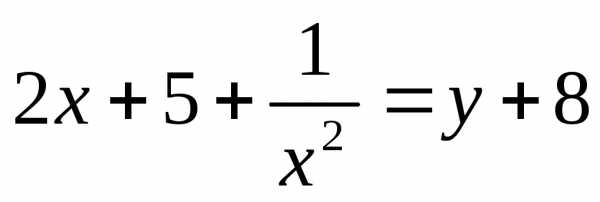, тогда

;

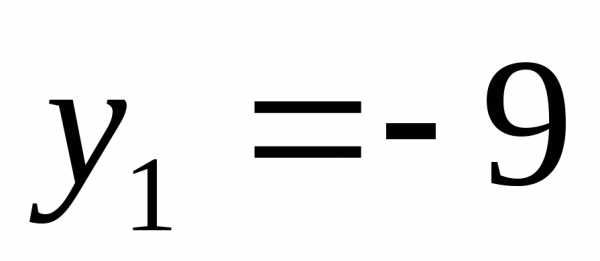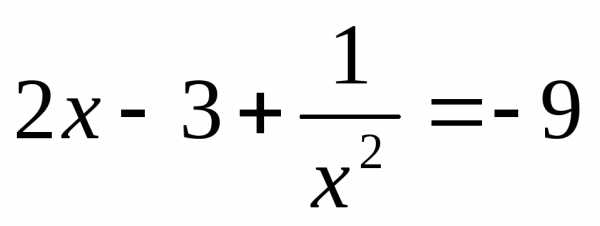или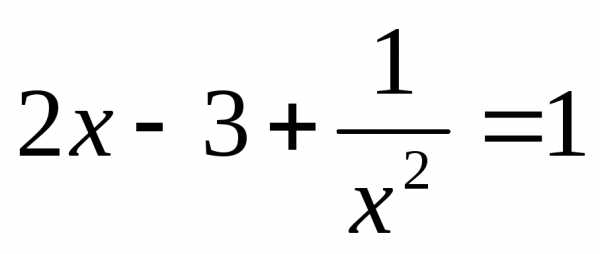

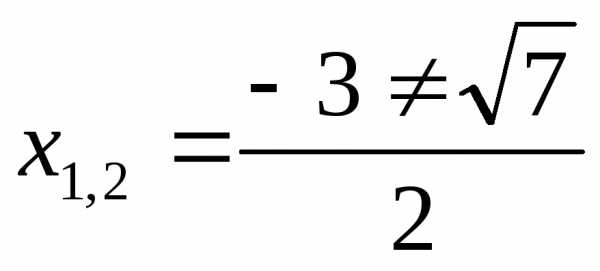
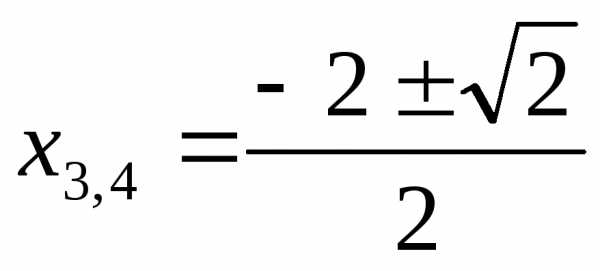
Ответ: ;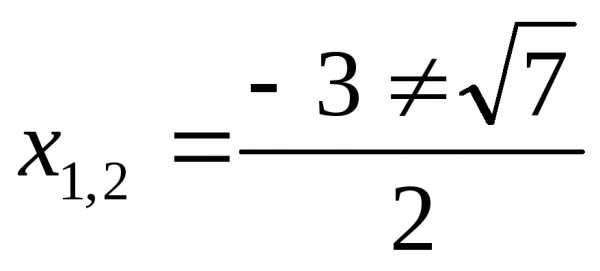

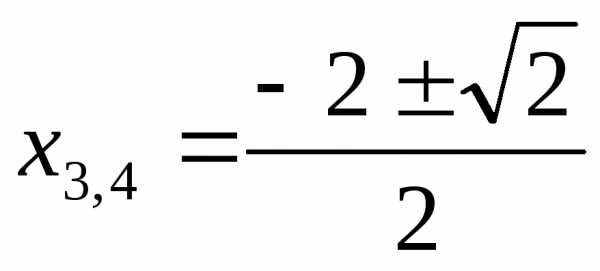
IX) Выделение полного квадрата.

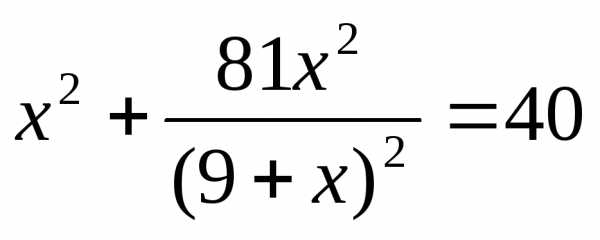
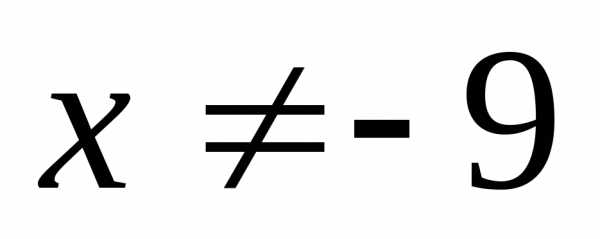
Введем замену.

Пусть 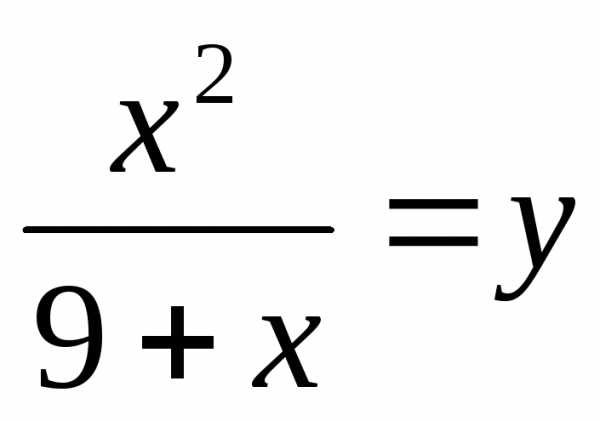, тогда

;

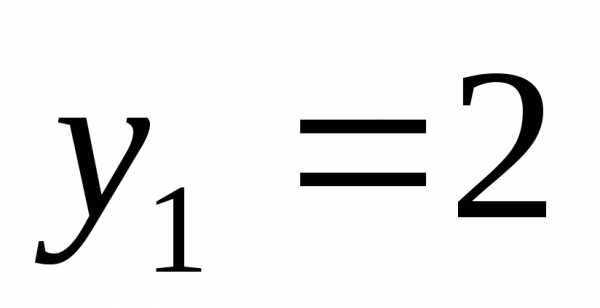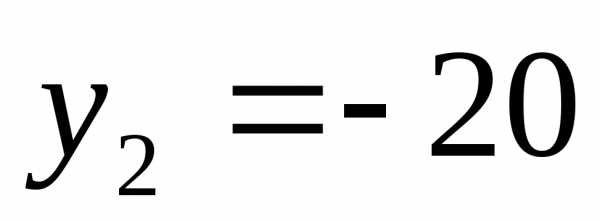
Вернемся к замене.

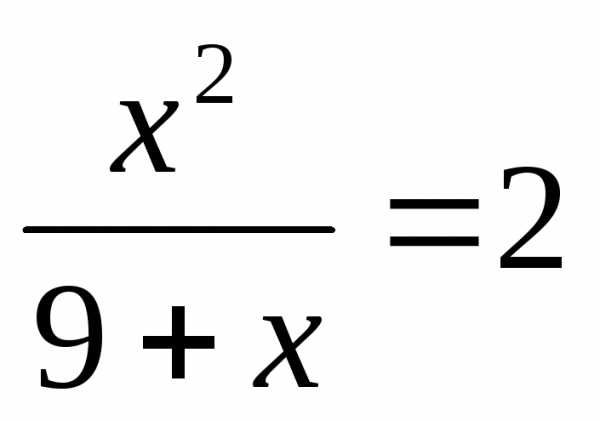или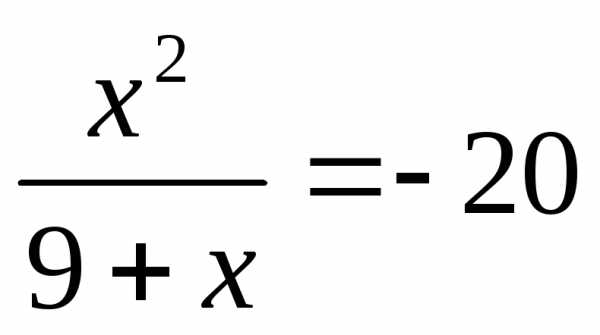

корней нет

Ответ:

X) Решение уравнений с помощью формулы

или

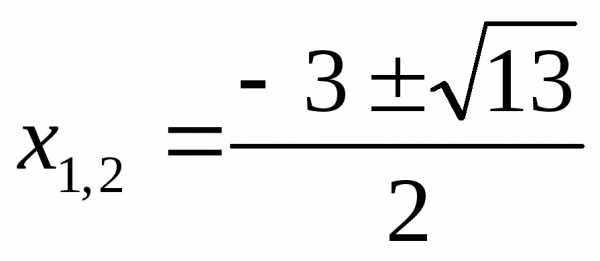корней нет

XI) Уравнения вида и к ним сводящиеся решаются при помощи замены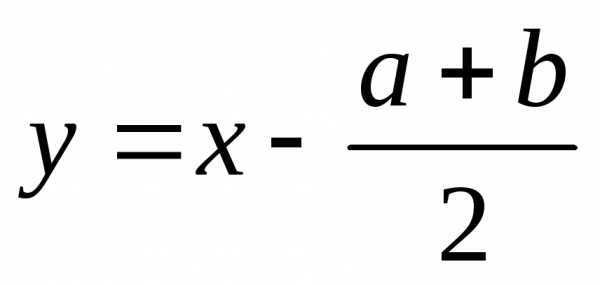

Введем замену.

Пусть 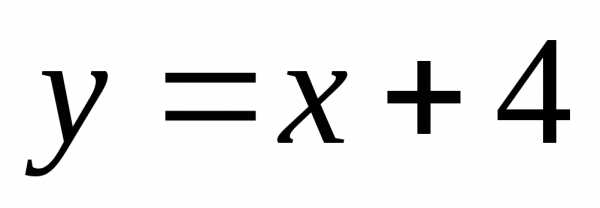, тогда

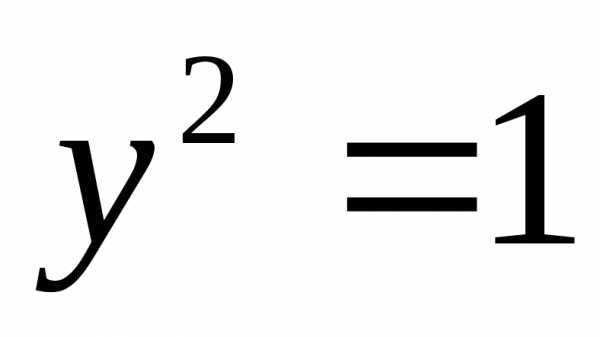иликорней нет

;

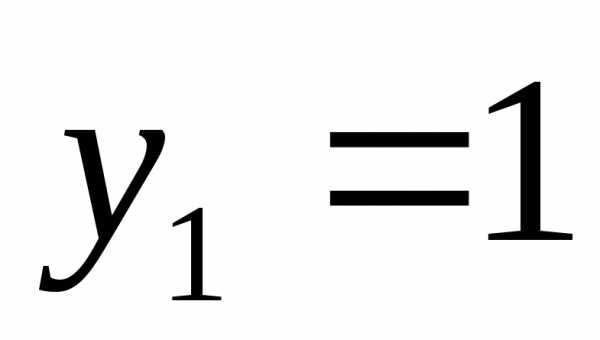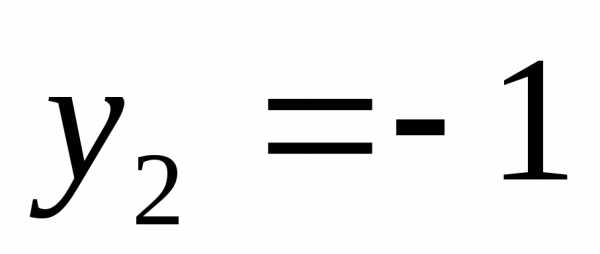
Вернемся к замене.

или

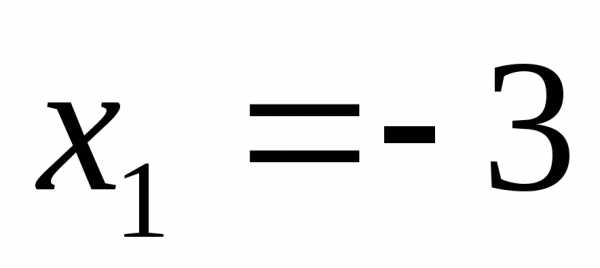
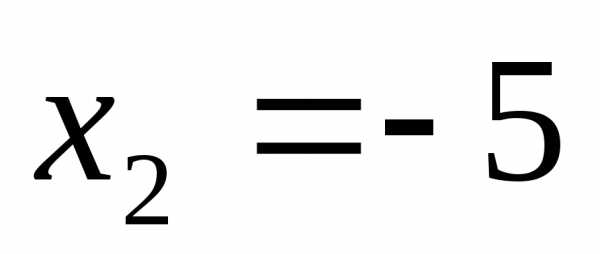
Ответ: ;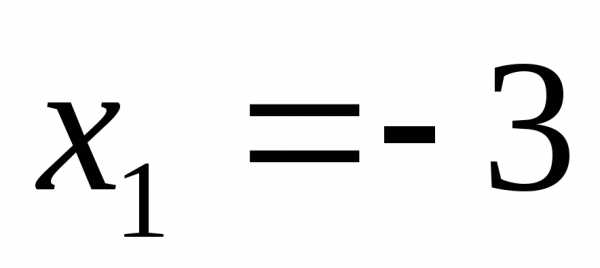

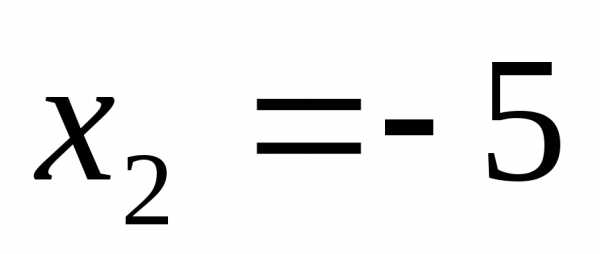
XII) Решение уравнений относительно коэффициентов.

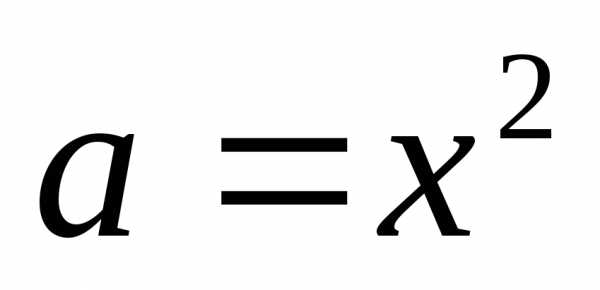
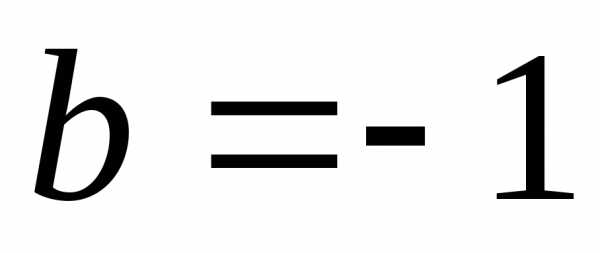
или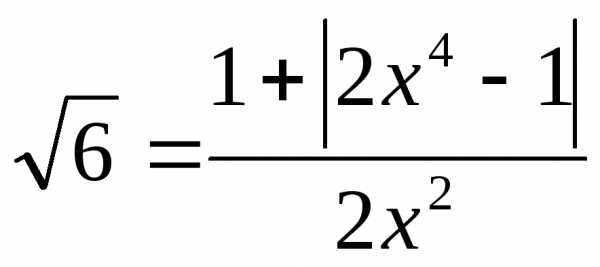

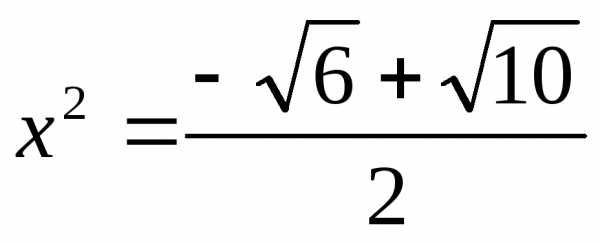
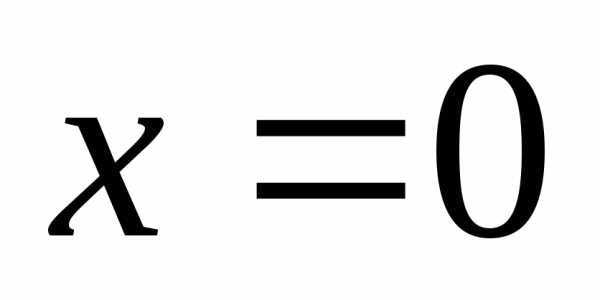;— посторонний корень

корней нет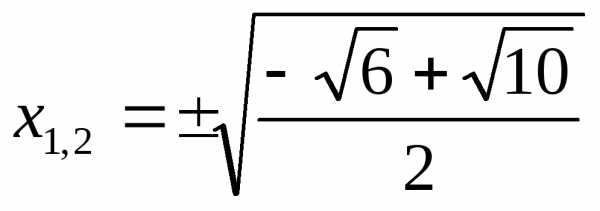

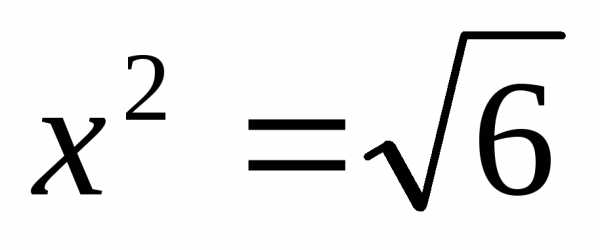
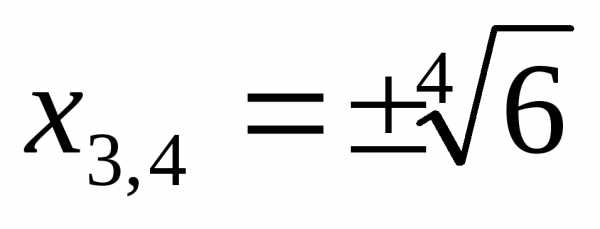
Ответ: ;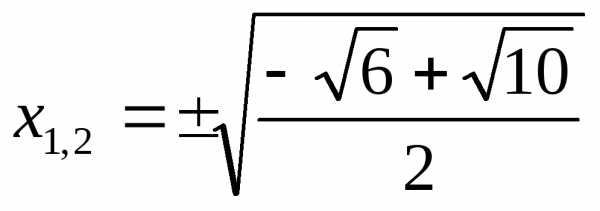

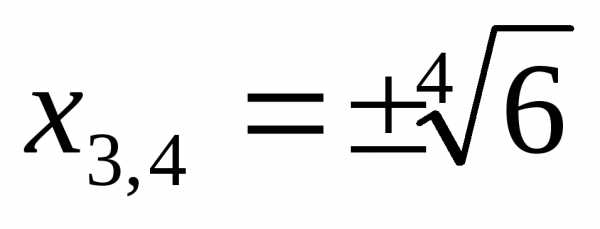
XIII) Метод разложения на простейшие дроби.

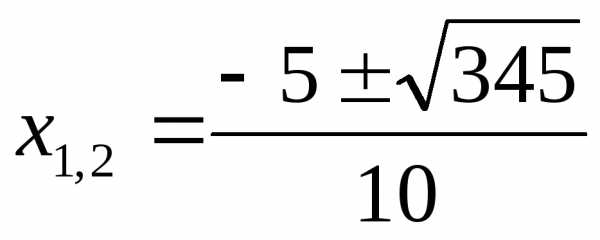
Ответ: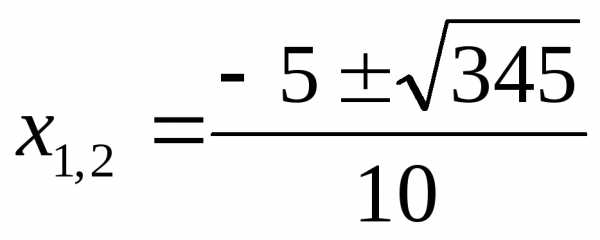

studfiles.net

Уравнения со степенями | Логарифмы

Рассмотрим показательные уравнения со степенями, содержащими две степени с разными основаниями и одинаковыми показателями:

(где a и b — положительные числа, отличные от единицы).

Уравнения такого вида называются однородными показательными уравнениями первой степени. Однородные уравнения решаются делением на одну из степеней:

(так как b>0, то

при любом показателе f(x), то есть деление на степень не приводит к потере корней).

В результате деление получаем с одной стороны частное степеней с одинаковыми показателями, с другой — единицу:

По свойству степеней,

а единицу можно представить как степень с любым основанием и показателем 0:

Приравниваем показатели:

Рассмотрим примеры решений такого вида уравнений со степенями.

ОДЗ: x∈R.

Разделим обе части уравнения на степень, стоящую в правой части уравнения:

Преобразуем левую часть уравнения

и представим единицу в виде степени с таким же основанием, что и степень в левой части

Из равенства степеней с одинаковыми основаниями следует равенство показателей этих степеней:

Ответ: 2,5.

ОДЗ: x∈R.

Делим обе части уравнения на степень, стоящую в правой части:

Приравняв показатели степеней, приходим к квадратному уравнению

корни которого —

Ответ: 1; 5.

ОДЗ: x∈R.

Это — простейшее тригонометрическое уравнение, корни которого

Ответ: πn, n∈Z.

www.logarifmy.ru