Умножения матрицы – примеры, алгоритм умножения на вектор, число, свойства произведения

Умножение матриц, онлайн калькулятор с решением

Наш онлайн калькулятор позволяет умножить матрицы всего за пару минут. Для умножения двух матриц выберите их размеры (количество столбцов первой матрицы должно быть равно количеству строк второй матрицы), введите все элементы и нажмите кнопку «Вычислить», калькулятор выдаст пошаговое решение и ответ! Каждый этап решения будет подробно расписан, это поможет вам понять, как был получен ответ и закрепить пройденный материал.

Заполните элементы матриц  

Первая матрица:

Вторая матрица:

A×B=?

Решили сегодня: раз, всего раз

Понравился сайт? Расскажи друзьям!

Как умножить матрицы онлайн

Умножать две матрицы можно только при условии, что в первой из них ровно такое же количество столбцов, сколько строк во второй. Сами же значения при этом могут быть не только целыми, но и дробными. Получив расшифровку вычисления этой задачи, вы сможете понять, как происходит перемножение. Это сэкономит ваше время и поможет лучше разобраться в вычислительных тонкостях.

Допустим, у вас имеется две матрицы, и вам предстоит найти их произведение. Сделать это оперативно и с наивысшей точностью вам поможет данный онлайн-калькулятор. Он не просто умножит две матрицы без затруднений за пару минут, но и позволит вам детальнее разобраться в самом алгоритме этих расчётов. Таким образом, применение онлайн-калькулятора способствует закреплению пройденного в теории материала. Можно также сначала производить вычисления вручную, а затем проверять их здесь, это превосходная тренировка для мозга.

Инструкция пользования данным онлайн-калькулятором не представляет сложности. Чтобы умножить матрицы онлайн для начала укажите количество имеющихся столбцов и строк в первой матрице посредством нажатия на иконки «+» или «-» слева от матрицы и под ней. Затем введите числа. Повторите те же операции для второй матрицы. Далее остаётся лишь кликнуть кнопку «Вычислить» — и перед вами откроется искомое значение вместе с детальным алгоритмом вычислений.

ru.solverbook.com

Умножение матриц онлайн

www.matcabi.net позволяет найти произведение матриц онлайн. Сайт производит умножение матриц онлайн. За неколько секунд сервер выдаст точное решение. Умножением матриц онлайн будет являться матрица, каждый элемент которой вычисляется как скалярное произведение строк первой матрицы на соответствующие столбцы второй матрицы по правилу умножения матриц. При умножении матриц онлайн, каждый элемент полученной матрицы будет результатом умножения строк одной матрицы на столбцы другой матрицы согласно правилу произведения матриц. Найти онлайн произведение двух матриц допустимых размерностей сводится к нахождению матрицы соответствующей им размерности. Операция умножения онлайн двух матриц размерностей NxK и KxM сводится к нахождению матрицы размерности MxN. Элементы этой матрицы составляют скалярное произведение соответствующих строк и столбцов умножаемых матриц, это результат умножения матриц онлайн. Задача по нахождению произведения матриц онлайн или операция умножения матриц онлайн заключается в умножении строк на столбцы матриц согласно правилу умножения матриц. www.matcabi.net находит произведение матриц заданных размерностей в режиме онлайн. Умножение матриц онлайн заданной размерности — это нахождение соответствующей размерности матрицы, элементами которой будут скалярные произведения соответствующих строк и столбцов умножаемых матриц. Нахождение произведения матриц онлайн широко распространено в теории матриц, а так же линейной алгебры. Произведение матриц онлайн используется для определения результирующей матрицы от умножения заданных матриц. Для того, чтобы вычислить произведение матриц или определить умножение матриц онлайн, необходимо затратить не мало времени, в то время как наш сервер в считанные секунды найдет произведение матриц онлайн от умножения двух заданных матриц онлайн. При этом ответ по нахождению произведения матриц будет правильным и с достаточной точностью, даже если числа при умножении матриц онлайн будут иррациональными. На сайте www.matcabi.net допускаются символьные записи в элементах матриц, то есть произведение матриц онлайн может быть представлено в общем символьном виде при умножении матриц онлайн. Полезно проверить ответ, полученный при решении задачи на умножение матриц онлайн, используя сайт www.matcabi.net. При совершении операции умножения матриц онлайн необходимо быть внимательным и предельно сосредоточенным при решении задачи. В свою очередь наш сайт поможет Вам проверить своё решение на тему умножение матриц онлайн. Если у Вас нет времени на долгие проверки решенных задач, то www.matcabi.net безусловно будет являться удобным инструментом для проверки умножения матриц онлайн.

www.matcabi.net

Умножение матриц » ProcMem.Ru Линейная Алгебра

Определение. Произведением строки длины n на столбец высоты n называется скаляр, вычисляемый по правилу:

.

Замечание. Из определения следует, что для умножения строки на столбец необходимо, чтобы длина строки была равна высоте столбца. В противном случае произведение строки на столбец не определено.

Пример.

Определение. Произведением матрицы  размера  на матрицу  размера  называют матрицу  размера , где элемент  является результатом произведения – й строки матрицы А на – й столбец матрицы В для всех значений индексов , , т.е.

или

.

Обозначение: .

Другими словами, чтобы умножить две матрицы, нужно каждую строку первой матрицы умножить на каждый столбец второй матрицы. Умножая первую строку первой матрицы на каждый столбец второй матрицы мы получим все элементы первой строки матрицы произведения, затем делаем то же самое для второй строки первой матрицы и т.д.

Замечание. Из определения следует, что умножение матриц возможно только тогда, когда ширина первой матрицы (т.е. число ее столбцов) равна высоте второй (т.е. числу ее строк)

Пример.

.

Определение. Квадратную матрицу – го порядка называют единичной матрицей n-го порядка и обозначают буквой Е, если для любой квадратной матрицы А – го порядка справедливо равенство: .

Множество всех квадратных матриц n-го порядка будем обозначать через .

Теорема. Множество  содержит единичную матрицу n-го порядка, которой является матрица

.

Доказательство этой теоремы предоставляется читателю.

Теорема. Единичная матрица Е является единственной в множестве .

Доказательство. Пусть  еще одна единичная матрица. Тогда, по определению, . Положим , тогда . Далее, по определению,  . Положим здесь . Получаем равенство, отсюда имеем , ч.т.д.

Заметим, что точно также доказывается единственность нейтрального элемента (при условии его существования) в любой алгебраической структуре.

Теорема доказана.

Из теоремы следует, что никакая другая матрица, кроме матрицы  не является единичной.

Теорема. (Свойства умножения матриц.)

Умножение матриц подчиняется следующим законам:

9) ассоциативность:

;

10) существование единичной матрицы:

:  ;

дистрибутивность умножения относительно сложения матриц:

11)  дистрибутивность умножения относительно сложения матриц:

 и

12)  умножение матриц связано с умножением матрицы на число естественным законом:  и  верно равенство:

.

Замечание. Для квадратных матриц одного порядка выполняются все 12 свойств. Это говорит о том, что множество всех квадратных матриц одного и того же порядка образует алгебру матриц над полем К.

Замечание. Умножение матриц не обладает свойством коммутативности. Для доказательства достаточно привести один контрпример.

Пусть , . Тогда , .

Аналогичный пример можно привести для квадратных матриц любого порядка.

Последнее равенство говорит о том, что квадратные матрицы имеют делители нуля.

Следствие. Множество всех квадратных матриц n-го порядка над полем K является некоммутативным кольцом с единицей и с делителями нуля.

Доказательство. На множестве  всех квадратных матриц n-го порядка над полем K определены две операции: сложение матриц и их умножение, которые подчиняются законам 1) – 4) и 9) – 11), откуда и следует, по определению, что  является кольцом с единицей (см. лекцию 1, п.14 и п.15). Пример, приведенный перед формулировкой данного следствия, показывает, что кольцо  имеет делители нуля.

Следствие доказано.

Определение. Натуральной степенью квадратной матрицы А называется матрица  .

Нулевую степень квадратной матрицы А – го порядка по определению полагают равной единичной матрице того же порядка: .

Еще записи по теме

procmem.ru

Умножение матриц Википедия

Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется

произведе́нием ма́триц.

Содержание

• 1 Определение
• 2 Иллюстрация
• 3 Обсуждение
• 4 Свойства
• 5 Обратная матрица
• 6 Алгоритмы быстрого перемножения матриц
• 7 Степени матриц
• 8 См. также
• 9 Литература
• 10 Примечания

Определение[ | ]

Пусть даны две прямоугольные матрицы A{\displaystyle A} и B{\displaystyle B} размерности l×m{\displaystyle l\times m} и m×n{\displaystyle m\times n} соответственно:

A=[a11a12⋯a1ma21a22⋯a2m⋮⋮⋱⋮al1al2⋯alm],B=[b11b12⋯b1nb21b22⋯b2n⋮⋮⋱⋮bm1bm2⋯bmn].{\displaystyle A={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1m}\\a_{21}&a_{22}&\cdots &a_{2m}\\\vdots &\vdots &\ddots &\vdots \\a_{l1}&a_{l2}&\cdots &a_{lm}\end{bmatrix}},\;\;\;B={\begin{bmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\end{bmatrix}}.}

Тогда матрица C{\displaystyle C} размерностью l×n{\displaystyle l\times n}:

C=[c11c12⋯c1nc21c22⋯c2n⋮⋮⋱⋮cl1cl2⋯cln],{\displaystyle C={\begin{bmatrix}c_{11}&c_{12}&\cdots &c_{1n}\\c_{21}&c_{22}&\cdots &c_{2n}\\\vdots &\vdots &\ddots &\vdots \\c_{l1}&c_{l2}&\cdots &c_{ln}\end{bmatrix}},}

в которой:

ru-wiki.ru

Умножение матрицы на число онлайн

Умножение матрицы на число

Операция умножения матрицы А на число k заключается в построении матрицы kA = [kaij]. Умножение матрицы на число допустимо для матриц любого размера, результатом умножения является матрица того же порядка, что и исходная матрица.

Таким образом, произведение матрицы А на число k – это результирующая матрица B = kA того же порядка, полученная умножением всех элементов aij исходной матрицы на заданное число.

Математически умножение матрицы на число можно представить следующими выражениями:
Аm×n × k = Вm×n
aij × k = bij,
где i принимает значение от 1 до m, j имеет значения от 1 до n

Пример умножения матрицы на число.

Даны матрица А и число k:

Найти произведение матрицы и числа.
Решение:

Свойства умножения матрицы на число:

1. Единица является нейтральным числом умножения любой матрицы, результатом умножения на нейтральное число является исходная матрица.
   1×А = А
2. Результатом умножения любой матрицы на ноль всегда является нулевая матрица, все элементы которой равняются нулю.
   0×А = О
3. Для матриц одного порядка и действительного числа выполняется свойство дистрибутивности умножения относительно сложения.
   k×(А+B) = k×A + k×B
4. Для любой матрицы и суммы действительных чисел выполняется свойство дистрибутивности. (k+n)×А = k×A + n×A
5. Для любой матрицы и произведения любых действительных чисел выполняется свойство ассоциативности умножения.
   (k×n)×А = k×(n×A)

Вы также можете

в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x (например, в ячейку матрицы можно ввести 2x, или sin(x), или даже ((x+2)^2)/lg(x)).
Полный список доступных функций можно найти в справке.

www.yotx.ru

Умножение матриц — это… Что такое Умножение матриц?

Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц.

Определение

Пусть даны две прямоугольные матрицы и размерности и соответственно:

Тогда матрица размерностью называется их произведением:

где:

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

Следует заметить, что из существования произведения вовсе не следует существование произведения

Иллюстрация

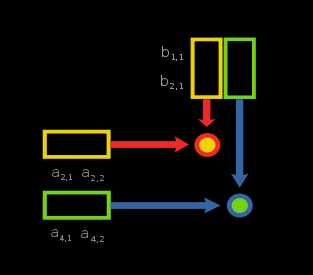
Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений строк матрицы A и столбцов матрицы B. Элемент матрицы AB с индексами i, j есть скалярное произведение i-ой строки матрицы A и j-го столбца матрицы B.

Иллюстрация справа демонстрирует вычисление произведения двух матриц A и B, она показывает как каждые пересечения в произведении матриц соответствуют строкам матрицы A и столбцам матрицы B. Размер результирующей матрицы всегда максимально возможный, то есть для каждой строки матрицы A и столбца матрицы B есть всегда соответствующее пересечение в произведении матрицы.

Значения на пересечениях отмеченных кружочками будут:

В общем случае, произведение матриц не является коммутативной операцией. К примеру:

Элемент произведения матриц приведённых выше вычисляется следующим образом

Первая координата в обозначении матрицы обозначает строку, вторая координата — столбец; этот порядок используют как при индексации, так и при обозначении размера. Элемент на пересечении строки и столбца результирующей матрицы является скалярным произведением -й строки первой матрицы и -го столбца второй матрицы. Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.

Мотивировка

Описанное правило матричного умножения прозрачнее всего мотивируется исходя из умножения вектора на матрицу.

Последнее естественно вводится исходя из того, что при разложении векторов по базису действие (любого) линейного оператора A дает выражение компонент вектора v’ = Av:

-то есть линейный оператор оказывается представлен матрицей, векторы — векторами-столбцами, а действие оператора на вектор — матричным умножением вектора-столбца слева на матрицу оператора (это частный случай матричного умножения, когда одна из матриц — вектор-столбец — имеет размер 1хn).

(Равно переход к любому новому базису при смене координат представляется полностью аналогичным выражением, только в этом случае уже не компоненты нового вектора в старом базисе, а компоненты старого вектора в новом базисе; при этом — элементы матрицы перехода к новому базису).

Далее, рассмотрев последовательное действие на вектор двух операторов: сначала A, а потом B (или преобразование базиса A, а затем преобразование базиса B), имеем, дважды применив нашу формулу:

откуда видно, что композиции BA действия линейных операторов A и B (или аналогичной композиции преобразований базиса) соответствует матрица, вычисляемая по рецепту произведения соответствующих матриц:

Определенное таким образом произведение матриц оказывается совершенно естественным и очевидно полезным (дает простой и универсальный способ вычисления композиций произвольного количества линейных преобразований).

Свойства

Сочетательное свойство:

Распределительное свойство:

.

Произведение матрицы на единичную матрицу подходящего порядка равно самой матрице:

Произведение матрицы на нулевую матрицу подходящей размерности равно нулевой матрице:

Если и — квадратные матрицы одного и того же порядка, то произведение матриц обладает ещё рядом свойств.

Умножение матриц в целом некоммутативно:

Если , то матрицы и называются перестановочными или коммутирующими между собой.

Определитель и след произведения не зависят от порядка умножения матриц:

Обратная матрица

Квадратная матрица называется неособенной (невырожденной), если она имеет единственную обратную матрицу такую, что выполняется условие:

В противном случае матрица называется особенной (вырожденной).

Матрица порядка является невырожденной в том и только в том случае, если в этом случае есть квадратная матрица того же порядка

где — алгебраическое дополнение элемента в определителе

Алгоритмы быстрого перемножения матриц

Сложность вычисления произведения матриц по определению составляет Θ(n³), однако существуют более эффективные алгоритмы^[1], применяющиеся для больших матриц.

• Алгоритм Штрассена (1969)

  Первый алгоритм быстрого умножения матриц был разработан В. Штрассеном^[2] в 1969. В основе алгоритма лежит рекурсивное разбиение матриц на блоки. На каждом этапе рекурсии выполняется семь умножений вместо восьми. В результате сложность этого алгоритма составляет . Недостатком данного метода является бо́льшая сложность программирования по сравнению со стандартным алгоритмом, численная неустойчивость и большой объём используемой памяти.

  Разработано большое количество алгоритмов на основе метода Штрассена, которые улучшают его численную устойчивость и уменьшают объём используемой памяти.

• Алгоритм Пана (1978)

  В 1978 Пан^[3] предложил свой метод умножения матриц, сложность которого составила Θ(n^2.78041).

• Алгоритм Бини (1979)

  В 1979 группа итальянских учёных во главе с Бини^[4] разработала алгоритм умножения матриц с использованием тензоров. Его сложность составляет Θ(n^2.7799).

• Алгоритмы Шёнхаге (1981)

  В 1981 Шёнхаге^[5] представил метод, работающий со сложностью Θ(n^2.695), который он назвал частичным матричным умножением. Позже ему удалось получить оценку Θ(n^2.6087).

  Затем Шёнхаге создал метод, названный методом прямых сумм, сложность которого составляет Θ(n^2.548). Романи сумел понизить оценку до Θ(n^2.5166), а Пан — до Θ(n^2.5161).

• Алгоритм Копперсмита — Винограда (1990)

  В 1990 Копперсмит и Виноград^[6] опубликовали алгоритм, умножающий матрицы со сложностью O(n^2.3727).^[7] Этот алгоритм использует идеи, схожие с алгоритмом Штрассена. На сегодняшний день алгоритм Копперсмита-Винограда является наиболее асимптотически быстрым, но он эффективен только на очень больших матрицах и поэтому не применяется.

• Алгоритмы с использованием теории групп (2003)

  В 2003 Кох и др. рассмотрели в своих работах^[8] алгоритмы Штрассена и Копперсмита-Винограда в контексте теории групп. Они показали возможность существования алгоритмов умножения матриц со сложностью Θ(n²)^[9].

См. также

Литература

• Корн Г., Корн Т. Алгебра матриц и матричное исчисление // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 392—394..

Примечания

1. ↑ Кибернетический сборник. Новая серия. Вып. 25. Сб. статей 1983 — 1985 гг.: Пер. с англ. — М.: Мир, 1988 — В.Б. Алекссев. Сложность умножения матриц. Обзор.
2. ↑ Strassen, Volker, Gaussian Elimination is not Optimal, Numer. Math. 13, p. 354-356, 1969
3. ↑ Pan V. Ya, Strassen’s algorithm is not optimal — trilinear technique of aggregating uniting and canceling for constructing fast algorithms for matrix operations. — Proc. 19th Annual Symposium on Foundations of Computer Science, Ann Arbor, Mich., 1978
4. ↑ Bini D., Capovani M., Lotti G., Romani F. — complexity for approximate matrix multiplication. — Inform. Process. Lett., 1979
5. ↑ Schonhage A. Partial and total matrix multiplication. — SIAM J. Comput., 1981
6. ↑ Don Coppersmith and Shmuel Winograd. Matrix multiplication via arithmetic progressions. Journal of Symbolic Computation, 9:251–280, 1990.
7. ↑ Williams, Virginia (2011), Breaking the Coppersmith-Winograd barrier.
8. ↑ Group-theoretic Algorithms for Matrix Multiplication
9. ↑ Toward an Optimal Algorithm for Matrix Multiplication

dic.academic.ru