Умножение матрицы на единичную матрицу – 25. Матричная алгебра. Сложение матриц и умножение матрицы на число. Перемножение матриц. Диагональная и единичная матрицы. Обратная матрица.
Умножение на единичную матрицу
На основании правила умножения матриц получаем:
АЕ = | а11 | а12 . | 1 | 0 | = | а11 | а12 |
а21 | а22 | 0 | 1 | а21 | а22 | ||
EA= | 1 | 0 . | а11 | а12 | = | а11 | а12 |
0 | 1 | а21 | а22 | а21 | а22, | ||
т.е. АЕ = ЕА = А (11)
Произведение квадратной матрицы любого порядка на соответствующую единичную матрицу равняется первоначальной матрице. Таким образом, при умножении матриц единичная матрица играет роль единицы, поэтому и называется единичной.
Понятие обратной матрицы
Если А – квадратная матрица, то
А-1А = АА-1 = Е (12)
Если обратная матрица А-1 существует, то матрица А называется обратимой. Операция вычисления обратной матрицы называется обращением матрицы. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица
Нахождение матрицы, обратной данной
Пусть дана невырожденная матрица
а11 | а12 | а13 | ||
А= | а21 | а22 | а23 | |
а31 | а32 | а33 |
а11 | а12 | а13 | |||
DА = | а21 | а22 | а23 | ≠ 0 | |
а31 | а32 | а33 | |||
Обратной матрицей А-1 будет матрица
A | A21/DА | A31/DА | ||||
A-1 = | A12/DА | A22/DА | A32/DА | , | ||
A13/DА | A23/DА | A33/DА |
где Аij – алгебраическое дополнение элемента аij определителя DA.
Убедиться в этом
можно, умножая матрицу А на матрицу А-1.
Например, элементы с11
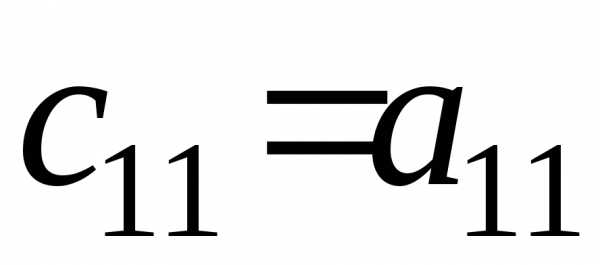 ·
·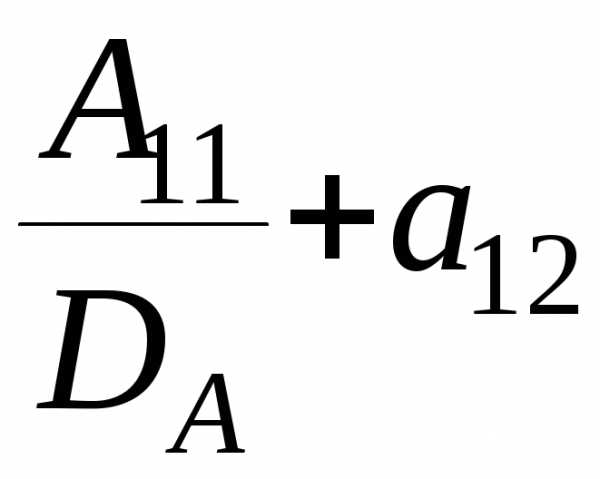 ·
·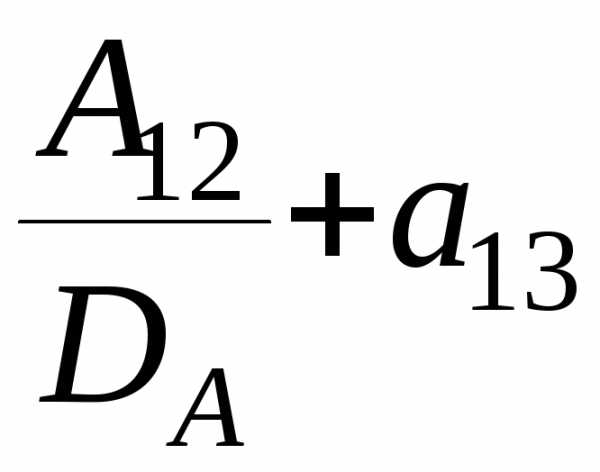 ·
·
c23=a21·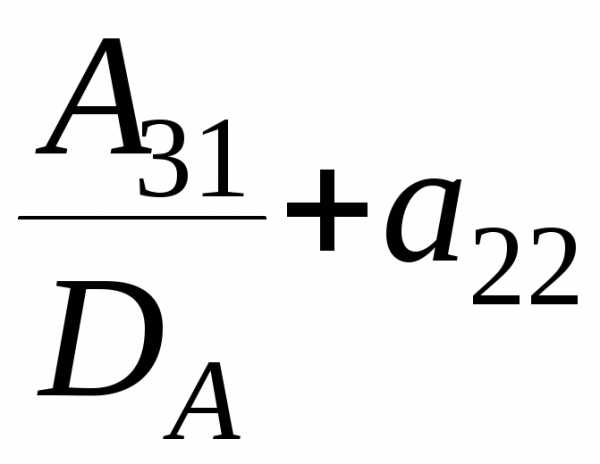 ·
· ·=
·=
=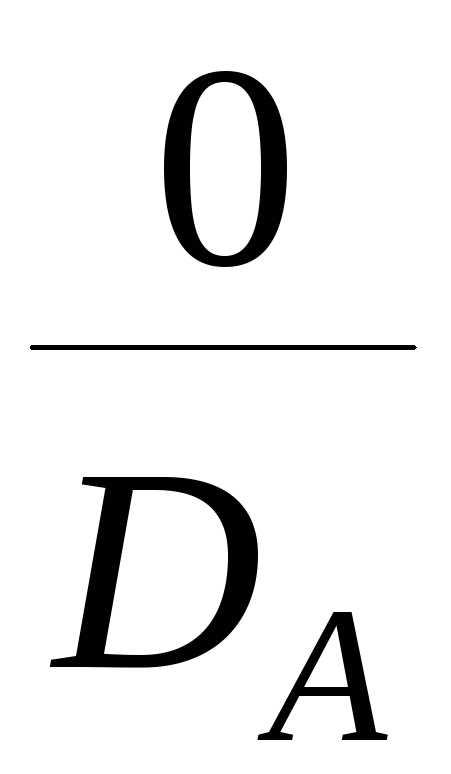 = 0
= 0
В итоге
а11 | а12 | а13 | A11/DА | A21/DА | A31/DА | 1 | 0 | 0 | |||
С=AA | а21 | а22 | а23 | A12/DА | A22/DА | A32/DА | = | 0 | 1 | 0 | =E |
а32 | а33 | A13/DА | A23/DА | A33/DА | 0 | 0 | 1 |
Матрица
A21 | A31 | |||||
| A12 | A22 | A32 | ( 14 ) | ||
A13 | A23 | A33 |
называется матрицей, присоединённой к А.
(Используется также обозначение  ).
Обратная матрица А-1 через присоединённую
).
Обратная матрица А-1 через присоединённую  выражается так:
выражается так:
| 1 |
| ( 15 ) |
DA |
Обратную матрицу будем находить по следующей схеме:
1. Находим определитель матрицы А.
2. Находим алгебраические дополнения всех элементов аij матрицы и записываем новую матрицу.
3. Меняем местами строки и столбцы полученной матрицы (транспонируем матрицу).
4. Умножаем полученную матрицу на 1/DA.
Пример 6. (Лена Иванова, КШ-061).
Дана матрица
Найти обратную матрицу.
1. Вычисляем определитель матрицы А:
2 | 5 | 7 | 2 | 5 | 7 | ||||
DA = | 6 | 3 | 4 | = | 0 | -12 | -17 | = | (492 — 493) = -1 |
5 | -2 | -3 | 0 | -29/2 | -41/2 |
Так как DA ≠ 0, то матрица А является невырожденной, и, значит, можно найти матрицу А-1.
2. Находим алгебраические дополнения элементов этого определителя:
A11 = | 3 | 4 | = -1, | A21= — | 5 | 7 | = 1, | A31= | 5 | 7 | = -1, |
-2 | -3 | -2 | -3 | 3 | 4 |
A12= — | 6 | 4 | = 38, | A22= | 2 | 7 | = -41, | A32= — | 2 | 7 | = 34, |
5 | -3 | 5 | -3 | 6 | 4 |
A13 = | 6 | 3 | = -27, | A23=- | 2 | 5 | = 29, | A33= | 2 | 5 | = -24. |
5 | -2 | 5 | -2 | 6 | 3 |
Следовательно,
-1 | 1 | -1 | 1 | -1 | 1 | ||
A-1 = (-1) | 38 | -41 | 34 | = | -38 | 41 | -34 |
-27 | 29 | -24 | 27 | -29 | 24 |
Лекция 4.
studfiles.net
Умножение матрицы на матрицу онлайн
Умножение матрицы на матрицу
Операция умножения двух матриц А и В представляет собой вычисление
результирующей матрицы С, каждый элемент cij которой равен сумме произведений
элементов в соответствующей строке первой матрицы aik и элементов в столбце второй матрицы
bkj.
Две матрицы можно умножать между собой только тогда, когда количество столбцов в первой матрице совпадает с количеством
строк во второй матрице. Другими словами первая матрица обязательно должна быть согласованной со второй матрицей.
Таким образом, результатом операции умножения матрицы размера m×n на матрицу размером n×k
является матрица размером m×k.
Итак, произведение матрицы Аm×n на матрицу Вn×k – это матрица
Сm×k, элемент cij которой, находящийся в i-ой строке и
j-ом столбце, равен сумме произведений i-ой строки матрицы А на соответствующие
элементы j-ого столбца матрицы В.
Каждый элемент матрицы Сm×k равен:
где k принимает значение от 1 до n.
Рассмотрим пример умножения двух матриц.
Даны две матрицы А и В.
Найти произведение матриц А × В.
Решение.
Свойства умножения матриц (свойства справедливы, если матрицы подходящего порядка):
-
Ассоциативность
(А × В) × С = А × (В × С) -
Дистрибутивность
А × (В+С) = А×В + А×С(А+В) × С = А×С + В×С -
Ассоциативность и коммутативность относительно умножения на число
(k×A) × B = k × (A×B) = A × (k×B) -
В общем случае умножение матриц не коммутативно
А×В ≠ В×А -
Произведение коммутативно в случае умножения на единичную матрицу
Em × Am×n = Am×n × En = Am×n
Вы также можете
в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x
(например, в ячейку матрицы можно ввести 2x, или sin(x), или даже ((x+2)^2)/lg(x)).
Полный список доступных функций можно найти в справке.
www.yotx.ru
Умножение матриц
Каталин Дэвид
Чтобы можно было умножить две матрицы, количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Алгоритм умножения матриц
Умножаем элементы в строках первой матрицы на элементы в столбцах второй матрицы.
- Умножаем элементы первой строки на элементы первого столбца.
- Умножаем первый элемент первой строки на первый элемент первого столбца.
- Умножаем второй элемент первой строки на второй элемент первого столбца.
- Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и первого столбца второй матрицы.
- Складываем полученные произведения.
- Полученный результат будет первым элементом первой строки произведения матриц.
- Умножаем элементы первой строки первой матрицы на элементы второго столбца второй матрицы.
- Умножаем первый элемент первой строки на первый элемент второго столбца.
- Умножаем второй элемент первой строки на второй элемент второго столбца.
- Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и второго столбца второй матрицы.
- Складываем полученные произведения.
- Полученный результат будет вторым элементом первой строки произведения матриц.
- Применяя тот же самый алгоритм, умножаем элементы первой строки первой матрицы на элементы остальных столбцов второй матрицы. Полученные числа составят первую строку вычисляемой матрицы.
- Вторая строка вычисляемой матрицы находится аналогично умножением элементов второй строки первой матрицы на элементы каждого столбца второй матрицы: результаты записываются в новую матрицу после каждого суммирования.
- Делаем это с каждой строкой первой матрицы, пока все строки новой матрицы не будут заполнены.
Пример 7
$A= \begin{pmatrix} 1 & 2 & 2\\ 3 & 1 & 1 \end{pmatrix}$
$B=\begin{pmatrix} 4 & 2 \\ 3 & 1 \\ 1 & 5\\ \end{pmatrix}$
Заметим, что матрица A имеет 3 столбца, а матрица B имеет 3 строки, значит, их можно перемножить.
$A \cdot B=$ $\begin{pmatrix} \color{red}1 &\color{blue}2 & \color{green}2\\ \color{red}3 &\color{blue}1 & \color{green}1 \end{pmatrix} \begin{pmatrix} \color{red}4 & \color{red}2 \\ \color{blue}3 & \color{blue}1 \\ \color{green}1 & \color{green}5 \end{pmatrix}=$ $\begin{pmatrix} \color{red}{1\cdot4}+\color{blue}{2\cdot3}+\color{green}{2\cdot1} & \color{red}{1\cdot2}+\color{blue}{2\cdot1}+\color{green}{2\cdot5}\\ \color{red}{3\cdot4}+\color{blue}{1\cdot3}+\color{green}{1\cdot1} & \color{red}{3\cdot2}+\color{blue}{1\cdot1}+\color{green}{1\cdot5} \end{pmatrix}=$ $\begin{pmatrix} 12 & 14\\ 16 & 12\\ \end{pmatrix}$$B \cdot A = \begin{pmatrix} \color{red}4 &\color{blue}2 \\ \color{red}3 & \color{blue}1 \\ \color{red}1 & \color{blue}5 \end{pmatrix} \begin{pmatrix} \color{red}1 &\color{red}2 & \color{red}2\\ \color{blue}3 &\color{blue}1 & \color{blue}1 \end{pmatrix}=$
$\begin{pmatrix} \color{red}{4\cdot1}+\color{blue}{2\cdot3} & \color{red}{4\cdot2}+\color{blue}{2\cdot1} & \color{red}{4\cdot2}+\color{blue}{2\cdot1}\\ \color{red}{3\cdot1}+\color{blue}{1\cdot3} & \color{red}{3\cdot2}+\color{blue}{1\cdot1} & \color{red}{3\cdot2}+\color{blue}{1\cdot1}\\ \color{red}{1\cdot1}+\color{blue}{5\cdot3} & \color{red}{1\cdot2}+\color{blue}{5\cdot1} & \color{red}{1\cdot2}+ \color{blue}{5\cdot1} \end{pmatrix} =$ $\begin{pmatrix} 10 & 10 & 10 \\ 6 & 7 & 7 \\ 16 & 7 & 7 \end{pmatrix}$
Заметим, что $A \cdot B \neq B \cdot A$
Пример 8
$A= \begin{pmatrix} 5 & 2 \\ 3 & 1 \end{pmatrix} B= \begin{pmatrix} 4 & 6 \\ 5 & 2 \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}5 & \color{blue}2 \\ \color{red}3 & \color{blue}1 \end{pmatrix} \cdot \begin{pmatrix} \color{red}4 & \color{red}6 \\ \color{blue}5 & \color{blue}2 \end{pmatrix} =\begin{pmatrix} \color{red}{5\cdot4}+\color{blue}{2\cdot5} & \color{red}{5\cdot6}+\color{blue}{2\cdot2} \\ \color{red}{3\cdot4}+\color{blue}{1\cdot5} & \color{red}{3\cdot6}+\color{blue}{1\cdot2} \end{pmatrix} =$ $\begin{pmatrix} 30 & 34\\ 17 & 20 \end{pmatrix}$
$B \cdot A= \begin{pmatrix} \color{red}4 & \color{bl
www.math10.com
Умножение на единичную матрицу
На основании правила умножения матриц получаем:
АЕ = | а11 | а12 . | 1 | 0 | = | а11 | а12 |
а21 | а22 | 0 | 1 | а21 | а22 | ||
EA= | 1 | 0 . | а11 | а12 | = | а11 | а12 |
0 | 1 | а21 | а22 | а21 | а22, | ||
т.е. АЕ = ЕА = А (11)
Произведение квадратной матрицы любого порядка на соответствующую единичную матрицу равняется первоначальной матрице. Таким образом, при умножении матриц единичная матрица играет роль единицы, поэтому и называется единичной.
Понятие обратной матрицы
Если А – квадратная матрица, то обратной по отношению к А называется матрица, которая, будучи умноженной на А (как справа, так и слева), даёт единичную матрицу. Обозначив обратную матрицу через А-1, запишем
А-1А = АА-1 = Е (12)
Если обратная матрица А-1 существует, то матрица А называется обратимой. Операция вычисления обратной матрицы называется обращением матрицы. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной.
Нахождение матрицы, обратной данной
Пусть дана невырожденная матрица
а11 | а12 | а13 | ||
А= | а21 | а22 | а23 | |
а31 | а32 | а33 |
а11 | а12 | а13 | |||
DА = | а21 | а22 | а23 | ≠ 0 | |
а31 | а32 | а33 | |||
Обратной матрицей А-1 будет матрица
A11/DА | A21/DА | A31/DА | ||||
A-1 = | A12/DА | A22/DА | A32/DА | , | ( 13 ) | |
A13/DА | A23/DА | A33/DА |
где Аij – алгебраическое дополнение элемента аij определителя DA.
Убедиться в этом можно, умножая матрицу А на матрицу А-1. Например, элементы с11 и с23 определяются так:
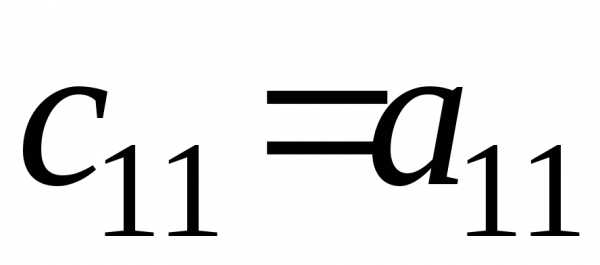 ·
·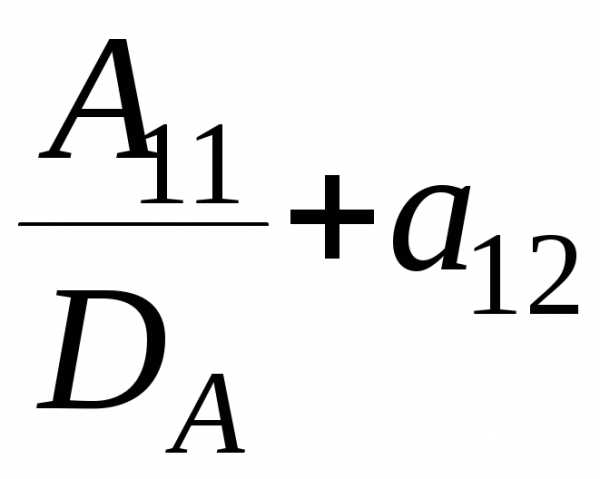 ·
·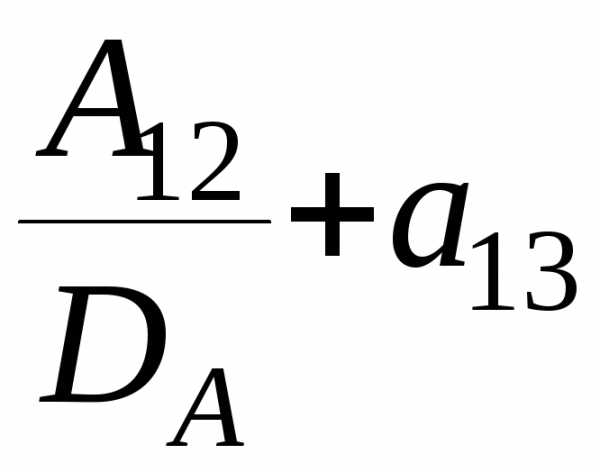 ·
·
c23=a21·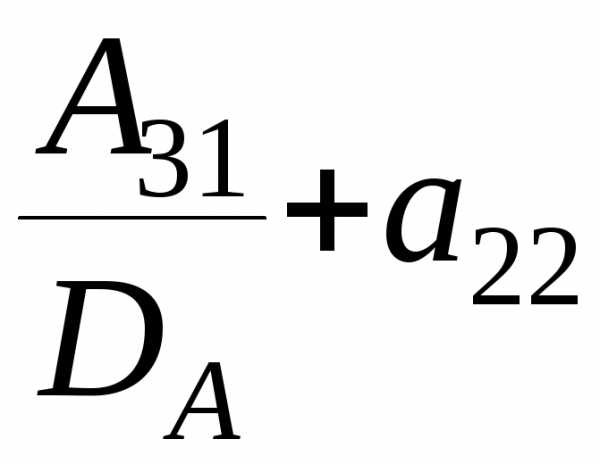 ·
·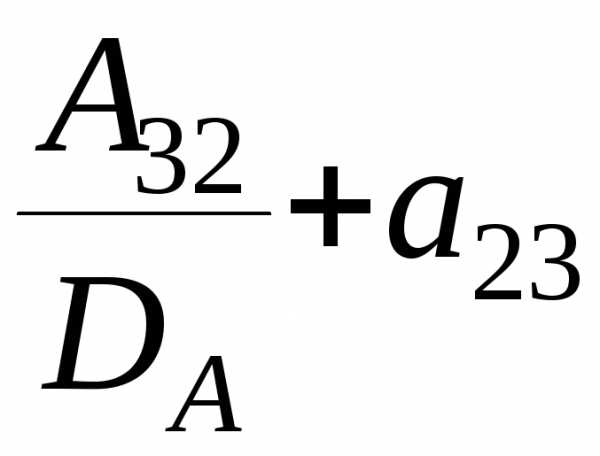 ·=
·=
= = 0
= 0
В итоге
а11 | а12 | а13 | A11/DА | A21/DА | A31/DА | 1 | 0 | 0 | |||
С=AA-1= | а21 | а22 | а23 | A12/DА | A22/DА | A32/DА | = | 0 | 1 | 0 | =E |
а31 | а32 | а33 | A13/DА | A23/DА | A33/DА | 0 | 0 | 1 |
Матрица
A11 | A21 | A31 | ||||
| A12 | A22 | A32 | ( 14 ) | ||
A13 | A23 | A33 |
называется матрицей, присоединённой к А.
(Используется также обозначение  ).
Обратная матрица А-1 через присоединённую
).
Обратная матрица А-1 через присоединённую  выражается так:
выражается так:
| 1 |
| ( 15 ) |
DA |
Обратную матрицу будем находить по следующей схеме:
1. Находим определитель матрицы А.
2. Находим алгебраическое дополнение всех элементов аij матрицы и записываем новую матрицу.
3. Меняем местами строки и столбцы полученной матрицы (транспонируем матрицу).
4. Умножаем полученную матрицу на 1/DA.
Пример 6. (Лена Иванова, КШ-061).
Дана матрица
Найти обратную матрицу.
1. Вычисляем определитель матрицы А:
2 | 5 | 7 | 2 | 5 | 7 | ||||
DA = | 6 | 3 | 4 | = | 0 | -12 | -17 | = | (492 — 493) = -1 |
5 | -2 | -3 | 0 | -29/2 | -41/2 |
Так как DA ≠ 0, то матрица А является невырожденной, и, значит, можно найти матрицу А-1.
2. Находим алгебраические дополнения элементов этого определителя:
A11 = | 3 | 4 | = -1, | A21= — | 5 | 7 | = 1, | A31= | 5 | 7 | = -1, |
-2 | -3 | -2 | -3 | 3 | 4 |
A12= — | 6 | 4 | = 38, | A22= | 2 | 7 | = -41, | A32= — | 2 | 7 | = 34, |
5 | -3 | 5 | -3 | 6 | 4 |
A13 = | 6 | 3 | = -27, | A23=- | 2 | 5 | = 29, | A33= | 2 | 5 | = -24. |
5 | -2 | 5 | -2 | 6 | 3 |
Следовательно,
-1 | 1 | -1 | 1 | -1 | 1 | ||
A-1 = -1 | 38 | -41 | 34 | = | -38 | 41 | -34 |
-27 | 29 | -24 | 27 | -29 | 24 |
Лекция 4.
studfiles.net
Умножение матриц, формулы и примеры
ОПРЕДЕЛЕНИЕ Произведением матрицы размером на матрицу размером называется матрица () размером элементы которой определяются формулой:
Иначе говоря, элемент матрицы стоящий в -той строке и -том столбце, равен сумме произведений элементов -той строки матрицы на соответствующие элементы -го столбца матрицы Таким образом, умножение осуществляется по правилу умножения строки на столбец.
Не всякие две матрицы можно перемножить. Произведение двух матриц возможно только в том случае, если число столбцов матрицы совпадает с числом строк в матрице . Для того чтобы перемножить две квадратные матрицы необходимо, чтобы они были одного порядка. При этом в результате получится матрица того же порядка, что и перемножаемые матрицы.
Как умножать матрицы, примеры
ПРИМЕР 1| Задание | Найти произведение матрицы и вектора-столбца .
|
| Решение | Матрица имеет размерность матрица имеет размерность значит размерность произведения будет Действительно,
Заметим, что произведение этих матриц в обратном порядке невозможно. |
| Ответ |
Произведение двух матриц в общем случае зависит от порядка сомножителей, то есть оно не коммутативно:
ПРИМЕР 2
| Задание | Заданы матрицы и . Найти их произведения и
|
| Решение | Матрица имеет размерность а матрица – размерность тогда размерность произведения будет . Действительно, умножая по принципу, строка первой матрицы на столбец второй, получим
Произведение так же будет существовать и его размерность будет .
|
| Ответ |
Но бывают матрицы, для которых выполняется равенство
такие матрицы называются перестановочными или коммутирующими. Такие матрицы будут обязательно квадратными.
ПРИМЕР 3| Задание | Проверить являются ли перестановочными матрицы и , если
|
| Решение | Найдем произведения этих матриц и .
Таким образом, для заданных матриц выполняется равенство поэтому они являются перестановочными. |
| Ответ | Матрицы и перестановочные. |
Определитель матрицы и способы вычисления
Обратная матрица и способы вычисления
Ранг матрицы
Транспонирование матрицы
Сложение матриц
Единичная матрица
ru.solverbook.com
Как умножать матрицы?
Наверное, не один студент в наше время испытывает трудности по высшей математике и в частности задается вопросом о том, как умножать матрицы. Разумеется, что в наше прогрессивное время практически все можно сделать во всемирной сети. В интернете сейчас можно без проблем выполнить большинство действий высшей математики, в том числе и умножить матрицы онлайн. На множестве современных ресурсов и сервисов для решения обсуждаемой задачи необходимо будет всего лишь ввести конкретные условия и сделать еще пару кликов. Но в нашей статье мы попытаемся осветить данную тему с более традиционной точки зрения.
Отличие умножений
Умножение матриц в некоторой степени отличается от обыкновенного умножения переменных или чисел. Причиной этому является структура элементов, которые принимают участие в операциях, а потому здесь свои особенности и правила.
Наиболее просто и кратко сформулировать сущность данной операции можно следующим образом: необходимо умножать строки матрицы на их столбцы. Поговорим об этом правиле немного подробнее, а также укажем некоторые особенности и возможные ограничения.
Умножение на единичные матрицы
Как умножить матрицу на матрицу в том случае, когда одна из них единична? При такой операции исходная матрица переходит в саму себя. Соответственно умножение любой произвольной матрицы на нулевую даст в результате также нулевую матрицу. При этом не особенно даже надо задумываться о том, как умножить матрицу на строку.
Классическое умножение
Главным условием, накладываемым на матрицы, участвующие в операции, является соответствие количества строк в одной матрице количеству столбцов в другой. Ведь догадаться не трудно, что в противных случаях просто не на что будет умножать.
Следует отдельно отметить немаловажный момент. Умножение матриц не обладает свойством коммутативности («перестановочности» множителей). Выражаясь более просто, произведение А на В не будет равно произведению В на А. Не путайте с правилами для умножения обыкновенных чисел. Рассмотрим теперь конкретней процесс того, как умножить матрицу на столбец.
Пускай по условию задачи нам необходимо матрицу А умножить на матрицу В. Для этого нужно взять первую строку первой матрицы и ее элементы умножать на элементы первого столбца второй матрицы. Все произведения, которые получились, следует сложить и записать на место а-1-1 в итоговое произведение (итоговую матрицу).
После этого аналогичным образом умножайте первую строку первой же матрицы на второй столбец второй матрицы. Получаемый результат записывайте справа от первого полученного числа в итоговой матрице, то есть, помещайте его на позицию а-1-2.
Затем аналогичным образом
elhow.ru
25. Матричная алгебра. Сложение матриц и умножение матрицы на число. Перемножение матриц. Диагональная и единичная матрицы. Обратная матрица.
Сложение матриц и умножение на число Сложение определено только для матриц одинаковых размеров. Определение 14.2 Суммой матриц иразмеровявляется матрицатаких же размеров, у которой,,.Определение 14.3 Произведением матрицы размеровна число называется матрицатаких же размеров, у которой,,.
Другими словами, при умножении матрицы на число все ее элементы умножаются на это число. Операцию вычитания матриц можно определить следующим способом: что соответствует вычитанию элементов, стоящих на одинаковых местах.
Используя операции сложения и умножения, мы можем находить линейные комбинации матриц, то есть выражения вида , где— числа,— матрицы одинаковых размеров. Операции сложения матриц и умножения матрицы на число, называемыелинейными операциями, обладают следующими свойствами:
— свойство коммутативности;
— свойство ассоциативности;
;
;
— свойство дистрибутивности;
;
;
.
Умножение матриц Определение 14.4 Произведением матрицы размеровна матрицуразмеровназывается матрицаразмеров, элементы которой вычисляются по формуле
(14.5) |
где ,. Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой — второй. Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено. В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя. Правило вычисления элементов произведения можно сформулировать следующим образом. Для того, чтобы вычислить элемент произведения, стоящий в-ой строке и-ом столбце, нужно взять-ую строку первого сомножителя и-ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить. (Точно так же мы поступаем, когда находим скалярное произведение двух векторов по их координатам, см. формулу (14.2).) Предложение 14.4 Умножение матриц обладает следующими свойствами: — ассоциативность умножения;, где— число;,— дистрибутивность умножения;,, где— единичная матрица соответствующего порядка. Предполагается, что все указанные произведения имеют смысл. Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной. Квадратная матрица называется верхней треугольной (нижней треугольной), если все ее элементы, стоящие ниже (выше) главной диагонали, равны нулю. Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны 1. Для обозначения единичной матрицы обычно используется буква . Порядок матрицы при этом обычно ясен из контекста. Из определения единичной матрицы видно, что ее элементыравны нулю, если индексы различны, и равны 1, если индексы совпадают. В математике таким свойством обладает величина, называемаясимволом Кронекера: Поэтому.Обратная матрица Определение14.8 Матрица называетсяобратной матрицей для квадратной матрицы , если. Из определения следует, что обратная матрицабудет квадратной матрицей того же порядка, что и матрица(иначе одно из произведенийилибыло бы не определено). Обратная матрица для матрицыобозначается. Таким образом, еслисуществует, то. Из определения обратной матрицы следует, что матрицаявляется обратной для матрицы, то есть. Про матрицыиможно говорить, что они обратны друг другу или взаимно обратны. Предложение14.20 Если матрица имеет обратную, тои. Доказательство. Так как определитель произведения матриц равен произведению определителей, то ., поэтому, что невозможно при. Из предыдущего равенства следует также. Последнее предложение можно сформулировать в следующем виде. Если определитель матрицы равен нулю, то обратная к ней не существует. Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения. Определение14.9 Квадратную матрицу назовемвырожденной или особенной матрицей, если , иневырожденной или неособенной матрицей, если . Предложение14.21 Если обратная матрица существует, то она единственна. Доказательство. Пусть две матрицы иявляются обратными для матрицы. ТогдаиСледовательно,. Предложение14.22 Если квадратная матрица является невырожденной, то обратная для нее существует и
(14.14) |
где — алгебраические дополнения к элементам. Доказательство. Так как для невырожденной матрицыправая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы . Обозначим правую часть равенства (14.14) буквой . Тогда нужно проверить, чтои что. Докажем первое из этих равенств, второе доказывается аналогично. Пусть. Найдем элементы матрицы, учитывая, что:
Если , то сумма справа равна нулю, то естьпри. Если, тоСумма справа представляет собой разложение определителя матрицыпо-ой строке. Таким образом,Итак, в матрицедиагональные элементы равны 1, а остальные равны нулю, то есть.Теорема 14.1 Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица— невырожденная, обратная матрица единственна, и справедлива формула (14.14)
studfiles.net

 =
=  =
= 
 =
= 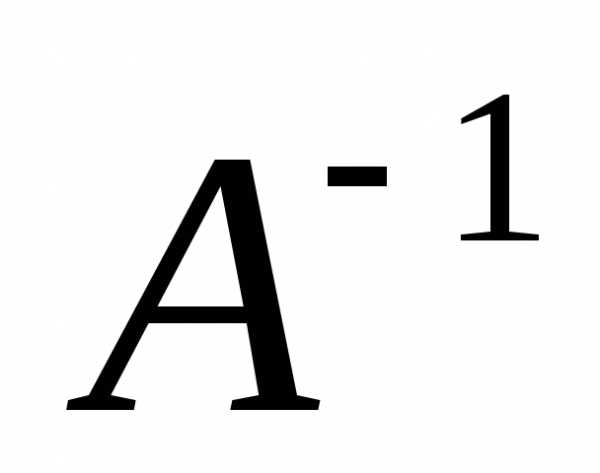 =
= 