Тригонометрическая единичная окружность – Тригонометрическая окружность. Подробная теория с примерами.

Тригонометрическая окружность Википедия

Единичная окружность — окружность с радиусом 1 и центром в начале координат. Понятие единичной окружности обобщается до n{\displaystyle n}-мерного пространства (n>2{\displaystyle n>2}), в таком случае говорят о «единичной сфере».

Для координат всех точек на окружности, согласно теореме Пифагора, выполняется равенство x2+y2=1{\displaystyle x^{2}+y^{2}=1}.

Тригонометрические функции

Все тригонометрические функции угла θ могут быть сконструированы геометрически при помощи единичной окружности.

С помощью единичной окружности могут быть наглядно описаны тригонометрические функции (в контексте такого описания единичную окружность иногда называют «тригонометрическим кругом», что не слишком удачно, так как рассматривается именно окружность, а не круг).

Синус и косинус могут быть описаны следующим образом: если соединить любую точку (x,y){\displaystyle (x,y)} на единичной окружности с началом координат (0,0){\displaystyle (0,0)}, получается отрезок, находящийся под углом α{\displaystyle \alpha } относительно положительной полуоси абсцисс. Тогда действительно:

cos⁡α=x{\displaystyle \cos \alpha =x},

sin⁡α=y{\displaystyle \sin \alpha =y}.

При подстановке этих значений в уравнение окружности x2+y2=1{\displaystyle x^{2}+y^{2}=1} получается:

cos2⁡α+sin2⁡α=1{\displaystyle \cos ^{2}\alpha +\sin ^{2}\alpha =1}.

(Используется следующая общепринятая нотация: cos2⁡x=(cos⁡x)2{\displaystyle \cos ^{2}x=(\cos x)^{2}}.)

Тут же наглядно описывается периодичность тригонометрических функций, так как соответствующее углу положение отрезка не зависит от количества «полных оборотов»:

sin⁡(x+2πk)=sin⁡(x){\displaystyle \sin(x+2\pi k)=\sin(x)}

cos⁡(x+2πk)=cos⁡(x){\displaystyle \cos(x+2\pi k)=\cos(x)}

для всех целых чисел k{\displaystyle k}, то есть для k∈Z{\displaystyle k\in \mathbb {Z} }.

Комплексная плоскость

В комплексной плоскости единичная окружность — это следующее множество G⊂C{\displaystyle G\subset \mathbb {C} }:

G={z:Re{z}2+Im{z}2=1}={z:z=eiϕ,0≤ϕ<2π}{\displaystyle G=\{z:\mathrm {Re} \{z\}^{2}+\mathrm {Im} \{z\}^{2}=1\}=\{z:z=e^{i\phi },0\leq \phi <2\pi \}}

Множество G{\displaystyle G} является подгруппой группы комплексных чисел по умножению, её нейтральный элемент — это ei0=1{\displaystyle e^{i0}=1}).

См. также

wikiredia.ru

Тригонометрический круг Википедия

Единичная окружность — окружность с радиусом 1 и центром в начале координат. Понятие единичной окружности обобщается до n{\displaystyle n}-мерного пространства (n>2{\displaystyle n>2}), в таком случае говорят о «единичной сфере».

Для координат всех точек на окружности, согласно теореме Пифагора, выполняется равенство x2+y2=1{\displaystyle x^{2}+y^{2}=1}.

Тригонометрические функции

Все тригонометрические функции угла θ могут быть сконструированы геометрически при помощи единичной окружности.

С помощью единичной окружности могут быть наглядно описаны тригонометрические функции (в контексте такого описания единичную окружность иногда называют «тригонометрическим кругом», что не слишком удачно, так как рассматривается именно окружность, а не круг).

Синус и косинус могут быть описаны следующим образом: если соединить любую точку (x,y){\displaystyle (x,y)} на единичной окружности с началом координат (0,0){\displaystyle (0,0)}, получается отрезок, находящийся под углом α{\displaystyle \alpha } относительно положительной полуоси абсцисс. Тогда действительно:

cos⁡α=x{\displaystyle \cos \alpha =x},

sin⁡α=y{\displaystyle \sin \alpha =y}.

При подстановке этих значений в уравнение окружности x2+y2=1{\displaystyle x^{2}+y^{2}=1} получается:

cos2⁡α+sin2⁡α=1{\displaystyle \cos ^{2}\alpha +\sin ^{2}\alpha =1}.

(Используется следующая общепринятая нотация: cos2⁡x=(cos⁡x)2{\displaystyle \cos ^{2}x=(\cos x)^{2}}.)

Тут же наглядно описывается периодичность тригонометрических функций, так как соответствующее углу положение отрезка не зависит от количества «полных оборотов»:

sin⁡(x+2πk)=sin⁡(x){\displaystyle \sin(x+2\pi k)=\sin(x)}

cos⁡(x+2πk)=cos⁡(x){\displaystyle \cos(x+2\pi k)=\cos(x)}

для всех целых чисел k{\displaystyle k}, то есть для k∈Z{\displaystyle k\in \mathbb {Z} }.

Комплексная плоскость

В комплексной плоскости единичная окружность — это следующее множество G⊂C{\displaystyle G\subset \mathbb {C} }:

G={z:Re{z}2+Im{z}2=1}={z:z=eiϕ,0≤ϕ<2π}{\displaystyle G=\{z:\mathrm {Re} \{z\}^{2}+\mathrm {Im} \{z\}^{2}=1\}=\{z:z=e^{i\phi },0\leq \phi <2\pi \}}

Множество G{\displaystyle G} является подгруппой группы комплексных чисел по умножению, её нейтральный элемент — это ei0=1{\displaystyle e^{i0}=1}).

См. также

wikiredia.ru

Единичная окружность и тригонометрические функции [Love Soft]

Окружность называется единичной, если её радиус равен единице.

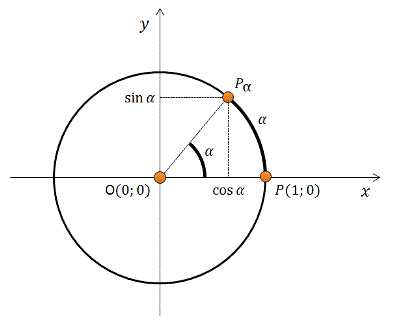
Повернем точку (1;0) вокруг начала координат на заданный угол.

Интерактивная модель — показывает как измеряют углы на единичной окружности.

• Синусом угла называется ордината полученной точки.

• Косинусом угла называется абсцисса полученной точки.

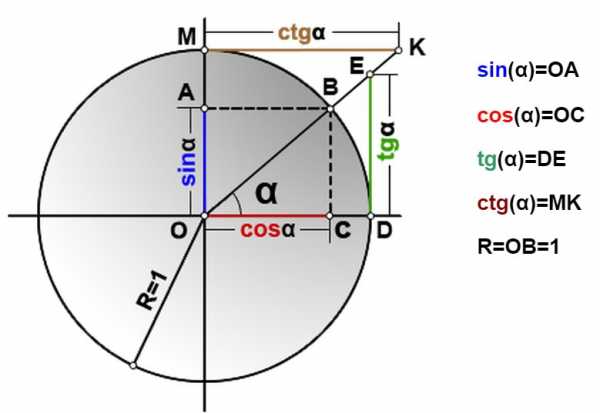
• Тангенс угла – это отношение синуса этого угла к косинусу этого же угла.

$$ \operatorname{tg}(\alpha) = \frac{\sin \alpha} {\cos \alpha} $$ $$\cos \alpha \ne 0$$ $$\alpha \ne \frac \pi 2 + \pi k, k \in \mathbb{Z} $$

khanacademy.org — упражнения: на единичной окружности опытным путем определить значение тригонометрических функций

Задачи

1. Расположить в порядке возрастания cos 1, cos 2, cos 3, cos 4, cos 5 и cos 6, без калькулятора и таблиц.

2. Расположить в порядке возрастания sin 1, sin 2, sin 3, sin 4, sin 5, sin 6

3. Сравнить sin 2 и cos 2

4. Сравнить sin 1 и cos 1

ответ

Чтобы найти углы в 1, 2, 3, 4, 5 и 6 радиан на единичной окружности, можно вспомнить, что π приближенно равно 3,14, и привязать их местонахождение к π, π/2, 3π/2 и 2π. Можно пойти другим путем: угол в 1 радиан соответствует длине дуги, равной радиусу окружности. Соответственно, отмечаем 6 раз на окружности длину радиуса. Конечно, рисунок получается очень приблизительным, но наглядным. Итак, косинус 1, косинус 2, косинус 3, косинус 4, косинус 5 и косинус 6 — это абсциссы отмеченных точек.

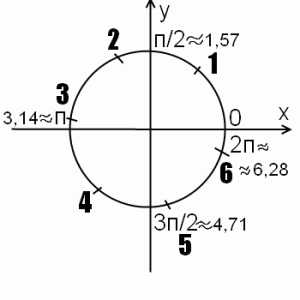
Вопрос сравнения косинусов с разными знаками решается элементарно: любое положительное число больше любого отрицательного: например, cos1 > cos3. При сравнении косинусов с одинаковыми знаками можно использовать геометрическую интерпретацию.

См. также wolframalpha

См. также Сравнение тригонометрических выражений

Мнемоническое правило

Легко запомнить синус и косинус с помощью ассоциации. Косинус — колобок (и начинаются оба слова с ко-). Колобку как удобнее двигаться: прыгать вверх-вниз или катиться влево-вправо? Правильно, с его фигурой ему легче передвигаться по горизонтали, то есть по оси OX.

Ассоциация: косинус — колобок — x. Ну а синус, соответственно — y.Таким образом, синус произвольного угла — это ордината y точки P на единичной окружности, полученной из точки A поворотом вокруг начала координат на угол альфа, косинус произвольного угла — ее абсцисса x.

Эта ассоциация поможет нам легко определять знаки синуса и косинуса.

Синусоида и тригонометрическая окружность

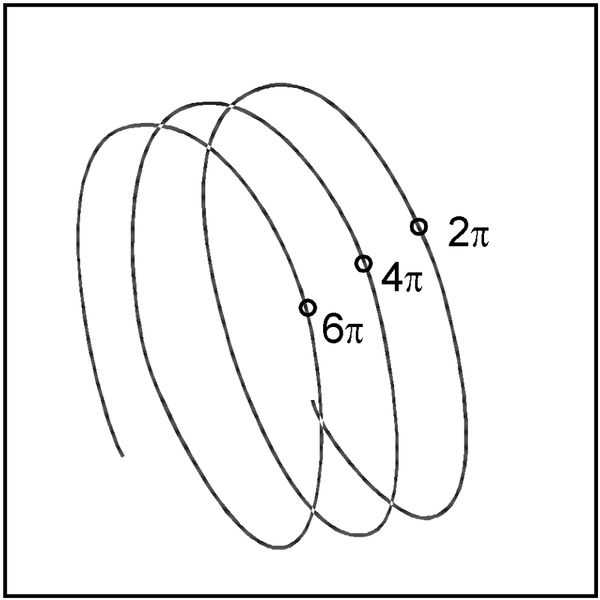
Тригонометрическая окружность как спираль

Тригонометрическую окружность можно представить себе как спираль, которую мы видим с «торца»:

Интерактивные модели

Интерпретации синуса и косинуса

(1) Синус — это высота объекта над уровнем наблюдателя, косинус — расстояние до объекта от наблюдателя.

(2) Имеются два радиуса единичной окружности с некоторым углом между ними. Какова длина хорды, заключённой между ними? Сейчас мы отображение угла в длину хорды называем функцией синуса угла.

И вот обратная задача: для некоторой длины хорды — каков будет угол? Несомненно, сейчас мы это называем арксинусом.

И, от индийского слова «chord», буквально переведённого на арабский и затем неправильно переведённого на латынь, появилось слово «sine». Это было в 12-ом веке, а в начале 13-го века его активно начал использовать Фибоначчи.

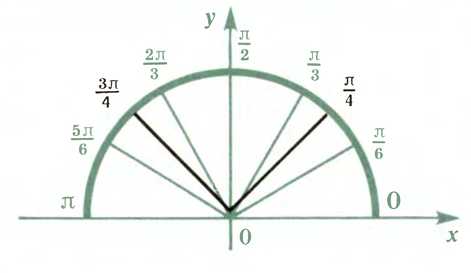
Основные углы

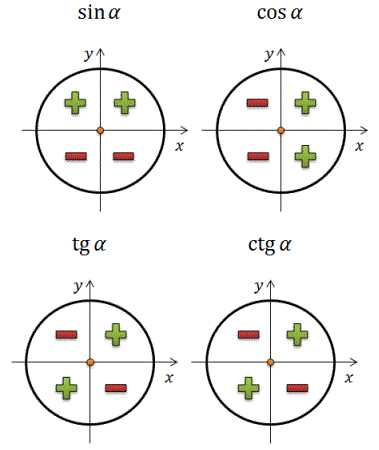
Знаки тригонометрических функций

Четность и нечетность тригонометрических функций

Итак, косинус — Колобок. Вы себе представляете похудевшего Колобка? Да, это будет уже не Колобок. Поэтому, чтобы сохранить свою круглую форму, Колобку надо усиленно питаться. Что он и делает. Поэтому он даже минус съедает:

cos(-x) = cos x.

Все остальные тригонометрические функции, глядя на минус, говорят: «Фу, какая гадость!» И минус выплевывают:

sin(-x) = -sin x

tg(-x) = -tg x

ctg(-x) = -ctg x.

Что в переводе на язык математики означает четность косинуса и нечетность остальных тригонометрических функций.

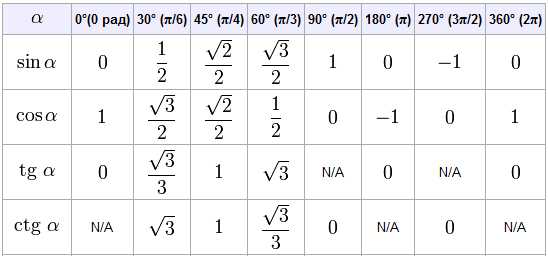
Таблица значений тригонометрических функций

еще раз

$\alpha$	$0^\circ$	$30^\circ$	$45^\circ$	$60^\circ$	$90^\circ$	$180^\circ$	$270^\circ$	$360^\circ$
$radians$	$0$	$\frac\pi 6$	$\frac\pi 4$	$\frac\pi 3$	$\frac\pi 2$	$\pi$	$\frac{3\pi}{2}$	$2\pi$
$\sin\alpha$	$0$	$\frac{1}{2}$	$\frac{\sqrt2}{2}$	$\frac{\sqrt3}{2}$	$1$	$0$	$-1$	$0$
$\cos\alpha$	$1$	$\frac{\sqrt3}{2}$	$\frac{\sqrt2}{2}$	$\frac{1}{2}$	$0$	$-1$	$0$	$1$
$\mathrm{tg}\,\alpha$	$0$	$\frac{\sqrt3}{3}$	$1$	$\sqrt3$	–	$0$	–	$0$
$\mathrm{ctg}\,\alpha$	–	$\sqrt3$	1	$\frac{\sqrt3}{3}$	$0$	–	$0$	–

Как легко запомнить эту таблицу:

---

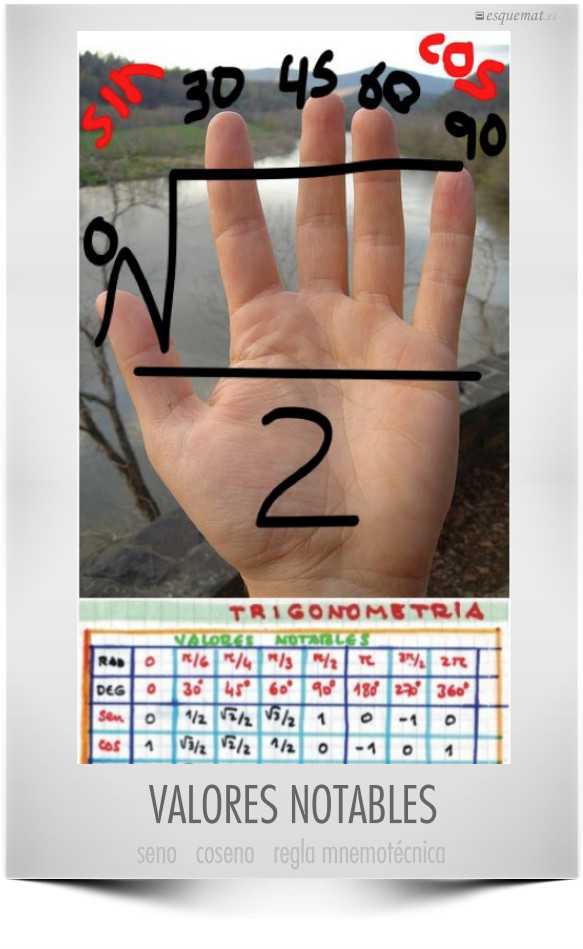
Учебники:
Единичная окружность, синус, косинус любого угла — Геометрия Мерзляк 9 класс, параграф 1
Синус, косинус, тангенс острого угла — Геометрия 8 класс

mat/trig/edin-circle.txt · Последние изменения: 2015/08/27 12:26 — kc

xlench.bget.ru

Единичная окружность — это… Что такое Единичная окружность?

Единичная окружность — это окружность с радиусом 1 и центром в начале координат. Понятие единичной окружности можно легко обобщить до n-мерного пространства (). В таком случае используется термин «единичная сфера».

Для всех точек на окружности действительно согласно с теоремой Пифагора: .

Не путайте термины «окружность» и «круг»!

• Окружность — геометрическое место точек, расположенное на данном расстоянии от данной точки, на одной плоскости — кривая.
• Круг — геометрическое место точек, расположенное не дальше чем окружность, на одной плоскости — фигура.

Все тригонометрические функции, сконструированные геометрически к углу θ в единичном кругу.

Синус и косинус могут быть описаны следующим образом: соединив любую точку на единичной окружности с началом координат , мы получаем отрезок, находящийся под углом относительно положительной полуоси абсцисс. Тогда действительно:

Подставив эти значения в вышеуказанное уравнение , мы получаем:

Обратите внимание на общепринятое написание .

Тут же наглядно описывается периодичность тригонометрических функций, так как угол отрезка не зависит от количества «полных оборотов»:

для всех целых чисел , иными словами, принадлежит .

В комплексной плоскости единичную окружность описывает множество :

Множество удоволетворяет условиям мультипликативной группы (с нейтральным элементом ).

Ссылки

См. также

dic.academic.ru

Единичная окружность — Gpedia, Your Encyclopedia

Единичная окружность — окружность с радиусом 1 и центром в начале координат. Понятие единичной окружности обобщается до n{\displaystyle n}-мерного пространства (n>2{\displaystyle n>2}), в таком случае говорят о «единичной сфере».

Для координат всех точек на окружности, согласно теореме Пифагора, выполняется равенство x2+y2=1{\displaystyle x^{2}+y^{2}=1}.

Тригонометрические функции

Все тригонометрические функции угла θ могут быть сконструированы геометрически при помощи единичной окружности.

С помощью единичной окружности могут быть наглядно описаны тригонометрические функции (в контексте такого описания единичную окружность иногда называют «тригонометрическим кругом», что не слишком удачно, так как рассматривается именно окружность, а не круг).

Синус и косинус могут быть описаны следующим образом: если соединить любую точку (x,y){\displaystyle (x,y)} на единичной окружности с началом координат (0,0){\displaystyle (0,0)}, получается отрезок, находящийся под углом α{\displaystyle \alpha } относительно положительной полуоси абсцисс. Тогда действительно:

cos⁡α=x{\displaystyle \cos \alpha =x},

sin⁡α=y{\displaystyle \sin \alpha =y}.

При подстановке этих значений в уравнение окружности x2+y2=1{\displaystyle x^{2}+y^{2}=1} получается:

cos2⁡α+sin2⁡α=1{\displaystyle \cos ^{2}\alpha +\sin ^{2}\alpha =1}.

(Используется следующая общепринятая нотация: cos2⁡x=(cos⁡x)2{\displaystyle \cos ^{2}x=(\cos x)^{2}}.)

Тут же наглядно описывается периодичность тригонометрических функций, так как соответствующее углу положение отрезка не зависит от количества «полных оборотов»:

sin⁡(x+2πk)=sin⁡(x){\displaystyle \sin(x+2\pi k)=\sin(x)}

cos⁡(x+2πk)=cos⁡(x){\displaystyle \cos(x+2\pi k)=\cos(x)}

для всех целых чисел k{\displaystyle k}, то есть для k∈Z{\displaystyle k\in \mathbb {Z} }.

Комплексная плоскость

В комплексной плоскости единичная окружность — это следующее множество G⊂C{\displaystyle G\subset \mathbb {C} }:

G={z:Re{z}2+Im{z}2=1}={z:z=eiϕ,0≤ϕ<2π}{\displaystyle G=\{z:\mathrm {Re} \{z\}^{2}+\mathrm {Im} \{z\}^{2}=1\}=\{z:z=e^{i\phi },0\leq \phi <2\pi \}}

Множество G{\displaystyle G} является подгруппой группы комплексных чисел по умножению, её нейтральный элемент — это ei0=1{\displaystyle e^{i0}=1}).

См. также

www.gpedia.com