Теория множеств чисел – ТЕОРИЯ МНОЖЕСТВ это что такое ТЕОРИЯ МНОЖЕСТВ: определение — Философия.НЭС

Теория множеств: основные понятия и определения

Понятие множества является исходным не определяемым строго понятием. Приведем здесь определение множества (точнее, пояснение идеи множества), принадлежащее Г. Кантору: «Под многообразием или множеством я понимаю вообще все многое, которое возможно мыслить как единое, т.е. такую совокупность определенных элементов, которая посредством одного закона может быть соединена в одно целое».

Множества будем, как правило, обозначать большими буквами латинского алфавита, а их элементы — малыми, хотя иногда от этого соглашения придется отступать, так как элементами некоторого множества могут быть другие множества. Тот факт, что элемент а принадлежит множеству , записывается в виде .

В математике мы имеем дело с самыми различными множествами. Для элементов этих множеств мы используем два основных вида обозначений: константы и переменные.

Индивидная константа (или просто константа) с областью значений  обозначает фиксированный элемент множества . Таковы, например, обозначения (записи в определенной системе счисления) действительных чисел: . Для двух констант  и  с областью значений  будем писать , понимая под этим совпадение обозначаемых ими элементов множества .

Индивидное переменное (или просто переменное) с областью значений  обозначает произвольный, заранее не определенный элемент множества . При этом говорят, что переменное  пробегает множество  или переменное  принимает произвольные значения на множестве . Можно фиксировать значение переменного , записав , где  — константа с той же областью значений, что и . В этом случае говорят, что вместо переменного подставлено его конкретное значение , или произведена подстановка  вместо , или переменное  приняло значение .

Равенство переменных  понимается так: всякий раз, когда переменное  принимает произвольное значение , переменное  принимает то же самое значение , и наоборот. Таким образом, равные переменные «синхронно» принимают всегда одни и те же значения.

Обычно константы и переменные, область значений которых есть некоторое числовое множество, а именно одно из множеств  и , называют соответственно натуральными, целыми (или целочисленными), рациональными, действительными и комплексными константами и переменными. В курсе дискретной математики мы будем использовать различные константы и переменные, область значений которых не всегда является числовым множеством.

Для сокращения записи мы будем пользоваться логической символикой, позволяющей коротко, наподобие формул, записывать высказывания. Понятие высказывания не определяется. Указывается только, что всякое высказывание может быть истинным или ложным (разумеется, не одновременно!).

Логические операции (связки) над множествами

Для образования из уже имеющихся высказываний новых высказываний используются следующие логические операции (или логические связки).

1. Дизъюнкция : высказывание  (читается: » или «) истинно тогда и только тогда, когда истинно хотя бы одно из высказываний  и .

2. Конъюнкция : высказывание  (читается: » и «) истинно тогда и только тогда, когда истинны оба высказывания  и .

3. Отрицание : высказывание  (читается: «не «) истинно тогда и только тогда, когда  ложно.

4. Импликация : высказывание  (читается: «если , то » или » влечет «) истинно тогда и только тогда, когда истинно высказывание или оба высказывания ложны.

5. Эквивалентность (или равносильность) : высказывание  (читается: «, если и только если «) истинно тогда и только тогда, когда оба высказывания  и  либо одновременно истинны, либо одновременно ложны. Любые два высказывания  и , такие, что истинно , называют логически эквивалентными или равносильными.

Записывая высказывания с помощью логических операций, мы предполагаем, что очередность выполнения всех операций определяется расстановкой скобок. Для упрощения записи скобки зачастую опускают, принимая при этом определенный порядок выполнения операций («соглашение о приоритетах»).

Операция отрицания всегда выполняется первой, и потому ее в скобки не заключают. Второй выполняется операция конъюнкции, затем дизъюнкции и, наконец, импликации и эквивалентности. Например, высказывание  записывают так: . Это высказывание есть дизъюнкция двух высказываний: первое является отрицанием , а второе — . В отличие от него высказывание  есть отрицание дизъюнкции высказываний  и .

Например, высказывание  после расстановки скобок в соответствии с приоритетами примет вид

Сделаем некоторые комментарии по поводу введенных выше логических связок. Содержательная трактовка дизъюнкции, конъюнкции и отрицания не нуждается в специальных разъяснениях. Импликация  истинна, по определению, всякий раз, когда истинно высказывание  (независимо от истинности ) или  и  одновременно ложны. Таким образом, если импликация  истинна, то при истинности  имеет место истинность , но обратное может и не выполняться, т.е. при ложности  высказывание  может быть как истинным, так и ложным. Это и мотивирует прочтение импликации в виде «если , то «. Нетрудно также понять, что высказывание  равносильно высказыванию  и тем самым содержательно «если , то » отождествляется с «не  или «.

Равносильность  есть не что иное, как «двусторонняя импликация», т.е.  равносильно . Это означает, что из истинности  следует истинность  и, наоборот, из истинности  следует истинность .

Пример 1.1. Для определения истинности или ложности сложного высказывания в зависимости от истинности или ложности входящих в него высказываний используют таблицы истинности.

В первых двух столбцах таблицы записывают все возможные наборы значений, которые могут принимать высказывания  и . Истинность высказывания обозначают буквой «И» или цифрой 1, а ложность — буквой «Л» или цифрой 0. Остальные столбцы заполняют слева направо. Так для каждого набора значений  и  находят соответствующие значения высказываний.

Наиболее простой вид имеют таблицы истинности логических операций (табл. 1.1-1.5).

Рассмотрим сложное высказывание . Для удобства вычислений обозначим высказывание  через , высказывание  через , а исходное высказывание запишем в виде . Таблица истинности этого высказывания состоит из столбцов  и  (табл. 1.6).

Предикаты и кванторы

Сложные высказывания образуются не только посредством логических связок, но и с помощью предикатов и кванторов.

Предикат есть высказывание, содержащее одно или несколько индивидных переменных. Например, » есть четное число» или » есть студент МГТУ им. Баумана, поступивший в 1999 г.». В первом предикате  есть целочисленное переменное, во втором — переменное, пробегающее множество «человеческих индивидов». Примером предиката, содержащего несколько индивидных переменных, может служить: » есть сын «, » и  учатся в одной и той же группе», » делится на «, » меньше » и т.п. Предикаты будем записывать в виде , полагая, что в скобках перечислены все переменные, входящие в данный предикат.

Подставляя вместо каждого переменного, входящего в предикат , конкретное значение, т.е. фиксируя значения , где  — некоторые константы с соответствующей областью значений, получаем высказывание, не содержащее переменных. Например, «2 есть четное число», «Исаак Ньютон есть студент МГТУ им. Баумана, поступивший в 1999 г.», «Иванов есть сын Петрова», «5 делится на 7» и т.п. В зависимости от того, истинно или ложно полученное таким образом высказывание, говорят, что предикат  выполняется или не выполняется на наборе значений переменных . Предикат, выполняющийся на любом наборе входящих в него переменных, называют тождественно истинным, а предикат, не выполняющийся ни на одном наборе значений входящих в него переменных, — тождественно ложным.

Высказывание из предиката можно получать не только подстановкой значений его переменных, но и посредством кванторов. Вводят два квантора — существования и всеобщности, обозначаемые  и  соответственно.

Высказывание  («для каждого элемента , принадлежащего множеству , истинно «, или, более коротко, «для всех истинно «) истинно, по определению, тогда и только тогда, когда предикат  выполняется для каждого значения переменного .

Высказывание  («существует, или найдется, такой элемент  множества , что истинно «, также «для некоторого  истинно «) истинно, по определению, тогда и только тогда, когда на некоторых значениях переменного  выполняется предикат .

Связывание переменных предикатов кванторами

При образовании высказывания из предиката посредством квантора говорят, что переменное предиката связывается квантором. Аналогично связываются переменные в предикатах, содержащих несколько переменных. В общем случае используют формы высказываний вида

где вместо каждой буквы  с индексом может быть подставлен любой из кванторов  или .

Например, высказывание  читается так: «для всякого  существует , такой, что истинно «. Если множества, которые пробегают переменные предикатов, фиксированы (подразумеваются «по умолчанию»), то кванторы записываются в сокращенной форме:  или .

Заметим, что многие математические теоремы можно записать в форме, подобной только что приведенным высказываниям с кванторами, например: «для всех  и для всех  истинно: если  — функция, дифференцируемая в точке , то функция  непрерывна в точке «.

Способы задания множеств

Обсудив особенности употребления логической символики, вернемся к рассмотрению множеств.

Два множества  и  считают равными, если любой элемент  множества  является элементом множества  и наоборот. Из приведенного определения равных множеств следует, что множество полностью определяется своими элементами.

Рассмотрим способы задания конкретных множеств. Для конечного множества, число элементов которого относительно невелико, может быть использован способ непосредственного перечисления элементов. Элементы конечного множества перечисляют в фигурных скобках в произвольном фиксированном порядке. Подчеркнем, что поскольку множество полностью определено своими элементами, то при задании конечного множества порядок, в котором перечислены его элементы, не имеет значения. Поэтому записи  и т.д. все задают одно и то же множество. Кроме того, иногда в записи множеств используют повторения элементов. Будем считать, что запись  задает то же самое множество, что и запись .

В общем случае для конечного множества используют форму записи . Как правило, при этом избегают повторений элементов. Тогда конечное множество, заданное записью , состоит из  элементов. Его называют также n-элементным множеством.

Однако способ задания множества путем непосредственного перечисления его элементов применим в весьма узком диапазоне конечных множеств. Наиболее общим способом задания конкретных множеств является указание некоторого свойства, которым должны обладать все элементы описываемого множества, и только они.

Эта идея реализуется следующим образом. Пусть переменное  пробегает некоторое множество , называемое универсальным множеством. Мы предполагаем, что рассматриваются только такие множества, элементы которых являются и элементами множества . В таком случае свойство, которым обладают исключительно элементы данного множества , может быть выражено посредством предиката , выполняющегося тогда и только тогда, когда переменное  принимает произвольное значение из множества . Иначе говоря,  истинно тогда и только тогда, когда вместо  подставляется индивидная константа .

Предикат  называют в этом случае характеристическим предикатом множества , а свойство, выражаемое с помощью этого предиката, — характеристическим свойством или коллективизирующим свойством.

Множество, заданное через характеристический предикат, записывается в следующей форме:

Например,  означает, что » есть множество, состоящее из всех таких элементов , что каждое из них есть четное натуральное число».

Термин «коллективизирующее свойство» мотивирован тем, что это свойство позволяет собрать разрозненные элементы в единое целое. Так, свойство, определяющее множество  (см. ниже), в буквальном смысле слова формирует некий «коллектив»:

G = {х: х есть студент 2-го курса специальности ИУ5 МГТУ им. Баумана, поступивший в 1999 г.},

Если мы вернемся к канторовскому определению множества, то характеристический предикат множества и есть тот закон, посредством которого совокупность элементов соединяется в единое целое. Предикат, задающий коллективизирующее свойство, может быть тождественно ложным. Множество, определенное таким образом, не будет иметь ни одного элемента. Его называют пустым множеством и обозначают .

В противоположность этому тождественно истинный характеристический предикат задает универсальное множество.

Обратим внимание на то, что не каждый предикат выражает какое-то коллективизирующее свойство.

Замечание 1.1. Конкретное содержание понятия универсального множества определяется тем конкретным контекстом, в котором мы применяем теоретико-множественные идеи. Например, если мы занимаемся только различными числовыми множествами, то в качестве универсального может фигурировать множество  всех действительных чисел. В каждом разделе математики рассматривается относительно ограниченный набор множеств. Поэтому удобно полагать, что элементы каждого из этих множеств суть также и элементы некоторого «объемлющего» их универсального множества. Зафиксировав универсальное множество, мы тем самым фиксируем область значений всех фигурирующих в наших математических рассуждениях переменных и констант. В этом случае как раз и можно не указывать в кванторах то множество, которое пробегает связываемое квантором переменное. В дальнейшем изложении мы встретимся с разными примерами конкретных универсальных множеств.

studfiles.net

Элементы теории множеств

Элементы теории множеств

Множество – основное математическое понятие. В обычной жизни его смысл заложен в словах: «совокупность», «класс», «стая», «табун», «стадо» и т.п. Теория множеств как математическая дисциплина создана немецким математиком Г. Кантором, которая получила признание в качестве самостоятельного раздела математики к 1890 году, когда были получены ее приложения в анализе и геометрии. Главная заслуга Георга Кантора заключается в установлении того факта, что понятие бесконечность является не абстракцией, придуманной философами, а реальностью; бесконечные совокупности предметов существуют наравне с конечными.

Множество относится к математическим объектам, для которых нет строго определения. Мы можем лишь в какой-то мере дать описание основных его свойств.

Кантор описывает множество следующим образом:

Определение.

Множество Sесть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое.

 Понятие множества. Способы задания множества

Мы под множествомбудем понимать следующее:

Определение.

Множество – набор (совокупность) определенных, различимых между собой объектов, рассматриваемых как единое целое, и обладающий некоторым общим свойством. . Объекты, составляющие данное множество, называют его элементами. .

Для того, чтобы указать, что х– элемент множестваА, записываюти читают «хпринадлежитА». Чтобы указать, чтохне является элементом множестваА, записываюти читают «хне принадлежит множествуА».

Для ряда числовых множеств в математике приняты стандартные обозначения:

Обозначения числовых множеств: N – множество натуральных чисел. Z – множество целых чисел. Q– множество рациональных чисел (дроби). R – множество действительных чисел

Существует два способа задания множества:

Рисунок 1. Способы задания множеств

Множества можно разделить на конечные и бесконечные.

Определение.

Конечныммножеством называется множество, состоящее из конечного числа элементов. Множество называется бесконечным, если оно состоит из бесконечного числа элементов

Пример 1.

• Конечные множества:множество букв алфавита, множество студентов 2 курса специальности «Юриспруденция» и т.д.

• Бесконечные множества:множество натуральных чисел, множество точек прямой и т.д.

К конечным множествам относится и множество, не содержащее элементов вообще. Такое множество называют пустыми обозначают Ø.

Пример 2.

Ø = , поскольку среди действительных чисел нет решения данного уравнения.

Определение.

Если каждый элемент множества Вявляется также и элементом множестваА, то говорят, что множествоВназываетсяподмножествоммножестваА. (Ввключено вА).

Пример 3.

Множество 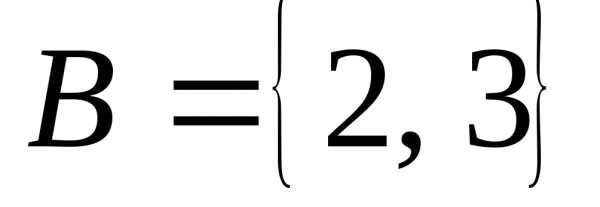,, тогда, т.е..

Определение.

Множества АиВназываютсяравными(илисовпадающими), если они состоят из одних и тех же элементов, т.е.и.

Если множества не равны, то пишут .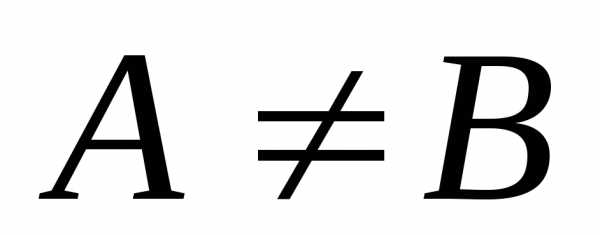

Пример 4.

Множества и, гдеиудовлетворяют уравнению, т.е.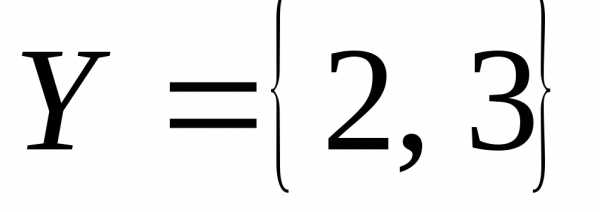, значит.

Определение.

Множество всех подмножеств множества Аназываетсямножеством-степеньюмножестваА.

Пример 5.

Пусть , тогда{Ø}, т.е. если множество состоит из двух элементов, то множество-степень состоит из четырех подмножеств.

Пусть , тогда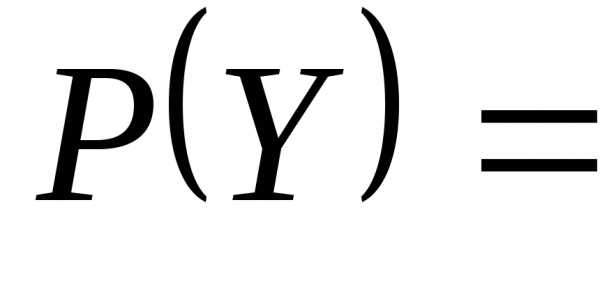{{4}, {2,3}, {3,4}, {2,4}, Ø}, т.е. если множество состоит из трех элементов, то множество-степень состоит из восьми подмножеств.

Таким образом, если конечное множество Асостоит изnэлементов, то число всех его подмножеств равно.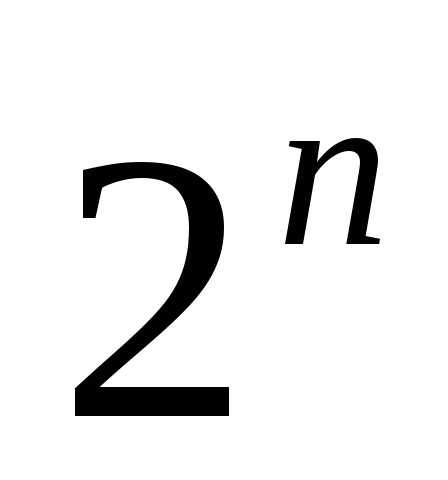

Определение.

Множество Uназываетсяуниверсальнымдля системы множествА,B,C, …, если каждое множество системы является подмножествомU, т.е.,,, …. .

studfiles.net

Множества Элементы теории множеств. Операции над множествами.

Определение 1.Множеством называется совокупность некоторых объектов, объединенных в одно целое по какому ‒ либо признаку.

Объекты, из которых состоит множество, называются его элементами.

Обозначаются заглавными буквами латинского алфавита: A, B, …, X, Y, …, а их элементы обозначаются соответствующими прописными буквами: a, b, …, x, y.

Определение 1.1.Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ø.

Множество можно задать перечислением и описанием.

Пример:; .

Определение 1.2.Множеством A называется подмножеством B, если каждый элемент множества A является элементом множества B. Символически это обозначают так: AB (A содержится в B).

Определение 1.3.Два множества A и B называются равными, если они состоят из одних и тех же элементов: (A =B).

Операции над множествами.

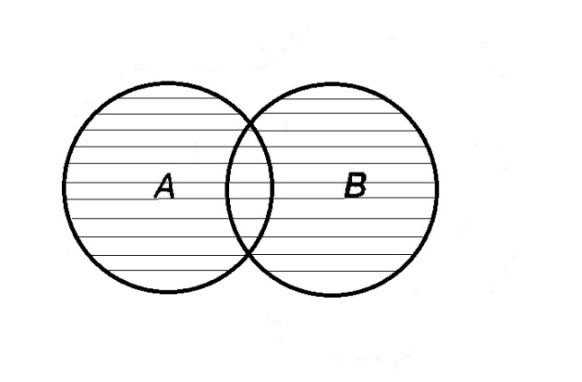
Определение 1.4.Объединением или суммой множеств A и B называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств.

Объединение множеств обозначают AB(или A +B). Кратко можно записать AB = .

AB= A +B

Если BA, то A +B=A

Определение 1.5. Пересечением или произведением множеств A и B называется множество, состоящее из элементов, каждый из которых принадлежит множеству A и множеству B одновременно. Пересечение множеств обозначают AB (или A·B). Кратко можно записать:

AB =.

AB =A ·B

Если BA, то A · B= B

Определение 1.6. Разностью множеств A и B называется множество, каждый элемент которого является элементом множества A и не является элементом множества B. Разность множеств обозначают A\B. По определению A\B = .

A\B =A–B

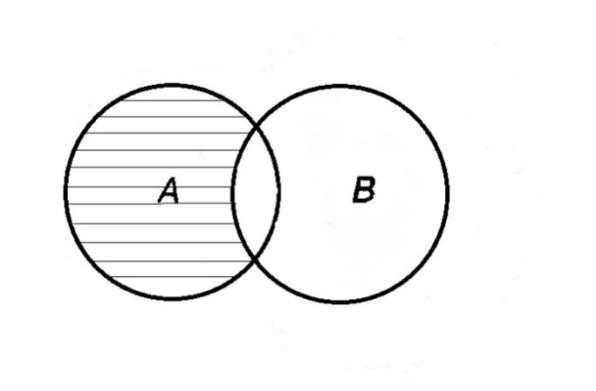
Множества, элементами которых являются числа, называются числовыми.

Примерами числовых множеств являются:

N = — множество натуральных чисел.

Z= — множество целых чисел.

Q= — множество рациональных чисел.

R‒ множество действительных чисел.

Множество Rсодержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, ;… ‒ рациональные числа.

Иррациональное число выражается бесконечной непериодической десятичной дробью. Так, = 1,41421356…; = 3,14159265…. – иррациональное число.

K– множество комплексных чисел (вида Z=a+bi)

RK

Определение 1.7.Ɛ ‒ окрестностью точки x₀ называется симметричный интервал (x₀ – Ɛ; x₀ + Ɛ), содержащий точку x₀.

В частности, если интервал (x₀ –Ɛ; x₀ +Ɛ), то выполнятся неравенство x₀ –Ɛ<x<x₀ +Ɛ, или, что то же, │x– x₀ │<Ɛ. Выполнение последнего означает попадание точки xв Ɛ – окрестность точки x₀.

Пример 1:

= 2, Ɛ = 0,1.

(2 – 0,1; 2 + 0,1) или (1,9; 2,1) – Ɛ– окрестность.

│x– 2│< 0,1

–0,1<x – 2<0,1

2 –0,1<x< 2 + 0,1

1,9<x< 2,1

Пример 2:

A– множество делителей 24;

B– множество делителей 18.

A=.

B=.

AB= A +B =

AB =A ·B =

A /B =A –B =

Функция Понятие функции. Основные свойства функции.

Определение 1. Пусть даны два непустых множестваХ и Y.Соответствие f, при котором каждому элементу xХсоответствует один единственный элемент уY, называется функцией и записывается у = f(x),

xХили f:x→ у (x → у).

x— аргумент функции; у — значение функции.

Пример:

y = 2 x – 1

Множество Х называется областью определения функцииfи обозначается D(f). Множество всех уY называется множеством значений функции f и обозначается E(f).

Если элементами множеств Х и Yявляются действительные числа, то функцию f называют числовой функцией.

studfiles.net

МНОЖЕСТВ ТЕОРИЯ • Большая российская энциклопедия

МНО́ЖЕСТВ ТЕО́РИЯ, раз­дел ма­те­ма­ти­ки, в ко­то­ром изу­ча­ют­ся свой­ст­ва мно­жеств, пре­им. бес­ко­неч­ных. По­ня­тие мно­же­ст­ва, или со­во­куп­но­сти, при­над­ле­жит к чис­лу ис­ход­ных ма­те­ма­тич. по­ня­тий; оно фор­маль­но не оп­ре­де­ля­ет­ся, но мо­жет быть по­яс­не­но при по­мо­щи при­ме­ров. Так, мож­но го­во­рить о мно­же­ст­ве всех книг, со­став­ляю­щих дан­ную биб­лио­те­ку, мно­же­ст­ве всех то­чек дан­ной ли­нии, мно­же­ст­ве всех ре­ше­ний дан­но­го урав­не­ния. Кни­ги дан­ной биб­лио­те­ки, точ­ки дан­ной ли­нии, ре­ше­ния дан­но­го урав­не­ния яв­ля­ют­ся эле­мен­та­ми со­от­вет­ст­вую­ще­го мно­же­ст­ва. Что­бы оп­ре­де­лить мно­же­ст­во, до­ста­точ­но ука­зать ха­рак­те­ри­стич. свой­ст­во его эле­мен­тов, т. е. та­кое свой­ст­во, ко­то­рым об­ла­да­ют все эле­мен­ты это­го мно­же­ст­ва и толь­ко они. Мо­жет слу­чить­ся, что дан­ным свой­ст­вом не об­ла­да­ет во­об­ще ни один объ­ект; то­гда го­во­рят, что это свой­ст­во оп­ре­де­ля­ет пус­тое мно­же­ст­во. То, что дан­ный объ­ект $x$ есть эле­мент мно­же­ст­ва $M$, за­пи­сы­ва­ют как $x∈М$.

Ес­ли ка­ж­дый эле­мент мно­же­ст­ва $A$ яв­ля­ет­ся в то же вре­мя эле­мен­том мно­же­ст­ва $B$, то мно­же­ст­во $A$ на­зы­ва­ет­ся под­мно­же­ст­вом мно­же­ст­ва $B$. Это за­пи­сы­ва­ют как $A⊂B$ или $B⊃A$. Под­мно­же­ст­вом дан­но­го мно­же­ст­ва $B$ яв­ля­ет­ся и са­мо мно­же­ст­во $B$. Ес­ли $A⊂B$ и $A⊃B$, то мно­же­ст­ва $А$ и $B$ на­зы­ва­ют рав­ны­ми и пи­шут $A=B$. Пус­тое мно­же­ст­во, по оп­ре­де­ле­нию, счи­та­ют под­мно­же­ст­вом лю­бо­го мно­же­ст­ва. Вся­кое не­пус­тое под­мно­же­ст­во $A$ дан­но­го мно­же­ст­ва $B$, от­лич­ное от все­го мно­же­ст­ва $B$, на­зы­ва­ют пра­виль­ной ча­стью по­след­не­го (вме­сто сим­во­ла вклю­че­ния $⊂$ ино­гда ис­поль­зу­ют сим­вол вклю­че­ния $⊆$; в этом слу­чае за­пись $A⊂B$ оз­на­ча­ет, что $A$ есть пра­виль­ная часть $B$).

Мощность множеств

Пер­вым во­про­сом, воз­ник­шим в при­ме­не­нии к бес­ко­неч­ным мно­же­ст­вам, был во­прос о воз­мож­но­сти их срав­не­ния ме­ж­ду со­бой. От­вет на этот и близ­кие во­про­сы дал в кон. 1870-х гг. Г. Кан­тор, ос­но­вав­ший М. т. как ма­те­ма­тич. нау­ку. Воз­мож­ность срав­ни­тель­ной оцен­ки мно­жеств опи­ра­ет­ся на по­ня­тие вза­им­но од­но­знач­но­го со­от­вет­ст­вия ме­ж­ду дву­мя мно­же­ст­ва­ми. Пусть ка­ж­до­му эле­мен­ту мно­же­ст­ва $A$ по­став­лен в со­от­вет­ст­вие с по­мо­щью к.-л. пра­ви­ла или за­ко­на не­ко­то­рый оп­ре­де­лён­ный эле­мент мно­же­ст­ва $B$; ес­ли при этом ка­ж­дый эле­мент мно­же­ст­ва $B$ ока­зы­ва­ет­ся по­став­лен­ным в со­от­вет­ст­вие од­но­му и толь­ко од­но­му эле­мен­ту мно­же­ст­ва $A$, то го­во­рят, что ме­ж­ду мно­же­ст­ва­ми $A$ и $B$ ус­та­нов­ле­но вза­им­но од­но­знач­ное со­от­вет­ст­вие. Ме­ж­ду дву­мя ко­неч­ны­ми мно­же­ст­ва­ми мож­но ус­та­но­вить вза­им­но од­но­знач­ное со­от­вет­ст­вие то­гда и толь­ко то­гда, ко­гда оба мно­же­ст­ва со­сто­ят из оди­на­ко­во­го чис­ла эле­мен­тов. Обоб­щая этот факт, оп­ре­де­ля­ют эк­ви­ва­лент­ность или рав­но­мощ­ность двух бес­ко­неч­ных мно­жеств как воз­мож­ность ус­та­но­вить ме­ж­ду ни­ми вза­им­но од­но­знач­ное со­от­вет­ст­вие.

Ещё до соз­да­ния М. т. Б. Боль­ца­но вла­дел, с од­ной сто­ро­ны, впол­не точ­но сфор­му­ли­ро­ван­ным по­ня­ти­ем вза­им­но од­но­знач­но­го со­от­вет­ст­вия, с др. сто­ро­ны, счи­тал не­со­мнен­ным су­ще­ст­во­ва­ние бес­ко­неч­но­стей разл. сту­пе­ней; од­на­ко он не толь­ко не сде­лал вза­им­но од­но­знач­ное со­от­вет­ст­вие ос­но­вой ус­та­нов­ле­ния рав­но­силь­но­сти мно­жеств, но ре­ши­тель­но воз­ра­жал про­тив это­го. Боль­ца­но ос­та­нав­ли­ва­ло то, что бес­ко­неч­ное мно­же­ст­во мо­жет на­хо­дить­ся во вза­им­но од­но­знач­ном со­от­вет­ст­вии со сво­ей пра­виль­ной ча­стью. Напр., ес­ли ка­ж­до­му на­ту­раль­но­му чис­лу $n$ по­ста­вить в со­от­вет­ст­вие на­ту­раль­ное чис­ло $2n$, то по­лу­ча­ет­ся вза­им­но од­но­знач­ное со­от­вет­ст­вие ме­ж­ду мно­же­ст­вом всех на­ту­раль­ных и мно­же­ст­вом всех чёт­ных чи­сел. Вме­сто то­го что­бы в при­ме­не­нии к бес­ко­неч­ным мно­же­ст­вам от­ка­зать­ся от по­ло­же­ния, со­стоя­ще­го в том, что часть мень­ше це­ло­го, Боль­ца­но от­ка­зал­ся от вза­им­ной од­но­знач­но­сти как кри­те­рия рав­но­мощ­но­сти. В ка­ж­дом бес­ко­неч­ном мно­же­ст­ве $M$ име­ет­ся пра­виль­ная часть, рав­но­мощ­ная все­му мно­же­ст­ву $M$, то­гда как ни в од­ном ко­неч­ном мно­же­ст­ве та­кой пра­виль­ной час­ти не су­ще­ст­ву­ет. По­это­му на­ли­чие пра­виль­ной час­ти, рав­но­мощ­ной це­ло­му, мож­но при­нять за оп­ре­де­ле­ние бес­ко­неч­но­го мно­же­ст­ва.

Для двух бес­ко­неч­ных мно­жеств $A$ и $B$ воз­мож­ны сле­дую­щие 3 слу­чая: ли­бо в $A$ есть пра­виль­ная часть, рав­но­мощ­ная $B$, но в $B$ нет пра­виль­ной час­ти, рав­но­мощ­ной $A$; ли­бо, на­обо­рот, в $B$ есть пра­виль­ная часть, рав­но­мощ­ная $A$, а в $A$ нет пра­виль­ной час­ти, рав­но­мощ­ной $B$; ли­бо, на­ко­нец, в $A$ есть пра­виль­ная часть, рав­но­мощ­ная $B$, и в $B$ есть пра­виль­ная часть, рав­но­мощ­ная $A$. До­ка­зы­ва­ет­ся, что в 3-м слу­чае мно­же­ст­ва $A$ и $B$ рав­но­мощ­ны (тео­ре­ма Кан­то­ра – Берн­штей­на). В 1-м слу­чае го­во­рят, что мощ­ность мно­же­ст­ва $A$ боль­ше мощ­но­сти мно­же­ст­ва $B$, во 2-м – что мощ­ность мно­же­ст­ва $B$ боль­ше мощ­но­сти мно­же­ст­ва $A$. Фор­маль­но воз­мож­ный 4-й слу­чай – в $A$ нет пра­виль­ной час­ти, рав­но­мощ­ной $B$, а в $B$ нет пра­виль­ной час­ти, рав­но­мощ­ной $A$, – в дей­ст­ви­тель­но­сти для бес­ко­неч­ных мно­жеств осу­ще­ст­вить­ся не мо­жет.

Цен­ность по­ня­тия мощ­но­сти мно­же­ст­ва свя­за­на с су­ще­ст­во­ва­ни­ем не­рав­но­мощ­ных бес­ко­неч­ных мно­жеств. Напр., мно­же­ст­во всех под­мно­жеств дан­но­го мно­же­ст­ва $M$ име­ет мощ­ность бо́ль­шую, чем мно­же­ст­во $M$. Мно­же­ст­во, рав­но­мощ­ное мно­же­ст­ву всех на­ту­раль­ных чи­сел, на­зы­ва­ет­ся счёт­ным мно­же­ст­вом. Мощ­ность счёт­ных мно­жеств есть наи­мень­шая мощ­ность, ко­то­рую мо­жет иметь бес­ко­неч­ное мно­же­ст­во; вся­кое бес­ко­неч­ное мно­же­ст­во со­дер­жит счёт­ную пра­виль­ную часть. Кан­тор до­ка­зал, что мно­же­ст­во всех ра­цио­наль­ных и да­же всех ал­геб­раи­че­ских чи­сел счёт­но, то­гда как мно­же­ст­во всех дей­ст­ви­тель­ных чи­сел не­счёт­но. Из это­го сле­ду­ет, в ча­ст­но­сти, до­ка­за­тель­ст­во су­ще­ст­во­ва­ния т. н. транс­цен­дент­ных чи­сел, т. е. дей­ст­ви­тель­ных чи­сел, не яв­ляю­щих­ся кор­ня­ми ни­ка­ко­го ал­геб­ра­ич. урав­не­ния с це­лы­ми ко­эф­фи­ци­ен­та­ми (и да­же не­счёт­ность мно­же­ст­ва та­ких чи­сел). Мощ­ность мно­же­ст­ва всех дей­ст­ви­тель­ных чи­сел на­зы­ва­ет­ся мощ­но­стью кон­ти­нуу­ма. Мно­же­ст­ву всех дей­ст­ви­тель­ных чи­сел рав­но­мощ­ны мно­же­ст­во всех под­мно­жеств счёт­но­го мно­же­ст­ва, мно­же­ст­во всех ком­плекс­ных чи­сел и, сле­до­ва­тель­но, мно­же­ст­во всех то­чек плос­ко­сти, а так­же мно­же­ст­во всех то­чек $n$-мер­но­го про­стран­ст­ва при лю­бом $n$. Кан­тор вы­ска­зал ги­по­те­зу о том, что вся­кое мно­же­ст­во, со­стоя­щее из дей­ст­ви­тель­ных чи­сел, ли­бо ко­неч­но, ли­бо счёт­но, ли­бо рав­но­мощ­но мно­же­ст­ву всех дей­ст­ви­тель­ных чи­сел; по по­во­ду этой ги­по­те­зы и о свя­зан­ных с нею ре­зуль­та­тах см. Кон­ти­ну­ум-ги­по­те­за, Кон­ти­нуу­ма про­бле­ма.

Отображения множеств

В М. т. по­ня­тие функ­ции, гео­мет­рич. по­ня­тие ото­бра­же­ния или пре­об­ра­зо­ва­ния фи­гу­ры при­во­дят к об­ще­му по­ня­тию ото­бра­же­ния од­но­го мно­же­ст­ва в дру­гое. Пусть да­ны два мно­же­ст­ва $X$ и $Y$ и ка­ж­до­му эле­мен­ту $x∈X$ по­став­лен в со­от­вет­ст­вие не­ко­то­рый оп­ре­де­лён­ный эле­мент $y=f(x)$ мно­же­ст­ва $Y$; то­гда го­во­рят, что име­ет­ся ото­бра­же­ние мно­же­ст­ва $X$ в мно­же­ст­во $Y$ или что име­ет­ся функ­ция, ар­гу­мент $x$ ко­то­рой про­бе­га­ет мно­же­ст­во $X$, а зна­че­ния $y$ при­над­ле­жат мно­же­ст­ву $Y$; при этом для ка­ж­до­го дан­но­го $x∈X$ эле­мент $y=f(x)$ мно­же­ст­ва $Y$ на­зы­ва­ет­ся об­ра­зом эле­мен­та $x$ при дан­ном ото­бра­же­нии или зна­че­ни­ем дан­ной функ­ции для дан­но­го зна­че­ния $x$ её ар­гу­мен­та.

При­ме­ры.

1) Пусть в плос­ко­сти с дан­ной на ней пря­мо­уголь­ной сис­те­мой ко­ор­ди­нат за­дан квад­рат с вер­ши­на­ми $(0; 0), (0; 1), (1; 0), (1; 1)$ и этот квад­рат спро­ек­ти­ро­ван, напр., на ось абс­цисс; эта про­ек­ция есть ото­бра­же­ние мно­же­ст­ва $X$ всех то­чек квад­ра­та в мно­же­ст­во $Y$ всех то­чек его ос­но­ва­ния; точ­ке с ко­ор­ди­на­та­ми $(x; y)$ со­от­вет­ст­ву­ет точ­ка $(x; 0)$.

2) Пусть $X$ – мно­же­ст­во всех дей­стви­тель­ных чи­сел; ес­ли для ка­ж­до­го дей­ст­ви­тель­но­го чис­ла $x∈X$ по­ло­жить $y=f(x)=x^3$, то тем са­мым бу­дет ус­та­нов­ле­но ото­бра­же­ние мно­же­ст­ва $X$ в се­бя.

3) Пусть $X$ – мно­же­ст­во всех дей­ст­ви­тель­ных чи­сел; ес­ли для ка­ж­до­го $x∈X$ по­ло­жить $y=f(x)=\text {arctg}$ $x$, то этим бу­дет ус­та­нов­ле­но ото­бра­же­ние мно­же­ст­ва $X$ в ин­тер­вал $(-π/2, π/2)$.

Вза­им­но од­но­знач­ное со­от­вет­ст­вие ме­ж­ду дву­мя мно­же­ст­ва­ми $X$ и $Y$ есть та­кое ото­бра­же­ние мно­же­ст­ва $X$ в мно­же­ст­во $Y$, при ко­то­ром ка­ж­дый эле­мент мно­же­ст­ва $Y$ яв­ля­ет­ся об­ра­зом од­но­го и толь­ко од­но­го эле­мен­та мно­же­ст­ва $X$. Ото­бра­же­ния при­ме­ров 2) и 3) вза­им­но од­но­знач­ны, при­ме­ра 1) – нет.

Операции над множествами

Сум­мой, или объ­е­ди­не­ни­ем, ко­неч­но­го или бес­ко­неч­но­го мно­же­ст­ва мно­жеств на­зы­ва­ет­ся мно­же­ст­во всех тех эле­мен­тов, ка­ж­дый из ко­то­рых есть эле­мент хо­тя бы од­но­го из дан­ных мно­жеств-сла­гае­мых. Объ­е­ди­не­ние мно­жеств $A$ и $B$ обо­зна­ча­ет­ся $A∪B$. Пе­ре­се­че­ни­ем лю­бо­го ко­неч­но­го или бес­ко­неч­но­го мно­же­ст­ва мно­жеств на­зы­ва­ет­ся мно­же­ст­во всех эле­мен­тов, при­над­ле­жа­щих всем дан­ным мно­же­ст­вам. Пе­ре­се­че­ние мно­жеств $A$ и $B$ обо­зна­ча­ет­ся $A∩B$. Пе­ре­се­че­ние не­пус­тых мно­жеств мо­жет быть пус­тым. Раз­но­стью ме­ж­ду мно­же­ст­вом $B$ и мно­же­ст­вом $A$ на­зы­ва­ет­ся мно­же­ст­во всех эле­мен­тов из $B$, не яв­ляю­щих­ся эле­мен­та­ми из $A$; эта раз­ность обо­зна­ча­ет­ся $BA$; раз­ность ме­ж­ду мно­же­ст­вом $B$ и его ча­стью $A$ на­зы­ва­ет­ся до­пол­не­ни­ем мно­же­ст­ва $A$ в мно­же­ст­ве $B$ и обо­зна­ча­ет­ся .

Опе­ра­ции сло­же­ния и пе­ре­се­че­ния мно­жеств об­ла­да­ют ас­со­циа­тив­но­стью и ком­му­та­тив­но­стью. Опе­ра­ция пе­ре­се­че­ния, кро­ме то­го, об­ла­да­ет ди­ст­ри­бу­тив­но­стью по от­но­ше­нию к сло­же­нию и вы­чи­та­нию. Ес­ли эти опе­ра­ции про­из­во­дить над мно­же­ст­ва­ми, яв­ляю­щи­ми­ся под­мно­же­ст­ва­ми од­но­го и то­го же мно­же­ст­ва $M$, то и ре­зуль­тат бу­дет под­мно­же­ст­вом мно­же­ст­ва $M$. Ука­зан­ным свой­ст­вом не об­ла­да­ет т. н. внеш­нее ум­но­же­ние мно­жеств, внеш­ним про­из­ве­де­ни­ем мно­жеств $X$ и $Y$ или пря­мым про­из­ве­де­ни­ем мно­жеств $X$ и $Y$ на­зы­ва­ет­ся мно­же­ст­во $X×Y$ все­воз­мож­ных пар $(x, y)$, где $x∈X, y∈Y$. Дру­гим в этом смыс­ле внеш­ним дей­ст­ви­ем яв­ля­ет­ся воз­ве­де­ние в сте­пень: сте­пе­нью $Y^X$ на­зы­ва­ет­ся мно­же­ст­во всех ото­бра­же­ний мно­же­ст­ва $X$ в мно­же­ст­во $Y$. Мож­но оп­ре­де­лить внеш­нее ум­но­же­ние лю­бо­го мно­же­ст­ва мно­жеств так, что в слу­чае сов­па­де­ния множи­те­лей оно пе­рей­дёт в воз­ве­де­ние в сте­пень. Ес­ли $ξ$ и $η$ суть мощ­но­сти мно­жеств $X$ и $Y$, то $ξ·η$ и $η^ξ$ оп­ре­де­ля­ют­ся со­от­вет­ст­вен­но как мощ­но­сти мно­жеств $X×Y$ и $Y^X$, что в слу­чае ко­неч­ных мно­жеств со­гла­су­ет­ся с ум­но­же­ни­ем и воз­ве­де­ни­ем в сте­пень на­ту­раль­ных чи­сел. Ана­ло­гич­но оп­ре­де­ля­ет­ся сум­ма мощ­но­стей как мощ­ность сум­мы по­пар­но не­пе­ре­се­каю­щих­ся мно­жеств с за­дан­ны­ми мощ­но­стя­ми.

Упорядоченные множества

В дан­ном мно­же­ст­ве $X$ мож­но ус­та­но­вить по­ря­док, т. е. оп­ре­де­лить для не­ко­то­рых пар $x′, x″$ эле­мен­тов это­го мно­же­ст­ва к.-л. пра­ви­ло пред­ше­ст­во­ва­ния (сле­до­ва­ния), вы­ра­жае­мое сло­ва­ми эле­мент $x′$ пред­ше­ст­ву­ет эле­мен­ту $x″$ (или, что то же, эле­мент $x″$ сле­ду­ет за эле­мен­том $x’$ ), что за­пи­сы­ва­ет­ся $x′≺x″$; при этом пред­по­ла­га­ет­ся, что для дан­но­го от­но­ше­ния по­ряд­ка вы­пол­не­но ус­ло­вие тран­зи­тив­но­сти, т. е. ес­ли $x≺x′$ и $x′≺x″$, то $x≺x″$. Мно­же­ст­во, рас­смат­ри­вае­мое вме­сте с к.-л. ус­та­нов­лен­ным в нём по­ряд­ком, на­зы­ва­ет­ся час­тич­но упо­ря­до­чен­ным мно­же­ст­вом; ино­гда – упо­ря­до­чен­ным мно­же­ст­вом. Од­на­ко ча­ще упо­ря­до­чен­ным мно­же­ст­вом на­зы­ва­ет­ся час­тич­но упо­ря­до­чен­ное мно­же­ст­во, в ко­то­ром по­ря­док удов­ле­тво­ря­ет сле­дую­щим до­пол­нит. тре­бо­ва­ни­ям (ли­ней­но­го по­ряд­ка): 1) ни­ка­кой эле­мент не пред­ше­ст­ву­ет са­мо­му се­бе; 2) из вся­ких двух разл. эле­мен­тов $x, x′$ один пред­ше­ст­ву­ет дру­го­му, т. е. ес­ли $x≠x′$, то или $x≺x′$, или $x″≺x$.

При­ме­ры.

1) Лю­бое мно­же­ст­во, эле­мен­та­ми ко­то­ро­го яв­ля­ют­ся не­ко­то­рые мно­же­ст­ва $x$, яв­ля­ет­ся час­тич­но упо­ря­до­чен­ным по вклю­че­нию, ес­ли счи­тать, что $x≺x′$, ес­ли $x⊂x′$.

2) Лю­бое мно­же­ст­во функ­ций $f$, оп­ре­де­лён­ных на чи­сло­вой пря­мой, ста­но­вит­ся час­тич­но упо­ря­до­чен­ным, ес­ли счи­тать, что $f_1≺f_2$, то­гда и толь­ко то­гда, ко­гда для ка­ж­до­го дей­ст­ви­тель­но­го чис­ла $x$ спра­вед­ли­во не­ра­вен­ст­во $f_1(x)⩽f_2(x)$.

3) Лю­бое мно­же­ст­во дей­ст­ви­тель­ных чи­сел ли­ней­но упо­ря­до­че­но, ес­ли счи­тать, что мень­шее из двух чи­сел пред­ше­ст­ву­ет боль­ше­му.

Два упо­ря­до­чен­ных мно­же­ст­ва на­зы­ва­ют­ся по­доб­ны­ми, или имею­щи­ми один и тот же по­ряд­ко­вый тип, ес­ли ме­ж­ду ни­ми мож­но ус­та­но­вить вза­им­но од­но­знач­ное со­от­вет­ст­вие, со­хра­няю­щее по­ря­док. Эле­мент упо­ря­до­чен­но­го мно­же­ст­ва на­зы­ва­ет­ся пер­вым, ес­ли он пред­ше­ст­ву­ет всем ос­таль­ным эле­мен­там; ана­ло­гич­но оп­ре­де­ля­ет­ся и по­след­ний эле­мент. Напр., в упо­ря­до­чен­ном мно­же­ст­ве всех дей­ст­ви­тель­ных чи­сел нет ни пер­во­го, ни по­след­не­го эле­мен­та; в упо­ря­до­чен­ном мно­же­ст­ве всех не­от­ри­ца­тель­ных чи­сел нуль есть пер­вый эле­мент, а по­след­не­го эле­мен­та нет; в упо­ря­до­чен­ном мно­же­ст­ве всех дей­ст­ви­тель­ных чи­сел $x$, удов­ле­тво­ряю­щих не­ра­вен­ст­вам $a⩽x⩽b$, чис­ло $a$ есть пер­вый эле­мент, $b$ – по­след­ний.

Упо­ря­до­чен­ное мно­же­ст­во на­зы­ва­ет­ся впол­не упо­ря­до­чен­ным, ес­ли оно са­мо и вся­кое его пра­виль­ное под­мно­же­ст­во име­ют пер­вый эле­мент. По­ряд­ко­вые ти­пы впол­не упо­ря­до­чен­ных мно­жеств на­зы­ва­ют­ся по­ряд­ко­вы­ми, или ор­ди­наль­ны­ми, чис­ла­ми. Ес­ли впол­не упо­ря­до­чен­ное мно­же­ст­во ко­неч­но, то его по­ряд­ко­вое чис­ло есть на­ту­раль­ное чис­ло. По­ряд­ко­вый тип бес­ко­неч­но­го впол­не упо­ря­до­чен­но­го мно­же­ст­ва на­зы­ва­ет­ся транс­фи­нит­ным чис­лом.

Точечные множества

Тео­рия то­чеч­ных мно­жеств, т. е. мно­жеств, эле­мен­та­ми ко­то­рых яв­ля­ют­ся дей­ст­ви­тель­ные чис­ла (точ­ки чи­сло­вой пря­мой), а так­же точ­ки мно­го­мер­ных про­странств, ос­но­ва­на Г. Кан­то­ром, ко­то­рый ввёл по­ня­тие пре­дель­ной точ­ки мно­же­ст­ва и свя­зан­ные с ним по­ня­тия замк­ну­то­го мно­же­ст­ва и пр. Раз­ви­тие тео­рии то­чеч­ных мно­жеств при­ве­ло к по­ня­ти­ям мет­ри­че­ско­го про­стран­ст­ва и то­по­ло­ги­че­ско­го про­стран­ст­ва, изу­че­ни­ем ко­то­рых за­ни­ма­ет­ся об­щая то­по­ло­гия. Са­мо­стоя­тель­но су­ще­ст­ву­ет де­ск­рип­тив­ная тео­рия мно­жеств, ос­но­ван­ная франц. ма­те­ма­ти­ком Р. Бэ­ром и А. Ле­бе­гом в свя­зи с клас­си­фи­ка­ци­ей раз­рыв­ных функ­ций (1905). Де­ск­рип­тив­ная тео­рия мно­жеств на­ча­лась с изу­че­ния и клас­си­фи­ка­ции т. н. бо­ре­лев­ских мно­жеств ($B$-мно­жеств). Бо­ре­лев­ские мно­же­ст­ва оп­ре­де­ля­ют­ся как мно­же­ст­ва, ко­то­рые мо­гут быть по­строе­ны, от­прав­ля­ясь от замк­ну­тых мно­жеств, при­ме­не­ни­ем опе­ра­ций объ­е­ди­не­ния и пе­ре­се­че­ния в лю­бых ком­би­на­ци­ях, но ка­ж­дый раз к ко­неч­но­му или к счёт­но­му мно­же­ст­ву мно­жеств. Даль­ней­шее раз­ви­тие де­ск­рип­тив­ной тео­рии мно­жеств осу­ще­ст­в­ля­лось пре­им. рус. и польск. ма­те­ма­ти­ка­ми, осо­бен­но мо­с­ков­ской ма­те­ма­тич. шко­лой, соз­дан­ной Н. Н. Лу­зи­ным (П. С. Алек­сан­д­ров, А. Н. Кол­мо­го­ров, М. А. Лав­рен­ть­ев, П. С. Но­ви­ков, М. Я. Сус­лин). Алек­сан­д­ров до­ка­зал (1916), что вся­кое бес­ко­неч­ное не­счёт­ное бо­ре­лев­ское мно­же­ст­во име­ет мощ­ность кон­ти­нуу­ма. Ап­па­рат это­го до­ка­за­тель­ст­ва был при­менён Сус­ли­ным для по­строе­ния тео­рии т. н. $A$-мно­жеств, ох­ва­ты­ваю­щих как ча­ст­ный слу­чай бо­ре­лев­ские или $B$-мно­же­ст­ва, счи­тав­ши­е­ся до то­го един­ст­вен­ны­ми мно­же­ст­ва­ми, ко­то­рые мо­гут встре­тить­ся в ма­те­ма­тич. ана­ли­зе. Сус­лин по­ка­зал, что мно­же­ст­во, до­пол­ни­тель­ное к $A$-мно­же­ст­ву $M$, яв­ля­ет­ся са­мо $A$-мно­же­ст­вом толь­ко в том слу­чае, ко­гда мно­же­ст­во $M$ – бо­ре­лев­ское (до­пол­не­ние к бо­ре­лев­ско­му мно­же­ст­ву все­гда есть бо­ре­лев­ское мно­же­ст­во). При этом ока­за­лось, что $A$-мно­же­ст­ва сов­па­да­ют с не­пре­рыв­ны­ми об­раз­ами мно­же­ст­ва всех ир­ра­цио­наль­ных чи­сел. Тео­рия $A$-мно­жеств в те­че­ние не­скoль­ких лет ос­та­ва­лась в цен­тре вни­ма­ния де­ск­рип­тив­ной тео­рии мно­жеств до то­го, как Лу­зин при­шёл к об­ще­му оп­ре­де­ле­нию про­ек­тив­ных мно­жеств, ко­то­рые мо­гут быть по­лу­че­ны, от­прав­ля­ясь от мно­же­ст­ва всех ир­ра­цио­наль­ных чи­сел при по­мо­щи по­втор­но­го при­ме­не­ния опе­ра­ций вы­чи­та­ния и не­пре­рыв­но­го ото­бра­же­ния. К тео­рии $A$-мно­жеств и про­ек­тив­ных мно­жеств от­но­сят­ся так­же ра­бо­ты Но­ви­ко­ва и др. Де­ск­рип­тив­ная тео­рия мно­жеств тес­но свя­за­на с ис­сле­до­ва­ния­ми по ос­но­ва­ни­ям ма­те­ма­ти­ки (с во­про­са­ми эф­фек­тив­ной оп­ре­де­ли­мо­сти ма­те­ма­тич. объ­ек­тов и раз­ре­ши­мо­сти ма­те­ма­тич. про­блем).

Роль теории множеств в развитии математики

Влия­ние М. т. на раз­ви­тие совр. ма­те­ма­ти­ки очень ве­ли­ко. Пре­ж­де все­го М. т. яви­лась фун­да­мен­том ря­да ма­те­ма­тич. дис­ци­п­лин, напр. тео­рии функ­ций дей­ст­ви­тель­но­го пе­ре­мен­но­го, об­щей то­по­ло­гии, об­щей ал­геб­ры, функ­цио­наль­но­го ана­ли­за. Тео­ре­ти­ко-мно­же­ст­вен­ные ме­то­ды при­ме­ня­ются и в клас­сич. раз­де­лах ма­те­ма­ти­ки. Напр., они ши­ро­ко при­ме­ня­ют­ся в ка­че­ст­вен­ной тео­рии диф­фе­рен­ци­аль­ных урав­не­ний, ва­риа­ци­он­ном ис­чис­ле­нии, тео­рии ве­ро­ят­но­стей. М. т. ока­за­ла глу­бо­кое влия­ние на по­ни­ма­ние са­мо­го пред­ме­та ма­те­ма­ти­ки, в ча­ст­но­сти, та­ких её раз­де­лов, как гео­мет­рия. Толь­ко М. т. по­зво­ли­ла от­чёт­ли­во сфор­му­ли­ро­вать по­ня­тие изо­мор­физ­ма сис­тем объ­ек­тов, за­дан­ных вме­сте со свя­зы­ва­ю­щи­ми их от­но­ше­ния­ми, и при­ве­ла к по­ни­ма­нию то­го, что ка­ж­дая ма­те­ма­тич. тео­рия в её чис­той аб­ст­ракт­ной фор­ме изу­ча­ет ту или иную сис­те­му объ­ек­тов лишь с точ­но­стью до изо­мор­физ­ма, т. е. мо­жет быть без вся­ких из­ме­не­ний пе­рене­се­на на лю­бую сис­те­му объ­ек­тов, изо­морф­ную той, для изу­че­ния ко­то­рой тео­рия бы­ла пер­во­на­чаль­но соз­да­на. В во­про­сах обос­но­ва­ния ма­те­ма­ти­ки, т. е. соз­да­ния стро­го­го, ло­ги­че­ски безу­преч­но­го по­строе­ния ма­те­ма­тич. тео­рий, сле­ду­ет иметь в ви­ду, что са­ма М. т. ну­ж­да­ет­ся в обос­но­ва­нии при­ме­няе­мых в ней ме­то­дов рас­су­ж­де­ния. Бо­лее то­го, все ло­гич. труд­но­сти, свя­зан­ные с по­ня­ти­ем бес­ко­неч­но­сти, при пе­ре­хо­де на точ­ку зре­ния об­щей М. т. при­об­ре­та­ют бо́ль­шую от­чёт­ли­вость.

bigenc.ru

Раздел 1: Элементы теории множеств

Каждый с самого рождения бессознательно пользуется теорией множеств, так же как Мольеров Журден из «Мещанина во дворянстве» разговаривает прозой, сам того не ведая.

М. Стоун

1.1 Основные понятия теории множеств

В конце XIX века в математической науке возникла необходимость уточнить смысл таких ведущих понятий, как функция, непрерывность и т. д. Для этого нужно было строго определить, что такое натуральное число. Поиски ответа на эти сложные вопросы способствовали развитию новых математических идей, поэтому в конце XIX начале XX столетий происходил пересмотр старых представлений буквально во всех областях математических знаний. В результате в конце XIX века возникла новая область математики – теория множеств, одним из создателей которой был немецкий математик Георг Кантор (1845 – 1918). За небольшой срок теория множеств стала фундаментом всей математики.

Понятие множества является ключевым в математике, без которого невозможно изложение ни одного из ее разделов. Подсознательно первые представления о множестве у человека начинают формироваться с рождения, когда он погружается в многообразный мир окружающих его объектов и явлений. С первых же шагов мы не просто пополняем список знакомых нам объектов и явлений, а начинаем дифференцировать и классифицировать (горячие и холодные, сладкие и горькие, тяжелые и легкие и т. п.), объединяя тем самым объекты в некоторые совокупности.

В математике понятие множество используется для описания предметов или объектов. При этом предполагается, что предметы (объекты) данной совокупности можно отличить друг от друга и от предметов, не входящих в эту совокупность.

Создатель теории множеств Г. Кантор определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией или мыслью», а так же «множество есть многое мыслимое нами как единое». Эти слова не могут рассматриваться как математически строгое определение множества, такого определения не существует. Понятие множества относится к исходным (не определяемым), на основании которых строятся остальные понятия математики.

Множество – это совокупность каких-либо объектов. Так, можно говорить о множестве всех книг данной библиотеки, множестве всех вершин данного многоугольника, множестве всех натуральных чисел, множестве всех точек данной прямой и т. д. Объекты, входящие в данное множество называются элементами множества. Книги данной библиотеки, вершины данного многоугольника, натуральные числа, точки данной прямой являются элементами соответствующих множеств.

Множества обычно обозначаются большими буквами A, B, X, а их элементы – малыми буквами а, b, x.

Множество называется конечным, если количество его элементов можно выразить целым неотрицательным числом (причем неважно, известно это число или нет, главное, оно существует), в противном случае множество называется бесконечным.

Пример 1: Множество книг в библиотеке, множество студентов в группе являются конечными. Множество натуральных чисел, множество точек прямой являются бесконечными.

Количество элементов множества обозначается |A|.

Пример 2: Пусть В – множество правильных многоугольников. Тогда В = {тетраэдр, куб, октаэдр, додекаэдр, икосаэдр}. |B| = 5.

Запись xХ, означает что объект х есть элемент множества Х, читается «х принадлежит множеству Х», «х входит в множество Х». Если х не принадлежит множеству Х, то пишут х Х.

Например, если через N обозначим множество натуральных чисел, то 3 N, 20 N, 0 N, N.

Если все элементы множества А принадлежат какому-то множеству В, то говорят, что множество А является подмножеством множества В. Записывают А В (множество А содержится во множестве В). Любое множество является подмножеством самого себя, т. е. справедливо утверждение А А.

Если множество не содержит ни одного элемента, то его называют пустым и обозначают символом Ø. Пустое множество является подмножеством любого множества.

Подмножества, которые содержат не все элементы множества В, называют собственными подмножествами множества В.

Пример 3: Дано множество М = {a; c; m}. Найти все его подмножества.

Решение:

M₁ = {a}, M₂ = {c}, M₃ = {m}, M₄ = {a; c}, M₅ = {a; m}, M₆ = {c; m}, M₇ = {a; c; m}, M₈ = Ø.

Множества M₇ и M₈ называются несобственными подмножествами множества М.

Множества А и В называют равными (А = В), если. они состоят из одних и тех же элементов, т.е. В Аи А В.

Например, множества А = {3, 5, 7, 9} и В = {7, 3, 9, 5} равны, т. к. состоят из одинаковых элементов.

Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:

Ν={1; 2; 3; …; n; …} – множество натуральных чисел – множество чисел, использующихся при счете предметов;

Ζ₀={0; 1; 2; …; n; …} – множество целых неотрицательных чисел – множество натуральных чисел с нулем;

Ζ={0; ±1; ±2; …; ±n; …} – множество целых чисел – множество целых неотрицательных чисели им противоположных;

Q={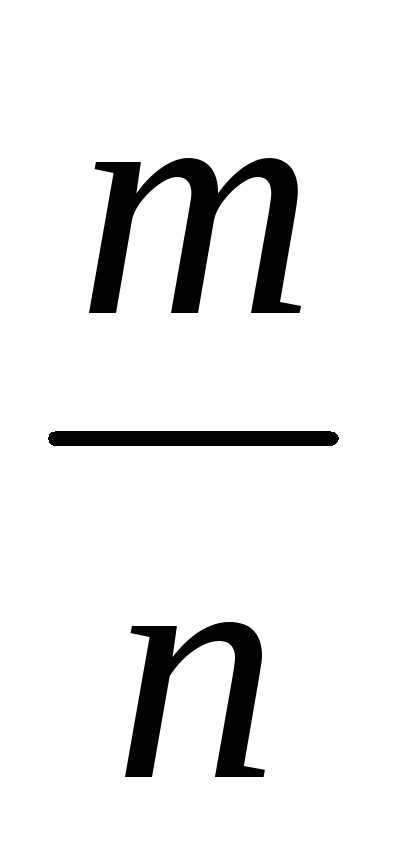:m Z, n N} – множество рациональных чисел – множество чисел, которые можно представить в виде обыкновенной дроби – множество конечных и бесконечных периодических десятичных дробей;

R – множество действительных чисел – объединение множеств рациональных и иррациональных чисел.

Между этими множествами существует соотношение: .

Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, ½=0,5 (=0,5000…), ⅓=0,333… – рациональные числа.

Действительные числа, не являющиеся рациональными, называются иррациональными. Иррациональное число выражается бесконечной непериодической дробью. Например, 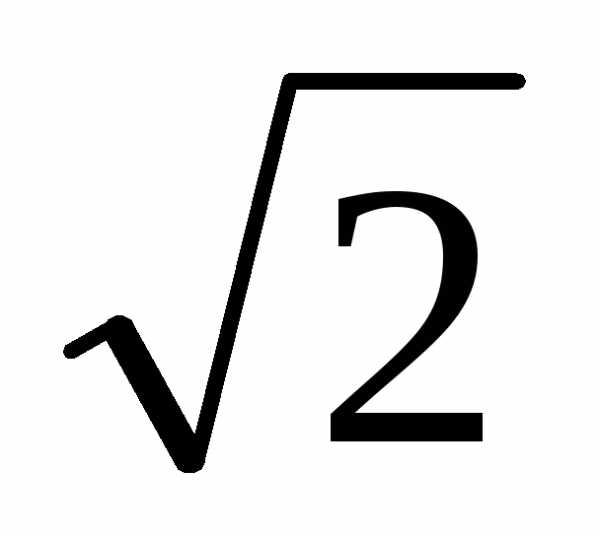= 1,4142356…, π = 3,1415926… – иррациональные числа.

studfiles.net

МНОЖЕСТВ ТЕОРИЯ | Энциклопедия Кругосвет

Содержание статьи

МНОЖЕСТВ ТЕОРИЯ. Под множеством понимается совокупность каких-либо объектов, называемых элементами множества. Теория множеств занимается изучением свойств как произвольных множеств, так и множеств специального вида независимо от природы образующих их элементов. Терминология и многие результаты этой теории широко используются в математике, например в математическом анализе, геометрии и теории вероятностей.

Терминология.

Если каждый элемент множества B является элементом множества A, то множество B называется подмножеством множества A. Например, если множество A состоит из чисел 1, 2 и 3, то у него существует 8 подмножеств (три из них содержат по 1 элементу, три – содержат по 2 элемента, одно подмножество, по определению, есть само множество A и восьмое подмножество – это пустое множество, не содержащее ни одного элемента). Запись x О A означает, что x – элемент множества A, а B М A – что B является подмножеством множества A. Если универсальное множество, из которого мы берем элементы всех множеств, обозначить через I, то элементы, принадлежащие I, но не входящие в A, образуют множество, называемое дополнением множества A и обозначаемое C(A) или Aў. Множество, не содержащее ни одного элемента, называется пустым множеством.

Над множествами можно производить операции, напоминающие операции, производимые в арифметике над числами. Объединением AB множеств A и B называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств A и B (элемент, принадлежащий множествам A и B одновременно засчитывается при включении в AB только один раз). Пересечением AB множеств A и B называется множество, состоящее из всех элементов, принадлежащих как A, так и B. Предположим, например, что множество I состоит из всех букв русского алфавита, A – из всех согласных, а множество B – из букв, встречающихся в слове «энциклопедия». Тогда объединение AB состоит из всех букв алфавита, кроме а, ё, у, ъ, ь, ы, ю, пересечение AB – из букв д, к, л, н, п, ц, а дополнение C(A) – из всех гласных. Раздел теории множеств, который занимается исследованием операций над множествами, называется алгеброй множеств. Пустое множество играет в алгебре множеств роль нуля, и поэтому его часто обозначают символом О; например, AO = A, AO = O.

Булева алгебра.

Алгебра множеств является подразделом булевых алгебр, впервые возникших в трудах Дж.Буля (1815–1864). В аксиомах булевой алгебры отражена аналогия между понятиями «множества», «событие» и «высказывания». Логические высказывания можно записать с помощью множеств и проанализировать с помощью булевой алгебры.

Даже не вдаваясь в детальное изучение законов булевой алгебры, мы можем получить представление о том, как она используется на примере одной из логических задач Льюиса Кэрролла. Пусть у нас имеется некоторый набор утверждений:

-2831. Не бывает котенка, который любит рыбу и которого нельзя научить всяким забавным штукам;

2. Не бывает котенка без хвоста, который будет играть с гориллой;

3. Котята с усами всегда любят рыбу;

4. Не бывает котенка с зелеными глазами, которого можно научить забавным штукам;

5. Не бывает котят с хвостами, но без усов.

Какое заключение можно вывести из этих утверждений?

Рассмотрим следующие множества (универсальное множество I включает в себя всех котят): A – котята, любящие рыбу; B – котята, обучаемые забавным штукам; D – котята с хвостами; E – котята, которые будут играть с гориллой; F – котята с зелеными глазами и G – котята с усами. Первое утверждение гласит, что множество котят, которые любят рыбу, и дополнение множества котят, обучаемых забавным штукам, не имеют общих элементов. Символически это записывается как

-2831. AC(B) = O.

Аналогичным образом остальные утверждения можно записать так:

-2832. C(D)E = O;

3. G М A;

4. BF = O;

5. D М G.

Принимая во внимание теоретико-множественный смысл символов (или воспользовавшись законами булевой алгебры), мы можем переписать утверждения 1, 2 и 4 в виде

1. A М B;

2. E М D;

4. B М C(F).

Таким образом, мы переформулировали исходные утверждения в следующие:

-2831. Котят, которые любят рыбу, можно обучить забавным штукам;

2. У котят, которые будут играть с гориллой, есть хвосты;

4. У котят, которых можно обучить забавным штукам, глаза не зеленые;

Теперь можно расположить символические записи утверждений в таком порядке, чтобы последний символ предыдущего утверждения совпадал с первым символом следующего (этому условию удовлетворяет расположение утверждений в порядке 2, 5, 3, 1, 4). Возникает цепочка включений E М D М G М A М B М C(F), из которой можно сделать вывод, что E М C(F) или «Не бывает котенка с зелеными глазами, который будет играть с гориллой». Такое заключение едва ли очевидно, если рассматривать пять исходных утверждений в их словесной формулировке.

Сравнение множеств.

Если из элементов двух множеств можно составить пары таким образом, чтобы каждому элементу первого множества соответствовал определенный элемент второго множества, а каждому элементу второго множества соответствовал один и только один элемент первого множества, то говорят, что между такими двумя множествами установлено взаимно однозначное соответствие. Чтобы установить взаимно однозначное соответствие, необязательно пересчитывать элементы множеств. Например, мы знаем, что американские штаты находятся во взаимно однозначном соответствии с их столицами, хотя можем оставаться в неведении относительно общего их числа. Мы могли бы утверждать: «Столиц штатов ровно столько, сколько штатов». Между двумя конечными множествами можно установить взаимно однозначное соответствие тогда и только тогда, когда оба множества состоят из одного и того же числа элементов. В теории множеств аналогичные утверждения используются, даже когда множества содержат бесконечно много элементов. Если между двумя множествами можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны. Если же при любом способе образования пар некоторые элементы из первого множества остаются без пары, то говорят, что первое множество содержит больше элементов, чем второе, или, что первое множество имеет большую мощность. С понятием мощности связаны, казалось бы, удивительные результаты. Например, на первый взгляд положительных целых чисел в два раза больше, чем четных положительных чисел, так как четно каждое второе число. Но, согласно теории множеств, четных положительных чисел столько же, сколько всех положительных целых чисел. Действительно, можно образовать пары чисел 2 и 1, 4 и 2, 6 и 3 и, вообще каждому четному числу 2n поставить в соответствие целое число n. Именно это обстоятельство имел в виду Б.Рассел (1872–1970), сформулировав факт, названный им парадоксом Тристрама Шенди. Герой романа Стерна сетовал на то, что ему потребовался целый год, чтобы изложить события первого дня его жизни, еще один год понадобился, чтобы описать второй день, и что при таком темпе он никогда не завершит свое жизнеописание. Рассел возразил, заметив, что если бы Тристрам Шенди жил вечно, то смог бы закончить свое жизнеописание, так как события n-го дня Шенди мог бы описать за n-й год и, таким образом, в летописи его жизни ни один день не остался бы не запечатленным. Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней. Эти примеры показывают, что бесконечное множество можно поставить во взаимно однозначное соответствие со своим бесконечным подмножеством. Иногда это свойство принимают за определение бесконечного.

Если можно установить взаимно однозначное соответствие между некоторым множеством и множеством положительных целых чисел, то говорят, что такое множество счетно. Для обозначения количества элементов в счетном множестве часто используют символ А0 (алеф-нуль). Так называемые «трансфинитные» числа, например А0, могут не подчиняться обычным законам арифметики. Например, так как существует А0 четных чисел, А0 нечетных и А0 целых чисел, то приходится признать, что А0 + А0 = А0. Идея сравнения множеств путем установления взаимно однозначного соответствия между ними используется в различных разделах математики. Число всех действительных чисел, как показал основатель научной теории множеств Г.Кантор (1845–1918), больше, чем А0 чисел. Следовательно, если можно показать, что множество действительных чисел, обладающих некоторым особым свойством, является всего лишь счетным множеством, то заведомо должны существовать действительные числа, этим свойством не обладающие. Например, так как множество алгебраических чисел счетно, должны существовать неалгебраические числа. Такие числа называются трансцендентными.

Поразительная и далеко не очевидная теорема, высказанная в качестве гипотезы Кантором и доказанная Э.Шрёдером и Ф.Бернштейном около 1896, утверждает, что если можно установить взаимно однозначное соответствие между множеством A и подмножеством множества B, и между множеством B и подмножеством множества A, то существует взаимно однозначное соответствие между всем множеством A и всем множеством B.

Парадоксы.

Мы уже упоминали о том, что в теории множеств встречаются такие утверждения, как парадокс Тристрама Шенди, которые выглядят противоречащими здравому смыслу. Эти парадоксы возникают просто потому, что теория множеств, подобно многим математическим и физическим теориям, облекает свои идеи в обычные слова, вкладывая в них особый смысл. Однако существуют и парадоксы, возникающие из-за внутренних логических трудностей самой теории множеств. Обильным источником парадоксов такого типа служит широко распространенная практика задания множества путем указания некоторого свойства его элементов, например, «множество, состоящее из английских слов, содержащих менее 19 букв».

Некритическое использование такого рода определений может привести к трудностям. Например, некоторые статьи в этой энциклопедии содержат ссылки на себя, другие таких ссылок не содержат. Мы могли бы включить в нашу энциклопедию дополнительную статью, состоящую только из перечня статей, не содержащих ссылок на себя. Принадлежала бы такая статья множеству статей, не содержащих ссылок на себя, или не принадлежала бы? Любой ответ противоречил бы отличительному свойству, которым по их определению наделены элементы множества. Это – одна из форм так называемого парадокса Рассела, названного в честь своего автора Бертрана Рассела. «Множество всех множеств» – еще одно понятие, также приводящее к парадоксу. Существование парадоксов показывает, с какой осторожностью следует пользоваться терминологией теории множеств. Тем не менее теория множеств настолько полезна, что большинство математиков не хотели бы отказываться от нее. Было затрачено много усилий, чтобы развить методы, позволяющие исключить возникновение парадоксов в теории множеств. В приложениях теории множеств к другим разделам математики универсальное множество I обычно само является некоторым определенным множеством и парадоксальные ситуации здесь не возникают.

Аксиома выбора.

Неожиданные трудности в теории множеств могут возникнуть, казалось бы, в самых простых случаях. Если, например, задано семейство непересекающихся множеств, ни одно из которых не пусто, то интуитивно кажется очевидным, что мы можем построить новое множество, содержащее ровно по одному элементу из каждого множества, входящего в это семейство. Но если наше семейство содержит бесконечно много множеств, то для построения нового множества может потребоваться бесконечное число произвольных выборов, а законность такого процесса при тщательном анализе становится отнюдь не очевидной. Аксиома выбора, утверждающая, что такое множество существует, была впервые сформулирована в 1904 Э.Цермело (1871–1953). До сих пор не удалось показать, что аксиома выбора следует из остальных аксиом теории множеств. Но около 1938 К.Гёдель (1906–1978) показал, что если теория множеств непротиворечива (т.е. не содержит внутренних противоречий) без аксиомы выбора, то она остается непротиворечивой и после присоединения к ней аксиомы выбора. См. также АБСТРАКТНЫЕ ПРОСТРАНСТВА; ФУНКЦИЯ.

www.krugosvet.ru

Теория множеств — это… Что такое Теория множеств?

Тео́рия мно́жеств — раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики.^{[источник не указан 479 дней]}

История

Наивная теория множеств

Первый набросок теории множеств принадлежит Бернарду Больцано («Парадоксы бесконечного», 1850). В этой работе рассматриваются произвольные (числовые) множества, и для их сравнения определено понятие взаимно-однозначного соответствия.

В 1870 году немецкий математик Георг Кантор разработал свою программу стандартизации математики, в рамках которой любой математический объект должен был оказываться тем или иным «множеством». Этот подход изложен в двух его статьях, опубликованных в 1879—1897 годах в известном немецком журнале «Математические анналы» (нем. «Mathematische Annalen»).^[1] Например, натуральное число, по Кантору, следовало рассматривать как множество, состоящее из единственного элемента другого множества, называемого «натуральным рядом» — который, в свою очередь, сам представляет собой множество, удовлетворяющее так называемым аксиомам Пеано. При этом общему понятию «множества», рассматривавшемуся им в качестве центрального для математики, Кантор давал мало что определяющие определения вроде «множество есть многое, мыслимое как единое», и т. д. Это вполне соответствовало умонастроению самого Кантора, подчёркнуто называвшего свою программу не «теорией множеств» (этот термин появился много позднее), а учением о множествах (Mengenlehre)^{[источник не указан 1087 дней]}.

Программа Кантора вызвала резкие протесты со стороны многих современных ему крупных математиков. Особенно выделялся своим непримиримым к ней отношением Леопольд Кронекер, полагавший, что математическими объектами могут считаться лишь натуральные числа и то, что к ним непосредственно сводится (известна его фраза о том, что «бог создал натуральные числа, а всё прочее — дело рук человеческих»). Полностью отвергли теорию множеств и такие авторитетные математики, как Герман Шварц и Анри Пуанкаре. Тем не менее, другие крупные математики — в частности, Готлоб Фреге, Рихард Дедекинд и Давид Гильберт — поддержали Кантора в его намерении перевести всю математику на теоретико-множественный язык. В частности, теория множеств стала фундаментом теории меры и интеграла, топологии и функционального анализа.

Однако вскоре выяснилось, что установка Кантора на неограниченный произвол при оперировании с бесконечными множествами (выраженный им самим в принципе «сущность математики состоит в её свободе») является изначально порочной (см. Кризис математических основ). А именно, был обнаружен ряд теоретико-множественных антиномий: оказалось, что при использовании теоретико-множественных представлений некоторые утверждения могут быть доказаны вместе со своими отрицаниями (а тогда, согласно правилам классической логики высказываний, может быть «доказано» абсолютно любое утверждение).

После обнаружения антиномии Рассела часть математиков (например, Л. Э. Я. Брауэр и его школа) решила полностью отказаться от использования теоретико-множественных представлений. Другая же часть математиков, возглавленная Д. Гильбертом, предприняла ряд попыток строго обосновать ту часть теоретико-множественных представлений, которая казалась им наиболее ответственной за возникновение антиномий, на основе заведомо надёжной финитной математики. Логический аппарат усовершенствовал Бертран Рассел в работах, позднее собранных в его монографии «Начала математики» (1910—1913). В 1904—1908 гг. Эрнст Цермело предложил первую версию аксиоматической теории множеств.

Аксиоматическая теория множеств

Особенностью аксиоматического подхода является отказ от лежащего в основе программы Кантора представления о действительном существовании множеств в некотором идеальном мире. В рамках аксиоматических теорий множества «существуют» исключительно формальным образом, и их «свойства» могут существенно зависеть от выбора аксиоматики. Этот факт всегда являлся мишенью для критики со стороны тех математиков, которые не соглашались (как на том настаивал Гильберт) признать математику лишённой всякого содержания игрой в символы. В частности, Н. Н. Лузин писал, что «мощность континуума, если только мыслить его как множество точек, есть единая некая реальность», место которой в ряду кардинальных чисел не может зависеть от того, признаётся ли в качестве аксиомы континуум-гипотеза, или же её отрицание.

В настоящее время наиболее распространённой аксиоматической теорией множеств является ZFC — теория Цермело — Френкеля с аксиомой выбора. Вопрос о непротиворечивости этой теории (а тем более — о существовании модели для неё) остаётся нерешённым.

Не всеми математиками аксиома выбора принимается безоговорочно. Так, например Эмиль Борель и Анри Лебег считают, что доказательства, полученные при помощи этой аксиомы, имеют другую познавательную ценность, чем доказательства, независимые от неё. Другие же математики, такие как Феликс Хаусдорф и Адольф Френкель, принимают аксиому выбора безоговорочно, признавая за ней ту же степень очевидности, что и за другими аксиомами Цермело — Френкеля.^[2]

Основные понятия

В основе теории множеств лежат первичные понятия: множество и отношение быть элементом множества (обозначается как ^[3] — «x есть элемент множества A», «x принадлежит множеству A»). Среди производных понятий наиболее важны следующие:

• пустое множество, обычно обозначается символом ;
• подмножество и надмножество;
• семейство множеств;
• пространство (Универсум);
• операции:

  Для множеств определены следующие бинарные отношения:

  • править] Расширения

    Основная статья: Теория комплектов

    Теория комплектов — естественное расширение (обобщение) теории множеств. Подобно множеству, комплект — набор элементов из некоторой области. Отличие от множества: комплекты допускают присутствие нескольких экземпляров одного и того же элемента (элемент входит от нуль раз, то есть, не входит в комплект, до любого заданного числа раз)^[4]. (см. например, Мультисочетания).

    Приложения

    См. также

    Примечания

    1. ↑ Georg Cantor, Ueber unendliche, lineare Punktmannichfahltigkeiten. — Mathematische Annalen, Bd. 15 (1879), 17 (1880), 20 (1882), 21 (1883), 23 (1884).
       Georg Cantor, Beiträge zur Begründung der transfiniten Mengenlehre. — Mathematische Annalen, Bd. 46 (1895), 49 (1895). (Имеется русский перевод: Кантор Г. Труды по теории множеств. М.: Наука, 1985.)
    2. ↑ К. Куратовский, А. Мостовский Теория множеств / Перевод с английского М. И. Кратко под редакцией А. Д. Тайманова. — М.: Мир, 1970. — С. 61..
    3. ↑ Символ (от греч. εστι — «быть») введён итальянским математиком Джузеппе Пеано.
    4. ↑ Джеймс Питерсон Теория сетей Петри и моделирование систем:Пер. с англ.-М.:Мир, 1984.-264с., ил. (стр. 231 «Обзор теории комплектов»)

    Литература

dic.academic.ru