Сходящаяся числовая последовательность – 11. Сходящиеся и расходящиеся последовательности. Предел последовательности | Читать онлайн, без регистрации
Лекция 09. Сходящиеся последовательности
Лекция 9. Сходящиеся последовательности.
9.1. Определения и свойства сходящихся последовательностей.
Определение 9.1. Последовательность  называется сходящейся,
если существует такое число
называется сходящейся,
если существует такое число  ,
что последовательность
,
что последовательность является бесконечно малой. При этом
число а называетсяпределом
последовательности
является бесконечно малой. При этом
число а называетсяпределом
последовательности 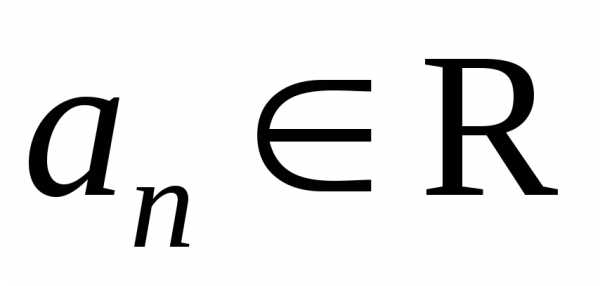 .
.
В силу определения
любая бесконечно малая последовательность
имеет пределом 0. Запись: 
 при.
при. Определение 9.2. Последовательность  называетсясходящейся,
если
называетсясходящейся,
если  :
для
:
для
 :
при всех
:
при всех
 .
. Последнее неравенство
означает, что элементы xn при  лежат в интервале,
который назовем
лежат в интервале,
который назовем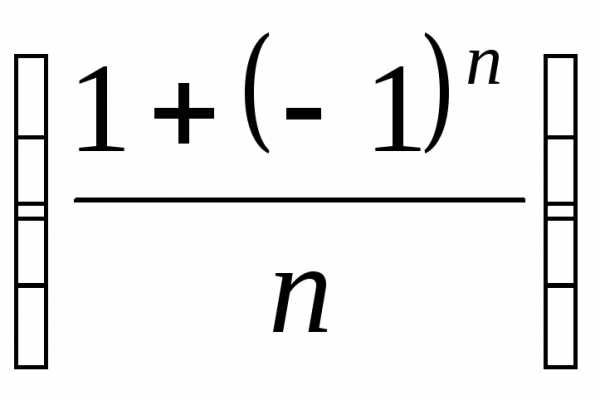 -окрестностью
точкиа.
-окрестностью
точкиа.
Определения 9.1 и 9.2 эквивалентны.
♦ Утверждение 9.1. Элемент xn сходящейся последовательности может
быть представлен в виде
,
где
 (
( – бесконечно малая последовательность).
– бесконечно малая последовательность).☼ Замечание 9.1. Последовательности, не являющиеся сходящимися, называют расходящимися. ☼
☼ Замечание 9.2. Будем считать, что бесконечно большие
последовательности сходятся к пределу  :
: или
или 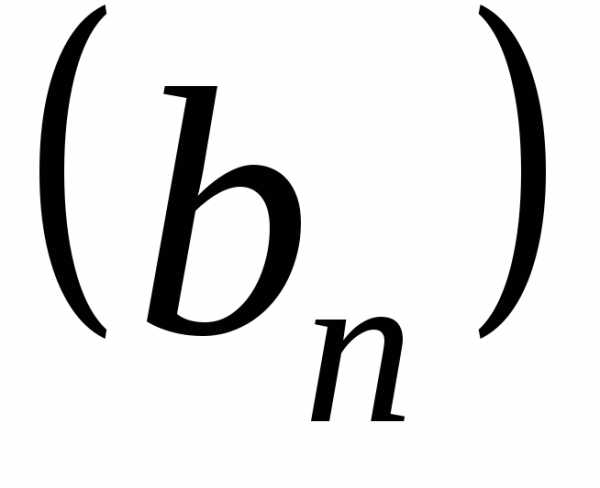
Пример 9.1. Рассмотрим последовательность  .
Докажем, что
.
Докажем, что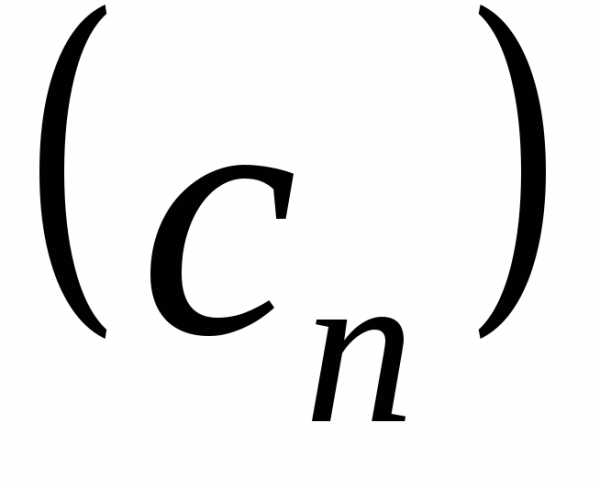 .
.
Доказательство. По определению 2 имеем
,  ;
; ;
;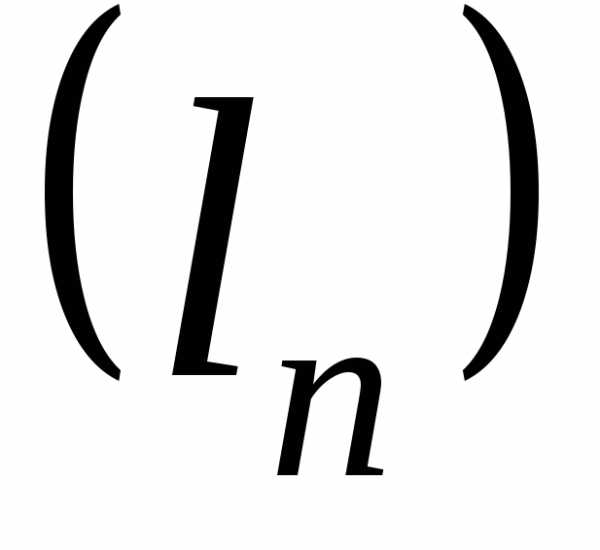 ;
;
 ,
то
,
то ,
где
,
где .
Таким образом, начиная с номера
.
Таким образом, начиная с номера ,
выполняется неравенство
,
выполняется неравенство и
и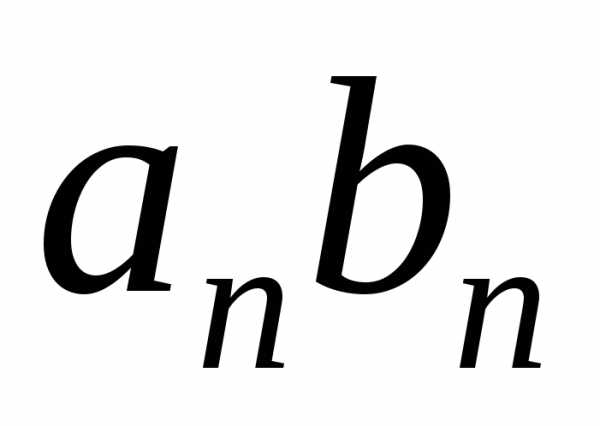 .■
.■ ♦ Теорема 9.1. Сходящиеся последовательности имеют только один предел.
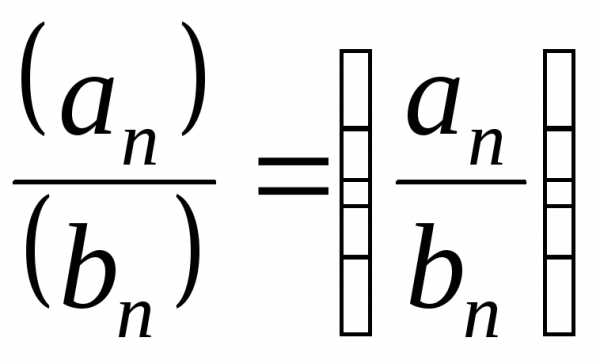 и
и
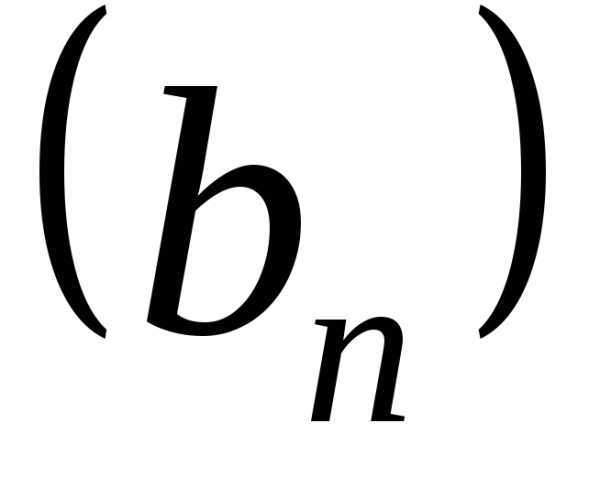 . Тогда
,,
где
. Тогда
,,
где ,
, – бесконечно малые последовательности.
Получаем:,
все элементы бесконечно малой
последовательности
– бесконечно малые последовательности.
Получаем:,
все элементы бесконечно малой
последовательности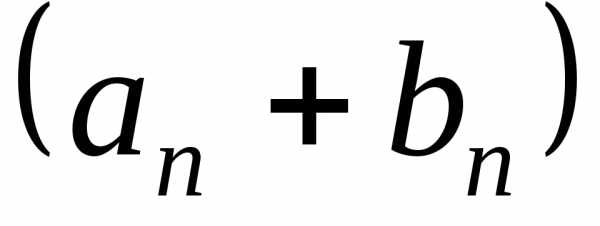 равны
равны
♦ Теорема 9.2. Всякая сходящаяся последовательность является ограниченной.
Доказательство. Пусть 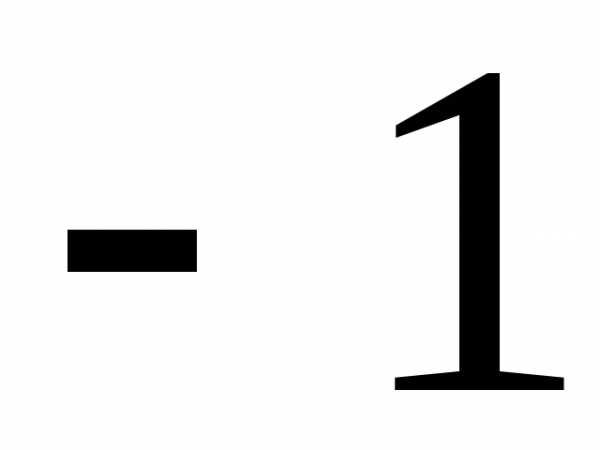 .
Фиксируем
.
Фиксируем ,
, :
: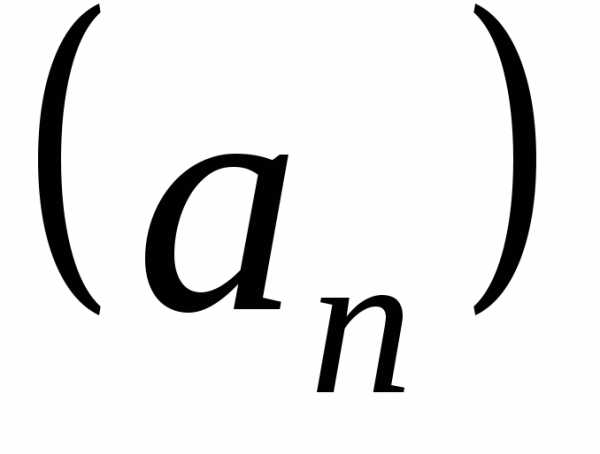 при
при , ,.
Тогда
, ,.
Тогда
 n.
■
n.
■☼ Замечание 9.3. Не всякая ограниченная последовательность является сходящейся.
Например: .☼
9.2. Теоремы об арифметических операциях над элементами сходящихся последовательностей.
♦ Теорема 9.3. Сумма
(разность) сходящихся последовательностей  и
и представляет собой сходящуюся
последовательность, предел которой
равен сумме (разности) пределов
последовательностей
представляет собой сходящуюся
последовательность, предел которой
равен сумме (разности) пределов
последовательностей
 ,
то есть.
,
то есть. Доказательство. Пусть а и b – соответственно пределы последовательностей  и
и .
Тогдаи,
где
.
Тогдаи,
где и
и
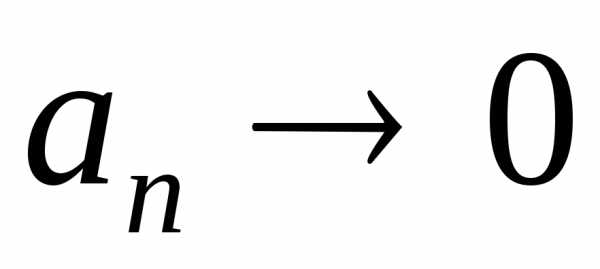 – бесконечно малая, таким образом,
последовательность
– бесконечно малая, таким образом,
последовательность сходится и имеет своим пределом число
сходится и имеет своим пределом число .
■
.
■ ♦ Теорема 9.4. Произведение
сходящихся последовательностей 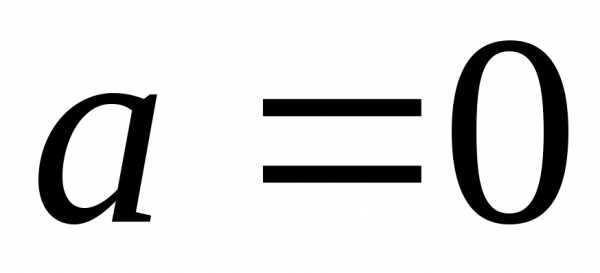 и
и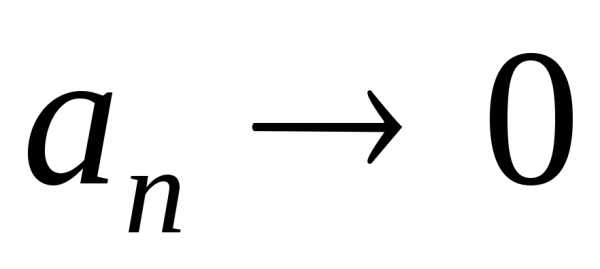 представляет собой сходящуюся
последовательность, предел которой
равен произведению пределов
представляет собой сходящуюся
последовательность, предел которой
равен произведению пределов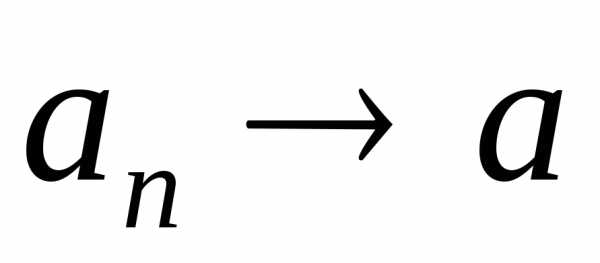
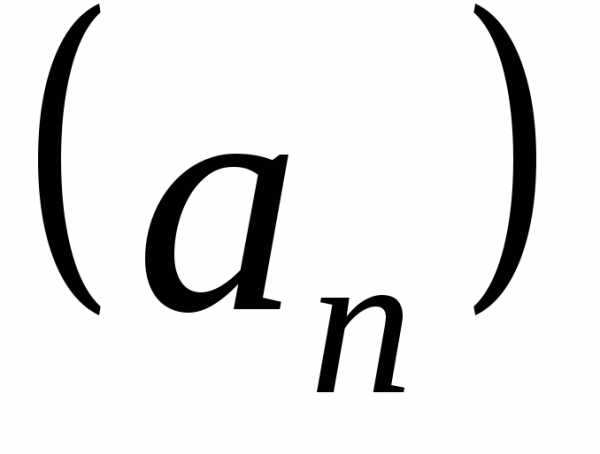 ,
то есть.
,
то есть. Доказательство. Пусть а и b – пределы последовательностей  и
и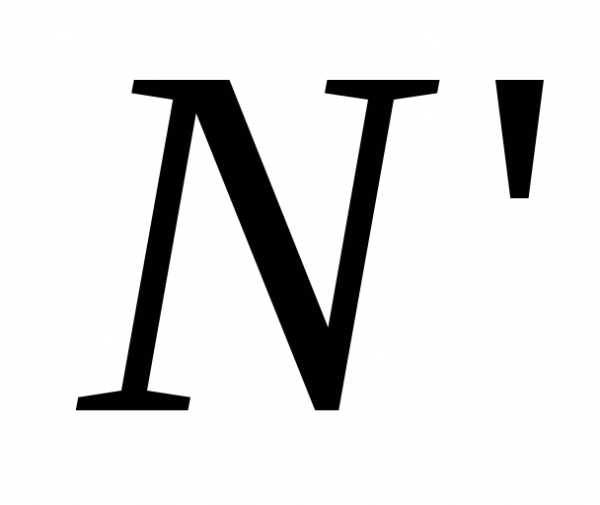 .
Тогдаи
.
Тогдаи ,
где
,
где и
и
 сходится и имеет своим пределом число
сходится и имеет своим пределом число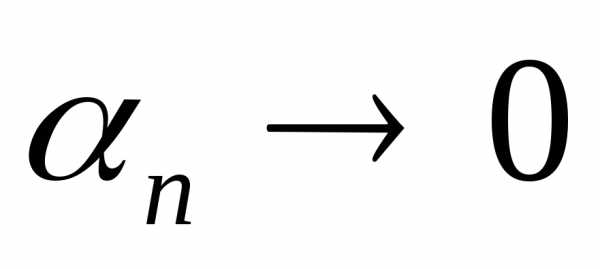 .
■
.
■ ♦ Лемма 9.1. Если
последовательность  сходится к отличному от нуля пределуb,
то, начиная с некоторого номера, определено
частное
сходится к отличному от нуля пределуb,
то, начиная с некоторого номера, определено
частное 
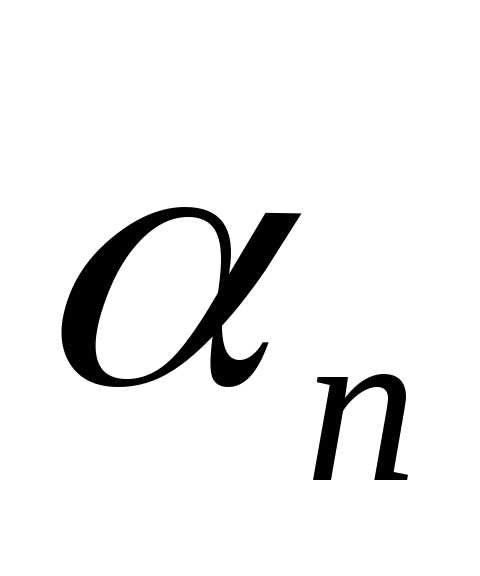 и
и ,
которое представляет собой ограниченную
последовательность.
,
которое представляет собой ограниченную
последовательность. Доказательство. Пусть  ,
т.к.
,
т.к. .
Тогда
.
Тогда при
при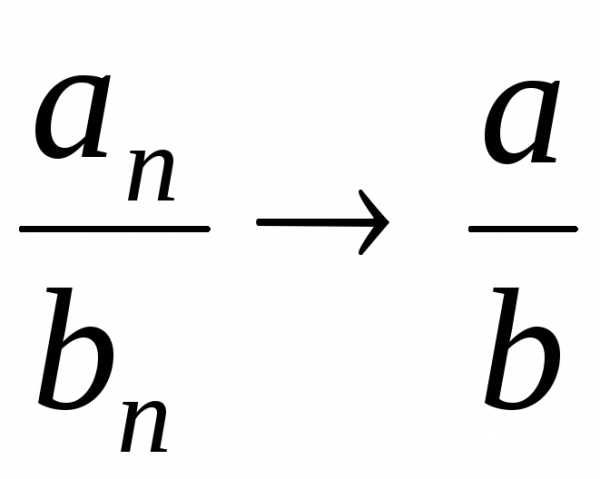 ,
,

Значит, начиная с 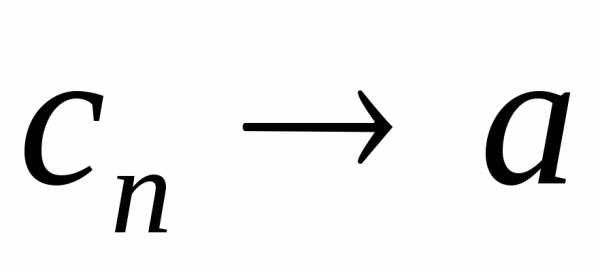 ,
, последовательность
последовательность ограничена. ■
ограничена. ■
♦ Теорема 9.5. Частное
двух сходящихся последовательностей 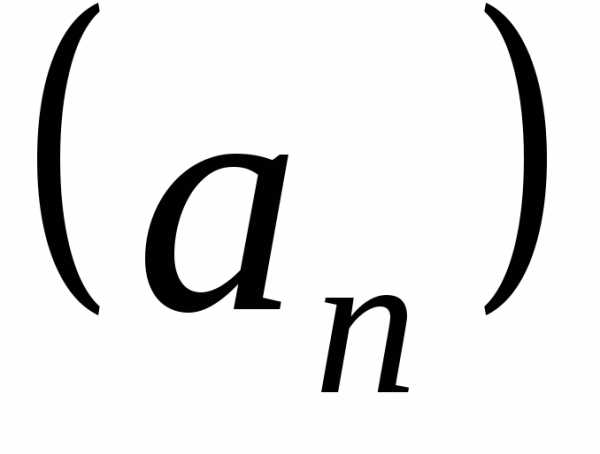 и
и при условии, что
при условии, что ,
есть сходящаяся последовательность,
предел которой равен частному пределов
последовательностей
,
есть сходящаяся последовательность,
предел которой равен частному пределов
последовательностей и
и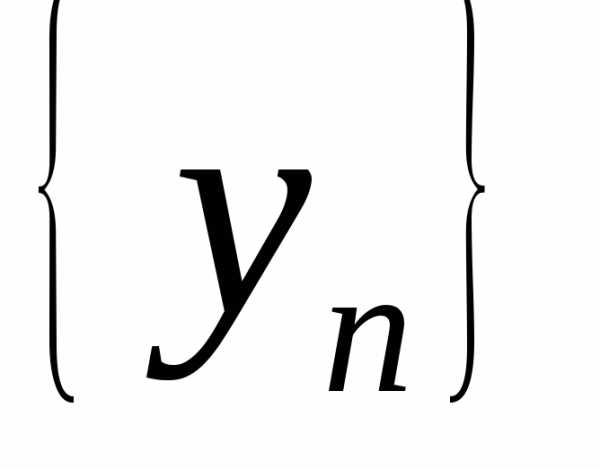 .
.
Доказательство. Пусть  .
По лемме при
.
По лемме при
 – ограниченная последовательность.
– ограниченная последовательность.
Рассмотрим при 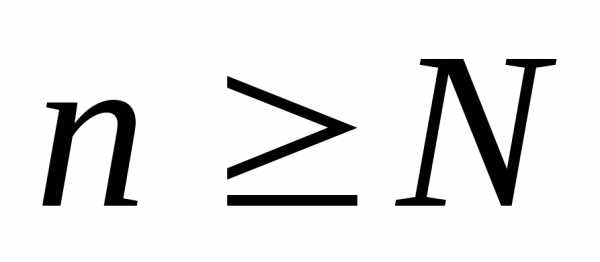 частное
частное ;
докажем, что
;
докажем, что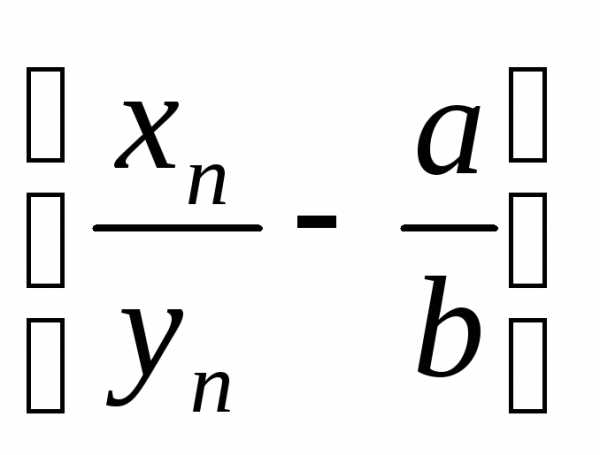 – бесконечно малая.
– бесконечно малая.
Рассмотрим разность
.
Так как  – ограниченная, а
– ограниченная, а – бесконечно малая, то последовательность
– бесконечно малая, то последовательность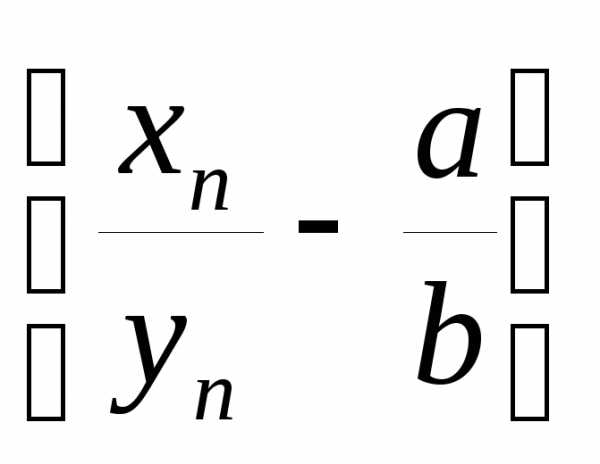 также бесконечно малая, значит,
последовательность
также бесконечно малая, значит,
последовательность сходится и её предел
сходится и её предел .
■
.
■
Пример 9.2.
1) Найти  .
Причислитель и знаменатель стремятся к
бесконечности и сразу применить теорему
о пределе частного нельзя, так как в
условии теоремы 9.5 предполагается
существование конечных пределов.
Преобразуем данную последовательность,
разделив все члены дроби на
.
Причислитель и знаменатель стремятся к
бесконечности и сразу применить теорему
о пределе частного нельзя, так как в
условии теоремы 9.5 предполагается
существование конечных пределов.
Преобразуем данную последовательность,
разделив все члены дроби на .
Затем, применяя теоремы о пределе
частного и о пределе суммы, найдём:
.
Затем, применяя теоремы о пределе
частного и о пределе суммы, найдём:
.
Когда вырабатывается определённый навык, подробную запись можно сократить.
2) Найти 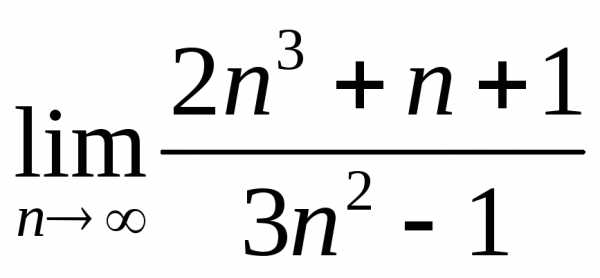 .
Разделим все члены дроби на
.
Разделим все члены дроби на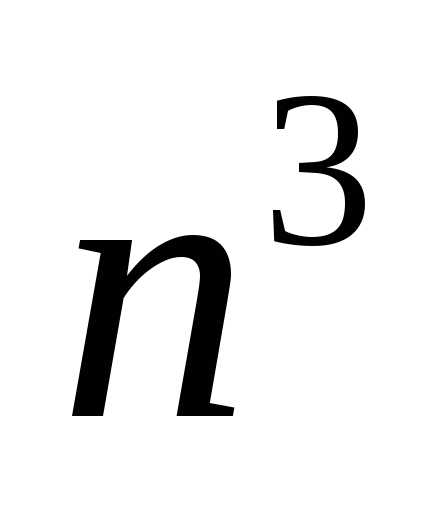 и используем необходимые теоремы:.
и используем необходимые теоремы:.
3) Найти 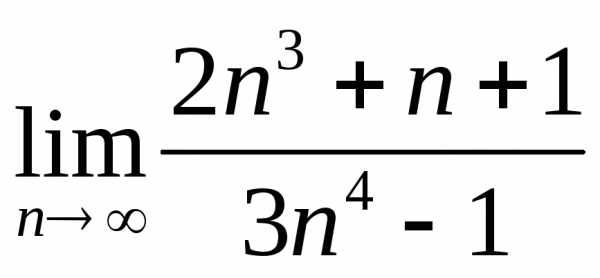 .
Разделим все члены дроби на
.
Разделим все члены дроби на ,
получим:.
,
получим:.
При решении задач
можно воспользоваться результатами
приведённых примеров. Сделаем вывод: если старшие
степени n в числителе и знаменателе равны, то
ответ равен отношению коэффициентов
при данных степенях; если старшая степень n находится в числителе, то ответ будет  ,
если старшая степень – в знаменателе,
то ответ будет0.
,
если старшая степень – в знаменателе,
то ответ будет0.
9.3. Предельный переход в неравенствах.
♦ Теорема 9.6. Если все
элементы сходящейся последовательности  ,
начиная с некоторого номера, удовлетворяют
неравенству
,
начиная с некоторого номера, удовлетворяют
неравенству
 ,
то и предел
,
то и предел этой последовательности удовлетворяет
неравенству
этой последовательности удовлетворяет
неравенству
 .
.
Доказательство. Пусть при  выполняется неравенство
выполняется неравенство .
.
Предположим
противное: пусть
.
Положим.
При ,
но тогда
,
но тогда ,
, – получается противоречие
– получается противоречие
 (случай
(случай рассматривается аналогично). ■
рассматривается аналогично). ■
☼ Замечание 9.4. Элементы сходящейся последовательности  могут удовлетворять строгому неравенству
могут удовлетворять строгому неравенству ,
однако при этом может оказатьсяa=b. Например,
если
,
однако при этом может оказатьсяa=b. Например,
если  ,
то при
,
то при получаем
получаем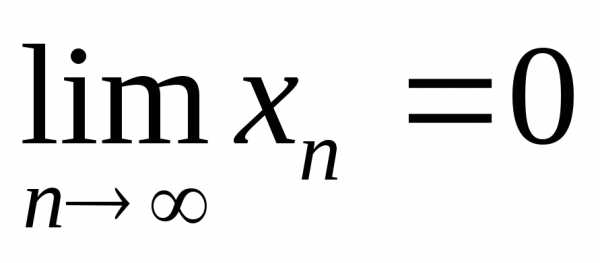 .☼
.☼
Следствие 1. Если элементы  и
и сходящихся последовательностей
сходящихся последовательностей и
и ,
начиная с некоторого номера, удовлетворяют
неравенству
,
начиная с некоторого номера, удовлетворяют
неравенству ,
то их пределы удовлетворяют такому же
неравенству:.
,
то их пределы удовлетворяют такому же
неравенству:.
Действительно,
если
,
то .
.
Следствие 2. Если все
элементы сходящейся последовательности  находятся на сегменте
находятся на сегменте ,
то и её предел с также находится на этом
сегменте.
,
то и её предел с также находится на этом
сегменте.
Это очевидно: так
как  ,
то и.
,
то и.
♦ Теорема 9.7 (принцип
двустороннего ограничения). Пусть  и
и – две сходящиеся последовательности,
имеющие общий пределa.
Пусть, кроме того, все элементы третьей
последовательности
– две сходящиеся последовательности,
имеющие общий пределa.
Пусть, кроме того, все элементы третьей
последовательности  ,
по крайней мере начиная с некоторого
номера, удовлетворяют неравенству.
Тогда последовательность
,
по крайней мере начиная с некоторого
номера, удовлетворяют неравенству.
Тогда последовательность сходится и имеет пределa.
сходится и имеет пределa.
Доказательство. Достаточно
доказать, что  бесконечно малая последовательность.
Пусть
бесконечно малая последовательность.
Пусть – номер, начиная с которого выполняется
неравенство. Тогда, начиная
с
– номер, начиная с которого выполняется
неравенство. Тогда, начиная
с  ,
выполняется и неравенство.
Отсюда следует, что при
,
выполняется и неравенство.
Отсюда следует, что при . Фиксируем
. Фиксируем  .
Тогда
.
Тогда

Обозначим
,
тогда при
 .
■
.
■
41
studfiles.net
Как доказать, что последовательность сходится? Основные свойства сходящихся последовательностей
Для многих людей математический анализ представляет собой лишь набор непонятных цифр, значков и определений, далёких от реальной жизни. Однако, мир, в котором существуем мы, построен на числовых закономерностях, выявление которых помогает не просто познавать окружающий мир и решать его сложные проблемы, но и упрощать бытовые практические задачи. Что имеет в виду математик, когда говорит, что числовая последовательность сходится? Об этом следует поговорить подробнее.

Представим себе матрёшек, которые помещаются одна в другой. Размеры их, записанные в виде цифр, начиная с большей и кончая меньшей из них, формируют последовательность. Если вообразить бесконечное количество подобных ярких фигурок, то получившийся ряд окажется фантастически длинным. Это сходящаяся числовая последовательность. И стремится она к нулю, так как размеры каждой последующей матрёшки, катастрофически уменьшаясь, постепенно превращаются в ничто. Таким образом, легко можно объяснить: что такое бесконечно малое.
Похожим примером может стать дорога, уходящая вдаль. А визуальные размеры автомобиля, уезжающего по ней от наблюдателя, постепенно сокращаясь, превращаются в бесформенное пятнышко, напоминающее точку. Таким образом, машина, как некий объект, удаляясь в неизвестном направлении, становится бесконечно маленькой. Параметры указанного тела никогда не будут нулевыми в прямом смысле этого слова, но неизменно стремятся к этой величине в конечном пределе. Поэтому данная последовательность сходится снова к нулю.

Рассчитаем всё по каплям
Вообразим теперь житейскую ситуацию. Больному врач прописал принимать микстуру, начиная с десяти капель в день и прибавляя по две в каждые последующие сутки. И так доктор предложил продолжать до тех пор, пока не кончится содержимое пузырька с лекарством, объём которого составляет 190 капель. Из изложенного следует, что количество таковых, расписанное по дням составит следующий числовой ряд: 10, 12, 14 и так далее.
Как выяснить время прохождения всего курса и количество членов последовательности? Здесь, конечно, можно подсчитывать капли примитивным образом. Но гораздо легче, учитывая закономерность, воспользоваться формулой суммы арифметической прогрессии с шагом d = 2. И с применением такого метода выяснить, что количество членов числового ряда равно 10. При этом а10 = 28. Номер члена указывает на количество дней приёма лекарства, а 28 соответствует числу капель, которые больной должен употребить в последний день. Данная последовательность сходится? Нет, потому что, несмотря на то, что снизу она ограничена числом 10, а сверху – 28, такой числовой ряд не имеет предела, в отличие от предыдущих примеров.
В чём разница?
Попробуем теперь уточнить: когда числовой ряд оказывается сходящейся последовательностью. Определение такого рода, как можно заключить из вышеописанного, напрямую связано с понятием конечного предела, наличие которого и выявляет суть вопроса. Так в чём принципиальное отличие ранее приведённых примеров? И почему в последнем из них число 28 не может считаться пределом числового ряда Xn = 10 + 2(n-1)?
Для выяснения этого вопроса рассмотрим другую последовательность, заданную нижеуказанной формулой, где n принадлежит множеству натуральных чисел.

Данное сообщество членов представляет собой набор обыкновенных дробей, числитель которых 1, а знаменатель постоянно увеличивается: 1, ½ …
Причём каждый последующий представитель этого ряда по расположению на числовой прямой всё больше приближается к 0. А это значит, что появляется такая окрестность, где точки скучиваются вокруг нуля, который и является пределом. И чем ближе они к нему, тем плотнее становится их концентрация на числовой прямой. А расстояние между ними катастрофически сокращается, превращаясь в бесконечно малое. Это признак того, что последовательность сходится.

Подобным же образом разноцветные прямоугольники, изображённые на рисунке, при удалении в пространстве визуально располагаются кучнее, в гипотетическом пределе превращаясь в ничтожно малые.
Бесконечно большие последовательности
Разобрав определение сходящейся последовательности, перейдём теперь к противоположным примерам. Многие из них были известны человеку с самых древних времён. Простейшими вариантами расходящихся последовательностей являются ряды натуральных и чётных чисел. Они по-другому именуются бесконечно большими, так как члены их, постоянно увеличиваясь, всё больше приближаются к положительной бесконечности.
Примерами таковых также могут служить любая из арифметических и геометрических прогрессий с шагом и знаменателем соответственно больше нуля. Расходящимися последовательностями считаются, к тому же, числовые ряды, которые и вовсе не имеют предела. К примеру, Xn= (-2)n-1.
Последовательность Фибоначчи
Практическая польза указанных ранее числовых рядов для человечества несомненна. Но существует огромное множество и других замечательных примеров. Одним из них является последовательность Фибоначчи. Каждый из её членов, которые начинаются с единицы, представляет собой сумму предыдущих. Первыми двумя её представителями являются 1 и 1. Третий 1+1=2, четвёртый 1+2=3, пятый 2+3=5. Далее, согласно этой же логике, следуют числа 8, 13, 21 и так далее.

Данный ряд чисел неограниченно возрастает и не имеет конечного предела. Зато он обладает ещё одним замечательным свойством. Отношение каждого предыдущего числа к последующему всё более приближается по своему значению к 0, 618. Здесь можно уяснить разницу между сходящейся и расходящейся последовательностью, ведь если составить ряд из полученных частных от делений, указанный числовой строй будет иметь конечный предел равный 0,618.
Последовательность коэффициентов Фибоначчи
Указанный выше числовой ряд широко используется в практических целях для технического анализа рынков. Но этим не ограничиваются его возможности, которые знали и умели применять на практике ещё в глубокой древности египтяне и греки. Это доказывают построенные ими пирамиды и Парфенон. Ведь число 0, 618 является постоянным коэффициентом хорошо известного в старину золотого сечения. Согласно этому правилу, любой произвольный отрезок возможно поделить так, что отношение между его частями будет совпадать с отношением между большим из отрезков и общей длиной.
Построим ряд из указанных отношений и попытаемся проанализировать данную последовательность. Числовой ряд получится следующим: 1; 0,5; 0,67; 0,6; 0,625; 0,615; 0,619 и так далее. Продолжая, таким образом можно убедиться, что предел сходящейся последовательности действительно будет 0,618. Однако, необходимо заметить и прочие свойства этой закономерности. Здесь цифры как бы идут вразнобой, а вовсе не в порядке возрастания или убывания. Это означает, что данная сходящаяся последовательность монотонной не является. О том, почему это так и пойдёт разговор далее.
Монотонность и ограниченность
Члены числового ряда с увеличением номера могут чётко убывать (если x1>x2>x3>…>xn>…) или возрастать (если x1<x2<x3<…<xn<…). В этом случае последовательность называется строго монотонной. Могут наблюдаться также другие закономерности, где числовой ряд будет неубывающим и невозрастающим (x1≥x2≥x3≥…≥xn≥… или x1≤x2≤x3≤…≤xn≤…), тогда сходящаяся последовательно монотонна тоже, только уже не в строгом смысле. Хорошим примером первого из указанных вариантов может служить числовой ряд, задаваемый следующей формулой.

Расписав числа данного ряда можно заметить, что любой из его членов, неограниченно приближаясь к 1, никогда не превысит этого значения. В этом случае говорят об ограниченности сходящейся последовательности. Подобное бывает всякий раз, когда находится такое положительное число М, которое оказывается всегда больше любого из членов ряда по модулю. Если числовой ряд обладает признаками монотонности и имеет предел, а следовательно – сходится, то он обязательно наделён таким свойством. Причём обратное не обязательно должно быть верным. Об этом говорит теорема об ограниченности сходящейся последовательности.
Применение подобных наблюдений на практике оказывается очень полезным. Приведём конкретный пример, исследовав свойства последовательности Xn = n/n+1, и докажем её сходимость. То, что она монотонна легко показать, так как (xn+1 – xn) есть число положительное при любых значениях n. Предел последовательности равен числу 1, а значит, соблюдаются все условия вышеуказанной теоремы, называемой также теоремой Вейерштрасса. Теорема об ограниченности сходящейся последовательности утверждает, что если она имеет предел, то в любом случае оказывается ограниченной. Однако, приведём следующий пример. Числовой ряд Xn = (-1)n является ограниченным снизу числом -1 и сверху 1. Но данная последовательность не является монотонной, не имеет предела и поэтому не сходится. То есть из ограниченности не всегда следует наличие предела и сходимости. Чтобы это выполнялось необходимо совпадение нижнего и верхнего предела, как в случае коэффициентов Фибоначчи.
Числа и законы Вселенной
Простейшими вариантами сходящейся и расходящейся последовательности являются, пожалуй, числовые ряды Xn = n и Xn = 1/n. Первая из них представляет собой натуральный ряд чисел. Она же является, как уже говорилось, бесконечно большой. Вторая сходящаяся последовательность ограничена, а члены её по величине приближаются к бесконечно малому. Каждая из этих формул олицетворяет одну из сторон многогранной Вселенной, помогая человеку на языке цифр и знаков представить себе и просчитать нечто непознаваемое, недоступное для ограниченного восприятия.
Законы мироздания, начиная от ничтожно малого и кончая невероятно большим, выражает также золотой коэффициент 0,618. Учёные считают, что он заложен в основу сути вещей и используется природой для формирования её частей. Упомянутые уже нами ранее отношения между последующим и предыдущим членами ряда Фибоначчи, не завершают на этом демонстрацию удивительных свойств этого уникального ряда. Если рассмотреть частное от деления предыдущего члена на последующей через один, то получим ряд 0,5; 0, 33; 0,4; 0,375; 0,384; 0,380; 0,382 и так далее. Интересно то, что эта ограниченная последовательность сходится, монотонной она не является, но отношение крайних от определённого члена соседних чисел всегда приблизительно оказывается равным 0,382, что тоже может быть использовано в архитектуре, техническом анализе и других отраслях.

Существуют и другие интересные коэффициента ряда Фибоначчи, все они играют в природе особую роль, а также применяются человеком в практических целях. Математики уверены, что Вселенная развивается по некоей «золотой спирали», формируемой из указанных коэффициентов. С их помощью возможно рассчитать многие явления, происходящие на Земле и в космосе, начиная от роста численности определённых бактерий и кончая движением далёких комет. Подобным же законам подчиняется, как выясняется, код ДНК.
Убывающая геометрическая прогрессия
Существует теорема, утверждающая единственность предела сходящейся последовательности. Это значит, что двух и более пределов у неё существовать не может, что несомненно важно для нахождения её математических характеристик.
Рассмотрим некоторые случаи. Любой числовой ряд, составленный из членов арифметической прогрессии, является расходящимся, за исключением случая с нулевым шагом. Это же касается геометрической прогрессии, знаменатель которой больше 1. Пределами таких числовых рядов являются «плюс» или «минус» бесконечности. Если же знаменатель меньше -1, то никакого предела вообще не существует. Возможны и другие варианты.
Рассмотрим числовой ряд, задаваемой формулой Xn = (1/4)n-1. С первого взгляда легко понять, что эта сходящаяся последовательность ограничена, потому что является строго убывающей и никаким образом не способна принимать отрицательные значения.
Распишем некоторое число её членов в ряд.
Получится: 1; 0,25; 0,0625; 0,015625; 0,00390625 и так далее. Достаточно совсем несложных расчётов, чтобы понять, как быстро данная геометрическая прогрессия со знаменателей 0<q<1 уменьшается. В то время как знаменатель членов неограниченно возрастает, сами они превращаются в бесконечно малое. Это значит, что предел числового ряда равен 0. Данный пример ещё раз демонстрирует ограниченность сходящейся последовательности.

Фундаментальные последовательности
Огюстен Луи Коши, французский учёный, явил миру много работ связанных с математическим анализом. Он дал определения таким его понятиям, как дифференциал, интеграл, предел и непрерывность. Исследовал он также основные свойства сходящихся последовательностей. Для того, чтобы понять суть его идей, необходимо обобщить некоторые важные детали.
В самом начале статьи было показано, что есть такие последовательности, для которых существует окрестность, где точки, изображающие члены определённого ряда на числовой прямой, начинают скучиваться, выстраиваясь всё плотнее. При этом расстояние между ними при увеличении номера очередного представителя всё уменьшается, превращаясь в бесконечно малое. Таким образом, оказывается, что в данной окрестности группируется бесконечное число представителей данного ряда, в то время, как за её пределами их насчитывается конечное количество. Такие последовательности именуются фундаментальными.
Знаменитый критерий Коши, созданный французским математиком, однозначно указывает, что наличия подобного свойства достаточно, чтобы доказать, что последовательность сходится. Верно также обратное.
Следует заметить, что данное заключение французского математика представляет по большей части чисто теоретический интерес. Его применение на практике считается достаточно сложным делом, поэтому для выяснения сходимости рядов гораздо важнее доказать существование у последовательности конечного предела. В противном же случае она считается расходящейся.
При решении задач следует также учитывать основные свойства сходящихся последовательностей. Они представлены ниже.

Бесконечные суммы
Такие знаменитые учёные древности, как Архимед, Евклид, Евдокс использовали суммы бесконечных числовых рядов для вычисления длин кривых, объёмов тел и площадей фигур. В частности, именно таким образом удалось узнать площадь параболического сегмента. Для этого была использована сумма числового ряда геометрической прогрессии с q=1/4. Подобным способом находились объёмы и площади других произвольных фигур. Данный вариант назывался методом «исчерпывания». Идея заключалось в том, что исследуемое сложное по формам тело разбивалось на части, которые представляли собой фигуры с легко измеряемыми параметрами. По этой причине нетрудно было вычислить их площади и объёмы, потом же они складывались.
Кстати, похожие задачи очень знакомы современным школьникам и встречаются в заданиях ЕГЭ. Уникальный способ, найденный ещё далёкими предками, является и на сегодняшний день самым простейшим вариантом решения. Даже если частей, на которые разбивается числовая фигура, всего две или три, сложение их площадей всё равно представляет собой сумму числового ряда.
Гораздо позднее древнегреческих учёных Лейбниц и Ньютон, основываясь на опыте мудрых предшественников, познавали закономерности интегрального вычисления. Знания свойств последовательностей помогали им решать дифференциальные и алгебраические уравнения. В настоящее время созданная усилиями многих поколений талантливых учёных теория рядов даёт шанс решить огромное количество математических и практических проблем. А изучение числовых последовательностей составляет основную задачу, решаемую математическим анализом с момента его создания.
fb.ru
Сходящиеся последовательности, их свойства
Определение 1. Последовательность называется сходящейся к числу а, если последовательность является бесконечно малой. При этом число а называют пределом последовательности и пишут или при .
Из определения 1 следует, что любая бесконечно малая последовательность сходится к нулю, так как = , то есть . В частности, и, в силу свойств бесконечно малых последовательностей, для любых и .
Определение 2. Последовательность называется сходящейся к числу а, если для любого найдется номер N, такой, что для всех значений .
Из определения 2 получаем, что предел любой постоянной величины А равен этой постоянной величине, то есть , так как для любого для всех значений .
Определение 3. Последовательность называется сходящейся к числу а, если в любой -окрестности точки а находятся все члены последовательности, начиная с некоторого номера.
Определение 4. Число а называется пределом последовательности , если для любого найдется номер N, такой, что для всех значений .
Нетрудно заметить, что определения 1-4 равносильны.
Замечание. Из определения 1 следует, что если последовательность сходится к а, то , где – бесконечно малая последовательность, отсюда . Верно и обратное, т.е. если последовательность можно представить в виде суммы постоянной а и бесконечно малой последовательности, то последовательность сходится к числу а. Действительно, по определению 1.
Теорема 1. Сходящаяся последовательность имеет только один предел.
Доказательство. Предположим, что последовательность имеет два предела: с и d. Тогда и , где и – бесконечно малые последовательности (см. замечание выше). Отсюда . Поскольку – бесконечно малая последовательность, по теореме 5 §4 . Теорема доказана.
Теорема 2. Всякая сходящаяся последовательность ограничена.
Доказательство. По определению 1 последовательность бесконечно малая, по теореме 4 §4 она ограничена, то есть существует число M > 0, такое, что одновременно ограничена и снизу и сверху, поэтому ограничена. Теорема доказана.
Теорема 3. Сумма (разность) сходящихся последовательностей есть сходящаяся последовательность, причем
.
Доказательство. Пусть . Тогда (см. замечание в начале параграфаи свойства бесконечно малых последовательностей). Теорема доказана.
Теорема 4. Произведение сходящихся последовательностей есть сходящаяся последовательность, причем
.
Доказательство. Имеем , , так как – бесконечно малая последовательность (см. замечание и свойства бесконечно малых последовательностей). Теорема доказана.
Следствие. Постоянный множитель можно выносить за знак предела, то есть .
Это очевидно, так как .
Теорема 5. Частное двух сходящихся последовательностей и , таких, что , определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, причем
.
Для доказательства теоремы 5 нам потребуется вспомогательное утверждение.
Лемма. Если последовательность сходится к числу , то последовательность ограничена , где N – некоторое натуральное число.
Доказательство. Положим . По определению предела для него найдется номер N, такой, что для всех выполняется неравенство , т.е. . Поскольку , то для всех , т.е. и существует при , а также для всех . Лемма доказана.
Доказательство теоремы 5. Пусть . Тогда , . Рассмотрим = = . В последнем выражении первый множитель – бесконечно малая последовательность, второй и третий – ограниченная для всех последовательность. Поэтому – бесконечно малая последовательность, а так как , то . Теорема доказана.
Рассмотрим теперь свойства сходящихся последовательностей, связанных знаком неравенства.
Теорема 6. Пусть и – две сходящиеся последовательности, имеющие одинаковый предел а. Если, хотя бы начиная с некоторого номера, выполнено неравенство
, (5.1)
то последовательность – сходящаяся, причем .
Доказательство. Пусть , неравенство выполняется, начиная с номера . Возьмем произвольно. Для него существуют и ,такие, что
, (5.2)
. (5.3)
Положим . Тогда одновременно выполнены все неравенства (5.1) – (5.3), значит,
,
то есть , следовательно, . Теорема доказана.
Теорема 6 часто называется «теоремой о сжатой переменной», или «теоремой о промежуточной переменной», или «теоремой о двух милиционерах». Мы ею часто будем пользоваться в дальнейшем.
Теорема 7. Если все члены двух сходящихся последовательностей и , по крайней мере, начиная с некоторого номера, удовлетворяют неравенству , то и пределы этих последовательностей удовлетворяют такому же неравенству, то есть .
Доказательство. Пусть , . Надо доказать, что . Предположим противное, т.е. что , и возьмем . Тогда и . По определению предела последовательности для этого найдутся и такие, что
, откуда для всех ,
, откуда для всех .
Обозначим . Тогда для всех эти неравенства выполняются одновременно и, следовательно, , т.е. , что противоречит условию теоремы. Полученное противоречие доказывает утверждение теоремы. Теорема доказана.
Следствие. Если, начиная с некоторого номера, то и ( ).
Это очевидно, так как вместо одной из последовательностей можно рассмотреть постоянную последовательность .
Заметим, что если , то ( ). Например, для всех n, однако .
Теорема 8. Если ( ), то, начиная с некоторого номера, .
Действительно, если ( ), то, взяв окрестность точки а, не содержащую точку А, по определению 3 получим, что, начиная с некоторого номера, все члены последовательности попадут в эту окрестность, т.е. будут больше А (будут меньше А).
§ 6. Монотонные последовательности. Число е
Определение 1. Последовательность называется убывающей (невозрастающей), если для всех выполняется неравенство .
Определение 2. Последовательность называется возрастающей (неубывающей), если для всех выполняется неравенство .
Определение 3. Убывающие, невозрастающие, возрастающие и неубывающие последовательности называются монотонными последовательностями, убывающие и возрастающие последовательности называют также строго монотонными последовательностями.
Очевидно, что неубывающая последовательность ограничена снизу, невозрастающая последовательность ограничена сверху. Поэтому всякая монотонная последовательность заведомо ограничена с одной стороны.
Пример 1. Последовательность возрастает, не убывает, убывает, не возрастает, – немонотонная последовательность.
Для монотонных последовательностей важную роль играет следующая
Теорема 1. Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), то она сходится.
Доказательство. Пусть последовательность не убывает и ограничена сверху, т.е. и множество ограничено сверху. По теореме 1 § 2 существует . Докажем, что .
Возьмем произвольно. Поскольку а – точная верхняя граница, существует номер N такой, что . Так как последовательность неубывающая, то для всех имеем , т.е. , поэтому для всех , а это и означает, что .
Для невозрастающей последовательности, ограниченной снизу, доказательство проводится аналогично (студенты могут доказать это утверждение дома самостоятельно). Теорема доказана.
Замечание. Теорему 1 можно сформулировать иначе.
Теорема 2. Для того чтобы монотонная последовательность сходилась, необходимо и достаточно, чтобы она была ограничена.
Достаточность установлена в теореме 1, необходимость – в теореме 2 § 5.
Условие монотонности не является необходимым для сходимости последовательности, так как сходящаяся последовательность не обязательно монотонна. Например, последовательность не монотонная, однако сходится к нулю.
Следствие. Если последовательность возрастает (убывает) и ограничена сверху (снизу), то ( ).
Действительно, по теореме 1 ( ).
Определение 4. Если и при , то последовательность называется стягивающейся системой вложенных отрезков.
Теорема 3 (принцип вложенных отрезков). У всякой стягивающейся системы вложенных отрезков существует, и притом единственная, точка с, принадлежащая всем отрезкам этой системы.
Доказательство. Докажем, что точка с существует. Поскольку , то и, следовательно, последовательность не убывает, а последовательность не возрастает. При этом и ограничены, так как . Тогда по теореме 1 существуют и , но так как , то = . Найденная точка с принадлежит всем отрезкам системы, так как по следствию теоремы 1 , , т.е. для всех значений n.
Покажем теперь, что точка с – единственная. Предположим, что таких точек две: с и d и пусть для определенности . Тогда отрезок принадлежит всем отрезкам , т.е. для всех n, что невозможно, так как и, значит, начиная с некоторого номера, . Теорема доказана.
Отметим, что здесь существенно то, что рассматриваются замкнутые промежутки, т.е. отрезки. Если рассмотреть систему стягивающихся интервалов, то принцип, вообще говоря, неверен. Например, интервалы , очевидно, стягиваются в точку , однако точка не принадлежит ни одному интервалу этой системы.
Рассмотрим теперь примеры сходящихся монотонных последовательностей.
1) Число е.
Рассмотрим теперь последовательность . Как она себя ведет? Основание
степени , поэтому ? С другой стороны, , а , поэтому ? Или предел не существует?
Чтобы ответить на эти вопросы, рассмотрим вспомогательную последовательность . Докажем, что она убывает и ограничена снизу. При этом нам будет нужна
Лемма. Если , то для всех натуральных значений n имеем
(неравенство Бернулли).
Доказательство. Воспользуемся методом математической индукции.
Если , то , т.е. неравенство верно.
Предположим, что оно верно для и докажем его справедливость для +1.
Верно . Умножим это неравенство на :
.
Таким образом, . Значит, согласно принципу математической индукции, неравенство Бернулли верно для всех натуральных значений n. Лемма доказана.
Покажем, что последовательность убывает. Имеем
׀неравенство Бернулли׀ ,а это и означает, что последовательность убывает.
Ограниченность снизу следует из неравенства ׀неравенство Бернулли׀ для всех натуральных значений n.
По теореме 1 существует , который обозначают буквой е. Поэтому .
Число е иррационально и трансцендентно, е = 2,718281828… . Оно является, как известно, основанием натуральных логарифмов.
Замечания. 1) Неравенство Бернулли можно использовать для доказательства того, что при . Действительно, если , то . Тогда, по неравенству Бернулли, при . Отсюда при имеем , то есть при .
2) В рассмотренном выше примере основание степени стремится к 1, а показатель степени n – к , то есть имеет место неопределенность вида . Неопределенность такого вида, как мы показали, раскрывается с помощью замечательного предела .
2) (*)
Докажем, что эта последовательность сходится. Для этого покажем, что она ограничена снизу и не возрастает. При этом воспользуемся неравенством для всех , которое является следствием неравенства .
Имеем |см. неравенство выше| , т.е. последовательность ограничена снизу числом .
Далее, |так как | , т.е. последовательность не возрастает.
По теореме 1 существует , который обозначим х. Переходя в равенстве (*) к пределу при , получим
, т.е. , откуда (берем знак «плюс», так как все члены последовательности положительны).
Последовательность (*) применяется при вычислении приближенно. За берут любое положительное число. Например, найдем . Пусть . Тогда , . Таким образом, .
3) .
Имеем . Поскольку при , существует номер N, такой, что для всех выполняется неравенство . Таким образом, последовательность , начиная с некоторого номера N, убывает и ограничена снизу, так как для всех значений n. Значит, по теореме 1 существует . Поскольку , имеем .
Итак, .
4) , справа – n корней.
Методом математической индукции покажем, что для всех значений n. Имеем . Пусть . Тогда , отсюда получаем утверждение по принципу математической индукции. Используя этот факт, находим , т.е. последовательность возрастает и ограничена сверху. Поэтому существует , так как .
Таким образом, .
Похожие статьи:
poznayka.org
11. Сходящиеся и расходящиеся последовательности. Предел последовательности | Читать онлайн, без регистрации
11. Сходящиеся и расходящиеся последовательности. Предел последовательности
Последовательность {аn} называется сходящейся, если существует такое вещественное число А, что последовательность {аn – А} является бесконечно малой. Число А будет пределом последовательности: .
Сходящуюся последовательность можно представить в виде {an} = {A + γn}, где {γn} – бесконечно малая последовательность.
Бесконечно малые последовательности являются сходящимися с пределом, равным нулю, бесконечно большие – расходящимися (сходящимися к бесконечности).
Точка бесконечной прямой называется предельной точкой последовательности, если в любой ее ε–окрестности содержится бесконечно много элементов данной последовательности.
Лемма. Каждая сходящаяся последовательность имеет только одну предельную точку, совпадающую с ее пределом.
Основные свойства сходящихся последовательностей:
1) всякая сходящаяся последовательность имеет один предел;
2) сходящаяся последовательность {an} ограниченна;
3) пусть последовательности {an} и {bn} сходятся и , тогда сходятся и последовательности {cxn} (c = const) {an ± bn} {an × bn} {an / bn} (в случае частного B ≠ 0, bn ≠ 0, n = 1, 2, …). И их пределы вычисляются по общим правилам.
Теорема сравнения (предельный переход в неравенствах). Пусть заданы последовательности {an}, {bn}. Тогда если последовательности {an}, {bn} таковы, что an ≤ (≥) bn, то (данное утверждение неверно для строгих неравенств).
Теорема (принцип двустороннего ограничения). Пусть заданы последовательности {an}, {bn}, {cn}. Тогда если an ≤ bn ≤ cn и последовательности {an} и {cn} сходятся к одному и тому же пределу В, то последовательность {bn} тоже сходится к тому же пределу: .
Следствия:
1) если все члены сходящейся последовательности {an} не отрицательны (не положительны), то предел последовательности есть число неотрицательное (неположительное), ;
2) если все элементы сходящейся последовательности {an} находятся на отрезке [a, b], то и предел этой последовательности {an} лежит на данном отрезке, ;
3) если все члены сходящейся последовательности {an} an ≤ (і) В, то , где В – некоторое число.
Теорема о сходимости монотонной ограниченной последовательности. Всякая неубывающая (невозрастающая) последовательность {an}, ограниченная сверху (снизу) сходится. Иначе для того чтобы монотонная последовательность сходилась необходимо и достаточно, чтобы она была ограниченна.
velib.com
12.4. Сходимость числовых последовательностей
Сходящаяся последовательность – это последовательность элементов множества имеющая предел в этом множестве.
Расходящаяся последовательность – это последовательность, не являющаяся сходящейся.
Свойства сходящихся последовательностей.
1) Всякая бесконечно малая последовательность является сходящейся. Ее предел равен нулю.
2) Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.
3) Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.
4) Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом ее верхний и нижний пределы совпадают.
5) Если последовательность сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность
которая является ограниченной.
6)Сумма сходящихся последовательностей также является сходящейся последовательностью.
7)Разность сходящихся последовательностей также является сходящейся последовательностью.
8)Произведение сходящихся последовательностей также является сходящейся последовательностью.
9)Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.
10)Если сходящаяся последовательность ограничена сверху, то ее предел не превышает ни одной из ее верхних граней.
11)Если сходящаяся последовательность ограничена снизу, то никакая из ее нижних граней не превышает ее предела.
12)Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к одному и тому же пределу последовательностей, то и эта последовательность также сходится к такому же пределу.
12.5. Предел функции. Односторонние пределы
Пусть функция определена на некотором множествеи пусть точка
или
Возьмем из последовательность точек, отличных от
сходящихся к Значения функции в точках этой последовательности также образуют числовую последовательность
и можно ставить вопрос о существовании ее предела.
Число называется пределом функции в точке если для любой сходящейся кпоследовательностизначений аргументаотличных отсоответствующая последовательность
значений функции сходится к числу
Функция может иметь в точкетолько один предел.
Число называетсяпределом функции в точке если для любого числасуществует числотакое, что для всехудовлетворяющих неравенствувыполняется неравенство
Первое и второе определение предела эквивалентны.
Односторонние пределы.
Число называется правым (левым) пределом функциив точкеесли для любой сходящейся кпоследовательности
которая больше (меньше) соответствующая последовательность
сходится к
Можно дать другое определение.
Число называется правым (левым) пределом функциив точке, если для любогосуществует числотакое, что для всехудовлетворяющих неравенствам
выполняется неравенство
Функция имеет в точкепредел тогда и только тогда, когда в этой точке существует как правый, так и левый пределы, и они равны. В этом случае предел функции равен односторонним пределам
Существует понятие предела при стремлении аргумента к бесконечности.
Число называется пределом функцииприесли для любой бесконечно большой последовательности
значений аргумента соответствующая последовательность
значений функции сходится к
Число называется пределом функцииприесли для любого числа
существует число такое, что для всехудовлетворяющих неравенству
выполняется неравенство
studfiles.net
Числовая последовательность — это… Что такое Числовая последовательность?
ПоследовательностьЧисловая последовательность — это последовательность элементов числового пространства.
Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.
Определение
Пусть множество — это либо множество вещественных чисел , либо множество комплексных чисел . Тогда последовательность элементов множества называется числовой последовательностью.
Примеры
- Функция является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид .
- Функция является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид .
- Функция, сопоставляющая каждому натуральному числу одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида . В частности, пятым членом этой последовательности является слово «май».
Операции над последовательностями
На множестве всех последовательностей элементов множества можно определить арифметические и другие операции, если таковые определены на множестве . Такие операции обычно определяют естественным образом, т. е. поэлементно.
Например, так определяются арифметические операции для числовых последовательностей.
Суммой числовых последовательностей и называется числовая последовательность такая, что .
Разностью числовых последовательностей и называется числовая последовательность такая, что .
Произведением числовых последовательностей и называется числовая последовательность такая, что .
Частным числовой последовательности и числовой последовательности , все элементы которой отличны от нуля, называется числовая последовательность . Если в последовательности на позиции всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность .
Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или даже кольца.
Подпоследовательности
Подпоследовательность последовательности — это последовательность , где — возрастающая последовательность элементов множества натуральных чисел.
Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.
Примеры
- Последовательность простых чисел является подпоследовательностью последовательности натуральных чисел.
- Последовательность натуральных чисел, кратных 12, является подпоследовательностью последовательности чётных натуральных чисел.
Свойства
- Всякая последовательность является своей подпоследовательностью.
- Для всякой подпоследовательности верно, что .
- Подпоследовательность сходящейся последовательности сходится к тому же пределу, что и исходная последовательность.
- Если все подпоследовательности некоторой исходной последовательности сходятся, то их пределы равны.
- Любая подпоследовательность бесконечно большой последовательности также является бесконечно большой.
- Из любой неограниченной числовой последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
- Из любой числовой последовательности можно выделить либо сходящуюся подпоследовательность, либо бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.
Предельная точка последовательности
Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности. Для сходящихся числовых последовательностей предельная точка совпадает с пределом.
Предел последовательности
Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.
Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.
Верхний предел последовательности — это наибольшая предельная точка этой последовательности.
Нижний предел последовательности — это наименьшая предельная точка этой последовательности.
Некоторые виды последовательностей
- Стационарная последовательность — это последовательность, все члены которой, начиная с некоторого, равны.
- стационарная
Ограниченные и неограниченные последовательности
В предположении о линейной упорядоченности множества элементов последовательности можно ввести понятия ограниченных и неограниченных последовательностей.
Критерий ограниченности числовой последовательности
Числовая последовательность является ограниченной тогда и только тогда, когда существует такое число, что модули всех членов последовательности не превышают его.
- ограниченная
Свойства ограниченных последовательностей
Бесконечно большие и бесконечно малые последовательности
Свойства бесконечно малых последовательностей
Бесконечно малые последовательности отличаются целым рядом замечательных свойств, которые активно используются в математическом анализе, а также в смежных с ним и более общих дисциплинах.
- Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
- Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
- Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.
- Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.
- Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
- Любая бесконечно малая последовательность ограничена.
- Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.
- Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.
- Если — бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность , которая является бесконечно малой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера , и всё равно будет бесконечно малой.
- Если — бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность , которая является бесконечно большой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера , и всё равно будет бесконечно большой.
Сходящиеся и расходящиеся последовательности
- Сходящаяся последовательность — это последовательность элементов множества , имеющая предел в этом множестве.
- Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.
Свойства сходящихся последовательностей
- Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю.
- Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.
- Любая сходящаяся последовательность элементов хаусдорфова пространства имеет только один предел.
- Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.
- Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределы совпадают.
- Если последовательность сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность , которая является ограниченной.
- Сумма сходящихся последовательностей также является сходящейся последовательностью.
- Разность сходящихся последовательностей также является сходящейся последовательностью.
- Произведение сходящихся последовательностей также является сходящейся последовательностью.
- Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.
- Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела.
- Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней.
- Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй.
- Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к одному и тому же пределу последовательностей, то и эта последовательность также сходится к такому же пределу.
- Любую сходящуюся последовательность можно представить в виде , где — предел последовательности , а — некоторая бесконечно малая последовательность.
- Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства).
Монотонные последовательности
Монотонная последовательность — это невозрастающая, либо неубывающая последовательность. При этом предполагается, что на множестве, из которого берутся элементы последовательности, введено отношение порядка.
Фундаментальные последовательности
Фундаментальная последовательность (сходящаяся в себе последовательность, последовательность Коши) — это последовательность элементов метрического пространства, в которой для любого наперёд заданного расстояния найдётся такой элемент, расстояние от которого до любого из следующих за ним элементов не превышает заданного. Для числовых последовательностей понятия фундаментальной и сходящейся последовательностей эквивалентны, однако в общем случае это не так.
Вариации и обобщения
Примечания
См. также
dic.academic.ru
Числовые последовательности
Рассмотрим ряд натуральных чисел: 1, 2, 3, , n – 1, n, .
Если заменить каждое натуральное число n в этом ряду некоторым числом an, следуя некоторому закону, то получим новый ряд чисел:
a1, a2, a3, , an–1, an, ,
кратко обозначаемый  и называемыйчисловой
последователь-
ностью.
Величина an называется общим членом числовой
последовательности. Обычно числовая
последовательность задается некоторой
формулой an = f(n)
позволяющей найти любой член
последовательности по его номеру n;
эта формула называется формулой общего
члена. Заметим, что задать числовую
последовательность формулой общего
члена не всегда возможно; иногда
последовательность задается путем
описания ее членов.
и называемыйчисловой
последователь-
ностью.
Величина an называется общим членом числовой
последовательности. Обычно числовая
последовательность задается некоторой
формулой an = f(n)
позволяющей найти любой член
последовательности по его номеру n;
эта формула называется формулой общего
члена. Заметим, что задать числовую
последовательность формулой общего
члена не всегда возможно; иногда
последовательность задается путем
описания ее членов.
По определению, последовательность всегда содержит бесконечное множество элементов: любые два разных ее элемента отличаются, по крайней мере, своими номерами, которых бесконечно много.
Числовая последовательность является частным случаем функции. Последовательность является функцией, определенной на множестве натуральных чисел и принимающей значения в множестве действительных чисел, т. е. функцией вида f : N R.
Последовательность  называетсявозрастающей (убывающей),
если для любого n N Такие последовательности называютсястрого
монотонными.
называетсявозрастающей (убывающей),
если для любого n N Такие последовательности называютсястрого
монотонными.
Иногда в качестве номеров удобно использовать не все натуральные числа, а лишь некоторые из них (например, натуральные числа, начиная с некоторого натурального числа n0). Для нумерации также возможно использование не только натуральных, но и других чисел, например, n = 0, 1, 2, (здесь в качестве еще одного номера к множеству натуральных чисел добавлен ноль). В таких случаях, задавая последовательность, указывают, какие значения принимают номера n.
Если в некоторой последовательности для любого n N то последовательность называетсянеубывающей (невозрастающей). Такие последовательности называются монотонными.
Пример 1. Числовая последовательность 1, 2, 3, 4, 5, … является рядом натуральных чисел и имеет общий член an = n.
Пример 2. Числовая последовательность 2, 4, 6, 8, 10, … является рядом четных чисел и имеет общий член an = 2n.
Пример 3. 1.4, 1.41, 1.414, 1.4142, … − числовая последовательность приближенных значений с увеличивающейся точностью.
В последнем примере невозможно дать формулу общего члена последовательности.
Пример 4. Записать
первых 5 членов числовой последовательности
по ее общему члену  .
Для вычисленияa1 нужно в формулу для общего члена an вместо n подставить 1, для вычисления a2 − 2 и т. д. Тогда имеем:
.
Для вычисленияa1 нужно в формулу для общего члена an вместо n подставить 1, для вычисления a2 − 2 и т. д. Тогда имеем: 
Тест 6. Общим членом последовательности 1, 2, 6, 24, 120, является:
1) 
2)
3)
4) 
Тест 7. Общим членом последовательности является:
1) 
2) 
3) 
4) 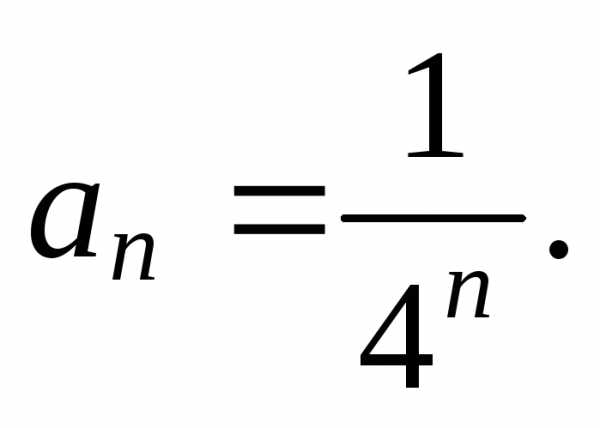
Тест 8. Общим членом последовательности является:
1) 
2) 
3)
4) 
Предел числовой последовательности
Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу А при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
Число А называется пределом числовой
последовательности :
:
 (1)
(1)
если для любого
> 0 найдется такое число n0 = n0(),
зависящее от ,
что 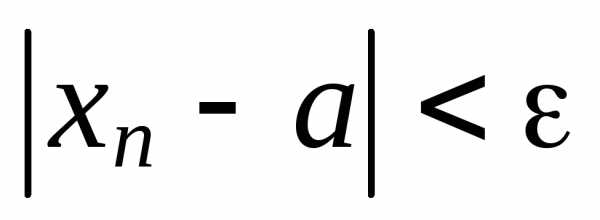 приn > n0.
приn > n0.
Это определение означает, что А есть предел числовой последовательности, если ее общий член неограниченно приближается к А при возрастании n. Геометрически это значит, что для любого > 0 можно найти такое число n0, что, начиная с n > n0, все члены последовательности расположены внутри интервала (А – , А + ). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
Числовая последовательность может иметь только один предел (конечный или бесконечный) определенного знака.
Пример 5. Гармоническая последовательность  имеет пределом число 0. Действительно,
для любого интервала (–;
+)
в качестве номера N0 можно взять какое-либо целое число,
больше
имеет пределом число 0. Действительно,
для любого интервала (–;
+)
в качестве номера N0 можно взять какое-либо целое число,
больше  .
Тогда для всехn > n0 >
.
Тогда для всехn > n0 >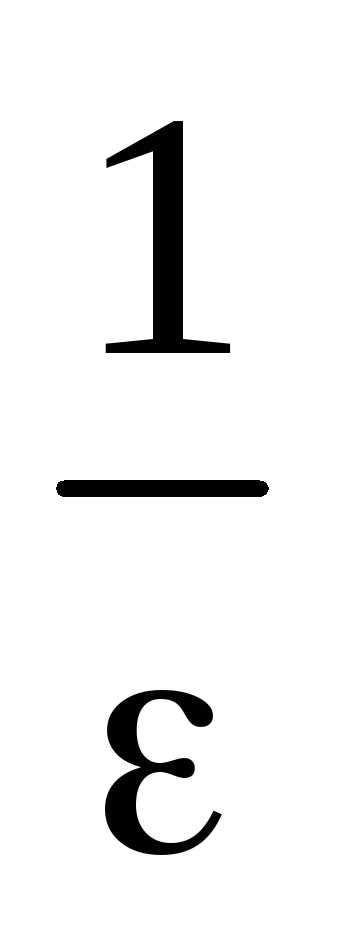 имеем
имеем
Пример 6. Последовательность 2, 5, 2, 5, является расходящейся. Действительно, никакой интервал длины, меньшей, например, единицы, не может содержать всех членов последовательности, начиная с некоторого номера.
Последовательность
называется ограниченной,
если существует такое число М,
что  для
всехn.
Всякая сходящаяся последовательность
ограничена. Всякая монотонная и
ограниченная последовательность имеет
предел. Всякая сходящаяся последовательность
имеет единственный предел.
для
всехn.
Всякая сходящаяся последовательность
ограничена. Всякая монотонная и
ограниченная последовательность имеет
предел. Всякая сходящаяся последовательность
имеет единственный предел.
Пример 7. Последовательность  является возрастающей и ограниченной.
Она имеет предел
является возрастающей и ограниченной.
Она имеет предел =е.
=е.
Число e называется числом Эйлера и приблизительно равно 2,718 28.
Тест 9. Последовательность 1, 4, 9, 16, является:
1) сходящейся;
2) расходящейся;
3) ограниченной;
4) арифметической прогрессией;
5) геометрической прогрессией.
Тест 10. Последовательность  является:
является:
1) сходящейся;
2) расходящейся;
3) ограниченной;
4) арифметической прогрессией;
5) геометрической прогрессией.
Тест 11. Последовательность  не
является:
не
является:
1) сходящейся;
2) расходящейся;
3) ограниченной;
4) гармонической.
Тест 12. Предел
последовательности, заданной общим
членом  равен:
равен:
1) 1;
2) 0;
3) e;
4) .
studfiles.net
