Свойства кубического корня – Свойства кубического корня. Существование единственного значения кубического корня из числа
Свойства кубического корня. Существование единственного значения кубического корня из числа
Покажем теперь, что из числа a можно извлечь только один кубический корень.
Рассмотрим три разных варианта значений, которые может принимать подкоренное выражение:
Пусть:
Тогда рассмотрим кубический корень из нуля:
Чтобы определить этот корень воспользуемся определением, т.е. найдем такое число, которое при возведении в третью степень даст подкоренное выражение – нуль:
Очевидно, что это число нуль. следовательно, можем заключить, что при извлечении кубического корня, получаем только одно значение, равное нулю.
Теперь рассмотрим положительные значения подкоренного выражения и покажем, что кубический корень из положительного выражения не может быть ни отрицательным числом, ни нулем.
Пусть b — кубический корень из числа a:
Тогда из определения кубического корня:
Так как:
То:
Данное неравенство возможно только при b>0, так как только положительное число в нечетной степени является положительным числом.
Следовательно, кубический корень из положительного числа a является положительным числом.
Теперь предположим, что помимо числа b существует еще один кубический корень из числа a, и обозначим его буквой c. Причем c является положительным числом, так как мы рассматриваем положительные значения подкоренного выражения, и мы доказали, что кубический корень из положительного числа является положительным числом.
Тогда по определению кубического корня:
И:
Вычтем из первого равенства второе:
Воспользуемся формулой разности кубов:
Значит:
Произведение равно нулю, если хотя бы один из множителей равен нулю:
Из первого равенства имеем:
Второе равенство не верно, так как по условию c>0, b>0, а значит:
Следовательно, мы показали, что для положительного подкоренного выражения значение кубического корня – единственное и положительное.
&nbs
mathvox.ru
Основные свойства кубического корня — СТЕПЕНИ, КОРНИ, ЛОГАРИФМЫ — МАТЕМАТИКА
МАТЕМАТИКА
СТЕПЕНИ, КОРНИ, ЛОГАРИФМЫ
Основные свойства кубического корня
Для любых действительных чисел a и b:
1) а = ()3;
2) = а;
3) = ;
4) если b ≠ 0, то ;
5) = только тогда, когда а = b;
6) < только тогда, когда а < b;
7) < только тогда, когда а ≤ b.
Логарифм числа b > 0 по основанию а (а > 0 и а ≠ 1) —показатель степени, в который надо возвести число а, чтобы получить число b. Логарифм числа b по основанию а обозначаемое logab.
Основное логарифмическое тождество
логарифм числа b по основанию а можно записать в
виде равенства: а
Десятичный логарифм — логарифм числа по основанию 10. Десятичный логарифм числа п сказывается lg n. — логарифм единицы равна нулю: lg 1 = 0; — логарифмы 10, 100, 1000 равны 1, 2, 3, т. е. имеют столько положительных единиц, сколько нулей стоит после единицы. — логарифмы чисел 0,1; 0,01; 0,001 равны -1, -2, -3. — логарифмы остальных чисел имеют дробную долю, что называется мантисою, целая часть логарифма называется характеристикой. — числа, больше 1, имеют положительные логарифмы; — положительные числа, меньшие 1, имеют отрицательные логарифмы. | |
При положительной основой отрицательные числа не имеют логарифма, поскольку: х = ав; а > 0; y > 0. | Логарифм доли равна логарифму делимого без логарифма делителя: Logax/y = logax – logay. |
При любом значении основы, что не равен 1, логарифма единицы есть нуль: loga1 = 0. а > 0; х = аy при а ≠ 1 и х = 1 y = 0. | Логарифм корня равен частному от деления логарифма подкоренного выражения на показатель корня: log = loga/m.
|
С основанием, большим 1, логарифмы чисел, больших 1, положительны, а меньше 1 — отрицательные: | Логарифм степени: Переход от одного основания логарифма к другой:
|
С основанием, большим 1, большем числу соответствует больший логарифм:
| |
С основанием 0 < а < 1 большему числу соответствует меньший логарифм: | |
Логарифм произведения равен сумме логарифмы: | |
schooled.ru
Кубический корень — это… Что такое Кубический корень?
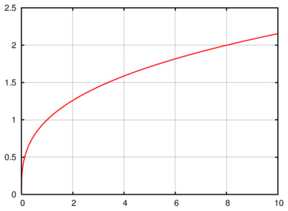 График функции y =
График функции y =Куби́ческий (куби́чный) ко́рень из a — решение уравнения (обычно подразумеваются вещественные решения). Операция извлечения кубического корня эквивалентна операции возведения числа в степень, при условии, что число неотрицательно.
Свойства
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический может быть извлечён и из отрицательных чисел:
Общее правило — из отрицательных чисел корни нечётной степени (в том числе и кубический) извлекаются, корни чётной степени — нет. Данное утверждение справедливо только для диапазона вещественных чисел.
Кубический корень из комплексного числа (из любого числа) имеет ровно три значения (частный случай свойства корня n-ой степени):
Здесь под понимается арифметический корень из положительного числа
В частности
Два комплексных значения кубического корня получаются из вещественных по формуле:
Эти значения необходимо знать для решения кубических уравнений по формуле Кардано.
Интересные факты
Кубический корень не может быть извлечён с помощью циркуля и линейки. Именно поэтому неразрешимы сводимые к извлечению кубического корня классические задачи: удвоение куба, трисекция угла, а также построение правильного семиугольника.
При постоянной плотности вещества размеры двух подобных тел относятся друг к другу как кубические корни их масс. Так, если один арбуз весит вдвое больше, чем другой, то его диаметр (а также окружность) будет всего лишь чуть больше, чем на четверть (на 26%) больше, чем у первого; и на глаз будет казаться, что разница в весе не столь существенна. Поэтому при отсутствии весов (продажа на глазок) обычно более выгодно покупать бо́льший плод.
См. также
Литература
- Корн Г., Корн Т. 1.3-3. Представление суммы, произведения и частного. Степени и корни // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 32—33.
dic.academic.ru
|
Десятичный логарифм — логарифм числа по основанию 10. Десятичный логарифм числа п сказывается lg n. — логарифм единицы равна нулю: lg 1 = 0; — логарифмы 10, 100, 1000 равны 1, 2, 3, т.е. имеют столько положительных единиц, сколько нулей стоит после единицы. — логарифмы чисел 0,1; 0,01; 0,001 равны -1, -2, -3. — логарифмы других чисел имеют дробную долю, что называется мантисою, целая часть логарифма называется характеристикой. — числа, больше 1, имеют положительные логарифмы; — положительные числа, меньшие 1, имеют отрицательные логарифмы. |
При положительной основой отрицательные числа не имеют логарифма, поскольку: х = ав; а > 0; y > 0. |
Логарифм доли равна логарифму делимого без логарифма делителя: Logax/y = logax — logaв. |
При любом значении основы, что не равен 1, логарифма единицы есть нуль: loga1 = 0. а > 0; х = аy при а ≠ 1 и х = 1 y = 0. |
Логарифм корня равен доле от деления логарифма подкоренного выражения на показатель корня: log = loga/m.
|
За основой, большей 1, логарифмы чисел, больших 1, положительны, а меньше 1 — отрицательные: |
Логарифм степени: Переход от одного основания логарифма к другой:
|
na-uroke.in.ua
9 класс. Алгебра. Степенная функция. — Функция кубического корня.
Комментарии преподавателя
На данном уроке вы ознакомитесь с понятием кубического корня из действительного числа, также вы узнаете, что такое функция . Мы изучим различные основные ее свойства и рассмотрим график. Также решим типовые примеры по данной теме
Практическая задача
Необходимо сконструировать кубический резервуар, объем которого равен (). Как отмерить величину ребра?
Решение:
Предположим, что ребро куба имеет длину (м). В этом случае объем будет равен (). Получается, что необходимо подобрать такое число , куб которого равен ().
Например: если объем равен , то длина ребра будет равна 2 м ().
На основании этого примера можно сделать вывод, что необходимо уметь находить число, если известен его куб.
На данном этапе эту задачу можно сравнить с квадратным корнем. И нахождение искомого числа будет происходить по аналогии.
Определение:
Число называется кубическим корнем или корнем третьей степени числа , если выполняется соотношение . Это можно записать как, в этом случае – подкоренное выражение, 3 – показатель корня.
Таким образом, выражения эквивалентны, то есть выражают одну и ту же зависимость между действительными числами и .
Например:
Кубический корень из существует для любого действительного числа .
Как и в случае квадратного корня, при извлечении кубического корня из рационального числа часто будет появляться иррациональный результат.
Доказательство иррациональности
Построим доказательство методом от противного. Предположим, что – рациональное число, то есть его можно представить в виде , где чисто целое, – натуральное. Причем – это несократимая обыкновенная дробь. Тогда по определению: , откуда следует, что . Последнее равенство означает, что пятерка является делителем числа , то есть натуральное число делится на пять без остатка. Однако это возможно тогда и только тогда, когда пятерка является делителем самого числа , то есть , где – некоторое натуральное число.
Подставим значение из последнего равенства в начальное:
Последнее равенство означает, что двадцать пять является делителем числа и тем более, что делится на пять, тогда и число делится без остатка на пять.
Таким образом, мы получили, что и делятся на пять, а это значит, что – сократимая дробь, так как и числитель и знаменатель можно сократить на пять, но это противоречит нашему предположению. Значит, – иррациональное число.
Результат возведения в куб отрицательного числа будет числом отрицательным, следовательно, и корень кубический из отрицательного числа будет отрицательным числом.
Доказать:
Доказательство:
Пусть , , тогда, по определению кубического корня, , . Отсюда следует, что или . Из последнего равенства следует, что , а значит, справедливо исходное тождество .
Задача о проектировании кубического резервуара
Необходимо автоматизировать процесс сварки. На вход поступает число – объем куба – автомат должен сам посчитать длину ребра.
Как научить автомат извлекать корень кубический из любого действительного числа? Для этого введем понятие функции, область определения которой – все действительные числа.
Рассмотрим функцию , выясним ее свойства и постоим график.
1. Область определения функции – множество действительных чисел ().
2. Данная функция является нечетной.
3. Функция возрастает на луче от нуля до плюс бесконечности ( при ).
Доказательство
Возьмем два значения аргумента, расположенные следующим образом: . Необходимо доказать: .
Построим доказательство методом от противного. Предположим, что , тогда, по свойству числовых неравенств, при возведении левую и правую часть в куб знак неравенства сохраняется . Таким образом, , что противоречит условию задачи. Исходя из этого, можно сделать вывод, что наше предположение неверно и .
В силу нечетности функции, свойство можно обобщить на всю область определения ( при ).
4. Функция не ограничена сверху на луче от нуля до плюс бесконечности ()
Доказательство
Дано: .
Доказать: .
Построим доказательство методом от противного. Предположим, что существует такое положительное число , что для любого выполняется неравенство . Возьмем на луче от нуля до плюс бесконечности некую точку . Тогда значение функции в этой точке будет равно , а это больше . Значит, мы нашли точку, такую, что что противоречит нашему предположению.
Функция монотонно возрастает на всей области определения и не ограничена ни сверху, ни снизу.
Не ограничена сверху при , не ограничена снизу при .
Доказывается это аналогично приведенным доказательствам для положительной полуоси .
5. Функция ограничена снизу ()
Построим график функции на луче от нуля до плюс бесконечности (). Для этого сперва составим таблицу значений:
|
X |
0 |
1 |
8 |
|
|
Y |
0 |
1 |
2 |
Построим четыре точки на координатной плоскости, координаты которых возьмем из таблицы. По данным точкам можно построить некоторую линию, которую можно построить, учитывая возрастающий характер функции и ее неограниченность сверху. Воспользовавшись нечетностью функции, добавим к приведенной линии ветвь, симметричную ей относительно начала координат (рис. 1).
www.kursoteka.ru
Кубический корень Википедия
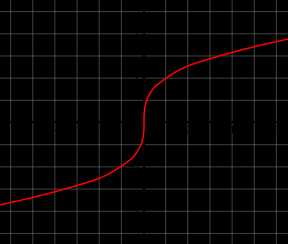 График функции y=x3{\displaystyle y={\sqrt[{3}]{x}}}
График функции y=x3{\displaystyle y={\sqrt[{3}]{x}}}Куби́ческий ко́рень из a, обозначающийся как a3{\displaystyle {\sqrt[{3}]{a}}} или как a1/3 — это число x,{\displaystyle x,} куб которого равен a.{\displaystyle a.} Другими словами, это решение уравнения x3=a{\displaystyle x^{3}=a} (обычно подразумеваются вещественные решения).
Вещественный корень
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел (так, чтобы получился действительный результат):
- −x3=−x3{\displaystyle {\sqrt[{3}]{-x}}=-{\sqrt[{3}]{x}}}
Комплексный корень
Кубический корень из комплексного числа (из любого числа) c{\displaystyle c} имеет ровно три значения (частный случай свойства корня n-ой степени):
- c3=|c|3(cosϕ+2kπ3+isinϕ+2kπ3),k=0,1,2,ϕ=argc.{\displaystyle {\sqrt[{3}]{c}}={\sqrt[{3}]{\left|c\right|}}\left(\cos {\frac {\phi +2k\pi }{3}}+i\sin {\frac {\phi +2k\pi }{3}}\right),\quad k=0,1,2,\quad \phi =\arg {c}.}
Здесь под |c|3{\displaystyle {\sqrt[{3}]{\left|c\right|}}} понимается арифметический корень из положительного числа |c|.{\displaystyle \left|c\right|.}
В частности
- 13={1cos2π3+isin2π3=−12+i32cos2π3−isin2π3=−12−i32{\displaystyle {\sqrt[{3}]{1}}={\begin{cases}1\\\cos {\frac {2\pi }{3}}+i\sin {\frac {2\pi }{3}}=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\cos {\frac {2\pi }{3}}-i\sin {\frac {2\pi }{3}}=-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{cases}}}
- −13={−1cosπ3+isinπ3=12+i32cosπ3−isinπ3=12−i32{\displaystyle {\sqrt[{3}]{-1}}={\begin{cases}-1\\\cos {\frac {\pi }{3}}+i\sin {\frac {\pi }{3}}={\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\cos {\frac {\pi }{3}}-i\sin {\frac {\pi }{3}}={\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{cases}}}
Два комплексных значения кубического корня получаются из вещественных по формуле:
- x32,3=x3(−12±i32).{\displaystyle {\sqrt[{3}]{x}}_{2,3}={\sqrt[{3}]{x}}\left(-{\frac {1}{2}}\pm i{\frac {\sqrt {3}}{2}}\right).}
Эти значения необходимо знать для решения кубических уравнений по формуле Кардано.
Показательная форма
Корень из комплексных чисел можно определить так:
- x1/3=exp(13lnx){\displaystyle x^{1/3}=\exp({\tfrac {1}{3}}\ln {x})}
Где ln — главная ветвь натурального логарифма.
Если представить x{\displaystyle x} как
- x=rexp(iθ){\displaystyle x=r\exp(i\theta )}
то формула кубического числа такова:
- x3=r3exp(13iθ).{\displaystyle {\sqrt[{3}]{x}}={\sqrt[{3}]{r}}\exp({\tfrac {1}{3}}i\theta ).}
Это геометрически означает, что в полярных координатах мы берем кубический корень радиуса и делим полярный угол на три, для того, чтобы определить кубический корень. Значит, если x{\displaystyle x} комплексное, то −83{\displaystyle {\sqrt[{3}]{-8}}} будет обозначать не −2{\displaystyle -2}, а будет 1+i3.{\displaystyle 1+i{\sqrt {3}}.}
Интересные факты
Кубический корень не может быть извлечён с помощью циркуля и линейки. Именно поэтому неразрешимы сводимые к извлечению кубического корня классические задачи: удвоение куба, трисекция угла, а также построение правильного семиугольника.
При постоянной плотности вещества размеры двух подобных тел относятся друг к другу как кубические корни их масс. Так, если один арбуз весит вдвое больше, чем другой, то его диаметр (а также окружность) будет всего лишь чуть больше, чем на четверть (на 26 %) больше, чем у первого; и на глаз будет казаться, что разница в весе не столь существенна. Поэтому при отсутствии весов (продажа на глазок) обычно более выгодно покупать бо́льший плод.
Способы вычисления
Столбиком
Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.
Алгоритм таков:
- Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
- Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
- Далее найденный промежуточный ответ заменим буквой a{\displaystyle a}. Вычислите по формуле 300×a2×x+30×a×x2+x3{\displaystyle 300\times a^{2}\times x+30\times a\times x^{2}+x^{3}} такое число x{\displaystyle x}, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x{\displaystyle x} справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
- Запишите под нижним числом результат вычисления по формуле 300×a2×x+30×a×x2+x3{\displaystyle 300\times a^{2}\times x+30\times a\times x^{2}+x^{3}} и произведите вычитание. Перейдите к пункту 3.
См. также
Литература
- Корн Г., Корн Т. 1.3-3. Представление суммы, произведения и частного. Степени и корни // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 32—33.
wikiredia.ru
Кубический корень
кубический корень, кубический корень онлайнКуби́ческий ко́рень из a, обозначающийся как или как a1/3 — решение уравнения (обычно подразумеваются вещественные решения).
Содержание
- 1 Вещественный корень
- 2 Комплексный корень
- 2.1 Показательная форма
- 3 Интересные факты
- 4 Алгоритмы решения
- 5 См. также
- 6 Литература
Вещественный корень
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел (так, чтобы получился действительный результат):
Комплексный корень
Кубический корень из комплексного числа (из любого числа) имеет ровно три значения (частный случай свойства корня n-ой степени):
Здесь под понимается арифметический корень из положительного числа
В частности
Два комплексных значения кубического корня получаются из вещественных по формуле:
Эти значения необходимо знать для решения кубических уравнений по формуле Кардано.
Показательная форма
Корень из комплексных чисел можно определить так:
Где ln — главная ветвь натурального логарифма.
Если представить как
то формула кубического числа такова:
Это геометрически означает, что в полярных координатах мы берем кубический корень радиуса и делим полярный угол на три, для того, чтобы определить кубический корень. Значит, если комплексное, то будет обозначать не , а будет
Интересные факты
Кубический корень не может быть извлечён с помощью циркуля и линейки. Именно поэтому неразрешимы сводимые к извлечению кубического корня классические задачи: удвоение куба, трисекция угла, а также построение правильного семиугольника.
При постоянной плотности вещества размеры двух подобных тел относятся друг к другу как кубические корни их масс. Так, если один арбуз весит вдвое больше, чем другой, то его диаметр (а также окружность) будет всего лишь чуть больше, чем на четверть (на 26 %) больше, чем у первого; и на глаз будет казаться, что разница в весе не столь существенна. Поэтому при отсутствии весов (продажа на глазок) обычно более выгодно покупать бо́льший плод.
Алгоритмы решения
Столбиком
Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.
Алгоритм таков:
- Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
- Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
- Далее найденный промежуточный ответ заменим буквой . Вычислите по формуле такое число , что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
- Запишите под нижним числом результат вычисления по формуле и произведите вычитание. Перейдите к пункту 3.
См. также
- Корень (математика)
- Квадратный корень
Литература
- Корн Г., Корн Т. 1.3-3. Представление суммы, произведения и частного. Степени и корни // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 32—33.
извлечь кубический корень, извлечь кубический корень из 80, как посчитать кубический корень, кубический корень, кубический корень из числа, кубический корень онлайн
Кубический корень Информацию О

Кубический корень Комментарии
Кубический корень
Кубический корень
Кубический корень Вы просматриваете субъект
Кубический корень что, Кубический корень кто, Кубический корень описание
There are excerpts from wikipedia on this article and video
www.turkaramamotoru.com
