Свойства корня n ой степени – .
Свойства арифметического корня n-ой степени: 5 свойств с доказательством
- Арифметическим корнем натуральной степени n>=2 из неотрицательного числа а называется некоторое неотрицательное число, при возведении которого в степень n получается число а.
Можно доказать, что для любого неотрицательного а и натурального n уравнение x^n=a будет иметь один единственный неотрицательный корень. Именно этот корень и называют арифметическим корнем n-ой степени из числа а.
Арифметический корень n-ой степени из числа а обозначается следующим образом n√a. Число а в данном случае называется подкоренным выражением.
Арифметический корень второй степени называется квадратным корнем, а арифметический корень третей степени – кубическим корнем.
Основные свойства арифметического корня n-ой степени
n√(a^n) = a.
Например, (5√2)^5 = 2.
Это свойство прямо следует из определения арифметического корня n-ой степени.
Если a больше либора равно нулю, b больше нуля и n, m – некоторые натуральные числа такие, что n больше либо равно 2 и m больше либо равно 2, тогда справедливы следующие свойства:
- 2. n√(a*b)= n√a*n√b.
Например, 4√27 * 4√3 = 4√(27*3) = 4√81 =4√(3^4) = 3.
- 3. n√(a/b) = (n√a)/(n√b).
Например, 3√(256/625) :3√(4/5) = 3√((256/625) : (4/5)) = (3√(64))/(3√(125)) = 4/5.
- 4. (n√a)^m = n√(a^m).
Например,7√(5^21) = 7√((5^7)^3)) = (7√(5^7))^3 = 5^3 = 125.
- 5. m√(n√a) = (n*m) √a.
Например, 3√(4√4096) = 12√4096 = 12√(2^12) = 2.
Заметим, что в свойстве 2, число b может быть равным нулю, а в свойстве 4 число m может быть любым целым, при условии, что a>0.
Доказательство второго свойства
Все последние четыре свойства доказываются аналогично, поэтому ограничимся доказательством только второго: n√(a*b)= n√a*n√b.
Используя определение арифметического корня докажем что n√(a*b)= n√a*n√b.
Для этого докажем два факта, что n√a*n√b. Больше либо равен нулю, и что (n√a*n√b.)^n = ab.
- 1. n√a*n√b больше либо равно нулю, так как и а и b больше либо равны нулю.
- 2. (n√a*n√b)^n = a*b, так как (n√a*n√b)^n = (n√a)^n *(n√b)^n = a*b.
Что и требовалось доказать. Значит свойство верно. Эти свойства очень часто придется использовать при упрощении выражений содержащих арифметические корни.
Нужна помощь в учебе?
Предыдущая тема: Определение корня n-ой степени: извлечение корня
Следующая тема:   Определение степени с дробным показателем: доказательство и особенности
Все неприличные комментарии будут удаляться.
www.nado5.ru
Корень n-ой степени и его свойства
Цели урока:
Образовательная: создать условия для формирования у обучающихся целостного представления о корне n-ой степени, навыков сознательного и рационального использования свойств корня при решении различных задач.
Развивающая: создать условия для развития алгоритмического, творческого мышления, развивать навыки самоконтроля.
Воспитательные: способствовать развитию интереса к предмету, активности, воспитывать аккуратность в работе, умение выражать собственное мнение, давать рекомендации.
Ход урока
1. Организационный момент.
Добрый день! Добрый час!
Как я рада видеть вас.
Прозвенел уже звонок
Начинается урок.
Улыбнулись. Подравнялись.
Друг на друга поглядели
И тихонько дружно сели.
2. Мотивация урока.
Выдающийся французский философ, ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя. Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:
— Что есть больше всего на свете? – Пространство.
— Что быстрее всего? – Ум.
— Что мудрее всего? – Время.
— Что приятнее всего? – Достичь желаемого.
Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.
3. Актуализация знаний.
1. Назовите взаимообратные алгебраические операции над числами. (Сложение и вычитание, умножение и деление)
2. Всегда ли можно выполнить такую алгебраическую операцию, как деление? (Нет, делить на нуль нельзя)
3. Какую еще операцию вы можете выполнять с числами? (Возведение в степень)
4. Какая операция будет ей обратной? (Извлечение корня)
5. Корень какой степени вы можете извлекать? (Корень второй степени)
6. Какие свойства квадратного корня вы знаете? (Извлечение квадратного корня из произведения, из частного, из корня, возведение в степень)
7. Найдите значения выражений:
, , , ,
Из истории. Ещё 4000 лет назад вавилонские ученые составили наряду с таблицами умножения и таблицами обратных величин (при помощи которых деление чисел сводилось к умножению) таблицы квадратов чисел и квадратных корней чисел. При этом они умели находить приблизительное значение квадратного корня из любого целого числа.
4. Изучение нового материала.
Очевидно, что в соответствии с основными свойствами степеней с натуральными показателями, из любого положительного числа существует два противоположных значения корня четной степени, например, числа 4 и -4 являются корнями квадратными из 16, так как (-4)2 = 42 = 16, а числа 3 и -3 являются корнями четвертой степени из 81, так как (-3)4 = З4 = 81.
Кроме того, не существует корня четной степени из отрицательного числа, поскольку четная степень любого действительного числа неотрицательна. Что же касается корня нечетной степени, то для любого действительного числа существует только один корень нечетной степени из этого числа. Например, 3 есть корень третьей степени из 27, так как З3 = 27, а -2 есть корень пятой степени из -32, так как (-2)5 = 32.
В связи с существованием двух корней четной степени из положительного числа, введем понятие арифметического корня, чтобы устранить эту двузначность корня.
Неотрицательное значение корня n-й степени из неотрицательного числа называется арифметическим корнем.
Обозначение: – корень n-й степени.
Число n называется степенью арифметического корня. Если n = 2, то степень корня не указывается и пишется. Корень второй степени принято называть квадратным, а корень третьей степени – кубическим.
= b, b2 = а, а ≥ 0, b ≥ 0
= b, bп = а, п – четное а ≥ 0, b ≥ 0
п – нечетное а, b – любые
Свойства
1. , а ≥ 0, b ≥ 0
2. , а ≥ 0, b >0
3. , а ≥ 0
4. , m, n, k – натуральные числа
5. Закрепление нового материала.
Устная работа
а) Какие выражения имеют смысл?
; ; ; ;
; ; ; ;
; ; ; ;
; ; ; .
б) При каких значениях переменной а имеет смысл выражение?
в) Вычислите:
Решить № 3, 4, 7, 9, 11.
6. Физкультминутка.
Во всех делах умеренность нужна,
Пусть будет главным правилом она.
Гимнастикой займись, коль мыслил долго,
Болезни чтоб прогнать и сохранить здоровье.
Гимнастика не изнуряет тела,
Но очищает организм всецело!
Закройте глаза, расслабьте тело,
Представьте – вы птицы, вы вдруг полетели!
Теперь в океане дельфином плывете,
Теперь в саду яблоки спелые рвете.
Налево, направо, вокруг посмотрели,
Открыли глаза, и снова за дело!
7. Самостоятельная работа.
Работа в парах с. 178 №1, №2.
8. Д/з. Выучить п.10 (с.160-161), решить № 5, 6, 8, 12, 16(1, 2).
9. Итоги урока. Рефлексия деятельности.
Достиг ли урок своей цели?
Чему вы научились?
xn--j1ahfl.xn--p1ai
Корень n-ой степени
Вопросы занятия:
· повторить, как извлекается корень n-ой степени из числа;
· повторить свойства арифметического корня n-ой степени;
· показать, как можно применить свойства корня при решении задач.
Материал урока
Определение.
Корнем n-ой степени из числа а называется такое число, энная степень которого равна А.
Говоря о корне энной степени нужно понимать, что показатель корня n является натуральным числом.
Вам хорошо известен такой частный случай корня n-ой степени, как корень второй степени, то есть квадратный корень из числа. Показатель корня в этом случае не пишут.
Определение.
Квадратным корнем из числа называют такое число, квадрат которого равен числу а.
Например,
Ещё одним частным случаем является корень третьей степени, мы привыкли называть его
Например,
Вы могли задаться вопросом, почему.
Чтобы ответить на этот вопрос, рассмотрим два случая корня энной степени: где показатель корня является нечётным числом и где показатель корня является чётным числом.
Но чтобы избавиться от неоднозначности в вычислениях, договорились неотрицательный корень n-ой степени обозначать как «корень n-ой степени из а». А отрицательный как «минус корень n-ой степени из а».
Исходя из этой договорённости и становится понятно, что
Из рассмотренных случаев можем сделать заключение, что:
Пример.
Вернёмся к определению корня энной степени
В первую запись вместо можно подставить:
Тогда получаем свойство, которым очень удобно пользоваться при вычислении корня энной степени.
Но ведь корень чётной степени мы договорились считать числом неотрицательным. Поэтому чтобы не возникало путаницы при вычислении корней, вместо этого свойства мы пользовались двумя:
Пример.
Вы видите, что корень энной степени из любого неотрицательного числа а
Любой корень можно выразить через арифметический.
Корни чётных степеней всегда являются арифметическими, ведь подкоренное выражение у них является числом неотрицательным, и под их значениями мы условились понимать неотрицательные числа.
Это же касается корней нечётных степеней из неотрицательных чисел.
А вот, например, корни нечётных степеней из отрицательных чисел можно записать так, при этом вынеся минус перед корнем.
Таким образом, при работе с любым корнем энной степени можно всегда перейти к рассмотрению арифметического корня.
Также при работе с корнями энной степени очень важно знать ещё несколько свойств. Напомним их.
Все эти свойства пригодятся вам при работе с выражениями, содержащими знак корня.
Итоги урока
На этом уроке мы с вами вспомнили, как извлекать корень n-ой степени из числа. Напомнили, что корень n-ой степени из неотрицательного числа считают числом неотрицательным, и называют «арифметическим корнем n-ой степени».
Так корень чётной степени из неотрицательного числа всегда является корнем арифметическим и поэтому равен числу неотрицательному. А корня чётной степени из отрицательного числа не существует. Корень нечётной степени из неотрицательного числа равен числу неотрицательному. Например, корень третьей степени из двадцати семи равен трём.
Ну, а корень нечётной степени из отрицательного числа равен числу отрицательному. Его нужно выражать с помощью арифметического корня n-ой степени, при этом вынося минус из-под знака корня. Также мы напомнили свойства арифметического корня энной степени и применили их на конкретных примерах.
videouroki.net
Свойства корня n-ой степени. Продолжение. Видеоурок. Алгебра 11 Класс
На данном уроке мы продолжим изучение свойств корня n-й степени из неотрицательного числа, научимся возводить его в степень и извлекать из него корень.
Напомним основное определение.
Определение:
Корнем n-й степени из неотрицательного числа а называется такое неотрицательное число b, которое при возведении в степень n дает число а.
Приведем математическую запись определения:
Например, , т. к. ; , т. к.
Неотрицательный корень n-й степени из неотрицательного числа а называют арифметическим корнем.
– арифметический корень;
Напомним геометрический смысл корня n-й степени из неотрицательного числа. Рассмотрим функцию на множестве всех действительных значений (рисунок 1) и только для неотрицательных х (рисунок 2).
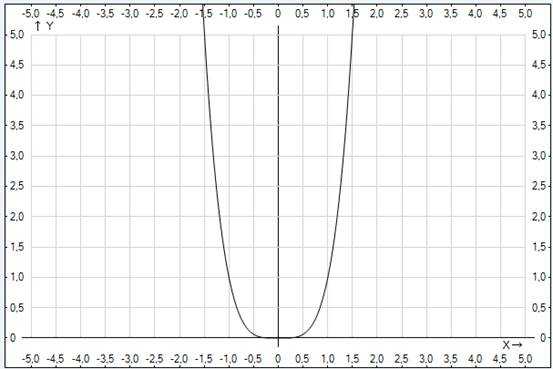
Рис. 1. График функции
Рис. 2. График функции на множестве
С рассматриваемыми функциями, как и с любой другой функцией, связаны две задачи – прямая (по заданному значению х найти у) и обратная (по заданному значению у определить х).
В случае, когда функция рассматривается для всех значений х, уравнение вида имеет два корня: , т. е. функция приобретает любое свое значение при двух противоположных значениях аргумента.
В случае же, когда рассматриваются только неотрицательные значения х, уравнение вида имеет единственный корень: , т. е. функция приобретает любое свое значение при одном значении аргумента, которое называют арифметическим корнем. Свойства этого корня мы и будем изучать.
Если а – неотрицательное число, k – любое натуральное число, n – натуральное чис
interneturok.ru
11 класс. Алгебра. Степени и корни. Степенные функции. Корни n-ой степени, их свойства. Функция y=ⁿ√x, ее свойства и график. — Свойства корня n-ой степени. Примеры решения типовых задач.
Комментарии преподавателя
При доказательстве свойств корня n-й степени мы будем опираться на его определение.
Определение:
Корнем n-й степени из неотрицательного числа а называется такое неотрицательное число b, которое при возведении в степень n дает число а.
Приведем математическую запись определения:
Например, , т. к. ; , т. к. ;
Обратим внимание, что под знаком корня может стоять отрицательное число, но только в том случае, если корень – нечетной степени. В этом случае следует вынести минус из-под знака корня, и мы получим корень из неотрицательного числа: .
Напомним геометрическую интерпретацию корня n-й степени и дадим пояснения к определению.
Рассмотрим функцию на множестве всех действительных значений. Рис. 1.

Рис. 1. График функции
Значение функция принимает при двух различных значениях аргумента: . Другими словами, уравнение имеет два решения, положительное и отрицательное, – неотрицательное значение – носит название арифметического корня.
Рассмотрим функцию на множестве . Рис. 2.
Рис. 2. График функции на множестве
Данная функция принимает значение при единственном значении аргумента . Система
имеет единственное решение .
Корень n-й степени (n=2, 3, 4…) из произведения двух неотрицательных чисел равен произведению корней n-й степени из этих чисел.
Дано:
Доказать:
Доказательство:
Обозначим исходные выражения через х, у и z:
Так как все выражения неотрицательные и возводятся в натуральную степень, имеем право записать:
Теорема доказана.
Рассмотрим несколько примеров на применение доказанной теоремы.
Пример 1 – вычислить:
Теорема удобна тем, что не нужно выполнять трудоемкое умножение, а иногда, наоборот, раскладывать большие числа на множители.
Пример 2 – вычислить:
Теорема 1 допускает обобщение, например, для произведения трех сомножителей.
Обобщение:
Дано: ,
Доказать:
Доказательство:
Согласно условию , если рассматривать ab как один множитель, а с как второй, можем применить к выражению теорему 1:
Теперь можем применить теорему 1 к корню из ab:
Обобщение доказано.
Пример 3 – вычислить:
Пример 4 – вычислить:
Если , то справедливо равенство:
Дано:
Доказать:
Доказательство:
Введем новые переменные:
Так как все выражения неотрицательные и возводятся в натуральную степень, имеем право записать:
Теорема доказана.
Теорему 2 можно доказать непосредственно через теорему 1:
Дано:
Доказать (используя теорему 1):
Доказательство:
Если вышеуказанное равенство верно, то, возведя его правую часть в степень n, мы должны получить подкоренное выражение:
Рассмотрим заданное выражение:
Теорема доказана.
Пример 5 – вычислить:
Пример 6 – вычислить:
www.kursoteka.ru
| 1. |
Корень из произведения, десятичные дроби и целые числа
Сложность: лёгкое |
2 |
| 2. |
Корень из произведения, целые числа и обыкновенные дроби
Сложность: лёгкое |
3 |
| 3. |
Корень из частного, обыкновенные дроби
Сложность: лёгкое |
2 |
| 4. |
Корень из произведения
Сложность: лёгкое |
4 |
| 5. |
Корень из корня
Сложность: лёгкое |
1 |
| 6. |
Извлечение корня из степени
Сложность: лёгкое |
3 |
| 7. |
Показатели корня
Сложность: лёгкое |
2 |
| 8. |
Корни с разными показателями
Сложность: лёгкое |
2 |
| 9. |
Корень из произведения степеней, корень в степени (целые числа)
Сложность: среднее |
3 |
| 10. |
Корень из дроби
Сложность: среднее |
5 |
| 11. |
Произведение корней
Сложность: среднее |
4 |
| 12. |
Частное корней
Сложность: среднее |
3 |
| 13. |
Произведение корня из произведения степеней и корня из степени
Сложность: среднее |
5 |
| 14. |
Корень из частного степеней
Сложность: среднее |
3 |
| 15. |
Корень из степени
Сложность: среднее |
4 |
| 16. |
Сравнение корней
Сложность: среднее |
3 |
| 17. |
Произведение корней с разными показателями
Сложность: среднее |
3 |
| 18. |
Частное корней с разными показателями
Сложность: среднее |
3 |
| 19. |
Произведение корней с разными показателями из произведений степеней
Сложность: среднее |
6 |
| 20. |
Степень произведения (число и корень)
Сложность: среднее |
6 |
| 21. |
Степень произведения (одночлен и корень)
Сложность: среднее |
4 |
| 22. |
Корень из произведения степеней (десятичные дроби)
Сложность: среднее |
4 |
| 23. |
Уравнение
Сложность: сложное |
5 |
| 24. |
Уравнение, сводимое к квадратному (метод введения новой переменной)
Сложность: сложное |
5 |
| 25. |
Уравнение, сводимое к квадратному (полное)
Сложность: сложное |
8 |
www.yaklass.ru
Свойства корня n-ой степени. Видеоурок. Алгебра 11 Класс
При доказательстве свойств корня n-й степени мы будем опираться на его определение.
Определение:
Корнем n-й степени из неотрицательного числа а называется такое неотрицательное число b, которое при возведении в степень n дает число а.
Приведем математическую запись определения:
Например, , т. к. ; , т. к. ;
Обратим внимание, что под знаком корня может стоять отрицательное число, но только в том случае, если корень – нечетной степени. В этом случае следует вынести минус из-под знака корня, и мы получим корень из неотрицательного числа: .
Напомним геометрическую интерпретацию корня n-й степени и дадим пояснения к определению.
Рассмотрим функцию на множестве всех действительных значений. Рис. 1.

Рис. 1. График функции
Значение функция принимает при двух различных значениях аргумента: . Другими словами, уравнение имеет два решения, положительное и отрицательное, – неотрицательное значение – носит название арифметического корня.
Рассмотрим функцию на множестве . Рис. 2.
Рис. 2. График функции на множестве
Данная функция принимает значение при единственном значении аргумента . Система
имеет единственное решение .
Корень n-й степени (n=2, 3, 4…) из произведения двух неотрицательных чисел равен произведению корней n-й степени из этих чисел.
Дано:
Доказать:
Доказательство:
Обозначим исходные выражения через х, у и z:
Так как все выражения неотрицательные и возводятся в натуральную степень, имеем право записать:
Теорема доказана.
Рассмотрим несколько примеров на применение доказанной теоремы.
Пример 1 – вычислить:
Теорема удобна тем, что не нужно выполнять трудоемкое умножение, а иногда, наоборот, раскладывать большие числа на множители.
Пример 2 – вычислить:
Теорема 1 допускает обобщение, например, для произведения трех сомножителей.
Обобщение:
Дано: ,
Доказать:
Доказательство:
Согласно условию , если рассматривать ab как один множитель, а с как второй, можем применить к выражению теорему 1:
Теперь можем применить теорему 1 к корню из ab:
Обобщение доказано.
Пример 3 – вычислить:
Пример 4 – вычислить:
Если , то справедливо равенство:
Дано:
Доказать:
Доказательство:
Введем новые переменные:
Так как все выражения неотрицательные и возводятся в натуральную степень, имеем право записать:
Теорема доказана.
Теорему 2 можно доказать непосредственно через теорему 1:
Дано:
Доказать (используя теорему 1):
Доказательство:
Если вышеуказанное равенство верно, то, возведя его правую часть в степень n, мы должны получить подкоренное выражение:
Рассмотрим заданное выражение:
Теорема доказана.
Пример 5 – вычислить:
Пример 6 – вычислить:
Докажем теорему 1 вторым способом:
Дано:
Доказать:
Доказательство:
Для доказательства будем использовать только определение корня.
Рассмотрим заданное выражение . Согласно определению корня, если правую часть выражения возвести в n-ю степень, мы должны получить подкоренное выражение, т. е.
Теорема доказана.
Итак, мы рассмотрели и доказали важные теоремы о корне n-й степени из произведения и частного. На следующих уроках мы продолжим изучение свойств корня n-й степени.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Terver.ru (Источник).
- Pm298.ru (Источник).
- School.xvatit.com (Источник).
Домашнее задание
1. Алгебра и начала анализа, 10–11 класс (А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 1990, № 381–384;
2. Вычислить:
а) ; б) ; в) ; г) ;
3. Вычислить:
а) ; б) ; в) ; г)
interneturok.ru
