Свойства корней степени н – .

1.1.5 Корень степени n > 1 и его свойства

Видеоурок 1: Степени и корни

Видеоурок 2: Свойства корня степени n > 1

Лекция: Корень степени n > 1 и его свойства

Корень 

Предположим, Вы имеете уравнение вида:

Решением данного уравнения будет х₁ = 2 и х₂ = (-2). В качестве ответа подходят оба решения, поскольку числа с равными модулями при возведении в четную степень дают одинаковый результат.

Это был простой пример, однако, что мы можем сделать в том случае, если, например,

Давайте попробуем построить график функции y=x². Её графиком является парабола:

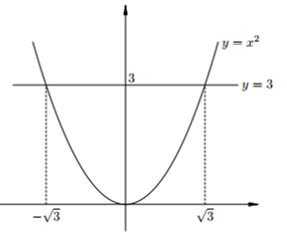
На графике необходимо найти точки, которым соответствует значение у = 3. Данными точками является:

 

Это означает, что данное значение нельзя назвать целым числом, но можно представить в виде корня квадратного.

Любой корень — это иррациональное число. К иррациональным числам относятся корни, непериодические бесконечные дроби.

Квадратный корень — это неотрицательное число «а», подкоренное выражение которого равно данному числу «а» в квадрате.

Например,

То есть в результате мы получим только положительное значение. Однако в качестве решения квадратного уравнения вида

 

Решением будет х₁ = 4, х₂ = (-4).

Свойства квадратного корня

1. Какое бы значение не принимала величина x, данное выражение верно в любом случае:

2. Сравнение чисел, содержащих квадратный корень. Чтобы сравнить данные числа, необходимо и одно, и второе число внести под знак корня. То число будет больше, чье подкоренное выражение больше.

Вносим число 2 под знак корня

А теперь давайте внесем число 4 под знак корня. В результате этого получим

И только теперь два полученных выражения можно сравнить:

3. Вынесение множителя из под корня.

Если подкоренное выражение может разложиться на два множителя, один из которых можно вынести из под знака корня, то необходимо пользоваться данным правилом.

4. Существует свойство, обратное данному — внесение множителя под корень. Этим свойством мы заведомо воспользовались во втором свойстве:

Корень степени n > 1

Под корнем n-ой степени некоторого числа «a» понимают число, которое при возведении в степень «n» даст число «а».

Иными словами можно сказать, что это решение следующего уравнения:

Например,

Если под корнем некоторой степени стоит степень, то для вынесения данного числа из под знака корня следует показатель степени разделить на степень корня.

cknow.ru

Свойства корней и степеней / Блог :: Бингоскул

• Блог
• →
• Свойства корней и степеней

Формулы корней n-ой степени и их свойства

1. Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение:
   (\sqrt[n]{a})^k =\sqrt[n]{a^k}
2. Чтобы извлечь корень из корня, достаточно перемножить показатели корней:
   \sqrt[n]{\sqrt[k]{a})} =\sqrt[n*k]{a}
3. Значение корня не изменится, если одновременно его показатель увеличить в k раз и подкоренное значение возвести в степень k:
4. \sqrt[n]{a^m} = \sqrt[n*k]{a^{m*k}}
5. Корень из произведения равен произведению корней:
   \sqrt[n]{a*b} = \sqrt[n]{a} * \sqrt[n]{b}
6. Корень из дроби — это корень из числителя и корень из знаменателя:
   \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}
7. Корень из n-ой степени в степени n
   (\sqrt[n]{a})^n =a
8. Корень из квадрата:
   (\sqrt{a^2}) = |a|

Формулы степеней и их свойства

1. Возведение в нулевую степень:
   a^0 = 1
2. Произведение степеней:
   a^m * a^n = a^{m+n}
3. Деление степеней:
   a^m : a^n = a^{m — n}
4. Возведение степени в степень:
   (a^m)^n = a^{m*n}
5. При возведении в степень произведения каждый из множителей возводится в степень и результаты перемножают:
   (a*b)^m = a^m * b^m
6. При возведении в степень частного возводят в эту степень и делимое, и делитель, результаты делят:
   (\frac{a}{b})^m = \frac{a^m}{b^m}
7. Степень с отрицательным рациональным показателем:
   a^{-n} = \frac{1}{a^n}
   Обыкновенная дробь с отрицательным показателем заменяется на обратную ей дробь с положительным показателем:
   (\frac{a}{b})^{-m} =(\frac{b}{a})^{m}
8. Степень с рациональным показателем: 
   a^{\frac{1}{n}} = \sqrt[n]{a}
   a^{\frac{m}{n}} = \sqrt[n]{a^m} 

---

 

Смотри также: Основные формулы по математике

 

Решай с разбором:

bingoschool.ru

Корень n-ой степени и его свойства.

Корень n-й степени и его свойства. 11 класс.

А.Г. Мордкович. Алгебра и начала анализа.

Цели урока:

• Образовательная: расширить и обобщить знания учащихся по данной теме, овладеть свойствами корня п-ой степени.

• Развивающая: развитие коммуникативных способностей.

• Воспитательная: формирование активной жизненной позиции, умение работать и преодолевать трудности, воспитание интереса к предмету.

Средства обучения: карточки, таблицы.

Тип урока

: урок обобщения и систематизации знаний.

Форма обучения: индивидуальная и групповая.

Ход урока

«Мышление начинается с удивления»

Аристотель

1. Организационный момент: приветствие, выявление готовности учащихся к уроку, постановка цели.

2. Разминка.

3. Актуализация опорных знаний.

4. Обобщение и закрепление материала.

Ход урока.

Вопросы для разминки.

1. Так называют выражение хn. (степень)

2. Есть у любого слова, у растения, может быть n-й степени. (корень)

3. Степень корня, кратная 2. (четная)

4. Степень корня 2 k+1. (нечетная).

5. Как можно иначе назвать корень третьей степени? (кубический)

6. Действие, посредством которого отыскивают корень. (извлечение).

7. Положительный корень. (арифметический).

8. Как можно иначе назвать арифметический корень второй степени? (квадратный).

Актуализация опорных знаний.

а) Свойства арифметического квадратного корня:

= ∙ , а ≥ 0 , в ≥0

= , а≥0, b0

б) свойства степени с натуральным показателем:

=

Формирование новых знаний. Аналогично определению квадратного корня из числа

a определяется корень n-ной степени из числа а, где n— произвольное натуральное число, n1.

Определение. Корнем n-ной степени из числа а называется такое число, n—ная степень которого равна а.

а)

б =2,

в) = -3

Рассмотрим уравнение = a. Число корней этого уравнения зависит от n и a.

Рассмотрим функцию f(x)=. При x и n –любое число- возрастает, и a имеет неотрицательный корень и только один x=.

Определение. Арифметическим корнем n-ной степени из числа

a называют неотрицательное число, n -ая степень которого равна a.

При четном n существует два корня n—ной степени из любого положительного числа a, корень четной степени из отрицательных чисел не существует. При нечетном n существует корень n—ной из любого числа a и притом только один.

Краткая запись (в тетради).

n— четное число

=a, a>0

=

X= —

а) = 7 , 7 =343 в)= -3 = -243

основные свойства арифметических корней n-ной степени.

Для любых чисел n € N , k € N, n >1 и k>1 , a>0, b>0 выполняются равенства :

1. =∙ ;

2. = ;

3. = ;

5. =( ) k

6. > 0≤ a a>b

Обобщение и закрепление материала.

Задание 1. Вычислите.

а)

б)

в)

Задание2. Докажите:

-=2

Задание3. Вычислите.

1) ∙ = = = 2

2) = = =

3) = = —

Трехуровневая самостоятельная работа с целью проверить знания, умения и навыки по теме

« Корень п-ой степени и его свойства»

№ 1. Вычислить (А)

1вариант 2 вариант

1. ∙ 1) ;

2. – 2 ; 2) ∙ ;

3. ; 3) -6 ∙ ;

№ 2 . Найдите значение выражения (В)

1) ∙ = 1) 7 ∙ =

2) = 2) =

№ 3. Упростите (С)

∙ ∙

Подведение итогов урока

Проверка работы учащихся: выставление оценок.

infourok.ru

35. Степени и корни. Корень n-й степени

Для всякого числа A Î R

определена степень с натуральным показателем An, N Î N.

Число B Î R называется Корнем N-й степени, N Î N, N ³ 2, из числа А, если обозначают

Нахождение корня N-й степени из данного числа А называют Извлечением корня N-й степени Из числа А. Число А, из которого извлекается корень N-й степени, называют Подкоренным выражением, а число N – Показателем корня.

Если то определен для всех A Î R и принимает любые действительные значения.

Если то определен для всех A ³ 0 (A Î R

). В курсе элементарной математики рассматривают Арифметическое значение корня, т. е. число

Свойства корней

Пусть A, B Î R, тогда:

1)

2)

3)

4)

5)

6) где A ³ 0 в случае

7) где в случае

8) где в случае

Пример 1. Вычислить

Решение. 1-й способ. Выделим полные квадраты подкоренных выражений:

Тогда получим

2-й способ. Обозначим вычисляемое выражение через A, т. е.

Заметим, что

Возведем обе части полученного равенства в квадрат:

Тогда

Поскольку исходное выражение положительно, в ответе получаем A = 4.

Пример 2. Упростить выражение

Решение. 1-й способ. Используем формулы квадрата разности и суммы, а также свойства корней. Получаем:

2-й способ. При упрощении иррациональных выражений часто бывает эффективным Метод рационализации, основанный на замене переменных.

Введем такую замену переменных, чтобы корни извлеклись:

Заданное выражение приобретает вид

Упрощаем его, используя формулы сокращенного умножения:

Возвращаясь к старым переменным, приходим к ответу

Пример 3. Избавиться от иррациональности в знаменателе:

1) 2) 3)

Решение. 1) Умножим числитель и знаменатель дважды на сопряженные выражения и воспользуемся формулой разности квадратов:

2) Домножим числитель и знаменатель на неполный квадрат разности и воспользуемся формулой суммы кубов:

3) Умножим числитель и знаменатель дважды на сопряженные выражения:

< Предыдущая		Следующая >

matica.org.ua

Свойства корня н степени – Telegraph

Свойства корня н степени

Скачать файл — Свойства корня н степени

Чтобы успешно использовать на практике операцию извлечения корня , нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе. Все свойства формулируются и доказываются только для неотрицательных значений переменных, содержащихся под знаками корней. Нам надо доказать, что для неотрицательных чисел х, у, z выполняется равенство х-уz. Теорема 1 остается справедливой и для случая, когда подкоренное выражение представляет собой произведение более чем двух неотрицательных чисел. Теорему 1 можно сформулировать, используя конструкцию ‘если Краткая хотя и неточная формулировка, которую удобнее использовать на практике: Приведем краткую запись доказательства теоремы 2, а вы попробуйте сделать соответствующие комментарии, аналогичные тем, что были приведены при доказательстве теоремы 1. ВЫ, конечно, обратили внимание на то, что доказанные два свойства корней п-й степени представляют собой обобщение известных вам из курса алгебры 8-го класса свойств квадратных корней. И если бы других свойств корней п-й степени не было, то как бы все было просто и не очень интересно. На самом деле есть еще несколько интересных и важных свойств, которые мы обсудим в этом параграфе. Но сначала рассмотрим несколько примеров на использование теорем 1 и 2. Воспользовавшись первым свойством корней теорема 1 , получим:. Можно, конечно, этот пример решить по-другому, особенно если у вас под рукой есть микрокалькулятор: Имеем Воспользовавшись вторым свойством корней теорема 2 , получим:. Так, первое свойство корней означает, что можно представить в виде и, наоборот, можно заменить выражением. То же относится и ко второму свойству корней. Учитывая это, выполним вычисления:. Решение , а Имеем: Здесь же предлагается умножить корень 2-й степени из числа а на корень 3-й степени из того же числа. Как это делать, мы пока не знаем. Вернемся к этой проблеме позднее. Продолжим изучение свойств радикалов. Иными словами, чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение. Это — следствие теоремы 1. Точно так же можно рассуждать в случае любого другого натурального значения показателя к. Иными словами, чтобы извлечь корень из корня, достаточно перемножить показатели корней. Как и в теореме 2, приведем краткую запись доказательства, а вы попробуйте самостоятельно сделать соответствующие комментарии, аналогичные тем, что были приведены при доказательстве теоремы 1. Чему мы научились благодаря доказанным теоремам? Мы узнали, что над корнями можно осуществлять четыре операции: А как же обстоит дело со сложением и вычитанием корней? Об этом мы говорили еще в 8-м классе по поводу операции извлечения квадратного корня. Например, вместо нельзя написать В самом деле, Но ведь очевидно, что Будьте внимательны! Самое, пожалуй, интересное свойство корней — это то, о котором пойдет речь в следующей теореме. Обозначим правую часть доказываемого тождества буквой у:. Тогда по определению корня должно выполняться равенство. Доказанная теорема позволит нам решить ту проблему, с которой мы столкнулись выше при решении примера 5, где требовалось выполнить умножение корней с разными показателями:. Вот как обычно рассуждают в подобных случаях. Воспользовавшись этим, умножим оба показателя на 3; получим: Воспользовавшись этим, умножим оба показателя на 2; получим: Вы не забыли, что все свойства корней, которые мы обсуждали в этом параграфе, рассмотрены нами только для случая, когда переменные принимают лишь неотрицательные значения? Почему пришлось сделать такое ограничение? Потому, что корень п-й степени из отрицательного числа не всегда имеет смысл — он определен только для нечетных значений п. Для таких значений показателя корня рассмотренные свойства корней верны и в случае отрицательных подкоренных выражений. Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум. При использовании материалов ресурса ссылка на edufuture. Ждем Ваши замечания и предложения на email: По вопросам рекламы и спонсорства пишите на email: Свойства корня n-й степени. Разработка — Гипермаркет знаний Ждем Ваши замечания и предложения на email: Свойства корня n-й степени Чтобы успешно использовать на практике операцию извлечения корня , нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе. Приведем краткую запись доказательства теоремы. Воспользовавшись первым свойством корней теорема 1 , получим: Имеем Воспользовавшись вторым свойством корней теорема 2 , получим: Учитывая это, выполним вычисления: Тогда по определению корня должно выполняться равенство Возведем обе части последнего равенства в одну и ту же степень р; получим: Доказанная теорема позволит нам решить ту проблему, с которой мы столкнулись выше при решении примера 5, где требовалось выполнить умножение корней с разными показателями:

Степени и корни

Гимнастика для рук при артрите

Стихи с бракосочетанием

Свойства корня n-ой степени

Схема зала дк ленсовета спб

Методы оценки в налоговом учете

Как правильно заполнить куплю продажи автомобиля

Тексты бесед с детьми

Корень степени n > 1 и его свойства. Начальный уровень.

Генеральный план софрино

Как сделать сломанный планшет

Статья 811 гк рф

Свойства корней, формулировки, доказательства, примеры.

Знаки препинания при косвенной речи таблица

Тест по обществознанию 7 класс личность подростка

Свойства графика y x3

telegra.ph

Корень степени n 1 и его свойства: квадратные корни формулы

Умножение корней: основные правила

Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.

Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)

Урок получился довольно большим, поэтому я разделил его на две части:

1. Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
2. Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще. С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.

Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.

Основное правило умножения

Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:

. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:

\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]

Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.

Примеры. Рассмотрим сразу четыре примера с числами:

\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}. \\ \end{align}\]

Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу.

Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.

Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.

Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:

Примеры.

\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]

И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.

Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка.

Случай произвольного показателя

Итак, с квадратными корнями разобрались. А что делать с кубическими? Или вообще с корнями произвольной степени $n$? Да всё то же самое. Правило остаётся прежним:

Чтобы перемножить два корня степени $n$, достаточно перемножить их подкоренные выражения, после чего результат записать под одним радикалом.

В общем, ничего сложного. Разве что объём вычислений может оказаться больше. Разберём парочку примеров:

Примеры. Вычислить произведения:

\[\begin{align} & \sqrt[4]{20}\cdot \sqrt[4]{\frac{125}{4}}=\sqrt[4]{20\cdot \frac{125}{4}}=\sqrt[4]{625}=5; \\ & \sqrt[3]{\frac{16}{625}}\cdot \sqrt[3]{0,16}=\sqrt[3]{\frac{16}{625}\cdot \frac{16}{100}}=\sqrt[3]{\frac{64}{{{25}^{2}}\cdot 25}}= \\ & =\sqrt[3]{\frac{{{4}^{3}}}{{{25}^{3}}}}=\sqrt[3]{{{\left( \frac{4}{25} \right)}^{3}}}=\frac{4}{25}. \\ \end{align}\]

И вновь внимание второе выражение. Мы перемножаем кубические корни, избавляемся от десятичной дроби и в итоге получаем в знаменателе произведение чисел 625 и 25. Это довольно большое число — лично я с ходу не посчитаю, чему оно равно.

Поэтому мы просто выделили точный куб в числителе и знаменателе, а затем воспользовались одним из ключевых свойств (или, если угодно — определением) корня $n$-й степени:

\[\begin{align} & \sqrt[2n+1]{{{a}^{2n+1}}}=a; \\ & \sqrt[2n]{{{a}^{2n}}}=\left| a \right|. \\ \end{align}\]

Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:

Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?

При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)

Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.

Умножение корней с разными показателями

Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt[7]{23}$? Можно ли вообще это делать?

Да конечно можно. Всё делается вот по этой формуле:

. Чтобы умножить $\sqrt[n]{a}$ на $\sqrt[p]{b}$, достаточно выполнить вот такое преобразование:

\[\sqrt[n]{a}\cdot \sqrt[p]{b}=\sqrt[n\cdot p]{{{a}^{p}}\cdot {{b}^{n}}}\]

Однако эта формула работает только при условии, что подкоренные выражения неотрицательны.

Корень степени n > 1 и его свойства. Начальный уровень.

Это очень важное замечание, к которому мы вернёмся чуть позже.

А пока рассмотрим парочку примеров:

\[\begin{align} & \sqrt[3]{3}\cdot \sqrt[4]{2}=\sqrt[3\cdot 4]{{{3}^{4}}\cdot {{2}^{3}}}=\sqrt[12]{81\cdot 8}=\sqrt[12]{648}; \\ & \sqrt{2}\cdot \sqrt[5]{7}=\sqrt[2\cdot 5]{{{2}^{5}}\cdot {{7}^{2}}}=\sqrt[10]{32\cdot 49}=\sqrt[10]{1568}; \\ & \sqrt{5}\cdot \sqrt[4]{3}=\sqrt[2\cdot 4]{{{5}^{4}}\cdot {{3}^{2}}}=\sqrt[8]{625\cdot 9}=\sqrt[8]{5625}. \\ \end{align}\]

Как видите, ничего сложного. Теперь давайте разберёмся, откуда взялось требование неотрицательности, и что будет, если мы его нарушим.:)

Почему подкоренные выражения должны быть неотрицательными?

Конечно, можно уподобиться школьным учителям и с умным видом процитировать учебник:

Требование неотрицательности связано с разными определениями корней чётной и нечётной степени (соответственно, области определения у них тоже разные).

Ну что, стало понятнее? Лично я, когда читал этот бред в 8-м классе, понял для себя примерно следующее: «Требование неотрицательности связано с *#&^@(*#@^#)~%» — короче, я нихрена в тот раз не понял.:)

Поэтому сейчас объясню всё по-нормальному.

Сначала выясним, откуда вообще берётся формула умножения, приведённая выше. Для этого напомню одно важное свойство корня:

\[\sqrt[n]{a}=\sqrt[n\cdot k]{{{a}^{k}}}\]

Другими словами, мы можем спокойно возводить подкоренное выражение в любую натуральную степень $k$ — при этом показатель корня придётся умножить на эту же степень. Следовательно, мы легко сведём любые корни к общему показателю, после чего перемножим. Отсюда и берётся формула умножения:

\[\sqrt[n]{a}\cdot \sqrt[p]{b}=\sqrt[n\cdot p]{{{a}^{p}}}\cdot \sqrt[p\cdot n]{{{b}^{n}}}=\sqrt[n\cdot p]{{{a}^{p}}\cdot {{b}^{n}}}\]

Но есть одна проблема, которая резко ограничивает применение всех этих формул. Рассмотрим вот такое число:

\[\sqrt[3]{-5}\]

Согласно только что приведённой формуле мы можем добавить любую степень. Попробуем добавить $k=2$:

\[\sqrt[3]{-5}=\sqrt[3\cdot 2]{{{\left( -5 \right)}^{2}}}=\sqrt[6]{{{5}^{2}}}\]

Минус мы убрали как раз потому, что квадрат сжигает минус (как и любая другая чётная степень). А теперь выполним обратное преобразование: «сократим» двойку в показателе и степени. Ведь любое равенство можно читать как слева-направо, так и справа-налево:

\[\begin{align} & \sqrt[n]{a}=\sqrt[n\cdot k]{{{a}^{k}}}\Rightarrow \sqrt[n\cdot k]{{{a}^{k}}}=\sqrt[n]{a}; \\ & \sqrt[n\cdot k]{{{a}^{k}}}=\sqrt[n]{a}\Rightarrow \sqrt[6]{{{5}^{2}}}=\sqrt[3\cdot 2]{{{5}^{2}}}=\sqrt[3]{5}. \\ \end{align}\]

Но тогда получается какая-то хрень:

\[\sqrt[3]{-5}=\sqrt[3]{5}\]

Этого не может быть, потому что $\sqrt[3]{-5} \lt 0$, а $\sqrt[3]{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:

1. констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
2. Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.

В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)

Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.

Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:

Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.

Пример. В числе $\sqrt[3]{-5}$ можно вынести минус из-под знака корня — тогда всё будет норм:

\[\begin{align} & \sqrt[3]{-5}=-\sqrt[3]{5} \lt 0\Rightarrow \\ & \sqrt[3]{-5}=-\sqrt[3\cdot 2]{{{5}^{2}}}=-\sqrt[6]{25}=-\sqrt[3\cdot 2]{{{5}^{2}}}=-\sqrt[3]{5} \lt 0 \\ \end{align}\]

Чувствуете разницу? Если оставить минус под корнем, то при возведении подкоренного выражения в квадрат он исчезнет, и начнётся хрень. А если сначала вынести минус, то можно хоть до посинения возводить/убирать квадрат — число останется отрицательным.:)

Таким образом, самый правильный и самый надёжный способ умножения корней следующий:

1. Убрать все минусы из-под радикалов. Минусы бывают только в корнях нечётной кратности — их можно поставить перед корнем и при необходимости сократить (например, если этих минусов окажется два).
2. Выполнить умножение согласно правилам, рассмотренным выше в сегодняшнем уроке. Если показатели корней одинаковые, просто перемножаем подкоренные выражения. А если разные — используем злобную формулу \[\sqrt[n]{a}\cdot \sqrt[p]{b}=\sqrt[n\cdot p]{{{a}^{p}}\cdot {{b}^{n}}}\].
3. 3.Наслаждаемся результатом и хорошими оценками.:)

Ну что? Потренируемся?

Пример 1. Упростите выражение:

\[\begin{align} & \sqrt[3]{48}\cdot \sqrt[3]{-\frac{4}{3}}=\sqrt[3]{48}\cdot \left( -\sqrt[3]{\frac{4}{3}} \right)=-\sqrt[3]{48}\cdot \sqrt[3]{\frac{4}{3}}= \\ & =-\sqrt[3]{48\cdot \frac{4}{3}}=-\sqrt[3]{64}=-4; \end{align}\]

Это самое простой вариант: показатели корней одинаковы и нечётны, проблема лишь в минусе у второго множителя. Выносим этот минус нафиг, после чего всё легко считается.

Пример 2. Упростите выражение:

\[\begin{align} & \sqrt[4]{32}\cdot \sqrt[3]{4}=\sqrt[4]{{{2}^{5}}}\cdot \sqrt[3]{{{2}^{2}}}=\sqrt[4\cdot 3]{{{\left( {{2}^{5}} \right)}^{3}}\cdot {{\left( {{2}^{2}} \right)}^{4}}}= \\ & =\sqrt[12]{{{2}^{15}}\cdot {{2}^{8}}}=\sqrt[12]{{{2}^{23}}} \\ \end{align}\]

Здесь многих смутило бы то, что на выходе получилось иррациональное число. Да, так бывает: мы не смогли полностью избавиться от корня, но по крайней мере существенно упростили выражение.

Пример 3. Упростите выражение:

\[\begin{align} & \sqrt[6]{a}\cdot \sqrt[3]{{{a}^{4}}}=\sqrt[6\cdot 3]{{{a}^{3}}\cdot {{\left( {{a}^{4}} \right)}^{6}}}=\sqrt[18]{{{a}^{3}}\cdot {{a}^{24}}}= \\ & =\sqrt[18]{{{a}^{27}}}=\sqrt[2\cdot 9]{{{a}^{3\cdot 9}}}=\sqrt{{{a}^{3}}} \end{align}\]

Вот на это задание хотел бы обратить ваше внимание. Тут сразу два момента:

1. Под корнем стоит не конкретное число или степень, а переменная $a$. На первый взгляд, это немного непривычно, но в действительности при решении математических задач чаще всего придётся иметь дело именно с переменными.
2. В конце мы умудрились «сократить» показатель корня и степень в подкоренном выражении. Такое случается довольно часто. И это означает, что можно было существенно упростить вычисления, если не пользоваться основной формулой.

Например, можно было поступить так:

\[\begin{align} & \sqrt[6]{a}\cdot \sqrt[3]{{{a}^{4}}}=\sqrt[6]{a}\cdot \sqrt[3\cdot 2]{{{\left( {{a}^{4}} \right)}^{2}}}=\sqrt[6]{a}\cdot \sqrt[6]{{{a}^{8}}} \\ & =\sqrt[6]{a\cdot {{a}^{8}}}=\sqrt[6]{{{a}^{9}}}=\sqrt[2\cdot 3]{{{a}^{3\cdot 3}}}=\sqrt{{{a}^{3}}} \\ \end{align}\]

По сути, все преобразования выполнялись лишь со вторым радикалом. И если не расписывать детально все промежуточные шаги, то в итоге объём вычислений существенно снизится.

На самом деле мы уже сталкивались с подобным задание выше, когда решали пример $\sqrt{5}\cdot \sqrt[4]{3}$. Теперь его можно расписать намного проще:

\[\begin{align} & \sqrt{5}\cdot \sqrt[4]{3}=\sqrt[2\cdot 4]{{{5}^{4}}\cdot {{3}^{2}}}=\sqrt[2\cdot 4]{{{\left( {{5}^{2}}\cdot 3 \right)}^{2}}}= \\ & =\sqrt[4\cdot 2]{{{\left( 75 \right)}^{2}}}=\sqrt[4]{75}. \end{align}\]

Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?

Смотрите также:

1. Что такое корень натуральной степени $n$
2. Сложные иррациональные уравнения — что с ними делать и как их решать?
3. Пробный ЕГЭ 2012. Вариант 1 (без логарифмов)
4. Как решать задачи B15 без производных
5. Как обеспечить себе достойную старость?
6. Выбор репетитора по математике для подготовки к ЕГЭ

laservirta.ru

Корень n-я степени, степень с рациональным показателем и их свойства [wiki.eduVdom.com]

Число, n-я степень которого равна a, называется корнем n-й степени из числа $a (n\in\mathbb{N}) и обозначается $\sqrt[n]{a}$.

Неотрицательное число, n-я степень которого равна неотрицательному числу а, называется арифметическим корнем n-и степени из числа а.

Свойства арифметического корня n-й степени:

1. Если $a\geq 0 ; b \geq 0 \text{ , то } \sqrt[n]{ab} = \sqrt[n]{a}\cdot\sqrt[n]{b}$

2. Если $a \geq 0; b \geq 0 \text{ , то } \sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}$

3. Если $n,\,k\in,\,a\geq 0\text{ , то } \sqrt[n]{\sqrt[k]{a}} = \sqrt[nk]{a}$

4. Если $n,\,k\in,\,a\geq 0\text{ , то } \sqrt[nk]{a^{mk}} = \sqrt[n]{a^m}$

Если $a>0\text{ , те }\mathbb{Z},\,n\in\mathbb{N}\text{ , то }a^{\frac{m}{n}} = \sqrt[n]{m} $.

Если $m\,,n\in\mathbb{N}\text{ , то }0^{\frac{m}{n}} = 0 $.

Свойства степени с рациональным показателем:

Для любого $a>0\text{ и }p, q\in\mathbb{Q}$:

• $a^pa^q = a^{p+q}$;

• $a^p:a^q = a^{p-q}$;

• $(a^p)^q = a^{pq}$;

Для любых a>0, b>0 и $p\in\mathbb{Q}$:

—- Пример 1. Найдите значение выражения $\sqrt[3]{8\cdot 0,001} \cdot \sqrt[5]{\frac{243}{32}}$

Решение:
$\sqrt[3]{8\cdot 0,001} \cdot \sqrt[5]{\frac{243}{32}} = \sqrt[3]{8}\cdot\sqrt[3]{0,001}\cdot\frac{\sqrt[5]{243}}{\sqrt[5]{32}} = 2\cdot0,1\cdot\frac{3}{2} = 0,3$

Ответ: 0,3

---

Пример 2. Упростите выражение $((a^{-0,4}b^{0,2})^5\cdot a^2b)^\frac{1}{3}$

Решение:
$((a^{-0,4}b^{0,2})^5\cdot a^2b)^\frac{1}{3} = ((a^{-0,4})^5\cdot(a^{0,2})^5\cdot a^2b)^{\frac{1}{3}} = (a^{-2}\cdot b\cdot a^2b)^{\frac{1}{3}} = (b^2)^{\frac{1}{3}} = b^{\frac{2}{3}}$

Ответ: $b^{\frac{2}{3}}$

wiki.eduvdom.com