Средние величины статистика – Тема № 5. Средние величины в статистике.

Средние величины

КУРСОВАЯ РАБОТА

ТЕОРИЯ СТАТИСТИКИ

На тему: Средние величины

Выполнил: Номер группы: СТП — 72

Юнусова Гульназия Чамилевна

Проверил: Серьга Людмила Константиновна

2008

Содержание

Введение

1. Сущность средних величин, общие принципы применения

2. Виды средних величин и сфера их применения

2.1 Степенные средние величины

2.1.1 Средняя арифметическая величина

2.1.2 Средняя гармоническая величина

2.1.3 Средняя геометрическая величина

2.1.4 Средняя квадратическая величина

2.2. Структурные средние величины

2.2.1 Медиана

2.2.2 Мода

3. Основные методологические требования правильного расчета средних величин

Заключение

Список использованной литературы

Введение

История практического применения средних насчитывает десятки столетий. Основная цель расчета средней состояла в изучении пропорций между величинами. Значимость расчетов средних величин возросла в связи с развитием теории вероятностей и математической статистики. Решение многих теоретических и практических задач было бы невозможно без расчетов средней и оценки колеблемости индивидуальных значений признака.

Ученые разных направлений стремились дать определение средней. Например, выдающийся французский математик О.Л.Коши (1789 — 1857) считал, что средней нескольких величин является новая величина, заключающаяся между наименьшей и наибольшей из рассматриваемых величин.

Однако создателем теории средних следует считать бельгийского статистика А. Кетле (1796 — 1874). Им предпринята попытка определить природу средних величин и закономерностей, в них проявляющихся. Согласно Кетле, постоянные причины действуют одинаково (постоянно) на каждое изучаемое явление. Именно они делают эти явления похожими друг на друга, создают общее для всех их закономерности.

Следствием учения А. Кетле об общих и индивидуальных причинах явилось выделения средних величин в качестве основного приема статистического анализа. Он подчеркивал, что статистические средние представляют собой не просто меру математического измерения, а категорию объективной действительности. Типическую, реально существующую среднюю он отождествлял с истинной величиной, отклонения от которой могут быть только случайными.

Ярким выражением изложенного взгляда на среднюю является его теория «среднего человека», т.е. человека среднего роста, веса, силы, среднего объема грудной клетки, емкости легких, средней остроты зрения и обычным цветом лица. Средние характеризуют «истинный» тип человека, все отклонения от этого типа указывают на уродливость или болезнь.

Взгляды А.Кетле получили дальнейшее развитие в работах немецкого статистика В.Лексиса (1837 — 1914).

Другая разновидность идеалистической теории средних основана на философии махизма. Ее основатель английский статистик А. Боули (1869 — 1957). В средних он видел способ наиболее простого описания количественных характеристик явления. Определяя значение средних или, как он выражается, «их функцию», Боули на первый план выдвигает махистский принцип мышлений. Так, он писал, что функция средних ясна: она заключается в том, чтобы выражать сложную группу при помощи немногих простых чисел. Ум не в состоянии сразу охватить величины миллионов статистических данных, они должны быть сгруппированы, упрощены, приведены к средним.

Последователем А.Кетле был и итальянский статистик К.Джини (1884-1965), автор крупной монографии «Средние величины». К.Джини подверг критике определение средней, данное советским статистиком А.Я. Боярским, и сформулировал свое: «Средняя нескольких величин является результатом действий, выполняемых по определенному правилу над данными величинами, и представляет собой либо одну из данных величин, которая не больше и не меньше всех остальных (средняя действительная или эффективная), либо какую-либо новую величину, промежуточную между наименьшей и наибольшей из данных величин (счетная средняя)».

В данной курсовой работе мы подробно рассмотрим основные проблемы теории средних величин. В первой главе выявим сущность средних величин и общие принципы применения. Во второй главе рассмотрим виды средних величин и сферу их применения на конкретных примерах. В третьей главе будут рассмотрены основные методологические требования расчета средних величин.

1. Сущность средних величин, общие принципы применения

Средние величины являются одними изнаиболее распространенных обобщающих статистических показателей. Они имеютсвоей целью одним числом охарактеризовать статистическую совокупность состоящуюиз меньшинства единиц. Средние величины тесно связаны с законом больших чисел.Сущность этой зависимости заключается в том, что при большом числе наблюденийслучайные отклонения от общей статистики взаимопогашаются и в среднем более отчетливо проявляется статистическая закономерность.

Средняя величина — это обобщающий показатель, характеризующий типический уровень явления в конкретных условиях места и времени. Он выражает уровень признака, типический для каждой единицы совокупности.

Средняя является объективной характеристикой только для однородных явлений. Средние для неоднородных совокупностей называются огульными и могут применяться только в сочетании с частными средними однородных совокупностей.

Средняя применяется в статистических исследованиях для оценки сложившегося уровня явления, для сравнения между собой нескольких совокупностей по одному и тому же признаку, для исследования динамики развития изучаемого явления во времени, для изучения взаимосвязей явлений.

Средние широко применяются в различных плановых, прогнозных, финансовыхрасчетах.

Главное значение средних величин состоит в их обобщающей функции,т.е. замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Всем известны особенности развития современных людей, проявляющиеся в том числе и в более высоком росте сыновей по сравнению с отцами, дочерей в сравнении с матерями в том же возрасте. Но как измерить это явление?

В разных семьях наблюдаются самые различные соотношения роста старшего и младшего поколения. Далеко не всякий сын выше отца и не каждая дочь выше матери. Но если измерить средний рост многих тысяч лиц, то по среднему росту сыновей и отцов, дочерей и матерей можно точно установить и сам факт акселерации, и типичную среднюю величину увеличения роста за одно поколение.

На производство одного и того же количества товара определенного вида и качества разные производители (заводы, фирмы) затрачивают неодинаковое количество труда и материальных ресурсов. Но рынок осредняет эти затраты, и стоимость товара определяется средним расходом ресурсов на производство.

Погода в определенном пункте земного шара в один и тот же день в разные годы может быть очень различной. Например, в Санкт-Петербурге 31 марта температура воздуха за сто с лишним лет наблюдений колебалась от -20,1° в 1883 г. до +12,24° в 1920 г. Примерно такие же колебания и в другие дни года. По таким индивидуальным данным о погоде в какой-то произвольно взятый год нельзя составить представление о климате Санкт-Петербурга. Характеристики климата — это средние за длительный период характеристики погоды — температуры воздуха, его влажность, скорость ветра, сумма осадков, число часов солнечного сияния за неделю, месяц и весь год и т.д.

Если средняя величина обобщает качественно однородные значения признака, то она является типической характеристикой признака в данной совокупности. Так, можно говорить об измерении типичного роста русских девушек рождения 1973 г. по достижении ими 20-летнего возраста. Типичной характеристикой будет средняя величина надоя молока от коров черно-пестрой породы на первом году лактации при норме кормления 12,5 кормовой единицы в сутки.

Однако неправильно сводить роль средних величин только характеристике типичных значений признаков в однородных по данному признаку совокупностях. На практике значительно чаще современная статистика использует средние величины, обобщающие явно неоднородные явления, как, например, урожайность всех зерновых культур по территории всей России. Или рассмотрим такую среднюю, как среднее потребление мяса на душу населения: ведь среди этого населения и дети до одного года, вовсе не потребляющие мяса, и вегетарианцы, и северяне, и южане, шахтеры, спортсмены и пенсионеры. Еще более ясна нетипичность такого среднего показателя, как произведенный национальный доход в среднем на душу населения.

Средняя величина национального дохода на душу, средняя урожайность зерновых по всей стране, среднее потребление разных продуктов питания — это характеристики государства, как единой народнохозяйственной системы, это так называемые системные средние.

Системные средние могут характеризовать как пространственные или объектные системы, существующие одномоментно (государство, отрасль, регион, планета Земля и т.п.), так и динамические системы, протяженные во времени (год, десятилетие, сезон и т.п.).

Примером системной средней, характеризующей период времени, может служить средняя температура воздуха в Санкт-Петербурге за 1992 г., равная +6,3°. Эта средняя обобщает крайне разнородные температуры зимних морозных дней и ночей, летних жарких дней, весны и осени. 1992 г. был теплым годом, его средняя температура не является типичной для Санкт-Петербурга. В качестве типической среднегодовой температуры воздуха в городе следует использовать многолетнюю среднюю, скажем, за 30 лет с 1963 по 1992 г., которая равна +5,05°. Эта средняя является типической средней, так как обобщает однородные величины; средние годовые температуры одного и того же географического пункта, варьирующие за 30 лет от +2,90° в 1976 г. до +7,44° в 1989 г.

mirznanii.com

Понятие средней величины в статистике

Количество просмотров публикации Понятие средней величины в статистике — 1680

Лекция 5. Средние величины

Понятие средней величины в статистике

Средняя арифметическая и ее свойства

Другие виды степенных средних величин

Мода и медиана

Квартили и децили

Большое распространение в статистике имеют средние величины. Средние величины характеризуют качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др.

Средняя — это один из распространенных приемов обобщений. Правильное понимание сущности средней определяет ее особую значимость в условиях рыночной экономики, когда средняя через единичное и случайное позволяет выявить общее и крайне важно е, выявить тенденцию закономерностей экономического развития.

Средняя величина — это обобщающие показатели, в которых находят выражение действия общих условий, закономерностей изучаемого явления.

Средняя величина (в статистике) – обобщающий показатель, характеризующий типичный размер или уровень общественных явлений в расчете на единицу совокупности при прочих равных условиях.

С помощью метода средних решаются следующие основные задачи:

1. Характеристика уровня развития явлений.

2. Сравнение двух или нескольких уровней.

3. Изучение взаимосвязей социально — экономических явлений.

4. Анализ размещения социально-экономических явлений в пространстве.

Статистические средние рассчитываются на базе массовых данных правильно статистически организованного массового наблюдения (сплошного и выборочного). При этом статистическая средняя будет объективна и типична, в случае если она рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений). К примеру, в случае если рассчитывать среднюю заработную плату в кооперативах и на госпредприятиях, а результат распространить на всю совокупность, то средняя фиктивна, так как рассчитана по неоднородной совокупности, и такая средняя теряет всякий смысл.

При помощи средней происходит как бы сглаживание различий в величинœе признака, которые возникают по тем или иным причинам у отдельных единиц наблюдения. К примеру, средняя выработка продавца зависит от многих причин: квалификации, стажа, возраста͵ формы обслуживания, здоровья и т.д.

Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов базовых. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.

Средняя величина является отражением значений изучаемого признака, следовательно, измеряется в той же размерности, что и данный признак.

Каждая средняя величина характеризует изучаемую совокупность по какому-либо одному признаку. Чтобы получить полное и всœестороннее представление об изучаемой совокупности по ряду существенных признаков, в целом крайне важно располагать системой средних величин, которые могут описать явление с разных сторон.

Существуют различные средние:

— средняя арифметическая;

— средняя геометрическая;

— средняя гармоническая;

— средняя квадратическая;

— средняя хронологическая.

referatwork.ru

Сущность и виды средних величин в статистике и способы их вычисления. Виды средних величин в статистике кратко: примеры, таблица

Начиная изучение такой науки, как статистика, следует понимать, что она содержит (как и любая наука) много терминов, которые необходимо знать и понимать. Сегодня мы разберём такое понятие, как средняя величина, и выясним, на какие виды она делится, как их вычислять. Ну а перед тем как начать, поговорим немного об истории, и о том, как и зачем возникла такая наука, как статистика.

История

Само слово «статистика» ведёт своё происхождение из латинского языка. Это производное от слова «статус», и означает «положение вещей» или «ситуация». Это короткое определение и отражает, по сути, весь смысл и назначение статистики. Она собирает данные о положении вещей и позволяет анализировать любые ситуации. Работой со статистическими данными занимались ещё в Древнем Риме. Там проводился учёт свободных граждан, их владений и собственности. Вообще изначально статистика использовалась для получения данных о количестве населения и их благах. Так, в Англии в 1061 году была проведена первая в мире перепись населения. Ханы, царствовавшие на Руси в 13 веке, тоже проводили переписи, чтобы брать дань с захваченных земель.

Каждый использовал статистику для своих целей, и в большинстве случаев это приносило ожидаемый результат. Когда люди осознали, что это не просто математика, а отдельная наука, которую нужно изучать основательно, начали появляться первые учёные, заинтересованные в её развитии. Люди, которые впервые заинтересовались этой областью и начали активно её постигать, были приверженцами двух основных школ: английской научной школы политических арифметиков и немецкой описательной школы. Первая возникла в середине 17-го века и ставила целью представить общественные явления, используя числовые показатели. Они стремились выявить закономерности в общественных явлениях на основе изучения статистических данных. Сторонники описательной школы также описывали социально-общественные процессы, но с использованием только слов. Они не могли представить динамику событий, чтобы лучше понять её.

В первой половине 19 века возникло ещё одно, третье направление этой науки: статистико-математическое. Огромный вклад в развитие этого направления внёс известный учёный, статистик из Бельгии Адольф Кетле. Именно он выделил виды средних величин в статистике, и по его инициативе начали проводиться международные конгрессы, посвящённые этой науке. С начала 20 века в статистике начали применяться более сложные математические методы, например, теория вероятностей.

Сегодня статистическая наука развивается благодаря компьютеризации. С помощью различных программ каждый может построить график на основе предложенных данных. В интернете также есть масса ресурсов, предоставляющих любые статистические данные о населении и не только.

В следующем разделе мы разберём, что означают такие понятия, как статистика, виды средних величин и вероятности. Далее коснёмся вопроса о том, как и где мы можем использовать полученные знания.

Это наука, основной целью которой является обработка информации для изучения закономерностей процессов, происходящих в обществе. Таким образом, можно сформулировать вывод о том, что статистика изучает общество и те явления, что протекают в нём.

Различают несколько дисциплин статистической науки:

1) Общая теория статистики. Разрабатывает методы сбора статистических данных и является основой всех остальных областей.

2) Социально-экономическая статистика. Она изучает макроэкономические явления с точки зрения предыдущей дисциплины и количественно характеризует общественные процессы.

3) Математическая статистика. Не всё в этом мире можно исследовать. Что-то приходится предугадывать. Математическая статистика изучает случайные величины и законы распределения вероятности в статистике.

4) Отраслевая и международная статистка. Это узкие области, которые изучают количественную сторону явлений, происходящих в определённых странах или отраслях жизни общества.

А сейчас мы рассмотрим виды средних величин в статистике, кратко расскажем об их применении в других, не столь тривиальных областях, как статистика.

Виды средних величин в статистике

Вот мы и подошли к самому главному, собственно, к теме статьи. Конечно, для освоения материала и усвоения таких понятий, как сущность и виды средних величин в статистике необходимы определённые знания математики. Для начала вспомним, что такое среднее арифметическое, гармоническое, геометрическое и квадратичное.

Среднее арифметическое мы проходили ещё в школе. Оно вычисляется очень просто: мы берём несколько чисел, среднее между которыми необходимо найти. Складываем эти числа и делим сумму на их количество. Математически это можно изобразить следующим образом. У нас есть ряд чисел, как пример, самый простой ряд: 1,2,3,4. Всего у нас 4 числа. Их среднее арифметическое находим таким образом: (1+2+3+4)/4 = 2,5. Всё просто. Мы начинаем с этого, потому что так легче понять виды средних величин в статистике.

Кратко расскажем также и о среднем геометрическом. Возьмём такой же ряд чисел, как и в предыдущем примере. Но теперь, чтобы вычислить среднее геометрическое, нам нужно извлечь корень степени, которая равна количеству этих чисел, из их произведения. Таким образом, для предыдущего примера получим: (1*2*3*4)^1/4~2,21.

Повторим понятие среднего гармонического. Как можно вспомнить из школьного курса математики, чтобы посчитать этот вид среднего, нам необходимо сначала найти числа, обратные числам ряда. То есть мы делим единицу на это число. Так получаем обратные числа. Отношение их количества к сумме и будет средним гармоническим. Возьмём для примера тот же ряд: 1, 2, 3, 4. Обратный ряд будет выглядеть так: 1, 1/2, 1/3, 1/4. Тогда среднее гармоническое можно посчитать так: 4/(1+1/2+1/3+1/4) ~ 1,92.

Все эти виды средних величин в статистике, примеры которых мы рассмотрели, являются частью группы под названием степенные. Также существуют структурные средние, которые мы разберём позже. Сейчас остановимся на первом виде.

Степенные средние величины

Мы уже разобрали арифметическое, геометрическое и гармоническое. Есть также более сложный вид, называемый средним квадратичным. Хоть его и не проходят в школе, вычислить его достаточно просто. Необходимо лишь сложить квадраты чисел ряда, разделить сумму на их количество, и извлечь из всего этого квадратный корень. Для нашего излюбленного ряда это будет выглядеть так: ((1²+2²+3²+4²)/4)^1/2= (30/4)^1/2 ~ 2,74.

На самом деле это всё только частные случаи среднего степенного. В общем виде это можно описать так: степенное n-ного порядка равно корню степени n из суммы чисел в n-ной степени, делённой на количество этих чисел. Пока всё не так сложно, как кажется.

Однако даже степенное среднее является частным случаем одного вида — среднего Колмогорова. По сути, все способы, которыми мы находили разные усреднённые величины до этого, можно представить в виде одной формулы: y^-1*((y(x₁)+y(x₂)+y(x₃)+…+y(x_n))/n). Здесь все переменные x — это числа ряда, а y(x) — некая функция, по которой мы считаем среднее значение. В случае, скажем, со средним квадратичным, это функция y=x², а со средним арифметическим y=x. Вот какие сюрпризы нам иногда преподносит статистика. Виды средних величин мы разобрали ещё не до конца. Помимо средних существуют ещё и структурные. Поговорим о них.

Структурные средние величины статистики. Мода

Тут всё немного сложнее. Чтобы разобрать эти виды средних величин в статистике и способы их вычисления, нужно основательно подумать. Существует две основных структурных средних: мода и медиана. Разберёмся с первым.

Мода встречается наиболее часто._{Она применяется чаще всего для определения спроса на ту или иную вещь. Чтобы найти её значение, нужно сначала найти модальный интервал. Что это такое? Модальный интервал — область значений, где какой-либо показатель имеет наибольшую частоту. Необходима наглядность, чтобы лучше представить моду и виды средних величин в статистике. Таблица, которую мы рассмотрим ниже, представляет собой часть задачи, условие которой такое:}

Определите моду по данным рабочих цеха о дневной выработке.

В нашем случае модальный интервал — это отрезок показателя дневной выработки с наибольшей численностью человек, то есть 40-44. Его нижняя граница — 44.

А теперь обсудим, как же вычислить эту самую моду. Формула не очень сложная и записать её можно так: M= x₁+ n*(f_M-f_M-1)/((f_M-f_M-1)+(f_M-f_M+1)). Здесь f_M — частота модального интервала, f_M-1 — частота интервала перед модальным (в нашем случае это 36-40), f_M+1 — частота интервала после модального (для нас — 44-48), n — величина интервала (то есть разность между нижней и верхней границей)? x₁ — значение нижней границы (в примере это 40). Зная все эти данные, мы можем смело вычислить моду на количество дневной выработки: M=40 +4*(24-20)/((24-20)+(24-19)) = 40 + 16/9 = 41,(7).

Структурные средние величины статистика. Медиана

Разберём ещё такой вид структурных величин, как медиана. Подробно на нём мы не будем останавливаться, расскажем лишь о различиях с предыдущим типом. В геометрии медиана делит угол пополам. Не зря в статистике этот вид средней величины так назвали. Если ранжировать ряд (к примеру, по численности населения того или иного веса в порядке возрастания численности), то медианой будет такое значение, которое делит этот ряд на две части, равные по численности.

Другие виды средних величин в статистике

Структурные типы вкупе со степенными дают далеко не всё, что требуется для расчётов в различных областях. Выделяют и другие типы этих данных. Таким образом, бывают средние взвешенные. Этот тип применяется тогда, когда числа в ряде имеют разный «вещественный вес». Это можно объяснить на простом примере. Возьмём автомобиль. Он движется с разной скоростью в разные промежутки времени. При этом друг от друга отличаются и значения этих временных отрезков, и значения скоростей. Так вот, эти промежутки и будут являться вещественными весами. Взвешенными можно сделать любой вид степенных средних.

В теплотехнике также применяется ещё один вид средних величин — среднее логарифмическое. Оно выражается достаточно сложной формулой, приводить которую мы не будем.

Где это применяется?

Статистика — наука, не привязанная к какой-либо одной сфере. Хоть и создана она была как часть социально-экономической сферы, но сегодня её методы и законы применяются в физике, химии, и биологии. Обладая знаниями в этой области, мы может легко определять тренды общества и вовремя предотвращать угрозы. Часто мы слышим фразы «угрожающая статистика», и это не пустые слова. Эта наука рассказывает нам о нас самих, и при должном её изучении способна предупредить о том, что может произойти.

Как связаны виды средних величин в статистике?

Соотношения между ними не всегда существуют, вот, например, структурные виды между собой не связаны никакими формулами. Но со степенными всё гораздо интереснее. Например, существует такое свойство: среднее арифметическое двух чисел всегда больше или равно их среднему геометрическому. Математически можно записать так: (a+b)/2 >= (a*b)^1/2. Доказывается неравенство переносом правой части влево и дальнейшей группировкой. В итоге получаем разность корней, возведённую в квадрат. А так как любое число в квадрате положительное, соответственно, неравенство становится верным.

Помимо этого есть более общее соотношение величин. Выясняется, что среднее гармоническое всегда меньше среднего геометрического, которое меньше среднего арифметического. А последнее оказывается, в свою очередь, меньше среднего квадратичного. Можете самостоятельно проверить правильность этих соотношений хотя бы на примере двух чисел — 10 и 6.

Что в этом интересного?

Интересно то, что виды средних величин в статистике, которые, казалось бы, показывают просто какой-то средний уровень, на самом деле могут сказать знающему человеку гораздо больше. Когда мы смотрим новости, никто и не задумывается над смыслом этих цифр и тем, как вообще их находить.

Что можно ещё почитать?

Для дальнейшего освоения темы мы рекомендуем прочитать (или прослушать) курс лекций по статистике и высшей математике. Ведь в этой статье мы рассказали лишь о крупинке того, что содержит в себе эта наука, и сама по себе она интереснее, чем кажется на первый взгляд.

Как эти знания мне помогут?

Возможно, они и пригодятся вам в жизни. Но если вам интересна сущность общественных явлений, их механизм и влияние на вашу жизнь, то статистика поможет вам глубже разобраться в этих вопросах. Вообще, она может описать практически любую сторону нашей жизни, если в её распоряжении имеются соответствующие данные. Ну а то, откуда и как добывается информация для анализа — тема отдельной статьи.

Заключение

Теперь мы знаем, что бывают разные виды средних величин в статистике: степенные и структурные. Разобрались в способах их вычисления и в том, где и как это можно применить.

fb.ru

Средние величины в статистике Лекция 5 Средняя

Средние величины в статистике Лекция 5.

Средняя величина – это обобщающая количественная характеристика совокупности по изучаемому признаку в конкретных условиях места и времени. Средняя величина отражает то общее и типичное, что присуще единицам данной совокупности.

Необходимые условия для расчета СВ – качественная однородность совокупности: все единицы совокупности должны обладать изучаемым признаком. Если изучают средний размер стипендии, то каждая единица должна обладать свойством – получением стипендии

Логическая формула • Расчет средней начинается с определения логической формулы. Прежде чем что-то умножать, делить или складывать, необходимо составить исходное соотношение средней, иначе называемое логической формулой

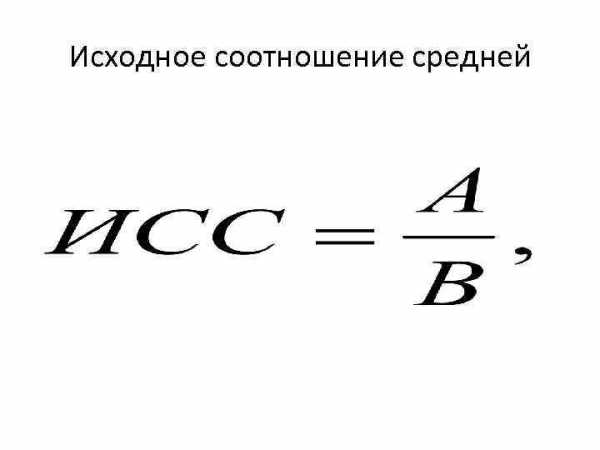Исходное соотношение средней

Исходное соотношение средней • где А – объем изучаемого события в совокупности: это суммарная абсолютная величина; • В – объем совокупности: это число единиц совокупности. • ИСС дает нам уровень изучаемого события в расчете на единицу совокупности

Примеры средних • Средняя зарплата показывает, сколько получает один работник. Что же мы возьмем в числителе и знаменателе ИСС? А – ? В – ?

Примеры средних • Средняя цена показывает, сколько в среднем стоит данный товар. • Что в числителе и знаменателе ИСС?

Примеры средних • Средняя себестоимость показывает, сколько в среднем стоит производство единицы продукции. • Что в числителе и знаменателе ИСС?

Примеры средних • Средняя продолжительность жизни, или средний срок службы показывает, сколько в среднем лет живет одушевленная единица совокупности и служит неодушевленная. • Что в числителе и знаменателе ИСС?

Логическая формула Для конкретного экономического показателя может быть составлена ТОЛЬКО ОДНА ИСТИННАЯ логическая формула

Виды средних величин Математикой доказано, что большую часть средних, которыми мы пользуемся, можно выразить в общем виде формулой средней степенной

Средние величины, применяемые в статистике, относятся к классу степенных средних. Общая формула степенной средней имеет следующий вид: где _ x k – степенная средняя k-ого порядка; k – показатель степени, определяющий форму средней; х – варианты; n – количество вариант

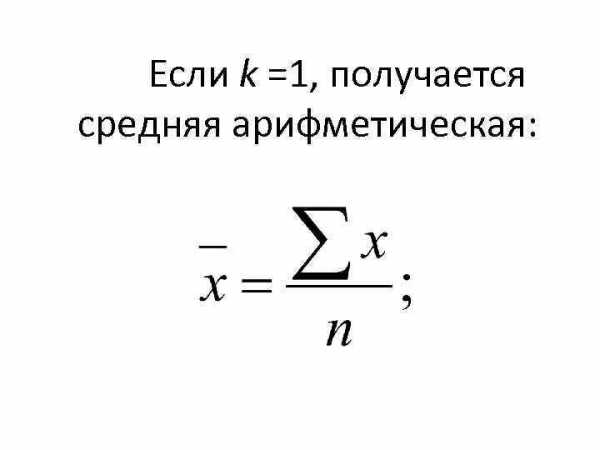Если k =1, получается средняя арифметическая:

Если k =2, получается средняя квадратическая:

если k =>0, получается средняя геометрическая:

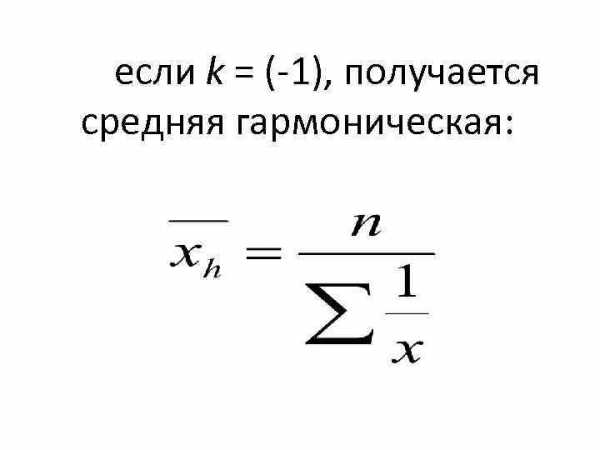если k = (-1), получается средняя гармоническая:

Правило мажорантности Чем выше показатель степени в формуле степенной средней, тем больше значение средней

Средняя арифметическая

Существуют две формулы средней арифметической: где f — частота

Средняя арифметическая простая • Средняя арифметическая простая применяется, когда есть перечисление вариант и нет никаких группировок. В числителе мы собираем сумму вариант, в знаменателе – количество вариант

Производительность труда 5 -и рабочих составляет: 58, 50, 46, 44, 42 изделий за смену. Определить среднюю производительность труда 5 -и рабочих. В этом случае решение имеет следующий вид:

Средняя арифметическая взвешенная • Средняя арифметическая взвешенная используется при появлении группировок. Это самая распространенная степенная средняя

Средняя квадратическая

• Нужно сохранить постоянной сумму квадратов.

Средняя гармоническая

Средняя гармоническая • СГ- это обратная величина средней арифметической. • Бывает простая и взвешенная СГ.

Существуют две формулы для расчета средней гармонической величины: где W- сложный вес, объем события по группе, по конкретному значению

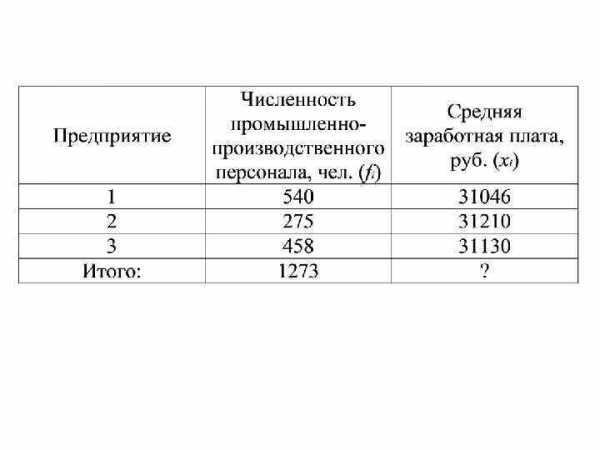
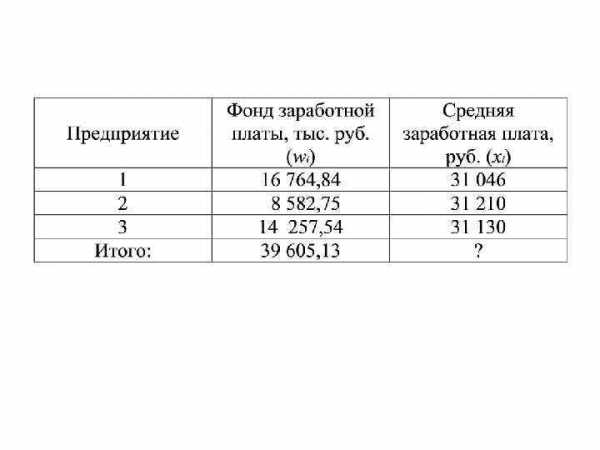
Арифметическая или гармоническая? • Подсказка: • Если по исходной информации дается осредняемая величина (варианта) и знаменатель логической формулы, то используется САВ. • Если дается варианта и числитель логической формулы, то используется СГВ

Арифметическая или гармоническая? • Иными словами: • Если не известен числитель, то используется САВ. • Если не известен знаменатель, то используется СГВ

Средняя геометрическая

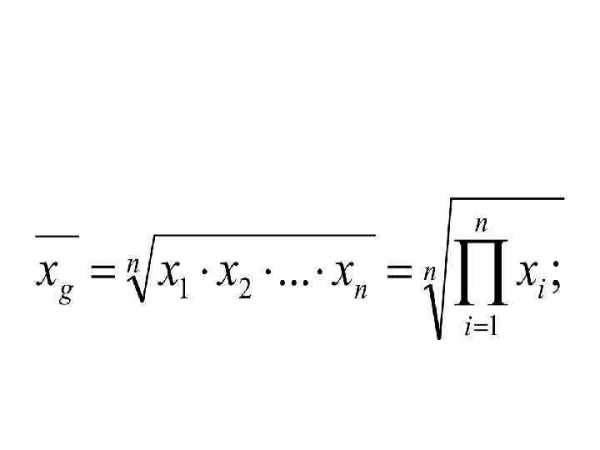
• Средний темп роста • Темпы прироста

Средняя хронологическая • Эта формула средней применяется для ряда моментных показателей

Средняя хронологическая • Необходимо взять половину первого и последнего показателя, плюс моментные показатели, находящиеся в середине ряда, полученную сумму разделить на количество моментных показателей минус 1

Средняя хронологическая • Широко применяется в рядах динамики, в социально-экономической статистике для определения средней численности населения и среднего размера остатков, а также для других показателей, исчисляемых на определенные моменты времени

Средняя хронологическая • Если необходимо подсчитать среднюю для двух моментных показателей, то формула средней хронологической превращается в формулу средней арифметической простой

Структурные средние Обычно средней степенной для анализа распределения недостаточно. Структурные средние применяются для первоначального анализа распределения признаков в совокупности.

Медиана • возможное значение признака, которое делит ранжированную совокупность на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.

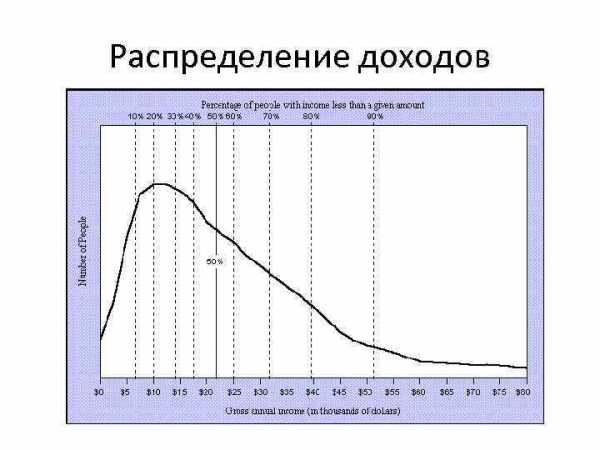Распределение доходов

Мода • значение во множестве наблюдений, которое встречается наиболее часто. • В вариационном ряду это будет варианта, имеющая наибольшую частоту. • Иногда в совокупности встречается более чем одна мода. В этом случае можно сказать, что совокупность мультимодальна. • Мода также может отсутствовать.

present5.com

Средние величины

Как уже неоднократно было сказано ранее, статистика изучает массовые явления и процессы. Каждое из таких явлений обладает как общими для всей совокупности, так и особенными, индивидуальными свойствами. Различие между индивидуальными явлениями называют вариацией, о ней подробно будет рассказано в теме 3. Здесь же рассмотрим другое свойство массовых явлений – присущую им близость характеристик отдельных явлений. В этом свойстве заключается причина широчайшего применения средних величин. Главное значение средних величин состоит в их обобщающей функции, то есть замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений.

            Виды средних величин различаются прежде всего тем, какое свойство, какой параметр исходной варьирующей массы индивидуальных значений признака должен быть сохранен неизменным.

            Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Иначе можно сказать, что средняя арифметическая величина – среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности. Исходя из определения, формула средней арифметической величины имеет вид (10):

.                                                      (10)

По формуле (10) вычисляются средние величины первичных признаков, если известны индивидуальные значения признака. Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения или группировку, как, например, табл. 3.

Таблица 3. Распределение студентов группы  дневного отделения по возрасту

            Средний возраст должен представлять собой результат равномерного распределения общего (суммарного) возраста всех студентов. Общий (суммарный) возраст всех студентов, согласно исходной информации табл. 3, можно получить как сумму произведений значений признака в каждой группе Xi, на число студентов с таким возрастом fi (частоты). Получим формулу (11):

,                                                                       (11)

где i – число групп.

            Такую форму средней арифметической величины называют взвешенной арифметической средней[11] в отличие от простой средней, рассчитанной по формуле (10). В качестве весов здесь выступают количество единиц совокупности в разных группах. Название «вес» выражает тот факт, что разные значения признака имеют неодинаковую «важность» при расчете средней величины. «Важнее», весомее возраст студентов 18, 19, 20 лет, а такие значения возраста как 17, 20 или 21 при расчете средней не играют большой роли – их «вес» мал.

            По формуле (11) по данным табл. 3 имеем:

= 18,857 (лет).

            Как видим, средняя арифметическая величина может быть дробным числом, если даже индивидуальные значения признака могут принимать только целые значения. Ничего необычного для метода средних в этом не заключено, так как из сущности средней не следует, что она обязана быть реальным значением признака, которое могло бы встретиться у какой-либо единицы совокупности.

            Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, то есть исходят из предположения о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспертным путем исходя из сущности, свойств признака и совокупности. При отсутствии возможности экспертной оценки значения признака в открытых интервалах, для нахождения недостающей границы открытого интервала применяют размах (разность между значениями конца и начала интервала) соседнего интервала (принцип «соседа»).

            Например, по данным табл. 4 можно минимальную и максимальную величину веса студентов определить затруднительно, поэтому воспользуемся принципом «соседа» – применим размах соседнего интервала, который у второго и предпоследнего составляет 10 кг, значит первый интервал будет от 50 до 60 кг, а последний – от 80 до 90 кг. Середины интервалов определяем как полусумму нижней и верхней границы интервалов.

Таблица 4. Распределение студентов по весу

Средний вес студентов, рассчитанный по формуле (11) с заменой точных значений признака в группах серединами интервалов, составил:

 кг,

что и записано в итоговую строку в 3-м столбце табл. 4. Следует обратить внимание, что итог объемного показателя – это сумма, а итог по столбцам относительных показателей или средних групповых величин – средняя.

            Средняя арифметическая величина обладает свойствами, знание которых полезно как при ее использовании, так и при ее расчете.

1.      Сумма отклонений индивидуальных значений признака от его среднего значения равна нулю. Доказательство[12]:

2.      Если каждое индивидуальное значение признака умножить или разделить на постоянное число, то и средняя увеличится или уменьшится во столько же раз. Доказательство:

Вследствие этого свойства индивидуальные значения признака можно сократить в c раз, произвести расчет средней и результат умножить на c.

3.      Если к каждому индивидуальному значению признака прибавить или из каждого значения вычесть постоянное число, то средняя величина возрастет или уменьшится на это же число. Доказательство:

Это свойство полезно использовать при расчете средней величины из многозначных и слабоварьирующих значений признака аналогично предыдущему свойству.

4.      Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится. Доказательство:

Используя это свойство, при расчетах следует сокращать веса на их общий сомножитель либо выражать многозначные числа весов в более крупных единицах измерениях.

5.      Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем от любого другого числа. Доказательство: составим сумму квадратов отклонений от переменной a: , чтобы найти экстремум этой функции, найдем ее производную по a и приравняем ее нулю, т.е. , отсюда получаем ; ; ; . Таким образом, экстремум суммы квадратов отклонений достигает максимума при a=. Так как логически ясно, что максимума функция иметь не может, этот экстремум является минимумом.

            Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменную сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной. Ее формула следующая:

.                                                               (12)

Главной сферой применения квадратической средней в силу пятого свойства средней арифметической величины является измерение вариации признака в совокупности.

            Аналогично, если по условиям задачи необходимо сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, мы приходим к средней кубической величине, имеющей вид:

.                                                               (13)

            Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить геометрическую среднюю величину, имеющую следующий вид:

 .                                  (14)

Основное применение средняя геометрическая находит при определении средних относительных изменений, о чем сказано в теме 6. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения признака, который качественно был бы равноудален как от максимального, так и от минимального значения признака.

            Когда статистическая информация не содержит частот f по отдельным вариантам Xi совокупности, а представлена как их произведение Xf, тогда применяется формула средней гармонической взвешенной, для получения которой обозначим Xf=w, откуда f=w/X, и, подставив эти обозначения в формулу (11), получим формулу (15):

.                                   (15)

Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны действительные веса f, а известно w=Xf. В тех случаях, когда вес каждого варианта w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой (16):

.                                     (16)

Все рассмотренные выше виды средних величин принадлежат к общему типу степенных средних, имеющему следующий вид:

=.                                                                (17)

При m = 1 получаем среднюю арифметическую; при m = 2 – среднюю квадратическую;

при m = 3 – среднюю кубическую; при m = 0 – среднюю геометрическую; при m = –1 – среднюю гармоническую. Чем выше показатель степени m, тем больше значение средней величины (если индивидуальные значения признака варьируют). В итоге, можно построить следующее соотношение, которое называется правилом мажорантности средних:

 ≤ ≤  ≤  ≤ .                                        (18)

www.ekonomstat.ru