Среднее статистическое – Средняя геометрическая, средняя гармоническая, средняя квадратичная и средняя кубическая

СТАТИСТИЧЕСКОЕ СРЕДНЕЕ — это… Что такое СТАТИСТИЧЕСКОЕ СРЕДНЕЕ?



СТАТИСТИЧЕСКОЕ СРЕДНЕЕ

СТАТИСТИЧЕСКОЕ СРЕДНЕЕ, в статистике — число, результат вычислений, которое дает типичное представление обо всем множестве чисел. Эта величина представляет собой АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ от этих чисел. Для получения представления о типичных величинах некоторого множества чисел определяют также модус (наиболее часто встречающееся число) и промежуточное число, приходящееся на середину диапазона значений всех чисел и разделяющее его на верхнюю и нижнюю части.

Научно-технический энциклопедический словарь.

• СТАТИСТИЧЕСКАЯ МЕХАНИКА
• СТАТИЧЕСКОЕ ЭЛЕКТРИЧЕСТВО

Смотреть что такое «СТАТИСТИЧЕСКОЕ СРЕДНЕЕ» в других словарях:

• статистическое среднее — statistinis vidurkis statusas T sritis fizika atitikmenys: angl. statistical average vok. statistischer Mittelwert, m rus. статистическое среднее, n pranc. moyenne statistique, f …   Fizikos terminų žodynas

• Среднее значение статической деформации, при которой происходило утомление образца до разрушения — Среднее статистическое значение статической деформации отдельного образца, к которой относятся усталостная выносливость образца Источник …   Словарь-справочник терминов нормативно-технической документации

• СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ — один из осн. разделов матем. статистики …   Физическая энциклопедия

• среднее — 3.3 среднее (mean): Среднее значение для (выбранного) времени усреднения результатов измерений анемометром. Источник: ГОСТ Р ИСО 1 …   Словарь-справочник терминов нормативно-технической документации

• среднее выходное качество — 2.7.4 среднее выходное качество Ожидаемый средний уровень качества выходящей продукции после контроля при данном значении входного уровня качества. Примечания 1 На практике могут быть использованы различные определения среднего выходного качества …   Словарь-справочник терминов нормативно-технической документации

• среднее процесса — 3.24 среднее процесса (process average): Уровень качества процесса, усредненный по определенному периоду времени или объему производства. [ИСО 2859 1, 3.1.25] Примечание В настоящем стандарте среднее процесса является средним уровнем… …   Словарь-справочник терминов нормативно-технической документации

• СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ — раздел статистического вывода , предназначенный для оценивания характеристик (параметров) генеральной совокупности по результатам выборочного исследования. С.О. параметров генеральной совокупности возможно, если выборка извлечена с использованием …   Социология: Энциклопедия

• ГОСТ Р 50779.11-2000: Статистические методы. Статистическое управление качеством. Термины и определения — Терминология ГОСТ Р 50779.11 2000: Статистические методы. Статистическое управление качеством. Термины и определения оригинал документа: 3.4.3 (верхняя и нижняя) границы регулирования Граница на контрольной карте, выше которой верхняя граница,… …   Словарь-справочник терминов нормативно-технической документации

• ГОСТ Р ИСО 16269-6-2005: Статистические методы. Статистическое представление данных. Определение статистических толерантных интервалов — Терминология ГОСТ Р ИСО 16269 6 2005: Статистические методы. Статистическое представление данных. Определение статистических толерантных интервалов оригинал документа: 3.1.2 толерантная граница (tolerance limit): Граница толерантного интервала.… …   Словарь-справочник терминов нормативно-технической документации

• ОЦЕНИВАНИЕ СТАТИСТИЧЕСКОЕ — один из основных разделов статистики математич. (см.), посвященный оцениванию по случайным наблюдениям тех или иных характеристик из распределения. В социологич. исследованиях чаще всего используются два вида О.с. точечное и интервальное.… …   Российская социологическая энциклопедия

dic.academic.ru

Средняя величина в статистике — это… Средние величины

Каждый человек в современном мире, планируя взять кредит или делая запасы овощей на зиму, периодически сталкивает с таким понятием, как «средняя величина». Давайте узнаем: что это такое, какие ее виды и классы существуют и зачем она применяется в статистике и других дисциплинах.

Средняя величина — это что такое?

Подобное название (СВ) носит обобщенная характеристика совокупности однородных явлений, определяемая по какому-либо одному количественному варьируемому признаку.

Однако люди далекие, от столь заумных определений, понимают это понятие, как среднее количество чего-то. Например, прежде чем взять кредит, сотрудник банка обязательно попросит потенциального клиента предоставить данные о среднем доходе за год, то есть общую сумму зарабатываемых человеком средств. Она вычисляется путем суммирования заработанного за весь год и разделения на количество месяцев. Таким образом, банк сможет определить, сумеет ли его клиент отдать долг в срок.

Зачем она используется?

Как правило, средние величины широко применяются для того, чтобы дать итоговую характеристику определенных общественных явлений, носящих массовый характер. Также они могут быть использованы для менее масштабных расчетов, как в случае с кредитом, в приведенном выше примере.

Однако чаще всего средние величины все же применяются для глобальных целей. В качестве примера одного из них можно привести вычисление количества потребляемой гражданами электроэнергии на протяжении одного календарного месяца. На основе полученных данных в дальнейшем устанавливаются максимальные нормы для категорий населения, пользующихся льготами от государства.

Также с помощью средних величин разрабатывается гарантийный срок службы тех или иных бытовых приборов, автомобилей, зданий и т. п. На основе собранных таким способом данных когда-то были разработаны современные нормы труда и отдыха.

Фактически любое явление современной жизни, носящее массовый характер, тем или иным образом обязательно связано с рассматриваемым понятием.

Сферы применения

Данное явление широко применяется практически во всех точных науках, особенно носящих экспериментальный характер.

Поиск среднего значения величины имеет огромное значение в медицине, инженерных дисциплинах, кулинарии, экономике, политике и т. п.

Основываясь на данных, полученных от подобных обобщений, разрабатывают лечебные препараты, учебные программы, устанавливают минимальные прожиточные минимумы и зарплаты, строят учебные графики, производят мебель, одежду и обувь, предметы гигиены и многое другое.

В математике данный термин именуется «средним значением» и применяется для осуществления решений различных примеров и задач. Наиболее простыми из них являются сложение и вычитание с обычными дробями. Ведь, как известно, для решения подобных примеров необходимо привести обе дроби к общему знаменателю.

Также в царице точных наук часто применяется близкий по смыслу термин «значение среднее случайной величины». Большинству он более знаком как «математическое ожидание», чаще рассматриваемое в теории вероятности. Стоит отметить, что подобное явление также применяется и при произведении статистических вычислений.

Средняя величина в статистике

Однако чаще всего изучаемое понятие используется в статистике. Как известно, эта наука сама по себе специализируется на вычислении и анализе количественной характеристики массовых общественных явлений. Поэтому средняя величина в статистике используется в качестве специализированного метода достижения ее основных задач — сбора и анализа информации.

Суть данного статистического метода заключается в замене индивидуальных уникальных значений рассматриваемого признака определенной уравновешенной средней величиной.

В качестве примера можно привести знаменитую шутку о еде. Итак, на неком заводе по вторникам на обед его начальство обычно ест мясную запеканку, а простые рабочие – тушеную капусту. На основе этих данных можно сделать вывод, что в среднем коллектив завода по вторникам обедает голубцами.

Хотя данный пример слегка утрирован, однако он иллюстрирует главный недостаток метода поиска средней величины – нивелирование индивидуальных особенностей предметов или личностей.

В статистике, данные средних величин применяются не только для анализа собранной информации, но и для планирования и прогнозирования дальнейших действий.

Также с его помощью производится оценка достигнутых результатов (например, выполнение плана по выращиванию и сбору урожая пшеницы за весенне-летний сезон).

Как правильно рассчитать

Хотя в зависимости от вида СВ существуют разные формулы ее вычисления, в общей теории статистики, как правило, применяется всего один способ расчета средней величины признака. Для этого нужно сначала сложить вместе значения всех явлений, а затем разделить получившуюся сумму на их количество. При произведении подобных вычислений стоит помнить, что средняя величина всегда имеет ту же размерность (или единицы измерения), что и отдельная единица совокупности.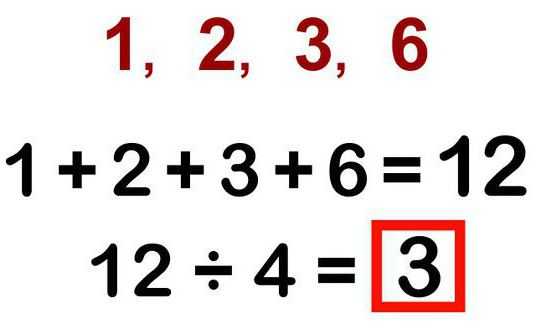

Условия правильного вычисления

Рассмотренная выше формула весьма проста и универсальна, так что ошибиться в ней практически невозможно. Однако всегда стоит учитывать два аспекта, иначе полученные данные не будут отражать реальную ситуацию.

• Искомые индивидуальные значения (на основе которых вычисляются средние) всегда должны относиться к однородной совокупности, а количество их должно быть значительным.

  В вышеупомянутой шутке мясная запеканка и капуста – относятся к одной категории – «еда». Однако если бы нужно было узнать, сколько килограмм капусты хранится в столовой завода, учитывать данные о мясе не было бы смысла, так как в данном случае они не относились бы к рассматриваемой однородной совокупности.

• В любом индивидуальном случае важно брать во внимание качественное содержания признака, среднюю величину которого необходимо рассчитать. При этом важно обращать внимание на взаимосвязь между изучаемыми признаками и имеющиеся для вычислений данные.

Классы СВ

Найдя ответы на основные вопросы: «Средняя величина — это что такое?», «Где применяется она?» и «Как можно вычислить ее?», стоит узнать, какие классы и виды СВ существуют.

Прежде всего это явление делится на 2 класса. Это структурные и степенные средние величины.

Виды степенных СВ

Каждый из вышеперечисленных классов, в свою очередь, делится на виды. У степенного класса их четыре.

• Средняя арифметическая величина – это наиболее распространенный вид СВ. Она являет собою среднее слагаемое, при определении коего общий объем рассматриваемого признака в совокупности данных поровну распределяется между всеми единицами данной совокупности.

  Этот вид делится на подвиды: простая и взвешенная арифметическая СВ.

• Средняя гармоническая величина – это показатель, обратный средней арифметической простой, вычисляемый из обратных значений рассматриваемого признака.

  Она применяется в тех случаях, когда известны индивидуальные значения признака и произведение, а данные частоты — нет.

• Средняя геометрическая величина чаще всего применима при анализе темпов роста экономических явлений. Она дает возможность сохранять в неизменном виде произведение индивидуальных значений данной величины, а не сумму.

  Также бывает простой и взвешенной.

• Средняя квадратическая величина используется при расчете отдельных показателе показателей, таких как коэффициент вариации, характеризующего ритмичность выпуска продукции и т. п.

  Также с ее помощью вычисляются средние диаметры труб, колес, средние стороны квадрата и подобных фигур.

  Как и все остальные виды средних СВ, среднеквадратическая бывает простой и взвешенной.

Виды структурных величин

Помимо средних СВ, в статистике довольно часто используются структурные виды. Они лучше подходят для расчета относительных характеристик величин варьирующего признака и внутреннего строения рядов распределения.

Таких видов существует два.

• Мода. Данный вид чаще всего используется для определения наиболее популярных у покупателей размеров одежды и обуви.

  Как правило, мода вычисляется по такой формуле.
  В ней М₀ – является значением моды, х₀ – нижней границей интервала модального, h – величиной рассматриваемого интервала, f_m – его частотой, f_m-1 – частотой предшествующего модальному интервалу и f_m+1 – частотой следующего.

• Медианой именуется значение признака, лежащее в основе ранжированного ряда и делящее его на две части, равные между собою по численному показателю.

  В формулах, данный вид обозначается, как М_е.

  В зависимости от того в каком ряду определяется данный вид структурной СВ (дискретный или интервальный вариационный), применяются различные формулы его вычисления.

fb.ru

Среднее статистическое — Справочник химика 21

    Взвешенные по числу значения й используют при определении среднего геометрического, среднего гармонического, степенного среднего (квадратичного и кубичного). Формулы для определения среднего статистического диаметра частиц смеси даны в табл. 5. В четвертой колонке этой таблицы указаны средние диаметры, рассчитанные как среднее арифметическое, взвешенное по весовым выходам   [c.27]

    Выбор начальных значений условно-входных переменных. Расчет оптимального режима схемы является многократно повторяемым итерационным процессом. Естественно в качестве начальных приближений для условно-входных переменных на г-ой итерации оптимизационного процесса принимать значения, которые они получили на (г — 1)-ой итерации. При выборе же начальных приближений па первой итерации необходимо привлекать физические соображения. Так, в качестве начальных приближений условно-входных переменных можно применять их средне-статистические значения, найденные из эксперимента. Этот способ удобен при незначительных отклонениях входных и управляющих переменных от своих средних значений. Однако такой выбор может привести к значительному увеличению числа итераций при расчете схемы в случае существенных отклонений переменных разрываемых потоков от средних значений что часто встречается при решении задач оптимизации. Например,, при расчете схемы отделения ректификации с изменением состава печного масла 2д в рабочем диапазоне число итераций требуемых для согласования условно-входных и условно-выходных переменных изменяется от 30 до 12 (расчет проводился методом простой итерации). 

[c.303]

    На рис. 74 представлена простейшая схема основных этапов работ по созданию новых производств в химической промышленности (по данным зарубежной литературы). В прямоугольниках наряду с названием этапа проставлен его порядковый номер и продолжительность работы (в скобках) в месяцах (средняя статистическая), над стрелкой — общая продолжительность с начала работы. Следует отметить, что формирование проблемы здесь взято за начало отсчета, хотя иа выполнение его требуется достаточно продолжительное время, поскольку именно на этом этапе проводится обоснование целен и потребности в новом производстве. [c.232]

    В процессе анализа структуры все приведенные интегральные характеристики материала рассчитываются по результатам анализа представительного объема и, таким образом, число составных частей фазы, среднее значение поверхностной кривизны, связность и другие характеристики обычно относятся к единице его объема, т. е. являются средними статистическими значениями удельных объемных характеристик. Строго говоря, связность G, рассматриваемая как род гомеоморфных поверхностей, не должна быть подвержена статистическим колебаниям. Однако в природе формирование контактов частиц является статистическим процессом, зависящим от таких стохастических факторов как перемешивание в системе, смачивание, диффузия, растворение и рост частиц фаз, взаимодействие фаз и др., поэтому в принципе возможно рассматривать Gy как статистическую величину. Потребность экспрессного определения связности фаз в многофазных средах в последнее время быстро растет в связи с определяющей ролью этой характеристики в описании и прогнозировании механического поведения структурно неоднородных материалов, выявления структуры многофазных потоков в его объеме. Вместе с тем существующие методы определения Gy до сих пор практически основывались на методе анализа параллельных сечений структуры. В работах [47, 481 предложен иной метод определения статистической характеристики связности на основании простых измерений характеристик одного случайного представительного сечения материала. Разрабатываются также методы стереоскопической оценки Gy. 

(adsbygoogle = window.adsbygoogle || []).push({}); [c.136]

    Эту характеристику определяют на основе условной замены реальной полидисперсной смеси системой частиц правильной формы и одинакового размера. Средние статистические диаметры определяют как средневзвешенные, с учетом веса , т. е. влияния частиц данного размера (фракции) на величину среднего диаметра  [c.27]

    В предложенной нами модифицированной модели сыпучей среды рассмотрены средние статистические значения напряжений и допускается возможность нарушения сплошности в виде резкого уменьшения концентрации твердых частиц на границах между агрегатами. При этом условие совместности деформаций выполняется только по их средним статистическим значениям. 

[c.74]

    Согласно нашим выводам, динамический свод является локальным образованием, однако он имеет значительную высоту, среднее статистическое значение которой равно (0,25—0,3)D. Кроме того, наиболее резкий скачок давления возникает не на верхней, а на нижней границе свода, примыкающей к зоне стока. [c.118]

    Следует отметить, что строение звеньев цепных молекул высокомолекулярных соединений отличается от строения молекул соответствующих мономеров, в связи с тем, что в процессе полимеризации происходит рекомбинация связей, приводящая к соединению отдельных звеньев с образованием длинной цепи. Следует также отметить, что при полимеризации происходит образование макромолекул разной длины, а следовательно, и разной массы. Таким образом, молекулярная масса полимера является средней статистической величиной, равно как и степень полимеризации. 

[c.370]

    В таких измерениях выход нейтронов является статистической величиной и изменяется от деления к делению, если даже падающий нейтрон имеет какую-то постоянную энергию. Принятые в результате измерений средние статистические значения V (среднее число нейтронов на одно деление) для основных трех видов ядерного горючего помещены в табл. 1.2. [c.14]

    Звуковое давление в заданной точке звукового поля есть разность между мгновенным полным давлением и средним статистическим давлением, которое наблюдается в среде при отсутствии звукового поля. [c.511]

    Учитывая недостатки приведенного точечного метода оценки вероятности разрушения образцов, более целесообразно в ряде случаев использовать для определения средних статистических значений доверительные интервалы, в которых находят с заданной вероятностью необходимые величины. [c.326]

    Температура газа определяется средней кинетической энергией его молекул. При неизменных внешних условиях температура остается постоянной, что связано со стационарным распределением молекул по скоростям, хотя отдельные молекулы имеют самые различные скорости. Давление газа — суммарный эффект ударов очень большого числа молекул о стенку сосуда. Статистической природой обладают также объем и плотность газа. Важнейшие термодинамические функции энтропия, изохорный и изобарный потенциал и другие — зависят от температуры, давления и объема. Значения этих функций представляют собой средние статистические величины, относящиеся к системам, состоящим из большого числа частиц. [c.148]

    Для таких полидисперсных веществ, как смолы и асфальтены, молекулярная масса является средней статистической величиной [c.151]

    Значения и AL зависят от сопротивления всасывающего и нагнетательного клапанов, холодильника, маслоотделителя и примыкающих к ним трубопроводов. В гл. VI приведены формулы для вычисления потерь энергии, возникающих в этих узлах в зависимости от их гидравлических сопротивлений. Но в начале проектирования форма и размеры этих узлов газового тракта еще неизвестны и поэтому приходится руководствоваться средними статистическими данными о потерях давления. [c.55]

    Окончательные размеры газовой коммуникации обычно устанавливаются лишь в рабочем проекте. Поэтому в эскизном и техническом проектах приходится ограничиваться вычислением потерь мощности только в клапанах, а потери в коммуникации ступени учитывать по средним статистическим значениям коэффициента потери индикаторной мощности АС г/нз (рис. 11.13), полагая, что на потери в коммуникации приходится 0,4 общей потери при всасывании и нагнетании [c.278]

    Следует иметь в виду, что влагосодержание наружного воздуха Хц в среднем летом выше, чем зимой. Величина х входит как вычитаемое в знаменатель правой части уравнения (XV,24). Следовательно, расчет удельного расхода воздуха (и соответственно подбор калориферов для его нагрева) надо вести по наибольшей величине х в летних условиях для того географического пункта, в котором должна работать сушилка. Средние статистические данные о значениях Хц в летнее и зимнее время года для различных городов СССР приводятся в справочных таблицах. [c.594]

    При расчете средних статистических величин необходимо учитывать различные взаимодействия в полимерной цепи. Во-первых, взаимодействие соседних боковых групп цепи затормаживает вращение вокруг простых связей такие взаимодействия называют ближними. Во-вторых, при расчете возможных конформаций цепи нужно учитывать, что разные звенья одновременно не могут находиться в одной и той же точке пространства и поэтому цепь не может пересекать самое себя. Иными словами, существует взаимодействие участков цепи, разделенных большим числом [c.125]

    Математическое ожидание (среднее статистическое) дискретной случайной величины определяют как сумму произведений всех ее возможных значений на вероятности этих значений  [c.17]

    Для расчета средней статистической величины х требуется знать вероятности всех возможных состояний системы. [c.17]

    Среднее статистическое (математическое ожидание) непрерывной случайной величины определяется как интеграл [c.17]

    Среднее статистическое значение функции М (р, д) динамических переменных рад молекулы может быть вычислено по формуле [c.90]

    Радиоспектроскопические измерения во многих случаях позволяют вычислить среднее статистическое значение квадрата дипольного мо- [c.108]

    Методы, основанные на определении и анализе средних статистических значений и анизотропии [c.110]

    Допустим, что в области V. образовалась флуктуация, так что величина х отличается от равновесного среднего статистического зна-чения . В замкнутой системе не зависит от времени. Если в начальный момент времени свойство х замкнутой системы почему-либо отличается от , то с течением времени замкнутая система будет стремиться к своему равновесному состоянию и л будет неограниченно приближаться к . Этот процесс называется релаксацией. Ясно, [c.130]

    Величина зависит от дипольного момента а молекул, имеющихся в жидкости. Если жидкость однокомпонентна, т. е. все молекулы одинаковы, то = где — число молекул в объеме V. Среднее статистическое значение квадрата дипольного момента связано с дипольными моментами ассоциатов и их концентрациями уравнением (У.З). [c.146]

    Давно уже существовала идея о том, что точное вычисление энергии меж-электронного взаимодействия не может основываться только на усредненной статистической модели расположения электронных плотностей в пространстве необходимо на самом деле принимать во внимание и мгновенные эффекты, зависяш,ие от кратковременных, но значительных отклонений быстро двигающихся электронов, от положений, отвечающих среднему статистическому. Корреляция движения во времени может идти так, чтобы один из взаимодействующих электронов, был, например, в данное мгновение справа от ядра, а другой слева (угловая корреляция) или в то время, когда один сблизился с ядром, другой, наоборот, отдалился от него (радиальная корреляция). Значение энергии при этом зависит как от усредненных, так и от мгновенных эффектов. [c.67]

    Нз-за спинового запрета обратный переход изолированной молекулы Од Б основное состояние также мало вероятен, и требует в среднем статистически около 45 мин [3], т. е. состояние Оа метастабильно переход совершается при этом с испусканием кванта света [4—6], обла- [c.176]

    При возрастании скоростп сдвига долнаю уд1еньшаться среднее статистическое значение константы для несферических частиц, поскольку в псевдоожиженных слоях с ориентацией частиц при низком значении трение между частицами меньше, чем в слое с высоким значением С . [c.242]

    Формула (11.42) принята впред-положении, что в новых компрессорах потери давления будут ниже средних статистических по выполненным компрессорам. [c.70]

    Чтобы использовать это соотношение для нахождения термодинамических величин, необходимо установить однозначное соответствие между термодинамическими переменными и статистическими средними. Поэтому средние статистические значения функций, определяемых из уравнений типа (VII.24), называют статистическими аналогами термодинамических величин. Их отождествление с термодинамическими величинами принимают как постулат. Важнейшее допушение подобного рода, хотя оно и представляется вполне естественным, состоит в том, что термодинамической внутренней энергии и соответствует среднее значение энергии системы в ансамбле с точностью до некоторой постоянной 11 о — энергии системы при 7=0 — абсолютном нуле  [c.206]

    Степень упорядоченности я имеет определенное значение для каждой конфигурации системы. В теории упорядоченности ставится задача нахождения среднего статистического (наиболее вероятного) значения этой величины, которое будет обнаруживаться на опыте. Требуется установить зависимость среднего значения з от температуры и выявить связь этой величины с термодинамическими функциями. Точка перехода порядок—беспорядок определяется в соответствии с условием 3 >0 при Т значение степени дальней упорядоченности. Особый интерес представляет нахождение связи между величиной и энергетическими характеристиками взаимодействия частиц, а также определение свойств системы вблизи точки перехода. [c.345]

    Согласно квантовой механике в силу делокализации электронов и для этих веществ, вероятно, существуют мгновенные диполи. Однако средняя статистическая картина такова, что молекулы и соединения, состоящие из одинаковых атомов, бездииольны и гомеоиолярны. [c.99]

    Оценим вклады различных типов вандерваальсовых взаимодействий в среднюю статистическую потенциальную энергию одного моля жидкой фазы (Здесь и далее волна над символом Е или каким-либо другим буквенным обозначением указывает, что речь идет о величине, отнесенной к одному молю вещества.) Для чистых жидкостей расчет может бьЕть выполнен по формуле [c.31]

    Так как объем сферы V макроскопический, то средаие по объему и средние статистические величины совпадают, т. е. / = это же [c.40]

    Зй -уровней З -элементов представляет собой продолжение незаселенной в нормальных состояниях линии М «Зо -ряда Na — Са «». Это становится особенно ясным, если уровниМ З для элементов, предшествующих скандию, отнести не к самому глубокому положению в мультиплетах 3d, а нанести средние статистические значения, учитывающие все составляющие муль-типлеты. [c.107]

---

chem21.info

Средние величины, применяемые в статистике

По дисциплине: Статистика

Вариант № 2

Средние величины, применяемые в статистике

Содержание

Введение………………………………………………………………………….3

Теоретическое задание

Средняя величина в статистике, ее сущность и условия применения.

1.1. Сущность средней величины и условия применения………….4

1.2. Виды средних величин……………………………………………8

Практическое задание

Задача 1,2,3………………………………………………………………………14

Заключение……………………………………………………………………….21

Список используемой литературы………………………………………………23

Данная контрольная работа состоит из двух частей – теоретической и практической. В теоретической части будет подробно рассмотрена такая важная статистическая категория как средняя величина с целью выявления её сущности и условий применения, а также выделения видов средних и способов их расчёта.

Статистика, как известно, изучает массовые социально-экономические явления. Каждое из этих явлений может иметь различное количественное выражение одного и того же признака. Например, заработная плата одной и той же профессии рабочих или цены на рынке на один и тот же товар и т.д. Средние величины характеризуют качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др.

Для изучения какой-либо совокупности по варьирующим (количественно изменяющимся) признакам статистика использует средние величины.

Сущность средней величины

Средняя величина — это обобщающая количественная характеристика совокупности однотипных явлений по одному варьирующему признаку. В экономической практике используется широкий круг показателей, вычисленных в виде средних величин.

Важнейшее свойство средней величины заключается в том, что она представляет значение определенного признака во всей совокупности одним числом, несмотря на количественные различия его у отдельных единиц совокупности, и выражает то общее, что присуще всем единицам изучаемой совокупности. Таким образом, через характеристику единицы совокупности она характеризует всю совокупность в целом.

Средние величины связаны с законом больших чисел. Суть этой связи заключается в том, что при осреднении случайные отклонения индивидуальных величин в силу действия закона больших чисел взаимопогашаются и в средней выявляется основная тенденция развития, необходимость, закономерность. Средние величины позволяют сравнивать показатели, относящиеся к совокупностям с различной численностью единиц.

В современных условиях развития рыночных отношений в экономике средние служат инструментом изучения объективных закономерностей социально-экономических явлений. Однако в экономическом анализе нельзя ограничиваться лишь средними показателями, так как за общими благоприятными средними могут скрываться и крупные серьезные недостатки в деятельности отдельных хозяйствующих субъектов, и ростки нового, прогрессивного. Например, распределение населения по доходу позволяет выявлять формирование новых социальных групп. Поэтому наряду со средними статистическими данными необходимо учитывать особенности отдельных единиц совокупности.

Средняя величина являются равнодействующей всех факторов, оказывающих влияние на изучаемое явление. То есть, при расчете средних величин взаимопогашаются влияние случайных (пертурбационных, индивидуальных) факторов и, таким образом, возможно определение закономерности, присущей исследуемому явлению. Адольф Кетле подчеркивал, что значение метода средних величин состоит в возможности перехода от единичного к общему, от случайного к закономерному, и существование средних величин является категорией объективной действительности.

Статистика изучает массовые явления и процессы. Каждое из таких явлений обладает как общими для всей совокупности, так и особенными, индивидуальными свойствами. Различие между индивидуальными явлениями называют вариацией. Другое свойство массовых явлений — присущая им близость характеристик отдельных явлений. Итак, взаимодействие элементов совокупности приводит к ограничению вариации хотя бы части их свойств. Эта тенденция существует объективно. Именно в её объективности заключается причина широчайшего применения средних величин на практике и в теории.

Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчёте на единицу качественно однородной совокупности.

В экономической практике используется широкий круг показателей, вычисленный в виде средних величин.[1]

С помощью метода средних величин статистика решает много задач.

Главное значение средних состоит в их обобщающей функции, то есть замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений.

Если средняя величина обобщает качественно однородные значения признака, то она является типической характеристикой признака в данной совокупности.

Однако неправильно сводить роль средних величин только к характеристике типичных значений признаков в однородных по данному признаку совокупностях. На практике значительно чаще современная статистика использует средние величины, обобщающие явно однородные явления.

Средняя величина национального дохода на душу населения, средняя урожайность зерновых культур по всей стране, среднее потребление разных продуктов питания – это характеристики государства как единой народнохозяйственной системы, это так называемые системные средние.[2]

Системные средние могут характеризовать как пространственные или объектные системы, существующие одномоментно (государство, отрасль, регион, планета Земля и т.д.), так и динамические системы, протяжённые во времени (год, десятилетие, сезон и т.д.).

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Например, курс акций корпорации в целом определяется ее финансовым положением. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу. Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.

Вычисление среднего — один из распространённых приёмов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости.

Средняя – это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает.[3]

Каждая средняя характеризует изучаемую совокупность по какому-либо одному признаку, но для характеристики любой совокупности, описания её типических черт и качественных особенностей нужна система средних показателей. Поэтому в практике отечественной статистики для изучения социально-экономических явлений, как правило, исчисляется система средних показателей. Так, например, показатель средней заработной платы оцениваются совместно с показателями средней выработки, фондовооружённости и энерговооружённости труда, степенью механизации и автоматизации работ и др.

Средняя должна вычисляться с учётом экономического содержания исследуемого показателя. Поэтому для конкретного показателя, используемого в социально экономическом анализе, можно исчислить только одно истинное значение средней на базе научного способа расчёта.

Средняя величина это один из важнейших обобщающих статистических показателей, характеризующий совокупность однотипных явлений по какому-либо количественно варьирующему признаку. Средние в статистике это обобщающие показатели, числа, выражающие типичные характерные размеры общественных явлений по одному количественно варьирующему признаку.

Виды средних величин

Виды средних величин различаются прежде всего тем, какое свойство, какой параметр исходной варьирующей массы индивидуальных значений признака должен быть сохранен неизменным.

Средняя арифметическая

Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объём признака в совокупности остаётся неизменным. Иначе можно сказать, что средняя арифметическая величина – среднее слагаемое. При её вычислении общий объём признака мысленно распределяется поровну между всеми единицами совокупности.

Средняя арифметическая применяется, если известны значения осредняемого признака (х) и количество единиц совокупности с определённым значением признака (f).

Средняя арифметическая бывает простой и взвешенной.

Средняя арифметическая простая

Простая используется, если каждое значение признака х встречается один раз, т.е. для каждого х значение признака f=1, или если исходные данные не упорядочены и неизвестно, сколько единиц имеют определённые значения признака.

Формула средней арифметической простой имеет вид:

,

mirznanii.com

Средние статистические величины — Мегаобучалка

 

Анализ данных правовой статистики невозможен без использования средних величин и связанных с ними показателей вариации. Только при помощи средних величин можно охарактеризовать совокупности по количественному варьирующему признаку, по которому их принято сравнивать.

Средней величиной в статистике называется обобщенная характеристика совокупности однородных явлений по какому-либо одному количественно варьирующему признаку в условиях места и времени.

Она обычно обобщает количественную вариацию признака. За любой средней величиной скрывается ряд распределения единиц совокупности по изучаемому признаку, т. е. вариационный ряд.

Одним из важных условий расчета средних величин является качественная однородность единиц совокупности в отношении осредняемого признака. Средние величины, которые вычислены для явлений разного типа, представляют собой фикцию. Они могут искажать или стирать различия разнородных совокупностей.

Практически и теоретически в криминологии, социологии права и других юридических дисциплинах допустимы в основном групповые средние, т. е. средние, которые вычислены на основе адекватных статистических группировок.

Средние величины базируются на массовом обобщении фактов. Только так они способны выявлять те или иные тенденции, которые лежат в основе наблюдаемого процесса. Средние величины отражают самую общую закономерность, которая присуща всей массе изучаемых явлений. Она видна в типичной количественной характеристике, так называемой средней величине всех варьирующих показателей.

Средние статистические величины имеют несколько видов, но все они входят в класс степенных средних, т. е. средних, построенных из различных степеней вариантов: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая и т. д.

При расчете различных степенных средних все основные показатели, на основе которых осуществляется расчет, не изменяются.

Разные виды средних при одних и тех же исходных показателях имеют

в связи с различными значениями степени далеко не одинаковые численные значения.

Чем меньше степень средней, тем меньше значение, соответствующее средней – это закономерность. Поэтому каждая средняя приведенного ряда мажорантна в отношении средних, которые стоят справа от нее. Все это называется правилом мажорантности средних.

Выбор обычной средней или взвешенной осуществляется статистическим материалом, а выбор вида степенной – целью исследования.

Кроме средних степенных, в правовой статистике применяются средние структурные, в качестве которых выступают мода и медиана.

Самым распространенным видом средней величины является средняя арифметическая. Она рассчитывается очень просто: сумму величин всех вариантов делят на общее число единиц вариантов.

Средняя арифметическая при дискретном вариационном ряде исчисляется по формуле средней арифметической взвешенной. Она не имеет принципиальных отличий от простой средней арифметической. В ней лишь суммирование одного и того же значения заменено умножением этого значения на его частоту. Таким образом, каждое значение взвешивается по частоте встречаемости. Когда частоты исчисляются сотнями и тысячами, то использование средней взвешенной намного упрощает расчет.

При расчете средней арифметической совсем не обязательно знать величину каждого индивидуального значения или иметь в своем распоряжении построенный на основе этих вариант вариационный ряд.

В официальной отчетности юридических учреждений обычно уже имеются многие суммарные величины. Суммирование происходит последовательно

в районах, городах, субъектах Федерации и в центре при сводке и группировке данных, которые получены из документов первичного учета.

Расчет средней на основе обобщенных в отчете данных осуществим, когда каждое отдельное значение варианты вообще не фиксируется. Поэтому можно сказать, что между средними и относительными величинами иногда

не существует строгих границ. Все они являются обобщающими. Кроме того, любая средняя величина представляет собой своеобразное отношение

двух абсолютных величин, т. е. она одновременно является определенной относительной величиной. Но, с другой стороны, любая относительная величина дает своеобразную усредненную характеристику процесса.

Существуют некоторые особенности и трудности для расчета средней арифметической при интервальном ряде статистических показателей, т. е. когда индивидуальные численные варианты сгруппированы в интервалы.

Правовая статистика использует интервальные ряды чаще, чем дискретные. Таким образом, учитываются сроки наказания, сроки следствия, сроки рассмотрения уголовных и гражданских дел, возраст правонаруши-телей и т. д.

С целью упрощения расчета средней арифметической можно использо-вать некоторые ее свойства, которые здесь приводятся без доказательств.

1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты.

2. Если от каждой варианты отнять или прибавить одно и то же число, то новая средняя уменьшится или увеличится на то же число.

3. Если каждую варианту разделить или умножить на какое-либо число, то средняя арифметическая уменьшится или увеличится во столько же раз.

4. Если все частоты разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится.

5. Сумма отклонений вариант от средней арифметической всегда равна нулю.

6. Общая средняя равна средней из частных средних, взвешенной по численности соответствующих частей совокупности.

Следующая средняя – средняя геометрическая – используется для вычисления средних темпов роста и прироста (снижения) наблюдаемых процессов. Исследование этих параметров в динамике преступности, выявленных правонарушителей, раскрываемости, судимости, общего числа заключенных, оправданных, освобожденных от уголовной ответственности, рассмотренных гражданских дел, удовлетворенных и неудовлетворенных исков и других меняющихся во времени юридически значимых процессов и явлений имеет важное значение в науке и практике.

Динамика юридически значимых явлений характеризуется многими показателями, среди которых – средние арифметические и геометрические. Средние арифметические показатели используются для расчета среднегодового абсолютного прироста или снижения, выраженного

в именованных числах. Они важны, но их недостаточно, особенно

в сравнительных целях, для достижения которых большую помощь оказывают темпы роста, прироста и снижения, выраженные в процентах. Расчет этих параметров производится по формуле средней геометрической, но на основе все тех же абсолютных показателей.

Для того, чтобы рассчитать среднегодовые темпы роста и прироста, необходимы абсолютные показатели первого и последнего годов, на базе которых рассчитывается относительная величина динамики в процентах и количество лет. В статистических сборниках и официальной отчетности уже имеются подсчитанные общие итоги и даже проценты роста или снижения наблюдаемого процесса. На основе их и числа лет можно легко найти искомые среднегодовые темпы роста и прироста интересующих процессов.

Мода и медиана. Модой в статистике именуется значение варианта, которое чаще всего встречается в данной совокупности. Иногда могут быть распределения, где все варианты встречаются примерно одинаково часто.

В подобных случаях мода не определяется, так как она практически отсутствует. В других распределениях мода может быть не единственной.

Моду применяют в тех случаях, когда нужно охарактеризовать более часто встречающуюся величину признака.

Определение моды для интервального ряда несколько сложнее, так как, чтобы определить моду, требуется определить модальный интервал данных рядов.

Медианой в статистике называется варианта, которая расположена

в середине ранжированного ряда. Она разделяет упорядоченный ряд пополам. По обе стороны от медианы находится одинаковое число единиц совокупности. При определении значения медианы предполагают, что значение признака в интервале расположено равномерно.

Медиана, которая рассчитана для вариационного ряда с существенно различающимися интервалами, отличается от медианы, исчисленной для того же ряда, но с равными интервалами.

В практике мода и медиана порой используются вместо средней арифметической или вместе с ней. При применении вместе они дополняют друг друга, особенно при совокупности небольшого числа единиц с очень малыми значениями исследуемого признака. Как дополнение к средней арифметической также лучше исчислять моду и медиану, которые, в отличие от средней, не зависят от крайних и характерных для совокупности значений признака. Медиану можно использовать в качестве приближенной средней арифметической, когда совокупность ранжирована и упорядочена, тогда медиана определяется по серединному значению варианты. Поэтому значения других вариант можно и не изменять.

Кроме медианного деления вариационного ряда на две равные части,

в статистике используются и более дробные деления: квартили, которые делят вариационный ряд по сумме частот на 4 равные части, децили – на

10 равных частей и центили – на 100 равных частей. Они употребляются для более выразительных и компактных описаний исследуемого процесса, но

в правовой статистике практически не применяются.

Показатели вариации признака. Средние величины представляют собой важную обобщающую характеристику совокупности по изменяющемуся признаку. Подсчитав их, необходимо уяснить, насколько они показательны, типичны или однородны, ведь одинаковые средние могут характеризировать совершенно разнородные совокупности.

Для того чтобы наши суждения о различиях вариационных рядов были статистически точными, нужно прибегать к показателям отклонений различных вариант от средней.

Первый и наиболее простой показатель вариации – это размах вариации, который исчисляется в виде разности между наибольшими и наименьшими значениями варьирующего признака.

Среднее арифметическое отклонение является второй мерой измерения вариаций признака. В статистическом анализе оно применяется довольно редко. Обычно применяют третий показатель вариации – дисперсию, или средний квадрат отклонений.

Путем извлечения квадратного корня из дисперсии мы получим следующий, четвертый, показатель вариации – среднее квадратическое отклонение.

Дисперсия и среднее квадратическое отклонение являются самыми распространенными показателями вариации изучаемого признака. В правовой статистике их используют при сравнительных статистических исследованиях, для обоснования ошибки репрезентативности выборочного наблюдения,

а также при изучении корреляционных и других статистических связей между признаками фактора и признаками следствия или между причиной и следствием.

Коэффициент вариации является пятым по счету показателем вариации. Он, в отличие от размаха вариации, среднего линейного, среднего квадратического отклонения и дисперсии, выражающихся в абсолютных и именованных числах, является показателем относительным. Коэффициент вариации предоставляет много возможностей для сравнительных изучений, потому что сравнивать, например, средние квадратические отклонения вариационных рядов с разными уровнями непосредственно нельзя. Коэффициент вариации в некоторой мере представляется критерием типичности средней. Если он относительно большой, это значит, что типичность этой средней очень невысока, а если, наоборот, – его значение мало, то средняя является типической и надежной.

 

 

megaobuchalka.ru

Статистическое Среднее

БНБ — Научно-Технический словарь «С» «СТ» — Photogallery — Естественные науки Археология Астрономия Биология Геология Медицина Молекулярная биология Физика Химия — Математика Алгоритмы Теория Приложения — Технология Авиация и машиностроение Высокие технологии Вычислительная техника Нанотехнология Роботехника Энергетика Электроника — Гуманитарные науки История Психология Социология Экономика Философия — Общество Образование Развитие науки Ученые Экология Знания

Значение термина Статистическое Среднее в Научно-Техническом словаре Статистическое Среднее — СТАТИСТИЧЕСКОЕ СРЕДНЕЕ, в статистике — число, результат вычислений, которое дает типичное представление обо всем множестве чисел. Эта величина представляет собой АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ от этих чисел. Для получения представления о типичных величинах некоторого множества чисел определяют также модус (наиболее часто встречающееся число) и промежуточное число, приходящееся на середину диапазона значений всех чисел и разделяющее его на верхнюю и нижнюю части. Рядом со словом Статистическое Среднее в Научно-Техническом словаре Статистическая Механика В начало буква «С» буквосочетание «СТ» Статическое Электричество Статья про Статистическое Среднее была прочитана 2192 раз

— TOP 200 — Импеданс — Цикл Кребса — Этаналь — Классификация Животных — Гермафродит — Типографский Набор — Правило Правой Руки — Суспензия — Синус — Классификация Растений

nts.sci-lib.com

Среднее значение — это… Что такое Среднее значение?

Сре́днее значе́ние — числовая характеристика множества чисел или функций; — некоторое число, заключённое между наименьшим и наибольшим из их значений.

Основные сведения

Исходным пунктом становления теории средних величин явилось исследование пропорций школой Пифагора. При этом не проводилось строгого различия между понятиями средней величины и пропорции. Значительный толчок развитию теории пропорций с арифметической точки зрения был дан греческими математиками — Никомахом Герасским (конец I — начало II в. н. э.) и Паппом Александрийским (III в. н. э.). Первым этапом развития понятия средней является этап, когда средняя стала считаться центральным членом непрерывной пропорции. Но понятие средней как центрального значения прогрессии не дает возможности вывести понятие средней по отношению к последовательности n членов, независимо от того, в каком порядке они следуют друг за другом. Для этой цели необходимо прибегнуть к формальному обобщению средних. Следующий этап — переход от непрерывных пропорций к прогрессиям — арифметической, геометрической и гармонической^[1].

В истории статистики впервые широкое употребление средних величин связано с именем английского ученого У. Петти. У. Петти один из первых пытался придать средней величине статистический смысл, связав её с экономическими категориями. Но описания понятия средней величины, его выделения Петти не произвел. Родоначальником теории средних величин принято считать А. Кетле. Он одним из первых начал последовательно разрабатывать теорию средних величин, пытаясь подвести под неё математическую базу. А. Кетле выделял два вида средних величин — собственно средние и средние арифметические. Собственно средние представляют вещь, число, действительно существующие. Собственно средние или средние статистические должны выводиться из явлений однокачественных, одинаковых по своему внутреннему значению. Средние арифметические — числа, дающие возможно близкое представление о многих числах, различных, хотя и однородных^[2].

Каждый из видов средней может выступать либо в форме простой, либо в форме взвешенной средней. Правильность выбора формы средней вытекает из материальной природы объекта исследования. Формулы простых средних применяются в случае, если индивидуальные значения усредняемого признака не повторяются. Когда в практических исследованиях отдельные значения изучаемого признака встречаются несколько раз у единиц исследуемой совокупности, тогда частота повторений индивидуальных значений признака присутствует в расчетных формулах степенных средних. В этом случае они называются формулами взвешенных средних.^[3]

Иерархия средних значений в математике

• среднее значение функции — понятие, определяемое многими способами.
  • Более конкретно, но на основе произвольных функций, определяются средние Колмогорова для набора чисел.
• Среднее взвешенное — обобщение средней величины на случай произвольной линейной комбинации:
• среднее хронологическое — обобщает значения признака для одной и той же единицы или совокупности в целом, изменяющихся во времени.
• среднее логарифмическое, определяемое по формуле ā=(a₁-a₂)/ln(a₁/a₂), используется в теплотехнике

См. также

Примечания

1. ↑ Джини К. Средние величины. — Москва: Статистика, 1970.
2. ↑ Измайлова М.О., Рахманкулов И.Ш. Категория «средняя величина» и ее методологическое значение в научном исследовании. — Казань: Издательство Казанского университета, 1982.
3. ↑ Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. — Москва: ИНФРА–М, 1996.

Столбчатая диаграмма · Совмещённая диаграмма · Диаграмма управления · Лесная диаграмма · Гистограмма · Q-Q диаграмма · Диаграмма выполнения · Диаграмма разброса · Стебель-листья · Ящик с усами

dikc.academic.ru