Сокращенные формулы умножения – Легкий способ запомнить формулы сокращенного умножения, или… Треугольник Паскаля.
Формулы сокращенного умножения. Примеры.
data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»2890988705″>
1) Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a+b)2 = a2+2ab+b2
a) (x + 2y)2 = x2 + 2 ·x·2y + (2y)2 = x2 + 4xy + 4y2
б) (2k + 3n)2 = (2k)2 + 2·2k·3n + (3n)2 = 4k2 + 12kn + 9n2
2) Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a-b)2 = a2
а) (2a – c)2 = (2a)2-2·2a·c + c2 = 4a2 – 4ac + c2
б) (3a – 5b)2 = (3a)2-2·3a·5b + (5b)2 = 9a2 – 30ab + 25b2
3) Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.
a2–b2 = (a–b)(a+b)
a) 9x2 – 16y2 = (3x)2 – (4y)2 = (3x – 4y)(3x + 4y)
б) (6k – 5n)( 6k + 5n) = (6k)2 – (5n)2 = 36k2 – 25n2
4) Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a+b)3 = a3+3a2b+3ab2+b3
a) (m + 2n)3 = m3 + 3·m2·2n + 3·m·(2n)2 + (2n)3 = m3 + 6m2n + 12mn2 + 8n3
б) (3x + 2y)3 = (3x)3 + 3·(3x)2·2y + 3·3x·(2y)2 + (2y)3 = 27x3 + 54x2y + 36xy2 + 8y3
5) Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a-b)3 = a3-3a2b+3ab2-b3
а) (2x – y)3 = (2x)3-3·(2x)2·y + 3·2x·y2 – y3 = 8x3 – 12x2y + 6xy2 – y3
б) (x – 3n)3 = x3-3·x2·3n + 3·x·(3n)2 – (3n)3 = x3 – 9x2n + 27xn2 – 27n3
6) Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.
a3+b3 = (a+b)(a2–ab+b2)
a) 125 + 8x3 = 53 + (2x)3 = (5 + 2x)(52 — 5·2x + (2x)2) = (5 + 2x)(25 – 10x + 4x2)
б) (1 + 3m)(1 – 3m + 9m2) = 13 + (3m)3 = 1 + 27m3
7) Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.
a3-b3 = (a-b)(a2+ab+b2)
а) 64с3 – 8 = (4с)3 – 23 = (4с – 2)((4с)2 + 4с·2 + 22) = (4с – 2)(16с
б) (3a – 5b)(9a2 + 15ab + 25b2) = (3a)3 – (5b)3 = 27a3 – 125b3
Дорогие друзья! Карта сайта поможет вам выбрать нужную тему.Запись имеет метки: Правила и формулы сокращенного умножения
www.mathematics-repetition.com
Формулы сокращённого умножения | Алгебра
При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются
Формулы сокращённого умножения – это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.
a2 + b2 = (a + b)2 — 2ab – сумма квадратов
a2 — b2 = (a + b)(a — b) – разность квадратов
(a + b)2 = a2 + 2ab + b2 – квадрат суммы
(a — b)2 = a2 — 2ab + b2 – квадрат разности
a3 + b3 = (a + b)(a2 — ab + b2) – сумма кубов
a3 — b3 = (a — b)(a2 + ab + b2) – разность кубов
(a + b)3 = a3 + 3a2b + 3ab2 + b3 – куб суммы
Обратите внимание, что a
и b
в формулах сокращённого умножения могут быть как числами так и выражениями.
Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения:
- Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:
a2 + b2 = (a + b)2 — 2ab
(a + b)2 — 2ab = (a + b)(a + b) — 2ab =
= a2 + ab + ab + b2 — 2ab = a2 + b2
- Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:
a2 — b2 = (a + b)(a — b)
Доказательство:
(a + b)(a — b) = a2 — ab + ab — b2 = a2 — b2
- Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(a + b)2 = a2 + 2ab + b2
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
- Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого числа на второе плюс квадрат второго числа:
(a — b)2 = a2 — 2ab + b2
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a — b)2 = (a
- Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:
a3 + b3 = (a + b)(a2 — ab + b2)
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)(a2 — ab
- Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:
a3 — b3 = (a — b)(a2 + ab + b2)
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a — b)(a2 + ab + b2) = a3 + a2b + ab2 — a2b — ab2 — b3 = a3 — b3
- Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a + b)3 = (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2) =
= a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3
- Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе число плюс утроенное произведение первого числа на квадрат второго минус куб второго числа:
(a — b)3 = a3 — 3a2b + 3ab2 — b3
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a — b)3 = (a — b)(a — b)2 = (a — b)(a2 — 2ab + b2) =
= a3 — 2a2b + ab2 — a2b + 2ab2 — b3 = a3 — 3a2b + 3ab2 — b3
Неполный квадрат суммы
Выражение:
a2 + 2ab + b2
это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:
a2 + ab + b2
которое называется неполным квадратом суммы. Неполный квадрат суммы – это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.
Неполный квадрат разности
Выражение:
a2 — 2ab + b2
это квадрат разности, которое также называется полным квадратом разности, относительно выражения:
a2 — ab + b2
которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа минус произведение первого числа на второе плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.
naobumium.info
Формулы сокращенного умножения
Формулы сокращенного умножения| Номер | Название формулы | Короткая запись | Раскрытие скобок/разложение на множители |
| (1) | Разность квадратов | a2-b2 | (a-b)(a+b) |
| (2) | Квадрат суммы/разности | (a±b)2 | a2±2ab+b2 |
| (3) | Квадрат суммы для n переменных | (a1+a2+…+an)2 | a12+a22+…+an2+2∑i,jaiaj |
| (4) | Сумма/разность кубов | a3±b3 | (a±b)(a2∓ab+b2) |
| (5) | Куб суммы/разности | (a±b)3 | a3±3a2b+3ab2±b3 |
| (6) | Куб суммы для n переменных | (a1+a2+…+an)3 | a13+a23+…+an3+3∑i,jai2aj+6∑i,j,kaiajak |
| (7) | Разность четвертых степеней | a4-b4 | (a-b)(a+b)(a2+b2) |
| (8) | Четвертая степень суммы/разности | (a±b)4 | a4±4a3b+6a2b2±4ab3+b4 |
| (9) | Сумма/разность nх степеней | an-bn | (a±b)(an-1+an-2b+an-3b2+…+bn-3a2+bn-2a+bn-1) |
| (10) | Сумма (2n+1)х степеней | a2n+1+b2n+1 | (a+b)(a2n-a2n-1b+a2n-2b2+…+b2n-2a2-b2n-1a+b2n) |
| (11) | Nая степень суммы/разности | (a±b)n | an±(n1)an-1b+(n2)an-2b2±..+(nn-2)a2bn-2±(nn-1)abn-1+bn |
— версия для печати
- Определение
- Nая степень числа — результат умножения числа на себя n раз. Также квадратом числа называется результат возведения числа в степень n (в nую степень).
- Пример:
- (4a—3b)3 = 64a3 — 144a2b + 108ab2 — 27b3
- Пояснение
- Под (nk) подразумевается биномиальный коэффициент, равный
| Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью. |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016
scolaire.ru
Все формулы сокращенного умножения
Квадрат суммы
Квадрат разности
Разность квадратов
Куб суммы
Куб разности
Сумма кубов
Разность кубов
Разность n степеней
- Подробности
- Автор: Administrator
www-formula.ru
Персональный сайт — Формулы сокращенного умножения
При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения. Всего таких формул семь. Их все необходимо знать наизусть.
Следует также помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.
Разность квадратов
Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.
a2 — b2 = (a — b)(a + b)
Квадрат суммы
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
(a + b)2 = a2 + 2ab + b2
Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик. Поясним на примере:
Найти 1122.
Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.2
112 = 100 + 1
Запишем сумму чисел в скобки и поставим над скобками квадрат.
1122 = (100 + 12)2
Воспользуемся формулой квадрата суммы:
1122 = (100 + 12)2 = 1002 + 2 x 100 x 12 + 122 = 10 000 + 2 400 + 144 = 12 544
Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.
(8a + с)2 = 64a2 + 16ac + c2
Предостережение!!!
(a + b)2 не равно a2 + b2
Квадрат разности
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.
(a — b)2 = a2 — 2ab + b2
Также стоит запомнить весьма полезное преобразование:
(a — b)2 = (b — a)2
Формула выше доказывается простым раскрытием скобок:
(a — b)2 = a2 — 2ab + b2 = b2 — 2ab + a2 = (b — a)2
Куб суммы
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Запомнить эту «страшную» на вид формулу довольно просто.
Выучите, что в начале идёт a3.
Два многочлена посередине имеют коэффициенты 3.
Вспомним, что любое число в нулевой степени есть 1. (a0 = 1, b0 = 1). Легко заметить, что в формуле идёт понижение степени a и увеличение степени b. В этом можно убедиться:
(a + b)3 = a3b0 + 3a2b1 + 3a1b2 + b3a0 = a3 + 3a2b + 3ab2 + b3
Предостережение!!!
(a + b)3 не равно a3 + b3
Куб разности
Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.
(a — b)3 = a3 — 3a2b + 3ab2 — b3
Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+» и «-». Перед первым членом a3стоит «+» (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «-», затем опять «+» и т.д.
(a — b)3 = + a3 — 3a2b + 3ab2 — b3 = a3 — 3a2b + 3ab2 — b3
Сумма кубов (Не путать с кубом суммы!)
Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.
a3 + b3 = (a + b)(a2 — ab + b2)
Сумма кубов — это произведение двух скобок.
Первая скобка — сумма двух чисел.
Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:
a2— ab + b2
Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.
Разность кубов (Не путать с кубом разности!!!)
Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.
a3 — b3 = (a — b)(a2 + ab + b2)
Будьте внимательны при записи знаков. Следует помнить, что все формулы, приведённые выше, используется также и справа налево.
Трудно запоминаются формулы сокращенного умножения? Делу легко помочь. Нужно просто запомнить, как изображается такая простая вещь, как треугольник Паскаля. Тогда вы вспомните эти формулы всегда и везде, вернее, не вспомните, а восстановите.
Что же такое треугольник Паскаля? Этот треугольник состоит из коэффициентов, которые входят в разложение любой степени двучлена вида в многочлен.
Разложим, например, :
В этой записи легко запоминается, что вначале стоит куб первого, а в конце – куб второго числа. А вот что посередине – запоминается сложно. И даже то, что в каждом следующем слагаемом степень одного множителя все время уменьшается, а второго – увеличивается – несложно заметить и запомнить, труднее дело обстоит с запоминанием коэффициентов и знаков (плюс там или минус?).
Итак, сначала коэффициенты. Не надо их запоминать! На полях тетрадки быстренько рисуем треугольник Паскаля, и вот они – коэффициенты, уже перед нами. Рисовать начинаем с трех единичек, одна сверху, две ниже, правее и левее — ага, уже треугольник получается:
Первая строка, с одной единичкой – нулевая. Потом идет первая, вторая, третья и так далее. Чтобы получить вторую строку, нужно по краям снова приписать единички, а в центре записать число, полученное сложением двух чисел, стоящих над ним:
Записываем третью строку: опять по краям единицы, и опять, чтобы получить следующее число в новой строке, сложим числа, стоящие над ним в предыдущей:
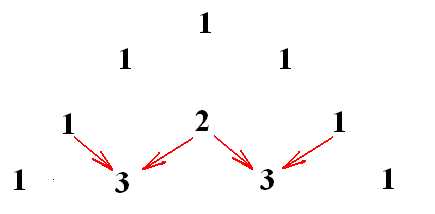
Как вы уже догадались, мы получаем в каждой строке коэффициенты из разложения двучлена в многочлен:
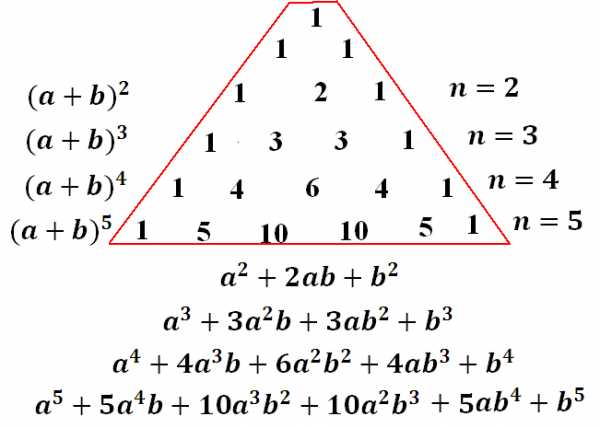
Ну а знаки запомнить еще проще: первый – такой же, как в раскладываемом двучлене (раскладываем сумму – значит, плюс, разность – значит, минус), а дальше знаки чередуются!
Вот такая это полезная штука – треугольник Паскаля. Пользуйтесь!
ychitelll.ucoz.ru
Формулы сокращённого умножения
Формулы сокращенного умножения. Применяются они довольно в широком спектре заданий: сокращение дробей, упрощение выражений, выделение квадрата при работе с квадратичной функцией и другие. Их нужно выучить, первые пять обязательно, они используются наиболее часто. Выводятся они просто. Сами формулы:
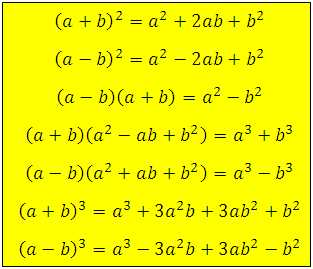
Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй.
Доказательство:
Разумеется, справедливо и обратное равенство:
Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй.
Доказательство:
Конечно же, справедливо:
Произведение суммы двух величин на их разность равно разности их квадратов.
Доказательство:
При преобразованиях часто используют:
*То есть если в условии имеется разность квадратов двух величин (или выражений), далее можно выполнить преобразование в произведение суммы и разности этих величин, затем полученное произведение уже используется в вычислительном процессе в зависимости от поставленного условия.
Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов.
*Квадрат разности (см выше) равен a2–2ab+b2, а выражение a2–ab+b2 называется неполным квадратом разности.
Доказательство:
Имеет место быть и равенство:
Произведение разности двух величин на неполный квадрат суммы равно разности их кубов.
*Квадрат суммы равен a2+2ab+b2, а выражение a2+ab+b2 называется неполным квадратом суммы.
Доказательство:
Имеет место быть и равенство:
Куб суммы двух величин равен кубу первой плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй.
Доказательство:
Имеет место быть и равенство:
Куб разности двух величин равен кубу первой минус утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй минус куб второй.
Доказательство:
Имеет место быть и обратное равенство:
В некоторых источниках указанные выше формулы представлены в следующем виде:
Очень часто приведение многочлена к стандартному виду («свернуть» его) можно осуществить путём применения формул сокращённого умножения. Скоро материал будет дополнен примерами.
С уважением, Александр.
*Делитесь информацией о сайте в социальных сетях.
matematikalegko.ru
Формулы сокращенного умножения
Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения. Формулы сокращенного умножения нужно знать наизусть.
Пусть а, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b)2 = a2 + 2ab + b2
2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a — b)2 = a2 — 2ab + b2
3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
a2 — b2 = (a -b) (a+b)
4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a — b)3 = a3 — 3a2b + 3ab2 — b3
6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.
a3 + b3 = (a + b) (a2 — ab + b2)
7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.
a3 — b3 = (a — b) (a2 + ab + b2)
8. Разность чисел в четвертой степени
(a — b)4 = a4 — 4a3b + 6a2b2 — 4ab3 + b4
9. Сумма чисел в четвертой степени
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
10. Разность чисел в пятой степени
(a — b)5 = a5 — 5a4b + 10a3b2 — 10a2b3 + 5ab4 — b5
11. Сумма чисел в пятой степени
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
12. Квадрат трехчлена
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
13. Квадрат линейной формы
(a + b + c + … + u + v)2 = a2 + b2 + c2 + … + u2 + v2 + 2(ab + ac + … + au + av + bc + … + bu + bv + … + uv)
14. Куб трехчлена
(a + b + c)3 = a3 + b3 + c3 + 3a2b + 3ab2 + 3a2c + 3ac2 + 3b2c + 3bc2 + 6abc
formuly-sokrashhennogo-umnozheniya.ru
