Система векторов – Линейная зависимость системы векторов и коллинеарные векторы: условия, свойства, примеры коллинеарности
Системы векторов.
Рассмотрим систему векторовa 1,a 2 , ,a k . Нулевая линейная комбинация 0a 1 + 0a 2 + + 0a k =0, имеющая только нулевые коэффициенты, называется тривиальной линейной комбинацией векторов этой системы.
Существуют ли
нетривиальные линейные комбинации
векторов системы a 1,a 2 ,
,a k , равные
нулевому вектору0?
Ответ на этот вопрос зависит от свойств
самой системы векторовa 1,a 2 ,
,a k
Система векторовa 1,a 2 , ,a k называется линейно зависимой, если существует нетривиальная нулевая линейная комбинация ее векторов, то есть существует линейная комбинация 1a 1 + 2a 2 + + ka k =0, в которой хотя бы один из коэффициентов отличен от нуля.
Система векторовa 1,a 2 ,
,a k называется линейно
независимой,
если не существует нетривиальной нулевой
линейной комбинации ее векторов, то
есть из равенства
1 = 2 = = k = 0.
Например, линейно зависимой является система, состоящая из двух коллинеарных векторов в R2 или в R3, система из трех компланарных векторов в R3. Любые два неколлинеарных вектора в R2 или в R3, а также три некомпланарных вектора в R3 образуют линейно независимую систему.
Докажите это в качестве упражнения.
ОСНОВНЫЕ УТВЕРЖДЕНИЯ О ЛИНЕЙНО ЗАВИСИМЫХ СИСТЕМАХ.
УТВЕРЖДЕНИЕ 1.
Система, состоящая из одного вектораa, линейно зависима тогда и только тогда, когдаa =0.
ДОКАЗАТЕЛЬСТВО.
Пусть система, состоящая из одного вектораa, линейно зависима, то есть существует линейная комбинация a =0, в которой 0. Тогдаa =0.
Обратно. Еслиa =0, то 1a =0. Существование этой линейной комбинации доказывает линейную зависимость системы.
УТВЕРЖДЕНИЕ 2.
Для того, чтобы система, состоящая из двух ненулевых векторовa иb, была линейно зависимой, необходимо и достаточно, чтобы векторыa иb были пропорциональны.
ДОКАЗАТЕЛЬСТВО.
Пусть система, состоящая из векторовa иb, линейно зависима. Тогда существует линейная комбинация 1a + 2b =0, в которой 1 0 или
2
0. Тогда либоa = 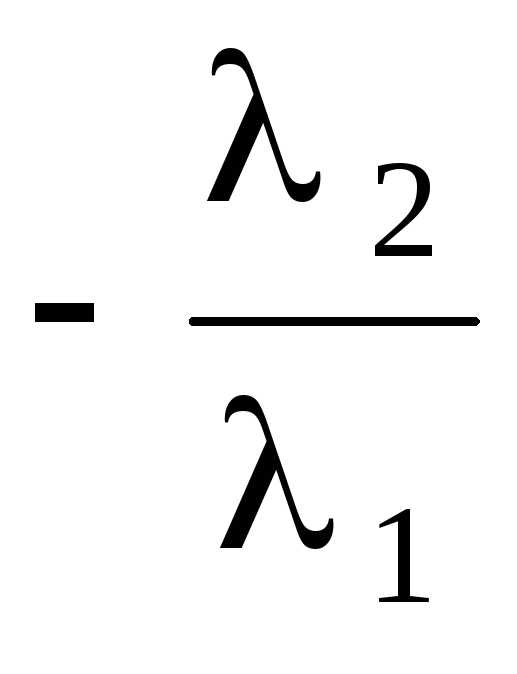 b,
либоb =
b,
либоb = 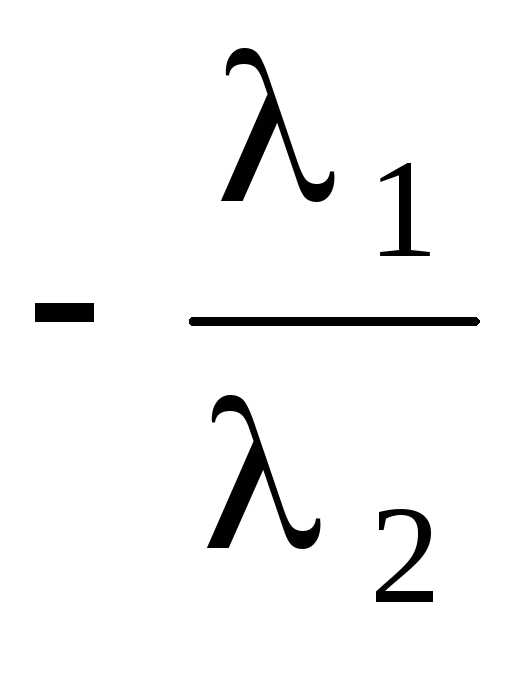
Обратно. Еслиa = b, тоa – b =0, 1 ·a – b =0, 1 0. Поскольку полученная нулевая линейная комбинация содержит ненулевой коэффициент, система, состоящая из векторовa иb, линейно зависима.
УТВЕРЖДЕНИЕ 3.
Если какая-либо часть системы векторов линейно зависима, то вся система линейно зависима.
ДОКАЗАТЕЛЬСТВО.
Пусть в системе векторовa 1,a 2 , ,a m , ,a
a 1,a 2 , ,a m образуют линейно зависимую подсистему. Это означает, что существует линейная комбинация 1a 1 + 2a 2 + + ma m =0, в которой хотя бы один из коэффициентов отличен от нуля. Тогда линейная комбинация
1a 1 + 2a 2 + ma m + 0a m + 1 + + 0a
a 1,a 2 , ,a m , ,a k линейно зависима.
СЛЕДСТВИЯ.
Любая часть линейно независимой системы векторов линейно независима.
Это утверждение легко доказывается рассуждением от противного.
Предполагая, что некоторая часть линейно независимой системы является линейно зависимой, получаем противоречие утверждению 3.
Если в системе векторов имеется нулевой вектор или два пропорциональных (в том числе два равных) вектора, то эта система линейно зависима.
УТВЕРЖДЕНИЕ 4.
Если система векторовa 1,a 2 , ,a k линейно независима, а система
a 1,a 2 , ,a k ,b линейно зависима, то векторb линейно выражается через векторыa 1,a 2 , ,a k .
Так как системаa 1,a 2 , ,a k ,b линейно зависима, то существует линейная комбинация 1a 1 + 2a 2 ++ ka k + 0b =0, в которой хотя бы один из коэффициентов отличен от нуля. Докажем, что 0 0. Действительно, если 0 = 0, то получаем нетривиальную линейную комбинацию
1a 1 + 2
0
0, и b = 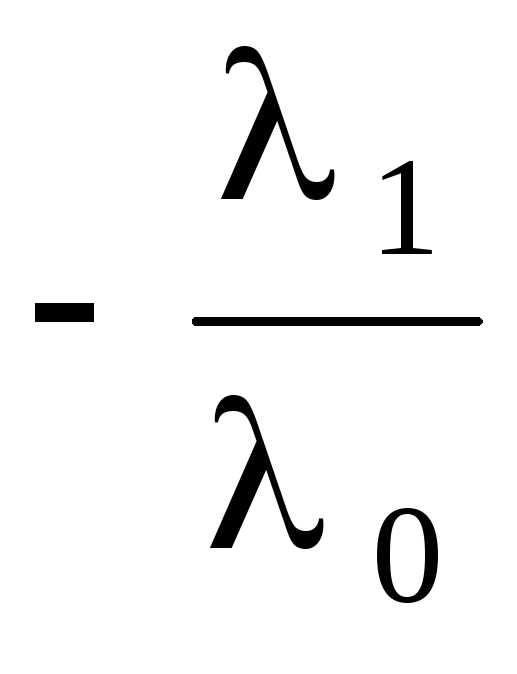 a 1
a 1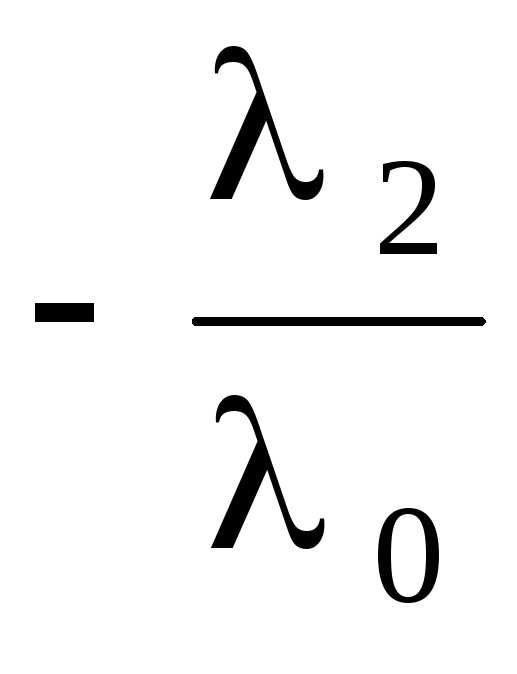 a 2 –
a 2 – 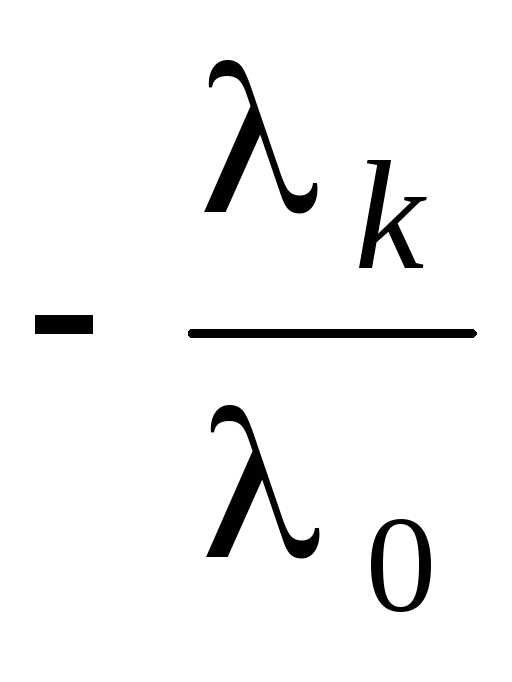 a k , что и требовалось доказать.
a k , что и требовалось доказать.
ТЕОРЕМА. Критерий линейной зависимости.
ДОКАЗАТЕЛЬСТВО.
Пусть система
векторовa 1,a 2 ,
,a k является линейно зависимой. Тогда
существует линейная комбинация 1a 1 + 2a 2 +
+ ka k =0,
в которой хотя бы один из коэффициентов
отличен от нуля. Для определенности
будем считать, что 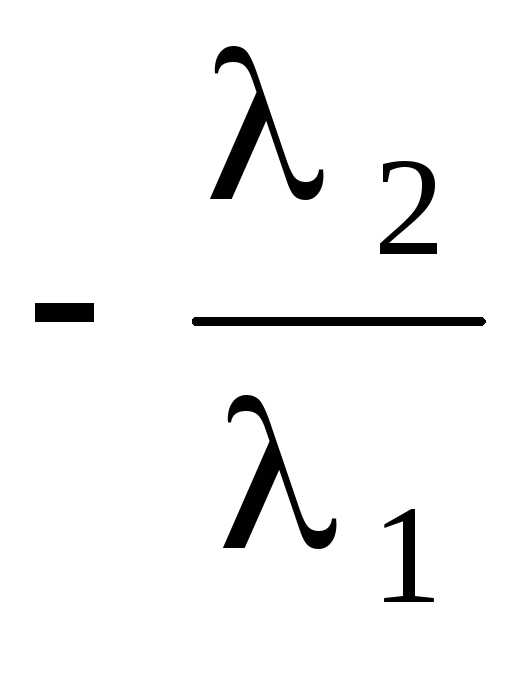 a 2
a 2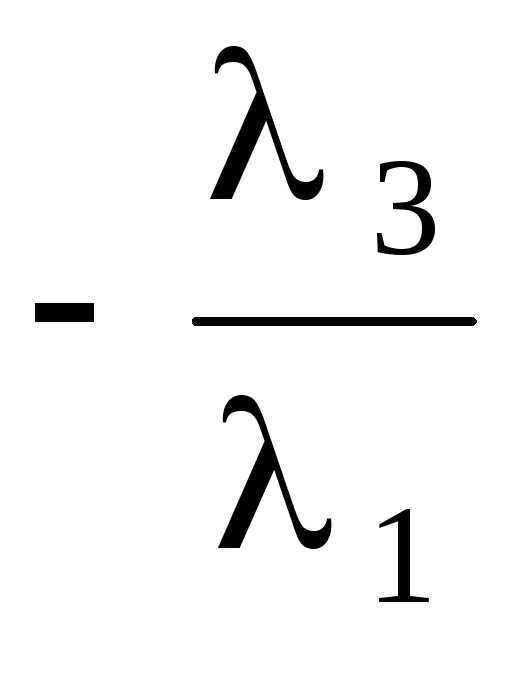 a 3 –
a 3 – 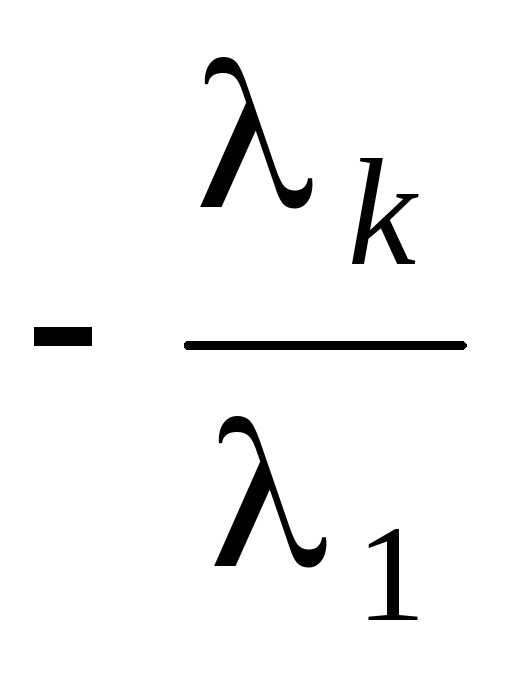 a k,
то
естьa 1 L (a 2 ,a 3 ,
,a k ).
a k,
то
естьa 1 L (a 2 ,a 3 ,
,a k ).
Пусть теперь один
из векторов (например,a 1 )
линейно выражается через остальные, то
естьa 1 = 2a
Тогда линейная комбинацияa 1 – 2a 2 – 3a 3 – – ka k =0 является нетривиальной, и система векторовa 1,a 2 , ,a k линейно зависима. Теорема доказана.
studfiles.net
02 Линейная зависимость и независимость системы векторов
6
Линейная зависимость и независимость векторов
Определения линейно зависимой и независимой систем векторов
Определение 22
Пусть имеем систему из n-векторов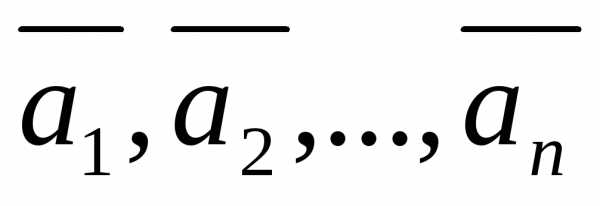 и имеем набор чисел, тогда
и имеем набор чисел, тогда
(11)
называется линейной комбинацией данной системы векторов с данным набором коэффициентов.
Определение 23 (через нулевую линейную комбинацию)
Система векторов 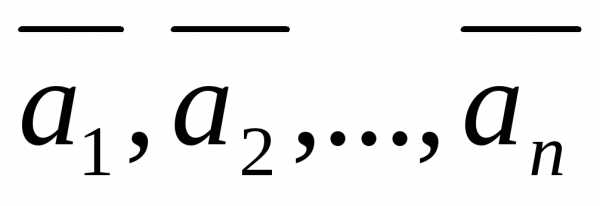 называетсялинейно зависимой,
если существует такой набор коэффициентов,
из которых хотя бы один не равен нулю,
что линейная комбинация данной системы
векторов с этим набором коэффициентов
равна нулевому вектору:
называетсялинейно зависимой,
если существует такой набор коэффициентов,
из которых хотя бы один не равен нулю,
что линейная комбинация данной системы
векторов с этим набором коэффициентов
равна нулевому вектору:
.(12)
Пусть 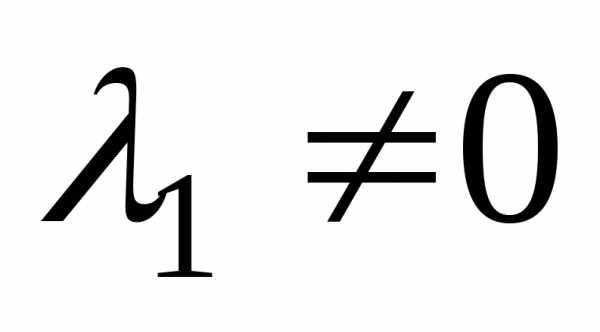 ,
тогда
,
тогда
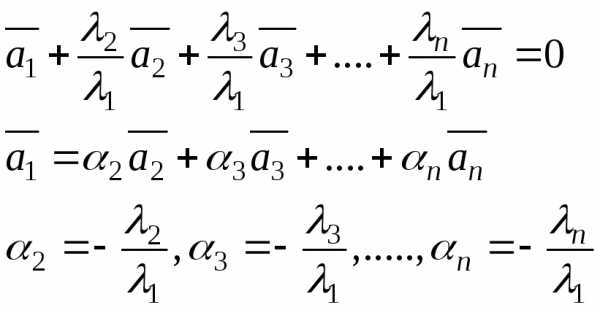
Определение 24 (через представление одного вектора системы в виде линейной комбинации остальных)
Система векторов 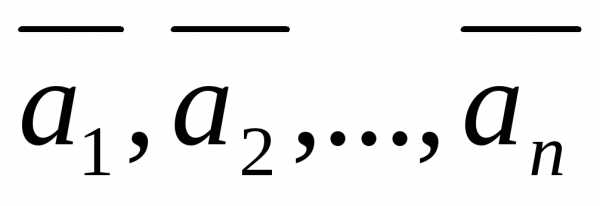 называетсялинейно зависимой,
если хотя бы один из векторов этой
системы можно представить в виде линейной
комбинации остальных векторов этой
системы.
называетсялинейно зависимой,
если хотя бы один из векторов этой
системы можно представить в виде линейной
комбинации остальных векторов этой
системы.
Утверждение 3
Определения 23 и 24 эквивалентны.
Определение 25 (через нулевую линейную комбинацию)
Система векторов 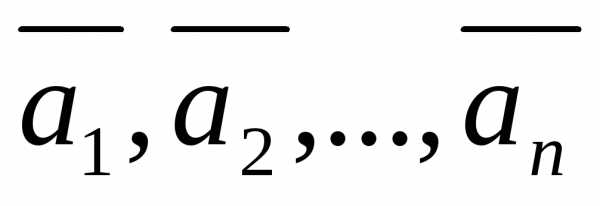 называетсялинейно
независимой, если нулевая линейная
комбинация этой системы возможна лишь
при всехравных нулю.
называетсялинейно
независимой, если нулевая линейная
комбинация этой системы возможна лишь
при всехравных нулю.
Определение 26(через невозможность представления одного вектора системы в виде линейной комбинации остальных)
Система векторов 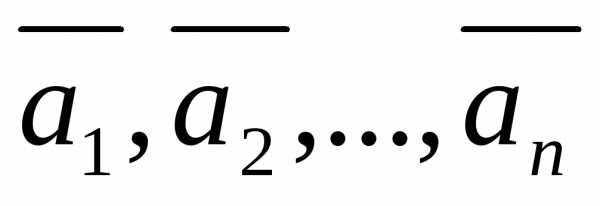 называетсялинейно
независимой, если не один из векторов
этой системы нельзя представить в виде
линейной комбинации других векторов
этой системы.
называетсялинейно
независимой, если не один из векторов
этой системы нельзя представить в виде
линейной комбинации других векторов
этой системы.
Свойства линейно зависимой и независимой систем векторов
Теорема 2 (нулевой вектор в системе векторов)
Если в системе векторов имеется нулевой вектор, то система линейно зависима.
Пусть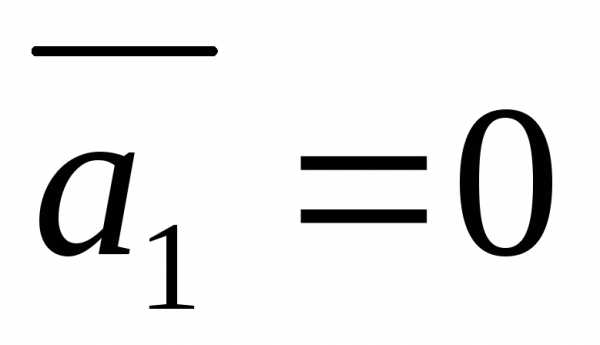 ,
тогда.
,
тогда.
Получим , следовательно, по определению линейно зависимой системы векторов через нулевую линейную комбинацию(12) система линейно зависима.
Теорема 3(зависимая подсистема в системе векторов)
Если в системе векторов имеется линейно зависимая подсистема, то и вся система линейно зависима.
Пусть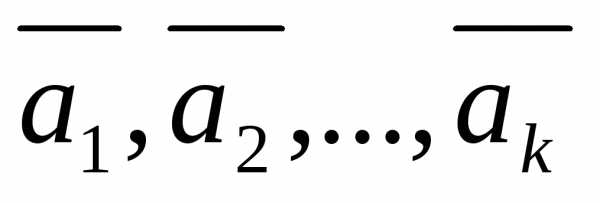 — линейно зависимая подсистема,
среди которых хотя бы одно не равно
нулю:
— линейно зависимая подсистема,
среди которых хотя бы одно не равно
нулю:
Пусть
Значит, по определению 23, система линейно зависима.
Теорема 4
Любая подсистема линейно независимой системы линейно независима.
От противного. Пусть система линейно независима и в ней имеется линейно зависимая подсистема. Но тогда по теореме 3 вся система будет также линейно зависимой. Противоречие. Следовательно, подсистема линейно независимой системы не может быть линейно зависимой.
Геометрический смысл линейной зависимости и независимости системы векторов
Теорема 5
Два вектора  и
и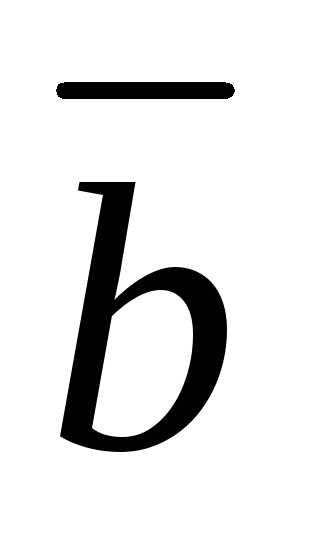 линейно зависимы тогда и только тогда,
когда
линейно зависимы тогда и только тогда,
когда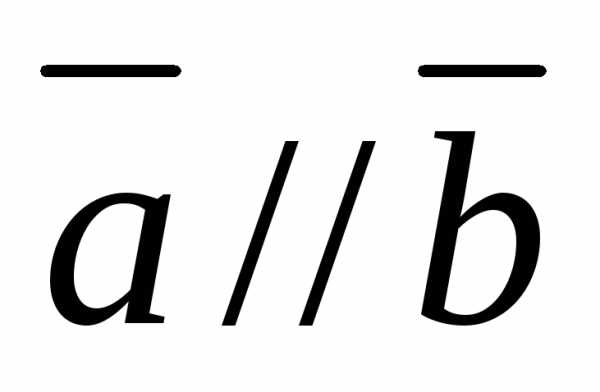 .
.
Необходимость.
 и
и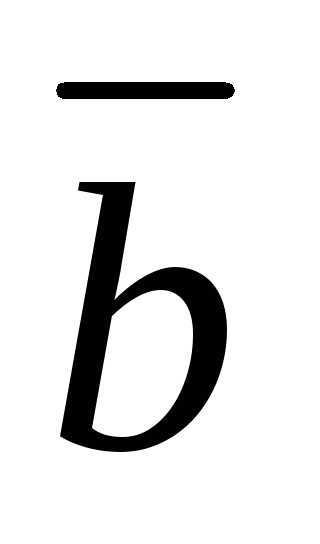 — линейно зависимы,
что выполняется условие.
Тогда
— линейно зависимы,
что выполняется условие.
Тогда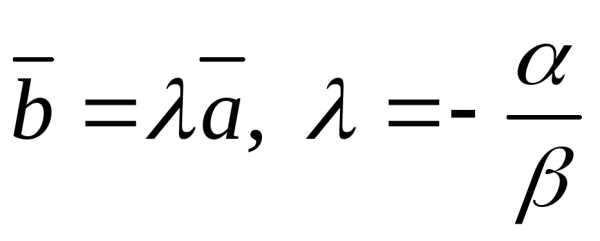 ,
т.е..
,
т.е..
Достаточность.
линейно зависимы.
Следствие 5.1
Нулевой вектор коллинеарен любому вектору
Следствие 5.2
Для того чтобы два вектора были линейно
независимы необходимо и достаточно,
чтобы 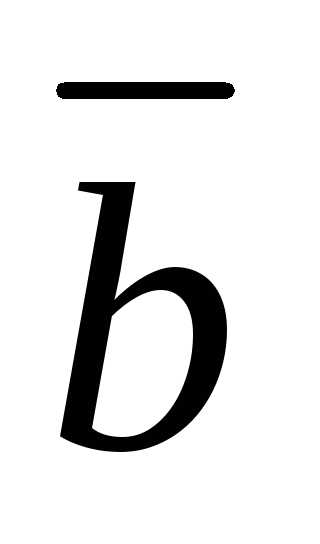 был не коллинеарен
был не коллинеарен .
.
Теорема 6
Для того чтобы система из трёх векторов была линейно зависима необходимо и достаточно, чтобы эти векторы были компланарными.
Необходимость.
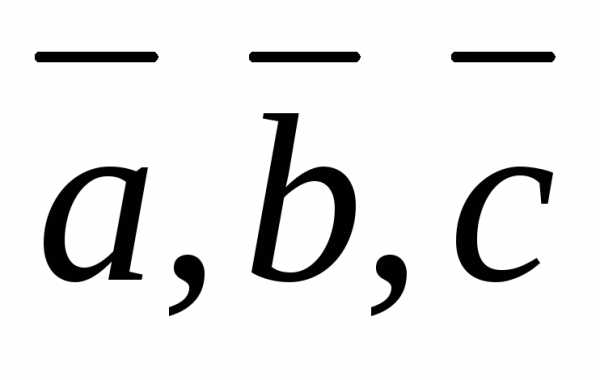 — линейно зависимы, следовательно, один
вектор можно представить в виде линейной
комбинации двух других.
— линейно зависимы, следовательно, один
вектор можно представить в виде линейной
комбинации двух других.
,(13)
где 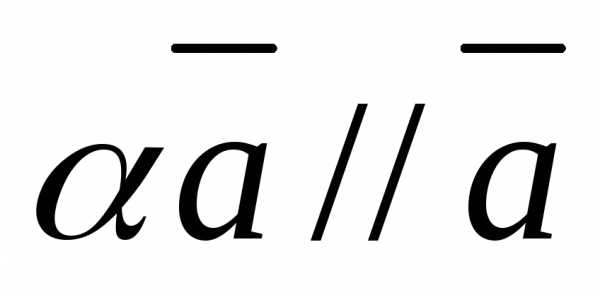 и
и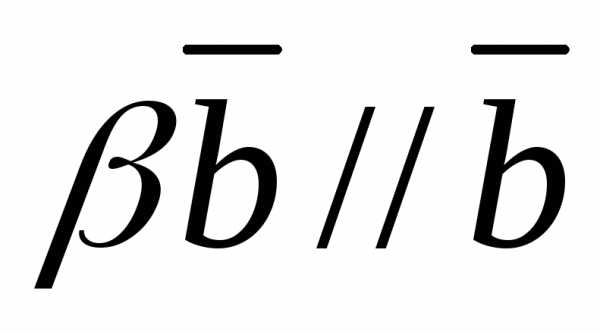 .
По правилу параллелограмма
.
По правилу параллелограмма есть диагональ параллелограмма со
сторонами
есть диагональ параллелограмма со
сторонами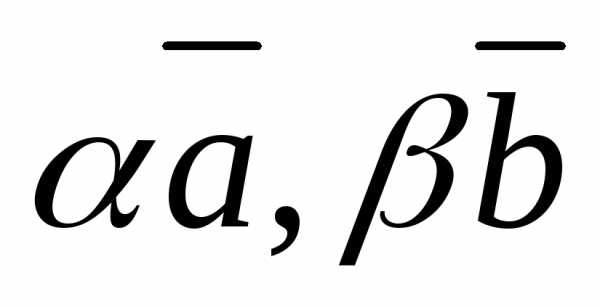 ,
но параллелограмм – плоская фигуракомпланарны
,
но параллелограмм – плоская фигуракомпланарны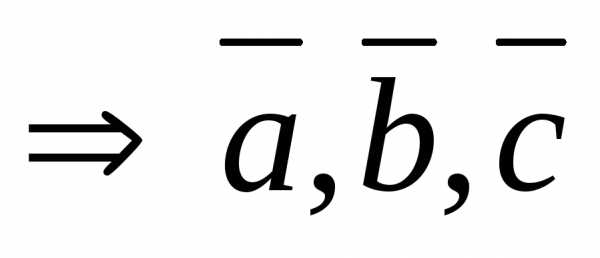 — тоже компланарны.
— тоже компланарны.
Достаточность.
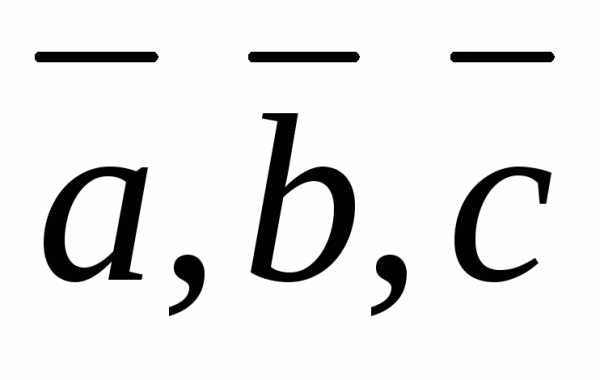 — компланарны. Приложим три вектора к
точке О:
— компланарны. Приложим три вектора к
точке О:
A`
A

 C
C
O
 B`
B`
B
 – линейно зависимы
– линейно зависимы
Следствие 6.1
Нулевой вектор компланарен любой паре векторов.
Следствие 6.2
Для того чтобы векторы 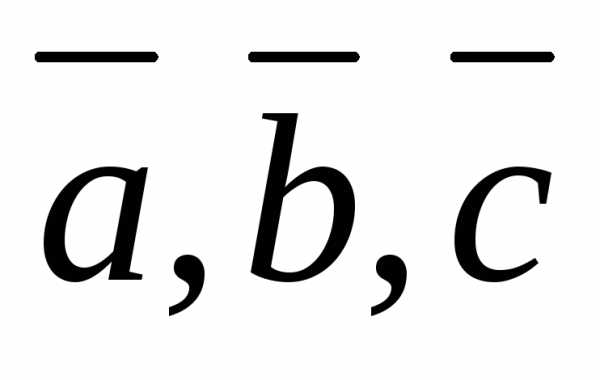 были линейно независимы необходимо и
достаточно, чтобы они были не компланарны.
были линейно независимы необходимо и
достаточно, чтобы они были не компланарны.
Следствие 6.3
Любой вектор плоскости можно представить в виде линейной комбинации любых двух неколлинеарных векторов этой же плоскости.
Теорема 7
Любые четыре вектора в пространстве линейно зависимы.
Рассмотрим 4 случая:
Если среди векторов есть нулевой вектор. Тогда система линейно зависима по теореме 2.
Если среди векторов имеется хотя бы 1 пара коллинеарных векторов. Тогда система линейно зависима по теоремам 5 и 3.
Если среди векторов имеется компланарная тройка векторов. Тогда система линейно зависима по теоремам 6 и 3.
Если среди векторов нет нулевых векторов, коллинеарных пар и компланарных троек. Приложим эти 4 вектора к точкеО.
. Проведем плоскость через векторы, затем плоскость через векторыи плоскость через векторы. Затем проведем плоскости, проходящие через точкуD, параллельные парам векторов;;соответственно. По линиям пересечения плоскостей строим параллелепипедOB1D1C1ABDC.
Рассмотрим OB1D1C1– параллелограмм по построениюпо правилу параллелограмма.
Рассмотрим OADD1– параллелограмм (из свойства параллелепипеда), тогда
EMBED Equation.3 .
По теореме 1 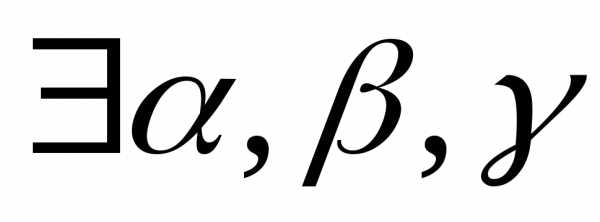 такие, что.
Тогда,
и по определению 24 система векторовлинейно
зависимая.
такие, что.
Тогда,
и по определению 24 система векторовлинейно
зависимая.
Следствие 7.1
Суммой трёх некомпланарных векторов в пространстве является вектор, совпадающий с диагональю параллелепипеда, построенного на этих трёх векторах, приложенных к общему началу, причём начало вектора суммы совпадает с общим началом этих трёх векторов.
Следствие 7.2
Если в пространстве взять 3 некомпланарных вектора, то любой вектор этого пространства можно разложить в линейную комбинацию данных трёх векторов.
studfiles.net
Линейная зависимость и независимость векторов
Определения и формулы линейно зависимых и независимых векторов
Набор векторов называется системой векторов.
Линейной комбинацией системы векторов называется выражение вида
Линейная комбинация (1) называется тривиальной, если все ее коэффициенты равны нулю одновременно:
в противном случае, если хотя бы один из коэффициентов не равен нулю, то линейная комбинация (1) называется нетривиальной.
Например. Нетривиальной линейной комбинацией некоторой системы векторов есть выражение вида
ОПРЕДЕЛЕНИЕ Векторы называются линейно независимыми, если только их тривиальная линейная комбинация равна нулевому вектору. ОПРЕДЕЛЕНИЕ Векторы называются линейно зависимыми, если хотя бы одна их нетривиальная линейная комбинация равна нулевому вектору.
Свойства линейно зависимых и линейно независимых векторов
- Если в систему векторов входит нулевой вектор, то она является линейно зависимой.
- Если в системе векторов имеется два равных вектора, то она линейно зависима.
- Если система векторов содержит два пропорциональных вектора и , то она является линейно зависимой.
- Система из векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.
- Если система векторов линейно независима и после присоединения к ней вектора она становится линейно зависимой, то вектор можно разложить по векторам этой системы и притом единственным образом.
Примеры решения задач
ПРИМЕР| Задание | Исследовать систему векторов на линейную зависимость. |
| Решение |
Три вектора будут линейно зависимыми, если они будут компланарными. Тройка векторов будет компланарна, если смешанное произведение указанных векторов равно нулю:
То есть смешанное произведение не равно нулю, тогда векторы некомпланарные, а тогда они являются линейно независимыми. |
| Ответ | Линейно независимы. |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Базис. Размерность | Математика, которая мне нравится
Будем рассматривать конечно порожденные системы векторов , т.е. существует конечная система векторов таких, что каждый вектор из является их линейной комбинацией. Будем предполагать, что .
Лемма. Существует линейно независимая система.
Возьмем любой ненулевой вектор.
Лемма. Если имеет систему образующих из векторов, то в любой линейно независимой системе число векторов не больше .
Доказательство. Пусть — линейно независимая система векторов, . Каждый вектор является линейной комбинацией векторов образующей системы
По теореме о линейной зависимости линейных комбинаций векторы будут линейно зависимыми.
Определение. Система векторов называется максимальной линейно независимой системой, если она линейно независима и ее нельзя включить в большую линейно независимую систему в качестве подсистемы.
Существование максимальных линейно независимых систем. Возьмем любой вектор . Будем добавлять к нему векторы , так, чтобы все векторы были линейно независимы. Придем к максимальной системе за конечное число шагов.
Определение. Базисом линейного пространства называется система векторов такая, что
1) — система образующих пространства ;
2) — линейно независимая система.
Теорема. Система векторов является базисом линейного пространства тогда и только тогда, когда это максимальная линейно независимая система векторов.
Доказательство.
Пусть — базис . Тогда по определению — линейно независимая система векторов. Любой вектор представим в виде линейной комбинации , т.е. любая большая система векторов линейно зависима, т.е. для векторов
Значит, базис — максимальная линейно независимая система.
Пусть — максимальная линейно независимая система. Второе свойство базиса выполняется. Любая большая система векторов линейно зависима:
т.е. каждый вектор является линейной комбинацией векторов этой системы — выполнено первое свойство.
Теорема. Базис линейного пространства может быть выбран из любой системы образующих.
Доказательство. Пусть . Выберем максимальную линейно независимую систему из векторов . Пусть это векторы .
Тогда система векторов , где , линейно зависима, иначе исходная не была бы максимальной. Тогда
Для любого вектора
Тогда система векторов — система образующих.
Теорема. В каждом базисе линейного пространства содержится одно и то же число векторов.
Доказательство. Пусть — базисы. Если , то поскольку каждый вектор можно представить в виде линейной комбинации векторов , то число линейных комбинаций больше числа комбинируемых векторов. Противоречие. Отсюда .
Определение. Число векторов в базисе линейного пространства называется размерностью линейного пространства.
Обозначение .
Если , то .
Теорема. Если , то любые линейно независимых векторов образуют базис.
Доказательство. Это максимальная линейно независимая система векторов.
Теорема. Разложение каждого вектора по базисным единственно.
Доказательство. Предположим противное. Пусть вектор раскладывается по базисным векторам двумя способами:
Векторы линейно независимы. Тогда
Определение. Коэффициенты в разложении вектора по базисным векторам называются координатами вектора в базисе .
Каждому вектору в фиксированном базисе соответствует один и только один столбец координат.
При сложении векторов складываем столбцы координат, при умножении на число — каждую координату умножаем на это число.
Задачи.
1. Найдите базис и размерность линейного пространства трехмерных вектор-столбцов, у которых вторая координата нулевая.
2. Найдите какой-нибудь базис и размерность линейного пространства всех векторов плоскости, начала и концы которых лежат на данной прямой.
3. Найдите все базисы системы векторов
hijos.ru
Базис системы векторов. Аффинные координаты
Определение 3. Векторное пространство называется n-мерным, если в нём существует в точности n линейно независимых векторов.
Базисом n-мерного пространства называется любая система из n независимых векторов этого пространства.
Пример 1. Доказать, что векторы
образуют базис в четырёхмерном пространстве.
Решение. Система векторов образует базис, если: 1) количество векторов равно размерности пространства; 2) эти векторы линейно независимы. Первое требование выполнено, остаётся доказать, что эти векторы линейно независимы. Попытаемся составить из них линейную нулевую комбинацию:
Подставим в это равенство вместо данных векторов их выражения в координатах и преобразуем левую часть:
или
Но вектор является нулевым, когда все его проекции равны нулю, т.е.
Таким образом, из данных векторов невозможно составить нулевую линейную комбинацию, у которой хотя бы один коэффициент был отличен от нуля. Поэтому векторы
линейно независимы и, следовательно, образуют базис в четырёхмерном пространстве.
Аналогичным образом определяется разложение вектора по базису на плоскости: базис образуется двумя векторами, а координат разложенного по базису вектора также две.
Основное значение базиса состоит в том, что линейные операции над векторами при задании базиса становятся обычными линейными операциями над числами — координатами этих векторов.
Пример 2 Разложить вектор
по базису где
Решение. Рассматриваемые векторы принадлежат двумерному пространству: базис в этом пространстве должен состоять из двух векторов. В примере 7 установлено, что векторы
и
линейно независимы и, следовательно, образуют базис. Запишем разложение вектора по этому базису:
Чтобы найти значения и , подставим в это разложение выражения векторов , и через координаты:
Выполнив преобразования в правой части равенства, получим
или
Равенство векторов означает равенство их соответствующих координат, т.е.
откуда
Следовательно, разложение вектора по базису , имеет вид
Замечание. В каждом векторном пространстве существует бесконечное множество различных базисов и в различных базисах один и тот же вектор имеет различные разложения (подобно тому, как точка имеет различные координаты в различных системах коорднат).
Аффинные координаты в пространстве определяются заданием базиса , , и некоторой точки O, называемой началом координат.
Аффинными координатами любой точки M называются координаты вектора (относительно базиса , , .)
Поделиться с друзьями
Начало темы «Векторы»
Продолжение темы «Векторы»
function-x.ru
Линейная зависимость векторов. Базис системы векторов. Основы линейной алгебры
Линейная зависимость векторов
Выражение видаλ1*A1+λ2*A2+…+λn*An называется линейной комбинацией векторов A1, A2,…,An с коэффициентами λ1, λ2,…,λn.
Определение линейной зависимости системы векторов
Система векторов A1, A2,…,An называется линейно зависимой, если существует ненулевой набор чисел λ1, λ2,…,λn, при кᴏᴛᴏᴩом линейная комбинация векторов λ1*A1+λ2*A2+…+λn*An равна нулевому вектору, то есть система уравнений: A1x1+A2x2+…+Anxn =Θ имеет ненулевое решение.
Набор чисел λ1, λ2,…,λnбудет ненулевым, если хотя бы одно из чисел λ1, λ2,…,λn отлично от нуля.
Определение линейной независимости системы векторов
Пример 29.1Система векторов A1, A2,…,An называется линейно независимой, если линейная комбинация данных векторов λ1*A1+λ2*A2+…+λn*An равна нулевому вектору только при нулевом наборе чисел λ1, λ2,…,λn, то есть система уравнений: A1x1+A2x2+…+Anxn =Θ имеет единственное нулевое решение.
Проверить, будет ли линейно зависимой система векторов
Решение:
1. Составляем систему уравнений:
2. Решаем ее методом Гаусса. Преобразования Жордано системы приведены в таблице 29.1. При расчете правые части системы не записываются так как они равны нулю и при преобразованиях Жордана не изменяются.
3. Из последних трех строк таблицы записываем разрешенную систему, равносильную исходной системе:
4. Стоит сказать — получаем общее решение системы:
5. Задав по ϲʙᴏему усмотрению значение ϲʙᴏбодной переменной x3 =1, получаем частное ненулевое решение X=(-3,2,1).
Ответ: Исходя из всего выше сказанного, мы приходим к выводу, что при ненулевом наборе чисел (-3,2,1) линейная комбинация векторов равняется нулевому вектору -3A1+2A2+1A3=Θ. Следовательно, система векторов линейно зависимая.
Свойства систем векторов
Свойство (1)
В случае если система векторов линейно зависимая, то хотя бы один из векторов разлагается по остальным и, наоборот, если хотя бы один из векторов системы разлагается по остальным, то система векторов линейно зависимая.
Свойство (2)
В случае если какая-либо подсистема векторов линейно зависимая, то и вся система линейно зависимая.
Свойство (3)
В случае если система векторов линейно независимая, то любая ее подсистема линейно независимая.
Свойство (4)
Любая система векторов, содержащая нулевой вектор, линейно зависимая.
Свойство (5)
Система m-мерных векторов всегда будет линейно зависимой, если число векторов n больше их размерности (n>m)
Базис системы векторов
Базисом системы векторов A1 , A2 ,…, An называется такая подсистема B1, B2 ,…,Br(каждый из векторов B1,B2,…,Br будет одним из векторов A1 , A2 ,…, An), кᴏᴛᴏᴩая удовлетворяет следующим условиям:
1. B1,B2,…,Br линейно независимая система векторов;
2. любой вектор Ajсистемы A1 , A2 ,…, An линейно выражается через векторы B1,B2,…,Brr — число векторов входящих в базис.
Отметим, что теорема 29.1 О единичном базисе системы векторов.В случае если система m-мерных векторов содержит m различных единичных векторов E1 E2 ,…, Em , то они образуют базис системы.
Алгоритм нахождения базиса системы векторов
Для того, ɥᴛᴏбы найти базис системы векторов A1 ,A2 ,…,An необходимо:
- Составить ϲᴏᴏᴛʙᴇᴛϲᴛʙующую системе векторов однородную систему уравнений A1x1+A2x2+…+Anxn =Θ
- Привести эту систему
xn--80aatn3b3a4e.xn--p1ai
Базис векторного пространства » ProcMem.Ru Линейная Алгебра
Определение. Система векторов векторного пространства над полем К называется порождающей (образующей) системой векторов этого векторного пространства, если она представляет любой его вектор, т.е. если найдется такой набор скаляров , что .
Определение. Система векторов векторного пространства называется минимальной порождающей системой, если при удалении из этой системы любого вектора она перестает быть порождающей системой.
Замечание. Из определения сразу же следует, что если порождающая система векторов не является минимальной, то найдется хотя бы один вектор системы, при удалении которого из системы, оставшаяся система векторов по прежнему будет порождающей.
Лемма (О линейно зависимой порождающей системе.)
Если в линейно зависимой и порождающей системе векторов один из векторов линейно выражается через другие, то его можно удалить из системы и оставшаяся система векторов будет порождающей.
Доказательство. Пусть система линейно зависимая и порождающая, и пусть один из ее векторов линейно выражается через другие векторы этой системы.
Для определенности и для простоты записи допустим, что
.
Так как – порождающая система, то найдется такой набор скаляров , что
.
Отсюда получаем,
,
т.е. любой вектор х линейно выражается через векторы системы , а это означает, что она является порождающей системой, ч.т.д.
Следствие 1. Линейно зависимая и порождающая система векторов не является минимальной.
Доказательство. Сразу же следует из леммы и определения минимальной порождающей системы векторов.
Следствие 2. Минимальная порождающая система векторов является линейно независимой.
Доказательство. Допустив противное, приходим к противоречию со следствием 1.
Определение. Система векторов векторного пространства называется максимальной линейно независимой системой, если при добавлении к этой системы любого вектора она становится линейно зависимой.
Замечание. Из определения сразу же следует, что если система является линейно независимой, но не максимальной, то найдется вектор, при добавлении которого к системе, получается линейно независимая система.
Определение. Базисом векторного пространства V над полем K называется упорядоченная система его векторов, представляющая любой вектор векторного пространства единственным способом.
Иначе говоря, система векторов векторного пространства V над полем K называется его базисом, если существует единственный набор скаляров , такой, что .
Теорема. (О четырех равносильных определениях базиса.)
Пусть – упорядоченная система векторов векторного пространства. Тогда следующие утверждения равносильны:
1. Система является базисом.
2. Система является линейно независимой и порождающей системой векторов.
3. Система является максимальной линейно независимой системой векторов.
4. Система является минимальной порождающей системой векторов.
Доказательство.
. Пусть система векторов является базисом. Из определения базиса сразу же следует, что эта система векторов является порождающей системой векторов векторного пространства, поэтому нам нужно только доказать ее линейную независимость.
Допустим, что данная система векторов линейно зависимая. Тогда существует два представления нулевого вектора – тривиальное и нетривиальное, что противоречит определению базиса.
. Пусть система векторов является линейно независимой и порождающей. Нам нужно доказать, что данная линейно независимая система является максимальной.
Допустим противное. Пусть данная линейно независимая система векторов не является максимальной. Тогда, в силу замечания выше, найдется вектор, который можно будет добавить к этой системе и полученная система векторов остается линейно независимой. Однако, с другой стороны, добавленный к системе вектор может быть представлен в виде линейной комбинации исходной системы векторов в силу того, что она является порождающей системой.
И мы получаем, что в новой, расширенной, системе векторов один из ее векторов линейно выражается через другие вектора этой системы. Такая система векторов является линейно зависимой. Получили противоречие.
. Пусть система векторов векторного пространства является максимальной линейно независимой. Докажем, что она является минимальной порождающей системой.
а) Сначала докажем, что она является порождающей системой.
Заметим, что в силу линейной независимости, система не содержит нулевого вектора. Пусть – произвольный ненулевой вектор. Добавим его к данной системе векторов: . Получившаяся система ненулевых векторов является линейно зависимой, т.к. исходная система векторов максимальная линейно независимая. Значит, в этой системе, найдется вектор линейно выражающийся через предыдущие. В исходной линейно независимой системе ни один из векторов не может выражаться через предыдущие, следовательно, линейно выражается через предыдущие только вектор х. Таким образом, система представляет любой ненулевой вектор. Осталось заметить, что данная система, очевидно, представляет и нулевой вектор, т.е. система является порождающей.
б) Теперь докажем ее минимальность. Допустим противное. Тогда один из векторов системы может быть удален из системы и оставшаяся система векторов по прежнему будет порождающей системой и, следовательно, удаленный из системы вектор тоже линейно выражается через оставшиеся вектора системы, что противоречит линейной независимости исходной системы векторов.
. Пусть система векторов векторного пространства является минимальной порождающей системой. Тогда она представляет любой вектор векторного пространства. Нам нужно доказать единственность представления.
Допустим противное. Пусть какой-нибудь вектор х линейно выражается через векторы данной системы двумя различными способами:
и .
Вычитая из одного равенства другое, получаем:
.
В силу следствия 2, система является линейно независимой, т.е. представляет нулевой вектор только тривмально, поэтому все коэффициенты этой линейной комбинации должны быть равны нулю:
.
Таким образом, любой вектор х линейно выражается через векторы данной системы единственным способом, ч.т.д.
Теорема доказана.
Еще записи по теме
procmem.ru
