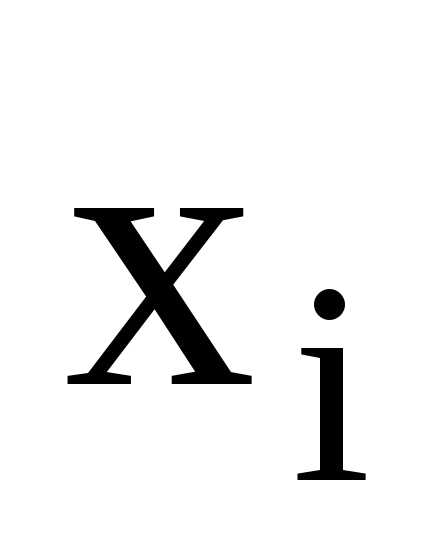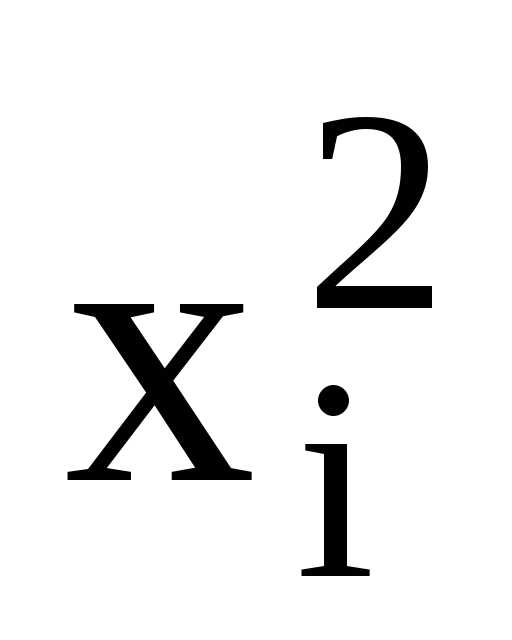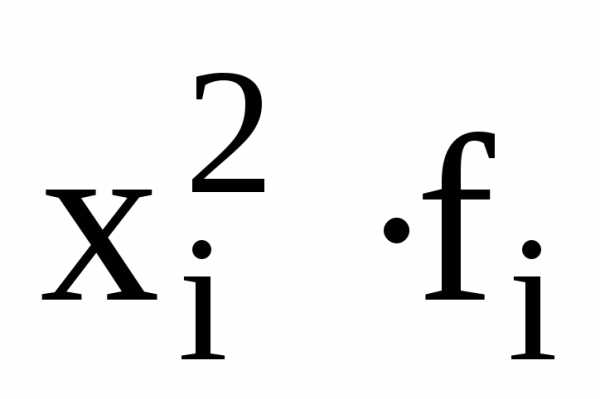Середина интервала статистика формула – Исчисление средней из интервального ряда, относительных величин. Средняя гармоническая, порядок исчисления. Средняя геометрическая. Средняя квадратическая.
Например, средняя арифметическая для интервального ряда
При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.
Пример 3. Определить средний возраст студентов вечернего отделения.
Возраст в годах | Число студентов | Среднее значение интервала | Произведение середины интервала (возраст) на число студентов |
до 20 | 65 | (18 + 20) / 2 =19 18 в данном случае граница нижнего интервала. Вычисляется как 20 — (22-20) | 1235 |
20 — 22 | 125 | (20 + 22) / 2 = 21 | 2625 |
22 — 26 | 190 | (22 + 26) / 2 = 24 | 4560 |
26 — 30 | 80 | (26 + 30) / 2 = 28 | 2240 |
30 и более | 40 | (30 + 34) / 2 = 32 | 1280 |
Итого | 500 | 11940 |
Средние, вычисляемые из интервальных рядов являются приближенными.
Структурные средние величины
Кроме степенных средних в статистике для относительной характеристики величины варьирующего признака и характеристики рядов распределения пользуются структурными средними: модой и медианой.
Мода
Мода— это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей.
Модой для дискретного ряда является варианта, обладающая наибольшей частотой.
При вычислении моды для интервального вариационного ряда необходимо:
сначала определить модальный интервал (по максимальной частоте),
затем — значение модальной величины признака по формуле:
где:
— значение моды
— нижняя граница модального интервала
i — величина интервала
— частота модального интервала
— частота интервала, предшествующего модальному
— частота интервала, следующего за модальным
Определение моды графически: Мода определяется по гистограмме распределения. Для этого
правую вершину модального
прямоугольника соединяют с правым
верхним углом предыдущего прямоугольника
, а левую
вершину модального прямоугольника —
с левым верхним углом
последующего прямоугольника. Абсцисса
точки пересечения этих прямых и будет
модой распределения.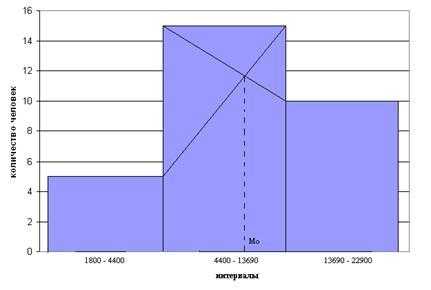
Медиана
Медиана — это значение признака, который делит вариационный ряд на две равные по численности части.
Медиана для дискретного ряда.
Для определения медианы в дискретном рядус нечетнымколичеством единиц наблюдения сначалапорядковый номер медианыпо формуле: , а затем определяют, какое значение варианта обладает накопленной частотой, равной номеру медианы.
Если ряд содержит
Медиана для интервального ряда
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана.
Для этого:
определяется номер медианы по формуле: , полученное значение округляется до целого большего числа.
затем по накопленной частоте определяется интервал, в который входит элемент с таким номером,
затем — значение медианы по формуле:
где:
— искомая медиана
— нижняя граница интервала, который содержит медиану
i — ширина интервала
— сумма частот или число членов ряда
— накопленная частота интервала, предшествующего медианному
— частота медианного интервала
Пример. Найти моду и медиану для интервального ряда.
Возрастные группы | Число студентов | Сумма накопленных частот ΣS |
До 20 лет | 346 | 346 |
20 — 25 | 872 | 1218 |
25 — 30 | 1054 | 2272 |
30 — 35 | 781 | 3053 |
35 — 40 | 212 | 3265 |
40 — 45 | 121 | 3386 |
45 лет и более | 76 | 3462 |
Итого | 3462 |
|
Решение:
Определим моду
В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).
Рассчитаем величину моды:
Это значит, что модальный возраст студентов равен 27 годам.
Определим медиану.
Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (Σfi/2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:
Это значит, что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.
Графически медиана определяется по кумуляте. Для ее определения высоту наибольшей ординаты, которая соответствует сумме всех частот, делят пополам. Через полученную точку
проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.
studfiles.net
STATISTIKA
ВВЕДЕНИЕ
Средняя величина как категория статистики. Средние величины являются одними из наиболее распространенных обобщающих статистических показателей. Они имеют своей целью одним числом охарактеризовать статистическую совокупность состоящую из меньшинства единиц. Средние величины тесно связаны с законом больших чисел. Сущность этой зависимости заключается в том, что при большом числе наблюдений случайные отклонения от общей статистики взаимопогашаются и в среднем более отчетливо проявляется статистическая закономерность. С помощью метода средних решаются следующие основные задачи: 1. Характеристика уровня развития явлений. 2. Сравнение двух или нескольких уровней. 3. Изучение взаимосвязей социально-экономических явлений. Анализ размещения социально-экономических явлений в пространстве.
Содержание
I.Статистические показатели: средние величины
1.1.Понятие о средних величинах
1.2.Виды средних и способы их вычисления
II. Основные категории статистики
1. Понятие о средних величинах
Признаки единиц статистических совокупностей различны по своему значению, например, заработная плата рабочих одной профессии какого-либо предприятия не одинакова за один и тот же период времени, различны цены на рынке на одинаковую продукцию, урожайность сельскохозяйственных культур в хозяйствах района и т.д. Поэтому, чтобы определить значение признака, характерное для всей изучаемой совокупности единиц, рассчитывают средние величины.
Средняя величина – это обобщающая характеристика множества индивидуальных значений некоторого количественного признака.
Совокупность, изучаемая по количественному признаку, состоит из индивидуальных значений; на них оказывают влияние, как общие причины, так и индивидуальные условия. В среднем значении отклонения, характерные для индивидуальных значений, погашаются. Средняя, являясь функцией множества индивидуальных значений, представляет одним значением всю совокупность и отражает то общее, что присуще всем ее единицам.
Средняя, рассчитываемая для совокупностей, состоящих из качественно однородных единиц, называется типической средней. Например, можно рассчитать среднемесячную заработную плату работника той или иной профессиональной группы (шахтера, врача библиотекаря). Разумеется, уровни месячной заработной платы шахтеров в силу различия их квалификации, стажа работы, отработанного за месяц времени и многих других факторов отличаются друг от друга, так и от уровня средней заработной платы. Однако в среднем уровне отражены основные факторы, которые влияют на уровень заработной платы, и взаимно погашаются различия, которые возникают вследствие индивидуальных особенностей работника. Средняя заработная плата отражает типичный уровень оплаты труда для данного вида работников. Получению типической средней должен предшествовать анализ того, насколько данная совокупность качественно однородна. Если совокупность состоит их отдельных частей, следует разбить ее на типические группы (средняя температура по больнице).
Средние величины, используемые в качестве характеристик для неоднородных совокупностей, называются системными средними. Например, средняя величина валового внутреннего продукта (ВВП) на душу населения, средняя величина потребления различных групп товаров на человека и другие подобные величины, представляющие обобщающие характеристики государства как единой экономической системы.
Средняя должна вычисляться для совокупностей, состоящих из достаточно большого числа единиц. Соблюдение этого условия необходимо для того, чтобы вошел в силу закон больших чисел, в результате действия которого случайные отклонения индивидуальных величин от общей тенденции взаимно погашаются.
2. Виды средних и способы их вычисления
Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. Однако любая средняя величина должна вычисляться так, чтобы при замене ею каждой варианты осредняемого признака не изменился итоговый, обобщающий, или, как его принято называть, определяющий показатель, который связан с осредняемым показателем. Например, при замене фактических скоростей на отдельных отрезках пути их средней скоростью не должно измениться общее расстояние, пройденное транспортным средством за одно и тоже время; при замене фактических заработных плат отдельных работников предприятия средней заработной платой не должен измениться фонд заработной платы. Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных, существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого социально-экономического явления.
Наиболее часто применяются средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая и средняя кубическая.
Перечисленные средние относятся к классу степенных средних и объединяются общей формулой:
где 
– среднее значение исследуемого
признака;
m – показатель степени средней;
–
текущее значение
(варианта) осредняемого признака;
n – число признаков.
В зависимости от значения показателя степени m различают следующие виды степенных средних:
при m
= -1 – средняя гармоническая 
;
при m
= 0 – средняя геометрическая 
;
при m
= 1 – средняя арифметическая 
;
при m
= 2 – средняя квадратическая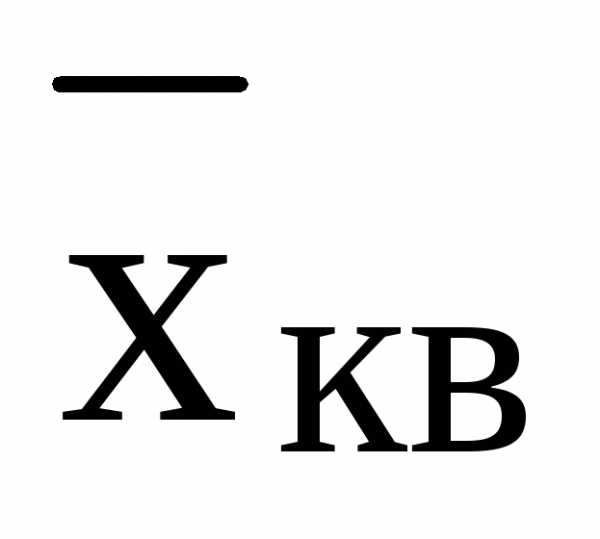 
;
при m
= 3 – средняя кубическая 
.
Средняя арифметическая
Средняя арифметическая применяется, когда объем совокупности представляет собой сумму всех индивидуальных значений варьирующего признака. Следует отметить, что если вид средней величины не указывается, подразумевается средняя арифметическая. Ее логическая формула имеет вид:
Средняя арифметическая простая рассчитывается по несгруппированным данным по формуле:
или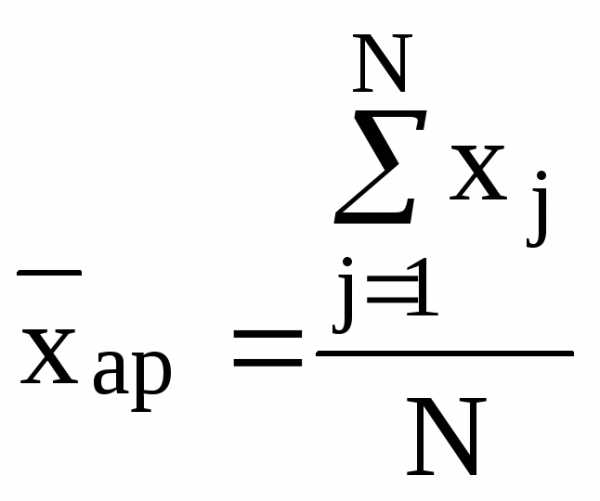 
,
где 
– отдельные значения признака;
j
– порядковый номер единицы наблюдения,
которая характеризуется значением 
;
N – число единиц наблюдения (объем совокупности).
Пример. В лекции «Сводка и группировка статистических данных» рассматривались результаты наблюдения стажа работы бригады из 10 человек. Рассчитаем средний стаж работы рабочих бригады. 5, 3, 5, 4, 3, 4, 5, 4, 2, 4.
По формуле средней арифметической простой вычисляются также средние в хронологическом ряду, если интервалы времени, за которое представлены значения признака, равны.
Пример. Объем реализованной продукции за первый квартал составил 47 ден. ед., за второй 54, за третий 65 и за четвертый 58 ден. ед. Среднеквартальный оборот составляет (47+54+65+58)/4 = 56 ден. ед.
Если в хронологическом ряду приведены моментные показатели, то при вычислении средней они заменяются полусуммами значений на начало и конец периода.
Если моментов больше двух и интервалы между ними равны, то средняя вычисляется по формуле средней хронологической
,
где n- число моментов времени
В
случае, когда данные сгруппированы по
значениям признака (т. е. построен
дискретный вариационный ряд распределения)
средняя арифметическая взвешенная рассчитывается
с использовании либо частот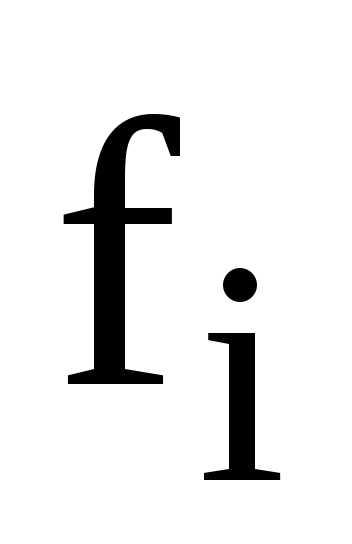 
,
либо частостей
наблюдения
конкретных значений признака
,
число которых (k)
значительно меньше числа наблюдений
(N)
.
,
,
где k – количество групп вариационного ряда,
i – номер группы вариационного ряда.
Поскольку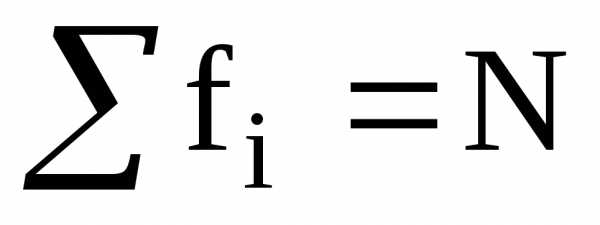 
,
а
,
получаем формулы, используемые для
практических расчетов:
и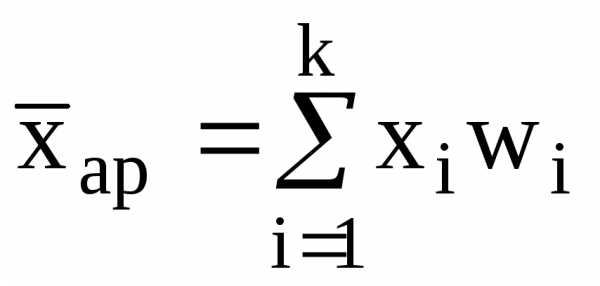 
Пример. Рассчитаем средний стаж рабочих бригад по сгруппированному ряду.
а) с использованием частот:
б) с использованием частостей:
В случае, когда данные сгруппированы по интервалам, т.е. представлены в виде интервальных рядов распределения, при расчете средней арифметической в качестве значения признака принимают середину интервала, исходя из предположения о равномерном распределении единиц совокупности на данном интервале. Расчет ведется по формулам:
и 
где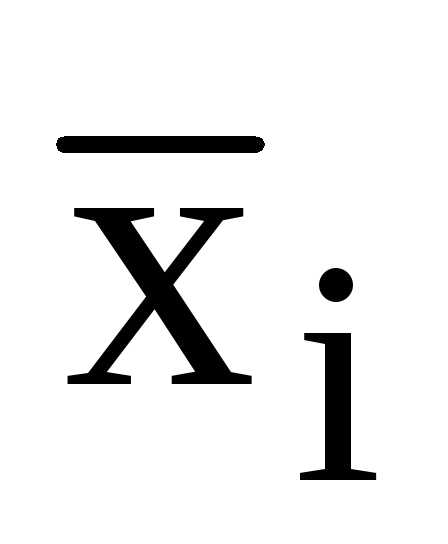 
— середина интервала:
,
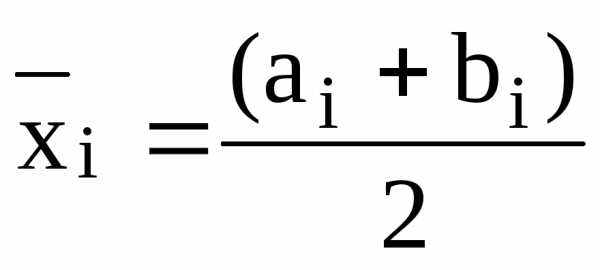где 
и– нижняя и верхняя границы интервалов
(при условии, что верхняя граница данного
интервала совпадает с нижней границей
следующего интервала).
Пример. Рассчитаем среднюю арифметическую интервального вариационного ряда, построенного по результатам исследования годовой заработной платы 30 рабочих.
Таблица 1 – Интервальный вариационный ряд распределения.
Интервалы, грн. | Частота, чел.
| Частость,
| Середина интервала,
|
|
|
600-700 700-800 800-900 900-1000 1000-1100 1100-1200 | 3 6 8 9 3 1 | 0,10 0,20 0,267 0,30 0,10 0,033 | (600+700):2=650 (700+800):2=750 850 950 1050 1150 | 1950 4500 6800 8550 3150 1150 | 65 150 226,95 285 105 37,95 |
| — | 26100 | 869,9 |
грн. или грн.
Средние арифметические, вычисленные на основе исходных данных и интервальных вариационных рядов, могут не совпадать из-за неравномерности распределения значений признака внутри интервалов. В этом случае для более точного вычисления средней арифметической взвешенной следует использовать не средины интервалов, а средние арифметические простые, рассчитанные для каждой группы (групповые средние). Средняя, вычисленная по групповым средним с использованием взвешенной формулы расчета, называется общей средней.
Средняя арифметическая обладает рядом свойств.
1. Сумма отклонений вариант от средней равна нулю:
.
2. Если все значения вариант увеличиваются или уменьшаются на величину А, то и средняя величина увеличивается или уменьшается на ту же величину А:
3. Если каждую варианту увеличить или уменьшить в В раз, то средняя величина также увеличится или уменьшатся в то же количество раз:
или
4. Сумма произведений вариант на частоты равна произведению средней величины на сумму частот:
5. Если все частоты разделить или умножить на какое-либо число, то средняя арифметическая не изменится:
6) если во всех интервалах частоты равны друг другу, то средняя арифметическая взвешенная равна простой средней арифметической:
,
где k – количество групп вариационного ряда.
Использование свойств средней позволяет упростить ее вычисление.
Допустим, что все варианты (х) сначала уменьшены на одно и то же число А, а затем уменьшены в В раз. Наибольшее упрощение достигается, когда в качестве А выбирается значение середины интервала, обладающего наибольшей частотой, а в качестве В – величина интервала (для рядов с одинаковыми интервалами). Величина А называется началом отсчета, поэтому этот метод вычисления средней называется способом отсчета от условного нуля или способом моментов.
После
такого преобразования получим новый
вариационный ряд распределения, варианты
которого равны 
.
Их средняя арифметическая, называемая
моментом первого порядка, выражается
формулой
и согласно второго и третьего свойств
средней арифметической равна средней
из первоначальных вариант, уменьшенной
сначала на А, а потом в В раз, т. е.
.
Для
получения действительной средней
(средней первоначального ряда) нужно
момент первого порядка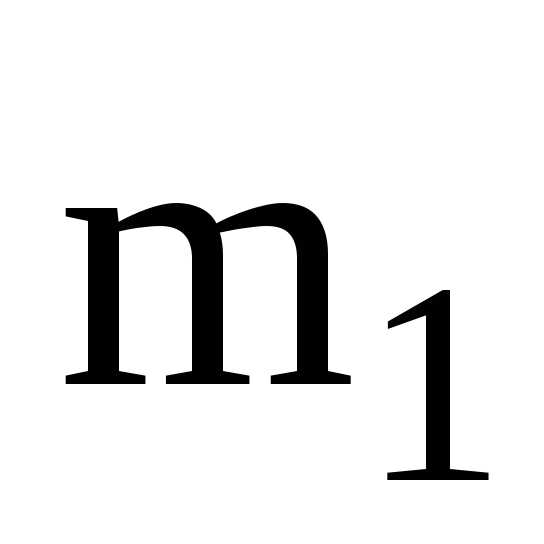 
умножить
на В и прибавить А:
Расчет средней арифметической по способу моментов иллюстрируется данными табл. 2.
Таблица 2 – Распределение работников цеха предприятия по стажу работы
Стаж работников, лет
| Количество работников
| Середина интервала
|
|
|
|
0 – 5 5 – 10 10 – 15 15 – 20 20 – 25 25 – 30 | 12 16 23 28 17 14 | 2,5 7,5 12,7 17,5 22,5 27,5 | -15 -10 -5 0 5 10 | -3 -2 -1 0 1 2 | -36 -32 -23 0 17 28 |
Итого | 110 | — | — | — | -46 |
Находим момент первого порядка . Затем, зная, что А=17,5, а В=5, вычисляем средний стаж работы работников цеха:
лет
Средняя гармоническая
Как было показано выше, средняя арифметическая применяется для расчета среднего значения признака в тех случаях, когда известны его варианты x и их частоты f.
Если
статистическая информация не содержит
частот f
по отдельным вариантам x
совокупности,
а представлена как их произведение 
,
применяется
формула средней гармонической взвешенной.
Чтобы вычислить среднюю, обозначим
,
откуда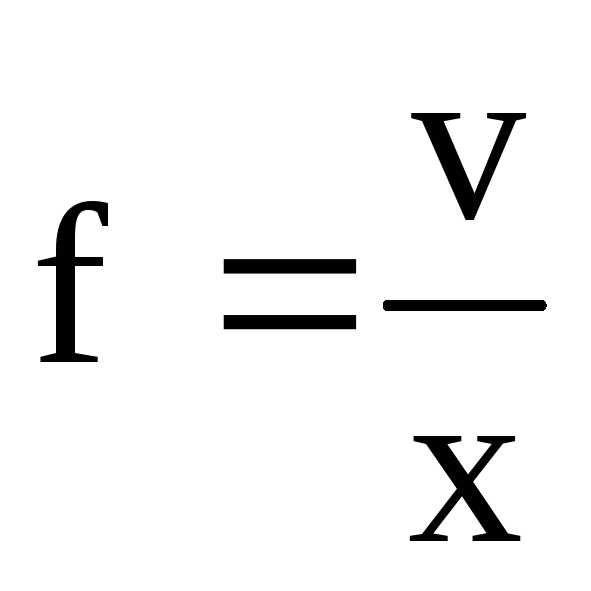
.
Подставив эти выражения в формулу
средней арифметической взвешенной,
получим формулу средней гармонической
взвешенной:
,
где 
— объем (вес) значений признака показателя
в интервале с номеромi
(i=1,2,
…, k).
Таким
образом, средняя гармоническая применяется
в тех случаях, когда суммированию
подлежат не сами варианты, а обратные
им величины: 
.
В тех случаях, когда вес каждой варианты равен единице, т.е. индивидуальные значения обратного признака встречаются по одному разу, применяется средняя гармоническая простая:
,
где 
– отдельные варианты обратного признака,
встречающиеся по одному разу;
N – число вариант.
Если
по двум частям совокупности численностью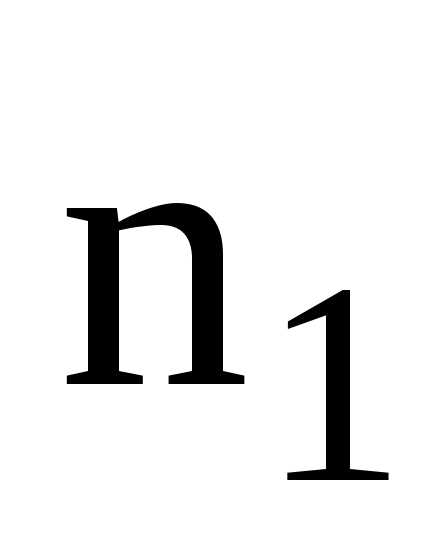 
и
имеются средние гармонические, то общая
средняя по всей совокупности рассчитывается
по формуле:
и называется взвешенной гармонической средней из групповых средних.
Пример. В ходе торгов на валютной бирже за первый час работы заключены три сделки. Данные о сумме продажи гривны и курсе гривны по отношению к доллару США приведены в табл. 3 (графы 2 и 3). Определить средний курс гривны по отношению к доллару США за первый час торгов.
Таблица 3 – Данные о ходе торгов на валютной бирже
Номер сделки | Сумма продажи, млн. грн.,
| Курс гривны, грн.,
| Частота (количество приобретенных долларов), млн. дол.,
|
1 | 2 | 3 | 4 |
1 2 3 | 45,0 25,2 40,4 | 5,00 5,04 5,05 | 9,0 5,0 8,0 |
Итого | 110,6 | — | 22,0 |
Средний курс доллара определяется отношением суммы проданных в ходе всех сделок гривен к сумме приобретенных в результате этих же сделок долларов. Итоговая сумма продажи гривны известна из графы 2 таблицы, а количество купленных в каждой сделке долларов определяется делением суммы продажи гривны к ее курсу (графа 4). Всего в ходе трех сделок куплено 22 млн. дол. Значит, средний курс гривны за один доллар составил
.
Полученное значение является реальным, т.к. замена им фактических курсов гривны в сделках не изменит итоговой суммы продаж гривны, выступающей в качестве определяющего показателя: млн. грн.
Если бы для расчета была использована средняя арифметическая, т.е. гривны, то по обменному курсу на покупку 22 млн. дол. нужно было бы затратить 110,66 млн. грн., что не соответствует действительности.
Средняя геометрическая
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака представляют собой относительные показатели динамики, построенные в виде цепных величин, как отношения каждого уровня к предыдущему.
Средняя геометрическая простая рассчитывается по формуле:
,
где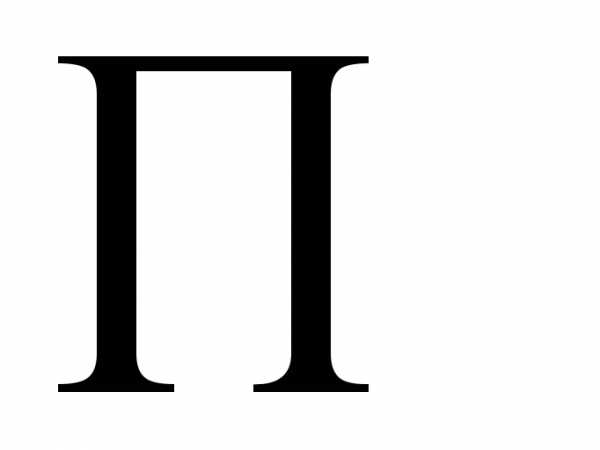 
– знак произведения,
N – число осредняемых величин.
Пример. Количество зарегистрированных преступлений за 4 года возросло в 1,57 раза, в т. ч. за 1-й – в 1,08 раза, за 2-й – в 1,1 раза, за 3-й – в 1,18 и за 4-й – в 1,12 раза. Тогда среднегодовой темп роста количества преступлений составляет: , т.е. число зарегистрированных преступлений ежегодно росло в среднем на 12%.
Средняя геометрическая взвешенная используется, когда временные интервалы неодинаковы:
,
где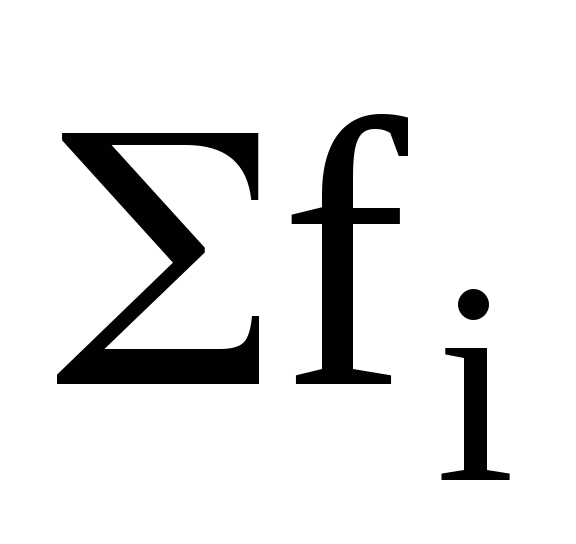 
– временной интервал.
Средняя квадратическая
Средняя квадратическая применяется, когда в качестве вариант используются отклонения фактических значений признака от средней арифметической или от заданной нормы.
Средняя квадратическая простая:
.
Средняя квадратическая взвешенная:
Пример. Вычислить среднюю величину измеренных отклонений фактической длины изделий от заданной нормы.
Отклонения,
мм, | Число
изделий, |
|
|
-1,8 -0,8 0,2 1,0 1,4 | 1 3 4 1 1 | 3,24 0,64 0,04 1 1,96 | 3,24 1,92 0,16 1 1,96 |
0 | 10 | 8,28 |
Для
расчета средней квадратической взвешенной
определяем и заносим в таблицу 
и
. Тогда средняя величина отклонений
длины изделий от заданной нормы равна:
Средняя арифметическая в данном случае была бы непригодна, т.к. в результате мы получили бы нулевое отклонение.
II. Основные категории статистики
Статистика оперирует определенными категориями – понятиями, отражающими существенные, всеобщие свойства и основные отношения явлений действительности.
Объект конкретного статистического исследования называют статистической совокупностью.
Статистическая совокупность – это множество единиц (объектов, явлений), объединённых единой закономерностью и варьирующих в пределах общего качества.
Специфическим свойством статистической совокупности является массовость единиц, поскольку явление характеризуется массовым процессом и всем многообразием определяющих его причин и форм.
Под единицами совокупности понимаются её неделимые первичные элементы, выражающие её качественную однородность, т. е. являющиеся носителями признаков.
Под качественной однородностью единиц совокупности понимается сходство единиц (объектов явлений) по каким-либо существенным признакам, но различающихся по каким-либо другим признакам.
Выделение качественно однородных статистических совокупностей является предпосылкой расчета обобщающих показателей, статистического изучения вариации, связей между признаками.
Единицы статистической совокупности характеризуются общими свойствами, именуемыми в статистике признаками.
Признак – это показатель, характеризующий некоторое свойство объекта совокупности, рассматриваемый, как случайная величина
Значение каждого признака отдельной единицы совокупности (варианты) могут быть различными.
Вариация – это различия в значениях того или иного признака у отдельных единиц, входящих в данную совокупность. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по разному сочетаются в каждом отдельном случае.
Наличие вариации является основной предпосылкой статистического исследования. Варьирующие признаки могут быть количественными , если их варианты выражаются числовыми значениями (возраст, стаж работы, оплата труда и прочее) и неколичественными (атрибутивными), не имеющими числового выражения и представляющими собой смысловые понятия (профессия, социальная принадлежность и т д.)Количественные признаки могут быть дискретными и непрерывными. Случаи, когда варианты признака могут принимать только одно из двух противоположных значений, говорят об альтернативном признаке. Признаки подразделяются на существенные, или главные, выражающие содержательную сторону явлений, и несущественные, или второстепенные, статистическому изучению подлежат существенные признаки.
studfiles.net
Группировка данных в статистике. Формула Стерджесса
Провести группировку жителей поселка по доходу с равными интервалами и оптимальным числом групп и представить полученные данные в виде статистического ряда распределения и гистограммы. На основе гистограммы построить полигон, кумуляту и огиву распределения жителей поселка по доходу.
№ | Дох. | № | Дох. |
1 | 3820 | 13 | 6660 |
2 | 9470 | 14 | 5490 |
3 | 3490 | 15 | 5980 |
4 | 7790 | 16 | 6250 |
5 | 4210 | 17 | 8390 |
6 | 3870 | 18 | 3630 |
7 | 4490 | 19 | 6090 |
8 | 9620 | 20 | 10450 |
9 | 6200 | 21 | 6800 |
10 | 6350 | 22 | 6470 |
11 | 7430 | 23 | 9160 |
12 | 7670 | 24 | 5110 |
Определяем число групп по формуле Стерджесса:
n = 1 + 3,322lgN = 1 + 3,322lg24 = 5,6
принимаем n = 5
Определяем шаг интервала:
Xmax, Xmin- максимальное и минимальное значение
n – число групп
Произведем группировку с равными интервалами
Интервалы | Диапазон | частота, f | Накопленная частота, f |
1 | 3490 — 4882 | 6 | 6 |
2 | 4882 – 6274 | 6 | 12 |
3 | 6274 – 7666 | 5 | 17 |
4 | 7666 – 9058 | 3 | 20 |
5 | 9058 — 10450 | 4 | 24 |
Гистограмма. Полигон. Кумулята. Огива
Если Вас интересуют задачи по статистике заходите сюда.
Примеры работ
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
univer-nn.ru
Решение статистических задач в EXCEL: Практикум, страница 3
Количественные данные следует определить как «Числовые».
2. Для выполнения расчета необходимо закрыть имеющиеся открытые интервалы – первый – «до 500», последний — «от 700».
Формула вычисления левой границы первого интервала вводится в ячейку Z19 : «=АА19-(АА20-Z20)» (– из ячейки АА19 вычесть разницу между содержимым ячейки АА20 и Z20).
Правая граница последнего интервала в ячейку АА23 устанавливается формулой «=Z23+АА22-Z22» (от значения в ячейке Z23 откладывается размер предшествующего интервала «АА22-Z22»).
3. 
Рассчитывается среднее по
каждой группе , как
середина интервала. Для этого в ячейку первой группы (АС19) устанавливается функция
СРЗНАЧ(Z19;AA19). После появления среднего значения первого интервала формула
копируется в соседние ячейки. При этом автоматически смещаются координаты
исходных данных в соответствии со смещением координат ячейки результата.
4. Рассчитывается величина средней взвешенной (в примере в ячейку АВ25)
СУММПРОИЗВ (АС19:АС23;АВ19:АВ23) реализует числитель
СУММ (АВ19:АВ23) – знаменатель;
«/» — знак деления.
Дисперсия. Среднее
квадратическое
отклонение.
Дисперсия и среднее квадратическое отклонение (СКО) могут вычисляться по простой и взвешенной формулам.
Дисперсия, среднее
квадратическое отклонение
по простой форме.
Для расчетов дисперсии по простой форме в Excel используется функция:
ДИСПР (диапазон данных).
СКО определяется как квадратный корень дисперсии, реализуемый оператором возведения в степень «^».
Рассмотрим методику расчета на примере расчета дисперсии и СКО зарплаты подразделения:
1. Исходные значения признака хi надо записать в массив ячеек расположенных в столбце или строке (в примере в строке (AF42:AQ42)).
Количественные данные следует определить как «Числовые».
2. В ячейку результата дисперсии (например «AF44») установить функцию ДИСПР(AF42:AQ42)
1. В ячейку результата СКО (например «AР44») установить функцию (ДИСПР(AF42:AQ42))^0,5.
Знак «^0,5» — означает возведение в степень 0,5 величины стоящей перед ним.
Дисперсия,
среднее квадратическое
отклонение по взвешенной форме.
Для расчетов дисперсии по взвешенной форме в Excel используется функция:
СУММ (диапазон данных) и
СУММПРОИЗВ (диапазоны перемножаемых данных),
оператор «/».
СКО определяется как квадратный корень дисперсии, реализуемый оператором возведения в степень «^».
Рассмотрим методику расчета на примере расчета дисперсии и СКО размера семьи группы
1. Исходные значения признака хi и частоту fi надо записать в массивы ячеек расположенных в столбце или строке (в примере в строках (АТ46:AY46) и (АТ47:AY47).
Количественные данные следует определить как «Числовые».
1. Рассчитать среднее арифметическое взвешенное — в примере в ячейке AW49 установлена формула =СУММПРОИЗВ (AT46:AY46;AT47:AY47)/СУММ(AT47:AY47)
vunivere.ru
Алгоритм построения интервального вариационного ряда с равными интервалами
Определяем число интервалов (групп) вариационного ряда
Число групп (интервалов) приближенно определяется по формуле Стерджесса:
m = 1 + 3,322 × lg(n)
где n — общее число единиц наблюдения (общее количество элементов в совокупности и т.д.), lg(n) – десятичный логарифм от n.
Полученную по формуле Стерджесса величину округляют обычно до целого большего числа, поскольку количество групп не может быть дробным числом.
Если ряд интервальный ряд с таким количеством групп по каким-то критериям не устраивает, то можно построить другой интервальный ряд, округлив m до целого меньшего числа и выбрать из двух рядов более подходящий.
Число групп не должно быть больше 15.
Также можно пользоваться следующей таблицей, если совсем нет возможности вычислить десятичный логарифм.
Объем выборки, n | 25-40 | 40-60 | 60-100 | 100-200 | Больше 200 |
Число интервалов, m | 5-6 | 6-8 | 7-10 | 8-12 | 10-15 |
Определяем ширину интервала
Ширина интервала для интервального вариационного ряда с равными интервалами определяется по формуле:
где Xмакс — максимальное из значений xi, Xмин — минимальное из значений xi; m — число групп (интервалов).
Величину интервала (i) обычно округляют до целого числа, исключение составляют лишь случаи, когда изучаются малейшие колебания признака (например, при группировке деталей по величине размера отклонений от номинала, измеряемого в долях миллиметра).
Часто применяется следующее правило:
Количество знаков до запятой | Количество знаков после запятой | Пример ширины интервала по формуле | До какого знака округляем | Пример округленной ширины интервала |
0 | 3 | 0,375 | 0,01 | 0,38 |
0 | 2 | 0,56 | 0,1 | 0,6 |
1 | 3 | 4,658 | 0,01 | 4,66 |
1 | 2 | 2,54 | 0,1 | 2,5 |
2 | любое | 12,54 | 1,0 | 13 |
3 | любое | 672,54 | 10,00 | 670 |
4 | любое | 3472,45 | 100,00 | 3500 |
и т.д. |
Определяем границы интервалов
Нижнюю границу первого интервала принимают равной минимальному значению признака (чаще всего его предварительно округляют до целого меньшего числа с таким же разрядом как ширина интервала). Например, хмин= 15, i=130, хн первого интервала = 10.
хн1 ≈ хмин
Верхняя граница первого интервала соответствует значению (Хmin + i).
Нижняя граница второго интервала всегда равно верхней границе первого интервала. Для последующих групп границы определяются аналогично, т е. последовательно прибавляется величина интервала.
xвi = xнi + i
xнi = xвi-1
Определяем частоты интервалов.
Считаем, сколько значений попало в каждый интервал. При этом помним, что если единица обладает значением признака, равным величине верхней границы интервала, то ее следует относить к следующему интервалу.
Строим интервальный ряд в виде таблицы.
Определяем середины интервалов.
Для дальнейшего анализа интервального ряда понадобится выбрать значение признака для каждого интервала. Это значение признака будет общим для всех единиц наблюдения, попавшим в этот интервал. Т.е. отдельные элементы «теряют» свои индивидуальные значения признака и им присваивается одно общее значение признака. Таким общим значением является середина интервала, которая обозначается x’i .
Рассмотрим на примере с ростом детей, как построить интервальный ряд с равными интервалами.
Имеются первоначальные данные.
90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 92, 93, 94, 95, 96, 98, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 100, 101, 102, 104, 110, 112, 114, 116, 117, 120, 122, 123, 124, 129, 110, 111, 113, 115, 116, 117, 121, 125, 126, 127, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 111, 113, 116, 127, 123, 122, 130, 131, 132, 133, 134, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 131, 133, 135, 136, 138, 139, 140, 141, 142, 143, 145, 146, 147, 148
studfiles.net
Как найти середину интервала | Сделай все сам
При статистической обработке итогов изысканий самого различного рода полученные значения зачастую группируются в последовательность промежутков. Для расчета обобщающих колляций таких последовательностей изредка доводится вычислять середину интервала — «центральную варианту». Способы ее расчета довольно примитивны, но имеют некоторые особенности, вытекающие как из применяемой для измерения шкалы, так и из нрава группировки (открытые либо закрытые промежутки).
Инструкция
1. Если промежуток является участком постоянной числовой последовательности, то для нахождения ее середины используйте обыкновенные математические способы вычисления среднеарифметического значения. Минимальное значение интервала (его предисловие) сложите с максимальным (окончанием) и поделите итог напополам — это один из методов вычисления среднеарифметического значения. Скажем, это правило применимо, когда речь идет о возрастных интервала х. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, потому что (21+33)/2=27.
2. Изредка бывает комфортнее применять иной способ вычисления среднеарифметического значения между верхней и нижней границами интервала . В этом варианте вначале определите ширину диапазона — отнимите от максимального значения минимальное. После этого поделите полученную величину напополам и прибавьте итог к минимальному значению диапазона. Скажем, если нижняя граница соответствует значению 47,15, а верхняя — 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, потому что 47,15+(31,98/2) = 47,15+15,99 = 63,14.
3. Если промежуток не является участком обыкновенной числовой последовательности, то вычисляйте его середину в соответствии с повторяемостью и размерностью применяемой измерительной шкалы. Скажем, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
4. Помимо обыкновенных (закрытых) промежутков статистические способы изысканий могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Скажем, открытый промежуток может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется способом аналогий — если все остальные диапазоны рассматриваемой последовательности имеют идентичную ширину, то предполагается, что и данный открытый промежуток имеет такую же размерность. В отвратном случае вам нужно определить динамику метаморфозы ширины промежутков, предшествующих открытому, и вывести его условную ширину, исходя из полученной склонности метаморфозы.
Изредка в повседневной деятельности может появиться надобность обнаружить середину отрезка прямой линии. Скажем, если предстоит сделать выкройку, эскиз изделия либо легко распилить на две равные части деревянный брусок. На поддержка приходит геометрия и немножко житейской смекалки.
Вам понадобится
- Циркуль, линейка; булавка, карандаш, нить
Инструкция
1. Воспользуйтесь обыкновенными инструментами, предуготовленными для измерения длины. Это самый легкой метод разыскать середину отрезка. Измерьте линейкой либо рулеткой длину отрезка, поделите полученное значение напополам и отмерьте от одного из концов отрезка полученный итог. Вы получите точку, соответствующую середине отрезка.
2. Существует больше точный метод нахождения середины отрезка, вестимый из курса школьной геометрии. Для этого возьмите циркуль и линейку, причем линейку может заменить всякий предмет подходящей длины с ровной стороной.
3. Установите расстояние между ножками циркуля так, дабы оно было равным длине отрезка либо же огромным, чем половина отрезка. После этого поставьте иглу циркуля в один из концов отрезка и проведите полуокружность так, дабы она пересекала отрезок. Переставьте иглу в иной конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность верно таким же образом.
4. Вы получили две точки пересечения полуокружностей по обе стороны от отрезка, середину которого мы хотим обнаружить. Объедините эти две точки при помощи линейки либо ровного бруска. Соединительная линия пройдет в точности посередине отрезка.
5. Если под рукой не оказалось циркуля либо длина отрезка значительно превышает возможный размах его ножек, дозволено воспользоваться простым приспособлением из подручных средств. Изготовить его дозволено из обыкновенной булавки, нитки и карандаша. Привяжите концы нитки к булавке и карандашу, при этом длина нитки должна немножко превышать длину отрезка. Таким импровизированным заменителем циркуля остается проделать шаги, описанные выше.
Видео по теме
Полезный совет
Довольно верно обнаружить середину доски либо бруска вы можете, использовав обыкновенную нитку либо шнур. Для этого отрежьте нить так, дабы она соответствовала длине доски либо бруска. Остается сложить нить верно напополам и разрезать на две равные части. Приложите один конец полученной мерки к концу измеряемого предмета, а 2-й конец будет соответствовать его середине.
jprosto.ru
Как найти середину интервала
При статистической обработке результатов исследований самого разного рода полученные значения часто группируются в последовательность интервалов. Для расчета обобщающих характеристик таких последовательностей иногда приходится вычислять середину интервала — «центральную варианту». Методы ее расчета достаточно просты, но имеют некоторые особенности, вытекающие как из используемой для измерения шкалы, так и из характера группировки (открытые или закрытые интервалы).
Спонсор размещения P&G Статьи по теме «Как найти середину интервала» Как найти боковые стороны равнобедренной трапеции Как построить медиану треугольника с помощью циркуля Как найти площадь разностороннего треугольникаИнструкция
1
Если интервал является участком непрерывной числовой последовательности, то для нахождения ее середины используйте обычные математические методы вычисления среднеарифметического значения. Минимальное значение интервала (его начало) сложите с максимальным (окончанием) и разделите результат пополам — это один из способов вычисления среднеарифметического значения. Например, это правило применимо, когда речь идет о возрастных интервалах. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.
2
Иногда бывает удобнее использовать другой метод вычисления среднеарифметического значения между верхней и нижней границами интервала. В этом варианте сначала определите ширину диапазона — отнимите от максимального значения минимальное. Затем поделите полученную величину пополам и прибавьте результат к минимальному значению диапазона. Например, если нижняя граница соответствует значению 47,15, а верхняя — 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, так как 47,15+(31,98/2) = 47,15+15,99 = 63,14.3
Если интервал не является участком обычной числовой последовательности, то вычисляйте его середину в соответствии с цикличностью и размерностью используемой измерительной шкалы. Например, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.4
Кроме обычных (закрытых) интервалов статистические методы исследований могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Например, открытый интервал может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется методом аналогий — если все остальные диапазоны рассматриваемой последовательности имеют одинаковую ширину, то предполагается, что и этот открытый интервал имеет такую же размерность. В противном случае вам надо определить динамику изменения ширины интервалов, предшествующих открытому, и вывести его условную ширину, исходя из полученной тенденции изменения. Как простоmasterotvetov.com