Решение системных линейных уравнений – Калькулятор онлайн — Решение системы двух линейных уравнений с двумя переменными (с подробным решением)

Примеры систем линейных уравнений: метод решения

Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.

Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.

Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.

Линейное уравнение

Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.

Виды систем линейных уравнений

Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.

F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.

Решить систему уравнений — это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.

Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.

Если системы имеют одно общее решение или решения не существует их называют равносильными.

Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.

Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.

Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.

Простые и сложные методы решения систем уравнений

Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.

Основная задача при обучении способам решения — это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода

Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.

Решение систем методом подстановки

Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе

Приведем решение примера системы линейных уравнений 7 класса методом подстановки:

Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.

Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.

Решение примера системы линейных неоднородных уравнений:

Решение с помощью алгебраического сложения

При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.

Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.

Алгоритм действий решения:

1. Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
2. Почленно сложить полученное выражение и найти одно из неизвестных.
3. Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.

Способ решения введением новой переменной

Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.

Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.

Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.

Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.

Решение для полученных в итоге системы находят методом сложения.

Наглядный метод решения систем

Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.

Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.

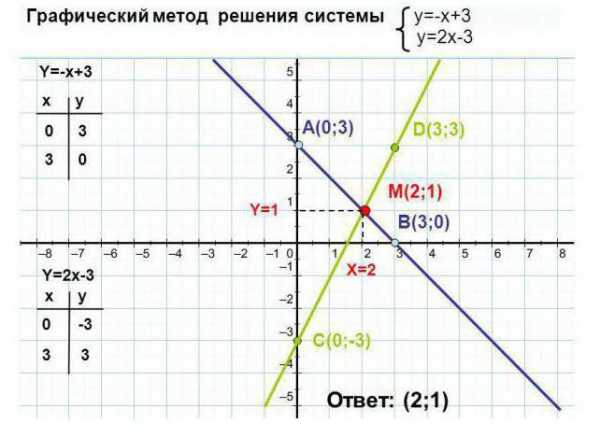
Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.

Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.

В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.

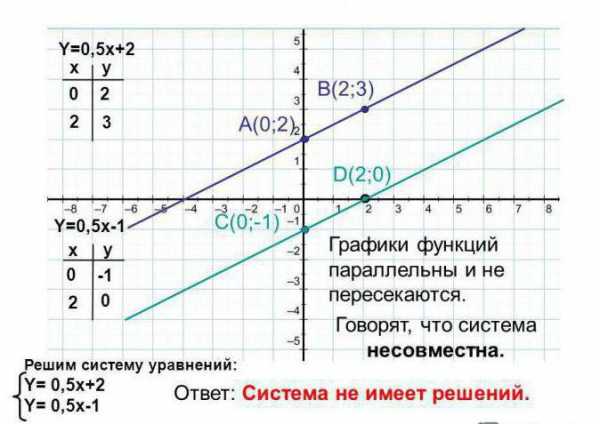
Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.

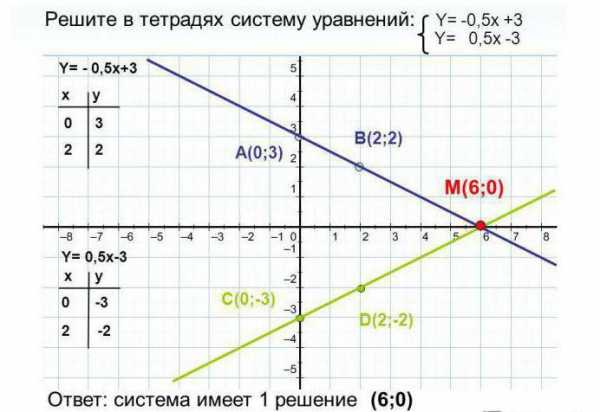
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.

Матрица и ее разновидности

Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. Матрица вида n*m имеет n — строк и m — столбцов.

Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей — вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.

Обратная матрица — это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.

Правила преобразования системы уравнений в матрицу

Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.

Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.

Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.

При умножении матрицы все элементы матрицы последовательно умножаются на число.

Варианты нахождения обратной матрицы

Формула нахождения обратной матрицы довольно проста: K^-1= 1 / |K|, где K^-1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.

Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a₁b₂c₃ + a₁b₃c₂ + a₃b₁c_{2 +} a₂b₃c₁ + a₂b₁c₃ + a₃b₂c₁. Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.

Решение примеров систем линейных уравнений матричным методом

Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.

В примере a_nm — коэффициенты уравнений, матрица — вектор x_n — переменные, а b_n — свободные члены.

Далее необходимо найти обратную матрицу и умножить на нее исходную. Найти значения переменных в полученной единичной матрицы легко выполнимая задача.

Решение систем методом Гаусса

В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.

Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.

После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.

В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:

Как видно из примера, на шаге (3) было получено два уравнения 3x₃-2x₄=11 и 3x₃+2x₄=7. Решение любого из уравнений позволит узнать одну из переменных x_n.

Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.

Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.

Для простоты записи вычислений принято делать следующим образом:

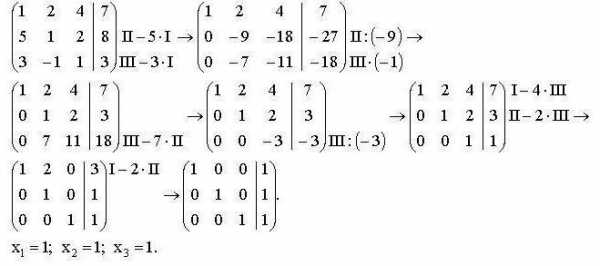
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. Вертикальная черта отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.

Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.

В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.

Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.

Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.

fb.ru

Решение СЛАУ методами подстановки и сложения

Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.

Например, уравнение

—

линейное, а уравнения и не являются линейными.

В общем виде система m линейных уравнений с n переменными записывается так:

. (1)

Числа
 
называются коэффициентами при переменных, а
 —
свободными членами.

Совокупность чисел

называется решением системы (1) линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.

Изучение систем линейных уравнений начинается в средней школе. В школьном курсе рассматриваются в основном системы двух линейных уравнений с двумя переменными и два метода их решения —

метод подстановки и метод сложения. Эти методы являются основой изучаемого в курсе высшей математике метода Гаусса. (Принципиально иной метод — метод Крамера — основан на использовании определителей).

Чтобы последовательно двигаться от простому к ещё более простому (сложному), повторим два школьных метода.

Решение. При решении системы линейный уравнений методом подстановки сначала из какого-нибудь уравнения выражают одну переменную через другую (другие, если неизвестных больше двух). Полученное выражение подставляют в другие уравнения, в результате чего приходят к уравнению с одной переменной. Затем находят соответствующее значение второй (и третьей, если она есть) переменной.

Начнём со вполне школьного примера системы двух линейных уравнений с двумя переменными.

Пример 1. Решить систему линейных уравнений методом подстановки:

Выразим из первого уравнения данной системы y через x (можно и наоборот) и получим:

Подставив во второе уравнение данной системы вместо y выражение , получим систему

Данная и полученная системы равносильны. В последней системе второе уравнение содержит только одну переменную. Решим это уравнение:

Соответствующее значение y найдём, подставив вместо x число -5 в выражение , откуда

Пара (-5; 2) является решением системы линейных уравнений.

Методом подстановки можно решать и системы трёх линейных уравнений с тремя переменными.

Пример 2. Решить систему линейных уравнений методом подстановки:

Из третьего уравнения системы выразим :

.

Подставим это выражение во второе уравнение данной системы:

.

Произведём преобразования и выразим из этого уравнения :

Полученные выражения для и подставим в первое уравнение системы и получим

.

Вместо можно вновь подставить его выражение, тогда получим уравнение с одним неизвестным:

откуда

.

Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:

Итак, решение данной системы линейных уравнений:

.

Пример 3. Решить систему линейных уравнений методом подстановки:

Из первого уравнения системы выразим :

.

Подставим это выражение во второе уравнение данной системы, после чего выполним преобразования и получим:

Из третьего уравнения выразим :

Полученное выражение для подставим в преобразованное второе уравнение системы и получим уравнение с одним неизвестным:

.

Произведём преобразования и найдём :

Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:

Итак, решение данной системы линейных уравнений:

.

При решении систем линейных уравнений методом сложения уравнения системы почленно складывают, причём одно или оба (несколько) уравнений могут быть умножены на различные числа. В результате приходят к эквивалентной (равносильной) системе линейных уравнений, в которой одно из уравнений содержит только одну переменную.

Пример 4. Решить систему линейных уравнений методом сложения:

Решение. В уравнениях данной системы в этом примере системы коэффициенты при

y — противоположные числа. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной:

, или , .

Заменим одно из уравнений исходной системы, например, первое, уравнением . Получим систему

Решим полученную систему. Подставив значение в уравнение , получим уравнение с одной переменной y:

Пара (2; 1) является решением полученной системы линейных уравнений. Она является также решением исходной системы, так как эти две системы линейных уравнений равносильны.

Пример 5. Решить систему линейных уравнений методом сложения

Почленное сложение уравнений системы не приводит к исключению одной из переменных. Но если умножить все члены первого уравнения на -3, а второго уравнения на 2, то коэффициенты при x в полученных уравнениях будут противоположными числами:

Почленное сложение уравнений полученной в результате преобразований системы приводит к уравнению с одной переменной: . Из этого уравнения находим, что . Получили

Решением полученной системы, а следовательно и исходной системы линейных уравнений является пара чисел (-3; 0).

Пример 6. Решить систему линейных уравнений методом сложения:

Решение. Для упрощения решения произведём замену переменных:

, .

Приходим к системе линейных уравнений:

или

Умножим второе уравнение полученной системы на -2 и сложим с первым уравнением, получим , . Тогда .

Следовательно, имеем систему уравнений

или

Умножим второе уравнение полученной системы на 3 и сложим с первым уравнением. Получим

.

Решив задачи из примеров на решение систем линейных уравнений методом подстановки и методом сложения, мы научились производить элементарные преобразования, необходимые для решениях систем линейных уравнений в курсе высшей математики.

Продолжение темы «Системы уравнений и неравенств»

Начало темы «Линейная алгебра»

Поделиться с друзьями

function-x.ru

Решение систем линейных уравнений

Существует три способа решения систем линейных уравнений:

• Способ подстановки
• Способ сложения
• Графический способ.

Остановимся на каждом из них подробно.

1. Способ подстановки удобно использовать в том случае, если в одном из уравнений системы коэффициент при одном из неизвестных равен 1. Тогда это неизвестное удобно выразить через другое.

Решим систему:

Заметим, что в первом уравнении системы коэффициент при равен 1, поэтому мы легко можем выразить через :

.

Подставим это выражение для вместо переменной во второе уравнение системы:

Решим это уравнение относительно :

.

Теперь вспомним, что . Подставим в правую часть равенства вместо переменной ее значение и найдем значение :

Внимание! При записи ответа на первом месте всегда указываем значение переменной , а на втором

Ответ: (3;-2)

2. Способ сложения более универсален, нежели способ подстановки.

Решим систему:

Мы имеем право умножать каждое уравнение системы на число и складывать уравнения. Воспользуемся этим правом.

Нам нужно сделать так, чтобы коэффициенты при одном из неизвестных были равны по модулю, но противоположны по знаку. Тогда при  сложении уравнений это неизвестное пропадет.

Сделаем так, чтобы, например, коэффициенты при были равны по модулю, но противоположны по знаку. Для этого нам нужно первое уравнение системы умножить на 3, а второе на 5. Получим систему:

Сложим уравнения системы, получим

, отсюда

Теперь подставим это значение , например, в первое уравнение исходной системы:

;

;

Ответ: (1;1)

А теперь решим такую систему:

Уравнения системы не являются линейными. Но мы можем сильно упростить себе жизнь, если введем замену переменной. Поэтому прежде чем решать эту систему, введем замену . Получим систему линейных уравнений:

Мы можем решать эту систему как способом подстановки (коэффициент при в первом уравнении равен 1, а при -1), так и способом сложения.

Решим способом сложения. Умножим первое уравнение на -2, тогда коэффициенты при будут равны по модулю, но противоположны по знаку.

Сложим уравнения. Получим:

;

Подставим это значение в первое уравнение исходной системы: ;

Итак,

Вернемся к исходной переменной:

отсюда

Ответ:

3. Графический способ.

Чтобы решить систему линейных уравнений графическим способом, нужно

• в каждом уравнении выразить
• построить графики соответствующих функций
• найти координаты точки пересечения графиков.

Решим систему

1. В каждом уравнении выразим :

2. Построим графики этих функций:

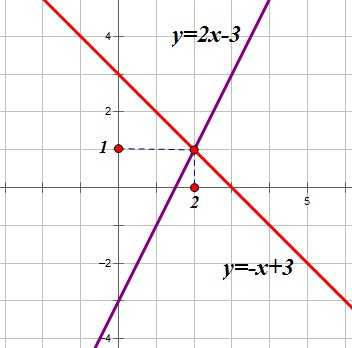
Координаты точки пересечения графиков (2;1)

Ответ: (2;1)

И.В. Фельдман, репетитор по математике

 

ege-ok.ru

Решение систем линейных уравнений

Определение и формула решения систем линейных уравнений

Школьные методы решения систем описаны в статье (\textbf{ссылка на статью «Решение систем уравнений» выше}).

Метод Гаусса для решения систем линейных уравнений

Метод Гаусса — это метод последовательного исключения переменных, когда расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к матрице (системе) треугольного вида, из которой последовательно, начиная с последней, находятся все остальные неизвестные системы. Метод назван в честь немецкого математика, механика, физика, астронома и геодезиста Иоганна Карла Фридриха Гаусса (1777-1855), хотя первое известное описание метода встречается уже в китайском трактате «Математика в девяти книгах» (10-2 в.в. до н.э.).

Метод Крамера для решения систем линейных уравнений

Матричный метод (метод обратной матрицы)

Матричный метод или метод обратной матрицы базируется на следующем алгоритме:

1. Система (1) записывается в матричной форме , где

   

2. Из матричного уравнения получаем, что

   

где матрица — это обратная матрица к матрице системы . Обратная матрица находится по формуле:

   

Матрица называется союзной матрицей к матрице , ее элементами есть алгебраические дополнения к соответствующим элементам матрицы .

Необходимым и достаточным условием применимости матричного метода является неравенство нулю определителя матрицы .

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Способы решения систем уравнений с двумя неизвестными

Линейные системы уравнений

Системы линейных уравнений. Метод подстановки 

+ показать

• Выражаем одну переменную через другую.

• Выраженную из одного уравнения переменную подставляем во второе уравнение. Получаем уравнение относительно одной переменной, которое и решаем.

• Опираясь на найденное значение одной переменной, находим значение второй, подставляя в оставшееся уравнение.

Решить систему уравнений: 

Решение: + показать

Системы линейных уравнений. Метод сложения 

+ показать

• Добиваемся, путем равносильных преобразований, наличия равных (или противоположных) коэффициентов при одной из неизвестных переменных в уравнениях.

• Вычитаем (или складываем) полученные уравнения с целью выхода на уравнение с одной неизвестной. 

• Решаем  полученное уравнение с одной неизвестной.

• Найденное значение одной переменной подставляем в любое из уравнений системы, находим значение второй.

1. Решить систему уравнений: 

Решение: + показать

Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

Ответ:  

2. Решить систему уравнений: 

Решение: + показать

Нелинейные системы уравнений

Системы уравнений, сводящихся к линейным

1. Решить систему уравнений: 

Решение: + показать

Можно сделать замену и Тогда выходим на систему линейных уравнений:

Систему можно решить методом сложения, например.

Но приведем решение без замены.

Умножим первое уравнение системы на , второе – на и произведем сложение полученных уравнений, оставим при этом в системе, например, первое уравнение исходной системы.

Ответ:  

2. Решить систему уравнений: 

Решение: + показать

Можно сделать замену и выйти на систему линейных уравнений:

Приведем решение без замены.

Выражаем из второго уравнения системы и подставляем в первое.

Ответ:  

Нелинейные системы уравнений. Метод подстановки

Решить систему уравнений: 

Решение: + показать

Выражаем из первого уравнения системы и подставляем во второе.

Ответ:  

Нелинейные системы уравнений. Метод сложения

Решить систему уравнений: 

Решение: + показать

Складываем уравнения системы, заменяя результатом одно из уравнений, оставляя другое.

Ответ:  

Нелинейные системы уравнений. Метод почленного умножения (деления)

1. Решить систему уравнений: 

Решение: + показать

Производим деление первой строки на вторую, оставляем в системе вторую строку без изменений.

Ответ:  

Симметрические системы. Метод введения переменной

Симметрическая система – система, все уравнения которой симметрические. Симметрическое уравнение от двух переменных и – уравнение, которое не изменяется при замене на и на .

Для таких систем удобно использовать замену  

Решить систему уравнений: 

Решение: + показать

При замене  приходим к следующей системе

 которую будем решать способом подстановки:

Производим обратную замену:

Ответ:

Системы однородных уравнений и приводящиеся к ним системы

Однородным уравнением с двумя неизвестными  будем называть уравнение вида

1. Решить систему уравнений: 

Решение: + показать

2. Решить систему уравнений: 

Решение: + показать

Применим прежде к системе метод сложения. После чего выйдем на однородное уравнение.

Ответ:

Графический метод решения систем уравнений

1. Решите графически систему уравнений: 

Решение: + показать

Выразим в обеих строках системы через :

Первое уравнение системы задает прямую, второе – гиперболу. Строим графики в одной системе координат, находим координаты точек пересечения графиков.

Ответ: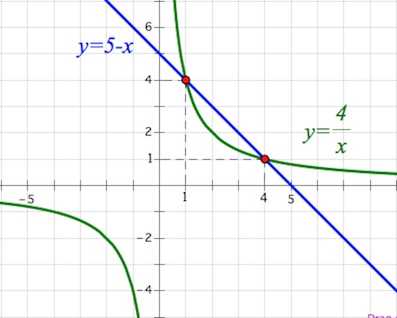 

2. Решите графически систему уравнений: 

Решение: + показать

3. Решите графически систему уравнений: 

Решение: + показать

——————————————————————————————————

Задания для самостоятельной работы

+ показать

Решите системы уравнений:

1.

Ответ:

2. 

Ответ:

3. 

Ответ:

4. 

Ответ:

5. 

Ответ:

6. 

Ответ:

7. 

Ответ:

8. 

Ответ:

Решите графически системы уравнений:

9. 

Ответ:

10. 

Ответ:

egemaximum.ru

Решение системы линейных уравнений. Метод подстановки, сложения, графический. Особые случаи, тесты

Тестирование онлайн

• Система линейных уравнений

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

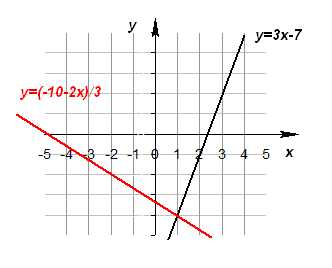
Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену , тогда

Переходим к первоначальным переменным

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если , то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.

fizmat.by

Решение систем линейных уравнений

Каталин Дэвид

Системы линейных уравнений имеют следующий общий вид:

$ \begin{cases} a_{1,1}\cdot x_{1} + a_{1,2}\cdot x_{2} + a_{1,3}\cdot x_{3} + \cdots a_{1,n} \cdot x_{n} =b_{1} \\ a_{2,1}\cdot x_{1} + a_{2,2}\cdot x_{2}+ a_{2,3}\cdot x_{3} + \cdots + a_{2,n}\cdot x_{n} = b_{2} \\ a_{3,1}\cdot x_{1} + a_{3,2}\cdot x_{2}+a_{3,3}\cdot x_{3}+ \cdots + a_{3,n}\cdot x_{n}=b_{3} \\ \cdots\\ a_{m,1}\cdot x_{1}+ a_{m,2}\cdot x_{2}+a_{m,3}\cdot x_{3}+\cdots + a_{m,n}\cdot x_{n} =b_{n} \end{cases}$

$ A= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n} \\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n} \\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ a_{m,1} & a_{m,2} & a_{m,3} & . & . & a_{m,n} \end{pmatrix}$ — матрица системы, а $b_{1}, b_{2},b_{3} \cdots b_{n}$ — свободные члены системы.

Если все свободные члены равны 0, то система однородна.

Матрица системы — квадратная (m=n)

Надо вычислить определитель матрицы системы.

$\Delta = \begin{vmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n} \\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n} \\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & a_{n,n} \end{vmatrix}$

Определитель матрицы системы не равен 0

Система называется невырожденной системой с единственным решением. Чтобы найти решение системы, используем метод Крамера.

Вычислим $ \Delta_{x_{1}}$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_{1}$ столбцом свободных членов.
$\Delta_{x_{1}}= \begin{vmatrix} b_{1} & a_{1,2} & a_{1,3} & . & . & a_{1,n} \\ b_{2} & a_{2,2} & a_{2,3} & . & . & a_{2,n} \\ b_{3} & a_{3,2} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ b_{n} & a_{n,2} & a_{n,3} & . & . & a_{n,n} \end{vmatrix}$

Получаем $ x_{1} = \dfrac{\Delta_{x_{1}}}{\Delta}$

Вычислим $ \Delta_{x_{2}}$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_{2}$ столбцом свободных членов.
$\Delta_{x_{2}}= \begin{vmatrix} a_{1,1} & b_{1} & a_{1,3} & . & . & a_{1,n} \\ a_{2,1} & b_{2} & a_{2,3} & . & . & a_{2,n} \\ a_{3,1} & b_{3} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ a_{n,1} & b_{n} & a_{n,3} & . & . & a_{n,n} \end{vmatrix}$

Получаем $ x_{2} = \dfrac{\Delta_{x_{2}}}{\Delta}$

Вычислим $ \Delta_{x_{3}}$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_{3}$ столбцом свободных членов.
$\Delta_{x_{3}}= \begin{vmatrix} a_{1,1} & a_{1,2} & b_{1} & . & . & a_{1,n} \\ a_{2,1} & a_{2,2} & b_{2} & . & . & a_{2,n} \\ a_{3,1} & a_{3,2} & b_{3} & . & . & a_{3,n} \\ \cdots \\ a_{n,1} & a_{n,2} & a_{n} & . & . & a_{n,n} \end{vmatrix}$

Получаем $ x_{3} = \dfrac{\Delta_{x_{3}}}{\Delta}$

Продолжаем делать это с остальными переменными, и в конце-концов записываем решение системы.
$x_{n}=\dfrac{\Delta_{x_{n}}}{\Delta}$

Пример 53
$\begin{cases} 2\cdot x + 3\cdot y -5\cdot z = \color{red}{-7}\\ -3 \cdot x + 2\cdot y + z = \color{red}{-9}\\ 4\cdot x — y + 2\cdot z = \color{red}{17} \end{cases}$

Матрица системы:
$ \begin{pmatrix} 2 & 3 & -5\\ -3 & 2 & 1\\ 4 & -1 & 2 \end{pmatrix}$

Вычисляем определитель матрицы и получаем $\Delta = 8 -15 + 12 +40 +2 + 18 = 65$
Вычисляем $ \Delta_{x}= \begin{vmatrix} \color{red}{-7} & 3 & -5\\ \color{red}{-9} & 2 & 1\\ \color{red}{17} & -1 & 2 \end{vmatrix}= -28 — 45 + 51 + 170 — 7 +54 = 195$

Вычисляем $ \Delta_{y}= \begin{vmatrix} 2 & \color{red}{-7} & -5\\ -3 & \color{red}{-9} & 1\\ 4 & \color{red}{17} & 2 \end{vmatrix}=-36 + 255 -28 -180 -34 -42 = -65$

Вычисляем $ \Delta_{z}= \begin{vmatrix} 2 & 3 &\color{red}{-7}\\ -3 & 2 & \color{red}{-9}\\ 4 & -1 & \color{red}{17} \end{vmatrix}= 68 -21 -108 + 56 -18 + 153 =130$

Решение системы:
$x = \dfrac{\Delta_{x}}{\Delta} =\dfrac{195}{65} = 3$
$y = \dfrac{\Delta_{y}}{\Delta} = -\dfrac{65}{65}= -1$
$z = \dfrac{\Delta_{z}}{\Delta} =\dfrac{130}{65}= 2$
$S=\{3;-1;2\}$

Пример 54
$\begin{cases} 4\cdot x + 5\cdot y -2\cdot z = \color{red}{3}\\ -2 \cdot x + 3\cdot y — z = \color{red}{-3}\\ -1\cdot x — 2\cdot y + 3\cdot z = \color{red}{-5} \end{cases}$

Матрица системы: $ \begin{pmatrix} 4 & 5 & -2\\ -2 & 3 & -1\\ -1 & -2 & 3 \end{pmatrix}$

Вычисляем определитель матрицы и получаем $\Delta = 36 -8 + 5 -6 -8 + 30 = 49$

Вычисляем $ \Delta_{x}= \begin{vmatrix} \color{red}{3} & 5 & -2\\ \color{red}{-3} & 3 &1\\ \color{red}{-5} & -2 & 3 \end{vmatrix}= 27 — 12 + 25 — 30 — 6 + 45 = 49$

Вычисляем $ \Delta_{y}= \begin{vmatrix} 4 & \color{red}{3} & -2\\ -2 & \color{red}{-3} & -1\\ -1 & \color{red}{-5} & 3 \end{vmatrix}=-36 -20+ 3 +6 -20 + 18 = -49$

Вычисляем $ \Delta_{z}= \begin{vmatrix} 4 & 5 & \color{red}{3}\\ -2 & 3 & \color{red}{-3}\\ -1& -2 & \color{red}{-5} \end{vmatrix}= -60 + 12 + 15 + 9 — 24 -50 = — 98$

Решение системы:
$x = \dfrac{\Delta_{x}}{\Delta} =\dfrac{49}{49} = 1$
$y = \dfrac{\Delta_{y}}{\Delta} = -\dfrac{-49}{49}= -1$
$z = \dfrac{\Delta_{z}}{\Delta} =\dfrac{-98}{4}= -2$
$S=\{1;-1;-2\}$

www.math10.com