Решение систем линейных уравнений – Калькулятор онлайн — Решение системы двух линейных уравнений с двумя переменными (с подробным решением)

Системы линейных алгебраических уравнений. Однородные системы линейных алгебраических уравнений

Ещё в школе каждый из нас изучал уравнения и, наверняка, системы уравнений. Но не многие знают, что существует несколько способов их решения. Сегодня мы подробно разберём все методы решения системы линейных алгебраических уравнений, которые состоят более чем из двух равенств.

История

На сегодняшний день известно, что искусство решать уравнения и их системы зародилось ещё в Древнем Вавилоне и Египте. Однако равенства в их привычном для нас виде появились после возникновения знака равенства «=», который был введён в 1556 году английским математиком Рекордом. Кстати, этот знак был выбран не просто так: он означает два параллельных равных отрезка. И правда, лучшего примера равенства не придумать.

Основоположником современных буквенных обозначений неизвестных и знаков степеней является французский математик Франсуа Виет. Однако его обозначения значительно отличались от сегодняшних. Например, квадрат неизвестного числа он обозначал буквой Q (лат.»quadratus»), а куб — буквой C (лат. «cubus»). Эти обозначения сейчас кажутся неудобными, но тогда это был наиболее понятный способ записать системы линейных алгебраических уравнений.

Однако недостатком в тогдашних методах решения было то, что математики рассматривали только положительные корни. Возможно, это связано с тем, что отрицательные значения не имели никакого практического применения. Так или иначе, но первыми считать отрицательные корни начали именно итальянские математики Никколо Тарталья, Джероламо Кардано и Рафаэль Бомбелли в 16 веке. А современный вид, основной метод решения квадратных уравнений (через дискриминант) был создан только в 17 веке благодаря работам Декарта и Ньютона.

В середине 18 века швейцарский математик Габриэль Крамер нашёл новый способ для того, чтобы сделать решение систем линейных уравнений проще. Этот способ был впоследствии назван его именем и по сей день мы пользуемся им. Но о методе Крамера поговорим чуть позднее, а пока обсудим линейные уравнения и методы их решения отдельно от системы.

Линейные уравнения

Линейные уравнения — самые простые равенства с переменной (переменными). Их относят к алгебраическим. Линейные уравнения записывают в общем виде так: а₁*x₁+а_2*x₂+…а_n*x_n=b. Представление их в этом виде нам понадобится при составлении систем и матриц далее.

Системы линейных алгебраических уравнений

Определение этого термина такое: это совокупность уравнений, которые имеют общие неизвестные величины и общее решение. Как правило, в школе все решали системы с двумя или даже тремя уравнениями. Но бывают системы с четырьмя и более составляющими. Давайте разберёмся сначала, как следует их записать так, чтобы в дальнейшем было удобно решать. Во-первых, системы линейных алгебраических уравнений будут выглядеть лучше, если все переменные будут записаны как x с соответствующим индексом: 1,2,3 и так далее. Во-вторых, следует привести все уравнения к каноническому виду: а₁*x₁+а_2*x₂+…а_n*x_n=b.

После всех этих действий мы можем начать рассказывать, как находить решение систем линейных уравнений. Очень сильно для этого нам пригодятся матрицы.

Матрицы

Матрица — это таблица, которая состоит из строк и столбцов, а на их пересечении находятся её элементы. Это могут быть либо конкретные значения, либо переменные. Чаще всего, чтобы обозначить элементы, под ними расставляют нижние индексы (например, а₁₁ или а₂₃). Первый индекс означает номер строки, а второй — столбца. Над матрицами, как и над любым другим математическим элементом можно совершать различные операции. Таким образом, можно:

1) Вычитать и складывать одинаковые по размеру таблицы.

2) Умножать матрицу на какое-либо число или вектор.

3) Транспонировать: превращать строчки матрицы в столбцы, а столбцы — в строчки.

4) Умножать матрицы, если число строк одной их них равно количеству столбцов другой.

Подробнее обсудим все эти приёмы, так как они пригодятся нам в дальнейшем. Вычитание и сложение матриц происходит очень просто. Так как мы берём матрицы одинакового размера, то каждый элемент одной таблицы соотносится с каждым элементом другой. Таким образом складываем (вычитаем) два этих элемента (важно, чтобы они стояли на одинаковых местах в своих матрицах). При умножении матрицы на число или вектор необходимо просто умножить каждый элемент матрицы на это число (или вектор). Транспонирование — очень интересный процесс. Очень интересно иногда видеть его в реальной жизни, например, при смене ориентации планшета или телефона. Значки на рабочем столе представляют собой матрицу, а при перемене положения она транспонируется и становится шире, но уменьшается в высоте.

Разберём ещё такой процесс, как умножение матриц. Хоть он нам и не пригодится, но знать его будет всё равно полезно. Умножить две матрицы можно только при условии, что число столбцов одной таблицы равно числу строк другой. Теперь возьмём элементы строчки одной матрицы и элементы соответствующего столбца другой. Перемножим их друг на друга и затем сложим (то есть, например, произведение элементов a₁₁ и а₁₂ на b₁₂ и b₂₂ будет равно: а₁₁*b₁₂ + а₁₂*b₂₂). Таким образом, получается один элемент таблицы, и аналогичным методом она заполняется далее.

Теперь можем приступить к рассмотрению того, как решается система линейных уравнений.

Метод Гаусса

Этой тему начинают проходить еще в школе. Мы хорошо знаем понятие «система двух линейных уравнений» и умеем их решать. Но что делать, если число уравнений больше двух? В этом нам поможет метод Гаусса.

Конечно, этим методом удобно пользоваться, если сделать из системы матрицу. Но можно и не преобразовывать её и решать в чистом виде.

Итак, как решается этим методом система линейных уравнений Гаусса? Кстати, хоть этот способ и назван его именем, но открыли его ещё в древности. Гаусс предлагает следующее: проводить операции с уравнениями, чтобы в конце концов привести всю совокупность к ступенчатому виду. То есть, нужно, чтобы сверху вниз (если правильно расставить) от первого уравнения к последнему убывало по одному неизвестному. Иными словами, нужно сделать так, чтобы у нас получилось, скажем, три уравнения: в первом — три неизвестных, во втором — два, в третьем — одно. Тогда из последнего уравнения мы находим первое неизвестное, подставляем его значение во второе или первое уравнение, и далее находим оставшиеся две переменные.

Метод Крамера

Для освоения этого метода жизненно необходимо владеть навыками сложения, вычитания матриц, а также нужно уметь находить определители. Поэтому, если вы плохо всё это делаете или совсем не умеете, придется поучиться и потренироваться.

В чём суть этого метода, и как сделать так, чтобы получилась система линейных уравнений Крамера? Всё очень просто. Мы должны построить матрицу из численных (практически всегда) коэффициентов системы линейных алгебраических уравнений. Для этого просто берём числа перед неизвестными и расставляем в таблицу в том порядке, как они записаны в системе. Если перед числом стоит знак «-«, то записываем отрицательный коэффициент. Итак, мы составили первую матрицу из коэффициентов при неизвестных, не включая числа после знаков равенства (естественно, что уравнение должно быть приведено к каноническому виду, когда справа находится только число, а слева — все неизвестные с коэффициентами). Затем нужно составить ещё несколько матриц — по одной для каждой переменной. Для этого заменяем в первой матрице по очереди каждый столбец с коэффициентами столбцом чисел после знака равенства. Таким образом получаем несколько матриц и далее находим их определители.

После того как мы нашли определители, дело за малым. У нас есть начальная матрица, и есть несколько полученных матриц, которые соответствуют разным переменным. Чтобы получить решения системы, мы делим определитель полученной таблицы на определитель начальной таблицы. Полученное число и есть значение одной из переменных. Аналогично находим все неизвестные.

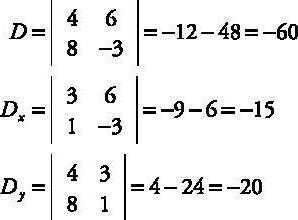
Другие методы

Существует ещё несколько методов для того, чтобы получить решение систем линейных уравнений. Например, так называемый метод Гаусса-Жордана, который применяется для нахождения решений системы квадратных уравнений и тоже связан с применением матриц. Существует также метод Якоби для решения системы линейных алгебраических уравнений. Он легче всех адаптируется для компьютера и применяется в вычислительной технике.

Сложные случаи

Сложность обычно возникает, если число уравнений меньше числа переменных. Тогда можно наверняка сказать, что, либо система несовместна (то есть не имеет корней), или количество её решений стремится к бесконечности. Если у нас второй случай — то нужно записать общее решение системы линейных уравнений. Оно будет содержать как минимум одну переменную.

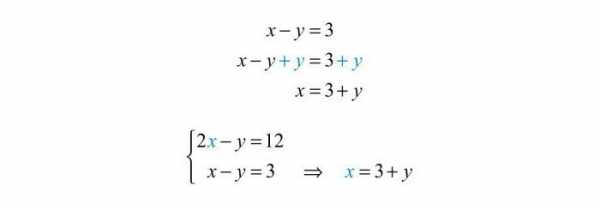
Заключение

Вот мы и подошли к концу. Подведём итоги: мы разобрали, что такое система и матрица, научились находить общее решение системы линейных уравнений. Помимо этого рассмотрели другие варианты. Выяснили, как решается система линейных уравнений: метод Гаусса и метод Крамера. Поговорили о сложных случаях и других способах нахождения решений.

На самом деле эта тема гораздо более обширна, и если вы хотите лучше в ней разобраться, то советуем почитать больше специализированной литературы.

fb.ru

Системы линейных уравнений (Лекция №14)

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных

x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется

несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

Найдем произведение

т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы

A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A^-1, обратную матрице A: . Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых

число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A^-1B.

Примеры. Решить системы уравнений.

1. Найдем матрицу обратную матрице A.

   ,

   Таким образом, x = 3, y = – 1.

2. 

   Итак, х₁=4,х₂=3,х₃=5.

3. Решите матричное уравнение: XA+B=C, где

   Выразим искомую матрицу X из заданного уравнения.

   Найдем матрицу А^-1.

   Проверка:

4. Решите матричное уравнение AX+B=C, где

   Из уравнения получаем .

   Следовательно,

ПРАВИЛО КРАМЕРА

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

1. 

   Итак, х=1, у=2, z=3.

2. Решите систему уравнений при различных значениях параметра p:

   Система имеет единственное решение, если Δ ≠ 0.

   . Поэтому .

   1. При
   2. При p = 30 получаем систему уравнений которая не имеет решений.
   3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y, yÎR.

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁

, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

1. Вернувшись к системе уравнений, будем иметь

2. Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

   Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

3. Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

   Вернемся к системе уравнений.

   Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

www.toehelp.ru

Решение системы линейных уравнений (СЛАУ) онлайн

Этот онлайн калькулятор позволит вам очень просто решить систему линейных уравнений онлайн (СЛУ онлайн) методом подстановки.

Для того чтобы решить систему линейных уравнений методом подстановки онлайн выберите количество неизвестных величин: 2345

Заполните систему линейных уравнений

Для изменения в уравнении знаков с «+» на «-» вводите отрицательные числа. Если в вашем уравнение отсутствует какой-то коэффициент, то на его месте в калькуляторе введите ноль. Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.

Решить систему

Воспользуйтесь также:
Решение системы линейных уравнений (метод Гаусса)
Решение системы линейных уравнений (метод Крамера)
Решение системы линейных уравнений (матричный метод)

Решение системы линейных уравнений онлайн

Метод подстановки

Решение системы линейных уравнений методом подстановки осуществляется следующим образом: сперва в одном из уравнений произвольная переменная выражается через остальные. Затем данное выражение подставляется во все остальные уравнения системы. Тем самым система из n уравнений превращается в систему n-1 уравнений с n-1 неизвестными. Затем аналогичные действия повторяются до тех пор, пока мы не приходим к конечному выражению для одной из переменных системы. Получив её значения, мы через неё выражаем пошагово все остальные неизвестные.

Данный метод решения СЛАУ называется методом подстановки (мы вместо некоторой переменной подставляем её выражение через другие переменные). Метод классический и простой в понимании, но на практике для больших систем уравнений очень громоздкий и сложный в вычислениях. Поэтому на практике при решении систем уравнений с большим количеством уравнений применяют более удобные методы, наподобие метода Гаусса, в котором преобразования уже выполняются в матрице, без лишних записей.

matematikam.ru

Методы решения систем линейных уравнений

Методы решения систем линейных уравнений

1. Решение системы линейных уравнений методом Гаусса

Задачи аппроксимации функции, а также множество других задач прикладной математики м вычислительной физики сводятся к задачам о решении систем линейных уравнений. Самым универсальным методом решения системы линейных уравнений является метод последовательного исключения неизвестных, называемый методом Гаусса.

Для иллюстрации смысла метода Гаусса рассмотрим систему линейных уравнений:

(1)

Эту систему запишем в матричном виде:

(2)

Как известно, обе части уравнения можно умножить на ненулевое число, а также можно из одного уравнения вычесть другое. Используя эти свойства, постараемся привести матрицу системы (2) к треугольному виду, т.е. к виду, когда ниже главной диагонали все элементы – нули. Этот этап решения называется прямым ходом.

На первом шаге прямого хода умножим первое уравнение на

и вычтем из второго, тогда исключится переменная из второго уравнения. Затем, умножим первое уравнение на и вычтем из третьего, тогда система (2) преобразуется в систему вида:
(3)

На втором шаге прямого хода из третьего уравнения исключаем

, т.е. из третьего уравнения вычитаем второе, умноженное, на , что приводит систему (3) к треугольному виду (4) (4)

Систему (4) переписываем в привычном виде:

(5)

Теперь, из системы (5) можем находить решение в обратном порядке, т.е. сначала находим из третьего уравнения

, далее, подставляя во второе уравнение, находим . Подставляя и в первое уравнение системы (5), находим . Нахождение решения из системы (5) называют обратным ходом.

Теперь, на основе рассмотренного примера, составим общий алгоритм метода Гаусса для системы:

(6)

Метод Гаусса состоит из двух этапов:

а) прямой ход – когда матрица системы (6) приводится к треугольному виду;

б) обратный ход – когда последовательно вычисляются неизвестные в обратном порядке, т.е. в последовательности:

.

а) Прямой ход: для приведения системы (6) к треугольному виду, уравнения с ненулевыми коэффициентами при переменной

переставляются таким образом, чтобы они были выше, чем уравнения с нулевыми коэффициентами . Далее, вычитаем первое уравнение, помноженное на , из второго уравнения, вычитаем первое уравнение, помноженное на , из третьего уравнения и т.д. В общем, вычитаем первое уравнение, помноженное на , из — го уравнения при , если . Вследствие этой процедуры, мы обнулили все коэффициенты при переменной в каждом из уравнений, начиная со второго, т.е. система (6) принимает вид: (7)

Далее, применяем туже самую процедуру, для уравнений системы (7), начиная со второго уравнения, т.е. первое уравнение исключается из «игры». Теперь стараемся обнулить коэффициенты при переменной

, начиная с третьего уравнения и т.д., пока не приведём систему к треугольному виду. Если , то система всегда приводима (теоретически) к треугольному виду. Общий алгоритм прямого хода можно представить в виде: (8)

б) Обратный ход: Вычисляем неизвестные по формулам:

(9)

Замечание: для вычисления определителя системы можно использовать треугольную форму полученной матрицы, тогда определитель этой матрицы равен произведению диагональных элементов, т.е.

(10)

2. Метод Гаусса с выбором главного элемента

Метод Гаусса настолько универсален, что для некоторых систем получаются практически «плохие» результаты, поэтому разрабатываются различные хитрые выходы из ситуации. В случае, когда некоторые коэффициенты матрицы системы близки между собой, как известно относительные погрешности сильно возрастают при вычитании, поэтому классический метод Гаусса даёт большие погрешности. Чтобы обойти эту трудность, стараются в прямом ходе Гаусса выбрать то уравнение, у которого коэффициент при

максимален и в качестве основного «игрока» выбирают именно это уравнение, тем самым обходя трудности вычитания близких чисел (если это возможно). Далее, когда нужно обнулить все коэффициенты переменной , кроме одного уравнения – этим особым уравнением опять выбирают то уравнение, у которого коэффициент при максимальный и т.д., пока не получим треугольную матрицу.

Обратный ход происходит так же, как и в классическом методе Гаусса.

3. Оценка погрешности при решении системы линейных уравнений

Для того, чтобы оценить погрешности вычислений решения системы линейных уравнений, нам нужно ввести понятия соответствующих норм матриц.

Прежде всего, вспомним три наиболее часто употребляемые нормы для вектора

: (11) (Евклидова норма) (12) (Чебышевская норма) (13)

Для всякой нормы векторов можно ввести соответствующую норму матриц:

(14)

которая согласована с нормой векторов в том смысле, что

(15)

Можно показать, что для трёх приведённых выше случаев нормы матрицы

задаются формулами:
(16) (17) (18)

Здесь

— являются сингулярными числами матрицы , т.е. это положительные значения квадратных корней — матрицы (которая является положительно-определённой матрицей, при ).

Для вещественных симметричных матриц

— где — собственные числа матрицы .

Абсолютная погрешность решения системы:

(19)

где

— матрица системы, — матрица правых частей, оценивается нормой:

mirznanii.com

Решение систем линейных уравнений.

Системы линейных алгебраических уравнений (СЛАУ) в научно-исследовательской инженерной практике встречаются весьма часто. К решению систем линейных уравнений сводится многочисленные практические задачи с использованием численных методов.

Например:

Коэффициенты сплайнов находятся путем решения СЛАУ. К СЛАУ приводят уравнения частных производных.

Задачи по нахождению собственных значений также приводят к СЛАУ. Таким образом, решение СЛАУ – одна из самых распространенных и важных задач вычислительной математики.

Запишем СЛАУ в общем виде:

 

 

— номер уравнения

— номер неизвестной, на которую умножается коэффициент.

Коэффициенты образуют матрицу

 

Матрица системы столбец неизвестных величин столбец правых частей

Введя эти величины, мы можем записать СЛАУ в виде матричного решения

Важнейшей характеристикой квадратной матрицы является её определитель( )

Число возможных значений

В курсе высшей математики показывается, что система СЛАУ имеет единственное решение, если определитель системы не равен нулю. В этом случае решение может быть найдено с помощью формул Крамера:

,

где — определитель матрицы, которая получается после исключения в матрице А -го столбца и его замены столбцом свободных членов.

Если определитель системы равен нулю, то в этом случае матрица называется вырожденной, а система либо не имеет решения, либо имеет бесконечное множество решений. Для некоторых систем решение оказывается очень чувствительным к малым погрешностям в исходных данных . Такие системы называются плохо-обусловленными. Определитель плохо-обусловленных систем близок к нулю. При численных вычислениях всегда надо иметь ввиду эту особенность систем линейных уравнений.

Существуют методы улучшения обусловленности систем. Некоторые некорректные задачи приводят к плохо обусловленным системам уравнений. Эти задачи могут иметь важное практическое значение. Существуют методы решения таких задач.

Методы решения СЛАУ делятся на 2 группы:

1)прямые

используют готовые формулы для вычисления неизвестных, эти методы наиболее универсальны, пригодны для решения широкого класса СЛАУ. Но они обладают недостатками: они требуют хранения в оперативной памяти сразу всей матрицы. Существенным недостатком прямых методов является накапливание погрешности в процессе решения. Это особенно опасно для больших систем, а также для плохо-обусловленных , поэтому прямые методы используют обычно если нескольких сотен.

Итерационные

в итерационных методах решение находят путем последовательных приближений. Накапливание погрешности не происходит, и с помощью них решают систему с большим числом уравнений и для решения плохо-обусловленных систем. Однако сходимость итерации может быть очень медленной. Поэтому время счета может быть очень большим. Другим недостатком является то, что с их помощью решается ограниченный класс уравнений.

Например:

Уравнений с преобладанием диагональных элементов, либо системы со слабо заполненными матрицами.

Метод Крамера относится к прямому методу, однако на практике метод Крамера практически никогда не используется, так как он требует большого объёма вычислений. Оценим объём вычислений с помощью метода Крамера. Для применения этого необходимо вычислить определитель, а для вычисления каждого определителя необходимо сделать произведений, а число полученных слагаемых . Значит, число арифметических операций будет с ростом резко возрастает при

Наиболее распространенным среди прямых методов является метод Гаусса.

Метод 14

Метод Гаусса.

Метод Гаусса основан на приведении матрицы системы к треугольному виду. Метод Гаусса состоит из двух этапов: прямой ход и обратный. Прямой ход – матрица приводится к треугольному виду, при обратном последовательно находятся неизвестные величины.

Прямой ход состоит в следующем:

1)на первом шаге с помощью первого уравнения исключается из всех последних уравнений системы, в результате получается новая система, имеющая то же решение, но в первом столбце матрицы будет не нулевым только первый элемент.

2)на втором шаге с помощью второго уравнения исключается из всех уравнений. Этот процесс продолжается до тех пор, пока в левой части последнего — го уравнения не останется лишь один член с неизвестным .

Рассмотрим процесс исключения подробнее:

На -ом шаге исключается

Запишем -ое уравнение:

Исключим с помощью этого уравнения из уравнения с номером

Для исключения из -го уравнения вычитаем -ое , умноженное на .

После такого вычитания первые слагаемые сокращаются. Запишем значение коэффициенты перед , используем для него прежнее обозначение

При этом изменяется свободный член

 

По завершению прямого хода получается система с треугольной матрицей. Далее производится обратный ход метода Гаусса.

Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных, начиная с . Сначала находится . Далее, используя это значение, находится и так далее.

Например:

На — ом шаге обратного хода неизвестные находятся с помощью выражения.

В процессе исключения неизвестных приходится делить на диагональный элемент, который может оказаться равным нулю. Чтобы исключить эту ситуацию, необходимо на каждом шаге прямого хода менять расположение уравнений таким образом, чтобы диагональный элемент не был равным нулю, а лучше, чтобы он имел максимально возможное значение.

Перестановка уравнений должна быть предусмотрена в вычислительном алгоритме и метод Гаусса, в котором производится перестановка уравнений таким образом, чтобы диагональный элемент имел максимальное значение, называется метод Гаусса с выбором главного элемента.

В методе Гаусса объём вычислений пропорционален . Существует практически значимые случаи, когда объём вычислений при решении СЛАУ можно резко сократить.

 

Метод 15

Метод прогонки.

Метод прогонки является модификацией метода Гаусса для частного случая с трёхдиагональной матрицей. Такие системы возникают при численном решении уравнений математической физики.

Другой пример: коэффициенты сплайна третьей степени находятся путём решения систем с трёхдиагональной матрицей.

В методе прогонки объём вычислений растет пропорционально . Запишем систему уравнений, которая решается методом прогонки.

 

 

Общий вид уравнений с трёхдиагональной матрицей

Решение системы с трёхдиагональной матрицей, как и в методе Гаусса, состоит из двух этапов. Прямой прогонки и обратной прогонки.

Рассмотрим первый этап (прямой ход метода прогонки)

Для этого неизвестный выражаем через , таким образом:

,

где , — неизвестные пока (прогоночные) коэффициенты. На первом как раз и находится эти коэффициенты. Сравним это уравнение при с первым уравнением системы

И из сравнения находим, что

Заменим i-ое уравнение системы, выразив в нём с помощью

Сравнивая с

Получаем рекуррентные соотношения для нахождения прогоночных коэффициентов.

После того как найдены все прогоночные коэффициенты в результате прямого хода метода, находят . Для этого сравниваем последние уравнения системы с последним прогоночным соотношением. В результате получаем систему из двух уравнений с двумя неизвестными.

Отсюда

Это фактически начало обратного хода метода прогонки.

После этого последовательно находим …….и т.д. вплоть до .

Метод 16

Похожие статьи:

poznayka.org

Численные методы: решение систем линейных уравнений

В прикладных задачах часто возникает необходимость решать системы линейных уравнений.

Система линейных алгебраических уравнений с n неизвестными  —  это система уравнений вида

                                     (1)

Слово система означает, что все уравнения рассматриваются как одно целое.

В общем случае у нас имеется m — уравнений, n — количество неизвестных. x₁, x₂,…, x_n — неизвестные, которые следует определить.

В системе (1)  – фиксированные коэффициенты,  b₁, b₂, …, b_m — свободные члены — предполагаются известными.

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Задача состоит в том, чтобы найти такие  которые удовлетворяют всем уравнениям (1).

В частном случае мы имеем одно линейное уравнение:

Конечно, такое уравнение легко решить, если предположить, что коэффициент  не равен 0, имеем:  = .

Очевидно, в общем случае имеются 3 варианта решений: система имеет ни одного решения, имеет одно решение, более одного решения.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если нет ни одного решения.

Система линейных уравнений может быть представлена в матричной форме как:

или:

Ax = b

Здесь A — это матрица системы, x — столбец неизвестных, а b — столбец свободных членов.

Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Рассмотрим, например, систему вида и поймем, как найти ее решение:

                                      (2)

Предположим на минуту, что в первом уравнении y отсутствует, а во втором отсутствует x, тогда мы имели бы решение именно то решение, которое нам нужно.

Вопрос: как исходную систему привести к такому виду и можно ли это сделать.

Заметим, что с тождествами мы можем делать следующие вещи: домножать на одно и то же число, отличное от 0, складывать, вычитать и тд, это похоже с тем, что вы раскладываете монеты по своим карманам, не меняя общей суммы.

От этих операций тождество не меняется.

В системе (2) у нас два тождества, домножим второе тождество на 2 и вычтем из первого, получим:

                                      (3)

Формально у нас есть еще старое тождество , но оно нам не понадобится (подумайте, почему).

Система (3) точно такая же, как система (2).

Из второго уравнения системы (3) сразу получим:

 

Никто не мешает нам подставить это значение в первое уравнение:

Отсюда сразу находим, что

Итак, путем простых действий мы нашли, что система (2) может быть представлена в виде:

Именно такие естественные соображения приводят к общему методу решения систем линейных уравнений, известному как метод исключения или метод Гаусса.

Метод Гаусса является одним из самых распространенных прямых методов решения систем линейных уравнений Ax = b:

Опишем этот метод в общем случае.

Вначале исходная система приводится к верхнетреугольному виду.

Это достигается следующей последовательностью преобразований (прямой ход).

Будем считать для удобства, что элемент a_ij исходной матрицы и компоненты вектора b_i есть, соответственно, элементы a_ij ⁽¹⁾ первого шага преобразованной матрицы A₁ и преобразованного вектора b₁:A = A₁, b=b₁. 

Далее, на втором шаге прибавим к второй строке первую, умноженную на  

Аналогично поступим со всеми оставшимися строками, т.е. прибавим к каждой i-ой строке i=2,3,…,N, первую, умноженную на коэффициент  

При этом соответственно изменится и вектор b1. 

Таким образом, 2 шаг.

Имеем систему уравнений A₂x = b₂:

где

3 шаг.

Прибавим к новой третьей строке новую вторую, умноженную на  

То же самое сделаем с остальными строками 4,5,…,N, т.е. прибавим к i-ой строке вторую, умноженную на  

При этом получим систему A₃x = b₃:

(k+1)-ый шаг:

Здесь

Поступая так и далее, на шаге N-1 получаем верхнетреугольную систему:

При этом, мы также получили матрицу C переводных коэффициентов, имеющую вид:

Решение полученной треугольной системы  как легко видеть, имеет вид (обратный ход метода Гаусса):

Заметим, что при прямом ходе метода Гаусса может возникнуть ситуация, когда происходит деление на нуль, да и вообще, желательно не делить на малое число, чтобы не накапливалась ошибка.

Поэтому метод Гаусса обычно проводят с частичным выбором главного элемента, то есть после каждого шага (пусть это был k-й шаг) переставляют строки с номерами k,k+1,…,N таким образом, чтобы на месте kk оказался элемент  наибольший из всех в k-ом столбце при m>k (при этом, естественно, переставляются и компоненты вектора b).

Можно для максимальной точности переставлять также и столбцы преобразуемой матрицы, чтобы на месте kk оказался максимальный элемент из всех с индексами больше, либо равными k.

Эта процедура называется методом Гаусса с выбором главного элемента. Она несколько повышает точность по сравнению с частичным выбором главного элемента, но весьма неудобна, в том числе для программирования, поскольку при перестановке строк компоненты искомого вектора x переставлять не надо, тогда как при перестановке столбцов надо переставлять и соответствующие компоненты вектора x.

Опишем обратный ход метода Гаусса в несколько иной форме (треугольное разложение).

Введем матрицы M_k по правилу:

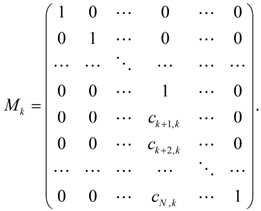
На каждом шаге метода Гаусса получается некоторая промежуточная матрица: 

 и вектор  

Нетрудно видеть, что

Вопрос. Почему

Если производить также выбор главных элементов, то необходимо использовать оператор P перестановки индексов l и m, матричные элементы которого равны:

При применении оператора перестановки индексов к матрице слева, меняются местами строки матрицы и компоненты свободного вектора (PAx = Pb), если же его применить справа к матрице, то меняются местами ее столбцы и компоненты решения

Существует большой класс так называемых итерационных методов решения систем уравнений, аналогичных итерационным методам нахождения корней нелинейных уравнений.

Итерационные методы последовательно уточняют решение, отправляясь от начального приближения.

При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций.

Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений.

Идея состоит в том, чтобы найти неподвижную точку матричного уравнения

                                     (5)

эквивалентного начальной системе линейных алгебраических уравнений.

При итерации  в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:

.

Термин неподвижная точка становится ясен, если вы внимательно посмотрите на уравнение (5), по самому своему смыслу величина Х является неподвижной точкой.

Более подробное описание методов решения систем линейных уравнений можно найти в специальной литературе, наша задача дать обзор методов и основные идеи решения такого рода задач.

Обусловленность линейных систем, погрешность

При решении абстрактной задачи Ax = b, где A — оператор произвольной природы, важным моментом является корректность ее постановки.

Задача считается корректной, если решение существует и единственно и , кроме того, решение непрерывно зависит от данных (то есть, при  также стремится к нулю).

Однако и непрерывная зависимость от входных данных может иметь свои нюансы.

Чем меньшее (большее) изменение решения вызывает вариация входных данных, тем более хорошо (плохо) обусловленной считается задача.

Понятие обусловленности является тем более существенным для численных методов, поскольку на практике входные данные известны, как правило, с некоторой погрешностью.

Кроме того, существуют ошибки округления, возникающие при вычислениях.

Таким образом, формально корректная задача, являясь плохо обусловленной, может оказаться разрешимой столь неточно, что в этом будет отсутствовать практический смысл.

Чем можно охарактеризовать количественно обусловленность для линейных систем?

Пусть A — квадратная NxN — матрица.

Рассмотрим задачу Ax = b.

Пусть также  некоторая норма в пространстве R_N 

Норма оператора A определяется стандартно:

Обозначим y = Ax и введем число m по правилу:

Величина  называется числом обусловленности.

Очевидно:

2.      
3. если A — диагональная, то  (Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть  вариация правой части, а соответствующее изменение решения.

Тогда справедливо следующее неравенство:

 

Доказательство. Имеем:

Так как

то    

Аналогично, поскольку  

Объединяя два неравенства, окончательно получаем для оценки погрешности:

 

В начало

Содержание портала

statistica.ru

Система линейных уравнений | Математика

Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в которой является линейным — алгебраическим уравнением первой степени.

В классическом варианте коэффициенты при переменных, свободные члены и неизвестные считаются вещественными числами, но все методы и результаты сохраняются (либо естественным образом обобщаются) на случай любых полей, например, комплексных чисел.

Решение систем линейных алгебраических уравнений — одна из классических задач линейной алгебры, во многом определившая её объекты и методы. Кроме того, линейные алгебраические уравнения и методы их решения играют важную роль во многих прикладных направлениях, в том числе в линейном программировании, эконометрике.

Соглашения и определенияПравить

Общий вид системы линейных алгебраических уравнений:

$ \begin{cases} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2\\ \dots\\ a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m \\ \end{cases} $

Здесь $ m $ — количество уравнений, а $ n $ — количество переменных, $ x_1, x_2, \dots, x_n $ — неизвестные, которые надо определить, коэффициенты $ a_{11}, a_{12}, \dots, a_{mn} $ и свободные члены $ b_1, b_2, \dots, b_m $ предполагаются известными. Индексы коэффициентов в системах линейных уравнений ($ a_{ij} $) формируются по следующему соглашению: первый индекс ($ i $) обозначает номер уравнения, второй ($ j $) — номер переменной, при которой стоит этот коэффициент. Система называется однородной, если все её свободные члены равны нулю, в остальных случаях — неоднородной.

Квадратной называется такая СЛАУ, где количество уравнений совпадает с количеством переменных. Если переменных больше, чем уравнений, такая система называется прямоугольной или недоопределённой, если наоборот — переопределённой.  Решение системы линейных алгебраических уравнений — совокупность $ n $ чисел $ c_1, c_2, \dots, c_n $, таких что их соответствующая подстановка вместо $ x_1, x_2, \dots, x_n $ в систему обращает все её уравнения в тождества.

Шаблон:ЯкорьСистема называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Решения считаются различными, если хотя бы одно из значений переменных не совпадает. Совместная система с единственным решением называется определённой, при наличии более одного решения — недоопределённой.

Матричная записьПравить

СЛАУ может быть представлена и в матричной форме:

$ \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{pmatrix} $

или:

$ Ax = b $.

Здесь $ A $ — это матрица системы, $ x $ — столбец неизвестных, а $ b $ — столбец свободных членов. Если к матрице $ A $ приписать справа столбец свободных членов, то получившаяся матрица называется расширенной. Теорема Кронекера — Капелли устанавливает необходимое и достаточное условие совместности системы линейных алгебраических уравнений посредством свойств матричных представлений: система совместна тогда и только тогда, когда ранг её матрицы совпадает с рангом расширенной матрицы.

Эквивалентные системы линейных уравненийПравить

Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот. Также считается, что системы, не имеющие решений, эквивалентны.

Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.

Система линейных алгебраических уравнений $ A \bold{x} \ = \bold{b} $ эквивалентна системе $ C A \bold{x} \ = C \bold{b} $, где $ C $ — невырожденная матрица. В частности, если сама матрица $ A $ — невырожденная, и для неё существует обратная матрица $ A^{-1} $, то решение системы уравнений можно формально записать в виде $ \bold{x} = A^{-1} \bold{b} $.

Прямые методы дают алгоритм, по которому можно найти точное решение систем линейных алгебраических уравнений. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.

Некоторые прямые методы:

Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения

$ \bold{x} = A^\prime \bold{x} + \bold{b}^\prime $,

эквивалентного начальной системе линейных алгебраических уравнений. При итерации $ \bold{x} $ в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:

$ \bold{x}_{n+1} = A^\prime \bold{x}_n + \bold{b}^\prime $.

Итерационные методы делятся на несколько типов, в зависимости от применяемого подхода:

• Основанные на расщеплении: $ (M-N)\bold{x}=\bold{b}\Leftrightarrow M\bold{x}=N\bold{x}+\bold{b} \Rightarrow M\bold{x}^{n+1}=N\bold{x}^n+\bold{b} $
• Вариационного типа: $ A\bold{x}=\bold{b}\Rightarrow \|A\bold{x}-\bold{b}\|\rightarrow \min $
• Проекционного типа: $ A\bold{x}=\bold{b}\Rightarrow (A\bold{x},\bold{m})=(\bold{b},\bold{m}) \forall\bold{m} $

Среди итерационных методов:

ru.math.wikia.com