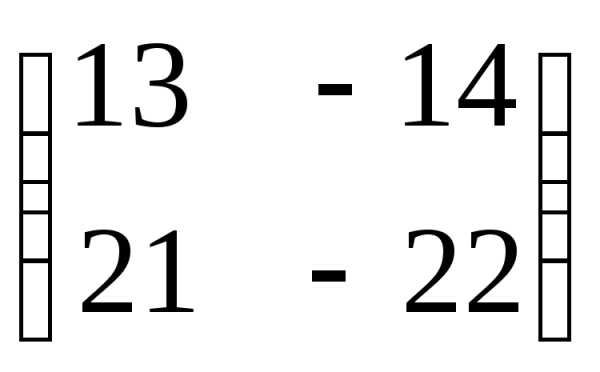Решение матричных уравнений примеры – Тема 3. Нахождение обратных матриц. Решение матричных уравнений. — КиберПедия

Решение матричных уравнений: теория и примеры

Матричным уравнением называется уравнение вида

A ⋅ X = B

или

X ⋅ A = B,

где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.

Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B, обе его части следует умножить на обратную к A матрицу слева:

.

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому

.

Так как E — единичная матрица, то E ⋅ X = X. В результате получим, что неизвестная матрица

X равна произведению матрицы, обратной к матрице A, слева, на матрицу B:

.

Как решить матричное уравнение во втором случае? Если дано уравнение

X ⋅ A = B,

то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A, и умножать матрицу B на неё справа:

,

,

.

Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X. То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A.

Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

A ⋅ X ⋅ B = C,

является

.

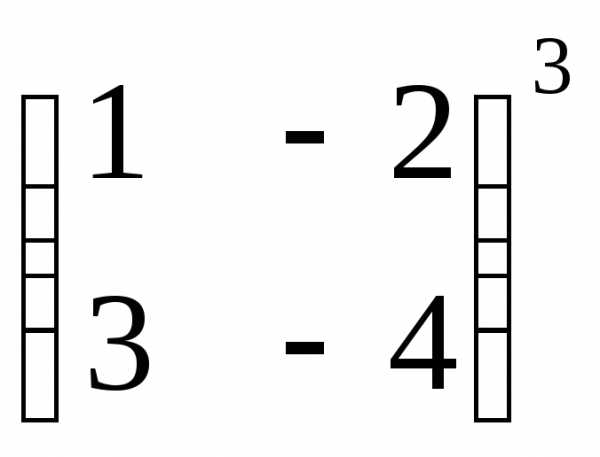
Пример 1. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы

B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.

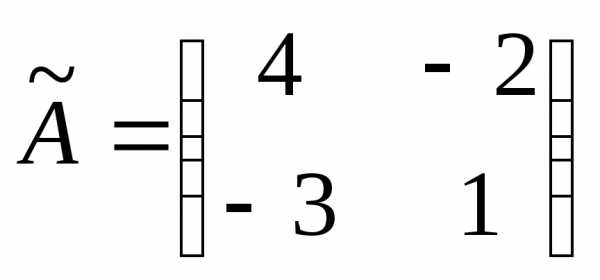
Сначала найдём определитель матрицы A:

.

Найдём алгебраические дополнения матрицы A:

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

.

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице

A:

.

Наконец, находим неизвестную матрицу:

---

Решить матричное уравнение самостоятельно, а затем посмотреть решение

---

Пример 3. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице

A.

Сначала найдём определитель матрицы A:

.

Найдём алгебраические дополнения матрицы A:

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

.

Находим матрицу, обратную матрице A:

.

Находим неизвестную матрицу:

До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.

Пример 4. Решить матричное уравнение

.

Решение. Это уравнение первого вида: A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

.

Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

.

Находим матрицу, обратную матрице A, и делаем это легко, так как определитель матрицы A равен единице:

.

Находим неизвестную матрицу:

Пример 5. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

.

Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

.

Находим матрицу, обратную матрице A:

.

Находим неизвестную матрицу:

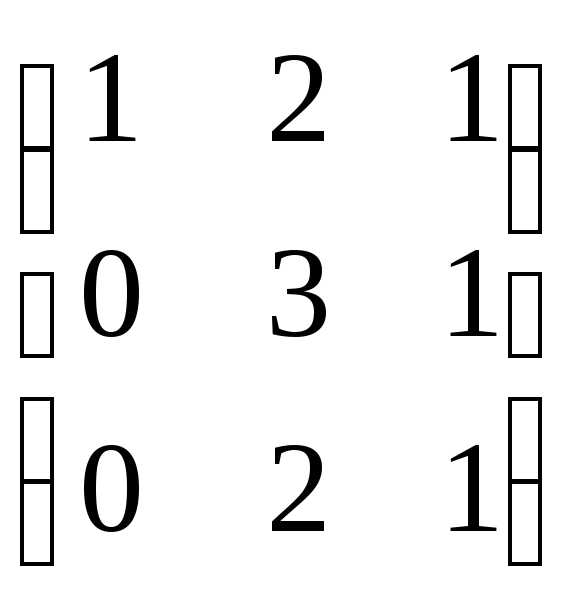
Пример 6. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C, то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

.

Найдём алгебраические дополнения матрицы A:

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

.

Находим матрицу, обратную матрице A:

.

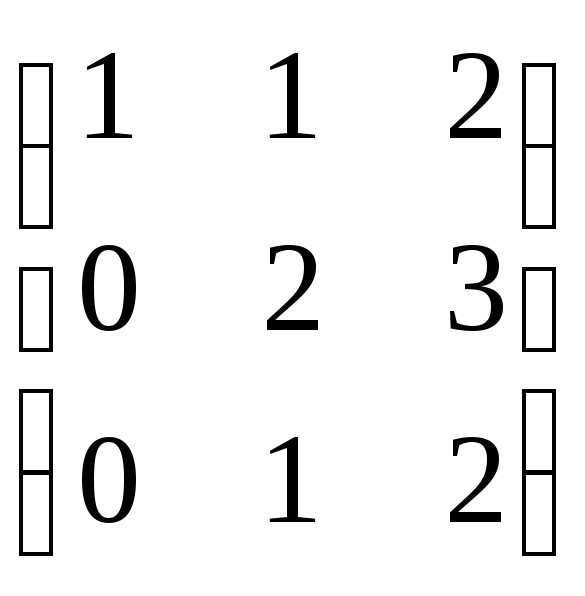
Найдём матрицу, обратную матрице B.

Сначала найдём определитель матрицы B:

.

Найдём алгебраические дополнения матрицы B:

Составим матрицу алгебраических дополнений матрицы B:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B:

.

Находим матрицу, обратную матрице B:

.

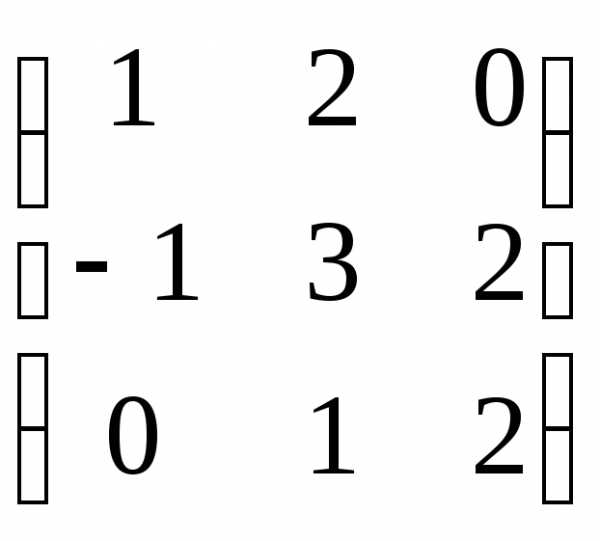
Находим неизвестную матрицу:

Поделиться с друзьями

Начало темы «Матрицы»

Продолжение темы «Матрицы»

Другие темы линейной алгебры

function-x.ru

Матричные уравнения и их решение

Определение и формулы матричных уравнений

ОПРЕДЕЛЕНИЕ Матричным уравнением называется уравнение, состоящее из нескольких матриц-коэффициентов и неизвестной матрицы

Простейшим матричным уравнением есть уравнение вида или ,

где — матрицы.

Алгоритм решения матричных уравнений

1. Матричное уравнение приводится к одному из простейших уравнений:

или

где — известные матрицы, — искомая (неизвестная) матрица.

ЗАМЕЧАНИЕ Существует также уравнение вида , но оно является комбинацией методов решения двух первых указанных простейших уравнений.

Чтобы привести произвольное матричное уравнение к одному из видов (1), надо все известные матрицы по свойствам уравнений перенести вправо, а неизвестную матрицу в левой части и свести подобные.

2. Разрешаем полученное простейшее уравнение относительно неизвестной матрицы .

2.1 Если в результате преобразований получили простейшее уравнение , то необходимо левую и правую часть этого равенства слева умножить на обратную матрицу к матрице :

   

ЗАМЕЧАНИЕ

Поскольку умножение матриц некоммутативно, то нужно строго соблюдать умножение слева или справа, иначе это влияет на результат.

2.2 Для простейшего уравнения после умножения справа на обратную матрицу получаем:

   

ЗАМЕЧАНИЕ Обратная матрица находится либо методом союзной матрицы, либо методом присоединенной матрицы.

3. Далее вычисляется одно из произведений или , что и определяет искомую матрицу.

4. Делаем проверку, для этого подставляем найденную матрицу в исходное уравнение.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ — ПриМат

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Олег Шпинарев (7), Людмила Рыбальченко (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Елизавета Снежинская (5), Вадим Покровский (5), Кирилл Волков (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Алиса Ворохта (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Валерия Заверюха (5), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Андрей Лисовой (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Иван Мясоедов (4), Павел Жуков (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Святослав Волков (4), Алёна Гирняк (4), Николай Царев (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Никита Савко (4), Кондрат Воронов (4), Иван Чеповский (4), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Василевский (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Стефания Амамджян (3), Валерия Сиренко (3), Андрей-Святозар Чернецкий (3), Вячеслав Иванов (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Константин Григорян (3), Карина Миловская (3), Стас Коциевский (3), Павел Бакалин (3), Антон Локтев (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Томас Пасенченко (3), Константин Мысов (3), Мария Карьева (3), Александра Рябова (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Кирилл Сплошнов (3), Дмитрий Козачков (3), Алёна Янишевская (3), Илья Черноморец (3), Дмитрий Байков (3), Павел Загинайло (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Артем Чернобровкин (3), Дмитрий Мороз (3), Станислав Чмиленко (3), Катя Писова (3), Данила Савчак (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Георгий Мартынюк (3), Виктор Булгаков (3), Валерия Ларикова (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Юрий Олейник (2), Татьяна Таран (2), Даниил Крутоголов (2), Настя Кондратюк (2), Сергей Запорожченко (2), Георгий Луценко (2), Настя Панько (2), Дэвид Ли (2), Александр Коломеец (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Антон Джашимов (2), Александр Гутовский (2), Таня Спичак (2), Радомир Сиденко (2), Алина Гончарова (2), Андрей Сидоренко (2), Юлия Стоева (2), Яна Колчинская (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Роман Гайдей (2), Гасан Мурадов (2), Алексей Никифоров (2), Настя Филипчук (2), Александр Дяченко (2), Михаил Абабин (2), Кирилл Бондаренко (2), Бриткариу Ирина (2), Андрей Данилов (2), Александра Филистович (2), Марк Носуленко (1), Артак Григорян (1), Юрий Холодков (1), Никита Пушкин (1),

ib.mazurok.com

Решение матричных уравнений

Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«Московский государственный технический университет имени Н.Э. Баумана»

(КФ МГТУ им. Н.Э. Баумана)

Влайков Н.Д.

Решение матричных уравнений

Методические указания для проведения упражнений

по курсу аналитической геометрии

Калуга 2011г.

Содержание.

Цели занятия стр.4

План занятия стр.4

Необходимые теоретические сведения стр.5

Практическая часть стр.6

Контроль освоения пройденного материала стр.10

Домашнее задание стр.11

Количество часов: 2

Цели занятия:

1. Систематизировать полученные теоретические знания о видах матричных уравнений и способах их решения.

2. Применить на практике методы решения матричных уравнений.

План занятия:

1. Кратко изложить теоретический материал.

2. Решить матричное уравнение видаметодом с использованием обратной матрицы.

3. Решить матричное уравнение видаметодом, основанным на элементарных преобразованиях строк матрицы.

4. Сравнить использованные методы.

5. Решить матричное уравнение видаметодом с использованием обратной матрицы.

6. Решить матричное уравнение вида методом с использованием обратной матрицы.

7. Проверить выполнение текущего домашнего задания.

8. Провести проверочную работу.

9. Представить тему следующего семинарского занятия.

10. Выдать текущее домашнее задание.

Необходимые теоретические сведения.

Рассмотрим два вида матричных уравнений относительно неизвестной матрицы :и, где матрицыи— известны, причем— квадратная и невырожденная.

Опр. Некоторую матрицу называют решением матричного уравнения относительно неизвестной матрицы 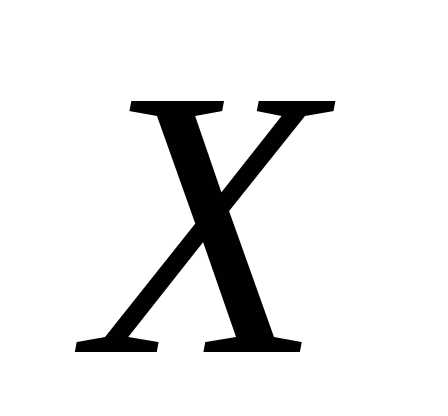, если при ее подстановке вместо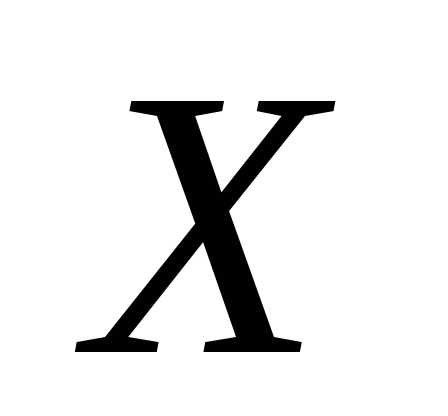матричное уравнение превращается в тождество.

Рассмотрим уравнение .

Первый метод предполагает вычисление обратной матрицы и дает запись решения матричного уравнения в виде. Причем данное решение единственно.

Второй метод основан на элементарных преобразованиях строк блочной матрицы 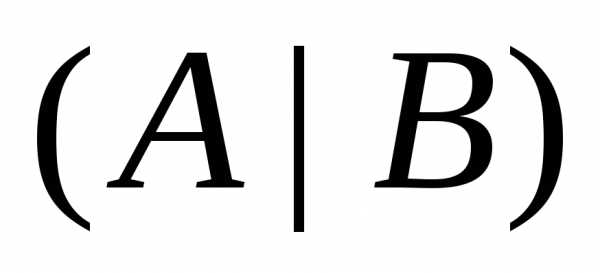и имеет своей целью преобразование ее к виду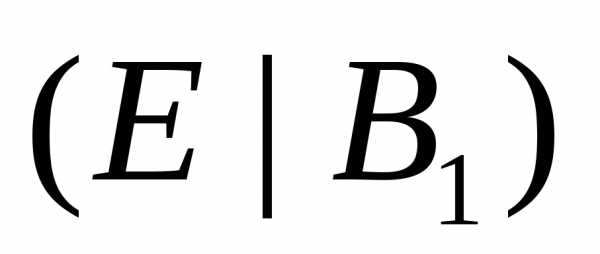, в котором вместо матрицыстоит единичная матрица. Тогда матрицаи будет решением уравнения.

Проверка ответа выполняется подстановкой найденного решения в исходное уравнение.

Матричное уравнение так же можно решить двумя способами. Если известна матрица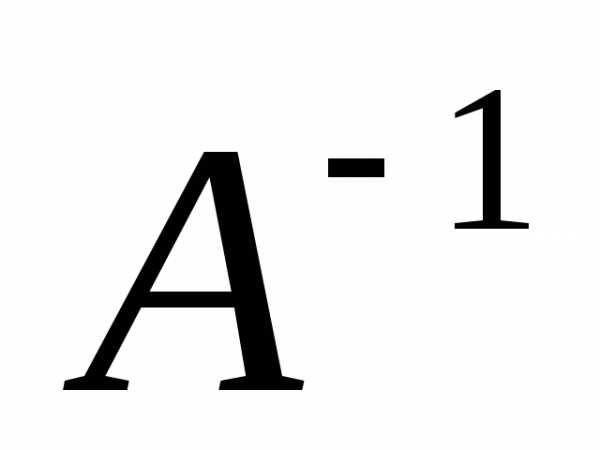, то умножаем справа на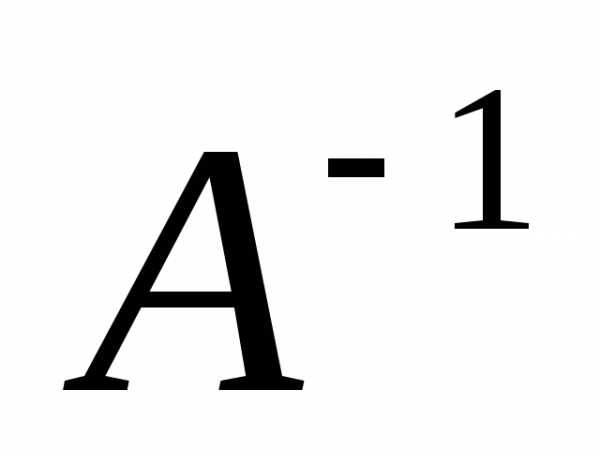матричное уравнениеи после очевидных преобразований получаем ответ в виде произведения двух матриц. Другой метод решения матричного уравнениясостоит в транспонировании его левой и правой частей,. После введения новой неизвестной матрицы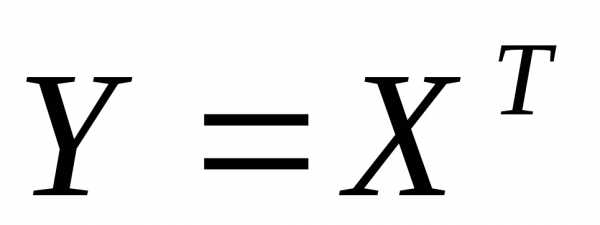получаем уравнение вида, которое решается методом элементарных преобразований.

Практическая часть.

Пример 1. Решить матричное уравнение: _,

где

; .

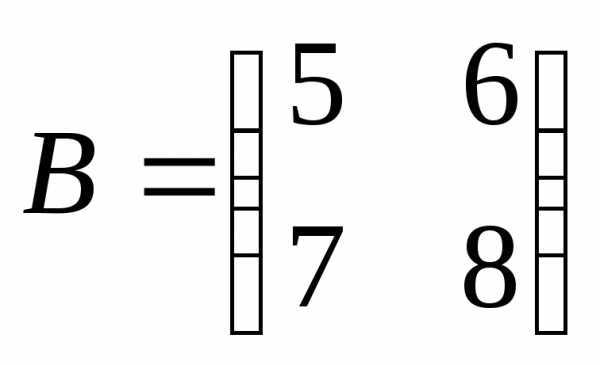Решение.

1-ый способ. Найдем решение, используя обратную матрицу:

_{Решение ищем в виде ;}

_{Найдем матрицу 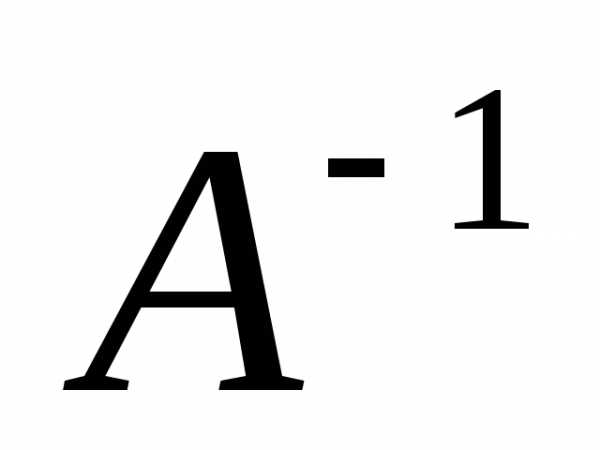(например, при помощи присоединенной матрицы)}

_.

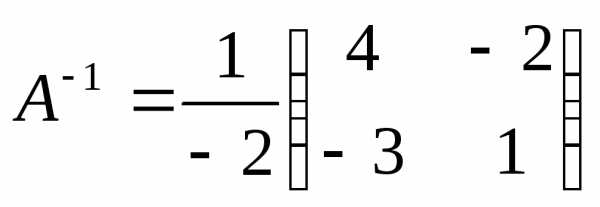_{Таким образом, получим:}

_.

_{2-ой способ. Найдем решение методом элементарных преобразований:}

_{Запишем матрицу 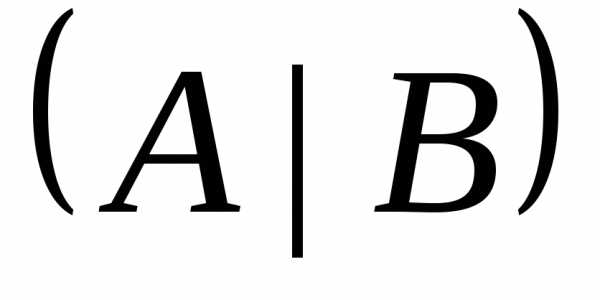и выполним элементарные преобразования ее строк с целью привести ее к виду .}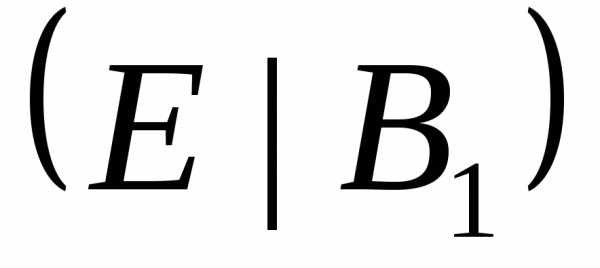

_.

_{Следовательно, .}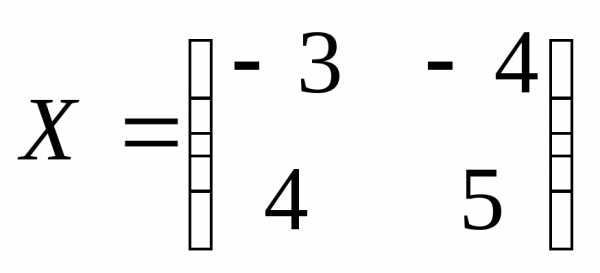

_{Проверка осуществляется подстановкой в исходное уравнение:}

_{— Верно.}

Пример 2. Решить матричное уравнение: _,

где

; ;.

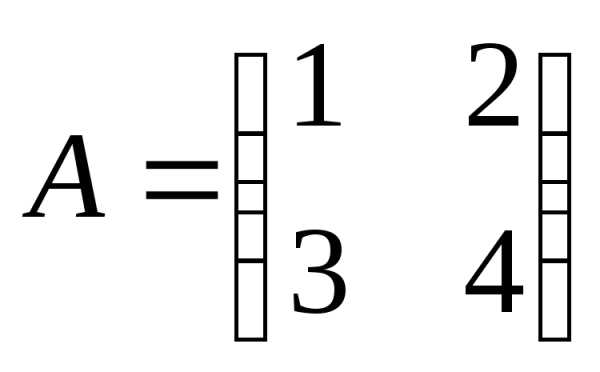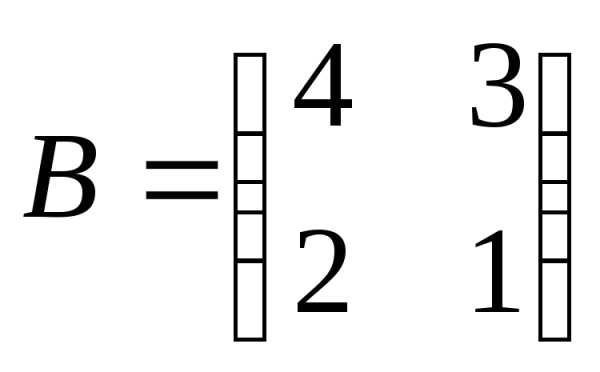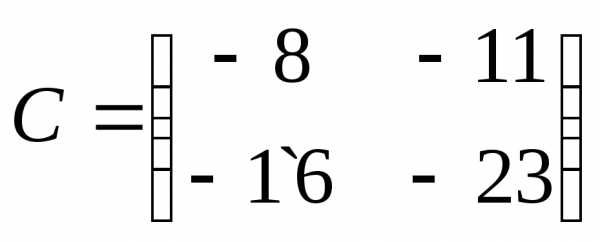Решение.

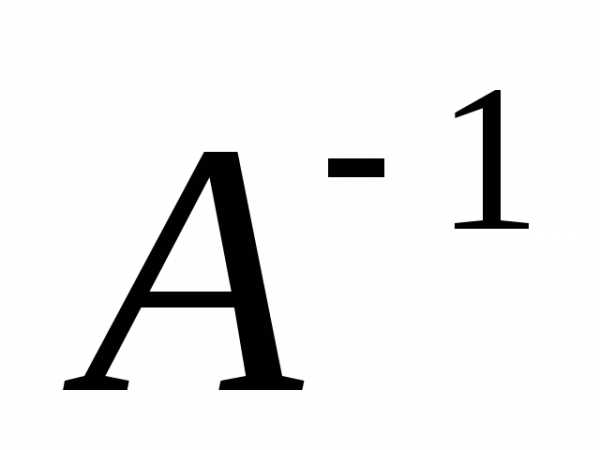Если для матриц исуществуют обратные матрицыи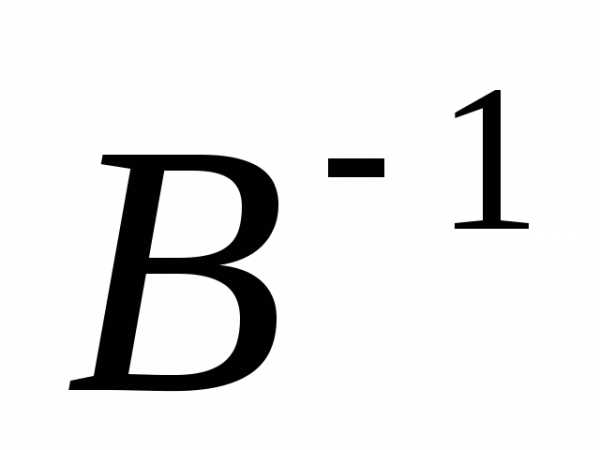соответственно, умножим обе части уравнения слева на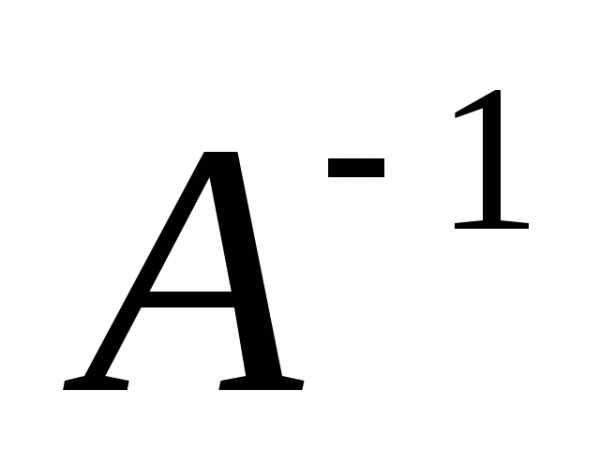, справа на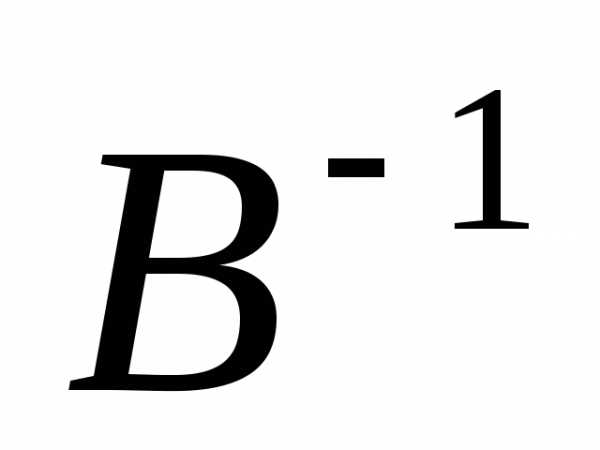. В результате получим:

. Учитывая, что ,

(— единичная матрица) можно записать:. Так как

— единичная матрица, окончательно имеем уравнение:

где матрица 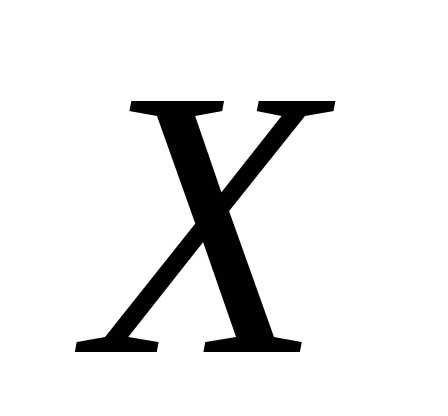— решение уравнения.

Если же хотя бы одна из матриц илине имеет обратную, уравнение не имеет решения.

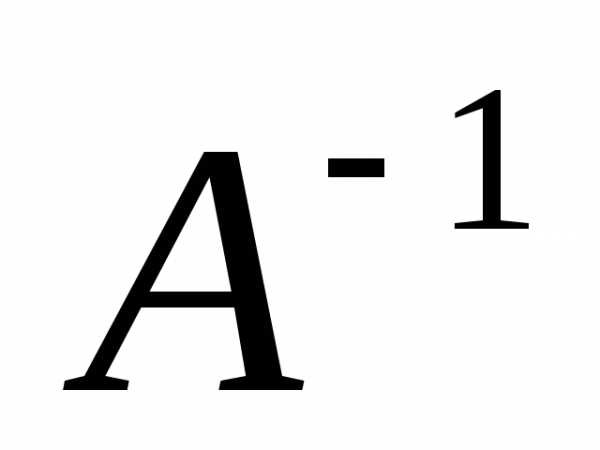Для матрицы найдем или докажем, что она не существует.

а) обратная матрица существует.

б) .

в) Найдем алгебраические дополнения для матрицы и составим из них присоединенную матрицу:

.

г) Известно, что 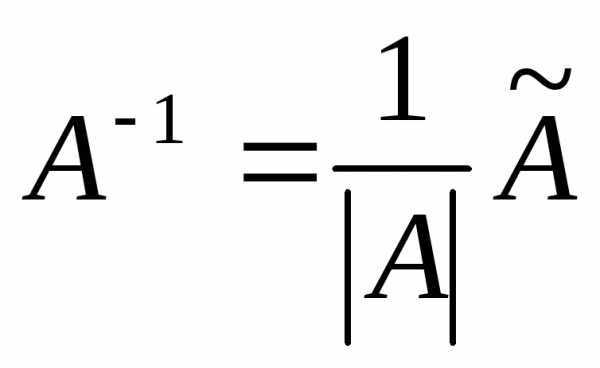; тогда

.

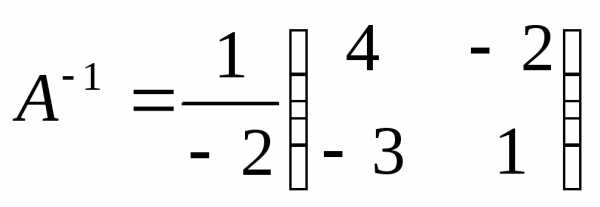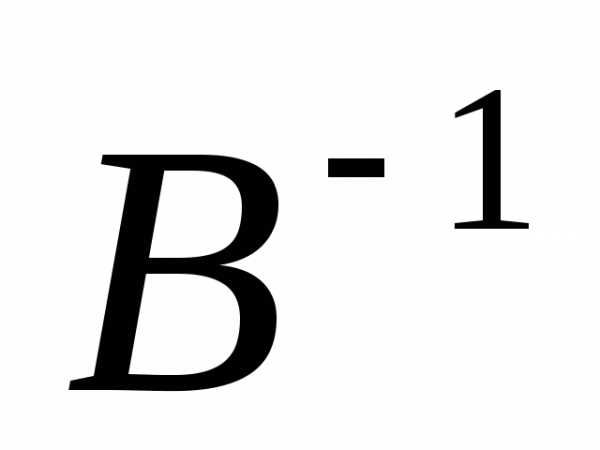Для матрицы найдем или докажем, что она не существует.

а) обратная матрица существует.

б) .

в) Найдем алгебраические дополнения для матрицы и составим из них присоединенную матрицу:

.

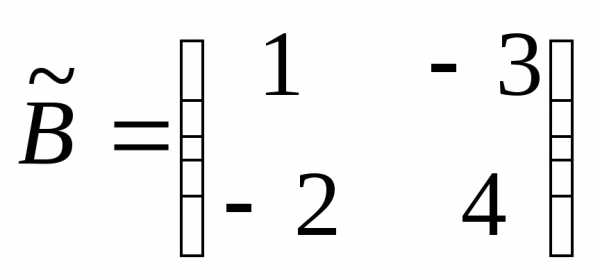г) По формуле ;

.

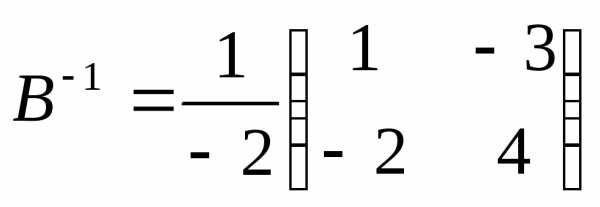Найдем неизвестную матрицу .

.

Ответ:.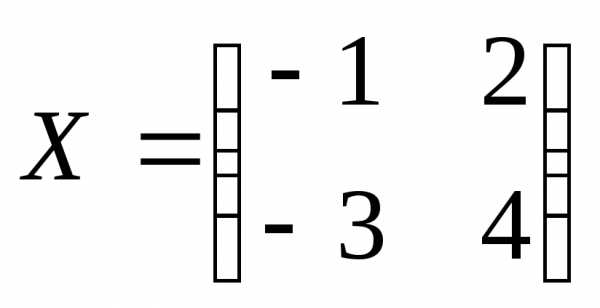

Решить матричные уравнения:

№2.121(2.39)

. Отв.: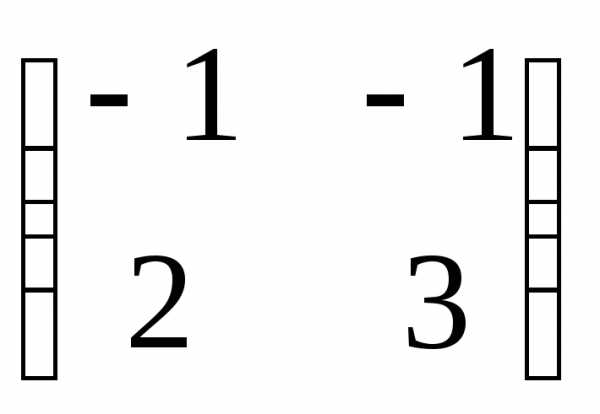

№2.122(2.40)

. Отв.: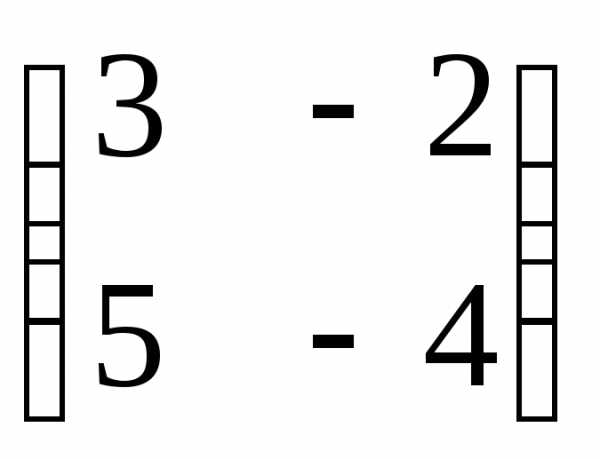

№2.123(2.41)

. Отв.: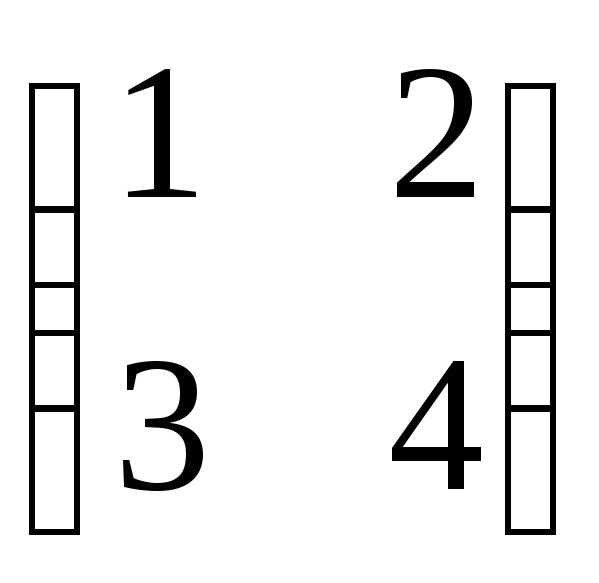

№2.124(2.42)

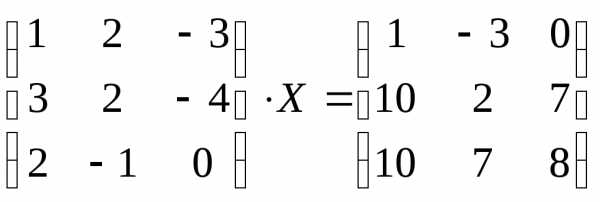. Отв.: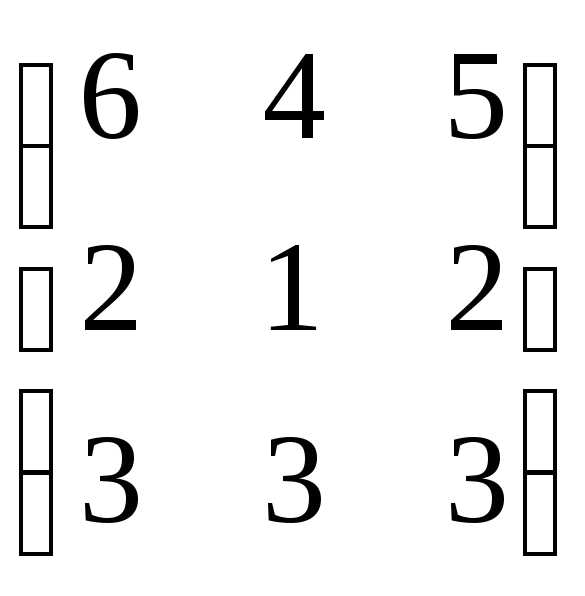

№2.125(2.43)

. Отв.:

Представление темы следующего семинара.

Решение систем линейных однородных уравнений.

Контроль освоения пройденного материала.

Проверочная работа 5 минут. Участвует 4 студента с четными номерами по журналу, начиная с №10

Задание:

Вар№1 Выполнить действия:	Вар№2 Выполнить действия:
Вар№3 Найти матрицу обратную данной:	Вар№4 Найти матрицу обратную данной:

Ответы:

Вар№1 Выполнить действия:	Вар№2 Выполнить действия:
Вар№3 Найти матрицу обратную данной:	Вар№4 Найти матрицу обратную данной:

Домашнее задание.

1.Решить матричное уравнение :

1) ; .

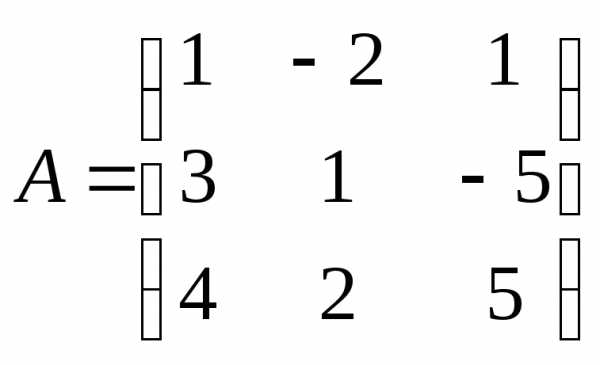2) ; .

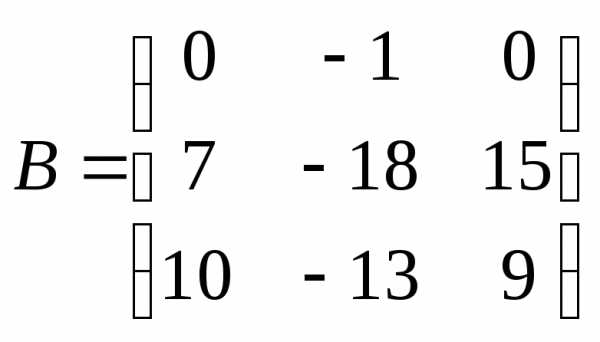
2.Решить матричное уравнение :

1) ;;.

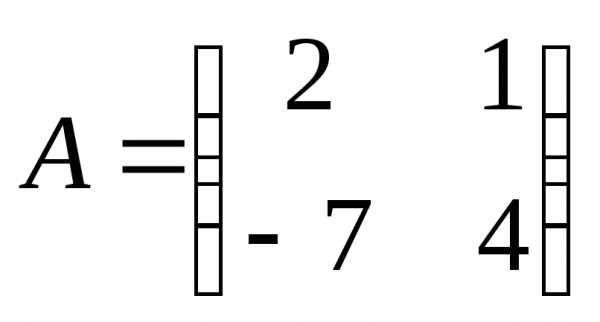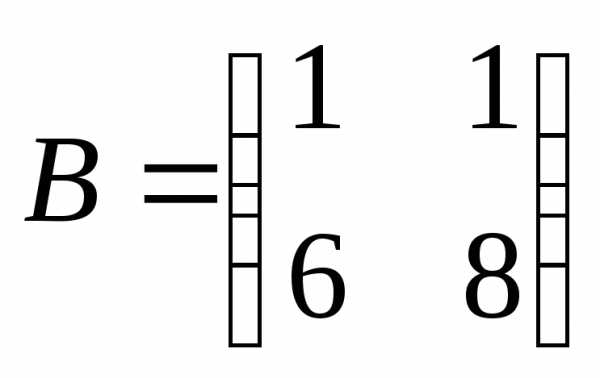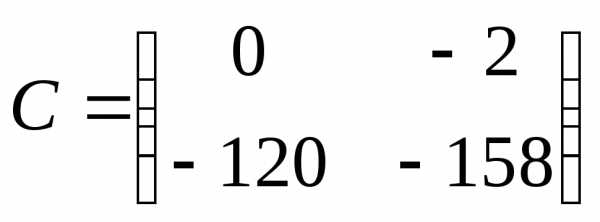2) ;;.

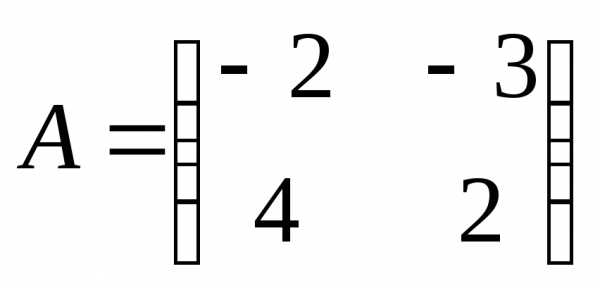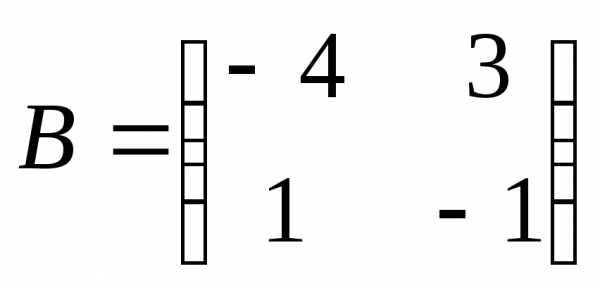3.Проработка лекций на темы:

Системы линейных алгебраических уравнений (СЛАУ). Координатная, матричная и векторная формы записи. Критерий Кронекера — Капелли совместности СЛАУ. Однородные СЛАУ. Критерий существования ненулевого решения однородной СЛАУ. Свойства решений однородной СЛАУ. Фундаментальная система решений однородной СЛАУ, теорема о ее существовании. Нормальная фундаментальная система решений. Теорема о структуре общего решения однородной СЛАУ.

11

studfiles.net

Простейшие матричные уравнения

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

 

Рассмотрим матрицы

; ;

Причем элементы матриц А и В заданы, а Х₁, Х₂, Х₃ – неизвестные.

Тогда уравнение А × Х = В называется простейшим матричным уравнением.

Чтобы его решить, т.е. найти элементы матрицы неизвестных Х, поступим следующим образом:

1. Умножим обе части уравнения на матрицу А^-1, обратную для матрицы А, слева:

А^-1 (А × Х) = А^-1 × В

2. Используя свойство умножения матриц, запишем

(А^-1 × А) Х = А^-1 × В

3. Из определения обратной матрицы

(А^-1 × А = Е) имеем Е × Х = А^-1 × В.

4. Используя свойство единичной матрицы (Е × Х = Х), окончательно получим Х = А^-1 × В

Замечание. Если матричное уравнение имеет вид Х × С = Д, то для нахождения неизвестной матрицы Х уравнение необходимо умножать на С^-1справа.

Пример. Решить матричное уравнение

Решение. Введем обозначения

А = ; В = ,

Их определения умножения матриц с учетом размерностей А и В матрица неизвестных Х будет иметь вид

Х =

С учетом введенных обозначений имеем

А × Х = В откуда Х = А^-1 × В

Найдем А^-1 по алгоритму построения обратной матрицы

Вычислим произведение

Тогда для Х получим

Х = откуда х₁ = 3, х₂ = 2

 

Ранг матрицы

 

Рассмотрим матрицу А размера (m x n)

Минором к-ого порядка матрицы А будем называть определитель порядка к, элементами которого являются элементы матрицы А, стоящие на пересечении любых К строк и любых К столбцов. Очевидно, к £ min (m, n).

Определение. Рангом r(A) матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля.

Определение. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется базисным минором.

Определение. Матрицы, имеющие одинаковые ранги, называются эквивалентными.

 

Вычисление ранга матрицы

 

Определение. Матрица называется ступенчатой, если под первым ненулевым элементом каждой ее строки стоят нули в нижележащих строках.

Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк.

Таким образом, преобразуя матрицу к ступенчатому виду, несложно определить ее ранг. Эта операция осуществляется с помощью элементарных преобразований матрицы, которые не изменяют ее ранга:

— умножение всех элементов ряда матрицы на число l ¹ 0;

— замена строк столбцами и наоборот;

— перестановка местами параллельных рядов;

— вычеркивание нулевого ряда;

— прибавление к элементам некоторого ряда соответствующих элементов параллельного ряда, умноженных на любое действительное число.

Пример. Вычислить ранг матрицы

А =

Решение. Преобразуем матрицу к ступенчатому виду. Для этого к третьей строке прибавим вторую, умноженную на (-3).

А ~

К четвертой строке прибавим третью.

А ~

Число ненулевых строк в полученной эквивалентной матрице равно трем, следовательно r(А) = 3.

 

 

Системы n линейных уравнений с n неизвестными.

Методы их решения

Рассмотрим систему n линейных уравнений с n неизвестными.

а₁₁х₁ + а₁₂х₂ + … + а_1nx_n = b₁

а₂₁х₁ + а₂₂х₂ + … + а_2nx_n = b₂ (1)

……………………………….

а_n1х₁ + а_n2х₂ + … + а_nnx_n = b_n

 

Определение: Решением системы (1) называется совокупность чисел (х₁, х₂, …, х_n), которая обращает каждое уравнение системы в верное равенство.

Матрица А, составленная из коэффициентов при неизвестных, называется основной матрицей системы (1).

A =

Матрица В, состоящая из элементов матрицы А и столбца свободных членов системы (1), называется расширенной матрицей.

В =

 

Матричный метод

Рассмотрим матрицы

Х = — матрица неизвестных;

С = — матрица свободных членов системы (1).

Тогда по правилу умножения матриц систему (1) можно представить в виде матричного уравнения

А × Х = С (2)

Решение уравнения (2) изложено выше, то есть Х = А^-1 × С, где А^-1 – обратная матрица для основной матрицы системы (1).

 

Метод Крамера

 

Система n линейных уравнений с n неизвестными, главный определитель которой отличен от нуля, всегда имеет решение и притом единственное, которое находится по формулам:

где D = det А – определитель основной матрицы А системы (1), который называется главным, Dх_i получаются из определителя D заменой i-ого столбца столбцом из свободных членов, т.е.

D = ;

Dх₁ = ;

Dх₂ = ; … ;

Dх_n = ;

Пример. Решить систему уравнений методом Крамера

 

2х₁ + 3х₂ + 4х₃ = 15

х₁ + х₂ + 5х₃ = 16

3х₁ — 2х₂ + х₃ = 1

Решение.

Вычислим определитель основной матрицы системы

D = det A = = 44 ¹ 0

Вычислим вспомогательные определители

Dх₁ = = 0;

Dх₂ = = 44;

Dх₃ = = 132.

По формулам Крамера найдем неизвестные

; ; .

Таким образом, х₁ = 0; х₂ = 1; х₃ = 3.

 

Метод Гаусса

 

Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы, т.е. в приведении основной матрицы системы к треугольному виду, когда под ее главной диагональю стоят нули. Это достигается с помощью элементарных преобразований матрицы над строчками. В результате таких преобразований не нарушается равносильность системы и она приобретает также треугольный вид, т.е. последнее уравнение содержит одну неизвестную, предпоследнее две и т.д. Выражая из последнего уравнения n-ую неизвестную и с помощью обратного хода, используя ряд последовательных подстановок, получают значения всех неизвестных.

Пример. Решить систему уравнений методом Гаусса

3х₁ + 2х₂ + х₃ = 17

2х₁ — х₂ + 2х₃ = 8

х₁ + 4х₂ — 3х₃ = 9

Решение. Выпишем расширенную матрицу системы и приведем, содержащуюся в ней матрицу А к треугольному виду.

В =

Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных выражений при последующих вычислениях

В ~

Первую строку полученной матрицы умножим последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом В будет иметь вид:

В ~

После умножения второй строки на и сложения ее с третьей строкой матрица А примет треугольный вид. Однако чтобы упростить вычисления можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим:

В ~

Далее, умножая вторую строку матрицы на 10 и складывая с третьей, окончательно получим:

В ~

Восстановим из полученной матрицы В систему уравнений, равносильную данной

х₁ + 4х₂ — 3х₃ = 9

х₂ — 2х₃ = 0

— 10х₃ = -10

Из последнего уравнения находим Найденное значение х₃ = 1 подставим во второе уравнение системы, из которого х₂ = 2х₃ = 2 × 1 = 2.

После подстановки х₃ = 1 и х₂ = 2 в первое уравнение для х₁ получим х₁ = 9 — 4х₂ + 3х₃ = 9 — 4 × 2 + 3 × 1 = 4.

Итак, х₁ = 4, х₂ = 2, х₃ = 1.

Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.

Проверка:

3 × 4 + 2 × 2 + 1 = 17 верно

2 × 4 — 2 + 2 × 1 = 8 верно

4 + 4 × 2 — 3 × 1 = 9 верно

Итак, система решена верно.

 

Рекомендуемые страницы:

lektsia.com

Матричные уравнения

Каталин Дэвид

AX = B, где матрица A обратима

Поскольку умножение матриц не всегда коммутативно, умножаем слева обе части уравнения на$ A^{-1}$.

$A^{-1}\cdot|A\cdot X = B$

$A^{-1}\cdot A\cdot X = A^{-1}\cdot B$

$I_{n}\cdot X = A^{-1}\cdot B$

Решение уравнения имеет общий вид
$\color{red}{X =A^{-1}\cdot B}$

Пример 50
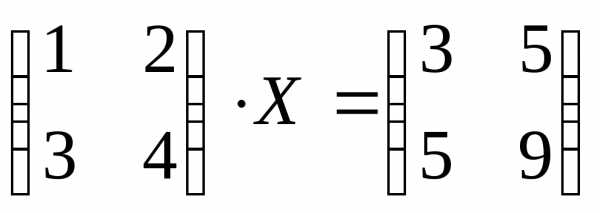
Решить уравнение
$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot X \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$

Убедимся, что первая матрица обратима.
$\left|A\right|=5-6=-1\neq 0$, следовательно, матрица обратима.

Умножаем слева на обратную ей матрицу.
$\begin{pmatrix} 1 & 3\\ 2 & 5\\ \end{pmatrix}^{-1}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot X= \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$

$I_{2}\cdot X = \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$

$X=\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$

$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}= \begin{pmatrix} -9 & -22\\ 4 & 9 \end{pmatrix}$

XA = B, где матрица A обратима

Поскольку умножение матриц не всегда коммутативно, умножаем справа обе части уравнения на$ A^{-1}$.

$X\cdot A = B |\cdot A^{-1}$

$X\cdot A\cdot A^{-1} = B\cdot A^{-1}$

$X \cdot I_{n} =B\cdot A^{-1}$

Решение уравнения имеет общий вид
$\color{red}{X =B\cdot A^{-1}}$

Пример 51
Решить уравнение
$X \begin{pmatrix} 1 & 3\\ 2 & 5\\ \end{pmatrix}= \begin{pmatrix} 3 & 5\\ 2 & 1\\ \end{pmatrix}$

Убедимся, что первая матрица обратима.
$\left|A\right|=5-6=-1\neq 0$, следовательно, матрица обратима.

Умножаем справа на обратную ей матрицу.
$X \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$

$X\cdot I_{2}= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$

$X=\begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$

$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix} \cdot \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}= \begin{pmatrix} -5 & 4\\ -8 & 5 \end{pmatrix}$

www.math10.com

Решение матричных уравнений

Следовательно, обратная матрица найдена верно.

Свойства обратной матрицы:

1.jA 1j =jA1j,

2.(A 1)1 = A,

3.(A B) 1 = B1 A1, где A и B – квадратные,

4.(A 1)T = (AT )1.

Спомощью обратной матрицы могут быть решены некоторые матричные уравнения. Рассмотрим их.

Уравнения вида A X = B.

Здесь X – матрица, значения элементов которой неизвестны, их требуется найти; матрицы A и B – заданные матрицы, причём матрица A – квадратная невырожденная, т.е jAj =6 0.

Умножим обе части уравнения на A 1 слева, равенство при этом сохранится:

A 1 A X = A1 B.

По определению обратной матрицы, A 1 A = E, где E – единичная матрица. Получим:

E X = A 1 B.

Так как E X = X, имеем:

X = A 1 B.

Итак, для решения матричного уравнения вида A X = B нужно умножить матрицу B на A 1 слева.

Пример. Решить уравнение						1	1			0	1	!.
						1	2 ! X =			0	3
Обозначим A =				1	1	!, B =		0	1	!. Тогда
			1		2			0	3
уравнение примет вид A X = B.
Найдём для матрицы A обратную:
	jAj = 2 + 1 = 1 6= 0;
	1		2		1	! =	2	1	!.
A 1 =				1			1 1
	1		1
Отсюда находим неизвестную матрицу X:
X = A 1 B =			2	1	!	0	1		0	1	!:
			1 1			0 3 ! =			0	2

Сделаем проверку: если матрица X найдена верно, то при подстановке её в данное уравнение получим верное равенство.

1	2 !		0	2 !	=	0	3 !	;
1	1		0	1		0	1

!!

Следовательно, уравнение решено верно.

37

Уравнения вида X A = B.

Отличие этого вида уравнений от предыдущего в том, что здесь матрица A умножается на матрицу X справа. Значит, и матрицу A 1 нужно умножать на B справа. В остальном решение проводится аналогично:

X A A 1 = B A1;

X E = B A 1;

X = B A 1:

Пример. Решить уравнение X							1	1	! =		0	1	!.
							1	2			0	3
			1 2								!. Тогда
Обозначим A =					!, B =				0	3
			1	1					0	1
уравнение примет вид X A = B.							!.
	A 1 =			1		1
					2	1
Отсюда находим неизвестную матрицу X:										3 3 !
X = B A 1 =	0 3		!		1 1 ! =								:
	0	1				2	1			1	1
Сделаем проверку:			1 2 !					0 3 !;
3 3 !							=
1	1		1	1				0	1

!!

Следовательно, уравнение решено верно.

Аналогичными рассуждениями можно получить решение уравнений вида A X B = C, где A и B – квадратные невырожденные матрицы:

X = A 1 C B1

.

Пример. Решить уравнение A X B = C, если

A =	0 3		0	2 1		; B =	0	1	2	2 1		;
	B	2	1	1	C		B	3	0	1	C
		1	4	2				0	1	0
	B				C		B				C
	@				A		@				A

01

8 1 2

BC

Для матрицы A получаем, что jAj = 8, обратная мат-

рица

			0	8	2	2	1
A 1 =	1		B				C	;
				4	3	1
	8
				12	7	3
			B				C
			@				A

для матрицы B: jBj = 7, обратная матрица

			0	2	1	2	1
		1	B				C
		7		1	3	6
B 1 =			B	0	0	7	C	:
			@				A

Следовательно, решением уравнения является матрица

				0			X = A 1 C B1 =							3 1
= 1						4	3	1	1 0 9				6
				B		8	2	2	C B			8	1		2	C
						12	7	3				11	10		15
8				B					C		B					C
				@				0	A @				1			A

2 1 2

						1					B			1					3	6			C
							7
											B			0					0			7	C		=
				0							@					1 0 0							A			7 1
=	1					16 32 32																			0			=
	56			B		24					0		8			C		B				2			1	2	C
						0 24 0																1			3	6
				B												C B											C
				@						0						A @								1			A
				=		1							0				112						0			=
					56 B							56							0				0	C
										B														C
										@	0		0						0	168				A
													1		0			0		1
										= B			0		2			0		C	:
											B									C
											@		0		0			3		A

Чтобы проверить, что найденная матрица X действи-

тельно является решением , подставим её в уравнение:

A X B = C;

0 3		0		2 1 0		0	2	0 1
B	2		1	1	C B	1	0	0	C
	1		4	2		0	0	3
B					C B				C
@					A @				A

0	1	2	2	1 =	0 9		6	3 1:
B	3	0	1	C B		8	1		2	C
	0	1	0			11	10		15
B				C	B					C
@				A	@					A

Перемножив матрицы A и X, получим:

0 3		0	6 1 0		1	2	2 1		=
B	2	2	3	C B	3	0	1	C
	1	8	6		0	1	0
B				C B				C
@				A @				A

01

8 1 2

BC

Таким образом,

0 9		6	3 1			=	0 9		6	3 1:
B	8	1		2	C		B	8	1		2	C
@					A		@					A
B	11	10		15	C		B	11	10		15	C

Значит уравнение решено верно.

4.3Задачи

1.Найдите матрицы, обратные для следующих матриц:

A =	2 4 ,						B =	4 6 ,
		4	0						3	2	0 1 ,
C =	0 3		9 4 1 ,				D =	0 0 2
	@	2	7	3	A			@	1	0	0	A
		1	5	3					0	0	3
F =	0 2		0		4 1	,	G =	0 0		1		6 1 .
		3	2		1				2	1		5
	@ 1		1		0 A			@ 0		0		2 A

2.Если A 1 BT (B A)T T B1 = E, то чему равен определитель матрицы B?

3.Для матрицы

01

найдите обратную. При каком значении параметра

обратная матрица не существует?

4.Решите матричные уравнения:

а)	3	4	X =		5	9 ;
	1	2	1		3	5	3
б) X 0				=	1			;
		1	1			2	0

studfiles.net