Решение матричным способом системы уравнений – примеры решения, обратная матрица, определение
5.2. Матричный метод решения систем линейных уравнений
Пусть
дана система 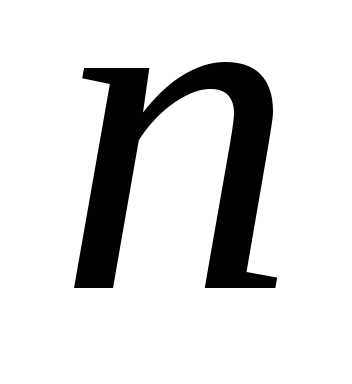 линейных уравнений с
линейных уравнений с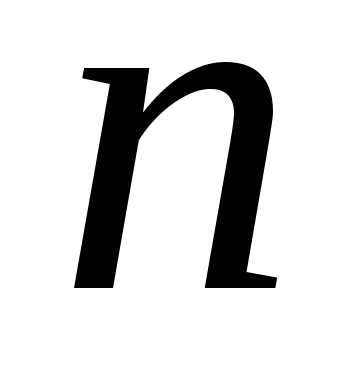 неизвестными:
неизвестными:
где

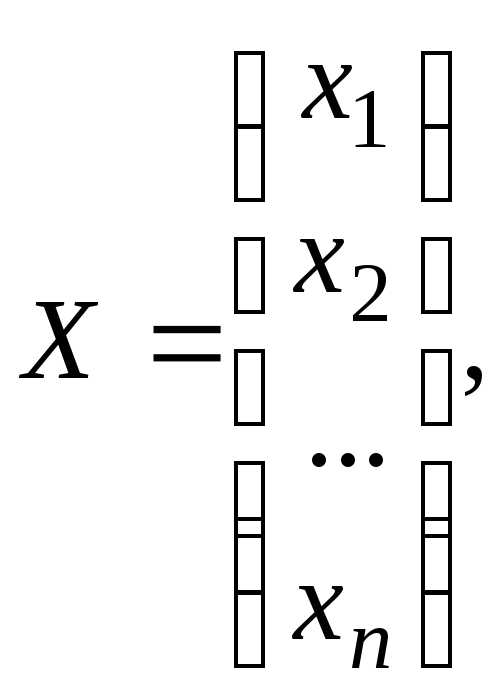
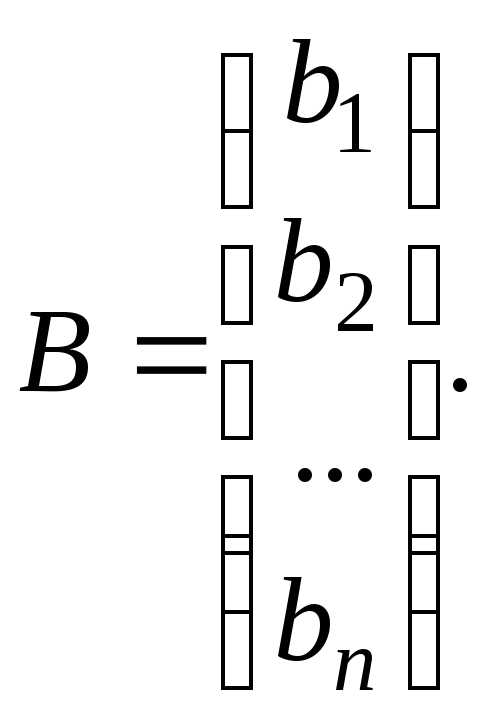
Будем
предполагать, что основная матрица  невырожденная.
Тогда, по теореме 3.1,
существует обратная матрица
невырожденная.
Тогда, по теореме 3.1,
существует обратная матрица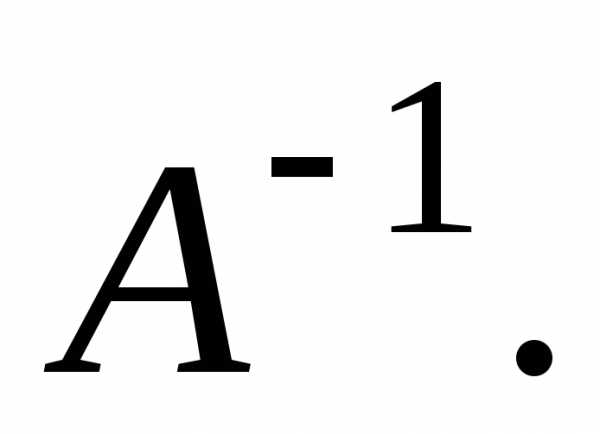
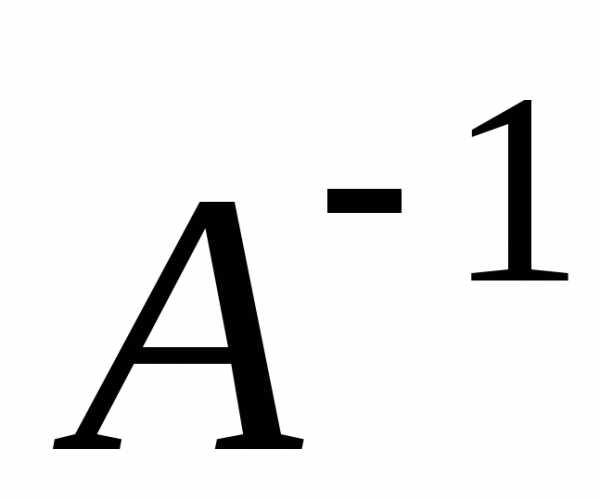 слева, воспользовавшись определением
3.2, а также утверждением 8) теоремы 1.1,
получим формулу, на которой основан
матричный метод решения систем линейных
уравнений:
слева, воспользовавшись определением
3.2, а также утверждением 8) теоремы 1.1,
получим формулу, на которой основан
матричный метод решения систем линейных
уравнений:Замечание. Отметим, что матричный метод решения систем линейных уравнений в отличие от метода Гаусса имеет ограниченное применение: этим методом могут быть решены только такие системы линейных уравнений, у которых, во-первых, число неизвестных равно числу уравнений, а во-вторых, основная матрица невырожденная.
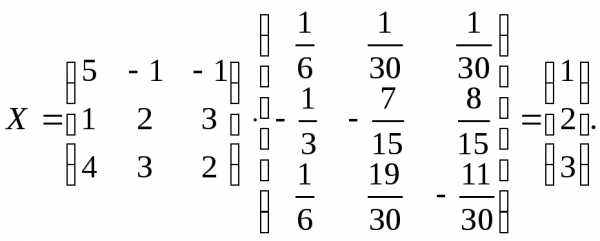
Пример. Решить систему линейных уравнений матричным методом.
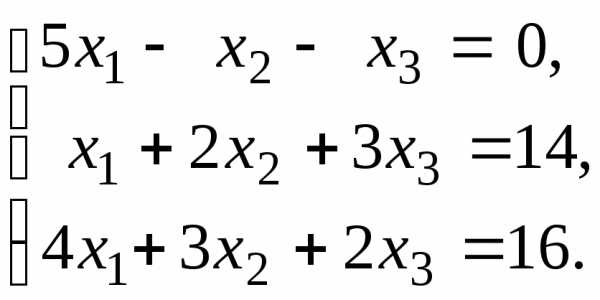
Задана система трёх линейных уравнений с тремя неизвестными где
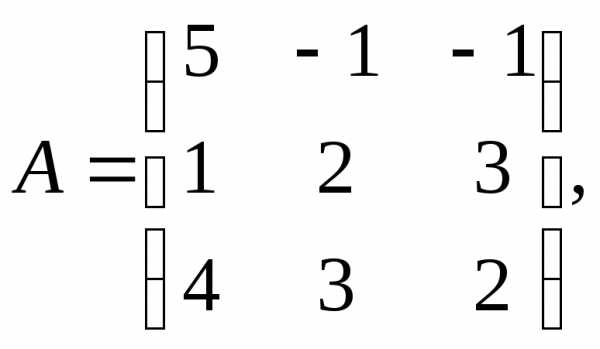
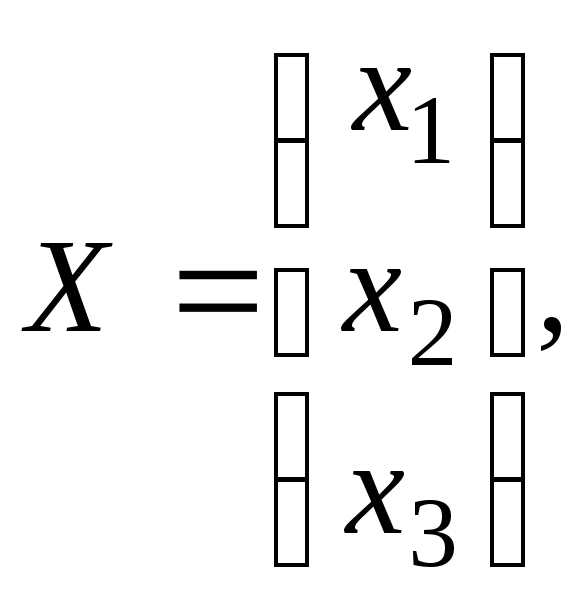
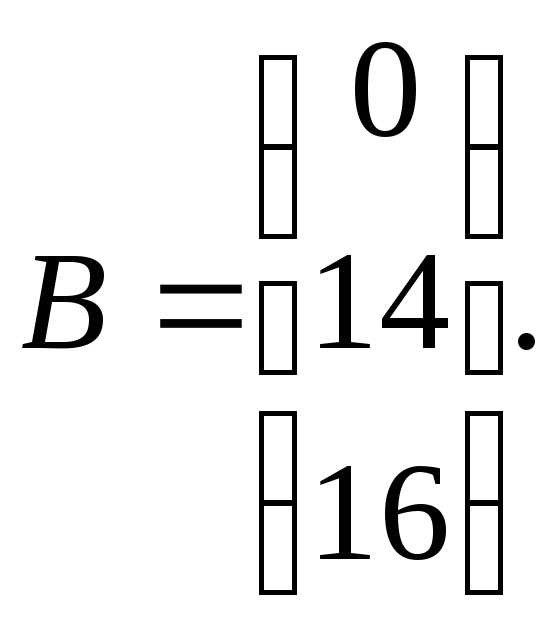
Основная матрица системы уравнений невырожденная, поскольку её определитель отличен от нуля:
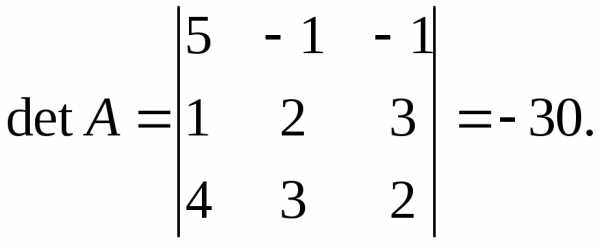
Обратную
матрицу 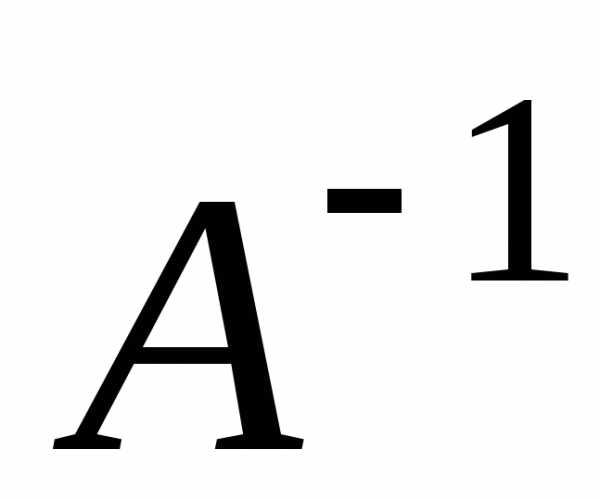 составим одним из методов, описанных в
пункте 3.
составим одним из методов, описанных в
пункте 3.
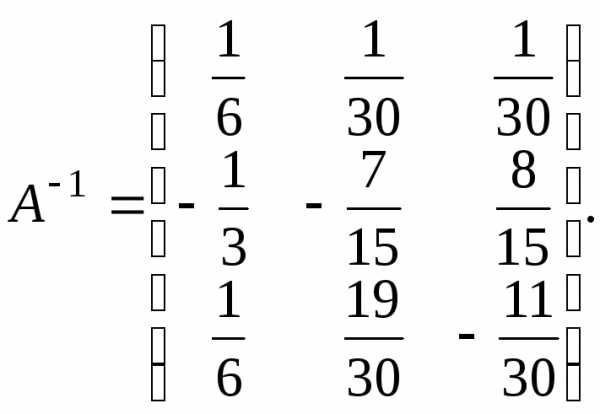
По формуле матричного метода решения систем линейных уравнений получим
5.3. Метод Крамера
Данный метод так же, как и матричный, применим только для систем линейных уравнений, у которых число неизвестных совпадает с числом уравнений. Метод Крамера основан на одноимённой теореме:
Теорема
5.2. Система  линейных уравнений с
линейных уравнений с неизвестными
неизвестными

основная матрица которой невырожденная, имеет единственное решение, которое может быть получено по формулам
где 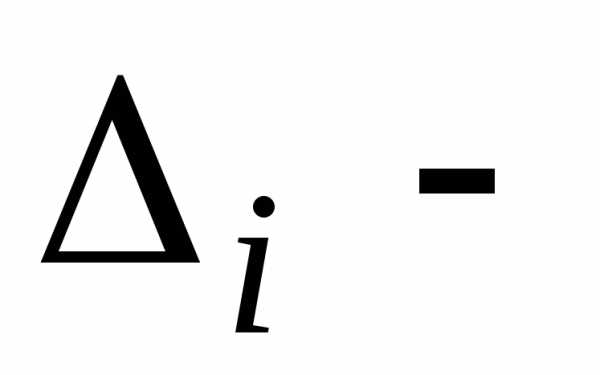 определитель
матрицы, полученной из основной матрицы
определитель
матрицы, полученной из основной матрицы
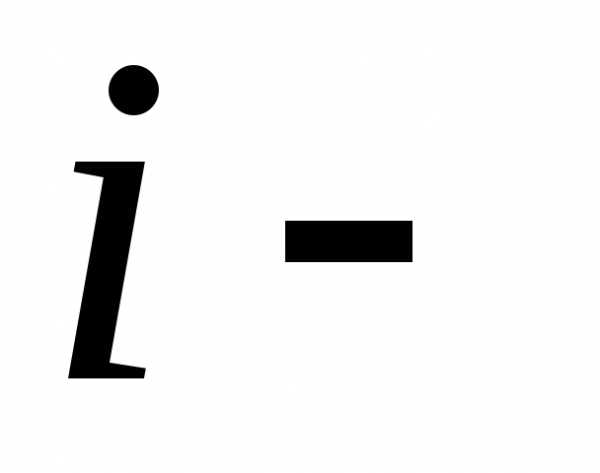 го
столбца столбцом свободных членов.
го
столбца столбцом свободных членов.Пример. Найдём решение системы линейных уравнений, рассмотренной в предыдущем примере, методом Крамера. Основная матрица системы уравнений невырожденная, поскольку Вычислим определители
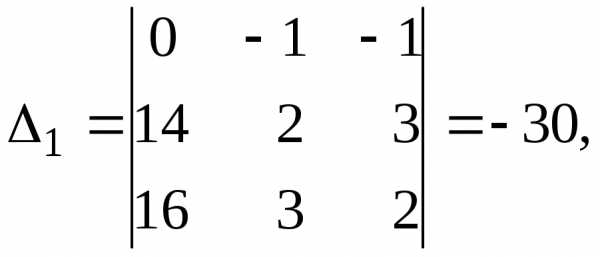
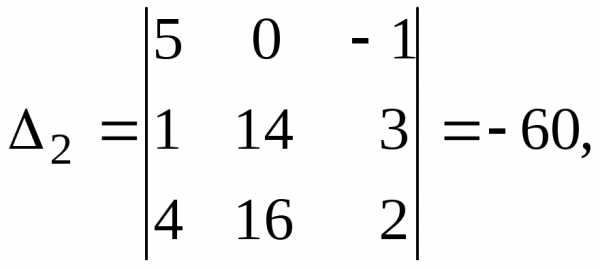
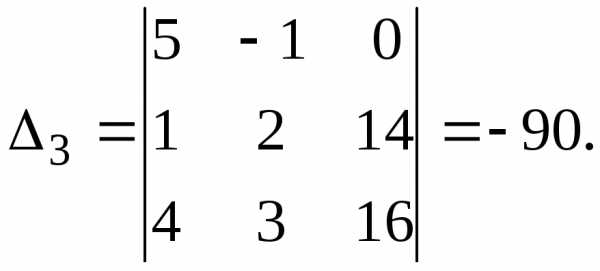
По формулам, представленным в теореме 5.2, вычислим значения неизвестных:
6. Исследование систем линейных уравнений.
Базисное решение
Исследовать систему линейных уравнений – означает определить, какой является эта система – совместной или несовместной, и в случае её совместности выяснить, определённая эта система или неопределённая.
Условие совместности системы линейных уравнений даёт следующая теорема
Теорема 6.1 (Кронекера–Капелли).
Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу её расширенной матрицы:
Для совместной системы линейных уравнений вопрос о её определённости или неопределённости решается с применением следующих теорем.
Теорема 6.2. Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой
Теорема 6.3. Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.
Таким образом, из сформулированных теорем вытекает способ исследования систем линейных алгебраических уравнений. Пусть n – количество неизвестных, Тогда:
при
 система несовместна;
система несовместна; система совместна, причём, если,
система
определённая; если же,
система неопределённая.
система совместна, причём, если,
система
определённая; если же,
система неопределённая.
Определение 6.1. Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные равны нулю.
Пример. Исследовать систему линейных уравнений. В случае неопределённости системы найти её базисное решение.
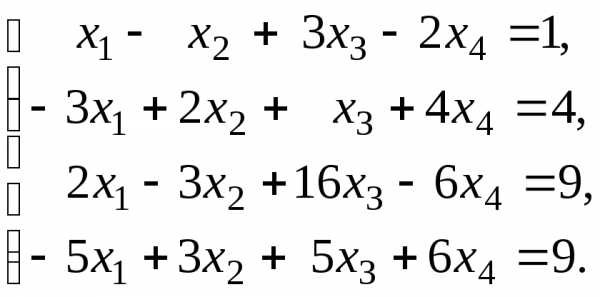
Вычислим
ранги основной 
 данной системы уравнений, для чего
приведём расширенную (а вместе с тем и
основную) матрицу системы к ступенчатому
виду:
данной системы уравнений, для чего
приведём расширенную (а вместе с тем и
основную) матрицу системы к ступенчатому
виду: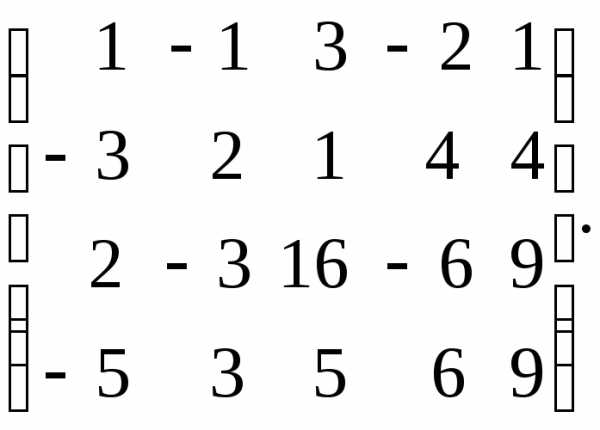
Вторую
строку матрицы сложим с её первой
строкой, умноженной на 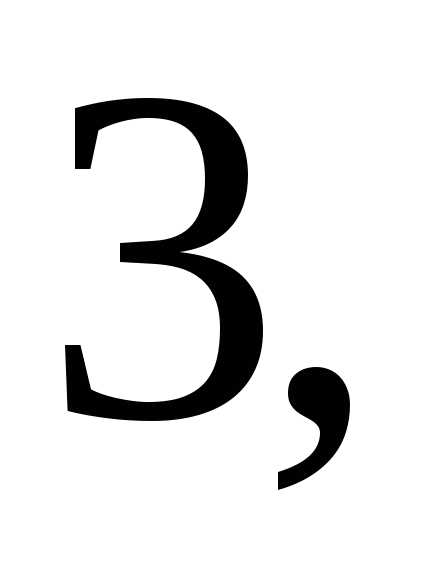 третью строку – с первой строкой,
умноженной на
третью строку – с первой строкой,
умноженной на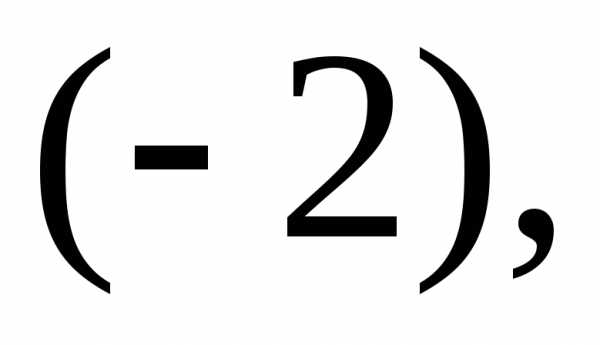
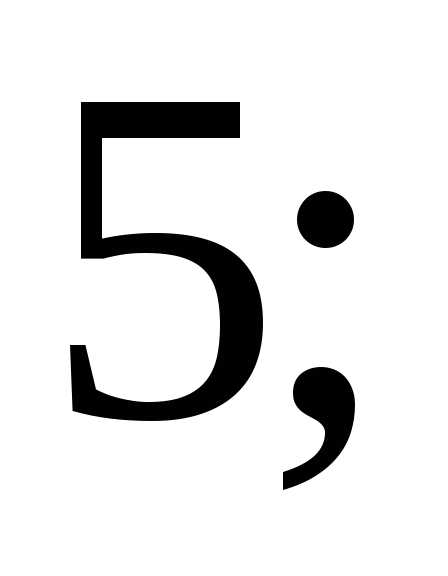 получим матрицу
получим матрицу
К
третьей строке этой матрицы прибавим
вторую строку, умноженную на 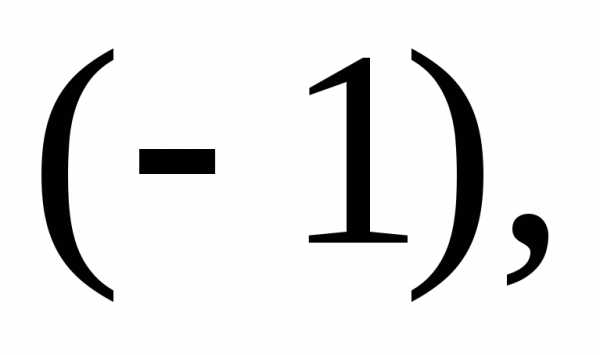 а к четвёртой строке – первую, умноженную
на
а к четвёртой строке – первую, умноженную
на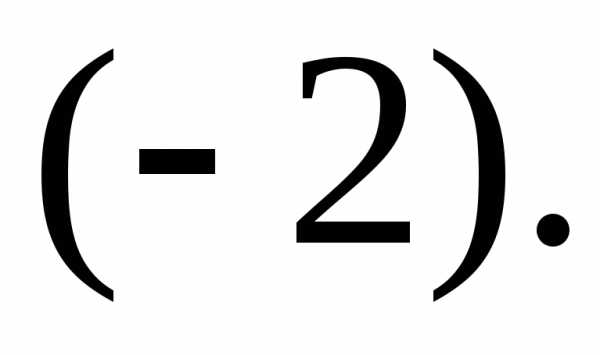 В результате получим матрицу
В результате получим матрицу

удаляя из которой третью и четвёртую строки получим ступенчатую матрицу
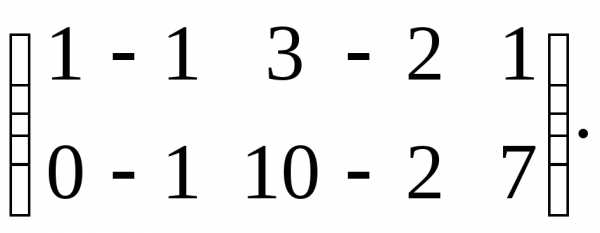
Таким образом, Следовательно, данная система линейных уравнений совместна, а поскольку величина ранга меньше числа неизвестных, система является неопределённой.Полученной в результате элементарных преобразований ступенчатой матрице соответствует система уравнений
Неизвестные 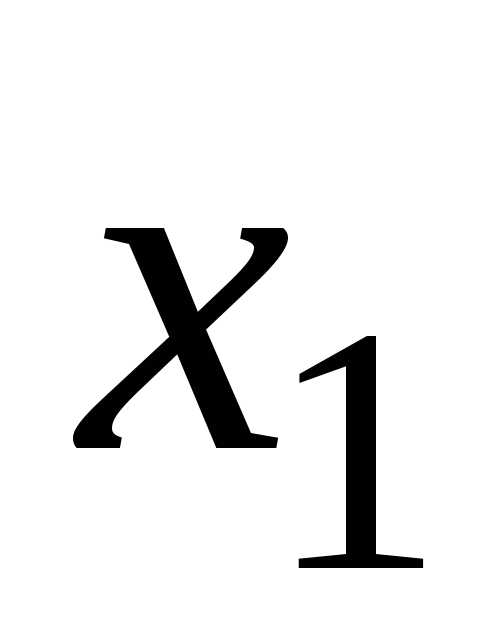 и
и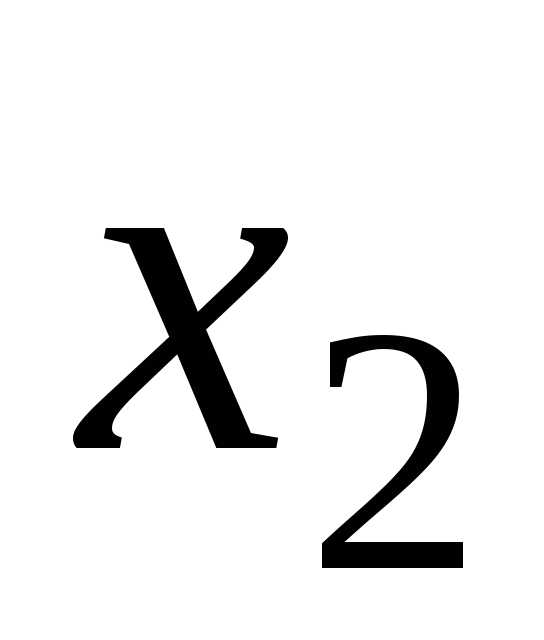 являются главными, а неизвестные
являются главными, а неизвестные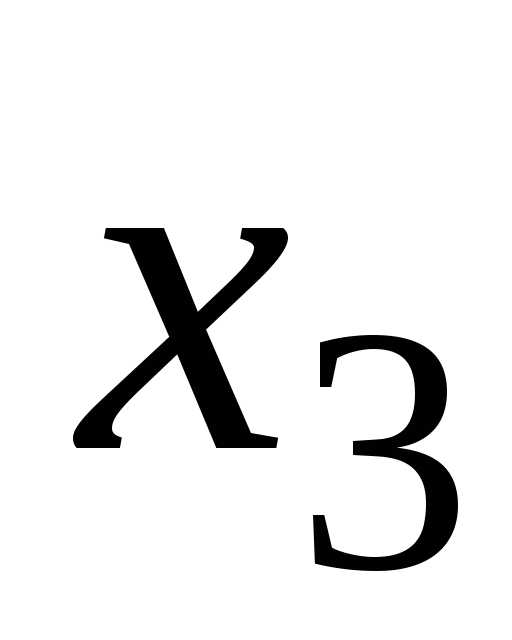
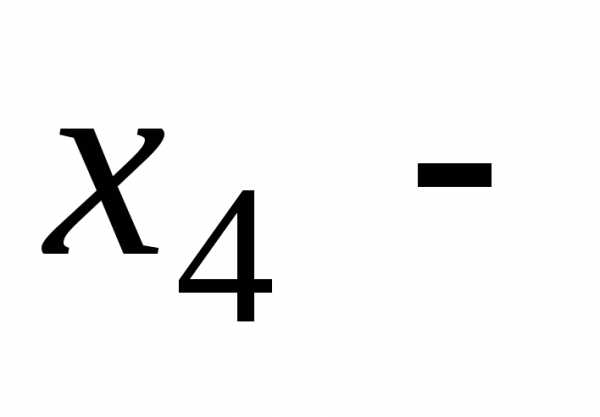 свободными. Придавая свободным неизвестным
нулевые значения, получим базисное
решение данной системы линейных
уравнений:
свободными. Придавая свободным неизвестным
нулевые значения, получим базисное
решение данной системы линейных
уравнений:studfiles.net
Матричный метод решения системы линейных алгебраических уравнений
Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.
Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.
Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.
Матричный метод решения — метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.
Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A-1 · B, где A-1 — обратная матрица.
Матричный метод решения состоит в следующем.
Пусть дана система линейных уравнений с nнеизвестными:
Её можно переписать в матричной форме: AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A-1 — матрицу, обратную к матрице A: A-1 (AX) = A-1B
Так как A-1A = E, получаем X = A-1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: detA≠ 0.
Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Пример решения неоднородной системы линейных алгебраических уравнений.
Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.
Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они понадобятся для нахождения обратной матрицы.
Теперь найдём союзную матрицу и транспонируем её, потом подставим в формулу для нахождения обратной матрицы.
Подставляя переменные в формулу, получаем:
Найдем неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.
Итак, x=2; y=1; z=4.
Если у Вас есть вопросы или Вам нужна помощь в решении линейных уравнений или систем, записывайтесь на мои занятия. Буду рад Вам помочь.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Решение систем линейных уравнений матричным методом
Дана СЛАУ: $\left\{\begin{array}{c} {x_{1} +3x_{3} =26} \\ {-x_{1} +2x_{2} +x_{3} =52} \\ {3x_{1} +2x_{2} =52} \end{array}\right. $. Решить систему в матричным способом, если это возможно.
Решение:
\[A=\left(\begin{array}{ccc} {1} & {0} & {3} \\ {-1} & {2} & {1} \\ {3} & {2} & {0} \end{array}\right),B=\left(\begin{array}{c} {26} \\ {52} \\ {52} \end{array}\right),X=\left(\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right). \]Вычислим определитель матрицы системы:
$\begin{array}{l} {\det A=\left|\begin{array}{ccc} {1} & {0} & {3} \\ {-1} & {2} & {1} \\ {3} & {2} & {0} \end{array}\right|=1\cdot 2\cdot 0+0\cdot 1\cdot 3+2\cdot (-1)\cdot 3-3\cdot 2\cdot 3-2\cdot 1\cdot 1-0\cdot (-1)\cdot 0=0+0-6-18-2-0=-26\ne 0} \end{array}$ Так как определитель не равен нулю, то матрица системы имеет обратную матрицу и, следовательно, система уравнений может быть решена матричным способом. Полученное решение будет единственным.Найдем обратную матрицу для матрицы системы:
\[A_{11} =(-1)^{1+1} \cdot \left|\begin{array}{cc} {2} & {1} \\ {2} & {0} \end{array}\right|=0-2=-2; A_{12} =(-1)^{1+2} \cdot \left|\begin{array}{cc} {-1} & {1} \\ {3} & {0} \end{array}\right|=-(0-3)=3;\] \[A_{13} =(-1)^{1+3} \cdot \left|\begin{array}{cc} {-1} & {2} \\ {3} & {2} \end{array}\right|=-2-6=-8; A_{21} =(-1)^{2+1} \cdot \left|\begin{array}{cc} {0} & {3} \\ {2} & {0} \end{array}\right|=-(0-6)=6; \] \[A_{22} =(-1)^{2+2} \cdot \left|\begin{array}{cc} {1} & {3} \\ {3} & {0} \end{array}\right|=0-9=-9; A_{23} =(-1)^{2+3} \cdot \left|\begin{array}{cc} {1} & {0} \\ {3} & {2} \end{array}\right|=-(2-0)=-2;\] \[A_{31} =(-1)^{3+1} \cdot \left|\begin{array}{cc} {0} & {3} \\ {2} & {1} \end{array}\right|=0-6=-6; A_{32} =(-1)^{3+2} \cdot \left|\begin{array}{cc} {1} & {3} \\ {-1} & {1} \end{array}\right|=-(1+3)=-4;\] \[A_{33} =(-1)^{3+3} \cdot \left|\begin{array}{cc} {1} & {0} \\ {-1} & {2} \end{array}\right|=2-0=2\]Искомая обратная матрица:
\[A^{-1} =\frac{1}{-26} \cdot \left(\begin{array}{ccc} {-2} & {6} & {-6} \\ {3} & {-9} & {-4} \\ {-8} & {-2} & {2} \end{array}\right)=\frac{1}{26} \cdot \left(\begin{array}{ccc} {2} & {-6} & {6} \\ {-3} & {9} & {4} \\ {8} & {2} & {-2} \end{array}\right)=\left(\begin{array}{ccc} {\frac{2}{26} } & {\frac{-6}{26} } & {\frac{6}{26} } \\ {\frac{-3}{26} } & {\frac{9}{26} } & {\frac{4}{26} } \\ {\frac{8}{26} } & {\frac{2}{26} } & {\frac{-2}{26} } \end{array}\right)=\left(\begin{array}{ccc} {\frac{1}{13} } & {-\frac{3}{13} } & {\frac{3}{13} } \\ {-\frac{3}{26} } & {\frac{9}{26} } & {\frac{2}{13} } \\ {\frac{4}{13} } & {\frac{1}{13} } & {-\frac{1}{13} } \end{array}\right).\]Найдем решение системы:
\[X=\left(\begin{array}{ccc} {\frac{1}{13} } & {-\frac{3}{13} } & {\frac{3}{13} } \\ {-\frac{3}{26} } & {\frac{9}{26} } & {\frac{2}{13} } \\ {\frac{4}{13} } & {\frac{1}{13} } & {-\frac{1}{13} } \end{array}\right)\cdot \left(\begin{array}{c} {26} \\ {52} \\ {52} \end{array}\right)=\left(\begin{array}{c} {\frac{1}{13} \cdot 26-\frac{3}{13} \cdot 52+\frac{3}{13} \cdot 52} \\ {-\frac{3}{26} \cdot 26+\frac{9}{26} \cdot 52+\frac{2}{13} \cdot 52} \\ {\frac{4}{13} \cdot 26+\frac{1}{13} \cdot 52-\frac{1}{13} \cdot 52} \end{array}\right)=\left(\begin{array}{c} {2-12+12} \\ {-3+18+8} \\ {8+4-4} \end{array}\right)=\left(\begin{array}{c} {2} \\ {23} \\ {8} \end{array}\right)\]$X=\left(\begin{array}{c} {2} \\ {23} \\ {8} \end{array}\right)$ — искомое решение системы уравнений.
spravochnick.ru
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть система линейных алгебраических уравнений задана в матричной форме , где матрицаAимеет размерностьnнаnи ее определитель отличен от нуля.
Так как , то матрицаА– обратима, то есть, существует обратная матрица. Если умножить обе части равенстванаслева, то получим формулу для нахождения матрицы-столбца неизвестных переменных. Так мы получили решение системы линейных алгебраических уравнений матричным методом.
Пример.
Решите систему линейных уравнений матричным методом.
Решение.
Перепишем систему уравнений в матричной форме:
Так как то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как.
Построим
обратную матрицу
с
помощью матрицы из алгебраических
дополнений элементов матрицыА(при
необходимости смотрите статьюметоды
нахождения обратной матрицы):
Осталось
вычислить
—
матрицу неизвестных переменных, умножив
обратную матрицуна
матрицу-столбец свободных членов(при
необходимости смотрите статьюоперации
над матрицами):
Ответ:
или в другой записи x1 = 4, x2 = 0, x3 = -1.
Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.
Более подробное описание теории и дополнительные примеры смотрите в статье матричный метод решения систем линейных уравнений.
К началу страницы
Решение систем линейных уравнений методом Гаусса.
Пусть нам требуется найти решение системы из nлинейных уравнений сnнеизвестными переменнымиопределитель основной матрицы которой отличен от нуля.
Суть метода Гауссасостоит в последовательном исключении неизвестных переменных: сначала исключаетсяx1из всех уравнений системы, начиная со второго, далее исключаетсяx2из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменнаяxn. Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называетсяпрямым ходом метода Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находитсяxn, с помощью этого значения из предпоследнего уравнения вычисляетсяxn-1, и так далее, из первого уравнения находитсяx1. Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называетсяобратным ходом метода Гаусса.
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменнуюx1из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на, к третьему уравнению прибавим первое, умноженное на, и так далее, кn-омууравнению прибавим первое, умноженное на. Система уравнений после таких преобразований примет видгде, а.
К такому же результату мы бы пришли, если бы выразили x1через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменнаяx1исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Будем считать, что (в противном случае мы переставим местами вторую строку сk-ой, где). Приступаем к исключению неизвестной переменнойx2из всех уравнений, начиная с третьего.
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на, и так далее, кn-омууравнению прибавим второе, умноженное на. Система уравнений после таких преобразований примет видгде, а. Таким образом, переменнаяx2исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x3, при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем xnиз последнего уравнения как, с помощью полученного значенияxnнаходимxn-1из предпоследнего уравнения, и так далее, находимx1из первого уравнения.
Пример.
Решите систему линейных уравнений методом Гаусса.
Решение.
Исключим
неизвестную переменную x1из второго и третьего уравнения системы.
Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные наи
насоответственно: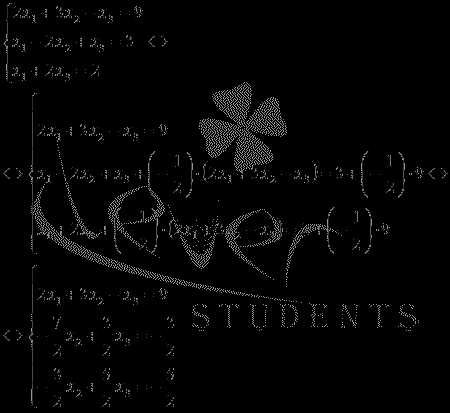
Теперь
из третьего уравнения исключим x2,
прибавив к его левой и правой частям
левую и правую части второго уравнения,
умноженные на:
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x3:
Из второго уравнения получаем .
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .
Ответ:
x1 = 4, x2 = 0, x3 = -1.
Более детальную информацию и дополнительные примеры смотрите в разделе решение элементарных систем линейных алгебраических уравнений методом Гаусса.
К началу страницы
studfiles.net
Матричный метод решения системы линейных уравнений
Задана система линейных алгебраических уравнений (СЛАУ) с неизвестными,коэффициентами при которых элементы матрицы , а свободными членами являются числа
Обозначим через – матрицу-столбец неизвестных, через –матрицу-столбец свободных членов. Тогда впереди систему уравнений можно записать в виде матричного уравнения:
Если квадратная матрица имеет отличный от нуля определитель ,то для нее существует обратная . Умножив слева в этом уравнении на , получим
Учитывая, что и, получим матричный решение системы
Нахождение матричного решения называется матричным способом решения системы линейных алгебраических уравнений (СЛАУ).
—————————————————————
Пример 1.
Решить СЛАУ матричным методом.
Решение.
Обозначим матрицу и векторы
Матричный решение системы уравнений ищем по формуле
Для нахождения обратной матрицы вычислим определитель
Поскольку , то заданная система уравнений совместная и имеет единственное решение.
Найдем транспонированную матрицу
Найдем алгебраические дополнения к элементам заданной матрицы:
Обратную матрицу вычисляем по формуле
Найдем решение СЛАУ
Решение СЛАУ:
Посмотреть материалы:
yukhym.com
Решение системы линейных уравнений методом обратной матрицы с примерами
Метод обратной матрицы не представляет ничего сложного, если знать общие принципы работы с матричными уравнениями и, конечно, уметь производить элементарные алгебраические действия.
Решение системы уравнений методом обратной матрицы. Пример.Удобнее всего постигать метод обратной матрицы на наглядном примере. Возьмем систему уравнений:
Первый шаг, который необходимо сделать для решения этой системы уравнений — найти определитель. Поэтому преобразим нашу систему уравнений в следующую матрицу:
И найдем нужный определитель:
Формула, использующаяся для решения матричных уравнений, выглядит следующим образом:
Х = А-1b.
Таким образом, для вычисления Х нам необходимо определить значение матрицы А-1 и умножить его на b. В этом нам поможет другая формула:
Ат в данном случае будет транспонированной матрицей — то есть, той же самой, исходной, но записанной не строками, а столбцами.
Не следует забывать о том, что метод обратной матрицы, как и метод Крамера, подходит только для систем, в которых определитель больше или меньше нуля. Если же определитель равен нулю, нужно использовать метод Гаусса.
Следующий шаг — составление матрицы миноров, представляющей собой такую схему:
В итоге мы получили три матрицы — миноров, алгебраических дополнений и транспонированную матрицу алгебраических дополнений. Теперь можно переходить к собственно составлению обратной матрицы. Формулу мы уже знаем. Для нашего примера это будет выглядеть так:
Работа почти закончена. Теперь осталось выполнить только умножение матрицы.
Таким образом, ответ для взятого нами примера получается следующим: х1 = 5, х2 = -1, х3 = 1.
Похожие статьи
infoogle.ru
Решение систем дифференциальных уравнений матричным способом
Матричная запись системы обыкновенных дифференциальных уравнений (СОДУ) с постоянными коэффициентами
Линейную однородную СОДУ с постоянными коэффициентами $\left\{\begin{array}{c} {\frac{dy_{1} }{dx} =a_{11} \cdot y_{1} +a_{12} \cdot y_{2} +\ldots +a_{1n} \cdot y_{n} } \\ {\frac{dy_{2} }{dx} =a_{21} \cdot y_{1} +a_{22} \cdot y_{2} +\ldots +a_{2n} \cdot y_{n} } \\ {\ldots } \\ {\frac{dy_{n} }{dx} =a_{n1} \cdot y_{1} +a_{n2} \cdot y_{2} +\ldots +a_{nn} \cdot y_{n} } \end{array}\right. $,
где $y_{1} \left(x\right),\; y_{2} \left(x\right),\; \ldots ,\; y_{n} \left(x\right)$ — искомые функции независимой переменной $x$, коэффициенты $a_{jk} ,\; 1\le j,k\le n$ — заданные действительные числа представим в матричной записи:
- матрица искомых функций $Y=\left(\begin{array}{c} {y_{1} \left(x\right)} \\ {y_{2} \left(x\right)} \\ {\ldots } \\ {y_{n} \left(x\right)} \end{array}\right)$;
- матрица производных решений $\frac{dY}{dx} =\left(\begin{array}{c} {\frac{dy_{1} }{dx} } \\ {\frac{dy_{2} }{dx} } \\ {\ldots } \\ {\frac{dy_{n} }{dx} } \end{array}\right)$;
- матрица коэффициентов СОДУ $A=\left(\begin{array}{cccc} {a_{11} } & {a_{12} } & {\ldots } & {a_{1n} } \\ {a_{21} } & {a_{22} } & {\ldots } & {a_{2n} } \\ {\ldots } & {\ldots } & {\ldots } & {\ldots } \\ {a_{n1} } & {a_{n2} } & {\ldots } & {a_{nn} } \end{array}\right)$.
Теперь на основе правила умножения матриц данную СОДУ можно записать в виде матричного уравнения $\frac{dY}{dx} =A\cdot Y$.
Общий метод решения СОДУ с постоянными коэффициентами
Пусть имеется матрица некоторых чисел $\alpha =\left(\begin{array}{c} {\alpha _{1} } \\ {\alpha _{2} } \\ {\ldots } \\ {\alpha _{n} } \end{array}\right)$.
Решение СОДУ отыскивается в следующем виде: $y_{1} =\alpha _{1} \cdot e^{k\cdot x} $, $y_{2} =\alpha _{2} \cdot e^{k\cdot x} $, \dots , $y_{n} =\alpha _{n} \cdot e^{k\cdot x} $. В матричной форме: $Y=\left(\begin{array}{c} {y_{1} } \\ {y_{2} } \\ {\ldots } \\ {y_{n} } \end{array}\right)=e^{k\cdot x} \cdot \left(\begin{array}{c} {\alpha _{1} } \\ {\alpha _{2} } \\ {\ldots } \\ {\alpha _{n} } \end{array}\right)$.
Отсюда получаем:
Теперь матричному уравнению данной СОДУ можно придать вид:
Полученное уравнение можно представить так:
Последнее равенство показывает, что вектор $\alpha $ с помощью матрицы $A$ преобразуется в параллельный ему вектор $k\cdot \alpha $. Это значит, что вектор $\alpha $ является собственным вектором матрицы $A$, соответствующий собственному значению $k$.
Число $k$ можно определить из уравнения$\left|\begin{array}{cccc} {a_{11} -k} & {a_{12} } & {\ldots } & {a_{1n} } \\ {a_{21} } & {a_{22} -k} & {\ldots } & {a_{2n} } \\ {\ldots } & {\ldots } & {\ldots } & {\ldots } \\ {a_{n1} } & {a_{n2} } & {\ldots } & {a_{nn} -k} \end{array}\right|=0$.
Это уравнение называется характеристическим.
Пусть все корни $k_{1} ,k_{2} ,\ldots ,k_{n} $ характеристического уравнения различны. Для каждого значения $k_{i} $ из системы $\left(\begin{array}{cccc} {a_{11} -k} & {a_{12} } & {\ldots } & {a_{1n} } \\ {a_{21} } & {a_{22} -k} & {\ldots } & {a_{2n} } \\ {\ldots } & {\ldots } & {\ldots } & {\ldots } \\ {a_{n1} } & {a_{n2} } & {\ldots } & {a_{nn} -k} \end{array}\right)\cdot \left(\begin{array}{c} {\alpha _{1} } \\ {\alpha _{2} } \\ {\ldots } \\ {\alpha _{n} } \end{array}\right)=0$ может быть определена матрица значений $\left(\begin{array}{c} {\alpha _{1}^{\left(i\right)} } \\ {\alpha _{2}^{\left(i\right)} } \\ {\ldots } \\ {\alpha _{n}^{\left(i\right)} } \end{array}\right)$.
Одно из значений в этой матрице выбирают произвольно.
Окончательно, решение данной системы в матричной форме записывается следующим образом:
$\left(\begin{array}{c} {y_{1} } \\ {y_{2} } \\ {\ldots } \\ {y_{n} } \end{array}\right)=\left(\begin{array}{cccc} {\alpha _{1}^{\left(1\right)} } & {\alpha _{1}^{\left(2\right)} } & {\ldots } & {\alpha _{2}^{\left(n\right)} } \\ {\alpha _{2}^{\left(1\right)} } & {\alpha _{2}^{\left(2\right)} } & {\ldots } & {\alpha _{2}^{\left(n\right)} } \\ {\ldots } & {\ldots } & {\ldots } & {\ldots } \\ {\alpha _{n}^{\left(1\right)} } & {\alpha _{2}^{\left(2\right)} } & {\ldots } & {\alpha _{2}^{\left(n\right)} } \end{array}\right)\cdot \left(\begin{array}{c} {C_{1} \cdot e^{k_{1} \cdot x} } \\ {C_{2} \cdot e^{k_{2} \cdot x} } \\ {\ldots } \\ {C_{n} \cdot e^{k_{n} \cdot x} } \end{array}\right)$,
где $C_{i} $ — произвольные постоянные.
Задача
Решить систему ДУ $\left\{\begin{array}{c} {\frac{dy_{1} }{dx} =5\cdot y_{1} +4y_{2} } \\ {\frac{dy_{2} }{dx} =4\cdot y_{1} +5\cdot y_{2} } \end{array}\right. $.
Записываем матрицу системы: $A=\left(\begin{array}{cc} {5} & {4} \\ {4} & {5} \end{array}\right)$.
В матричной форме данная СОДУ записывается так: $\left(\begin{array}{c} {\frac{dy_{1} }{dt} } \\ {\frac{dy_{2} }{dt} } \end{array}\right)=\left(\begin{array}{cc} {5} & {4} \\ {4} & {5} \end{array}\right)\cdot \left(\begin{array}{c} {y_{1} } \\ {y_{2} } \end{array}\right)$.
Получаем характеристическое уравнение:
$\left|\begin{array}{cc} {5-k} & {4} \\ {4} & {5-k} \end{array}\right|=0$, то есть $k^{2} -10\cdot k+9=0$.
Корни характеристического уравнения: $k_{1} =1$, $k_{2} =9$.
Составляем систему для вычисления $\left(\begin{array}{c} {\alpha _{1}^{\left(1\right)} } \\ {\alpha _{2}^{\left(1\right)} } \end{array}\right)$ при $k_{1} =1$:
\[\left(\begin{array}{cc} {5-k_{1} } & {4} \\ {4} & {5-k_{1} } \end{array}\right)\cdot \left(\begin{array}{c} {\alpha _{1}^{\left(1\right)} } \\ {\alpha _{2}^{\left(1\right)} } \end{array}\right)=0,\]то есть $\left(5-1\right)\cdot \alpha _{1}^{\left(1\right)} +4\cdot \alpha _{2}^{\left(1\right)} =0$, $4\cdot \alpha _{1}^{\left(1\right)} +\left(5-1\right)\cdot \alpha _{2}^{\left(1\right)} =0$.
Положив $\alpha _{1}^{\left(1\right)} =1$, получаем $\alpha _{2}^{\left(1\right)} =-1$.
Составляем систему для вычисления $\left(\begin{array}{c} {\alpha _{1}^{\left(2\right)} } \\ {\alpha _{2}^{\left(2\right)} } \end{array}\right)$ при $k_{2} =9$:
\[\left(\begin{array}{cc} {5-k_{2} } & {4} \\ {4} & {5-k_{2} } \end{array}\right)\cdot \left(\begin{array}{c} {\alpha _{1}^{\left(2\right)} } \\ {\alpha _{2}^{\left(2\right)} } \end{array}\right)=0, \]то есть $\left(5-9\right)\cdot \alpha _{1}^{\left(2\right)} +4\cdot \alpha _{2}^{\left(2\right)} =0$, $4\cdot \alpha _{1}^{\left(2\right)} +\left(5-9\right)\cdot \alpha _{2}^{\left(2\right)} =0$.
Положив $\alpha _{1}^{\left(2\right)} =1$, получаем $\alpha _{2}^{\left(2\right)} =1$.
Получаем решение СОДУ в матричной форме:
\[\left(\begin{array}{c} {y_{1} } \\ {y_{2} } \end{array}\right)=\left(\begin{array}{cc} {1} & {1} \\ {-1} & {1} \end{array}\right)\cdot \left(\begin{array}{c} {C_{1} \cdot e^{1\cdot x} } \\ {C_{2} \cdot e^{9\cdot x} } \end{array}\right).\]В обычной форме решение СОДУ имеет вид: $\left\{\begin{array}{c} {y_{1} =C_{1} \cdot e^{1\cdot x} +C_{2} \cdot e^{9\cdot x} } \\ {y_{2} =-C_{1} \cdot e^{1\cdot x} +C_{2} \cdot e^{9\cdot x} } \end{array}\right. $.
spravochnick.ru

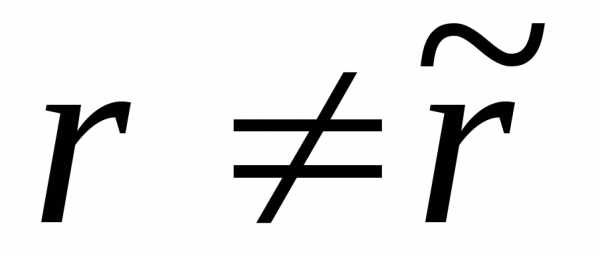 система несовместна;
система несовместна;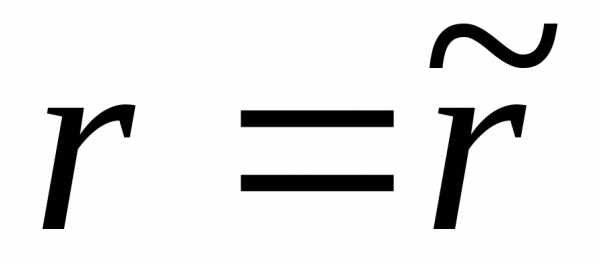 система совместна, причём, если,
система
определённая; если же,
система неопределённая.
система совместна, причём, если,
система
определённая; если же,
система неопределённая.