Регрессия в эконометрике – Эконометрика лекция!!!

Регрессия в эконометрике

Регрессия и ее виды

Определение 1

Регрессионный анализ – это основной математико-статистический инструмент в эконометрике. Регрессия представляет собой зависимость среднего значения величины $y$ от другой величины $x$ или же нескольких величин $x_i$.

Количество факторов, которые включены в равнение регрессии, определяет вид регрессии, которая может быть простой (парной) и множественной.

Простая регрессия – это модель, в которой среднее значение зависимой переменной y является функцией одной независимой переменной x.

Парная регрессия в неявном виде – это уравнение вида:

$y ̂= f(x)$

В явном виде: $y ̂= a + bx$, где $a$ и $b$ – это оценки коэффициента регрессии.

Множественной регрессией является модель, в которой среднее значение объясняемой переменной $y$ – это функция нескольких объясняющих переменных $x_1, x_2, …, x_n$. Множественная регрессия в неявном виде – это модель типа:

$y ̂= f(x_1, x_2,…, x_n)$

В явном виде: $y ̂= a + b_1x_1 + b_2x_2 + … + b_nx_n$

Примером модели множественной регрессии может выступать зависимость зарплаты работников от их возраста, уровня образования, степени квалификации, стажа работы, отрасли и т.д.

Относительно формы регрессия может быть линейной и нелинейной, предполагающей наличие нелинейных соотношений среди факторов. В большинстве случаев нелинейные модели можно привести к линейному виду.

Предпосылки регрессионного анализа

Чтобы проведение регрессионного анализа было наиболее результативным, необходимо выполнять определенные условия:

• В любом наблюдении математические ожидания случайной ошибки должны быть равны нулю;
• Дисперсия случайной ошибки для всех наблюдений должна быть постоянной;
• Случайные ошибки не должны иметь между собой статической зависимости;
• Объясняющая переменная x должна быть величиной неслучайной.

Если выполняются все вышеперечисленные условия, то модель является линейной классической регрессионной. Рассмотрим подробнее предположения и условия, составляющие основу регрессионного анализа.

Согласно первому условию, случайная ошибка не должна систематически смещаться. Если в уравнении регрессии имеется постоянный член, то данное условие автоматически выполняется.

Второе условие – это наличие в каждом наблюдении только одного значения дисперсии случайной ошибки. Дисперсия – это возможное изменение случайной ошибки до проведения выборки. Величина дисперсии является неизвестной, а задача регрессионного анализа – это ее оценка. Независимость дисперсии случайных ошибок от номера наблюдения – это гомоскедастичность, т.е. одинаковый разброс. Гетероскедастичность – это зависимость дисперсии случайных ошибок от номера наблюдения.

Если не выполняется условие гомоскедастичности, то оценка коэффициентов регрессии будет неэффективной.

Третье условие состоит в некоррелированности случайных отклонений для различных наблюдений. Данное условие часто не выполняется при ситуации, когда данные – это временные ряды. Если оно не выполняется, то это означает автокорреляцию остатков. Чтобы диагностировать и устранить автокорреляцию, существуют специальные методы.

Четвертое условие представляет особую важность, поскольку если не выполняется условие неслучайности объясняющих переменных, то оценка коэффициентов регрессии будет смещенной и несостоятельной. Данное условие нарушается при ошибках в измерении объясняющих переменных или же при использовании лаговых переменных.

Парная регрессионная модель

Как правило в естественных науках рассматриваются функциональные зависимости, в которых каждое значение одной переменной соответствует единственному значению другой. Однако в экономических переменных нет таких зависимостей, но есть статистические и корреляционные зависимости.

Наибольшую опасность в парной регрессии представляют ошибки в измерениях. Если ошибки спецификации возможно уменьшить с помощью изменения формы модели, ошибки выборки – при помощи увеличения объема исходных данных, то ошибки изменения невозможно исправить.

Случайный фактор в регрессионных моделях может отсутствовать по следующим причинам:

1. В модель не включены все объясняющие переменные. Любая модель эконометрики – это упрощение реальной ситуации, которая является сложнейшим переплетением факторов, большинство из которых не учитываются в модели, из-за чего реальные значения зависимой переменной отклоняются от модельных значений. Невозможно перечислить все виды объясняющих переменных, поскольку неизвестно заранее, какие факторы относятся к определяющим, а какие можно не учитывать.
2. Неправильное определение функционального типа модели. Слабая изученность исследуемого процесса, его переменчивость влияет на правильность подбора его моделирующей функции. Это отражается и на отклонении модели от реальной жизни.
3. Агрегирование переменных. Многие модели содержат зависимость между факторами, являющимися комбинацией других переменных. Например, чтобы рассмотреть в качестве зависимой переменной совокупный спрос, необходимо провести анализ зависимости, содержащей объясняемую переменную, являющуюся композицией индивидуальных спросов, которые оказывают влияние на нее. Это может послужить причиной отклонения значений реальных от модельных.
4. Ошибки в измерениях. Даже при качественной модели ошибки в измерениях сказываются на несоответствии получаемых значений эмпирическим.
5. Ограниченность статистической информации. Часто строятся модели, которые являются непрерывными функциями. Для этого применяется информация, имеющая дискретную структуру. Данное несоответствие выражается в случайном отклонении.
6. Непредсказуемость человеческих факторов. Данная причина может исказить любую качественную эконометрическую модель, поскольку даже правильный выбор формы модели, скрупулезный подбор объясняющих переменных не позволяют спрогнозировать поведение индивидов.

spravochnick.ru

Тема 1. Предмет и метод эконометрики

Эконометрика — быстроразвивающаяся отрасль науки, цель которой состоит в том, чтобы придать количественные меры эко­номическим отношениям.

Эконометрика — это наука, которая дает ко­личественное выражение взаимосвязей экономических явлений и процессов.

Предмет исследования эконометрики – экономические явления.

К основным задачам эконометрики можно отнести следующее:

• Построение эконометрических моделей, т.е. представление экономических моделей в математической форме, удобной для проведения эмпирического анализа. Данную проблему принято называть проблемной

  спецификации. Отметим, что зачастую она может быть решена несколькими способами.

• Оценка параметров построенной модели, делающих выбранную модель наиболее адекватной реальным данным. Это так называемый этап параметризации.

• Проверка качества найденных параметров модели и самой модели в целом. Иногда этот этап анализа называют этапом верификации.

• Использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания, а также для осмысленного проведения экономической политики.

TЕМА 2. ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ.

1. Спецификация модели.

Любое эконометрическое исследование начинается со специ­фикации модели, т. е. с формулировки вида модели, исходя из со­ответствующей теории связи между переменными. Практически в каж­дом отдельном случае величина y складывается из двух слага­емых:

где y_j — фактическое значение результативного признака;

ŷ_xj

. — теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и x, т. е. из уравнения регрессии;

ε_j — случайная величина (возмущение), характеризующая отклонения реального значения результативного признака от теоретического, найден­ного по уравнению регрессии. Ее присутствие в модели по­рождено тремя источниками: спецификацией модели ( а) непра­вильный выбор той или иной математической функции, б) недоучет в уравнении регрессии какого-либо существенного фактора), выбороч­ным характером исходных данных (если совокупность неоднородна, то уравнение регрессии не имеет практического смысла), особенностями измерения переменных (например, статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например в результате наличия сокрытых доходов).

В парной регрессии выбор вида математической функции может быть осуществлен тремя методами:

• графическим;

• аналитическим, т. е. исходя из теории изучаемой взаимосвязи;

• экспериментальным.

Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.

2. Линейная регрессия и корреляция.

Линейная регрессия находит широкое применение в экономет­рике в виде четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида

Построение линейной регрессии сводится к оценке ее пара­метров — а и b. Оценки параметров линейной регрессии могут быть найдены разными методами.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). То есть, получим следующую систему нор­мальных уравнений для оценки параметров а и b:

Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом оп­ределителей, найдем искомые оценки параметров а и b. Можно воспользоваться следующими готовыми формулами:

Параметр b называется коэффициентом регрессии. Его вели­чина показывает среднее изменение результата с изменением фактора на одну единицу. Формально а — значение у при x = 0.

Уравнение регрессии всегда дополняется показателем тесно­ты связи. При использовании линейной регрессии в качестве та­кого показателя выступает линейный коэффициент корреляции r_xy. Существуют разные модификации формулы линейного коэф­фициента корреляции:

Как известно, линейный коэффициент корреляции находит­ся в границах:

Если коэффициент регрессии b > 0, то , и, наоборот, при b < 0,

Для оценки качества подбора линейной функции рассчиты­вается квадрат линейного коэффициента корреляции r²_xy, назы­ваемый коэффициентом детерминации.

После того как найдено уравнение линейной регрессии, про­водится оценка значимости как уравнения в целом, так и отдель­ных его параметров.

Оценка значимости уравнения регрессии в целом дается с по­мощью F-критерия Фишера.

Расчетное значение критерия можно получить, используя формулу:

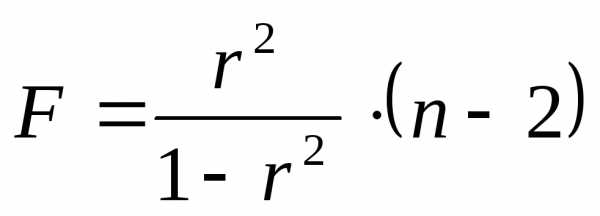
Расчетное значение сравнивается с табличным по таблицам распределения Фишера Для уровня значимости 0,05 и числа степеней свободы k1=1 и k2=n-2. Если расчетное значение больше табличного, уравнение регрессии признается значимым.

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: т_b и т_а.

Стандартная ошибка коэффициента регрессии определяется по формуле

где S² — остаточная дисперсия на одну степень свободы.

Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдента: 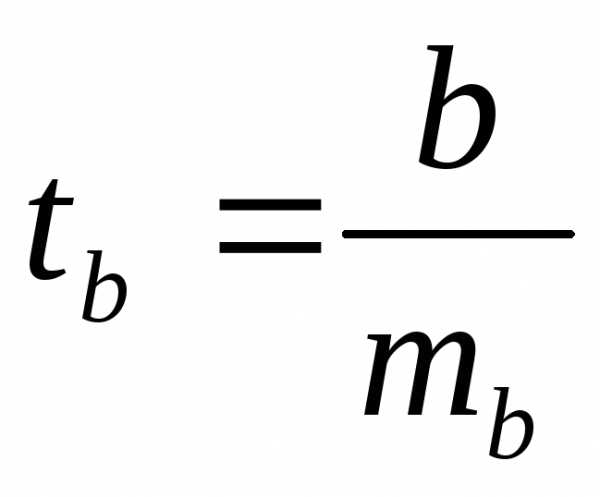, которое затем сравнивается с табличным значением при определен­ном уровне значимостиα и числе степеней свободы (n — 2).

Стандартная ошибка параметра а определяется по формуле:

Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрес­сии; вычисляется t-критерий: t_a = a/m_a, его величина сравнивается с табличным значением при df = n — 2 степенях свободы.

В прогнозных расчетах по уравнению регрессии определяется предсказываемое (у_р) значение как точечный прогнозприх_р =х_к, т. е. путем подстановки в уравнение регрессиисоответствующего значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом интегральной ошибки прогноза Е_Y, которая формируется как сумма двух ошибок: из ошибки прогноза как результата отклонения прогноза от уравнения регрессии —и ошибки прогноза положения регрессии.

Интегральная ошибка прогноза составит:

Предельная ошибка прогноза (при уровне значимости 0,05) составит:

Табличное значение определили по таблице распределения Стьюдента с учетом значимости 0,05 и числом степеней свободы v=n-2.

Фактическая реализация прогноза будет находиться в доверительном интервале: . Относительная величина различий значений верхней и нижней границ характеризует точность выполненного прогноза.

studfiles.net

Прикладная математика | 404 ошибка

Произошла ошибка. Причины ошибки могут быть разными. Например, была удалена страница, а вы попали на нее из поисковой системы. Вы получили ошибочный адрес страницы из других источников. Или, к примеру, произошел сбой на сервере. Не расстраивайтесь. Перейдите на любую другую страницу нашего сайта. Если ошибка возникает систематически — можете сообщить администратору сайта, воспользовавшись нашей формой [обратной связи]. Приносим наши извинения.

На нашем сайте очередная порция обновлений. Перечислим основные. Во-первых, изменился полностью дизайн сайта. Основная причина для смены дизайна — пер… […]

Подскажите пожалуйста на правильном ли пути решения? Вычислить массу m неоднородной пластины D, ограниченной линиями если поверхностная плотность в ка… […]

Здесь приведен список самых востребованных и популярных языков программирования по состоянию на октябрь 2015 года, а также сравнительная динамика популярности с октябрем прошлого года. … […]

Здесь можно проследить как менялась популярность основных языков программирования на последние тридцать лет. В таблице указано место языка в общем рейтинге наиболее популярных языков в те или иные годы. Таблица пригодится при выборе языка программирования для изучения. Ее можно использовать и для рефератов. … […]

В современных смартфонах используются литий-ионные аккумуляторы. И их срок хорошей работоспособности составляет 2-3 года. Но можно продлить их жизнь, если следовать некоторым правилам…. […]

Отличный способ понять как генератор случайных чисел работает — представить его результаты на графике в режиме реального времени. Ниже приведен такой … […]

Теперь решить систему линейных алгебраических уравнений очень просто. Вводите команду solve и через запятую записываете ваши уравнения. Затем нажимает… […]

Если вам понадобится найти обратную матрицу — используйте наш #решатель. Просто введите команду и получите результат. Приведем примеры, как можно найт… […]

Вам может понадобиться вычислить определитель 2-го, 3-го, 4-го порядка или даже пятого. Теперь вы можете это сделать очень просто. Надо только правиль… […]

Переводчик Skype помогает общаться с людьми из разных стран, преодолевая языковые барьеры. Просто организуйте голосовой или видеозвонок и начните обще… […]

Продолжаем рубрику — умникам. На это раз у нас видео-вопрос. Внимательно посмотрите ролик. Это не фото или видео-подделка. Это — попытка создать вечны… […]

Алан Матисон Тьюринг (1912—1954) английский математик, логик, криптограф, изобретатель машины Тьюринга. Машина Тьюринга — простое вычислительно… […]

Здесь представлена постоянно обновляющаяся лента вакансий для программистов. Следите за новыми предложениями работы в реальном времени. … […]

Вы не разговариваете во сне? — спрашивает врач пациента. — Нет, доктор, хотя я часто говорю, когда другие спят. — Это как же? — Я читаю лекции по мате… […]

«Если… то…» — если это не математика, то это шантаж. Ягодзиньский, Хенрик (р. 1928), польский сатирик
В пустую голову входит больше знаний…. […]

primat.org

Новосибирский государственный архитектурно-строительный университет — Сибстрин

Около 400 областных молодежных мероприятий было проведено в регионе в 2018 году Масштабные добровольческие проекты, подготовка специалистов по работе с молодежью, продвижение молодежных инициатив и развитие общественной деятельности – эти и другие актуальные вопросы обсудили на заседание совета по молодежной политике при Губернаторе Новосибирской области 20 декабря. Заседание открыл министр образования Сергей Федорчук, который отметил успешную работу молодежного направления в течение всего года. «2018 год был Годом добровольца, и новосибирская молодежь активно участвовала во всех проводимых мероприятиях. Помимо добровольчества, в регионе было реализовано большое количество и других молодежных проектов, и приятно отметить, что молодежное…

Премия «Я – волонтер» нашла своих героев В Новосибирской области прошло торжественное вручение региональной премии в сфере добровольчества «Я – волонтер». Участниками церемонии награждения стали более 400 активных представителей волонтёрского движения региона и почётные гости праздника. Участников волонтерского движения региона, людей с большим сердцем, которые каждый день дарят добро и делают мир лучше, приветствовал Губернатор Новосибирской области Андрей Травников. В своем выступлении он поздравил волонтеров с успешным завершением Год добровольца. «Важно, что ваши инициативность, активность, непосредственность, ответственность увлекают людей, которые, возможно, внутренне и не считают себя добровольцами.

Объявлены победители конкурса эскизных проектов создания образа «студента-строителя» Открытый конкурс эскизных проектов создания образа «студента-строителя» стартовал 1 октября 2018 года по инициативе СРО «Ассоциация строительных организаций Новосибирской области» и «Ассоциация профессиональных строителей Сибири». Его цель – создание художественно-планировочной концепции скульптурной группы привлекательного образа «студента-строителя» и НГАСУ (Сибстрин) – старейшего университета нашего города, в целом. Конкурс проводится в рамках подготовки к празднованию 90-летнего юбилея Сибстрина при поддержке Министерства науки и высшей школы РФ, Администрации Новосибирской области, мэрии г. Новосибирска, Ассоциации строителей и инвесторов Новосибирска и Новосибирской области, Новосибирского союза архитекторов России, союза художников России и союза дизайнеров.

www.sibstrin.ru

Эконометрика. Линейная Регрессия в MS Excel

 
На мой взгляд, как студента, эконометрика – это одна из самых прикладных наук из всех, с которыми мне удалось познакомиться в стенах своего университета. С помощью неё, действительно, можно решать задачи прикладного характера в масштабах предприятия. Насколько эффективными будут эти решения – вопрос третий. Суть в том, что большая часть знаний так и останется теорией, а вот эконометрика и регрессионный анализ всё-таки стоит изучить с особым вниманием.
 

Что объясняет регрессия?

 
Прежде, чем мы приступим к рассмотрению функций MS Excel, позволяющих, решать данные задачи, хотелось бы вам на пальцах объяснить, что, в сущности, предполагает регрессионный анализ. Так вам проще будет сдавать экзамен, а самое главное, интересней изучать предмет.

Будем надеяться, вы знакомы с понятием функции из математики. Функция – это взаимосвязь двух переменных. При изменении одной переменной что-то происходит с другой. Изменяем X, меняется и Y, соответственно. Функциями описываются различные законы. Зная функцию, мы можем подставлять произвольные значения X и смотреть на то, как при этом изменится Y.
 
Это имеет большое значение, поскольку регрессия – это попытка объяснить с помощью определённой функции на первый взгляд бессистемные и хаотичные процессы. Так, например, можно выявить взаимосвязь курса доллара и безработицы в России.
 
Если данную закономерность обнаружить удастся, то по полученной нами в ходе расчетов функции, мы сможем составить прогноз, какой будет уровень безработицы при N-ом курсе доллара по отношению к рублю.
Данная взаимосвязь будет называться корреляцией. Регрессионный анализ предполагает расчет коэффициента корреляции, который объяснит тесноту связи между рассматриваемыми нами переменными (курсом доллара и числом рабочих мест).

Данный коэффициент может быть положительным и отрицательным. Его значения находятся в пределах от -1 до 1. Соответственно, мы может наблюдать высокую отрицательную или положительную корреляцию. Если она положительная, то за увеличением курса доллара последует и появление новых рабочих мест. Если она отрицательная, значит, за увеличением курса, последует уменьшение рабочих мест.
 
Регрессия бывает нескольких видов. Она может быть линейной, параболической, степенной, экспоненциальной и т.д. Выбор модели мы делаем в зависимости от того, какая регрессия будет соответствовать конкретно нашему случаю, какая модель будет максимально близка к нашей корреляции. Рассмотрим это на примере задачи и решим её в MS Excel.
 

Линейная регрессия в MS Excel

 
Для решения задач линейной регрессии вам понадобится функционал «Анализ данных». Он может быть не включен у вас поэтому его нужно активировать.
 

• Жмём на кнопку «Файл»;
• Выбираем пункт «Параметры»;
• Жмём по предпоследней вкладке «Надстройки» с левой стороны;

 

 

• Снизу увидим Надпись «Управление» и кнопку «Перейти». Жмём по ней;
• Ставим галочку на «Пакет анализа»;
• Жмём «ок».

 

 

Пример задачи

Функция пакетного анализа активирована. Решим следующую задачу. У нас есть выборка данных за несколько лет о числе ЧП на территории предприятия и количестве трудоустроенных работников. Нам необходимо выявить взаимосвязь между этими двумя переменными. Есть объясняющая переменная X – это число рабочих и объясняемая переменная – Y – это число чрезвычайных происшествий. Распределим исходные данные в два столбца.
 

 
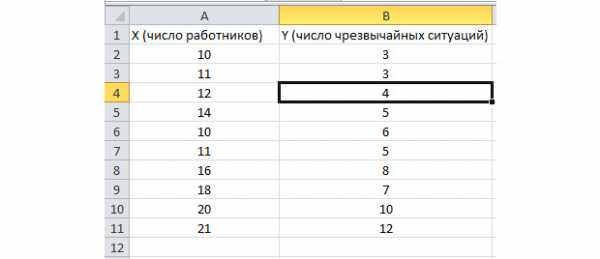
Перейдём во вкладку «данные» и выберем «Анализ данных»

 

 
В появившемся списке выбираем «Регрессия». Во входных интервалах Y и X выбираем соответствующие значения.
 

 
Нажимаем «Ок». Анализ произведён, и в новом листе мы увидим результаты.
 
Наиболее существенные для нас значения отмечены на рисунке ниже.
 

 
Множественный R – это коэффициент детерминации. Он имеет сложную формулу расчета и показывает, насколько можно доверять нашему коэффициенту корреляции. Соответственно, чем больше это значение, тем больше доверия, тем удачнее наша модель в целом.
 
Y-пересечение и Пересечение X1 – это коэффициенты нашей регрессии. Как уже было сказано, регрессия – это функция, и у неё есть определённые коэффициенты. Таким образом, наша функция будет иметь вид: Y = 0,64*X-2,84.
 
Что нам это даёт? Это даёт нам возможность составить прогноз. Допустим, мы хотим нанять на предприятие 25 работников и нам нужно примерно представить, каким при этом будет количество чрезвычайных происшествий. Подставляем в нашу функцию данное значение и получаем результат Y = 0,64 * 25 – 2,84. Примерно 13 ЧП у нас будет происходить.

Посмотрим, как это работает. Взгляните на рисунок ниже. В полученную нами функцию подставлены фактические значения по вовлеченным работникам. Посмотрите, как близки значения к реальным игрекам.
 

 
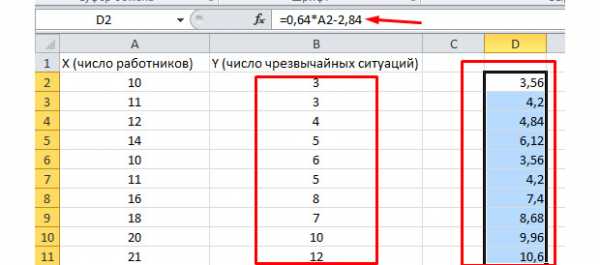
Вы так же можете построить поле корреляции, выделив область игреков и иксов, нажав на вкладку «вставку» и выбрав точечную диаграмму.
 

 
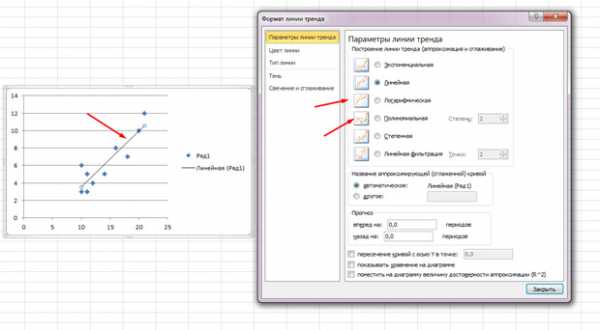
Точки идут вразброс, но в целом двигаются вверх, как будто посередине лежит прямая линия. И эту линию вы так же можете добавить, перейдя во вкладку «Макет» в MS Excel и выбрав пункт «Линия тренда»

 

 
Щелкните дважды по появившейся линии и увидите то, о чем говорилось ранее. Вы можете изменять тип регрессии в зависимости от того, как выглядит ваше поле корреляции.
 
Возможно, вам покажется, что точки рисуют параболу, а не прямую линию и вам целесообразней выбрать другой тип регрессии.
 

 

Заключение

Будем надеяться, что данная статья дала вам большее понимание о том, что такое регрессионный анализ и для чего он нужен. Всё это имеет большое прикладное значение.

reshatel.org

Эконометрика

1. Эконометрика как наука. Понятие взаимосвязи между случайными величинами. Ковариация и коэффициент корреляции. Эконометрическая модель

«Эконометрика позволяет проводить количественный анализ реальных экономических явлений, чтобы охарактеризовать их типичное поведение. Выделяют 2 вида статистического анализа зависимостей:

1. Корреляционный анализ – позволяет оценить значимость и силу взаимосвязи, без указания вида зависимости

2. Регрессионный анализ – позволяет оценить и проанализировать формулу зависимости одной переменной от других.

Коэффициент ковариации показывает направленность взаимосвязи между двумя переменными. Является состоятельной, смещенной оценкой.

Коэффициент корреляции показывает направленность и силу(!) взаимосвязи между двумя переменными. Значения коэффициента корреляции:

— Близкие к 0 – свидетельствуют об отсутствии линейной взаимосвязи

— Близкие к (+1) – о сильной прямой взаимосвязи

— Близкие к (–1) – о сильной обратной взаимосвязи

Эконометрическая модель – это математическое описание экономического явления, отражающее наиболее важные его черты. Модель упрощает, идеализирует изучаемое явление. О правильности построенной модели можно судить по близкому соответствию результатов моделирования и фактических данных.

Общим моментом для любых эконометрических моделей является разбиение зависимой переменной на две части: объясненную и случайную, и є – случайная составляющая. Y=f(x)+E

2. Понятие регрессии. Модель парной линейной регрессии. Диаграмма рассеяния и проблема выбора линии регрессии. Природа случайного члена регрессии

Регрессионный анализ – позволяет оценить и проанализировать формулу зависимости одной переменной от других.

Линейная парная модель

Уравнение регрессии:

y = β0 + β1x + ε

β1 – показывает, на сколько изменится значение зависимой переменной y при изменении объясняющей переменной x на единицу.

β0 – показывает среднее значение зависимой переменной y при нулевом значении объясняющей переменной x. Не всегда имеет экономический смысл. (компонент)

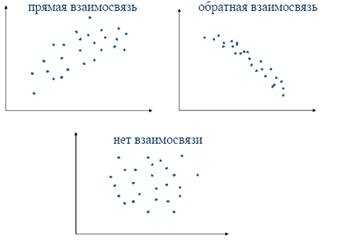
Проблема выбора линии заключаеться в том, что надо её максимально описать зависимость, чтобы по минимуму были отклонения.

Природа случайного члена регрессионной модели

1. Невключение объясняющих переменных

2. Неправильная функциональная спецификация модели

3. Случайность поведения рассматриваемых объектов

4. Ошибки измерения

3. Метод наименьших квадратов. Вывод формул метода наименьших квадратов для парного случая. Суть метода, графическое представление, условия применения

Метод наименьших квадратов — метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов ошибок (регрессионных остатков) минимальна.

Метод заключается в минимизации евклидова расстояния

между двумя векторами — вектором восстановленных значений зависимой переменной и вектором фактических значений зависимой переменной.

Применение. Задача метода наименьших квадратов состоит в выборе вектора

, минимизирующего ошибку .

Метод наименьших квадратов имеет следующие преимущества:

— не требуется знания закона распределения случайного возмущения

— дает оценки по крайней мере состоятельные

— в случае нормального распределения случайного возмущения оценки параметров линейной модели несмещенные и эффективные

Formula:

4. Свойства оценок коэффициентов регрессии, полученных с помощью метода наименьших квадратов. Теорема Гаусса-Маркова — формулировка, смысл теоремы. Условия Гаусса-Маркова и последствия их нарушения

Теорема Гаусса—Маркова

оценки по обычному методу наименьших квадратов являются не только несмещенными оценками коэффициентов регрессии, но и наиболее эффективными в том случае, если выполнены условия Гаусса—Маркова. С другой стороны, если условия Гаусса—Маркова не выполнены, то, вообще говоря, можно найти оценки, которые будут более эффективными по сравнению с оценками, полученными обычным методом наименьших квадратов. В данной работе не приводится общее рассмотрение этих вопросов. Тем не менее в том случае, если условия Гаусса—Маркова для остаточного члена выполнены, коэффициенты регрессии, построенной обычным методом наименьших квадратов, будут наилучшими линейными несмещенными оценками (best linear unbiased estimators, или BLUE): несмещенными, как уже было показано; линейными, так как они являются линейными функциями значений у; наилучшими, так как они являются наиболее эффективными в классе всех несмещенных линейных оценок. Теорема Гаусса—Маркова доказывает это (краткое изложение, не использующее матричной алгебры, дано в работе Дж. Томаса

для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие из всех возможных результаты, случайный член должен удовлетворять четырем условиям, известным как условия Гаусса—Маркова.

1-е условие Гаусса—Маркова: E(Ut) = 0 для всех наблюдений. Первое условие состоит в том, что математическое ожидание случайного члена в любом наблюдении должно быть равно нулю. Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в одном из двух возможных направлений. Vipolnjaetsjaavtomaticeski,esliuravasoderzitkonstantu

2-е условие Гаусса—Маркова: pop. var (u) постоянна для всех наблюдений. Второе условие состоит в том, что дисперсия случайного члена должна быть постоянна для всех наблюдений. Иногда случайный член будет больше, иногда меньше, однако не должно быть априорной причины для того, чтобы он порождал большую ошибку в одних наблюдениях, чем в других. Одна из задач регрессионного анализа состоит в оценке стандартного отклонения случайного члена. Если рассматриваемое условие не выполняется, то коэффициенты регрессии, найденные по обычному методу наименьших квадратов, будут неэффективны. Narushenieprivoditkgeteroskedasticnosti

3- е условие Это условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях. Например, если случайный член велик и положителен в одном наблюдении, это не должно обусловливать систематическую тенденцию к тому, что он будет большим и положительным в следующем наблюдении (или большим и отрицательным, или малым и положительным, или малым и отрицательным). Случайные члены должны быть абсолютно независимы друг от друга. Narushenieprivoditkavtokorreljacii

4-е условие случайный член должен быть распределен независимо от объясняющих переменных В большинстве глав книги мы будем в сущности использовать более сильное предположение о том, что объясняющие переменные не являются стохастическими, т. е. не имеют случайной составляющей. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии. Если это условие выполнено, то теоретическая ковариация между независимой переменной и случайным членом равна нулю. Дело в том, что если случайный член и нормально распределен, то так же будут распределены и коэффициенты регрессии.

Предположение о нормальности основывается на центральной предельной теореме. В сущности, теорема утверждает, что если случайная величина является общим результатом взаимодействия большого числа других случайных величин, ни одна из которых не является доминирующей, то она будет иметь приблизительно нормальное распределение, даже если отдельные составляющие не имеют нормального распределения.

5. Понятие качества регрессии, коэффициент детерминации, скорректированный коэффициент детерминации

Коэффициент детерминации (R2) Это оценка качества — это квадрат множественного коэффициента корреляции. Он показывает, какая доля дисперсии результативного признака объясняется влиянием независимых переменных. Формула для вычисления коэффициента детерминации:

где yi — выборочные данные, а fi — соответствующие им значения модели.

Коэффициент принимает значения из интервала [0;1]. Чем ближе значение к 1 тем ближе модель к эмпирическим наблюдениям. R2<50% Построенные при таких условиях регрессионные модели имеют низкое практическое значение.

Значение R2 монотонно возрастает с ростом числа переменных (регрессоров) в регрессии, что зачастую не означает улучшения качества предсказания. Потому правильнее использовать скорректированный коэффициент детерминации, учитывающий число использованных регрессоров и корректировать коэффициент множественной детерминации на потерю степеней свободы вариации.

6. Модель множественной регрессии. Смысл коэффициентов множественной регрессии. Матричный вид регрессии, метода наименьших квадратов и теоремы Гаусса-Маркова. Вывод формул метода наименьших квадратов в матричном виде

Идея множественной регрессии состоит в том, что зависимая переменная определяется более чем одной объясняющей переменной. Общий вид множественной регрессии:

Коэф. Регрессии показывают насколько изменится значение зависимой переменной y , если значение соответствующей независимой переменной изменится на 1, при условии, что все остальные переменные останутся неизменными.

Матричная форма записи

Пусть имеется выборка из п наблюдений, а модель включает k peгреccopов и константу. Введем обозначения:

mirznanii.com

Расчет коэффициентов множественной линейной регрессии в эконометрике матричным способом

Представим данные наблюдений и коэффициенты модели в матричной форме.

Здесь Y — n-мерный вектор-столбец наблюдений зависимой переменной; X — матрица размерности n х (m +1), в которой i-я строка i = 1, 2,…, n представляет i-е наблюдение вектора значений независимых переменных X₁, X₂,…,Xm, единица соответствует переменной при свободном члене b₀; B — вектор-столбец размерности (m + 1) параметров уравнения множественной регрессии; e — вектор-столбец размерности n отклонений выборочных значений y_i зависимой переменной от значений y_i, получаемых по уравнению регрессии: В матричном виде соотношение примет вид: Согласно методу наименьших квадратов: где e^T = (e₁, e₂,…, e_n), т. е. надстрочный значок T означает транспонированную матрицу.

Можно показать, что предыдущее условие выполняется, если вектор-столбец коэффициентов B найти по формуле:

Здесь X^T — матрица, транспонированная к матрице X,

(X^TX)^-1 — матрица, обратная к (X^TX). Соотношение справедливо для уравнений регрессии с произвольным количеством m объясняющих переменных.

Пример задачи на нахождение параметров множественной регрессии

Пусть объем предложения некоторого блага Y фирмы линейно зависит от цены X₁ и заработной X₂ сотрудников, производящих данное благо. Определим коэффициенты уравнения линейной регрессии.

Матрицы имеют вид: Таким образом, уравнение регрессии имеет вид: Y = 95,5 + 0,818X₁ — 7,680X₂Отметим, что в случае двух объясняющих переменных: Другие примеры решения задач по эконометрике смотрите здесь

univer-nn.ru