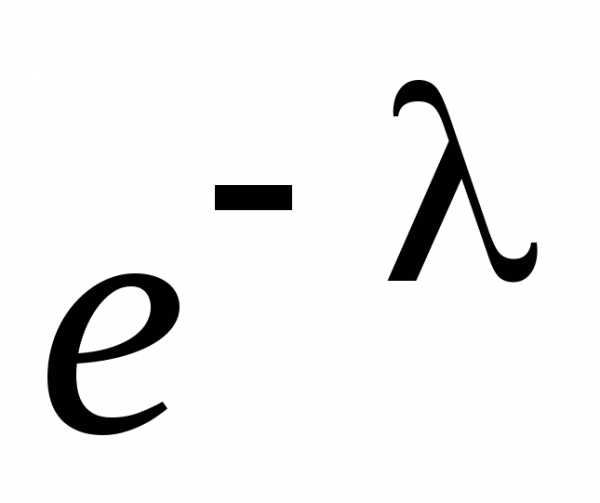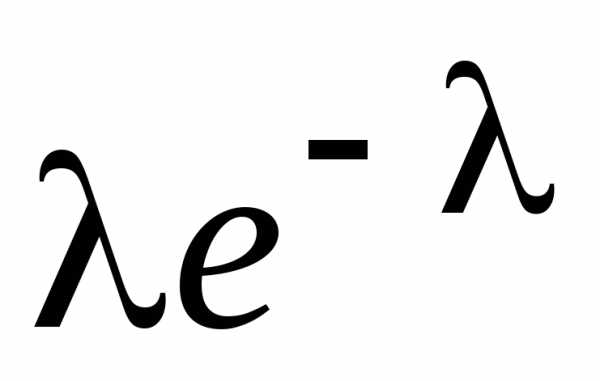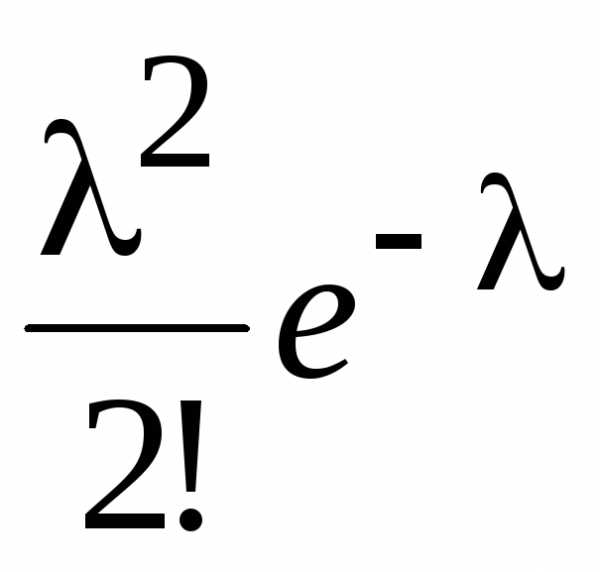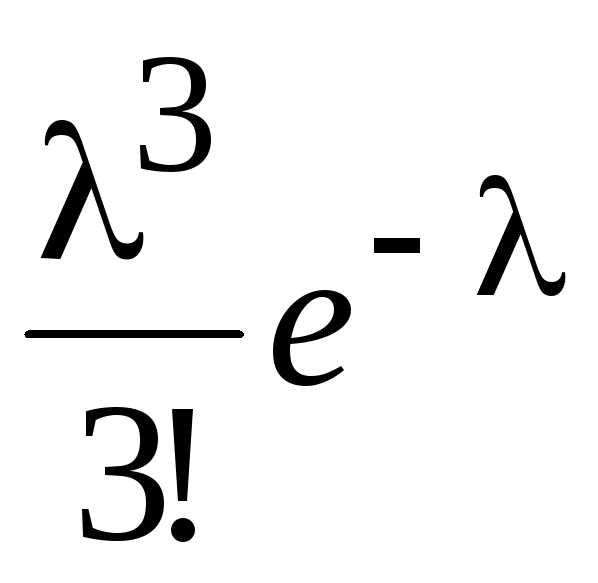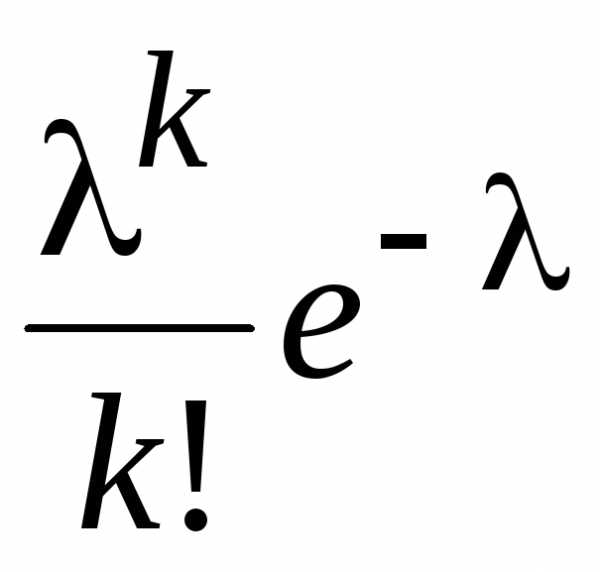Распределение пуассона формула – Формула Пуассона и закон распределения Пуассона. Задача по теории вероятностей с решением
Распределение Пуассона — Википедия
Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску| Распределение Пуассона | |
|---|---|
| Функция вероятности | |
| Функция распределения | |
| Обозначение | P(λ){\displaystyle \mathrm {P} (\lambda )} |
| Параметры | λ∈(0,∞){\displaystyle \lambda \in (0,\infty )} |
| Носитель | k∈{0,1,2,…}{\displaystyle k\in \{0,1,2,\ldots \}} |
| Функция вероятности | e−λλkk!{\displaystyle {\frac {e^{-\lambda }\lambda ^{k}}{k!}}} |
| Функция распределения | Γ(k+1,λ)k!{\displaystyle {\frac {\Gamma (k+1,\lambda )}{k!}}} |
ru.wikipedia.org
Распределение Пуассона
Ранее мы рассмотрели два типа дискретных числовых распределений: биномиальное и гипергеометрическое. Во многих практически важных приложениях большую роль играет распределение Пуассона. Многие из числовых дискретных величин являются реализациями пуассоновского процесса, обладающего следующими свойствами:[1]
- Нас интересует, сколько раз происходит некое событие в заданной области возможных исходов случайного эксперимента. Область возможных исходов может представлять собой интервал времени, отрезок, поверхность и т.п.
- Вероятность данного события одинакова для всех областей возможных исходов.
- Количество событий, происходящих в одной области возможных исходов, не зависит от количества событий, происходящих в других областях.
- Вероятность того, что в одной и той же области возможных исходов данное событие происходит больше одного раза, стремится к нулю по мере уменьшения области возможных исходов.
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Чтобы глубже понять смысл пуассоновского процесса, предположим, что мы исследуем количество клиентов, посещающих отделение банка, расположенное в центральном деловом районе, во время ланча, т.е. с 12 до 13 часов. Предположим, требуется определить количество клиентов, приходящих за одну минуту. Обладает ли эта ситуация особенностями, перечисленными выше? Во-первых, событие, которое нас интересует, представляет собой приход клиента, а область возможных исходов — одноминутный интервал. Сколько клиентов придет в банк за минуту — ни одного, один, два или больше? Во-вторых, разумно предположить, что вероятность прихода клиента на протяжении минуты одинакова для всех одноминутных интервалов. В-третьих, приход одного клиента в течение любого одноминутного интервала не зависит от прихода любого другого клиента в течение любого другого одноминутного интервала. И, наконец, вероятность того, что в банк придет больше одного клиента стремится к нулю, если временной интервал стремится к нулю, например, становится меньше 0,1 с. Итак, количество клиентов, приходящих в банк во время ланча в течение одной минуты, описывается распределением Пуассона.
Распределение Пуассона имеет один параметр, обозначаемый символом λ (греческая буква «лямбда») – среднее количество успешных испытаний в заданной области возможных исходов. Дисперсия распределения Пуассона также равна λ, а его стандартное отклонение равно . Количество успешных испытаний Х пуассоновской случайной величины изменяется от 0 до бесконечности. Распределение Пуассона описывается формулой:
где Р(Х) — вероятность X успешных испытаний, λ — ожидаемое количество успехов, е— основание натурального логарифма, равное 2,71828,
Вернемся к нашему примеру. Допустим, что в течение обеденного перерыва в среднем в банк приходят три клиента в минуту. Какова вероятность того, что в данную минуту в банк придут два клиента? А чему равна вероятность того, что в банк придут более двух клиентов?
Применим формулу (1) с параметром λ = 3. Тогда вероятность того, что в течение данной минуты в банк придут два клиента, равна
Вероятность того, что в банк придут более двух клиентов, равна Р(Х > 2) = Р(Х = 3) + Р(Х = 4) + … + Р(Х = ∞) . Поскольку сумма всех вероятностей должна быть равной 1, члены ряда, стоящего в правой части формулы, представляют собой вероятность дополнения к событию Х≤ 2. Иначе говоря, сумма этого ряда равна 1 – Р(Х ≤ 2). Таким образом, Р(Х> 2) = 1 – Р(Х≤2) = 1 – [Р(Х = 0) + Р(Х = 1) + Р(Х = 2)]. Теперь, используя формулу (1), получаем:
Таким образом, вероятность того, что в банк в течение минуты придут не больше двух клиентов, равна 0,423 (или 42,3%), а вероятность того, что в банк в течение минуты придут больше двух клиентов, равна 0,577 (или 57,7%).
Такие вычисления могут показаться утомительными, особенно если параметр λ достаточно велик. Чтобы избежать сложных вычислений, многие пуассоновские вероятности можно найти в специальных таблицах (рис. 1). Например, вероятность того, что в заданную минуту в банк придут два клиента, если в среднем в банк приходят три клиента в минуту, находится на пересечении строки
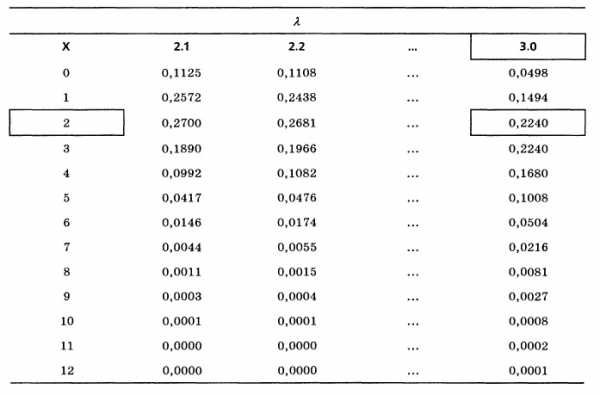
Рис. 1. Пуассоновская вероятность при λ = 3
Сейчас вряд ли кто-то будет пользоваться таблицами, если под рукой есть Excel с его функцией =ПУАССОН.РАСП() (рис. 2). Эта функция имеет три параметра: число успешных испытаний Х, среднее ожидаемое количество успешных испытаний λ, параметр Интегральная, принимающий два значения: ЛОЖЬ – в этом случае вычисляется вероятность числа успешных испытаний Х (только Х), ИСТИНА – в этом случае вычисляется вероятность числа успешных испытаний от 0 до
Рис. 2. Расчет в Excel вероятностей распределения Пуассона при λ = 3
Аппроксимация биноминального распределения с помощью распределения Пуассона
Если число n велико, а число р — мало, биномиальное распределение можно аппроксимировать с помощью распределения Пуассона. Чем больше число n и меньше число р, тем выше точность аппроксимации. Для аппроксимации биномиального распределения используется следующая модель Пуассона.
где Р(Х) — вероятность X успехов при заданных параметрах n и
Теоретически случайная величина, имеющая распределение Пуассона, принимает значения от 0 до ∞. Однако в тех ситуациях, когда распределение Пуассона применяется для приближения биномиального распределения, пуассоновская случайная величина — количество успехов среди n наблюдений — не может превышать число n. Из формулы (2) следует, что с увеличением числа n и уменьшением числа р вероятность обнаружить большое количество успехов уменьшается и стремится к нулю.
Как говорилось выше, математическое ожидание µ и дисперсия σ2 распределения Пуассона равны λ. Следовательно, при аппроксимации биномиального распределения с помощью распределения Пуассона для приближения математического ожидания следует применять формулу (3).
(3) µ = Е(Х) = λ = np
Для аппроксимации стандартного отклонения используется формула (4).
Обратите внимание на то, что стандартное отклонение, вычисленное по формуле (4), стремится к стандартному отклонению в биномиальной модели – , когда вероятность успеха p стремится к нулю, и, соответственно, вероятность неудачи 1 – р стремится к единице.
Предположим, что 8% шин, произведенных на некотором заводе, являются бракованными. Чтобы проиллюстрировать применение распределения Пуассона для аппроксимации биномиального распределения, вычислим вероятность обнаружить одну дефектную шину в выборке, состоящей из 20 шин. Применим формулу (2), получим
Если бы мы вычислили истинное биномиальное распределение, а не его приближение, то получили бы следующий результат:
Однако эти вычисления довольно утомительны. В то же время, если вы используете Excel для вычисления вероятностей, то применение аппроксимации в виде распределения Пуассона становится излишним. На рис. 3 показано, что трудоемкость вычислений в Excel одинакова. Тем не менее, этот раздел, на мой взгляд, полезен понимаем того, что при некоторых условиях биноминальное распределение и распределение Пуассона дают близкие результаты.
Рис. 3. Сравнение трудоемкости расчетов в Excel: (а) распределение Пуассона; (б) биноминальное распределение
Итак, в настоящей и двух предыдущих заметках были рассмотрены три дискретных числовых распределения: биномиальное, гипергеометрическое и Пуассона. Чтобы лучше представлять, как эти распределения соотносятся друг с другом приведем небольшое дерево вопросов (рис. 4).
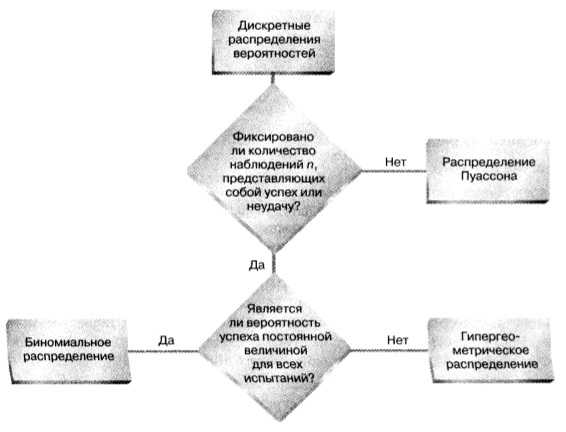
Рис. 4. Классификация дискретных распределений вероятностей
Предыдущая заметка Гипергеометрическое распределение
Следующая заметка Нормальное распределение
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 320–328
baguzin.ru
2. Закон распределения Пуассона.
Если число испытаний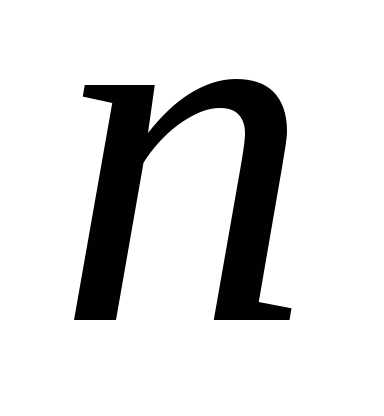 
Определение. Дискретная
случайная величина 
,
возможными значениями которой являются,
а вероятности соответствующих значений
определяются по формуле Пуассона
,
называется пуассоновской
случайной величиной с
параметром 
.
Пуассоновское
распределение широко используется в
теории массового обслуживания. Число 
называется интенсивностью.
Закон распределения Пуассона случайной величины можно записать в виде таблицы 2:
Таблица 2.
Свойства закона распределения Пуассона.
Свойство 1. Сумма вероятностей всех возможных значений пуассоновской случайной величины равна единице, т.е.
.
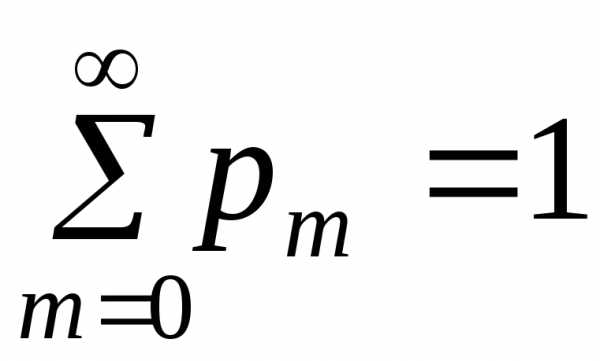Доказательство. Найдем сумму ряда
. ●
Установим теперь
теоретико-вероятностный смысл параметра 
закона распределения Пуассона.
Свойство 2. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны между собой, причем имеют место равенства
.
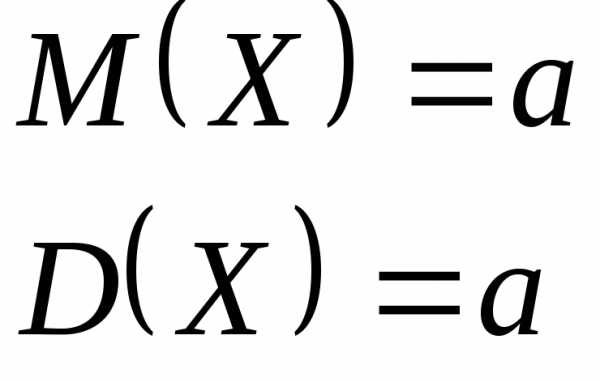Доказательство. Пользуясь определением математического ожидания, находим математическое ожидание пуассоновской случайной величины, заданной таблицей 2.
.
Итак, доказано, что
.
Найдем теперь дисперсию пуассоновской случайной величины
.
Вычислим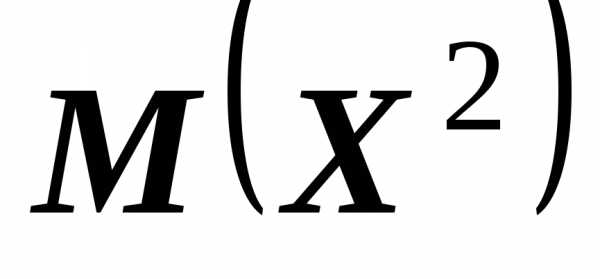 
,
получим
.
Поэтому
. ●
3. Равномерное распределение
Определение. Непрерывная
случайная величина называется равномерно
распределенной на отрезке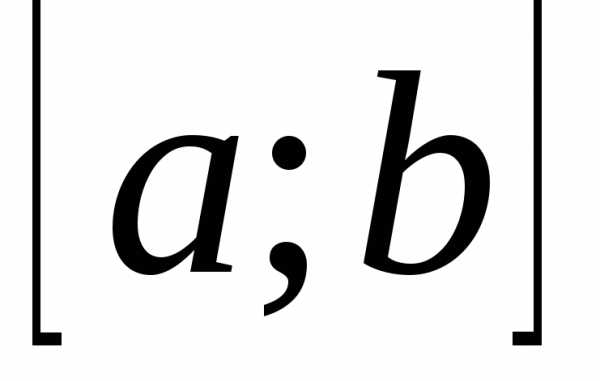 
,
если все ее возможные значения содержатся
на этом отрезке и плотность распределения
вероятности постоянна.
Из определения следует, что дифференциальная функция равномерно распределенной случайной величины имеет вид
Свойства равномерного распределения
Свойство 1. Дифференциальная
функция равномерно распределенной на
отрезке 
случайной величины записывается в виде
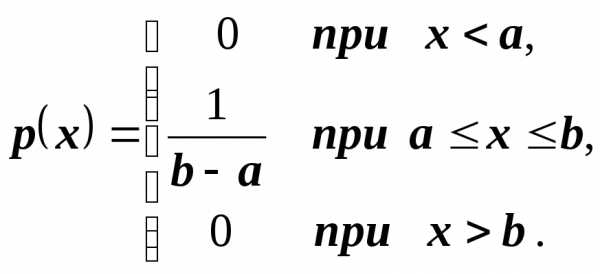(1)
Доказательство.
График плотности
вероятности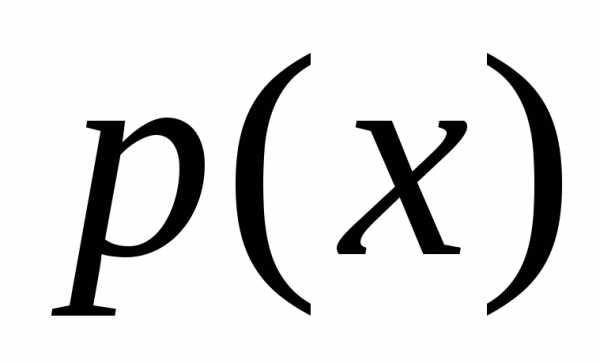 
равномерно
распределенной случайной величины
изображен на рисунке 1
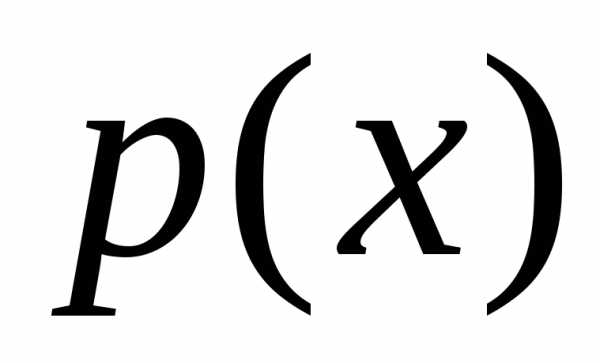
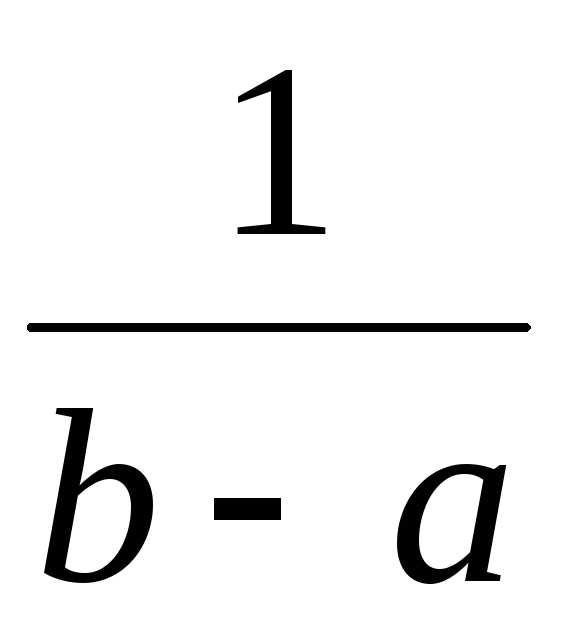
Рис. 1.
Свойство 2. Интегральная функция распределения
случайной величины, равномерно
распределенной на отрезке 
,
записывается в виде
.
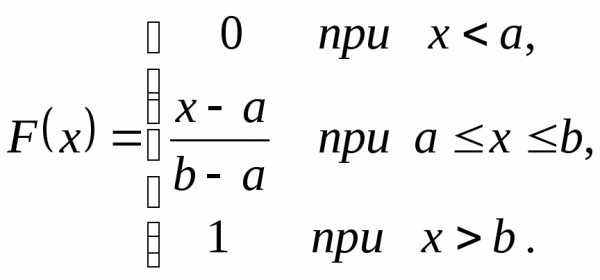Доказательство. | |
График интегральной
функции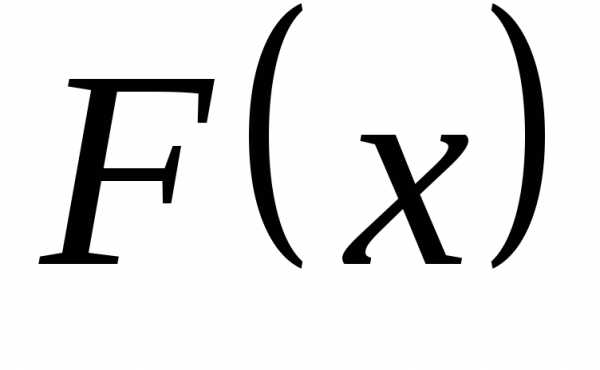 
равномерно распределенной случайной
величины изображен на рисунке 2.
Рис. 2.
Свойство 3. Математическое
ожидание случайной величины, равномерно
распределенной на отрезк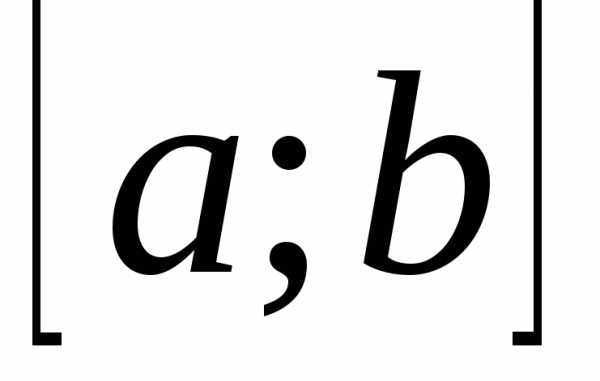е 
,
определяется по формуле
.
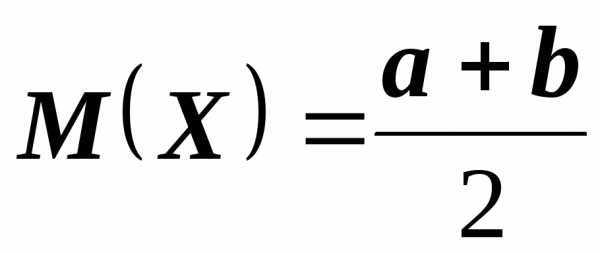Доказательство.
Свойство 4. Дисперсия
случайной величины, равномерно
распределенной на отрезк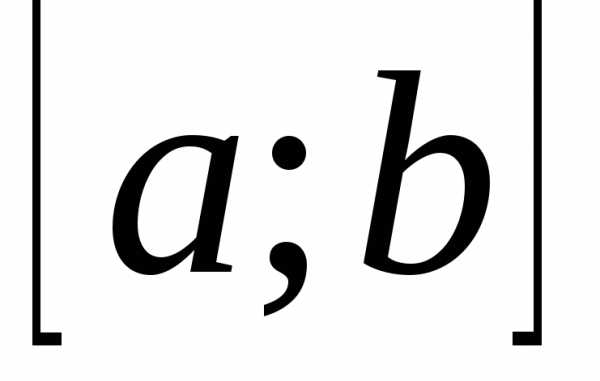е 
,
определяется по формуле
.
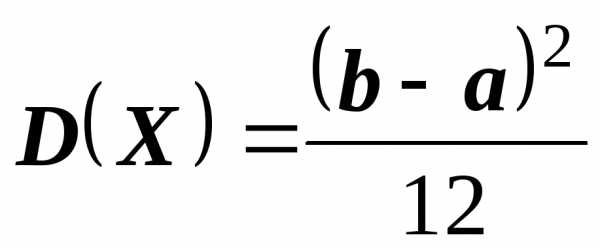Доказательство.
Свойство 5. Среднее квадратическое отклонение
случайной величины равномерно
распределенной на отрезке 
,
вычисляется по формуле
.
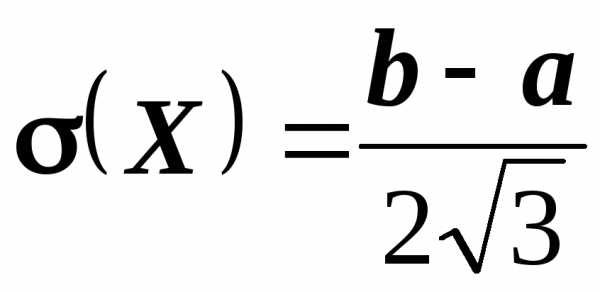Доказательство.
Пример. Случайная
величина равномерно распределена на
интервале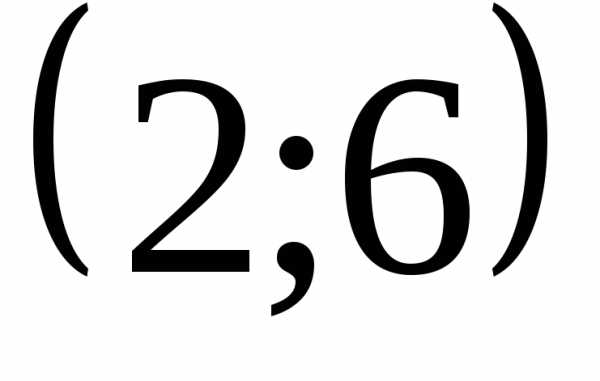 
.
Найти:
а) дифференциальную функцию распределения и построить ее график;
б) интегральную функцию распределения и построить ее график;
в) числовые характеристики заданной случайной величины.
studfiles.net
Распределение Пуассона
Введение
Теория вероятностей – это математическая наука, изучающая закономерности в случайных явлениях. На сегодняшний день это полноценная наука, имеющая большое практическое значение.
История теории вероятности восходит к XVII веку, когда были предприняты первые попытки систематического исследования задач, относящихся к массовым случайным явлениям, и появился соответствующий математический аппарат. С тех пор, многие основы были разработаны и углублены до нынешних понятий, были открыты другие важные законы и закономерности. Множество ученых работало и работает над проблемами теории вероятностей.
Среди них нельзя не обратить внимание на труды Симеона Дени Пуассона ((1781–1840) – французский математик), доказавшего более общую, чем у Якова Бернулли, форму закона больших чисел, а также впервые применившего теорию вероятностей к задачам стрельбы. С именем Пуассона связан один из законов распределения, играющий большую роль в теории вероятностей и ее приложениях.
Число наступлений определённого случайного события за единицу времени, когда факт наступления этого события в данном эксперименте не зависят от того, сколько раз и в какие моменты времени оно осуществлялось в прошлом, и не влияет на будущее. А испытания производятся в стационарных условиях, то для описания распределения такой случайной величины обычно используют закон Пуассона (данное распределение впервые предложено и опубликовано этим учёным в 1837 г.).
Этот закон можно также описывать как предельный случай биноминального распределения, когда вероятность p осуществления интересующего нас события в единичном эксперименте очень мала, но число экспериментов m, производимых в единицу времени, достаточно велико, а именно такое, что в процессе p
0 и m произведение mp стремится к некоторой положительной постоянной величине (т.е. mp).Поэтому закон Пуассона часто называют также законом редких событий.
Распределение Пуассона в теории вероятностей
Функция и ряд распределения
Распределение Пуассона – это частный случай биномиального распределения (при n >> 0 и при p –> 0 (редкие события)).
Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:
где a = n · p – параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию. Приведем математические выкладки, поясняющие этот переход. Биномиальный закон распределения
Pm = Cnm · pm · (1 – p )n – m
может быть написан, если положить p = a /n , в виде
или
Так как p очень мало, то следует принимать во внимание только числа m , малые по сравнению с n . Произведение
весьма близко к единице. Это же относится к величине
очень близка к e –a . Отсюда получаем формулу:
число Эйлера (2,71…). ,Для производящей функции
величины имеем:Интегральная функция вероятности распределения равна
Классическим примером случайной величины, распределенной по Пуассону, является количество машин, проезжающих через какой-либо участок дороги за заданный период времен. Также можно отметить такие примеры, как количество звезд на участке неба заданной величины, количество ошибок в тексте заданной длины, количество телефонных звонков в call-центре или количество обращений к веб-серверу за заданный период времени.
Ряд распределения случайной величины Х, распределенной по закону Пуассона, выглядит следующим образом:
На рис. 1 представлены многоугольники распределения случайной величины Х по закону Пуассона, соответствующие различным значениям параметра а .
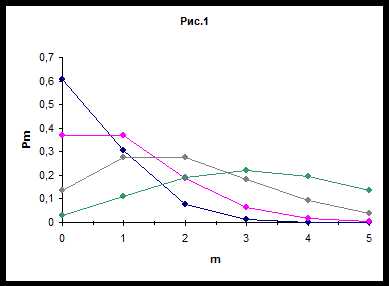
Для начала убедимся, что последовательность вероятностей, может представлять собой ряд распределения, т.е. что сумма всех вероятностей Р m равна единице.
Используем разложение функции ех в ряд Маклорена:
Известно, что этот ряд сходится при любом значении х , поэтому, взяв х=а , получим
следовательно
Числовые характеристики положения о распределении Пуассона
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
По определению, когда дискретная случайная величина принимает счетное множество значений:
Первый член суммы (соответствующий m =0 ) равен нулю, следовательно, суммирование можно начинать с m =1 :
Таким образом, параметр а представляет собой не что иное, как математическое ожидание случайной величины Х .
Кроме математического ожидания, положение случайной величины характеризуется модой и медианой.
Модой случайной величины называется её наиболее вероятное значение.
Для непрерывной величины модой называется точкой локального максимума функции плотности распределения вероятностей. Если многоугольник или кривая распределения имеют один максимум (рис. 2 а), то распределение называется унимодальным, при наличии более одного максимума – мультимодальным (в частности, распределение, имеющее две моды, называется бимодальным). Распределение, имеющее минимум, называется антимодальным (рис. 2 б)
F(x) Pi
xmod x 0 x1 x2 x3 x4 x
Наивероятнейшим значением случайной величины называется мода, доставляющая глобальный максимум вероятности для дискретной случайной величины или плотности распределения для непрерывной случайной величины.
Медиана – это такое значение хl , которое делит площадь под графиком плотности вероятности пополам, т.е. медиана является любым корнем уравнения. Математическое ожидание может не существовать, а медиана существует всегда и может быть неоднозначно определенной.
Медианой случайной величины
называется такое её значение = x med , что P (med ) = Р (> x med ) =.Числовые характеристики разброса
Дисперсией случайной величины Х называют математической ожидание квадрата отклонения случайной величины от ее математического ожидания:
Однако, удобнее ее вычислять по формуле:
Поэтому найдем сначала второй начальный момент величины Х :
По ранее доказанному
кроме того,
mirznanii.com
Формула Пуассона и закон распределения Пуассона. Задача по теории вероятностей с решением
Пусть производится независимых испытаний, в каждом из которых вероятность появления события равна . Для определения вероятности появлений события в этих испытаниях используют формулу Бернулли. Если же велико, то пользуются локальной формулой Лапласа. Однако эта формула непригодна, если вероятность случайного события мала. В этих случаях ( велико, мало) прибегают к асимптотической формуле Пуассона.
Поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно раз. Сделаем важное допущение: произведение сохраняет постоянное значение, а именно . Это означает, что среднее число появления события в различных сериях испытаний, т.е. при различных значениях , остается неизменным.
Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности:
Так как , то , следовательно:
Приняв во внимание, что имеет очень большое значение, вместо найдем
При этом будет найдено лишь приближенное значение отыскиваемой вероятности: хотя и велико, но конечно, а при отыскании предела мы устремим к бесконечности. Затем, что поскольку произведение сохраняет постоянное значение, то при вероятность .
Таким образом:
Эта формула выражает закон распределения Пуассона вероятностей массовых ( велико) и редких ( мало) событий.
Условие задачи
На базе получено 10000 электроламп. Вероятность того, что в пути лампа разобьется, равна 0,0003. Найдите вероятность того, что среди полученных ламп будет пять ламп разбито.
Если перед сессией вам объективно не до выполнения заданий по теории вероятностей, то существует возможность заказать контрольную работу на сайте 100task.ru. Подробнее по ссылке Выполнить контрольную работу по теории вероятностей…
Решение задачи
Условие применимости формулы Пуассона:
Если вероятность появления события в отдельном испытании достаточно близка к нулю, то даже при больших значениях количества испытаний вероятность, вычисляемая по локальной теореме Лапласа, оказывается недостаточно точной. В таких случаях используют формулу, выведенную Пуассоном.
Пусть событие – 5 ламп будет разбито
Воспользуемся формулой Пуассона:
В нашем случае:
Ответ
p=0.1008
100task.ru
6.2. Распределение Пуассона
Как было уже отмечено, биномиальное распределение приближается к нормальному при n. Однако это не имеет места, если наряду с увеличением n одна из величин p или q стремится к нулю. В этом случае имеет место асимптотическая формула Пуассона, т.е. при n, p0
,
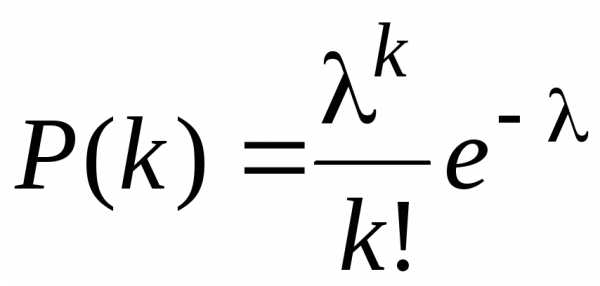(6.7)
где =np. Эта формула определяет закон распределения Пуассона, который имеет самостоятельное значение, а не только как частный случай биномиального распределения. В отличие от биномиального распределения здесь случайная величина k может принимать бесконечное множество значений: k=0,1,2,…
Закон Пуассона описывает число событий k, происходящих за одинаковые промежутки времени при условии, что события происходят независимо друг от друга с постоянной средней интенсивностью, которая характеризуется параметром . Многоугольник распределения Пуассона показан на рис. 6.2. Отметим, что при больших расп
Рис. 6.2
ределение Пуассона приближается к нормальному. Поэтому распределение Пуассона применяется, как правило, в тех случаях, когда имеет порядок единицы, при этом число испытаний n должно быть велико, а вероятность появления события p в каждом испытании мала. В связи с этим закон Пуассона часто называют еще законом распределения редких явлений.Примерами ситуаций, в которых возникает распределение Пуассона, могут служить распределения: 1) числа определенных микробов в единице объема; 2) числа вылетевших электронов с накаленного катода за единицу времени; 3) числа -частиц, испускаемых радиоактивным источником за определенных промежуток времени; 4) числа вызовов, поступающих на телефонную станцию за определенное время суток и т.д.
Запишем закон Пуассона в виде таблицы
X | 0 | 1 | 2 | 3 | … | k | … |
P |
|
|
|
| … |
| … |
Проверим, что сумма всех вероятностей равна единице:
Найдем числовые характеристики этого распределения. По определению математического ожидания для ДСВ имеем
.
Отметим, что в последней сумме суммирование начинается с k=1, т.к. первый член суммы, соответствующий k=0, равен нулю.
Для нахождения дисперсии найдем предварительно математического ожидание квадрата случайной:
Тогда
Таким образом, математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого распределения
. (6.8)
В этом состоит отличительная особенность распределения Пуассона. Так, если на основании опытных данных было получено, что математическое ожидание и дисперсия некоторой величины близки между собой, то есть основания предполагать, что данная случайная величина распределена в соответствии с законом Пуассона.
Воспользовавшись понятием начальных и центральных моментов, можно показать, что для распределения Пуассона коэффициент асимметрии и эксцесс равны:
.
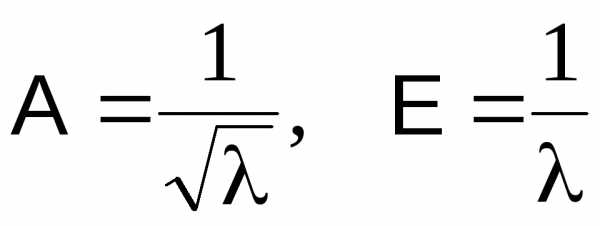(6.9)
Поскольку параметр всегда положителен, то у распределения Пуассона всегда положительная асимметрия и эксцесс.
Покажем теперь, что формулу Пуассона можно рассматривать как математическую модель простейшего потока событий.
Потоком событийназывают последовательность событий, которые наступают в случайные моменты времени. Поток называетсяпростейшим, если он обладает свойствамистационарности,отсутствия последействияиординарности.
Интенсивностью потока называют среднее число событий, которые появляются в единицу времени.
Если постоянная интенсивности потока известна, то вероятность появления k событий простейшего потока за время t определяется формулой Пуассона:
.
(6.10)
Эта формула отражает все свойства простейшего потока. Более того, любой простейший поток описывается формулой Пуассона, поэтому простейшие потоки часто называют пуассоновскими.
Свойство стационарности состоит в том, что вероятность появления k событий в любом промежутке времени зависит только от числа k и от длительности t промежутка времени и не зависит от начала его отсчета. Другими словами, если поток обладает свойством стационарности, то вероятность появления k событий за промежуток времени t есть функция, зависящая только от k и от t.
В случае простейшего потока из формулы Пуассона (6.10) следует, что вероятность k событий за время t, при заданной интенсивности является функцией только двух аргументов: k и t, что характеризует свойство стационарности.
Свойство отсутствия последействия состоит в том, что вероятность появления k событий в любом промежутке времени зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Другими словами, предыстория потока не влияет на вероятности появления событий в ближайшем будущем.
В случае простейшего потока в формуле Пуассона (6.10) не используется информация о появлении событий до начала рассматриваемого промежутка времени, что характеризует свойство отсутствия последействия.
Свойство ординарности состоит в том, что появление двух или более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появление более одного события за малый промежуток времени пренебрежимо мала по сравнению с вероятностью появления только одного события.
Покажем, что формула Пуассона (6.10) отражает свойство ординарности. Положив k=0 и k=1, найдем соответственно вероятности не появления событий и появления одного события:
Следовательно, вероятность появления более одного события равна
.
Используя
разложение функции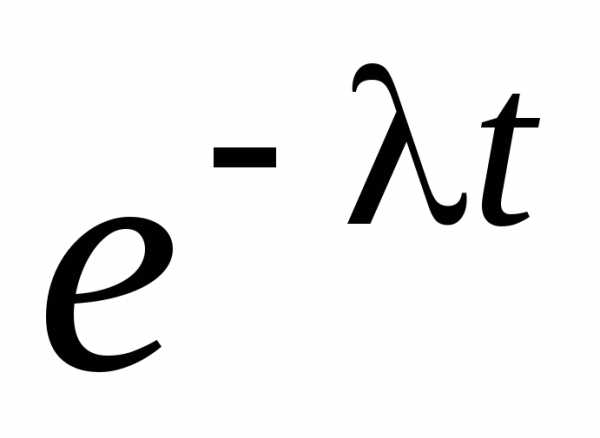 
в ряд Маклорена, после элементарных
преобразований получим
.
Сравнивая Pt(1) и Pt(k>1), заключаем, что при малых значениях t вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события, что характеризует свойство ординарности.
Пример 6.2. В наблюдениях Резерфорда и Гейгера радиоактивное вещество за промежуток времени 7,5 сек испускало в среднем 3,87 -частицы. Найти вероятность того, что за 1 сек это вещество испустит хотя бы одну частицу.
Решение. Как мы уже отмечали, распределение числа -частиц, испускаемых радиоактивным источником за определенных промежуток времени описывается формулой Пуассона, т.е. образует простейший поток событий. Поскольку интенсивность испускания -частиц за 1 сек равно
,
то формула Пуассона (6.10) примет вид
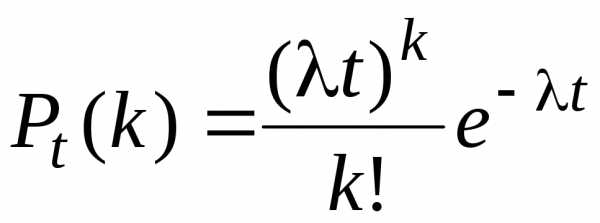
Таким образом, вероятность того, что за t=1 сек вещество испустит хотя бы одну частицу будет равно
.
studfiles.net
Распределения Пуассона. Решение задач
Дискретная случайная величина Х имеет закон распределения Пуассона, если вероятности ее возможных значений
вычисляется по формуле Пуассона, где a=np<10. Как правило, Пуассоновское распределение касается вероятности появления благоприятного события в большом количестве экспериментов, если в одном — вероятность успешного завершения стремится к нулю.
В табличной форме этот закон распределения имеет вид
Условие нормировки для пуассоновского закона распределения запишется следующим образом
Построим образующую функцию вероятностей для приведенного закона
Она принимает достаточно простой компактный вид
Воспользовавшись зависимостями для определения математического ожидания М (Х) и дисперсии D (X) через производные от образующей функции в единице, получим их простые зависимости
1. Математическое ожидание определяется по формуле
2. Имея вторую производную от образующей функции в единице
находят дисперсию
Среднее квадратическое отклонение вычисляем через квадратный корень из дисперсии
Следовательно, для пуассоновского закона распределения вероятностей математическое ожидание и дисперсия равны произведению количества опытов на вероятность благоприятной события
На практике, если математическое ожидание и дисперсия близкие по значению то принимают гипотезу, что исследуемая величина имеет закон распределения Пуассона.
3. Асимметрия и эксцесс для пуассоновский закон также уровни и вычисляются по формулам
Рассмотрим несколько задач.
—————————————-
Задача 1. Микропроцессор имеет 10000 ранзисторов, работающих независимо друг от друга. Вероятность того, что транзистор выйдет из строя во время работы прибора, является величиной маловероятной и составляет 0,0007. Определить математическое ожидание М (Х) и среднее квадратическое отклонение S (Х) случайной величины Х — исла транзисторов, выйдут из строя во время работы процессора.
Решение. Задача удовлетворяет всем законам пуассоновский распределения:
количество испытаний n=10000 велика;
вероятность р=0,0007 близка к нулю;
их произведение a=np=7<10.
На основе данных вычисляем заданные величины
————————————
Задача 2. В рыбацком городке 99,99% мужчин хотя бы раз в жизни были на рыбалке. Проводят социологические исследования среди 10000 наугад выбранных мужчин. Определить дисперсию D (X) и среднее квадратическое отклонени S (Х) случайной величины Х — числа мужчин, которые ни разу не были на рыбалке.
Решение. егко убедиться, что величина Х имеет пуассоновский закон распределения. С условия задачи находим
По формулам находим дисперсию и среднее квадратическое отклонение
Можно найти в гугле еще много подобных задач, всех их объединяет изменение случайной величины по закону Пуассона. Схема нахождения числовых характеристик приведена выше и является общей для всех задач, кроме того формулы для вычислений достаточно простыми даже для школьников.
yukhym.com