Радианная окружность – [Билет 17] Радианная и градусная меры углов. Тригонометрическая окружность. Соответствия между действительными числами и точками на тригонометрической окружности.

Содержание

Радианная мера угла

Цель урока «Радианная мера угла» 9 класс:

Усвоить определение угла в один радиан, запомнить формулы перехода от градусной меры угла к радианной и от радианной к градусной.

Научиться использовать полученные знания при выполнении упражнений

Наравне с градусной мерой угла используется радианная.

Возьмем на координатной плоскости окружность с центром в точке О и радиусом R. Отметим на ней дугу РМ, длина которой равна R и угол РОМ.

Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.

Градусная мера угла в 1 радиан равна:

Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.

И наоборот

Так как

π = 3,14, то 1 рад = 57,3°

Если угол содержит a радиан, то его градусная мера равна

И наоборот

Обычно при обозначении меры угла в радианах наименование «рад» опускают.

Например, 360° = 2π рад, пишут 360° = 2π

В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.

Градусы	0	15	30	45	60	75	90	120	135	150	180	270	360
Радианы	0	π/12	π/6	π/4	π/3	5π/12	π/2	2π/3	3π/4	5π/6	π	3π/2	2π

Пример 1.

Найти радианную меру угла равного а) 40° , б)120° , в)105°

Решение

а) 40° = 40·π / 180 = 2π/9

б) 120° = 120·π/180 = 2π/3

в) 105° = 105·π/180 = 7π/12

Пример 2.

Найти градусную меру угла выраженного в радианах а) π/6 , б) π/9, в) 2·π/3

Решение

а) π/6 = 180°/6 = 30°

б) π/9 = 180°/9 = 20°

в) 2π/3 = 2·180°/6 = 120°

mirurokov.ru

Длина дуги окружности и радианы

Тригонометрия — это умение пользоваться треугольниками для изменения (дословный перевод — «измеряю треугольник»). С давних времен, при помощи тригонометрии измеряли Землю и звездные объекты и проводили постройку зданий.

Но начинается тригонометрия даже не с треугольника, а с круга!

Про дугу окружности мы уже говорили ранее. Дуга окружности ограничена углом из двух радиусов. Если мы возьмем 360 таких углов по одному градусу и совместим их, то получим круг (словно колесо нашпигованное спицами).

Вспомним ещё одно интересное число π (Пи) = 3,1415,…. Оно постоянно и произошло от деления длины окружности на его диаметр. Длина/диаметр = π. Увеличиваем диаметр, соразмерно увеличится длина окружности, именно во столько раз (можете проверить, не верьте нам на слово!)

Так как диаметр окружности равен двум радиусам (2R), то длина всей окружности l = 2πR. Если не усложнять и взять R = 1, то l = 2π (фактически, эту единицу можно не учитывать).

Радиан и градусы

Угол в 1 радиан

— это центральный угол (лучи выходят из центра), длина дуги у этого угла равна радиусу окружности (AB = R).

т.е. ∠AOB = 1 рад

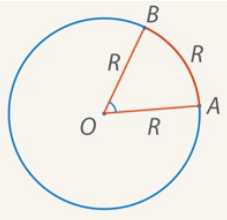
Теперь вспомнинаем из текста выше, что l = 2πR или теперь можно сказать, что l = 2π рад = 360°, а если взять половину окружности, то π рад = 180°. Т.е. половина окружности — это 3 радиана (длины радиуса окружности) и еще хвостик из примерно 0,1415 радиана.

Обратите внимание, что «рад» часто не пишется, просто имеется ввиду, поэтому, если увидите, например sinπ/4, то знайте, что это sin45°. Или sinπ/6 = sin30° и т.д.

Значит, 1° = π рад / 180° или просто π / 180°

Если прикинуть по-другому, то 180° / π и получаем примерно 60° (точнее 57,3° с копейками). Кстати, здесь градусы уже есть, поэтому π подразумевается, как обычное число π = 3,1415…

Если желаете хорошо запомнить и понять таблицу синусов, ксинусов, тангенсов и котангенсов, то смотрите этот урок по ссылке из геометрии/9 класс, а также до/после него.

Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно

Добавить новость и получить деньги

Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников

uchilegko.info

Длина дуги окружности. Радианная мера угла [wiki.eduVdom.com]

Найдем длину дуги окружности радиуса R, отвечающей центральному углу в n° (рис.1).

Рис.1
Развернутому углу соответствует длина полуокружности $\pi R$. Следовательно, углу в 1° соответствует дуга длины $\frac{\pi R}{180}$ , а углу в n° соответствует дуга длины $$ l = \frac{\pi R}{180}n \,\,\, (8) $$ Например, длина дуги окружности радиуса 12 м, отвечающей центральному углу в 30°, есть $$ l = \frac{12\pi}{180} \bullet = 2\pi \approx 6 \text{(м)} $$

Пример 1. По данной хорде к найти длину ее дуги, если она соответствует центральному углу в 60° (рис.2).
Рис.2
Решение. Так как АО = ВО = R(R — радиус окружности) и ∠ АОВ = 60°, то треугольник АОВ равносторонний: R = АВ = к. Теперь согласно формуле (8) имеем: $$ l = \frac{\pi R}{180} \bullet 60 = \frac{\pi k}{3} $$ Радианной мерой угла называется отношение длины соответствующей дуги к радиусу окружности. Из формулы для длины дуги окружности следует, что $$ \frac{l}{R} = \frac{\pi}{180}n $$ , т.е.
радианная мера угла получается из градусной умножением на $\frac{\pi}{180}$. В частности, радианная мера угла 180° равна $\pi$, радианная мера прямого угла равна $\frac{\pi}{2}$.
Единицей радианной меры углов является радиан. Угол в один радиан — это центральный угол, у которого длина дуги равна радиусу (рис.3).
Рис.3
Градусная мера угла в один радиан равна $\frac{180^{\circ}}{\pi} = 57°$ .
Пример 2. Найти радианные меры углов параллелограмма ABCD, если ∠ A = 36°.
Решение. Радианная мера угла А равна $36° \bullet \frac{\pi}{180°} = \frac{\pi}{5}$ ,а радианная мера угла В равна к $\pi — \frac{\pi}{5} = \frac{4\pi}{5}$ , так как в параллелограмме сумма углов, прилежащих к одной стороне, равна 180° (теорема 1). Наконец, радианные меры углов C и D соответственно равны $\frac{\pi}{5}$ и $\frac{4\pi}{5}$ (в параллелограмме противоположные углы равны).
wiki.eduvdom.com
8. Радианы, тригонометр.функции
Угол величиной в 1 радиан
1 радиан — величина центрального угла окружности, опирающегося на дугу, длина которой равна радиусу этой окружности.
Примечание. Очевидно, что угол в радиан не меняется при переходе к другой окружности. Измерение углов радианами — пропорциональное, аналогичное измерению градусами или измерению отрезков единичными отрезками. Например, угол опирающийся на дугу, длина которой равна двум радиусам, будет иметь мерурадиана.
Радианная мера угла, то есть, выражение величины угла в радианах, имеет преимущества перед градусной мерой или любой другой: численное значение радианной меры дуги единичной окружности совпадает с длиной соответствующей дуги. Таким образом, радианная мера даёт возможность отождествить (не различать) измерение углов и отрезков.
Перевод из градусной меры в радианную
Центральный угол окружности, равный , опирается на полуокружность. Длина полуокружности единичного радиуса равна. Следовательно,рад. В силу принципа пропорциональности радианной меры, получаем формулу для перевода градусной меры произвольного угла в радианную:рад.
Пример. Дан угол радрад.
Перевод из радианное меры в градусную
Центральный угол окружности, равный , опирается на полуокружность. Длина полуокружности единичного радиуса равна. Следовательно,рад. В силу принципа пропорциональности радианной меры, получаем формулу для перевода градусной меры произвольного угла в радианную:.
Пример. Дан угол рад. Выразить его величину в градусах.
Решение. рад.
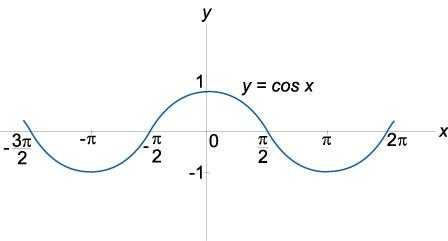
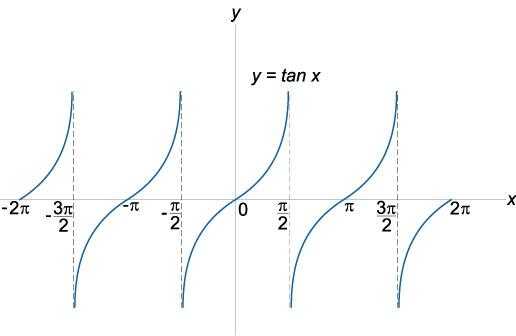
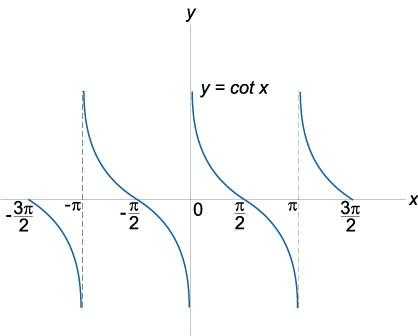
Определение и графики тригонометрических функций
Величины углов (аргументы функций): α, x Тригонометрические функции: sin α, cos α, tan α, cot α, sec α, cosec α Множество действительных чисел: ℜ Координаты точки окружности: x, y
Радиус круга: r Целые числа: k
Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решениидифференциальныхи функциональных уравнений.
К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс, котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.
Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r = 1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.

Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r: sin α = y/r. Поскольку r = 1, то синус равен ординате точки M(x,y).
Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r: cos α = x/r = x
Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x: tan α = y/x,   x ≠ 0
Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: cot α = x/y,   y ≠ 0
Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y): sec α = r/x = 1/x,   x ≠ 0
Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y): cosec α = r/y = 1/y,   y ≠ 0
В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x, y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: Синусом угла α называется отношение противолежащего катета к гипотенузе. Косинусом угла α называется отношение прилежащего катета к гипотенузе. Тангенсом угла α называется противолежащего катета к прилежащему. Котангенсом угла α называется прилежащего катета к противолежащему.
График функции синус y = sin x, область определения: x ∈ ℜ, область значений: −1 ≤ sin x ≤ 1

График функции косинус y = cos x, область определения: x ∈ ℜ, область значений: −1 ≤ cos x ≤ 1

График функции тангенс y = ttg x, область определения: x ∈ ℜ, x ≠ (2k + 1)π/2, область значений: −∞ < tg x < ∞

График функции котангенс y = ctg x, область определения: x ∈ ℜ, x ≠ kπ, область значений: −∞ < ctg x < ∞

Формулы приведения

   Основные тригонометрические тождества
studfiles.net
Радианная мера угла. Радиан.
Для его измерения рассмотрим единичную окружность, где вершина угла совпадает с его центром. Затем нарисуем дугу, равную радиусу окружности и соединим концы дуги с центром.

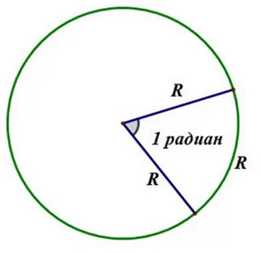
Это и есть один радиан, один градус равен $\frac{π}{180}$ радиан и $1$ радиан равен $\frac{180}{π}$ градусов.
Вся окружность равна $2π$.
Определение радиана:

Краткая история радиана
Слово «радиан» было придумано Томасом Муиром или Джеймсом Томпсоном около 1870 года, математики измеряли углы таким образом в течение длительного времени. Например, Леонард Эйлер (1707-1783) в своих исследованиях в алгебре измерял углы по длине дуги, отрезанной в единичной окружности. Это ему было необходимо для того, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции косинусов с экспоненциальной функцией.

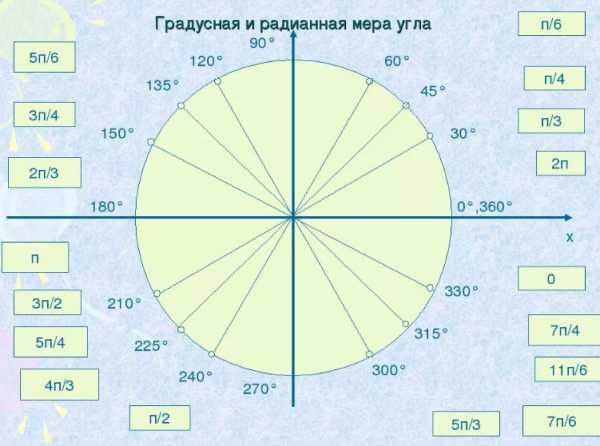
Найдите градусную меру углов, если его радианная мера равна: $\frac{π}{2};\frac{π}{4};\frac{π}{8};\frac{5π}{6};$
Решение.
$\frac{π}{2}*\frac{180}{π}=$$90°$

$\frac{π}{4}*\frac{180}{π}=$$45°$

$\frac{π}{8}*\frac{180}{π}=$$22,5°$

$\frac{5π}{6}*\frac{180}{π}=$$150°$

Таблица градусов в радианах

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Тригонометрия
Рассмотрим тригонометрические круги, изображенные на рисунке 1 и рисунке 2.
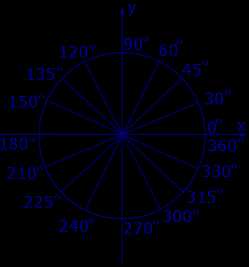
Рис.1
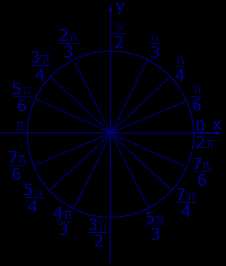
Рис.2
На тригонометрическом круге, изображенном на рисунке 1, центральные углы измерены в градусах, а на тригонометрическом круге, изображенном на рисунке 2, те же центральные углы измерены в радианах.
Углом в 1 градус называют угол, составляющий полного угла. Углом в k° называют угол в k раз больший угла в 1° .
Углом в 1 радиан называют центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной 1 . Углом в k радиан называют центральный угол тригонометрического круга в k раз больший угла в 1 радиан.
Следствие 1. Углом в k радиан является центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной k .
Следствие 2. Полный угол является углом в 2π радиан.
Для того, чтобы найти формулы, связывающие градусную и радианную меры угла, рассмотрим рисунки 3 и 4
Рис.3 Рис.4
Рис.3
Рис.4
На этих рисунках изображены прямые углы, причем на рисунке 3 прямой угол измерен в градусах и равен 90° , а на рисунке 4 прямой угол измерен в радианах и равен радиан. Следовательно,
Таким образом, формулы, связывающие градусную и радианную меры угла, имеют вид
Поскольку , то
По этой причине углы, составляющие целое число радиан, изображаются на тригонометрическом круге так, как это показано на рисунке 5.
Рис.5
Замечание. Тригонометрическая формула sin α означает, что рассматривается синус угла в α радиан, а тригонометрическая формула sin α° означает, что рассматривается синус угла в α градусов. По такому же правилу определяются значения косинуса, тангенса и котангенса.
Пример. Найти наименьшее из чисел:
Решение. Поскольку
то наименьшим числом является число cos 3 .
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными».
Запись по телефону (495) 509-28-10
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Тригонометрия: радианная мера измерения угла
В этой статье мы познакомимся с радианной мерой измерения углов, научимся переводить из радианной меры в градусную и обратно, и отмечать на тригонометрическом круге точки, соответствующие углам поворота, выраженным в радианах.
Чтобы лучше понять, что такое угол в 1 радиан, и как отмечать на тригонометрическом круге точки, соответствующие углу поворота, выраженному в радианах, посмотрите, пожалуйста, ВИДЕОУРОК.

Итак. Углом в 1 радиан называется центральный угол, который опирается на дугу, равную радиусу: Соотношение между радианной и градусной мерой измерения угла выражается равенством:
ß°∏=180°x,
где ß° — градусная мера измерения угла, x- радианная мера. Например, чтобы определить, сколько градусов содержит угол ∏/10 радиан, нужно в равенство вместо х подставить ∏/10. Получим:
ß°∏=180°∏/10 (1)
ß°=18°. Чтобы определить, сколько радиан содержит угол 60°, надо в равенство (1) вместо ß° поставить 60°:

60°∏=180°х
x=∏/3.
Таблица соответствия между радианной и градусной мерой измерения углов выглядит так:
Угол в радианах Угол в градусах
0 0
∏/6 30°
∏/4 45°
∏/3 60°
∏/2 90
∏    180°
2∏ 360°
∏/180 1°

Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и С1»
ege-ok.ru