Простейшие тригонометрические формулы – Основные тригонометрические тождества, формулы приведения, сложения, двойного угла, суммы и разности, половинного аргумента, тангенс половинного аргумента. Тест
Тригонометрические формулы. Основные тригонометрические тождества. Тригонометрические тождества
Основные тригонометрические тождества
- sin² α + cos² α = 1
- tg α · ctg α = 1
- tg α = sin α ÷ cos α
- ctg α = cos α ÷ sin α
- 1 + tg² α = 1 ÷ cos² α
- 1 + ctg² α = 1 ÷ sin² α
Формулы сложения
- sin (α + β) = sin α · cos β + sin β · cos α
- sin (α — β) = sin α · cos β — sin β · cos α
- cos (α + β) = cos α · cos β — sin α · sin β
- cos (α — β) = cos α · cos β + sin α · sin β
- tg (α + β) = (tg α + tg β) ÷ (1 — tg α · tg β)
- tg (α — β) = (tg α — tg β) ÷ (1 + tg α · tg β)
- ctg (α + β) = (ctg α · ctg β — 1) ÷ (ctg β + ctg α)
- ctg (α — β) = (ctg α · ctg β + 1) ÷ (ctg β — ctg α)
Формулы двойного угла
- cos 2α = cos² α — sin² α
- cos 2α = 2cos² α — 1
- cos 2α = 1 — 2sin² α
- sin 2α = 2sin α · cos α
- tg 2α = (2tg α) ÷ (1 — tg² α)
- ctg 2α = (ctg² α — 1) ÷ (2ctg α)
Формулы тройного угла
- sin 3α = 3sin α — 4sin³ α
- cos 3α = 4cos³ α — 3cos α
- ctg 3α = (3ctg α — ctg³ α) ÷ (1 — 3ctg² α)
Формулы понижения степени
- sin² α = (1 — cos 2α) ÷ 2
- sin³ α = (3sin α — sin 3α) ÷ 4
- cos² α = (1 + cos 2α) ÷ 2
- cos³ α = (3cos α + cos 3α) ÷ 4
- sin² α · cos² α = (1 — cos 4α) ÷ 8
- sin³ α · cos³ α = (3sin 2α — sin 6α) ÷ 32
Переход от произведения к сумме
- sin α · cos β = ½ (sin (α + β) + sin (α — β))
- sin α · sin β = ½ (cos (α — β) — cos (α + β))
- cos α · cos β = ½ (cos (α — β) + cos (α + β))
Переход от суммы к произведению
Другие заметки по алгебре и геометрии
edu.glavsprav.ru
Тригонометрические формулы функций, более 100 шт
Тригонометрия в буквальном переводе означает измерение треугольников. Но это надо понимать как решение треугольников, то есть определения их сторон, углов или других элементов. Возникновение тригонометрии связано с землеизмерением, астрономией и строительством.
Основные тригонометрические формулы
Основное тригонометрическое тождество
Эти тождества используются для преобразования тригонометрических выражений; позволяют по значению одной из тригонометрических функций найти значения всех остальных.
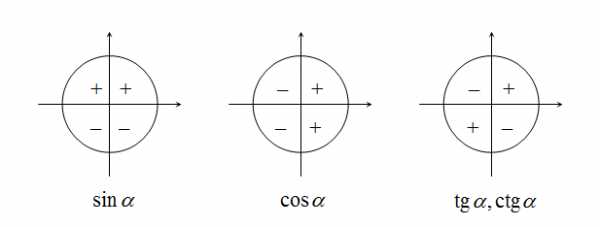
Знаки тригонометрических функций
Отсюда можем сделать вывод, что значения синусов углов лежащих в первой и второй четверти положительны (так как ординаты точек в этих четвертях больше нуля), а лежащих в третьей и четвёртой четверти – отрицательны.
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент.
Формулы, выражающие тригонометрические функции через другие тригонометрические функции
Данные формулы позволяют находить одну тригонометрическую функцию угла если известная какая-нибудь иная функция этого угла. Используются при упрощениях и вычислениях:
Формулы, выражающие тригонометрические функции через тангенс половинного аргумента
Эти формулы находят свое широкое применение в интегральном исчислении.
Формулы двойных и тройных аргументов
Данные формулы довольно легко получить при помощи формул сложения аргументов тригонометрических функций, заменой на Используются при тригонометрических упрощениях и преобразованиях.
Синус двойного угла:
Косинус двойного угла:
Формулы половинного аргумента
Названные формулы выражают функции половинного аргумента через тригонометрические функции аргумента При меняются в тригонометрических преобразованиях.
Формулы сложения и вычитания аргументов
Тригонометрические формулы сложения и вычитания углов представляют собой тригонометрические уравнения, в которых в качестве аргумента тригонометрической функции выступает сумма или разность двух углов и Данные формулы позволяют по известным тригонометрическим функциям аргументов и определять значения этих функций для сумм или разностей указанных аргументов.
Формулы преобразования суммы тригонометрических функций в произведение
Сумма (и разность) тригонометрических функций преобразуется в произведение функций от других аргументов по следующим формулам, которые выводятся из теорем сложения, а также определений тангенса и котангенса:
Формулы для разложения тригонометрических выражений на множители.
Формулы преобразования произведения тригонометрических функций в сумму
Эти формулы получаются из сложения/вычитания соответствующих формул сложения и вычитания аргументов и дальнейшего упрощения:
Используются при тригонометрических преобразованиях.
Формулы понижения степени тригонометрических функций
Данные формулы используются при различных тригонометрических преобразованиях:
Другие формулы
ru.solverbook.com
Формулы тригонометрии
Формулы тригонометрии (тригонометрические формулы) для решения математических задач. Основные тригонометрические тождества, формулы понижения степени, сложения, вычитания и умножения, а также другие формулы. Дополнительно приведены значения тригонометрических функций для наиболее распространённых углов.
Основные тождества
Формулы двойного угла
… Подготовка формул …Формулы тройного угла
… Подготовка формул …Формулы понижения степени
… Подготовка формул …Формулы понижения степени
… Подготовка формул …Формулы понижения степени
… Подготовка формул …Формулы половинного аргумента
Формулы понижения степени
половинного аргумента
… Подготовка формул …Формулы сложения
… Подготовка формул …Формулы вычитания
… Подготовка формул …Формулы преобразования суммы
в формулы произведения
… Подготовка формул …Формулы преобразования разности
в формулы произведения
… Подготовка формул …Формулы преобразования суммы
… Подготовка формул …Формулы преобразования произведения
в формулы суммы и разности
… Подготовка формул …Формулы преобразования произведения
функций в степени
… Подготовка формул …Формулы понижения степени
… Подготовка формул …Универсальная
тригонометрическая подстановка
… Подготовка формул … Значения тригонометрических функций
| α | 0 | ||||||||||||||||
| α° | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 225° | 240° | 270° | 300° | 315° | 330° | 360° | |
| sin α | 0 | 1 | 0 | −1 | 0 | ||||||||||||
| cos α | 1 | 0 | −1 | 0 | 1 | ||||||||||||
| tg α | 0 | 1 | − | −1 | 0 | 1 | − | −1 | 0 | ||||||||
| ctg α | − | 1 | 0 | −1 | − | 1 | 0 | −1 | − |
Теория
Тригонометрия – раздел математики, изучающий зависимости углов и сторон треугольников, которые выражены функциями, называемыми тригонометрическими.
Функция – это правило, описывающее зависимость одной величины от другой.
Тождество – это равенство, справедливое при любых значениях, входящих в него переменных
Тригонометрические тождества (равенства) описывают зависимости между синусом, косинусом, тангенсом и котангенсом.
Скачать тригонометрические формулы
Вы можете скачать тригонометрические формулы в виде картинки:








doza.pro
Тригонометрические формулы
Наиболее часто встречающиеся тригонометрические формулы:
\(\blacktriangleright\) Основные тождества: \[\begin{array}{|l|l|} \hline \sin^2 \alpha+\cos^2 \alpha =1& \mathrm{tg}\, \alpha \cdot \mathrm{ctg}\, \alpha =1 \\ &(\sin\alpha\ne 0, \cos\alpha\ne 0)\\[0.5ex] \hline &\\ \mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos \alpha} &\mathrm{ctg}\, \alpha =\dfrac{\cos \alpha}{\sin \alpha} \\&\\ 1+\mathrm{tg}^2\, \alpha =\dfrac1{\cos^2 \alpha} & 1+\mathrm{ctg}^2\, \alpha=\dfrac1{\sin^2 \alpha}\\&\\ (\cos\alpha\ne 0)& (\sin\alpha\ne 0) \\ \hline \end{array}\]
\(\blacktriangleright\) Формулы сложения углов: \[\begin{array}{|l|r|} \hline &\\ \sin{(\alpha\pm \beta)}=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha & \cos{(\alpha\pm \beta)}=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &\\ \hline &\\ \mathrm{tg}\, (\alpha\pm \beta)=\dfrac{\mathrm{tg}\, \alpha\pm \mathrm{tg}\, \beta}{1 \mp \mathrm{tg}\, \alpha\cdot \mathrm{tg}\, \beta} & \mathrm{ctg}\, (\alpha\pm\beta)=-\dfrac{1\mp \mathrm{ctg}\, \alpha\cdot \mathrm{ctg}\, \beta}{\mathrm{ctg}\, \alpha\pm \mathrm{ctg}\, \beta}\\&\\ \cos\alpha\cos\beta\ne 0&\sin\alpha\sin\beta\ne 0\\ \hline \end{array}\]
\(\blacktriangleright\) Формулы двойного и тройного углов: \[\begin{array}{|lc|cr|} \hline \sin {2\alpha}=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos{2\alpha}=\cos^2\alpha -\sin^2\alpha\\ \sin \alpha\cos \alpha =\dfrac12\sin {2\alpha} && & \cos{2\alpha}=2\cos^2\alpha -1\\ & & & \cos{2\alpha}=1-2\sin^2 \alpha\\ \hline &&&\\ \mathrm{tg}\, 2\alpha = \dfrac{2\mathrm{tg}\, \alpha}{1-\mathrm{tg}^2\, \alpha} && & \mathrm{ctg}\, 2\alpha = \dfrac{\mathrm{ctg}^2\, \alpha-1}{2\mathrm{ctg}\, \alpha}\\&&&\\ \cos\alpha\ne 0, \ \cos2\alpha\ne 0 &&& \sin\alpha\ne 0, \ \sin2\alpha\ne 0\\ \hline &&&\\ \sin {3\alpha}=3\sin \alpha -4\sin^3\alpha && & \cos{3\alpha}=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline \end{array}\]
\(\blacktriangleright\) Формулы понижения степени: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin^2\alpha=\dfrac{1-\cos{2\alpha}}2 &&& \cos^2\alpha=\dfrac{1+\cos{2\alpha}}2\\&&&\\ \hline \end{array}\]
\(\blacktriangleright\) Формулы произведения функций: \[\begin{array}{|c|} \hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}-\cos{(\alpha+\beta)}\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}+\cos{(\alpha+\beta)}\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin{(\alpha-\beta)}+\sin{(\alpha+\beta)}\bigg)\\\\ \hline \end{array}\]
\(\blacktriangleright\) Формулы суммы/разности функций: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin\alpha+\sin\beta=2\sin{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \sin\alpha-\sin\beta=2\sin{\dfrac{\alpha-\beta}2}\cos{\dfrac{\alpha+\beta}2}\\&&&\\ \cos\alpha+\cos\beta=2\cos{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \cos\alpha -\cos\beta=-2\sin{\dfrac{\alpha-\beta}2}\sin{\dfrac{\alpha+\beta}2}\\&&&\\ \mathrm{tg}\, \alpha \pm \mathrm{tg}\, \beta=\dfrac{\sin{(\alpha\pm\beta)}}{\cos\alpha\cos\beta} &&& \mathrm{ctg}\, \alpha\pm \mathrm{ctg}\, \beta= — \dfrac{\sin{(\alpha\pm \beta)}}{\sin\alpha\sin\beta}\\&&&\\ \hline \end{array}\]
\(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin{array}{|l|r|} \hline &\\ \sin{2\alpha}=\dfrac{2\mathrm{tg}\, \alpha}{1+\mathrm{tg}^2\, \alpha} & \cos{2\alpha}=\dfrac{1-\mathrm{tg}^2\, \alpha}{1+\mathrm{tg}^2\, \alpha}\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end{array}\]
\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin{array}{|c|} \hline \text{Частный случай}\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin{\left(\alpha\pm \dfrac{\pi}4\right)}\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin{\left(\alpha\pm \dfrac{\pi}6\right)}\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin{\left(x\pm \dfrac{\pi}3\right)}\\\\ \hline \text{Общий случай}\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt{a^2+b^2}\cdot \sin{(\alpha\pm \phi)}, \ \ \cos\phi=\dfrac a{\sqrt{a^2+b^2}}, \ \sin\phi=\dfrac b{\sqrt{a^2+b^2}}\\\\ \hline \end{array}\]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
\(\blacktriangleright\) Вывод формулы косинуса разности углов \(\cos{(\alpha -\beta)}=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
Рассмотрим тригонометрическую окружность и на ней углы \(\alpha\) и \(\beta\). Пусть этим углам соответствуют точки \(A\) и \(B\) соответственно. Тогда координаты этих точек: \(A(\cos\alpha;\sin\alpha), \ B(\cos\beta;\sin\beta)\).
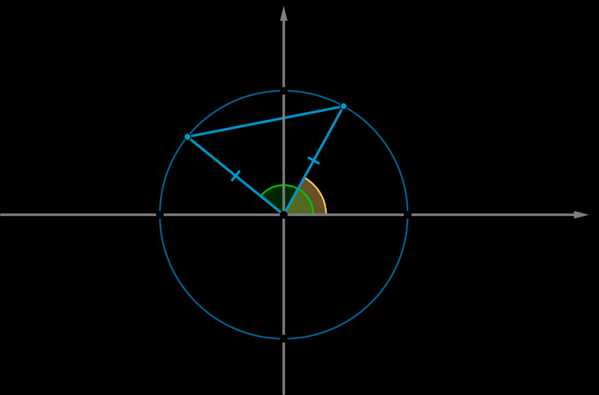
Рассмотрим \(\triangle AOB: \ \angle AOB=\alpha-\beta\). По теореме косинусов:
\(AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)\) (т.к. \(AO=BO=R\) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
\(AB^2=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2=\cos^2\alpha-2\cos\alpha\cos\beta+\cos^2\beta+\)
\(+\sin^2\alpha-2\sin\alpha\sin\beta+\sin^2\beta=\big(\cos^2\alpha+\sin^2\alpha\big)+\big(\cos^2\beta+\sin^2\beta\big)-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big)=\)
\(=1+1-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big) \ (2)\)
Таким образом, сравнивая равенства \((1)\) и \((2)\):
\(1+1-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big)=1+1-2\cos(\alpha-\beta)\)
Отсюда и получается наша формула.
\(\blacktriangleright\) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения \(\sin x=\cos(90^\circ-x)\) и \(\cos x=\sin (90^\circ-x)\):
1) \(\cos(\alpha+\beta)=\cos(\alpha-(-\beta))=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
2) \(\sin(\alpha+\beta)=\cos(90^\circ-(\alpha+\beta))=\cos((90^\circ-\alpha)-\beta)=\)
\(+\cos(90^\circ-\alpha)\cos\beta+\sin(90^\circ-\alpha)\sin\beta=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)
3) \(\sin(\alpha-\beta)=\sin(\alpha+(-\beta))=\sin\alpha\cos(-\beta)+\sin(-\beta)\cos\alpha=\sin\alpha\cos\beta-\sin\beta\cos\alpha\)
4) \(\mathrm{tg}\,(\alpha\pm\beta)=\dfrac{\sin (\alpha\pm\beta)}{\cos (\alpha\pm\beta)}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta\mp\sin\alpha\sin\beta}=\)
разделим числитель и знаменатель дроби на \(\cos\alpha\cos\beta\ne
0\)
(при \(\cos\alpha=0 \Rightarrow
\mathrm{tg}\,(\alpha\pm\beta)=\mp \mathrm{ctg}\,\beta\), при \(\cos\beta=0 \Rightarrow
\mathrm{tg}\,(\alpha\pm\beta)=\pm \mathrm{ctg}\,\alpha\)):
\(=\dfrac{\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta}{1\mp\mathrm{tg}\,\alpha\cdot \mathrm{tg}\,\beta}\)
Таким образом, данная формула верна только при \(\cos\alpha\cos\beta\ne 0\).
5) Аналогично, только делением на \(\sin\alpha\sin\beta\ne 0\), выводится формула котангенса суммы/разности двух углов.
\(\blacktriangleright\) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) \(\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha\)
2) \(\cos2\alpha=\cos(\alpha+\alpha)=\cos\alpha\cos\alpha-\sin\alpha\sin\alpha=\cos^2\alpha-\sin^2\alpha\)
Используя основное тригонометрическое тождество \(\sin^2\alpha+\cos^2\alpha=1\), получим еще две формулы для косинуса двойного угла:
2.1) \(\cos2\alpha=\cos^2\alpha-\sin^2\alpha=\cos^2\alpha-(1-\cos^2\alpha)=2\cos^2\alpha-1\)
2.2) \(\cos2\alpha=\cos^2\alpha-\sin^2\alpha=(1-\sin^2\alpha)-\sin^2\alpha=1-2\sin^2\alpha\)
3) \(\mathrm{tg}\,2\alpha=\dfrac{\sin2\alpha}{\cos2\alpha}=\dfrac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}=\)
разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0 \Rightarrow \mathrm{tg}\,2\alpha=0\)):
\(=\mathrm{tg}\,2\alpha=\dfrac{2\mathrm{tg}\,\alpha}{1-\mathrm{tg}^2\,\alpha}\)
Таким образом, эта формула верна только при \(\cos\alpha\ne 0\), а также при \(\cos2\alpha\ne 0\) (чтобы существовал сам \(\mathrm{tg}\,2\alpha\)).
4) \(\mathrm{ctg}\,2\alpha=\dfrac{\cos^2\alpha-\sin^2\alpha}{2\sin\alpha\cos\alpha}=\dfrac{\mathrm{ctg}^2\,\alpha-1}{2\mathrm{ctg}\,\alpha}\)
По тем же причинам при \(\sin\alpha\ne 0, \sin2\alpha\ne 0\).
5) \(\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=\)
\(=\sin\alpha-2\sin^3\alpha+2\sin\alpha(1-\sin^2\alpha)=3\sin\alpha-4\sin^3\alpha\)
6) Аналогично выводится, что \(\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha\)
\(\blacktriangleright\) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) \(\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac{1+\cos2\alpha}2\)
2) \(\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac{1-\cos2\alpha}2\)
Заметим, что в данных формулах степень синуса/косинуса равна \(2\) в левой части, а в правой части степень косинуса равна \(1\).
\(\blacktriangleright\) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
\(\sin\alpha\sin\beta=\dfrac12\Big(\cos(\alpha-\beta)-\cos(\alpha+\beta)\Big)\)
3) Сложим формулы синуса суммы и синуса разности двух углов:
\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha\)
\(\sin(\alpha-\beta)=\sin\alpha\cos\beta-\sin\beta\cos\alpha\)
Получим: \(\sin\alpha\cos\beta=\dfrac12\Big(\sin(\alpha-\beta)+\sin(\alpha+\beta)\Big)\)
\(\blacktriangleright\) Вывод формул суммы/разности функций:
Обозначим \(\alpha+\beta=x, \alpha-\beta=y\). Тогда: \(\alpha=\dfrac{x+y}2, \ \beta=\dfrac{x-y}2\). Подставим эти значения в предыдущие три формулы:
1) \(2\cos{\dfrac{x+y}2}\cos{\dfrac{x-y}2}=\cos x+\cos y\)
Получили формулу суммы косинусов.
2) \(2\sin {\dfrac{x+y}2}\sin {\dfrac{x-y}2}=\cos y-\cos x\)
Получили формулу разности косинусов.
3) \(2\sin {\dfrac{x+y}2}\cos {\dfrac{x-y}2}=\sin y+\sin x\)
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
\(\sin x-\sin y=\sin x+\sin(-y)=2\sin {\dfrac{x-y}2}\cos {\dfrac{x+y}2}\)
5) \(\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta=\dfrac{\sin\alpha}{\cos\alpha}\pm\dfrac{\sin\beta}{\cos\beta}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta}=\dfrac{\sin(\alpha\pm\beta)}{\cos\alpha\cos\beta}\)
Аналогично выводится формула суммы котангенсов.
\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
1) \(\sin2\alpha=\dfrac{\sin2\alpha}1=\dfrac{2\sin\alpha\cos\alpha}{\sin^2\alpha+\cos^2\alpha}=\)
(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\)):)
\(=\dfrac{2\mathrm{tg}\,\alpha}{1+\mathrm{tg}^2\,\alpha}\)
2) Так же, только делением на \(\sin^2\alpha\), выводится формула для косинуса.
\(\blacktriangleright\) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
Рассмотрим выражение \(a\sin x+b\cos x\). Домножим и разделим это выражение на \(\sqrt{a^2+b^2}\,\):
\(a\sin x+b\cos x=\sqrt{a^2+b^2}\left(\dfrac a{\sqrt{a^2+b^2}}\sin x+ \dfrac b{\sqrt{a^2+b^2}}\cos x \right)=\sqrt{a^2+b^2}\big(a_1\sin x+b_1\cos x\big)\)
Заметим, что таким образом мы добились того, что \(a_1^2+b_1^2=1\), т.к. \(\left(\dfrac a{\sqrt{a^2+b^2}}\right)^2+\left(\dfrac b{\sqrt{a^2+b^2}}\right)^2=\dfrac{a^2+b^2}{a^2+b^2}=1\)
Таким образом, можно утверждать, что существует такой угол \(\phi\), для которого, например, \(\cos \phi=a_1, \ \sin \phi=b_1\). Тогда наше выражение примет вид:
\(\sqrt{a^2+b^2}\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt{a^2+b^2}\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: \[{\large{a\sin x+b\cos x=\sqrt{a^2+b^2}\,\sin (x+\phi),}} \quad \text{где } \cos \phi=\dfrac a{\sqrt{a^2+b^2}}\] Заметим, что мы могли бы, например, принять за \(\cos \phi=b_1, \ \sin \phi=a_1\) и тогда формула выглядела бы как \[a\sin x+b\cos x=\sqrt{a^2+b^2}\,\cos (x-\phi)\]
\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:
\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1{\sqrt2}\sin x\pm\dfrac1{\sqrt2}\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac{\pi}4\right)\)
\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac{\sqrt3}2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac{\pi}6\right)\)
\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac{\sqrt3}2\cos x\right)=2\,\sin\left(x\pm\dfrac{\pi}3\right)\)
shkolkovo.net
Основные тригонометрические тождества, формулы приведения, сложения, двойного угла, суммы и разности, половинного аргумента, тангенс половинного аргумента. Тест
Тестирование онлайн
Основные тригонометрические тождества
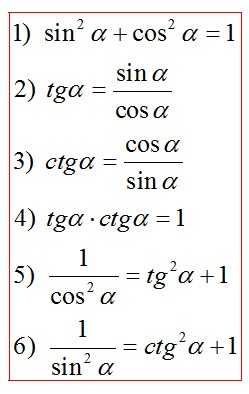
Четность, нечетность тригонометрических функций
Косинус является четной функцией; синус, тангенс, котангенс — нечетные.
Формулы приведения
Это соотношения, с помощью которых значения тригонометрических функций аргументов и др., выражаются через значения .
Правила преобразования:
1) Если аргумент содержит , где n — нечетное натуральное число , то функция меняется на «конфункцию», т.е. синус на косинус, тангенс на котангенс и наоборот. Если n — четное натуральное число , то название функции не изменяется.
2) Определяем знак («+» или «-«) значения первоначальной функции. Преобразованное выражение сохраняет знак своего родителя.
Формулы сложения и вычитания
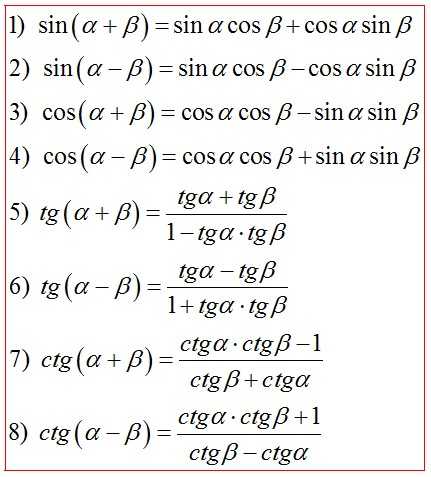
Формулы двойного угла
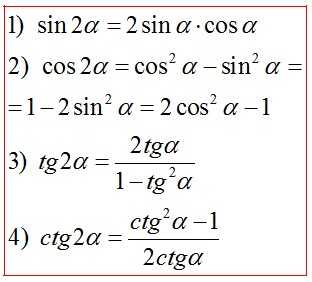
Формулы преобразования суммы и разности в произведение
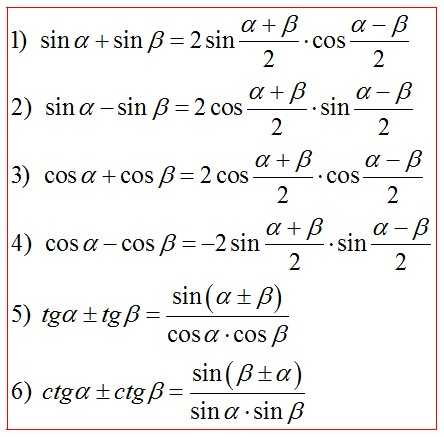
Формулы половинного аргумента
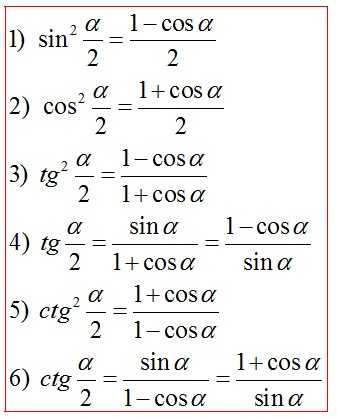
Формулы тройного угла*
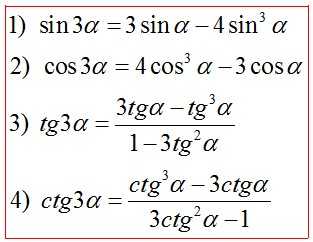
Формулы преобразования произведения в сумму (разность)*
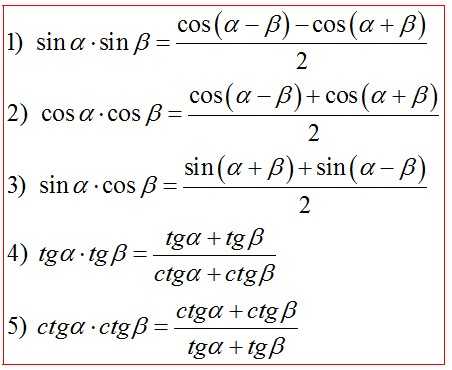
Универсальная подстановка через тангенс половинного аргумента*
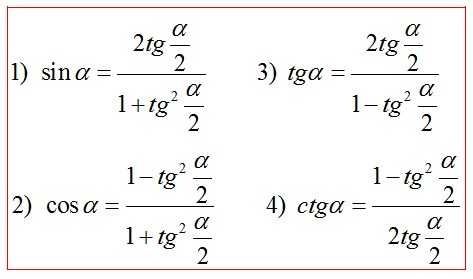
fizmat.by
?Тригонометрические формулы (более 100 шт.)
На этой странице вы найдете все основные тригонометрические формулы, которые помогут вам решать многие упражнения, значительно упростив само выражение.
Тригонометрические формулы — математические равенства для тригонометрических функций, которые выполняются при всех допустимых значениях аргумента.
Формулами задаются соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом, котангенсом.
Синус угла – это координата y точки (ордината) на единичной окружности. Косинус угла – это координата x точки (абсцисса).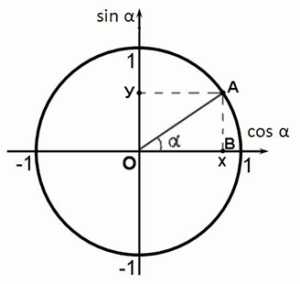
Тангенс и котангенс – это, соответственно, соотношения синуса к косинусу и наоборот.
`sin \ \alpha, \ cos \ \alpha`
`tg \ \alpha=\frac{sin\ \alpha}{cos \ \alpha},` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac{cos\ \alpha}{sin\ \alpha},` ` \alpha\ne\pi+\pi n, \ n \in Z`
И две, которые используются реже – секанс, косеканс. Они обозначают соотношения 1 к косинусу и синусу.
`sec \ \alpha=\frac{1}{cos\ \alpha},` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac{1}{sin \ \alpha},` ` \alpha\ne\pi+\pi n,\ n \in Z`
Из определений тригонометрических функций видно, какие знаки они имеют в каждой четверти. Знак функции зависит только от того, в какой из четвертей располагается аргумент.
Содержание статьи:
Тригонометрические функции угла `(-\alpha)`
При изменении знака аргумента с «+» на «-» только функция косинус не меняет своего значения. Она называется четной. Ее график симметричен относительно оси ординат.
Остальные функции (синус, тангенс, котангенс) нечетные. При смене знака аргумента с «+» на «-» их значение также изменяется на отрицательное. Их графики симметричны относительно начала координат.
`sin(-\alpha)=-sin \ \alpha`
`cos(-\alpha)=cos \ \alpha`
`tg(-\alpha)=-tg \ \alpha`
`ctg(-\alpha)=-ctg \ \alpha`
Основные тригонометрические тождества
Основные тригонометрические тождества – это формулы, устанавливающие связь между тригонометрическими функциями одного угла (`sin \ \alpha, \ cos \ \alpha, \ tg \ \alpha, \ ctg \ \alpha`) и которые позволяют находить значение каждой из этих функций через любую известную другую.
`sin^2 \alpha+cos^2 \alpha=1`
`tg \ \alpha \cdot ctg \ \alpha=1, \ \alpha\ne\frac{\pi n} 2, \ n \in Z`
`1+tg^2 \alpha=\frac 1{cos^2 \alpha}=sec^2 \alpha,` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`1+ctg^2 \alpha=\frac 1{sin^2 \alpha}=cosec^2 \alpha,` ` \alpha\ne\pi n, \ n \in Z`
Формулы суммы и разности углов тригонометрических функций
Формулы сложения и вычитания аргументов выражают тригонометрические функции суммы или разности двух углов через тригонометрические функции этих углов.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac{tg \ \alpha+tg \ \beta}{1-tg \ \alpha\ tg \ \beta}`
`tg(\alpha-\beta)=\frac{tg \ \alpha-tg \ \beta}{1+tg \ \alpha \ tg \ \beta}`
`ctg(\alpha+\beta)=\frac{ctg \ \alpha \ ctg \ \beta-1}{ctg \ \beta+ctg \ \alpha}`
`ctg(\alpha-\beta)=\frac{ctg \ \alpha\ ctg \ \beta+1}{ctg \ \beta-ctg \ \alpha}`
Формулы двойного угла
`sin \ 2\alpha=2 \ sin \ \alpha \ cos \ \alpha=` `\frac {2 \ tg \ \alpha}{1+tg^2 \alpha}=\frac {2 \ ctg \ \alpha}{1+ctg^2 \alpha}=` `\frac 2{tg \ \alpha+ctg \ \alpha}`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \ sin^2 \alpha=2 \ cos^2 \alpha-1=` `\frac{1-tg^2\alpha}{1+tg^2\alpha}=\frac{ctg^2\alpha-1}{ctg^2\alpha+1}=` `\frac{ctg \ \alpha-tg \ \alpha}{ctg \ \alpha+tg \ \alpha}`
`tg \ 2\alpha=\frac{2 \ tg \ \alpha}{1-tg^2 \alpha}=` `\frac{2 \ ctg \ \alpha}{ctg^2 \alpha-1}=` `\frac 2{ \ ctg \ \alpha-tg \ \alpha}`
`ctg \ 2\alpha=\frac{ctg^2 \alpha-1}{2 \ ctg \ \alpha}=` `\frac { \ ctg \ \alpha-tg \ \alpha}2`
Формулы тройного угла
`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac{3 \ tg \ \alpha-tg^3 \alpha}{1-3 \ tg^2 \alpha}`
`ctg \ 3\alpha=\frac{ctg^3 \alpha-3 \ ctg \ \alpha}{3 \ ctg^2 \alpha-1}`
Формулы половинного угла
`sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`
`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`
`tg \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}=` `\frac {sin \ \alpha}{1+cos \ \alpha}=\frac {1-cos \ \alpha}{sin \ \alpha}`
`ctg \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}=` `\frac {sin \ \alpha}{1-cos \ \alpha}=\frac {1+cos \ \alpha}{sin \ \alpha}`
Формулы половинных, двойных и тройных аргументов выражают функции `sin, \ cos, \ tg, \ ctg` этих аргументов (`\frac{\alpha}2, \ 2\alpha, \ 3\alpha,… `) через эти ж функции аргумента `\alpha`.
Вывод их можно получить из предыдущей группы (сложения и вычитания аргументов). Например, тождества двойного угла легко получить, заменив `\beta` на `\alpha`.
Формулы понижения степени
Формулы квадратов (кубов и т. д.) тригонометрических функций позволяют перейти от 2,3,… степени к тригонометрическим функциям первой степени, но кратных углов (`\alpha, \ 3\alpha, \ …` или `2\alpha, \ 4\alpha, \ …`).
`sin^2 \alpha=\frac{1-cos \ 2\alpha}2,` ` (sin^2 \frac \alpha 2=\frac{1-cos \ \alpha}2)`
`cos^2 \alpha=\frac{1+cos \ 2\alpha}2,` ` (cos^2 \frac \alpha 2=\frac{1+cos \ \alpha}2)`
`sin^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}4`
`cos^3 \alpha=\frac{3cos \ \alpha+cos \ 3\alpha}4`
`sin^4 \alpha=\frac{3-4cos \ 2\alpha+cos \ 4\alpha}8`
`cos^4 \alpha=\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`
Формулы суммы и разности тригонометрических функций
Формулы являют собой преобразования суммы и разности тригонометрических функций разных аргументов в произведение.
`sin \ \alpha+sin \ \beta=` `2 \ sin \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`sin \ \alpha-sin \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2`
`cos \ \alpha+cos \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2=` `2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\beta-\alpha}2`
`tg \ \alpha \pm tg \ \beta=\frac{sin(\alpha \pm \beta)}{cos \ \alpha \ cos \ \beta}`
`ctg \ \alpha \pm ctg \ \beta=\frac{sin(\beta \pm \alpha)}{sin \ \alpha \ sin \ \beta}`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac{cos(\alpha \mp \beta)}{cos \ \alpha \ sin \ \beta}`
Здесь происходит преобразование сложения и вычитаний функций одного аргумента в произведение.
`cos \ \alpha+sin \ \alpha=\sqrt{2} \ cos (\frac{\pi}4-\alpha)`
`cos \ \alpha-sin \ \alpha=\sqrt{2} \ sin (\frac{\pi}4-\alpha)`
`tg \ \alpha+ctg \ \alpha=2 \ cosec \2\alpha;` `tg \ \alpha-ctg \ \alpha=-2 \ ctg \2\alpha`
Следующие формулы преобразовывают сумму и разность единицы и тригонометрической функции в произведение.
`1+cos \ \alpha=2 \ cos^2 \frac{\alpha}2`
`1-cos \ \alpha=2 \ sin^2 \frac{\alpha}2`
`1+sin \ \alpha=2 \ cos^2 (\frac {\pi} 4-\frac{\alpha}2)`
`1-sin \ \alpha=2 \ sin^2 (\frac {\pi} 4-\frac{\alpha}2)`
`1 \pm tg \ \alpha=\frac{sin(\frac{\pi}4 \pm \alpha)}{cos \frac{\pi}4 \ cos \ \alpha}=` `\frac{\sqrt{2} sin(\frac{\pi}4 \pm \alpha)}{cos \ \alpha}`
`1 \pm tg \ \alpha \ tg \ \beta=\frac{cos(\alpha \mp \beta)}{cos \ \alpha \ cos \ \beta};` ` \ ctg \ \alpha \ ctg \ \beta \pm 1=\frac{cos(\alpha \mp \beta)}{sin \ \alpha \ sin \ \beta}`
Формулы преобразования произведений функций
Формулы преобразования произведения тригонометрических функций с аргументами `\alpha` и `\beta` в сумму (разность) этих аргументов.
`sin \ \alpha \ sin \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}`
`sin\alpha \ cos\beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}`
`cos \ \alpha \ cos \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}`
`tg \ \alpha \ tg \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)} =` `\frac{tg \ \alpha + tg \ \beta}{ctg \ \alpha + ctg \ \beta}`
`ctg \ \alpha \ ctg \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)} =` `\frac{ctg \ \alpha + ctg \ \beta}{tg \ \alpha + tg \ \beta}`
`tg \ \alpha \ ctg \ \beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}`
Универсальная тригонометрическая подстановка
Эти формулы выражают тригонометрические функции через тангенс половинного угла.
`sin \ \alpha= \frac{2tg\frac{\alpha}{2}}{1 + tg^{2}\frac{\alpha}{2}},` ` \alpha\ne \pi +2\pi n, n \in Z`
`cos \ \alpha= \frac{1 — tg^{2}\frac{\alpha}{2}}{1 + tg^{2}\frac{\alpha}{2}},` ` \alpha \ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac{2tg\frac{\alpha}{2}}{1 — tg^{2}\frac{\alpha}{2}},` ` \alpha \ne \pi +2\pi n, n \in Z,` ` \alpha \ne \frac{\pi}{2}+ \pi n, n \in Z`
`ctg \ \alpha = \frac{1 — tg^{2}\frac{\alpha}{2}}{2tg\frac{\alpha}{2}},` ` \alpha \ne \pi n, n \in Z,` `\alpha \ne \pi + 2\pi n, n \in Z`
Формулы приведения
Формулы приведения можно получить, используя такие свойства тригонометрических функций, как периодичность, симметричность, свойство сдвига на данный угол. Они позволяют функции произвольного угла преобразовать в функции, угол которых находится в пределе между 0 и 90 градусами.
Для угла (`\frac {\pi}2 \pm \alpha`) или (`90^\circ \pm \alpha`):
`sin(\frac {\pi}2 — \alpha)=cos \ \alpha;` ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha`
`cos(\frac {\pi}2 — \alpha)=sin \ \alpha;` ` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`
`tg(\frac {\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):
`sin(\pi — \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi — \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi — \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi — \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
Для угла (`\frac {3\pi}2 \pm \alpha`) или (`270^\circ \pm \alpha`):
`sin(\frac {3\pi}2 — \alpha)=-cos \ \alpha;` ` sin(\frac {3\pi}2 + \alpha)=-cos \ \alpha`
`cos(\frac {3\pi}2 — \alpha)=-sin \ \alpha;` ` cos(\frac {3\pi}2 + \alpha)=sin \ \alpha`
`tg(\frac {3\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {3\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {3\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {3\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Выражение одних тригонометрических функций через другие
`sin \ \alpha=\pm \sqrt{1-cos^2 \alpha}=` `\frac{tg \ \alpha}{\pm \sqrt{1+tg^2 \alpha}}=\frac 1{\pm \sqrt{1+ctg^2 \alpha}}`
`cos \ \alpha=\pm \sqrt{1-sin^2 \alpha}=` `\frac 1{\pm \sqrt{1+tg^2 \alpha}}=\frac {ctg \ \alpha}{\pm \sqrt{1+ctg^2 \alpha}}`
`tg \ \alpha=\frac {sin \ \alpha}{\pm \sqrt{1-sin^2 \alpha}}=` `\frac {\pm \sqrt{1-cos^2 \alpha}}{cos \ \alpha}=\frac 1{ctg \ \alpha}`
`ctg \ \alpha=\frac {\pm \sqrt{1-sin^2 \alpha}}{sin \ \alpha}=` `\frac {cos \ \alpha}{\pm \sqrt{1-cos^2 \alpha}}=\frac 1{tg \ \alpha}`
Тригонометрия в буквальном смысле переводится, как «измерение треугольников». Она начинает изучаться еще в школе, и продолжается более детально в ВУЗах. Поэтому основные формулы по тригонометрии нужны, начиная еще с 10 класса, а также для сдачи ЕГЭ. Они обозначают связи между функциями, а поскольку этих связей много, то и самых формул есть немало. Запомнить их все нелегко, да и не надо – при необходимости их все можно вывести.
Тригонометрические формулы применяются в интегральном исчислении, а также при тригонометрических упрощениях, вычислениях, преобразованиях.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Формулы для решения простейших тригонометрических уравнений
Прежде чем решать тригонометрические уравнения, вы должны хорошо разбираться в тригонометрическом круге.
Все тригонометрические уравнения, какими они не были – простыми или сложными, в итоге сводятся к решению четырех типов простейших тригонометрических уравнений.
Вы просто обязаны уметь решать уравнения вида
Формулы–алгоритмы будут разбросаны по трем статьям,
здесь же они собраны все вместе =>
+ показать
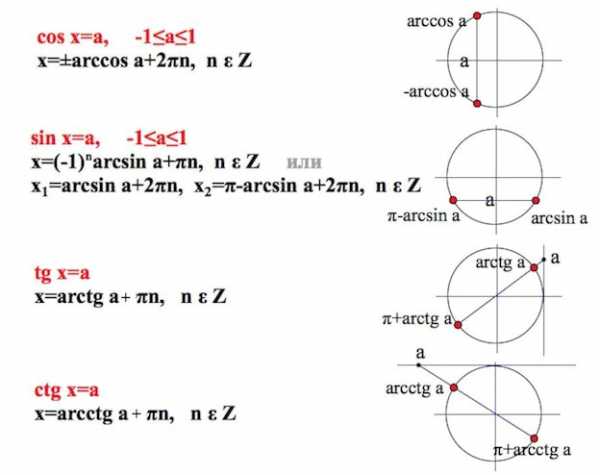
Давайте разбираться. В этой статье мы рассмотрим решение уравнения вида . Решение остальных типов простейших уравнений смотрим здесь: часть 2 (), часть 3 (, )
Уравнение вида
Решим уравнение
Мы должны подобрать такие значения аргумента , то есть такие значения углов, косинус которых равнялся бы .
Смотрим на тригонометрический круг, на оси косинусов находим :
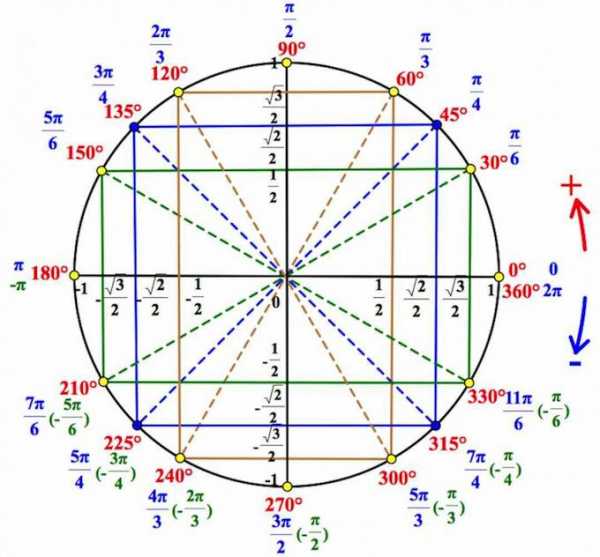
Выстраиваем через эту точку вертикаль, получаем две точки на круге:
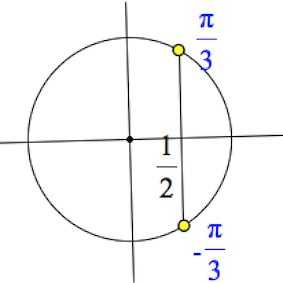
Но надо понимать, что за этими точками скрывается бесконечно много других точек, – таких, косинус в которых также равен . Мы об этом подробно говорили в предыдущей статье, когда знакомились с тригонометрическим кругом.
На координатной прямой подходящие нам точки располагаются так:
А с графической точки зрения решение уравнения выглядело бы так:
Как все точки взять в ответ?
Нам поможет счетчик . Возьмем , то есть
Решением уравнения будет
Возьмите, поперебирайте различные значения подставьте в вышеуказанную формулу.
Вы получите как раз точки при ,
при ,
при и т.д.
То что нам нужно!
Если бы мы решали, например, уравнение , то решением бы было
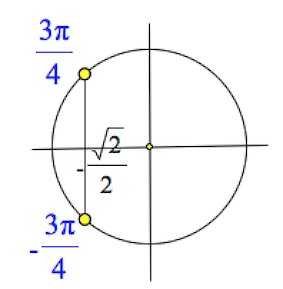
.
Я думаю, вы уже увидели общий принцип формирования ответа.
Давайте дадим формулу, которой можно руководствоваться, решая уравнения
, где – из
(в противном случае, когда – не из – решений нет)
Но вам формула будет понятна, если вы уже знакомы с понятием «арккосинус».
Если нам попадается уравнение с нетабличным значением косинуса, вроде этого , то решение будет следующее:
Частные случаи решения уравнения
1)
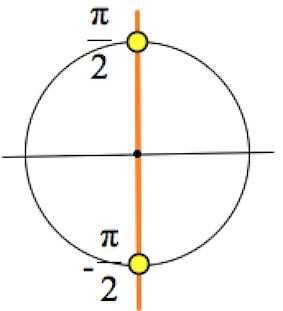
Мы должны бы записать так:
.
Но можно записать решение иначе (ведь в данном случае между точками расстояние – полкруга, значит нам можно использовать полукруговой счетчик ):
2)
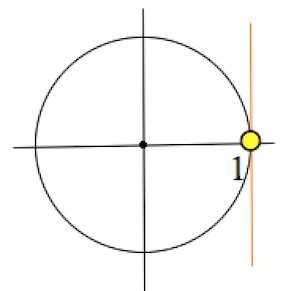
У нас только одна серия корней:
то есть
3)
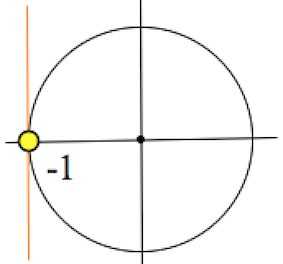
Аналогично решению примера 2, решение такое:
egemaximum.ru
