Производные формулы функции – Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Элементы математического анализа
Формулы производных функции
Рассмотрим функцию которая определена и непрерывна на некотором интервале произвольную точку и соответствующее значение функции в этой точке Зададим аргументу функции приращение в точке В результате получим величину и соответствующее значение функции
ОПРЕДЕЛЕНИЕ Производной функции в точке называется предел отношения приращения функции к вызвавшему его приращению аргумента в этой точке, при условии, что последний стремится к нулю:
Если данный предел конечен, то рассматриваемая функция называется дифференцируемой в точке .
Дифференцирование – это процесс нахождения производной функции. Его проводят с использованием таблицы производных и правил дифференцирования. На этой странице разобраны все формулы производных функции.
Таблица производных, список формул
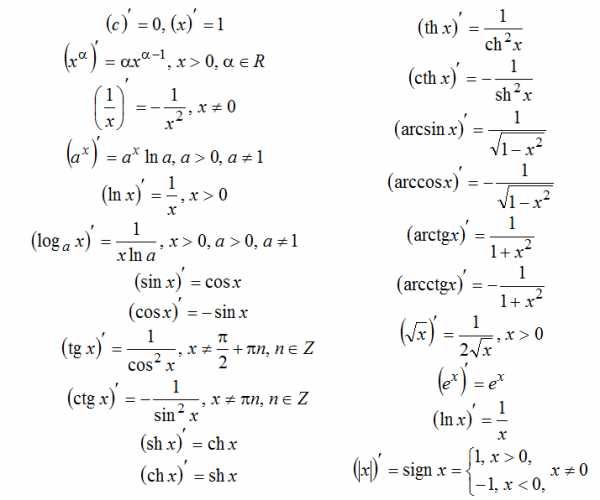
Правила дифференцирования
| Задание | Найти производную функции |
| Решение | Искомая производная равна:
|
| Ответ |
| Задание | Продифференцировать функцию
|
| Решение | Искомая производная
Производная разности равна разности производных:
Производную первого слагаемого найдем по таблице производных, второго – как производную частного:
|
| Ответ |
ru.solverbook.com
Формулы производных функций y (x)
Производные линейной функции.
Производные степенной функции.
Производные показательной функции.
Производные логарифмической функции.
Производные тригонометрической функции.
Производные обратной тригонометрической функции.
- Подробности
- Автор: Administrator
Формулы производных
Что такое производная функция — это основное математическое понятие, находится на одном уровне с интегралами, при анализе. Данная функция в определенной точке дает характеристику скорости изменений функции в данной точке.
Такие понятия как дифференцирование и интегрирование, первое расшифровывается как действие поиска производной, второе наоборот, восстанавливает функцию отталкиваясь от данной производной.
Вычислениям производной отводится важная часть в дифференциальных расчетах.
Для наглядного примера, изобразим производную на координатной плоскости.
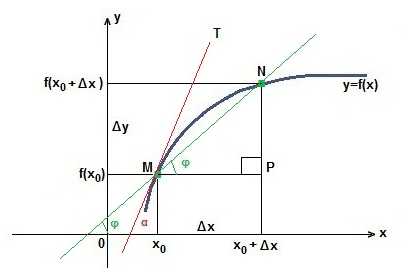
в функции у=f(х) фиксируем точки М в которой (х0; f(X0)) и N f (x0+?x) к каждой абсциссе есть приращение в виде ?x. Приращением называется процесс когда изменяется абсцисса, тогда меняется и ордината. Обозначается как ?у.
Найдем тангенс угла в треугольнике MPN используя для этого точки М и N.
tg? = NP/MP = ?у/?x.
При ?x идущем к 0. Пересекающая МN все ближе к касательной МТ и угол ? будет ?. Следовательно, tg ? максимальное значение для tg ?.
tg ? = lim от ?x-0 tg ? = lim от ?x-0 ?у/?x
Таблица производныхЕсли проговаривать формулировку каждой формулы производных. Таблица будет проще запоминаться.
1) Производная от постоянного значения равняется 0.
3) Если есть постоянный множитель, просто выносим ео за производную.
4) Чтобы найти производную степень, нужно показатель данной степени умножить на степень с таким же основанием, у которого показатель на 1 меньше.
5) Поиск корня равен одному, деленному 2 этих корня.
6) Производная одного, деленного на Х равняется одному разделенному на Х возведенный в квадрат, со знаком минус.
7) П синус равняется косинусу
8) П косинус равняется синусу со знаком минус.
9) П тангенс равняется одному, деленному на косинус в квадрате.
В дифференцировании также существуют правила, которые тоже проще выучить проговаривая их в слух.
1) Очень просто, п. слагаемых равняется их сумме.
2) Производная в умножении равняется умножению первого значения на второе, прибавляя к себе умножение второго значения на первое.
3) Производная в делении равняется умножению первого значения на второе, отнимая от себя умножение второго значения на первое. Дробь деления на второе значение в квадрате.
4) Формулировка является частным случаем третьей формулы.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Элементы математического анализа
Правила вычисления производных
Вычисление производных основано на применении следующих правил, которые мы будем использовать без доказательств, поскольку доказательства выходят за рамки школьного курса математики.
Правило 1 (производная от произведения числа на функцию). Справедливо равенство
(c f (x))’ = c f ‘ (x) ,
где c – любое число.
Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.
Правило 2 (производная суммы функций). Производная суммы функций вычисляется по формуле
(f (x) + g (x))’ = f ‘ (x) + g’ (x),
то есть производная от суммы функций равна сумме производных этих функций.
Правило 3 (производная разности функций). Производная разности функций вычисляется по формуле
(f (x) – g (x))’ = f ‘ (x) – g’ (x),
то есть производная от разности функций равна разности производных этих функций.
Правило 4 (производная произведения двух функций). Производная произведения двух функций вычисляется по формуле
(f (x) g (x))’ = f ‘ (x) g (x) + f (x) g’ (x),
Другими словами, производная от произведения двух функций равна производной от первой функции, умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.
Правило 5 (производная частного двух функций). Производная от дроби (частного двух функций) вычисляется по формуле
,
Определение. Рассмотрим функции f (x) и g (x) . Сложной функцией или «функцией от функции» называют функцию вида
f (g (x))
При этом функцию f (x) называют внешней функцией, а функцию g (x) – внутренней функцией.
Правило 6 (производная сложной функции). Производная сложной функции вычисляется по формуле
[ f (g (x))]’ = f ‘ (g (x)) g’ (x)
Другими словами, для того, чтобы найти производную от сложной функции f (g (x)) в точке x нужно умножить производную внешней функции, вычисленную в точке g (x) , на производную внутренней функции, вычисленную в точке x .
Таблица производных часто встречающихся функций
В следующей таблице приведены формулы для производных от степенных, показательных (экспоненциальных), логарифмических, тригонометрических и обратных тригонометрических функций. Доказательство большинства их этих формул выходит за рамки школьного курса математики.
| Функция | Формула для производной | Название формулы |
y = c , где c – любое число | y’ = 0 | Производная от постоянной функции |
y = x c , где c – любое число | y’ = c xc – 1 | Производная степенной функции |
| y = e x | y’ = e x | Производная от экспоненты (показательной функции с основанием e) |
y = a x где a – любое положительное число, не равное 1 | y’ = a x ln a | Производная от показательной функции с основанием a |
| y = ln x , x > 0 | , x > 0 | Производная от натурального логарифма |
y = log a x , x > 0 где a – любое положительное число, не равное 1 | , x > 0 | Производная от логарифма по основанию a |
| y = sin x | y’ = cos x | Производная синуса |
| y = cos x | y’ = – sin x | Производная косинуса |
y = tg x , | , | Производная тангенса |
y = ctg x , | , | Производная котангенса |
y = arcsin x , | Производная арксинуса | |
y = arccos x , | Производная арккосинуса | |
| y = arctg x | Производная арктангенса | |
| y = arcctg x | Производная арккотангенса |
| Производная от постоянной функции |
Функция: y = c , где c – любое число Формула для производной: y’ = 0 |
| Производная степенной функции |
Функция: y = x c , где c – любое число Формула для производной: y’ = c xc – 1 |
| Производная от экспоненты (показательной функции с основанием e) |
Функция: y = e x Формула для производной: y’ = e x |
| Производная от показательной функции с основанием a |
Функция: y = a x где a – любое положительное число, не равное 1 Формула для производной: y’ = a x ln a |
| Производная от натурального логарифма |
Функция: y = ln x , x > 0 Формула для производной: , x > 0 |
| Производная от логарифма по основанию a |
Функция: y = log a x , x > 0 где a – любое положительное число, не равное 1 Формула для производной: , x > 0 |
| Производная синуса |
Функция: y = sin x Формула для производной: y’ = cos x |
| Производная косинуса |
Функция: y = cos x Формула для производной: y’ = – sin x |
| Производная тангенса |
Функция: y = tg x , где Формула для производной: , |
| Производная котангенса |
Функция: y = ctg x , где Формула для производной: , |
| Производная арксинуса |
Функция: y = arcsin x , Формула для производной: |
| Производная арккосинуса |
Функция: y = arccos x , Формула для производной: |
| Производная арктангенса |
Функция: y = arctg x Формула для производной: |
| Производная арккотангенса |
Функция: y = arcctg x Формула для производной: |
Таблица производных сложных функций
В следующей таблице приведены формулы для производных сложных функций.
В отдельных строках (с желтым фоном) приведены формулы для производных сложных функций в случае, когда внутренняя функция является линейной функцией и имеет вид f (x) = kx + b , где k и b – любые числа, .
| Функция | Формула для производной |
y = (kx + b) c , где c – любое число. | y’ = kc (kx + b) c – 1 , |
y = ( f (x)) c , где c – любое число. | |
| y = ekx + b | y = kekx + b |
| y = e f (x) | |
y = akx + b где a – любое положительное число, не равное 1 | |
y = a f (x) где a – любое положительное число, не равное 1 | |
| y = ln (kx + b) , kx + b > 0 | , kx + b > 0 |
| y = ln ( f (x)) , f (x) > 0 | , f (x) > 0 |
y = log a (kx + b) , kx + b > 0 где a – любое положительное число, не равное 1 | , kx + b > 0 |
y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1 | , f (x) > 0 |
| y = sin (kx + b) | y’ = k cos (kx + b) |
| y = sin ( f (x)) | |
| y = cos (kx + b) | y’ = – k sin (kx + b) |
| y = cos ( f (x)) | |
y = tg (kx + b), где | , |
y = tg ( f (x)), где | , |
y = ctg (kx + b), где | , |
y = ctg ( f (x)), где | , |
| y = arcsin (kx + b), | |
| y = arcsin ( f (x)), | |
| y = arccos (kx + b), | |
| y = arccos ( f (x)), | |
| y = arctg (kx + b) | |
| y = arctg ( f (x)) | |
| y = arcctg (kx + b) | |
| y = arcctg ( f (x)) |
Функция: y = (kx + b) c , где c – любое число. Формула для производной: y’ = kc (kx + b) c – 1 , |
Функция: y = ( f (x)) c , где c – любое число. Формула для производной: |
Функция: y = ekx + b Формула для производной: y = kekx + b |
Функция: y = e f (x) Формула для производной: |
Функция: y = akx + b где a – любое положительное число, не равное 1 Формула для производной: |
Функция: y = a f (x) где a – любое положительное число, не равное 1 Формула для производной: |
Функция: y = ln (kx + b) , kx + b > 0 Формула для производной: , kx + b > 0 |
Функция: y = ln ( f (x)) , f (x) > 0 Формула для производной: , f (x) > 0 |
Функция: y = log a (kx + b) , kx + b > 0 где a – любое положительное число, не равное 1 Формула для производной: , kx + b > 0 |
Функция: y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1 Формула для производной: , f (x) > 0 |
Функция: y = sin (kx + b) Формула для производной: y’ = k cos (kx + b) |
Функция: y = sin ( f (x)) Формула для производной: |
Функция: y = cos (kx + b) Формула для производной: y’ = – k sin (kx + b) |
Функция: y = cos ( f (x)) Формула для производной: |
Функция: y = tg (kx + b), где Формула для производной: , |
Функция: y = tg ( f (x)), где Формула для производной: , |
Функция: y = ctg (kx + b), где Формула для производной: , |
Функция: y = ctg ( f (x)), где Формула для производной: , |
Функция: y = arcsin (kx + b), Формула для производной: |
Функция: y = arcsin ( f (x)), Формула для производной: |
Функция: y = arccos (kx + b), Формула для производной: |
Функция: y = arccos ( f (x)), Формула для производной: |
Функция: y = arctg (kx + b) Формула для производной: |
Функция: y = arctg ( f (x)) Формула для производной: |
Функция: y = arcctg (kx + b) Формула для производной: |
Функция: y = arcctg ( f (x)) Формула для производной: |
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Формулы производной | Формулы с примерами
ФормулыПриращение аргумента
Приращение функции
Производная функции ?(x) в точке x0
Касательная к графику
Геометрический смысл производной
Уравнение касательной к графику ? (x)
Физический смысл производной
Правила дифференцирования

Таблица производных

Достаточное условие монотонности функции ? (x)
Экстремумы функции ? (x)
Необходимое условие экстремума ? (x)
Достаточное условие экстремума непрерывной в точке x0 функции ? (x)

formula-xyz.ru
64. Вывод табличных производных. Производная постоянной.
Следует заметить, что под знаком предела получается выражение , которое не являетсянеопределенностью ноль делить на ноль, так как в числителе находится не бесконечно малая величина, а именно ноль. Другими словами, приращение постоянной функции всегда равно нулю.
Таким образом, производная постоянной функции равна нулю на всей области определения.
Производная степенной функции.
Формула производной степенной функции имеет вид , где показатель степени
Докажем сначала формулу для натурального показателя степени, то есть, для p = 1, 2, 3, …
Будем пользоваться определением производной. Запишем предел отношения приращения степенной функции к приращению аргумента:
Для упрощения выражения в числителе обратимся к формуле бинома Ньютона:
Следовательно, 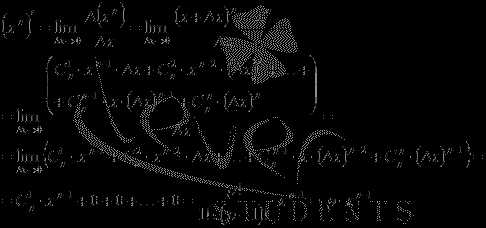
Этим доказана формула производной степенной функции для натурального показателя.
Производная показательной функции.
Вывод формулы производной приведем на основе определения:
Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда . В последнем переходе мы использовали формулу перехода к новому основанию логарифма.
Выполним
подстановку в исходный предел: 
Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:
Производная логарифмической функции.
Докажем
формулу производной логарифмической
функции для всех x из
области определения и всех допустимых
значениях основания a логарифма.
По определению производной имеем: 
Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство справедливо в силу второго замечательного предела.
Производные тригонометрических функций.
Для вывода формул производных тригонометрических функций нам придется вспомнить некоторые формулы тригонометрии, а также первый замечательный предел.
По определению производной для функции синуса имеем .
Воспользуемся
формулой разности синусов: 
Осталось обратиться к первому замечательному пределу:
Таким образом, производная функции sin x есть cos x.
Абсолютно
аналогично доказывается формула
производной косинуса. 
Следовательно, производная функции cos x есть –sin x.
Вывод
формул таблицы производных для тангенса
и котангенса проведем с использованием
доказанных правил дифференцирования
(производная
дроби).
Производные гиперболических функций.
Правила
дифференцирования и
формула производной показательной
функции из таблицы производных позволяют
вывести формулы производных гиперболического
синуса, косинуса, тангенса и котангенса. 
Производная обратной функции.
Перед началом изучения данной статьи рекомендуем вспомнить определение и свойства обратной функции.
Чтобы при изложении не было путаницы, давайте обозначать в нижнем индексе аргумент функции, по которому выполняется дифференцирование, то есть, — это производная функции f(x) по x.
Теперь сформулируем правило нахождения производной обратной функции.
Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x), то в точке существует конечная производная обратной функции g(y), причем . В другой записи .
Можно это правило переформулировать для любого x из промежутка , тогда получим .
Давайте проверим справедливость этих формул.
Найдем обратную функцию для натурального логарифма (здесь y – функция, а x— аргумент). Разрешив это уравнение относительно x, получим (здесь x – функция, а y – ее аргумент). То есть, и взаимно обратные функции.
Из таблицы производных видим, что и .
Убедимся, что формулы нахождения производных обратной функции приводят нас к этим же результатам:
Как видите, получили такие же результаты как и в таблице производных.
Теперь мы обладаем знаниями для доказательства формул производных обратных тригонометрических функций.
Начнем с производной арксинуса.
Для обратной функцией является . Тогда по формуле производной обратной функции получаем
Осталось провести преобразования.
Так как областью значений арксинуса является интервал , то (смотрите раздел основные элементарные функции, их свойства и графики). Поэтому , а не рассматриваем.
Следовательно, . Областью определения производной арксинуса является промежуток (-1; 1).
Для арккосинуса все делается абсолютно аналогично:
Найдем производную арктангенса.
Для обратной функцией является .
Выразим арктангенс через арккосинус, чтобы упростить полученное выражение.
Пусть arctgx
= z,
тогда 
Следовательно,
Схожим образом находится производная арккотангенса:
studfiles.net
Правила нахождения производных, формулы и примеры
Рассмотрим функции и которые являются дифференцируемыми в точке (то есть имеют производную в этой точке). Тогда для нахождения производных используют следующие правила.
1. Производная произведения константы на некоторую функцию равна произведению этой константы на производную от заданной функции, то есть константа выносится за знак производной:
2. Производная суммы/разности двух функций равна сумме/разности производных от каждой их них:
Замечание. Это свойство справедливо и для большего, чем два, числа функций.
Замечание. Первые два правила можно объединить в одно свойство линейности:
3. Производная произведения двух функций равна сумме произведений производной первой функции на вторую и первой функции на производную второй:
4. Производная частного двух функций равна отношению разности произведений производной числителя на знаменатель и числителя на производную знаменателя и квадрата исходного знаменателя, то есть
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
