Производная с нуля – Что такое производная 🚩 для чего нужна производная 🚩 Математика
Как найти производную функции, примеры решения
Процесс нахождения производной функции называется дифференцированием. Производную приходится находить в ряде задач курса математического анализа. Например, при отыскании точек экстремума и перегиба графика функции.
Как найти?
Чтобы найти производную функции нужно знать таблицу производных элементарных функций и применять основные правила дифференцирования:
- Вынос константы за знак производной:
- Производная суммы/разности функций:
- Производная произведения двух функций:
- Производная дроби:
- Производная сложной функции:
Примеры решения
| Пример 1 |
| Найти производную функции |
| Решение |
Производная суммы/разности функций равна сумме/разности производных: Используя правило производной степенной функции имеем: Так же было учтено, что производная от константы равна нулю. |
| Ответ |
| Пример 2 |
| Найти производную функции |
| Решение |
По правилу производной разности: По таблице интегрирования находим: С учетом того, что аргумент натурального логарифма отличен от , то нужно домножить ещё на производную самого аргумента: После упрощения получаем: |
| Ответ |
| Пример 3 |
| Найти производную функции |
| Решение |
В данном примере стоит произведение двух функций, а производная произведения находится по формуле номер 3: Производная первой функции вычисляется как разность фунций: Вторая функция является показательной, производная которой находится по формуле: : Продолжаем решение с учетом найденных производных: |
| Ответ |
| Пример 4 |
| Найти производную функции |
| Решение |
Производную дроби найдем по четвертой формуле. Положим и . Тогда их производные по таблице основных элементарных функций равны: Используя формулу №4 получаем: |
| Ответ |
| Пример 5 |
| Найти производную функции |
| Решение |
Данная функция является сложной, потому производную будем брать по цепочке. Сначала от внешней функции, затем от внутренней. При этом выполняя их перемножение. Заметим, что аргумент синуса отличен от , поэтому тоже является сложной функцией: Учитывая определение котангенса перепишем полученную производную в удобном компактном виде: |
| Ответ |
xn--24-6kcaa2awqnc8dd.xn--p1ai
Производная онлайн с подробным решением
Калькулятор решает производные c описанием действий ПОДРОБНО бесплатно!
Это он-лайн сервис в один шаг:
- Ввести функцию, для которой надо найти производную
Перейти: Онлайн сервис «Производная функции» →
Это он-лайн сервис в один шаг:- Ввести функцию, для которой надо найти частные производные
- Ввести функцию, для которой надо найти производную
- Ввести найденную первую производную в форму
- Ввести функцию, для которой надо найти производную
- Ввести найденную первую производную в форму
- Ввести найденную вторую производную функции в форму
Введите функцию, заданную в неявном виде, вы получите соответствующую производную
Это он-лайн сервис в три шага:
- Ввести функцию x = x(t)
- Ввести функцию y = y(t)
Перейти: Онлайн сервис «Производной параметрической функции» →
Производная сложной функции
Производную сложной функции онлайн вы сможете вычислить с помощью калькулятора производных здесь
Таблица производных
Вы также можете воспользоваться таблицей производных, чтобы самостоятельно вычислить любую производную, перейти:
www.kontrolnaya-rabota.ru
Что такое производная
Производная — главнейшее понятие математического анализа. Она характеризует изменение функции аргумента x в некоторой точке. При этом и сама производная является функцией от аргумента x
Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
То есть,
(1)
Наиболее употребительны следующие обозначения производной:
Пример 1. Пользуясь определением производной, найти производную функции
.
Решение. Из определения производной вытекает следующая схема её вычисления.
Дадим аргументу приращение (дельта) и найдём приращение функции:
.
Найдём отношение приращения функции к приращению аргумента:
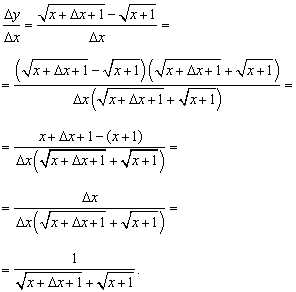
Вычислим предел этого отношения при условии, что приращение аргумента стремится к нулю, то есть требуемую в условии задачи производную:
К понятию производной привело изучение Галилео Галилеем закона свободного падения тел, а в более широком смысле — задачи о мгновенной скорости неравномерного прямолинейного движения точки.
Однако движение свободно падающего тела явно неравномерное. Скорость v падения
постоянно возрастает. И средней скорости уже недостаточно для характеристики быстроты движения на различных участках пути.
Такая характеристика тем точнее, чем меньше промежуток времени .
Поэтому вводится следующее понятие: мгновенной скоростью прямолинейного движения (или скоростью в данный момент времени
(при условии, что этот предел существует и конечен).
Так выясняется, что мгновенная скорость есть предел отношения приращения функции s(t) к приращению аргумента t при Это и есть производная, которая в общем виде записывается так:.
.
Решение обозначенной задачи представляет собой физический смысл производной. Итак, производной функции y=f(x) в точке x называется предел (если он существует и конечен) приращения функции к приращению аргумента при условии, что последнее стремится к нулю.
Пример 2. Найти производную функции
Решение. Из определения производной вытекает следующая схема для её вычисления.
Шаг 1. Дадим аргументу приращение и найдём
Шаг 2. Найдём приращение функции:
Шаг 3. Найдём отношение приращения функции к приращению аргумента:
Шаг 4. Вычислим предел этого отношения при , то есть производную:
Касательной к графику функции в точке М называется предельное положение секущей МР при , или, что то же при .
Из определения следует, что для существования касательной достаточно, чтобы существовал предел
,
причём предел равен углу наклона касательной к оси .
Теперь дадим точное определение касательной.
Из этого определения следует, что производная функции равна угловому коэффициенту касательной к графику этой функции в точке с абсциссой x. В этом состоит геометрический смысл производной:
где — угол наклона касательной к оси абсцисс, т.е. угловой коэффициент касательной.
Пример 3. Найти производную функции и значение этой производной при .
Решение. Воспользуемся схемой, приведённой в примере 1.
Шаг 1.
Шаг 2.
Шаг 3.
Шаг 4.
Выражение под знаком предела не определено при (неопределённость вида 0/0), поэтому преобразуем его, избавившись от иррациональности в числителе и затем сократив дробь:
Найдём значение производной при :
Весь блок «Производная»
function-x.ru
Производная функции. Геометрический смысл производной.
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.
Запомним определение:
Производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
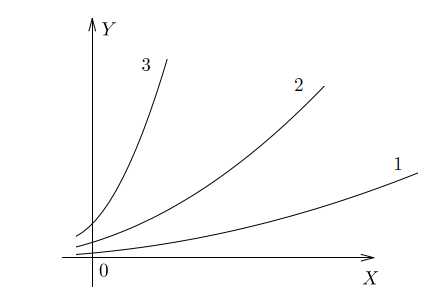
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
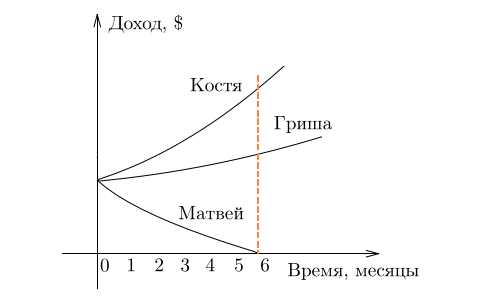
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.

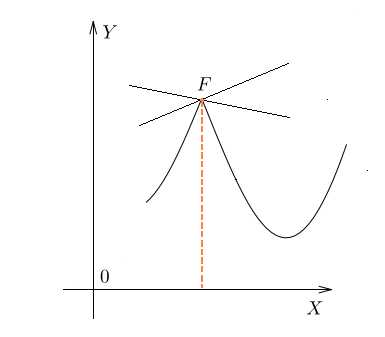
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
.
Величина в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
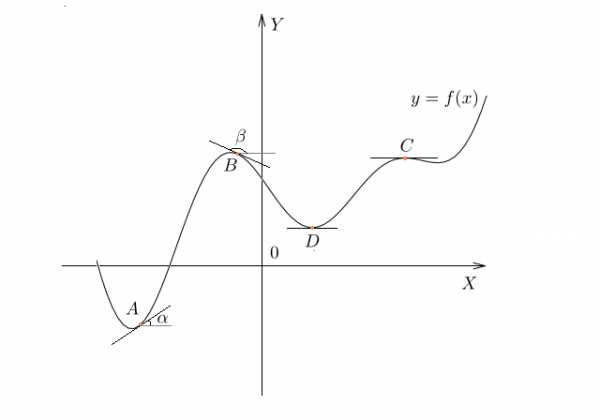
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол ; с положительным направлением оси . Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол ; с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | — | 0 | + |
Ты нашел то, что искал? Поделись с друзьями!
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задачи . Другое — на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Как брать производную? Высшая математика, производная.
На самом деле брать производную не так уж и трудно, главное хорошенько проработать алгоритм.
Кстати если после просмотра материала у вас будут трудности пишите МНЕ, я дешево помогу вам решить примеры.
Итак, без чего мы не сможем обойтись? Конечно же таблица производных!
Таблица производных
в данной таблице указаны значения производной простейших функций, внимательно изучите таблицу производных, после чего можно приступать к решению заданий.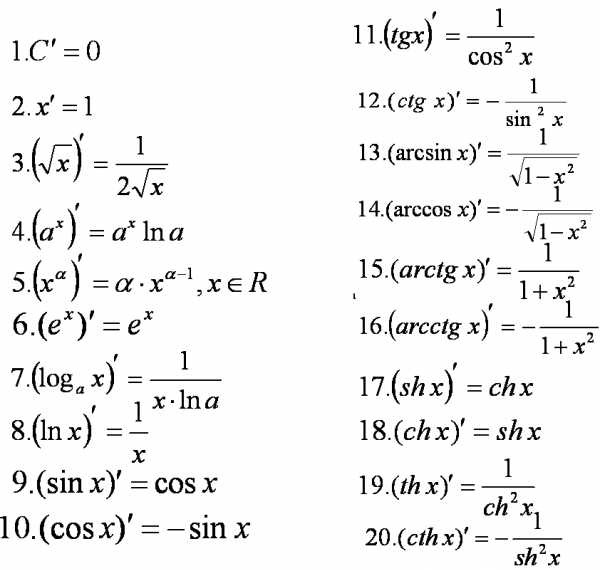
Данная таблица поможет нам брать производные от тригонометрических и логарифмических функций.
Теперь разберем поэтапно как брать производную, начиная с самых простых и элементарных функций.
Сперва разберем самые простые производные.
Если вы еще не поняли смотрим более легкие уроки.
matematikaprosta.ru
Производная функции одной переменной
В этой статье мы будем учиться находить производную от функции одной переменной. Дадим ее определение, вскользь затронем геометрический смысл. Разберемся с вопросом нахождения производной от сложной функции.
Итак, дадим определение производной: пусть в некоторой окрестности точки определена функция . Производной функции в точке называется предел, если он существует,
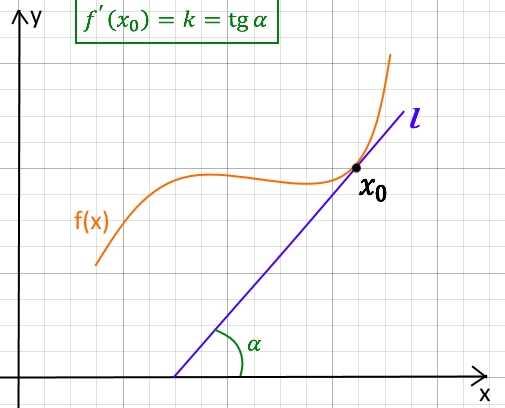
Из школы можно вспомнить формулу для нахождения касательной к функции в точке: . То есть если говорить о геометрическом смысле производной, то обозначим производную функции в точке как угловой коэффициент или тангенс угла наклона касательной прямой к графику функции в этой точке.
Правила дифференцирования:
- Производная суммы равна сумме производных, то есть:
- Производная произведения:
- Вынесение константы за знак производной:
- Производная частного:
Прежде чем перейти к задачам, необходимо обзавестись таблицей производных. В идеале вы должны ее знать наизусть, как таблицу умножения 🙂
Таблица производных

[свернуть]
Правилами дифференцирования и таблицей вооружились, двигаемся дальше.
Рассмотрим некоторую функцию . Как видим, функция зависит не просто от переменной , а от другой функции . Будем называть такую функцию сложной. Производная сложной функции вычисляется следующим образом:
Теперь всей необходимой теорией для решения стандартных задач на нахождение производной мы обладаем, а именно: правилами дифференцирования, таблицей производных и формулой производной от сложной функции. Давайте на примерах подробно разберемся с тем, как это работает.
Задачи на применение правила дифференцирования суммы
Пример 1. Найти производную функции
Решение: Применяем правило дифференцирования суммы функций:
Заглядываем в таблицу производных и ищем там производную от и от
Всё, производная найдена. В ответ запишем
Пример 2. Найти производную функции , где
Решение: Применяем правило дифференцирования суммы функций:
Открываем таблицу производных и находим производные от и
Производная найдена, в ответе записываем
Пример 3. Найти производную функции
Решение:
[свернуть]
Задачи на применение правила дифференцирования произведения
Пример 4. Найти производную функции
Решение: Применим правило дифференцирования произведения:
Обращаемся к таблице производных и ищем там производные тангенса и
или
Производная найдена.
Пример 5. Найти производную функции
Решение: Применим правило дифференцирования произведения:
Производная найдена.
Пример 6. Найти производную функции
Решение:
Производная найдена.
[свернуть]
Задачи с вынесением константы за знак производной
Это правило дифференцирования самое простое для понимания (редко у кого можно встретить здесь ошибки): мы просто выносим константу за знак производной и находим производную от оставшегося выражения.
Пример 7. Найти производную функции
Решение: Видим константу , поэтому поступаем в соответствии с нашим правилом:
Всё, задача решена 🙂 Давайте, на всякий случай, рассмотрим еще одну такую задачу.
Пример 8. Найти производную функции
Решение: Видим дробь. Производную от дроби находить пока не умеем, но может без проблем преобразовать выражение следующим образом:
Теперь константа очевидна, выносим и находим производную:
Производная найдена.
[свернуть]
Задачи на применения правила дифференцирования частного (дроби)
Ничего сложно в дифференцировании дробей нет, но на практике именно здесь чаще всего возникают ошибки, поэтому остановимся на этом моменте подробнее.
Пример 9. Найти производную функции
Решение: Видим дробь. Мысленно повторяем для себя: «Производная дроби равна производной числителя, умноженной на знаменатель, минус производная знаменателя, умноженная на числитель, и всё это деленное на квадрат знаменателя«.
Числителем здесь является , а знаменателем — . Тогда, в соответствии с формулой, напишем:
Всё, производная успешно найдена.
Пример 10. Найти производную функции
Решение: Рассматриваем выражение. Числителем служит , знаменателем — . По формуле получим:
В принципе, на этом этапе можно остановиться, производная найдена. Но, взглянув на числитель, несложно заметить и применить основное тригонометрическое тождество :
.
Вспомнив, что отношение синуса к косинусу есть тангенс, легко проверить получившийся ответ по таблице производных.
Пример 11. Найти производную функции
Решение: Числитель здесь , знаменатель . По формуле производной для дроби запишем:
Производная найдена, но можно упростить полученное выражение, сделаем это:
Пример 12. Найти производную функции
Решение: Числитель и знаменатель . Получаем:
Заметим, что здесь необязательно было пользоваться именно формулой для дроби, так как знаменатель представляет собой константу. Эту константу можно было вынести по предыдущему правилу дифференцирования.
[свернуть]
С правилами дифференцирования ознакомились. Переходим к дифференцированию сложной функции. Пока еще нет достаточного опыта, рекомендую на каждом шаге повторять для себя: «Производная сложной функции равна производной внешней функции на производную внутренней функции«.
Пример 13
Найти производную функции .
Решение: Видим обыкновенный косинус, но воспользоваться таблицей производных сразу не можем, потому что зависит косинус не просто от , а от . Применяем формулу для сложной функции.
Необходимо очень чётко уяснить вопрос с тем, что является в некотором выражении внешней функцией, а что внутренней. Для этого нужно посмотреть на функцию как бы в целом (это может быть нечто очень громоздкое), понять, что это прежде всего: произведение, степень, дробь или что-то другое.
В данной задаче всё просто. Прежде всего наше выражение — это косинус. То есть косинус является внешней функцией. Внутренней функцией будет являться аргумент косинуса . Тогда по формуле запишем:
.
[свернуть]
В 13 и 14 примерах для нахождения производной достаточно было применить формулу для сложной функции всего один раз. Однако на практике чаще всего имеются выражения вида «функция от функции, зависящей от еще одной функции, которая зависит функции и т.д.». В этих случаях принцип нахождения производной не изменяется — мы просто используем формулу несколько раз.
Пример 15
Найти производную функции
Решение: Имеем натуральный логарифм, который зависит от синуса, который зависит от некоторого выражения. Внешняя функция здесь сам логарифм, то есть , внутренняя — выражение под логарифмом, т.е. .
Производную первого множителя уже можем написать из таблицы производных (сделаем это позже, чтобы не возникло путаницы). Для нахождения производной второго множителя вновь используем формулу, полагая, что внешней функцией является синус, а внутренней — выражение :
Давайте для наглядности покажем на картинке процесс работы с выражением:
Функция слева от стрелки внешняя, справа внутренняя. Количество стрелок равно количеству применений формулы для сложной функции.
[свернуть]
Пример 16
Найти производную функции
Решение: Нарисуем такую же картинку, как и в предыдущем примере:
Имеем три стрелки, то есть формулу для сложной функции будем последовательно применять именно три раза. На каждом шаге функция слева от стрелки — внешняя, справа — внутренняя.
Ответ получился некрасивым, но это нестрашно, потому что задания придумывал сам 🙂 Здесь все производные мы высчитываем на последнем шаге, чтобы не запутаться. На практике же чаще всего будет удобнее это делать после каждого применения формулы (для внешних функций).
[свернуть]
В первое время будет нелишним рисовать на черновике картинки из примеров 15 и 16 (понятно, применительно к своей задаче). Далее разберем пару примеров на комбинирование правил дифференцирования и формулы дифференцирования сложной функции.
Пример 17
Найти производную функции
Решение: Видим произведение, поэтому по формуле дифференцирования произведения функций запишем:
Обе полученные функции под знаком производной сложные, поэтому дифференцируем их по соответствующему правилу:
[свернуть]
Пример 18
Найти производную функции
Решение: Видим дробь, поэтому по формуле дифференцирования дробей запишем:
Обе полученные функции под знаком производной сложные, поэтому дифференцируем их по соответствующему правилу:
Опять получился не очень красивый ответ, но зато правильный 🙂
Здесь стоит заметить, что мы могли избавиться от дроби и перейти к произведению функций с помощью перенесения арксинуса в числитель (арксинус в этом случае получает степень ).
[свернуть]
На этом всё, спасибо за внимание!
higher-math.ru
