Примеры по алгебре с дискриминантом – Решение квадратных уравнений, примеры, тесты. Особые случаи. Разложение квадратного трехчлена на множители. Теорема Виета прямая, обратная

Решение квадратных уравнений

6 июля 2011

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант.

Дискриминант

Пусть дано квадратное уравнение ax² + bx + c = 0. Тогда дискриминант — это просто число D = b

2 − 4ac.

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

1. Если D < 0, корней нет;
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x² − 8x + 12 = 0;
2. 5x² + 3x + 7 = 0;
3. x² − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:

a = 1, b = −8, c = 12;
D = (−8)² − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3² − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)² − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.

Задача. Решить квадратные уравнения:

1. x² − 2x − 3 = 0;
2. 15 − 2x − x² = 0;
3. x² + 12x + 36 = 0.

Первое уравнение:
x² − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2)² − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x² = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2)² − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left( -1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left( -1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:

x² + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12² − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

\[x=\frac{-12+\sqrt{0}}{2\cdot 1}=-6\]

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x² + 9x = 0;
2. x² − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax² + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax² = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax

2 + c = 0. Немного преобразуем его:

Решение неполного квадратного уравнения

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax² + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c/a) < 0, корней нет.

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0. Достаточно выразить величину x² и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax² + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x² − 7x = 0;
2. 5x² + 30 = 0;
3. 4x² − 9 = 0.

x² − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x₁ = 0; x₂ = −(−7)/1 = 7.

5x² + 30 = 0 ⇒ 5x² = −30 ⇒ x² = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x² − 9 = 0 ⇒ 4x² = 9 ⇒ x² = 9/4 ⇒ x₁ = 3/2 = 1,5; x₂ = −1,5.

Смотрите также:

1. Теорема Виета
2. Следствия из теоремы Виета
3. Стандартный вид числа
4. Комбинаторика в задаче B6: легкий тест
5. Задача C2: уравнение плоскости через определитель
6. Задачи на проценты считаем проценты с помощью формулы

www.berdov.com

Дискриминант квадратного уравнения. Формулы дискриминанта

Дискриминант квадратного уравнения – это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Дискриминант позволяет определить имеет ли уравнение корни и сколько их, не решая само уравнение:

1. Если дискриминант больше нуля, то уравнение имеет два корня.
2. Если дискриминант равен нулю, то уравнение имеет один корень.
3. Если дискриминант меньше нуля, то уравнение не имеет корней.

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

D = b² — 4ac

так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле, можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата либо искать корни по формуле, либо сделать вывод что корней нет.

Пример 1. Решить уравнение:

3x²

— 4x + 2 = 0

Определим чему равны коэффициенты:

a = 3, b = -4, c = 2

Найдём дискриминант:

D = b² — 4ac = (-4)² — 4 · 3 · 2 = 16 — 24 = -8, D < 0

Ответ: корней нет.

Пример 2.

x² — 6x + 9 = 0

Определим чему равны коэффициенты:

a = 1, b = -6, c = 9

Найдём дискриминант:

D = b² — 4ac = (-6)² — 4 · 1 · 9 = 36 — 36 = 0, D = 0

Уравнение имеет всего один корень:

Ответ: 3.

Пример 3.

x² — 4x — 5 = 0

Определим чему равны коэффициенты:

a = 1, b = -4, c = -5

Найдём дискриминант:

D = b² — 4ac = (-4)² — 4 · 1 · (-5) = 16 + 20 = 36, D > 0

Уравнение имеет два корня:

x₁ = (4 + 6) : 2 = 5,   x₂ = (4 — 6) : 2 = -1

Ответ: 5, -1.

naobumium.info

Решение квадратных уравнений с помощью дискриминанта.

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

Какие же квадратные уравнения называются полными? Это уравнения вида ах² + b x + c = 0, где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b² – 4ас .

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D < 0),то корней нет.

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х₁ = (-b — √D)/2a ,  и  х₂ = (-b + √D)/2a .

Например. Решить уравнение х² – 4х + 4= 0.

D = 4² – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х² + х + 3 = 0.

D = 1² – 4 · 2 · 3 = – 23

Ответ: корней нет.

Решить уравнение 2х² + 5х – 7 = 0.

D = 5² – 4 · 2 · (–7) = 81

х₁ = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х₂ = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1.

Итак представим решение полных квадратных уравнений схемой на рисунке1. 

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах² + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х² = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3² – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах², затем с меньшим  – bx, а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2. 

Полное квадратное уравнение называется приведенным, если коэффициент при х² равен единице и уравнение примет вид х² + px + q = 0. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а, стоящий при х².

На рисунке 3 приведена схема решения приведенных квадратных уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х² + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6² – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х₁ = (-6 — 6√3 )/(2 · 3) = (6 ( -1- √(3)))/6 = –1 – √3

х₂ = (-6 + 6√3 )/(2 · 3) = (6 ( -1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам , приведенным на схеме рисунка D₁ = 3² – 3 · (– 6) = 9 + 18 = 27

√(D₁) = √27 = √(9 · 3) = 3√3

х₁ = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х₂ = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3. Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x² + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного уравнения рисунок 3.

D₂ = 2² – 4 · (– 2) = 4 + 8 = 12

√(D₂) = √12 = √(4 · 3) = 2√3

х₁= (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х₂= (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

примеры решений. Как решать квадратные уравнения через дискриминант

Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.

О каких уравнениях пойдет речь?

На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.

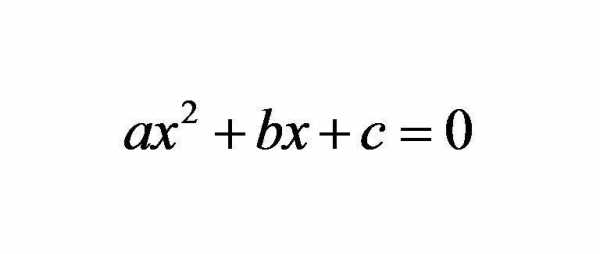
Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.

Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.

Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.

Способы решения уравнений второго порядка

Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:

• с помощью факторизации;
• используя формулу для полного квадрата;
• применяя график соответствующей квадратичной функции;
• используя уравнение дискриминанта.

Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.

Формула для получения корней уравнения

Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).

Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.

В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).

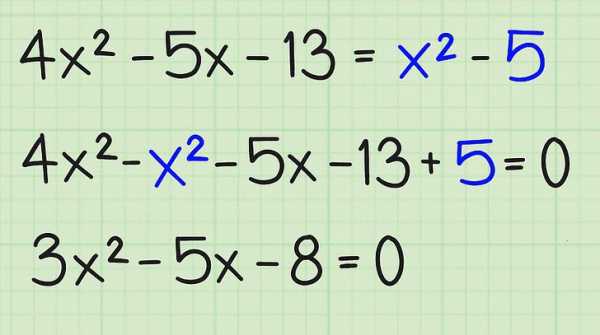
Как только усвоен описанный выше шаг, далее, следует научиться различать коэффициенты. Здесь все просто: при x² всегда стоит a, при x1 находится b, свободный член c представляет собой не связанное с x число.

В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.

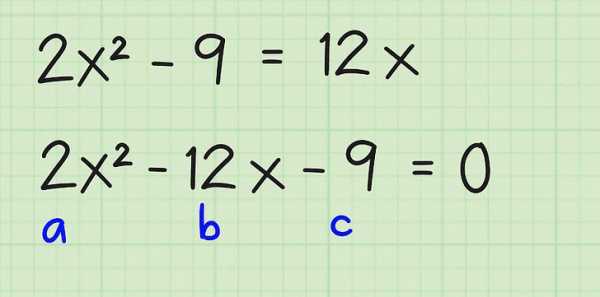
Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.

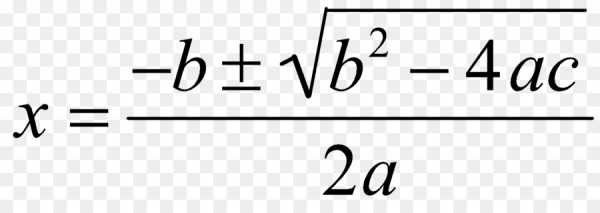
Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»). Для этого в него достаточно подставить коэффициенты b, c, и a.

Понятие о дискриминанте

В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.

Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:

1. D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
2. D
3. D=0: у уравнения всего один корень, и он является действительным числом.

Далее в статье приведены примеры с дискриминантом квадратных уравнений и дано их решение.

Задача на определение дискриминанта

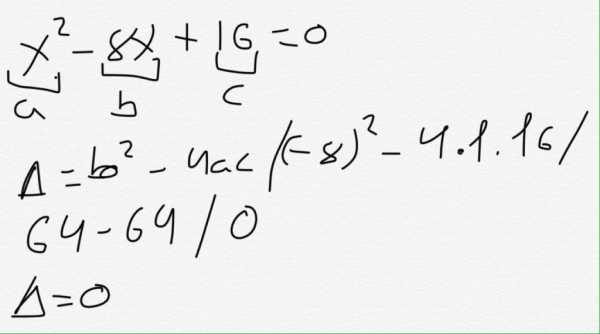
Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.

Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.

Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.

Пример неравенства через дискриминант

Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.

В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.

Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4

Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.

Пример решения уравнения

Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.

В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.

Геометрическая задача

Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.

У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.

Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.

Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.

Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см.

www.nastroy.net

Дискриминант на 4 | Алгебра

Дискриминант, делённый на 4 — D/4 — удобно использовать для упрощения вычислений при решении квадратных уравнений, если коэффициент b при x — чётное число.

Формула дискриминанта, деленного на 4 —

   

Как и для случая с обычным дискриминантом, количество корней  квадратного уравнения зависит от знака D/4.

• Если D/4>0, квадратное уравнение имеет два корня:

     

• Если D/4=0, квадратное уравнение имеет один корень

     

• Если D/4<0, квадратное уравнение не имеет действительных корней.

Рассмотрим примеры решения квадратных уравнений с помощью формулы четверти дискриминанта.

   

   

Так как b=16 — чётное число, вместо обычного дискриминанта вычислим дискриминант, делённый на 4 (иногда его еще обозначают через D1):

   

Так как D/4>0, уравнение имеет два корня:

   

   

   

Ответ: -0,2; -3.

   

   

   

   

Поскольку D/4>0, уравнение имеет два корня:

   

   

   

   

Ответ: 9; 1/3.

   

   

   

   

Так как D/4=0, данное квадратное уравнение имеет один корень

   

Ответ: -2 1/3.

   

   

   

   

Так как D/4<0, уравнение не имеет корней в действительных числах.

Ответ: нет корней.

Для решения квадратных уравнений вполне достаточно помнить обычную формулу дискриминанта и связанные с ним формулы корней. И все же, дополнительное знание формулы четверти дискриминанта не будет лишним.

Во-первых, с меньшими (по модулю) числами проще работать. Во-вторых, эта формула иногда ускоряет процесс нахождения корней уравнения.

   

   

   

   

Если находить корни через формулу обычного дискриминанта, придётся раскладывать его на множители, выносить множитель из-под корня, затем общий множитель — за скобки и сокращать дробь.

Ответ:

   

 

www.algebraclass.ru

Дискриминант квадратного уравнения с большими коэффициентами

Сложно встретить старшеклассника, НЕ умеющего находить корни квадратного уравнения через дискриминант.

Но, к сожалению, в отдельных случаях, получая громоздкий дискриминант,  многие начинают паниковать (без калькулятора).

А на ЕГЭ по математике, например, в задачах категории В14, вам вполне может встретиться причудливый дискриминант.

Нет безвыходных ситуаций!

На чем можно сэкономить силы при вычислении дискриминанта

 

Прежде чем разбирать примеры, вспомним все же  формулу дикриминанта для вычисления корней квадратного уравнения  

Тогда корни  уравнения находим по формуле

Надеюсь, вы помните, что удобно искать корни уравнения через дискриминант в случае, если имеем дело с полным  квадратным уравнением ( и – ненулевые).

Как решать неполные квадратные уравнения мы уже говорили.

1) Используем формулу «разность квадратов».

Допустим, нам нужно решить уравнение  

Ясно, что дискриминант следующий:

Не спешим возводить 53 в квадрат! Замечаем, что , поэтому

Корни данного уравнения, думаю, теперь каждый из вас найдет без труда…

2) Используем прием вынесения общего множителя за скобки.

Допустим, нам нужно решить уравнение (кстати, оно взято из реальной текстовой задачи из открытого банка заданий ЕГЭ по математике).

Ясно, что дискриминант следующий: 

Нет, мы не пойдем напролом!

Замечаем, что , а .

Мы можем вынести за скобку общий множитель

Корни найти – уже не проблема…

3) Формула сокращенного дискриимнанта.

Допустим, нам нужно решить уравнение

Вы знаете, что такое ? + показать

Его очень удобно применять в случае четности второго коэффициента (при x).

Вот формулы дискриминанта и корней в этом случае:

для уравнения , где – четное

Тогда корни следующие: , то есть или

Хоть на чуть-чуть, но упростили вычисления. Считаете, что неоправданно, – лишней формулой забивать голову… Выбор за вами.

4) Вместо дискриминанта – т. Виета.

Допустим, нам нужно решить уравнение

Вспоминаем  теорему  Виета:

Для приведенного квадратного уравнения (т.е. такого, коэффициент при  в котором равен единице)   сумма корней равна коэффициенту , взятому с обратным знаком, а произведение корней равно свободному члену , то есть ,

Так вот, очевидно, на роль корней уравнения  претендуют числа и , так как и

Вот, пожалуй, все основные случае, где можно сэкономить время и силы при решении квадратного уравнения, о которых я хотела рассказать.

За улыбкой –> + показать

egemaximum.ru

Квадратные уравнения, примеры решений

Теория по квадратным уравнениям

ОПРЕДЕЛЕНИЕ Квадратным уравнением называется уравнение вида , где .

Возможны такие случаи:

, тогда имеем квадратное уравнение вида и .

, тогда имеем квадратное уравнение вида , если ; если – корней нет.

, тогда имеем квадратное уравнение вида .

, тогда имеем полное квадратное уравнение , которое решается или с помощью дискриминанта:

   

Или по теореме Виета:

   

Примеры

ПРИМЕР 1

Задание	Решить следующие неполные квадратные уравнения
Решение	1) В уравнении вынесем за скобки . Произведение равно нулю, если один из сомножителей равен нулю, следовательно:     или     2) В уравнении перенесем свободный член вправо и раздели его на коэффициент при :     3) В уравнении перенесем свободный член вправо и раздели его на коэффициент при :     У данного квадратного уравнения нет корней. 4) уравнение равносильно уравнению , которое имеет два совпадающих корня .
Ответ	Корней нет

ПРИМЕР 2

Задание	Решить квадратное уравнение
Решение	Подсчитаем для заданного уравнения, чему равен дискриминант:     Так как , то уравнение имеет два совпадающих корня:
Ответ

ПРИМЕР 3

Задание	Решить уравнение
Решение	Вычислим дискриминант для исходного уравнения, получим:     Так как , данное уравнение решений не имеет.
Ответ	Корней нет.

ПРИМЕР 4

Задание	Решить квадратное уравнение
Решение	Дискриминант заданного уравнения, равен     Следовательно, уравнение имеет два различных корня
Ответ

ПРИМЕР 5

Задание	Решить уравнение, используя теорему Виета:
Решение	Пусть и – корни квадратного уравнения, по следствию из теоремы Виета     Проанализируем полученные равенства. Произведение корней отрицательно, следовательно, корни имеют разные знаки. Разложим –12 на множители, учитывая, что они должны быть числами разного знака. Возможны такие варианты: –12 и 1; 12 и –1; –6 и 2; 6 и –2; –4 и 3; 4 и –3. Так как сумма корней равна 1, то корнями будут числа и .
Ответ

ru.solverbook.com