Примеры квадратные уравнения 9 класс – Решение уравнений 9 класс. На уроке Линейные уравнения. Квадратные и сводимые к ним. Дробно – рациональные уравнения Уравнения высших степеней.». Скачать бесплатно и без регистрации.
Примеры уравнений, приводимых к квадратным. 9-й класс
Разделы: Математика
Цели:
- сформировать умение решать целые уравнения методом введения новой переменной;
- развивать познавательную активность и творческие способности учащихся;
- воспитывать навыки творческого усвоения знаний.
Оборудование: компьютер, проектор .
ХОД УРОКА
1. Сообщение темы и цели урока
2. Проверка домашнего задания
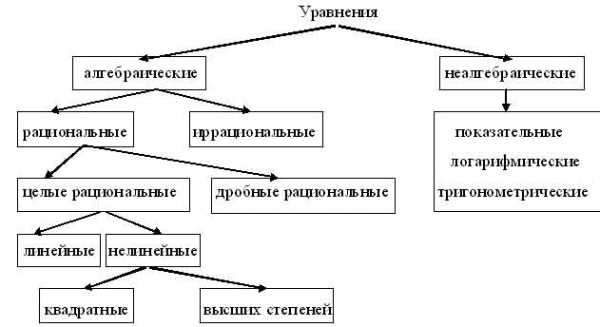
– Какие уравнения называют целыми?
– Что называют степенью уравнения?
№ 273 (2 ст.), № 274 (а) – решение представлено на
экране.
– Проверьте домашнее задание и поставьте
себе оценку в табеле.
Табель оценок
| №п/п | Виды работ на уроке |
Оценка |
| 1 | Домашнее задание | |
| 2 | Устная работа | |
| 3 | Составление алгоритма решения уравнения | |
| 4 | Работа у доски | |
| 5 | Парная работа | |
| 6 | Самостоятельная работа |
3. Устная работа
– Решим уравнения:
а) (х + 6) (х – 7) = 0 (Когда
произведение равно 0?)
б) (10 – х) (4 – х) = 0
в) х(25 + х) (2 + х) = 0
г) х2 = 25
д) х2 – 9 = 27
4. Работа по объяснению нового материала. (Создание проблемной ситуации)
– Какова степень уравнения x4 – 4х2
+ 5 = 0? (4)
– Умеем мы решать такие уравнения? (Нет)
Давайте попробуем.
– Можно переписать уравнение в таком виде: (х2)2
– 4х2
– На какое уравнение похожа эта запись? (На квадратное)
– Почему я выделила х2?
– Что я могу сделать с этим одночленом? (Заменить другой переменной)
– Пусть х2 = у, тогда у2 – 4у + 5 = 0
– Что мы получили при замене переменной? (Квадратное уравнение)
– Когда решим квадратное уравнение, значение какой переменной мы найдём? (у)
– Это будет ответ? (Нет)
– Что мы должны сделать дальше? (Вернуться к подстановке)
– Сколько у нас получится уравнений? (2)
– Чтобы найти значение х, мы должны решить оба эти уравнения.
– Отчего зависит количество корней уравнения? (От количества и знака корней уравнения с замененной переменной)
5. Презентация решений уравнений:
х4 – 4х2 + 5 = 0 и
(х2 + х + 6)(х2 + х – 4) = 144
6. Закрепление нового материала
У доски решение с комментированием и составлением алгоритма решения.
№276(а): (2х2 + 3) – 12(2х2 + 3) + 11 = 0
Алгоритм решения биквадратного уравнения
Метод решения – замены переменной
1. Ввести замену переменной: пусть х2 =
y,
2. Составить квадратное уравнение с новой
переменной: аy2 + by+ с = 0 (2)
3. Решить новое квадратное уравнение (2).
4. Вернуться к замене переменной.
5. Решить получившиеся квадратные уравнения.
6. Сделать вывод о числе решений биквадратного
уравнения.
7. Записать ответ.
7. Парная работа
Самостоятельное решение с взаимопроверкой. №276(б), 278(б)
8. Самостоятельная работа
в) г) д) е) одновременное решение у доски (на 4 досках). Проверка с помощью проектора.
7. Подведение итогов. Рефлексия
– Что нового узнали на уроке?
– Какие задания были сложными? Что запомнилось?
– Как работал класс на уроке?
– Кто работал лучше всех?
Поставить оценки за урок, используя табель оценок. (Табель сдается и проверяется учителем)
8. Домашнее задание: №279(обязательно), №280 (по выбору).
9.01.2015
Поделиться страницей:Конспект урока по теме Квадратные уравнения в 9 классе.
Конспект урока по теме «Квадратные уравнения»: обучение учащихся решению квадратных уравнений
Тема. Обобщающий урок по теме « Квадратные уравнения».
Образовательные цели:
Продолжать формировать общеучебные умения:
организовывать себя на работу;
работа с таблицей;
пользоваться умением самопроверки.
Развивающий аспект:
интеллектуальное, эмоциональное, личностное развитие ученика;
развитие логического и вариативного мышления;
развивать умение обобщать, систематизировать на основе сравнения, делать вывод;
активизация самостоятельной деятельности;
развивать познавательный интерес;
развивать наглядно-действенное творческое воображение.
Воспитательный аспект:
Воспитание коммуникативной и информационной культуры учащихся.
Эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задание на доске и в тетради, через наглядные и дидактические пособия.
Задачи:
1. Сформировать у школьников личностную мотивацию к изучению данной темы.
2. Развивать у учащихся умение пользоваться опорными знаниями для получения новых знаний.
3. Развивать у учащихся логическое мышление (умение выделять существенные признаки и делать обобщения).
4. Развивать у учащихся навыки творческого подхода к решению задач и навыки исследовательской работы над уравнениями.
Учебник: Алгебра 9 класс.
Дидактический материал: мультимедийная презентация.
Оборудование: мультимедийный терминал.
Формы работы: фронтальная, групповая, индивидуальная.
Эпиграфом к данному уроку я взяла слова:
Сухие строки уравнений –
В них сила разума влилась.
В них объяснение явлений,
Вещей разгаданная связь.
Л.М.Фридман.
Тип урока: урок обобщения и систематизации знаний.
Методы обучения: частично-поисковый (эвристический). Тестовая проверка уровня знаний, решение познавательных обобщающих задач, системные обобщения, самопроверка.
Знать: методы решения квадратных уравнений.
Уметь:
— решать различные виды квадратных уравнений и уравнений, сводящихся к ним;
— сравнивать уравнения, находить отличия.
Деятельность учителя: поддержание обратной связи с учащимися в непрерывном виде.
Формы организации труда: индивидуальная, фронтальная, звеньевая, групповая и индивидуализированная.
Х О Д У Р О К А.
I. Организационный момент.
Французский писатель Анатоль Франс ( 1844 – 1924 ) заметил, что « Учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом.»
Последуем совету писателя: будем на уроке активны, внимательны, будем
« поглощать » знания с большим желанием, ведь они скоро вам понадобятся при сдаче экзамена по математике.
Сегодня мы с вами повторим, обобщим классификацию квадратных уравнений, способы их решения, вспомним биквадратные уравнения.
II. Устная работа.
Цель: организовать внимание, повторить виды квадратных уравнений, способы их решения.
ОПРОС:
1).Что называется уравнением?
2)Что называется корнем уравнения?
3)Что значит решить уравнение?
4) Уравнение принадлежит множеству (вид уравнения)?
ПОВТОРЕНИЕ (презентация):
Цель: повторить определение, классификацию, способы решения квадратных и биквадратных уравнений.
Слайд 3: ОПРЕДЕЛЕНИЕ.
Квадратным уравнением называется уравнение вида ах2
где а,в,с –заданные числа, а ≠ 0, х – неизвестное.
Выражение в2 – 4ас называется дискриминантом квадратного
уравнения.
Слайд 4: КЛАССИФИКАЦИЯ КВАДРАТНЫХ УРАВНЕИЙ ПО КОЛИЧЕСТВУ СЛАГАЕМЫХ
Квадратные уравнения:
Полные: Неполные:
ах2 + вх + с=0, ах2 + вх=0, где а≠0, в≠0, с=0;
где а≠0, в≠0, с≠0. ах2 + с=0, где а≠0, в=0, с≠0;
ах2=0, где а≠0, в=0, с=0.
Слайд 5: КЛАССИФИКАЦИЯ КВАДРАТНЫХ УРАВНЕИЙ ПО =1 СТАРШЕГО КОЭФФИЦИЕНТА
Квадратные уравнения:
Приведенные: Неприведенные:
а=1 а ≠ 1
х2 +рх + q = 0 ах2 + вх + с =0
Слайд 6: СПОСОБЫ РЕШЕНИЯ ПОЛНЫХ УРАВНЕНИЙ
1)По формуле корней квадратного уравнения:
х1,2=
2)По формуле корней с четным вторым коэффициентом:
х1,2 =
Слайд 7: ЧИСЛО КОРНЕЙ ПОЛНОГО КВАДРАТНОГО УРАВНЕНИЯ
1) Если D > 0, то уравнение имеет 2 корня
2) Если D = 0, то уравнение имеет 1 корень, который можно
вычислить по формуле х = — в / 2а
3) Если D < 0,то уравнение корней не имеет.
Слайд 8: СПОСОБЫ РЕШЕНИЯ НЕПОЛНЫХ КВАДРАТНЫХ
УРАВНЕНИЙ
1)2х2 = 0, 2) 10х2 + 7х = 0, 3) 3х2 – 75 = 0,
х2 = 0, х(10х + 7) =0, 3х2 = 75,
х = 0. х=0 или 10х+7=0, х2=25,
х=-0,7. х1,2=± 5.
Слайд 9: СПОСОБЫ РЕШЕНИЯ ПРИВЕДЕННОГО КВАДРАТНОГО
УРАВНЕНИЯ
1) Пример: х2 – 8х – 9 =0 ,
Характеристика уравнения.
х1,2 = 4 ± √ 16 + 9,
х1,2 =4 ±5,
х1= 9, х2 = -1.
2). Пример: х2 – 7х + 10 =0
Характеристика уравнения.
По формулам Виета: х1=2, х2=5
Слайд 10: БИКВАДРАТНЫЕ УРАВНЕНИЯ
Уравнение вида ах4 +вх2 + с = 0 называется биквадратным.
Пример: х4 – 2х2 – 8 =0.
Пусть х2 = t, где t ≥0, тогда
t2 -2t -8 =0,
t1 =4, t2=-2.
t=-2 не удовлетворяет условию t ≥0.
Вернемся к принятым обозначениям: х2=t,
t=4
Решим уравнение: х2=4,
х1,2 = ±2
Ответ: -2; 2.
III. Следствие ведут знатоки.
Цель: проверить знания теории на практике.
1)Найдите ошибку в решении уравнений (слайд 11)
а)2х2 -9х+4=0 б) х2+2х-15=0
Д=81-4·2·4=81-32=49; =7. По обратной теореме Виета:
х1,2 =; х1+х2=2,
х1==8; х2==1. х1·х2=-15
Ответ: 1; 8. х1=5; х2=-3.
Ответ: -3; 5.
IV. Проба сил.
1.ТЕСТ ( карточки с тестом на каждом столе)
I вариант
1)Квадратное уравнение 2х2-3х+4=0 является:
А.полным; Б.неполным; В.приведенным
2)В уравнении 2х2-3х+4=0 по дискриминанту сделайте вывод о количестве корней.
А. 2корня; Б. 1корень; В. нет корней
3).Если дискриминант равен нулю, то корень квадратного уравнения вычисляется по формуле:
А. х = ; Б. х = ; В. х = ;
II вариант
1). Найдите дискриминант уравнения 3х2 +5х-2=0.
А. -49; Б. 1; В.49.
2) Квадратное уравнение 5х2-6х=0 является:
А.полным; Б.неполным; В.приведенным
3).Если дискриминант положителен, то полное квадратное уравнение имеет:
А. 2корня; Б. 1 корень; В. не имеет корней
Проверка теста — обмен тетрадями.
Ключ к ответам: I в.- А,В,Б; II в. – В,Б,А (Слайд 12)
2. Соревнование «Сильное звено »
Решить уравнения, работая в звеньях: (уравнения написаны на доске)
1) 2х2 + 3х – 5=0;
2) х2-8х +12=0;
3) 4х2 -8 =0;
4) 5х2 + 6х =0;
Ответы: 1)- 2,5; 1; 2) 2;6; 3) ; 4) -1,2; 0. (Слайд 13)
V. Исторические сведения
Цель: формирование учебно-познавательной мотивации школьников на уроке, воспитание интереса к предмету.
На данном этапе учащимся сообщается, а также демонстрируется в презентации материал из истории возникновения квадратных уравнений, сведения об известном французском математике Франсуа Виете.
Затем учащимся предлагается решить самостоятельно задачу Бхаскары. По словам математика Лейбница “Кто хочет ограничиваться настоящим без знания прошлого, тот никогда его не поймет”. Задачи на квадратные уравнения встречались уже в 499 году. В древней Индии были распространены публичные соревнования в решении трудных задач. Часто они были составлены в стихотворной форме.
Вот одна из задач про обезьян:
Обезьянок резвых стая,
Всласть поевши, развлекаясь,
Их в квадрате часть восьмая
На поляне забавлялась,
А 12 по лианам
Стали прыгать, повисая.
Сколько было обезьянок,
Ты скажи мне, в этой стае?
Решение:
– всего обезьян
Ответ: 48 или 16
VI. Физ.минутка.
VII. Самостоятельная работа в группах.
I-II группы –
1 вариант
1)2х4-19х2+9=0, 2)х4 -7х2+12=0,
Пусть х2=t,где t≥0,тогда Пусть х2=t, где t≥0,тогда
2t2-19t+9=0, t2 – 7t+12=0,
D=361-72=289, √289 =17, t1= 4; t2=3,
19±17 Вернемся к принятым
t1,2= 4
обозначениям:
t1=9, t2=1/2, а)х2=t, t=4, б)х2=t, t=3
Вернемся к принятым х2=4 х2=3,
обозначениям: х1,2=±2 х3,4=±√3
а)х2=t, t=9 б)х2=t, t=1/2, Ответ:-2;-√3; √3; 2.
х2=9 х2=1/2,
х1,2=±3 х3,4=±√1/2
Ответ: — 3; — √1/2; √1/2; 3.
II вариант
1)3х4-13х2+4=0, 2)х4 – 11х2 +18=0,
Пусть х2=t,где t≥0,тогда Пусть х2=t,гдеt≥0,тогда
3t2 — 13t +4=0, t2 – 11t+18 =0,
D=169 – 48 =121, √121=11, t1=2, t2= 9
Вернемся к принятым
обозначениям:
t1= 4, t2=1/3, а)х2=t, t=2, б)x2=t, t=9
Вернемся к принятым х2=2, х2=9,
обозначениям: х1,2=±√2, х3,4=±3.
а)х2=t, t=4 б)х2=t, t=1/3, Ответ: -3; -√2; √2; 3.
х2= 4, х2=1/3,
Х1,2=±2, х3,4=±√1.3
Ответ:-2; -√1/3; √1/3; 2.
III группа –
1 вариант:
1)10х2+5х=0, 2) 4 – 36х2=0 , 3)5х2-7х+2=0,
5х( 2х+1)=0, 36х2=4, D=49 – 4•5•2=9,
5х=0 или2х+1=0, х2=4/36, √9 =3,
Х=0 2х= -1, х2=1/9,
7±3
х = — 0,5. х1,2=±1/3. х1,2= 10
Ответ: — 0,5; 0. Ответ:±1/3 х1=1; х2=0,4
Ответ: 0,4; 1.
2 вариант:
1)х2-10х=0 , 2)3х2-75=0 , 3) 3х2+5х-2=0,
х(х-10)=0, 3х2=75, D=25+24=49,
х=0или х-10=0, х2=25 √49 =7,
х=10. х1,2=±5. -5±7
Ответ: 0; 10. Ответ: ±5. х1,2= 6
х1=1/3, х2= — 2. Ответ: -2; 1/3.
Индивидуальные задания:
1)(х2+х)2-11(х2+х)=12
Пусть х2+х = у, тогда
у2-11у-12=0,
у1=12; у2=-1.
Вернемся к принятым обозначениям, получим 2 уравнения:
а)х2+х=12, б)х2+х=-1,
х2+х-12=0, х2+х+1=0,
х1=-4; х2=3; D=1- 4=-3,
корней нет.
Ответ:-4; 3.
2) (х2+4х)(х2+4х-17)+60=0
Пусть х2+4х=у,тогда
у(у-17)+60=0,
у2-17у+60=0,
у1=12, у2=5.
Вернёмся к принятым обозначениям, получим
2 уравнения:
а)х2+4х=12 , б) х2+4х=5,
х2+4х-12=0, х2+4х-5=0,
х1=-6;х2=2 . х3=-5;х4=1.
Ответ:-6;-5;1;2
Проверка заданий по группам. ( Слайды 15- 19 )
VIII. Самооценка.
-Я работал самостоятельно без ошибок. Получил 5.
-Я работал с подсказками без ошибок. Получил 4.
— Я работал с подсказками, допустил ошибку. Получил 3.
IХ. Рефлексия.
Прежде, чем мы окончим сегодняшний урок, я хочу узнать, что же изменилось или сохранилось в вашем настроении в течение урока. Перед вами лежат листочки с солнышками. Каждое из них обозначает определенное настроение. Около рисунка, отражающего ваш настрой на урок, отметьте знаком V.
Продолжи фразы: (заранее раздать учащимся)
Теперь я точно знаю…
Я понял(а)…
Я узнал(а)…
Я научился(ась)…
Мое мнение…
Я почувствовал(а)…
ХI. Итог урока. Сегодня на уроке мы с вами повторили и обобщили знания по теме «Квадратные уравнения».
Х. Сам себе режиссер: (домашнее задание) (Слайд 20)
Критерии оценок:
А. – «5»; В. – «4»; С. – «3».
№77(1),№76(2),№78(2)
№71(1),№72(2),№79(2)
№393,№423,№429,№437
Дополнительно: решить уравнение 3х2 + 2х – 1 = 0 разными способами.
Закончить наш урок я хотела бы словами: Научился сам, научи другого.
Урок окончился, спасибо за работу. До свидания!
infourok.ru
Деятельность учеников | |
1. Организационный этап Подготовка к итоговой аттестации – неотъемлемая часть современного курса математики 9 класса. На этом уроке повторим и закрепим знания и умения решать квадратные уравнения различными способами. Эта тема очень важная в курсе математики, она является ступенькой в изучении более сложного материала. В старших классах будем решать логарифмические, показательные, тригонометрические уравнения, приводимые к квадратным. А сегодня вы покажете, насколько готовы шагать по ступенькам математики дальше. Эпиграфом к уроку послужат слова английского поэта средних веков Чосера: «Посредством уравнений, теорем я уйму всяких разрешал проблем». Всем желаю творческих успехов и надеюсь, что каждый урок математики поможет вам при прохождении итоговой аттестации. Учитель объясняет назначение раздаточного материала, который находится на рабочем месте каждого ученика, обращает внимание учащихся на лист результативности, в который постепенно в ходе урока будут заноситься баллы, полученные за выполнение заданий разноуровневых тестов, выполнения заданий у доски, за активную работу на уроке. | Приветствуют учителя и готовятся к началу работы. |
2. Эмоциональный настрой. Целеполагание. ДЕРЕВО ЖИЗНИ Чтобы определить главные и второстепенные цели и задачи, я нарисовал дерево. Корень дерева – момент вашего рождения, ствол – вся дальнейшая жизнь, вершина дерева – то самое важное, что вы представляете в своей жизни. Может быть несколько вершин. Ветви – те задачи, которые предстоит решать втечение жизни (личные, образовательные, профессиональные, нравственные, творческие, государственные). Каждый из вас должен задуматься, какие цели и задачи ставить, какие ветви будут толстыми, прочными, а какие, наоборот, будут более тонкими и хрупкими. В зависимости от этого определяется его личностная направленность. | Определяют свое настроение и демонстрируют его с помощью выбранных символов – разноцветных смайлов. |
3. Повторение теоретического материала. Учитель просит учащихся дать определение квадратного уравнения. -Объясните, в чем заключается смысл ограничения в определении квадратного уравнения. -Перечислите виды квадратных уравнений -Приведите примеры квадратных уравнений различных видов. -Какое квадратное уравнение называется приведенным? Приведите пример. -Какие способы решения неполных уравнений вы знаете? —От чего зависит количество корней полного квадратного уравнения? -Какие способы решения полных квадратных уравнений вам известны? | формулируют определение квадратного уравнения а 0. Перечисляют виды (полные и неполные). Приводят примеры. Формулируют понятие приведенных уравнений (а = 1) и приводят пример. Ответы учащиеся заполняют в таблицу 1. Ответы учащиеся заполняют в таблицу 2. Ответы учащиеся заполняют в таблицу 3. |
4. Устная работа Учитель предлагает учащимся применить только что сформулированные теоретические факты. Определите, какие из уравнений являются квадратными? 1) 2х2 –1 = 0, 2) х = 5х – 7, 3) = х2 + 4х, 4) 4 = 9х2 + 2х. Если уравнение является квадратным, то приведите его к стандартному виду. 2. Назовите коэффициенты квадратного уравнения: 1) 5х2 +4х –1 = 0, 2) х2 –3х = 0 3) 2 х –5 + х2 = 0, 4) – х2 + 5=0. 3. Найдите, сколько корней имеет квадратное уравнение? 1) х2 –3х + 2 = 0, 2) 4 х2 +4 х+1 = 0 3) 3 х2 –7х + 14 = 0, 4) 6 х2 + 5х –3 = 0 | Выявляют квадратные уравнения. Называют коэффициенты. Определяют количество корней уравнения. |
5. Упражнения для закрепления материала 1. Тест “Виды квадратных уравнений” 2. Учитель предлагает восемь квадратных уравнений: (самостоятельная работа) 3х2 + 4х – 1 = 0, 4х2 – 8 = 0, х2 – 10х + 100 = 0, 5х2 + 6х = 0, х2 – 8х + 12 = 0, 3х2 = 0, 14 – 2х2 + х = 0. Вопросы: Выпишите номера полных квадратных уравнений. Выпишите коэффициенты а, b, с в уравнении №8. Выпишите номер неполного квадратного уравнения, имеющего один корень. Какое из неполных квадратных уравнений решается разложением на множители? Выпишите коэффициенты а, b, с в уравнении № 5. Найдите дискриминант в уравнении № 6, сделайте вывод о количестве корней. Найдите D1 в уравнении № 3, сделайте вывод о количестве корней. Найдите сумму и произведение корней в уравнении № 7. Учитель предлагает обменяться учащимся работами, проверить товарища и поставить оценку. Сдать листочки и проверить правильность выполнения заданий по образцу. Критерии оценок: 8 заданий верно – 5б, 6 – 7 заданий – 4б, 4 – 5 заданий – 3б. 3. Соотнесите квадратные уравнения и способы их решения: 1. 2х2 – 3х + 11 = 0 разложение на множители 2. 7 х2 = 8х общая формула корней 3. х2 – 10х + 100 = 0 теорема Виета 4. х2 –5х –6 = 0 графический 5. х2 – 21х – 45 = 0 формула чётного коэффициента 6. х2 + 2008х – 2009= 0 формула для приведённого уравнения 7. – 2х2 + х +14= 0 свойства коэффициентов 4.Найдите ошибки в решении уравнений: х2 – 16х – 63 =0 D = 64 – 63=1, 2 корня; х=, х= х=4,5; х=3,5 Ответ: 4,5; 3,5 2) х2 – 23х – 45 =0 D = 529 + 180 =709, 2 корня; х=, х=, Ответ: , . Записать правильное решение в тетради, в записи на доске исправить ошибки другим цветом. Разноуровневая самостоятельная работа Учащиеся группы 1 решают два уравнения с последующей проверкой, а группы 2 и 3 применяют умение решать уравнения в нестандартной ситуации. | Выполняют тест Выполняют письменную работу, отвечая на поставленные учителем вопросы. Обмениваются работами, проверяют товарища и выставляют друг другу отметки по критериям. Устно выполняют соотнесение, аргументируя свой ответ. Выполняют самостоятельно в парах в тетради, затем исправляют ошибки на доске другим цветом. Решают задания своего уровня сложности. Если остается ещё время, то набирают дополнительные баллы, решая задания другого уровня сложности. Сильные учащиеся, выполнив задания менее сложного уровня, помогают своим товарищам из другой группы в случае необходимости. (По просьбе учителя они выступают в роли консультантов). У доски работают 4 учащихся из группы III, в случае необходимости они объясняют своё решение. |
6.Разноуровневый тест тематического контроля знаний «Квадратные уравнения». Во время выполнения работы учитель, если необходимо, помогает учащимся группы I, II выполнять задания и контролирует решение задач на доске. | У доски учащиеся группы III записывают и подробно объясняют решение своего варианта. Учащиеся двух других групп и остальные учащиеся группы III решают в это время разноуровневый тест. Проверка теста осуществляют учащиеся самостоятельно, тетради сдаются учителю для последующей проверки и анализа. |
7. Обсуждение решений задач представленных на доске. Если есть недочеты, учитель предлагает их найти. | Учащиеся, выполнявшие задачи у доски, комментируют свои решения, а остальные вносят, при необходимости, коррективы. |
8. Подведение итогов урока, комментарии по домашнему заданию. Итак, мы проделали большую работу. Повторили всю теорию, касающуюся квадратных уравнений. Выполнили различные их виды как вместе, так и вы сами. Вы старательно зарабатывали баллы, настало время подвести итог. Подсчитайте сумму баллов заработанных в течение урока. 1). Подсчет баллов Каждое задание самостоятельной работы и теста, выполненное верно оценивается в 1 балл. 2). Заполнение листа результативности «5» — 15 – 20 баллов «4» — 9 — 14 баллов «3» — 5 – 8 баллов Учитель еще раз обращает внимание, на те типы заданий, и те теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их. Отмечает наиболее успешную работу на уроке отдельных учащихся. Решения разноуровневых самостоятельной работы и теста учащиеся забирают с собой, чтобы дома сделать работу над ошибками, листы результативности сдают учителю. Учитель после урока анализирует их и выставляет оценки, докладывая о результатах анализа на следующем уроке. | Подсчитывают баллы, заработанные в течение урока. |
9. Рефлекия Давайте поставим общую оценку за урок. С каким настроением вы уходите с урока? Выберите смайлик, который, по вашему мнению, соответствует вашему настроению. | Аргументируя, ставят общую оценку за урок. Выбирают смайлик по своему настроению. |
10. Домашнее задание Работа над ошибками в тестах. Решение уравнений различными способами с книги по подготовке к итоговой аттестации.( по своему уровню) | Записывают домашнее задание |
doc4web.ru
Решение квадратных уравнений с параметрами с учащимися 8-9 классов
Квадратные уравнения применяются для решения задач практического характера с незапамятных времен. Для большинства современных учащихся их решение едва ли может представлять особую сложность, однако ситуация может кардинально измениться, если в уравнении появится параметр… На примере 3-ех задач различного уровня сложности автор попытался осветить наиболее частые проблемы, с которыми могут столкнуться школьники в рамках подготовки к Единому государственному экзамену.
Говоря о проблемах и трудностях, с которыми учащиеся 8-9 классов могут столкнуться на уроках алгебры, безусловно, следует упомянуть вопросы, касающиеся решения квадратных уравнений с параметрами. Казалось бы, сами по себе квадратные уравнения вряд ли могут представлять сложность для учащихся 8-9 классов, однако в случае если в квадратном уравнении фигурирует параметр, дело принимает совсем иной оборот.
Итак, попробуем разобраться.
Ученые полагают, что квадратные уравнения применялись астрономами, специалистами по аграрному и военному дела (а впоследствии и многими другими, включая, конечно, математиков) еще во времена существования Древнего Вавилона в III-II вв. до н.э. В соревнованиях по решению квадратных уравнений участвовали ученые Древней Индии, задачи с уравнениями второй степени решали также в Древней Греции, Древнем Риме, Древнем Китае, одним словом этим занимались ученые-представители всех крупных древних цивилизаций. С развитием математики проблемой квадратных уравнений занимались видные мировые ученые, такие как Франсуа Виет, Михаэль Штифель, Альбер Жирар, Рене Декарт и другие. А теперь и мы прикоснемся к тому, что занимало умы великих ученых-математиков на протяжении тысячелетий.
Итак, квадратные уравнения.
Согласно общему определению квадратное уравнение – это уравнение вида ax^2+bx+c=0, где x- переменная, a, b, c – коэффициенты, причем a≠0. Известно, что для решения уравнения подобного вида необходимо вычислить дискриминант и в зависимости от его значения (если D ≥0 воспользоваться формулой корней, если D <0, корней нет) получить соответствующий ответ. Однако в случае решения квадратных уравнений с параметрами ситуация не будет столь однозначной. Давайте рассмотрим несколько примеров.
Необходимо исследовать и определить, при каких значениях параметра уравнения имеют решения:
Задача №1
x^2- (m-2)*x-(m-2)=0
Квадратное уравнение имеет решения, если D ≥0, т.е. D=(m-2)^2+4(m-2)=(m-2)(m+2)≥0
Таким образом, уравнение имеет решения при m∈(-∞;-2]∪[2;+∞) и решением будет являться значения x_1,2=(m-2±√(m^2-4))/2
Соответственно, при m∈(-2;2) D<0, т.е. решений нет.
При m=-2 x=-2 (единственное решение).
При m=2 x=0 (единственное решение).
Задача №2
x/(x^2-4)+a/(x^2+2x)+1/(2x-x^2 )=0
Найдем ОДЗ: x≠±2
x≠0
Путем приведения к общему знаменателю получим: x^2+(x-2)a-(x+2)=0.
Упростив выражение, получим: x^2+(a-1)x-2a-2=0
Если D=(a-1)^2+8a+8=(a+3)^2>0, тогда при
a≠-3 x_1,2=(1-a±√((a+3)^2 ))/2 , т.е. x_1=- a-1; x_2=2,но x_2=2 не принадлежит ОДЗ.
Таким образом, решением данного уравнения будет являться корень x_1=- a-1 в случае, если:
x_1=- a-1≠0, т.е. a≠-1
x_1=- a-1≠2, т.е. a≠-3
x_1=- a-1≠-2, т.е. a≠1
Ответ: При a≠±1 ∃ единственное решение x=- a-1
a≠-3
Задача №3
x/m(x+1) -2/(x+2)=(3-m^2)/m(x+1)(x+2)
Найдем ОДЗ: m≠0
x≠-1
x≠-2
Приведем уравнение к общему знаменателю: x(x+2)-2m(x+1)=3-m^2
Упростив выражение, получим: x^2-2(m-1)x+m^2-2m-3=0
Если D=4(m-1)^2-4(m^2-2m-3)=16>0, тогда x_1,2= (2(m-1)±4)/2=(m-1)±2
x_1= m+1
x_2= m-3
Выясним, при каких значениях параметра m x принадлежит ОДЗ (см.действие 1).
x≠-1 , тогда x_1= m+1≠-1,тогда m≠-2,а значит x_2= m-3≠-2-3≠-5 или x_2= m-3≠-1,тогда m≠2,а значит x_1= m+1≠2+1≠3
x≠-2,тогда x_1= m+1≠-2,тогда m≠-3,а значит x_2= m-3≠-3-3≠-6 или x_2= m-3≠-2,тогда m≠1,а значит x_1= m+1≠1+1≠2
При m=0 уравнение не определено.
Ответ: При m≠±2 существует 2 корня: x_1= m+1 и x_2= m-3
m≠-3
m≠1
m≠0
Итак, мы рассмотрели несколько примеров решений квадратных уравнений с параметрами. Эта тема включена в учебную программу по алгебре для учащихся 8-9 классов, что делает ликвидацию пробелов по данной тематике необходимым фактором в условиях современного образовательного процесса, а также в рамках подготовки к Единому государственному экзамену.
Всего комментариев: 0www.uchportal.ru
Алгебра 7-9 классы. 19. Квадратные уравнения. Разложение квадратного трехчлена на множители
- Главная
- Видеотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Обществознание
- Обществознание — как наука
- Иностранные языки
- История
- Психология и педагогика
- Русский язык и литература
- Культурология
- Экономика
- Менеджмент
- Логистика
- Статистика
- Философия
- Бухгалтерский учет
- Технические науки
- Черчение
- Материаловедение
- Сварка
- Электротехника
- АСУТП и КИПИА
- Технологии
- Теоретическая механика и сопромат
- САПР
- Метрология, стандартизация и сертификация
- Геодезия и маркшейдерия
- Программирование и сеть
- Информатика
- Языки программирования
- Алгоритмы и структуры данных
- СУБД
- Web разработки и технологии
- Архитектура ЭВМ и основы ОС
- Системное администрирование
- Создание программ и приложений
- Создание сайтов
- Тестирование ПО
- Теория информации и кодирования
- Функциональное и логическое программирование
- Программы
- Редакторы и компиляторы
- Офисные программы
- Работа с аудио видео
- Работа с компьютерной графикой и анимацией
- Автоматизация бизнеса
- Прочие
- Музыка
- Природное земледелие
- Рисование и живопись
- Естествознание
- Библиотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Астрономия
- Обществознание
- Иностранные языки
- Технические науки
- Теоретическая механика и сопромат
- Сварка
- Железная дорога
- Паспорта и техническая документация
- Металлообра-батывающие станки
- Деревообра-батывающие станки
- Сварочное оборудование
- Естествознание
- Правила
- Контакты
- Вы здесь:
- Главная
- Видеотека
forkettle.ru
