Правила сокращенного умножения – «Исторические сведения Формулы сокращённого умножения Некоторые правила сокращённого умножения были известны еще около 4 тыс. лет тому назад. Их знали вавилоняне.». Скачать бесплатно и без регистрации.
Правила и формулы сокращенного умножения
Записи с меткой «Правила и формулы сокращенного умножения»
data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»2890988705″>
1) Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a+b)2 = a2+2ab+b2
a) (x + 2y)2 = x2 + 2 ·x·2y + (2y)2 = x2 + 4xy + 4y2
б) (2k + 3n)2 = (2k)2 + 2·2k·3n + (3n)2 = 4k2 + 12kn + 9n2
2) Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a-b)2 = a2-2ab+b2
а) (2a – c)2
б) (3a – 5b)2 = (3a)2-2·3a·5b + (5b)2 = 9a2 – 30ab + 25b2
3) Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.
a2–b2 = (a–b)(a+b)
a) 9x2 – 16y2 = (3x)2 – (4y)2 = (3x – 4y)(3x + 4y)
б) (6k – 5n)( 6k + 5n) = (6k)2 – (5n)2 = 36k2 – 25n2
4) Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a+b)3 = a3+3a2b+3ab2+b3
a) (m + 2n)3 = m3 + 3·m2·2n + 3·m·(2n)2 + (2n)3 = m3 + 6m2n + 12mn2 + 8n3
б) (3x + 2y)3 = (3x)3 + 3·(3x)2·2y + 3·3x·(2y)2 + (2y)3 = 27x3 + 54x2y + 36xy2 + 8y3
5) Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a-b)3 = a3-3a2b+3ab2-b3
а) (2x – y)3 = (2x)3-3·(2x)2·y + 3·2x·y2 – y3 = 8x3 – 12x2y + 6xy2 – y3
б) (x – 3n)3 = x3-3·x2·3n + 3·x·(3n)2 – (3n)3 = x3 – 9x2n + 27xn2 – 27n3
6) Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.
a3+b3 = (a+b)(a
a) 125 + 8x3 = 53 + (2x)3 = (5 + 2x)(52 — 5·2x + (2x)2) = (5 + 2x)(25 – 10x + 4x2)
б) (1 + 3m)(1 – 3m + 9m2) = 13 + (3m)3 = 1 + 27m3
7) Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.
a3-b3 = (a-b)(a2+ab+b2)
а) 64с3 – 8 = (4с)3 – 23 = (4с – 2)((4с)2 + 4с·2 + 22) = (4с – 2)(16с2 + 8с + 4)
б) (3a – 5b)(9a2
www.mathematics-repetition.com
Формулы сокращенного умножения
Формулы сокращенного умноженияФормулы сокращенного умножения применяются в математике, а точнее в алгебре, для быстрого получения результата некоторых алгебраических выражений. Получаются формулы сокращенного умножения из алгебраических правил умножения многочленов. Применение формул сокращенного умножения позволяет более быстро решать математические задачи, производить сокращение громоздких алгебраических выражений. Правила алгебры разрешают произвольно выполнять преобразования выражений по формулам сокращенного умножения: можно левую часть равенства представить в виде правой части или правую часть равенства преобразовать в виде левой части равенства. Формулы сокращенного умножения рекомендуется знать наизусть, поскольку они часто применяются при решении задач и уравнений по алгебре, математике. Наиболее часто встречаются первые три
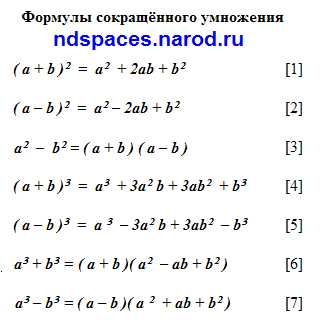
Рекомендуется сохранить приведенный рисунок на свой компьютер в качестве шпаргалки по математике, алгебре. Представленные на рисунке формулы не являются полным перечнем формул сокращенного умножения. В алгебре существуют и другие формулы сокращенного умножения и деления. Все эти формулы имеют свои собственные названия. Рассмотрим более подробно названия приведенных формул сокращенного умножения.
Первым [1] на картинке представлен квадрат суммы. Квадрат суммы равняется квадрату первого члена двучлена плюс удвоенное произведение первого члена на второй член двучлена плюс квадрат второго члена двучлена:
(a + b)² = a² + 2ab + b²
Вторая [2] формула сокращенного умножения называется квадрат разности.
(a — b)² = a² — 2ab + b²
В общем виде квадрат суммы и квадрат разности можно записать так:
(a ± b)² = a² ± 2ab + b²
Формула номер три [3] называется разность квадратов. Разность квадратов равняется сумме двух первых членов двучлена умноженной на разность первого и второго членов двучлена:
a² — b² = (a + b)·(a – b)
Четвертая [4] формула называется куб суммы. Куб суммы равняется сумме кубов первого и второго членов двучлена, утроенных произведений квадрата первого члена двучлена на второй и квадрата второго члена двучлена на первый:
(a + b)³ = a³ + 3a²b + 3b²a + b³
Пятая [5] формула похожа на куб суммы и называется куб разности. Куб разности равен кубу первого члена двучлена минус утроенное произведение квадрата первого члена двучлена на второй плюс утроенное произведение первого члена двучлена на квадрат второго минус куб второго члена двучлена:
(a — b)³ = a³ — 3a²b + 3b²a — b³
Одной формулой куб суммы и куб разности можно записать, используя знаки плюс-минус:
(a ± b)³ = a³ ± 3a²b + 3b²a ± b³
Шестая [6] формула называется сумма кубов. Сумма кубов равняется сумме первого и второго членов двучлена умноженной на квадрат первого члена двучлена минус произведение первого и второго членов двучлена плюс квадрат второго члена двучлена:
a³ + b³ = (a + b)·( a² — 2ab + b²)
Седьмая [7] формула похожа на предыдущую и называется разность кубов. Разность кубов равняется разности первого и второго членов двучлена умноженной на квадрат первого члена двучлена плюс произведение первого и второго членов двучлена плюс квадрат второго члена двучлена:
a³ — b³ = (a — b)·( a² + 2ab + b²)
Одной формулой куб суммы и куб разности можно записать, используя знаки плюс-минус и минус-плюс.
Если вам понравилась публикация и вы хотите знать больше, помогите мне в работе над другими материалами.
9 августа 2010 года — 28 февраля 2017 года.
© 2006 — 2018 Николай Хижняк. Все права защишены.
ndspaces.narod.ru
Дроби. Формулы сокращенного умножения
Факт 1.
\(\bullet\) Множество натуральных чисел \(\mathbb{N}\) – это числа \(1,
\ 2, \ 3, \ 4 \ \) и т.д.
\(\bullet\) Рациональные числа \(\mathbb{Q}\) – числа вида \(\dfrac ab\), где \(a\in \mathbb{Z}\), \(b\in \mathbb{N}\). Таким образом, существует включение: \(\mathbb{N}\) содержится в \(\mathbb{Z}\), а \(\mathbb{Z}\) содержится в \(\mathbb{Q}\).
Факт 2.
\(\bullet\) Правила сложения дробей: \[\begin{aligned} &\dfrac ab+\dfrac cb=\dfrac{a+c}b\\[2ex]
&\dfrac ab+\dfrac cd=\dfrac{ad+bc}{bd}\end{aligned}\] Пример: \(\dfrac {31}6+\dfrac {67}6=\dfrac{31+67}6=\dfrac{98}6\)
\(\bullet\) Правила умножения дробей: \[\dfrac ab\cdot \dfrac cd=\dfrac{ac}{bd}\] Пример: \(\dfrac 47\cdot \dfrac{14}5=\dfrac{4\cdot 14}{7\cdot 5}\)
\(\bullet\) Правила деления дробей: \[\dfrac ab: \dfrac cd=\dfrac ab\cdot \dfrac dc\] Пример: \(\dfrac 45 :\dfrac 67=\dfrac 45\cdot \dfrac 76\)
Факт 2.
\(\bullet\) Сокращение дробей – деление числителя и знаменателя на одно и то же число, отличное от нуля.
Пример:
\(\begin{aligned} &\dfrac{98}6=\dfrac{49\cdot
2\llap{/}}{3\cdot
2\llap{/}}=\dfrac{49}3\\[2ex]
&\dfrac{4\cdot 14}{7\cdot 5}=\dfrac{4\cdot 2\cdot
7\llap{/}}{7\llap{/}\cdot
5}=\dfrac 85\\[2ex]
&\dfrac{4\cdot 7}{5\cdot 6}=\dfrac {2\llap{/}\cdot 2\cdot 7}{5\cdot
3\cdot
2\llap{/}}=\dfrac{14}{15}\end{aligned}\)
\(\bullet\) Если \(\dfrac ab\) – несократимая дробь, то ее можно представить в виде конечной десятичной дроби тогда и только тогда, когда знаменатель \(b\) делится только на числа \(2\) и \(5\).
Пример: дробь \(\dfrac2{65}\) нельзя представить в виде конечной десятичной дроби, так как \(65=5\cdot 13\), то есть \(\dfrac2{65}=0,0307…\)
дробь \(\dfrac3{160}\) можно представить в виде конечной десятичной дроби, так как \(160=2^5\cdot 5\), то есть \(\dfrac3{160}=0,01875\).
Факт 3.
\(\bullet\) Формулы сокращенного умножения:
\(\blacktriangleright\) Квадрат суммы и квадрат разности: \[(a+b)^2=a^2+2ab+b^2\] \[(a-b)^2=a^2-2ab+b^2\]
\(\blacktriangleright\) Куб суммы и куб разности: \[(a+b)^3=a^3+3a^2b+3ab^2+b^3\quad {\small{\text{или}}}\quad (a+b)^3=a^3+b^3+3ab(a+b)\] \[(a-b)^3=a^3-3a^2b+3ab^2-b^3\quad {\small{\text{или}}}\quad (a-b)^3=a^3-b^3-3ab(a-b)\]
Заметим, что применение данных формул справа налево часто помогает упростить вычисления:
\(13^3+3\cdot 13^2\cdot 7+3\cdot 13\cdot 49+7^3=(13+7)^3=20^3=8000\)
\(\blacktriangleright\) Разность квадратов: \[a^2-b^2=(a-b)(a+b)\]
\(\blacktriangleright\) Сумма кубов и разность кубов: \[a^3+b^3=(a+b)(a^2-ab+b^2)\] \[a^3-b^3=(a-b)(a^2+ab+b^2)\]
Заметим, что не существует формулы суммы квадратов \(a^2+b^2\).
Заметим, что применение данных формул слева направо часто помогает упростить вычисления:
\(\dfrac{7^6-2^6}{7^4+14^2+16}= \dfrac{(7^2-2^2)(7^4+7^2\cdot2^2+2^4)} {7^4+(7\cdot2)^2+2^4}=7^2-2^2=45\)
Факт 4.
\(\bullet\) Квадрат суммы нескольких слагаемых равен сумме квадратов этих слагаемых и удвоенных попарных произведений: \[\begin{aligned}
&(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc\\[2ex]
&(a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd\\[2ex]
&{\small{\text{и т.д.}}}\end{aligned}\]
shkolkovo.net
Все формулы сокращенного умножения
Квадрат суммы
Квадрат разности
Разность квадратов
Куб суммы
Куб разности
Сумма кубов
Разность кубов
Разность n степеней
- Подробности
- Автор: Administrator
www-formula.ru
