Потока формула – Денежный поток (Cash Flow) — что это такое, определение и формула расчета, суть понятия, виды потоков

Содержание

Магнитный поток

Автор: Субботин Б.П.

На картинке показано однородное магнитное поле. Однородное означает одинаковое во всех точках в данном объеме. В поле помещена поверхность с площадью S. Линии поля пересекают поверхность.

Определение магнитного потока:

Магнитным потоком Ф через поверхность S называют количество линий вектора магнитной индукции B, проходящих через поверхность S.

Формула магнитного потока:

Ф = BS cos α

здесь α — угол между направлением вектора магнитной индукции B и нормалью к поверхности S.

Из формулы магнитного потока видно, что максимальным магнитный поток будет при cos α = 1, а это случится, когда вектор B параллелен нормали к поверхности S. Минимальным магнитный поток будет при cos α = 0, это будет, когда вектор B перпендикулярен нормали к поверхности S, ведь в этом случае линии вектора B будут скользить по поверхности S, не пересекая её.

А по определению магнитного потока учитываются только те линии вектора магнитной индукции, которые пересекают данную поверхность.

Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с. Кроме того, для измерения магнитного потока применяют максвелл: 1 вб = 108 мкс. Соответственно 1 мкс = 10-8 вб.

Магнитный поток является скалярной величиной.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА

Вокруг проводника с током существует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля. Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.

Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? — выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)

4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность

Основные формулы

·            Закон электромагнитной индукции (закон Фарадея):

,                                        (39)

где – эдс индукции;– полный магнитный поток (потокосцепление).

·            Магнитный поток, создаваемый током в контуре,

,                                               (40)

где  – индуктивность контура;– сила тока.

·            Закон Фарадея применительно к самоиндукции

.                                            (41)

·            Эдс индукции, возникающая при вращении рамки с током в магнитном поле,

,                                         (42)

где – индукция магнитного поля;– площадь рамки;– угловая скорость вращения.

·            Индуктивность соленоида

,                                             (43)

где – магнитная постоянная;– магнитная проницаемость вещества;– число витков соленоида;– площадь сечения витка;– длина соленоида.

·            Сила тока при размыкании цепи

 ,                                            (44)

где – установившаяся в цепи сила тока;– индуктивность контура,– сопротивление контура;– время размыкания.

·            Сила тока при замыкании цепи

.                                         (45)

·            Время релаксации

.                                                  (46)

Примеры решения задач

Пример 1.

Магнитное поле изменяется по закону , где= 15 мТл,. В магнитное поле помещен круговой проводящий виток радиусом = 20 см под угломк направлению поля (в начальный момент времени). Найти эдс индукции, возникающую в витке в момент времени= 5 с.

Решение

По закону электромагнитной индукции возникающая в витке эдс индукции , где–  магнитный поток, сцепленный в витке.

,

где – площадь витка,;– угол между направлением вектора магнитной индукциии нормалью к контуру:.

.

Подставим числовые значения: = 15 мТл,,= 20 см =   = 0,2 м,.

Вычисления дают .

 

Пример 2

В однородном магнитном поле с индукцией = 0,2 Тл расположена прямоугольная рамка, подвижная сторона которой длиной= 0,2 м перемещается со скоростью= 25 м/с перпендикулярно линиям индукции поля (рис. 42). Определить эдс индукции, возникающую в контуре.

Решение

При движении проводника АВ в магнитном поле площадь рамки увеличивается, следовательно, возрастает магнитный поток сквозь рамку и возникает эдс индукции.

По закону Фарадея ,  где, тогда, но, поэтому.

Так, .

Знак «–» показывает, что эдс индукции и индукционный ток направлены против часовой стрелки.

 

САМОИНДУКЦИЯ

Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.

При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.  Это явление называется самоиндукцией.Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции

Проявление явления самоиндукции

Замыкание цепи При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи ( вихревое поле тормозит электроны). В результате

Л1 загорается позже, чем Л2.

Размыкание цепи При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток ( стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи. В результате Л при выключении ярко вспыхивает. Вывод в электротехнике явление самоиндукции проявляется при замыкании цепи (эл.ток нарастает постепенно) и при размыкании цепи (эл.ток пропадает не сразу).

ИНДУКТИВНОСТЬ

От чего зависит ЭДС самоиндукции?  Эл.ток создает собственное магнитное поле . Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике (B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I). ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника  (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник. Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью. Индуктивность — физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду. Также индуктивность можно рассчитать по формуле:

где Ф — магнитный поток через контур, I — сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды  ( возможен сердечник).

ЭДС САМОИНДУКЦИИ

ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.

 

Для характеристики намагниченности вещества в магнитном поле используетсямагнитный момент (Рм). Он численно равен механическому моменту, испытываемому веществом в магнитном поле с индукцией в 1 Тл.

Магнитный момент единицы объема вещества характеризует его намагниченность — I, определяется по формуле:

I= Рм /V, (2.4)

где V — объем вещества.

Намагниченность в системе СИ измеряется, как и напряженность, в А/м, величина векторная.

Магнитные свойства веществ характеризуются объемной магнитной восприимчивостью — cо , величина безразмерная.

Если какое-либо тело поместить в магнитное поле с индукцией В

0, то происходит его намагничивание. Вследствие этого тело создает свое собственное магнитное поле с индукцией В‘, которое взаимодействует с намагничивающим полем.

В этом случае вектор индукции в среде (В)будет слагаться из векторов:

В = В0 + В‘(знак вектора опущен), (2.5)

где В‘ —индукция собственного магнитного поля намагнитившегося вещества.

Индукция собственного поля определяется магнитными свойствами вещества, которые характеризуются объемной магнитной восприимчивостью — cо , справедливо выражение:В‘ = cо В0 (2.6)

Разделим на m0 выражение (2.6):

В‘/ mо= cо В0 /m0

Получим: Н‘ = cо Н0 , (2.7)

но Н‘ определяет намагниченность вещества I, т.е. Н‘ = I, тогда из (2.7):

I = cо Н0. (2.8)

Таким образом, если вещество находится во внешнем магнитном поле с напряженностьюН0, то внутри него индукция определяется выражением:

В=В0 + В‘ = m0Н0 +m0Н‘ = m0 (Н0 + I) (2.9)

 

Последнее выражение строго справедливо, когда сердечник (вещество) находится полностью во внешнем однородном магнитном поле (замкнутый тор, бесконечно длинный соленоид и т.д.).

studfiles.net

Магнитный поток и электромагнитная индукция: физические формулы

Среди физических величин важное место занимает магнитный поток. В этой статье рассказывается о том, что это такое, и как определить его величину.

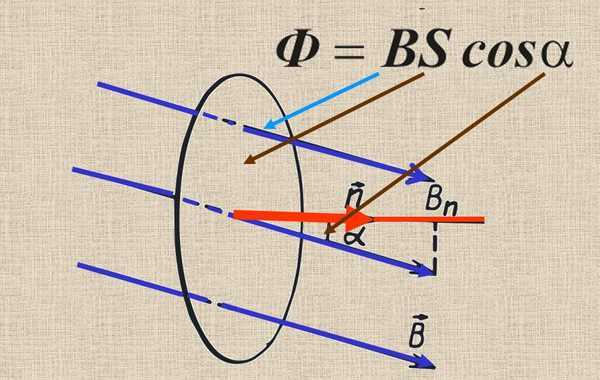
Формула магнитного потока

Что такое магнитный поток

Это величина, определяющая уровень магнитного поля, проходящего через поверхность. Обозначается «ФФ» и зависит от силы поля и угла прохождения поля через эту поверхность.

Рассчитывается она по формуле:

ФФ=B⋅S⋅cosα, где:

  • ФФ – магнитный поток;
  • В – величина магнитной индукции;
  • S – площадь поверхности, через которую проходит это поле;
  • cosα – косинус угла между перпендикуляром к поверхности и потоком.

Единицей измерения в системе СИ является «вебер» (Вб). 1 вебер создаётся  полем величиной 1 Тл, проходящим перпендикулярно поверхности площадью 1 м².

Таким образом, поток максимален при совпадении его направления с вертикалью и равен «0», если он параллелен с поверхностью.

Интересно. Формула магнитного потока аналогична формуле, по которой рассчитывается освещённость.

Постоянные магниты

Одним из источников поля являются постоянные магниты. Они известны много веков. Из намагниченного железа изготавливалась стрелка компаса, а в Древней Греции существовала легенда об острове, притягивающем к себе металлические части кораблей.

Постоянные магниты есть различной формы и изготавливаются из разных материалов:

  • железные – самые дешёвые, но обладают меньшей притягивающей силой;
  • неодимовые – из сплава неодима, железа и бора;
  • альнико – сплав железа, алюминия, никеля и кобальта.

Все магниты являются двухполюсными. Это заметнее всего в стержневых и подковообразных устройствах.

Если стержень подвесить за середину или положить на плавающий кусочек дерева или пенопласта, то он развернётся по направлению «север-юг». Полюс, показывающий на север, называют северным и на лабораторных приборах красят в синий цвет и обозначают «N». Противоположный, показывающий на юг, – красный и обозначен » S». Одноимёнными полюсами магниты притягиваются, а противоположными – отталкиваются.

В 1851 году Майкл Фарадей предложил понятие о замкнутых линиях индукции. Эти линии выходят из северного полюса магнита, проходят по окружающему пространству, входят в южный и внутри устройства возвращаются к северному. Ближе всего линии и напряжённость поля у полюсов. Здесь также выше притягивающая сила.

Если на устройство положить кусок стекла, а сверху тонким слоем насыпать железные опилки, то они расположатся вдоль линий магнитного поля. При расположении рядом нескольких приборов опилки покажут взаимодействие между ними: притяжение или отталкивание.

Магнит и железные опилки

Магнитное поле Земли

Нашу планету можно представить в виде магнита, ось которого наклонена на 12 градусов. Пересечения этой оси с поверхностью называют магнитными полюсами. Как и у любого магнита, силовые линии Земли идут от северного полюса к южному. Возле полюсов они проходят перпендикулярно поверхности, поэтому там стрелка компаса ненадёжна, и приходится использовать другие способы.

Частицы «солнечного ветра» имеют электрический заряд, поэтому при движении вокруг них появляется магнитное поле, взаимодействующее с полем Земли и направляющее эти частицы вдоль силовых линий. Тем самым это поле защищает земную поверхность от космической радиации. Однако возле полюсов эти линии направлены перпендикулярно поверхности, и заряженные частицы попадают в атмосферу, вызывая северное сияние.

Электромагниты

В 1820 году Ганс Эрстед, проводя эксперименты, увидел воздействие проводника, по которому протекает электрический ток, на стрелку компаса. Через несколько дней Андре-Мари Ампер обнаружил взаимное притяжение двух проводов, по которым протекал ток одного направления.

Интересно. Во время электросварочных работ рядом расположенные кабеля двигаются при изменении силы тока.

Позже Ампер предположил, что это связано с магнитной индукцией тока, протекающего по проводам.

В катушке, намотанной изолированным проводом, по которому протекает электрический ток, поля отдельных проводников усиливают друг друга. Для увеличения силы притяжения катушку наматывают на незамкнутом стальном сердечнике. Этот сердечник намагничивается и притягивает железные детали или вторую половину сердечника в реле и контакторах.

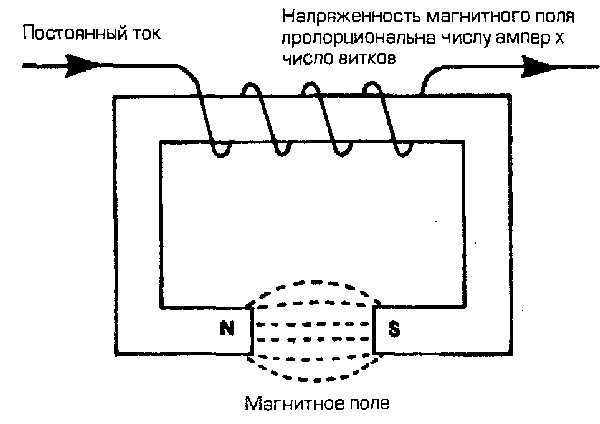
Электромагниты

Электромагнитная индукция

При изменении магнитного потока в проводе наводится электрический ток. Этот факт не зависит от того, какими причинами было вызвано это изменение: перемещением постоянного магнита, движением провода или изменением силы тока в рядом расположенном проводнике.

Это явление было открыто Майклом Фарадеем 29 августа 1831 года. Его эксперименты показали, что ЭДС (электродвижущая сила), появляющаяся в контуре, ограниченном проводниками, прямопропорциональна скорости изменения потока, проходящего через площадь этого контура.

Важно! Для возникновения ЭДС провод должен пересекать силовые линии. При движении вдоль линий ЭДС отсутствует.

Если катушка, в которой возникает ЭДС, включена в электрическую цепь, то в обмотке возникает ток, создающий в катушке индуктивности своё электромагнитное поле.

Правило правой руки

При движении проводника в магнитном поле в нём наводится ЭДС. Её направленность зависит от направления движения провода. Метод, при помощи которого определяется направление магнитной индукции, называется «метод правой руки».

Правило правой руки

Расчёт величины магнитного поля важен для проектирования электрических машин и трансформаторов.

Видео

Оцените статью:

elquanta.ru

Поток векторного поля. Формула Гаусса-Остроградского

Пусть в области задано некоторое векторное поле , где – непрерывно дифференцируемые в области функции. Пусть – гладкая ориентированная поверхность, на которой выбрана одна из сторон, задаваемая единичным вектором нормали* ( –направляющие косинусы этого вектора).

Потоком векторного поля через поверхность называется поверхностный интеграл

 

. (4.16)

Поверхностный интеграл 1-го рода в формуле (4.16) может быть выражен через поверхностный интеграл 2-го рода:

, (4.17)

что дает еще один способ вычисления потока.

Понятие потока вектора взято из гидродинамики. В гидродинамике рассматривается векторное поле скорости текущей жидкости . Поток этого векторного поля дает объем жидкости, протекающей через поверхность за единицу времени.

Если – замкнутая поверхность, являющаяся границей тела , то имеет место формула Гаусса – Остроградского:

, (4.18)

(интеграл от дивергенции векторного поля по некоторому объему равен потоку этого поля через поверхность , ограничивающую данный

объем). Эта формула часто используется для вычисления потока векторного поля через замкнутую поверхность.

 

*) Нормаль к поверхности в некоторой ее точке – прямая, проходящая через и перпендикулярная к касательной плоскости в этой точке.

 

 

Формула Гаусса – Остроградского позволяет выразить следующей формулой:

 

= , (4.19)

которую правильнее всего и считать определением понятия дивергенция: дивергенция вектора в данной точке поля есть предел, к которому стремится отношение потока вектора через произвольную, окружающую эту точку, поверхность к величине ограниченного этой поверхностью объема (при ).

Формула (4.19), определяющая дивергенцию, в гидродинамике имеет непосредственный физический смысл: дивергенция скорости жидкости = равна рассчитанному на единицу объема количеству жидкости, вытекающей в единицу времени из элемента объема , окружающего рассматриваемую точку. Название «дивергенция», что значит по-латыни расхождение или расходимость, было выбрано для этой величины именно потому, что жидкость растекается или расходится из тех и только из тех точек или участков занимаемого ею пространства, в которых .Очевидно, что в этих точках должны быть расположены источники жидкости. По аналогии, те точки произвольного векторного поля , в которых , принято называть истоками этого поля. Численная же величина называется силой, или обильностью, истоков поля; в зависимости от знака дивергенции сила истоков может быть как положительной, так и отрицательной. Иногда отрицательным истокам поля дают название стоков поля. Векторные поля, у которых , называются свободными от источников, или соленоидальными (трубчатыми).

 

Пример. Вычислить поток векторного поля через часть плоскости, заданной уравнением , расположенную в октанте , если единичный вектор нормали к рассматриваемой поверхности образует острый угол с осью .

◄ Вычислим поток при помощи формулы (4.17). Учитывая, что для данного векторного поля , будем иметь . Последний интеграл вычислим сведением его к двойному по области (рис.2), являющуюся проекцией поверхности на плоскость . Так как единичная нормаль образует с осью тупой угол (это очевидно из рис. 2) и, следовательно, , перед двойным интегралом необходимо

 

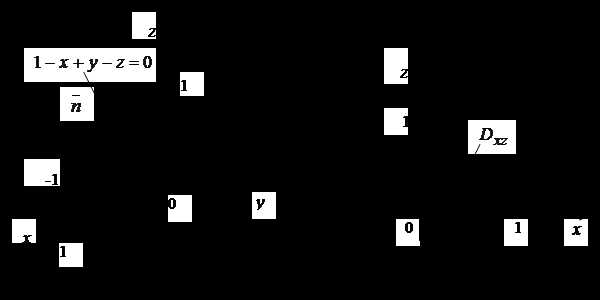
поставить знак минус: =

. ►

 

Пример. Положительный электрический заряд , помещенный в начале координат, создает векторное поле, напряженность которого в каждой точке пространства определяется законом Кулона: , где – постоянный коэффициент, величина которого зависит от выбора системы единиц измерения, – радиус-вектор точки пространства. Найти поток этого векторного поля через сферу радиуса с центром в начале координат.

◄ Так как , будем иметь =

= . Скалярное произведение в последнем интеграле равно 1, т. к. единичные векторы и в каждой точке сферы совпадают. Следовательно, (площадь поверхности (сферы)). Окончательно, поток . ►

 


Похожие статьи:

poznayka.org

Денежный поток: формула и методы расчета

Оптимизация финансовых, производственных и инвестиционных процессов немыслима без качественного анализа. На основе данных проведенных исследований и отчетов проводится процесс планирования, устраняются неблагоприятные, сдерживающие развитие факторы.

Одним из видов оценки эффективности финансовой деятельности является расчет денежного потока. Формула и особенности применения этой методики будут представлены далее.

Цель анализа

Формула денежного потока рассчитывается в соответствии с определенными методиками. Целью проведения подобного анализа является определение источников поступления денежных средств в организацию, а также их расхода для расчета дефицита или избытка денег за исследуемый период.

Для осуществления подобного исследования на предприятии формируется отчет о движении денежных средств. Также составляется соответствующая смета. При помощи подобных документов можно определить, достаточно ли для организации полноценной инвестиционной, финансовой деятельности компании существующих в наличии денежных средств.

Проводимое исследование позволяет определить, зависима ли организация от внешних источников капитала. Также анализируется динамика поступления и выбытия средств в разрезе каждого вида деятельности. Это позволяет выработать дивидендную политику, спрогнозировать ее в будущем периоде. Анализ денежного потока имеет целью определить фактическую платежеспособность организации, а также ее прогноз в краткосрочной перспективе.

Что дает расчет?

Денежный поток, формула расчета которого представлена в различных методиках, требует правильного анализа для возможности эффективного управления. В случае проведения представленного исследования организация получает возможность соблюдать сбалансированность своих финансовых средств в текущем и плановом периоде.

Денежные потоки должны быть синхронизованы по своему времени поступления и объему. Благодаря этому можно добиться хороших показателей развития компании, ее финансовой стабильности. Высокая степень синхронизации входных и исходящих потоков позволяет ускорить выполнение задач в стратегической перспективе, снизить потребность в платных (кредитных) источниках финансирования.

Управление потоками финансов позволяет оптимизировать расход денежных ресурсов. Уровень риска в этом случае сокращается. Эффективное управление позволит избежать неплатежеспособности компании, повысить финансовую стойкость.

Классификация

Существует 8 основных критериев, по которым можно сгруппировать денежные потоки по категориям. Беря во внимание методику, по которой производилось исчисление, различают валовой и чистый денежный поток. Формула для первого подхода предполагает суммировать все денежные потоки предприятия. Вторая методика учитывает разность между доходами и расходами.

По масштабу влияния на хозяйственную деятельность организации различают общий для компании поток, а также его составляющие (по каждому подразделению и экономическим операциям).

По видам деятельности различают производственную (операционную), финансовую и инвестиционную группы. По направлению движения различают положительный (поступивший) и отрицательный (выбывший) поток.

Рассматривая достаточность средств, различают избыток и дефицит средств. Расчет может производиться в текущем или плановом периоде. Также потоки могут классифицировать на дискретную (единоразовую) и регулярную группы. Капитал может поступать и выбывать из организации с одинаковым интервалом времени или хаотично.

Чистый поток

Одним из ключевых показателей в представленном анализе является чистый денежный поток. Формула этого коэффициента применяется при инвестиционном анализе деятельности. Она дает исследователю информацию о финансовом состоянии компании, ее способности увеличивать свою рыночную стоимость, привлекательность для инвесторов.

Чистый денежный поток рассчитывается как разность между поступившими и выбывшими из организации финансами за выбранный промежуток времени. Это фактически сумма между показателями финансовой, операционной и инвестиционной деятельности.

Информацию о размере и характере этого показателя применяют при принятии стратегических решений собственники организации, инвесторы и кредитные компании. При этом становится возможным рассчитать, целесообразно ли вкладывать средства в деятельность конкретного предприятия или в подготовленный проект. Представленный коэффициент учитывается при проведении расчетов стоимости предприятия.

Управление потоками

Коэффициент денежного потока, формула которого применяется при расчетах практически всеми крупными организациями, позволяет эффективно управлять финансовыми потоками. Для расчетов потребуется определить величину поступивших и выбывших средств за установленный период, основные их составляющие. Также разбивку выполняют в соответствии с видом деятельности, которая генерирует определенное движение капитала.

Расчет показателей может производиться двумя способами. Их называют косвенным и прямым методом. Во втором случае в расчет берут данные счетов организации. Основополагающим компонентом для проведения подобного исследования является показатель выручки от реализации.

Методика косвенного расчета предполагает использовать для анализа статьи бухгалтерского баланса, а также отчета о доходах и расходах предприятия. Для аналитиков этот способ является более информативным. Он позволит определить связь между прибылью в исследуемом периоде и количеством денег предприятия. Влияние изменения активов баланса на показатель чистой прибыли также получится рассмотреть при использовании представленной методики.

Прямой расчет

Если расчет производится в конкретный момент операционного периода, определяется текущий денежный поток. Формула его достаточно проста:

ЧДП = ЧПО + ЧПФ + ЧПИ, где ЧПД – чистый денежный поток в исследуемом периоде, ЧПО – поток от операционной деятельности, ЧПФ – от финансовых операций, ЧПИ – в разрезе инвестиционной деятельности.

Чтобы определить чистый показатель денежного потока необходимо воспользоваться формулой:

ЧПД = ВДП – ИДП, где ВДП – входящий поток денег, ИДП – исходящий поток средств.

При этом расчет производят для одного или нескольких расчетных периодов. Это простая формула. Составляющие от каждого типа деятельности необходимо рассчитывать отдельно. При этом необходимо учесть все составляющие.

Расчет чистого инвестиционного потока

Основная масса средств организации, находящаяся в распоряжении компании в данный момент, поступает от операционного денежного потока. Формула расчета чистого показателя движения средств (была представлена выше) обязательно учитывает эту величину.

Чтобы рассчитать показатель ЧПИ применяется определенная формула:

ЧПИ = ВОС + ПНА + ПДФА + РА + ДП – ПОС + ОНП – ПНА – ПДФА – ВСА, где ВОС – выручка, полученная от использования основных средств, ПНА – доход от продажи нематериальных активов, ПДФА – доход от продажи долгосрочных финансовых активов, РА – доход за реализацию акций, ДП – проценты и дивиденды, ПОС – приобретенные основные средства, ОНП – остаток незавершенного производства, ПНА – покупка нематериальных активов, ПДФА – покупка долгосрочных финансовых активов, ВСА – величина выкупленных собственных акций.

Расчет чистого финансового потока

Формула денежного потока применяет в себе данные о чистом финансовом потоке. Расчет производят по такой формуле:

ЧПФ = ДВФ + ДДКР + ДККР + БЦФ – ВДКД – ВККД – ДА, где ДВФ – дополнительное внешнее финансирование, ДДКР – дополнительно привлекаемые долгосрочные кредиты, ДККР – дополнительно привлекаемые краткосрочные кредиты, БЦФ – безвозвратное целевое финансирование, ВДКД – выплаты долга по долгосрочным кредитам, ВККД – выплаты по краткосрочным кредитам, ДА – дивидендные выплаты акционерам.

Косвенный метод

Косвенный метод расчета также позволяет определить чистый денежный поток. Формула по балансу предполагает проведение корректировок. Для этого применяются данные об амортизации, изменения структуры и количества текущих пассивов и активов.

Расчет чистой прибыли от операционной деятельности производится по следующей формуле:

ЧПО = ЧП + АОС + АНА – ДЗ – З – КЗ + РФ, где ЧП – чистая прибыль предприятия, АОС – амортизация основных средств, АНА – амортизация нематериальных активов, ДЗ – изменение дебиторской задолженности в исследуемом периоде, З – изменение запасов, КЗ – изменение количества кредиторской задолженности, РФ – изменение показателя резервного капитала.

На показатель чистого денежного потока прямо влияют изменения в стоимости текущих пассивов и активов компании.

Свободный денежный поток

Некоторые аналитики применяют в процессе изучения финансового состояния организации показатель свободного денежного потока. Формула расчета представленного показателя рассматривается в двух основных аспектах. Различают свободный денежный поток фирмы и капитала.

В первом случае рассматривается показатель операционной деятельности компании. Из него вычитают инвестиции в основной капитал. Этот показатель предоставляет информацию аналитику о количестве финансов, которые остаются в распоряжении компании после вложений капитала в активы. Представленная методика применяется инвесторами для определения целесообразности финансирования деятельности компании.

Свободный денежный поток капитала предполагает вычитать из общего количества финансов предприятия только собственные вложения средств. Этот расчет применяется чаще всего акционерами компании. Эту методику применяют в процессе оценки акционерной стоимости организации.

Дисконтирование

Чтобы сопоставить будущие финансовые платежи с текущим состоянием стоимости, применяется методика дисконтирования. Эта методика учитывает, что в перспективе деньги постепенно теряют свою стоимость относительно текущего состояния цены. Поэтому в анализе применяется дисконтированный денежный поток. Формула при этом содержит специальный коэффициент. Он умножается на сумму финансового потока. Это позволяет соотнести расчет с современным уровнем инфляции.

Коэффициент дисконтирования определяется по формуле:

К = 1/(1 + СД)ВП, где СД – ставка дисконтирования, ВП – временной период.

Ставка дисконтирования является одним из важнейших элементов при расчете. Она характеризует, какой доход получит инвестор при вложении своих средств в определенный проект. Этот показатель содержит в себе информацию об инфляции, прибыльность в разрезе безрисковых операций, прибыль от повышения риска. Также при расчетах учитывают ставку рефинансирования, стоимость (средневзвешенную) капитала, депозитные проценты.

Подходы к оптимизации

При определении финансового состояния организации в расчет берут дисконтируемый денежный поток. Формула может не учитывать этого расчета, если показатель приводится в краткосрочной перспективе.

Процесс оптимизации денежного потока предполагает установления баланса между расходами и доходами компании. Дефицит и избыток отрицательно влияют на финансовое состояние и стабильность организации.

При появлении дефицита денежных средств уменьшаются показатели ликвидности. Платежеспособность также становится низкой. Избыток средств влечет за собой фактическое обесценивание временно незадействованных средств из-за инфляции. Поэтому руководство компании должно сбалансировать величину входящих и исходящих потоков.

Рассмотрев, что собой представляет денежный поток, формулу его определения, можно принять решения в вопросе оптимизации этого показателя.

fb.ru

Формула чистого денежного потока и примеры

Понятие чистого денежного потока

С помощью этого показателя можно определить финансовое состояние любой компании, включая ее способность к увеличению собственной стоимости и инвестиционной привлекательности.

Формула чистого денежного потока включает в себя сумму денежного потока от нескольких видов деятельности, среди которых:

  • Операционная.
  • Финансовая,
  • Инвестиционная.

Формула чистого денежного потока

Существует 2 варианта расчета формулы чистого денежного потока. В первом случае формула чистого денежного потока рассчитывается путем суммирования всех потоков компании со знаком плюс и минус (приток и отток):

NCF = ∑ (CI+ — CO—)

ЗдесьNCF – величина чистого денежного потока,

CI – входящий денежный поток (положительная величина)

CO – отток денежных средств (отрицательная величина).

Если расписать чистый поток подробно в соответствии с видами деятельности компании, то формула чистого денежного потока примет вид:

NCF = CFO + CFF + CFI

Здесь CFO – денежные потоки операционной деятельности,

CFF – денежные потоки финансовой деятельности

CFI – денежные потоки инвестиционной деятельности

Норматив показателя чистого денежного потока

Можно рассмотреть три ситуации состояния значения денежного потока. При этом, чем выше его значение, тем больше привлекательности для потенциальных инвесторов заключается в реализации проекта.

Значение показателя чистого денежного потока может быть:

  • Больше нуля, что говорит о высокой привлекательности проекта для инвестиций,
  • Меньше или равен нулю, что говорит о необходимости отклонения проекта, поскольку он не увеличит свою денежную стоимость,
  • Если показатель одного проекта (предприятия) больше, чем другого, то это говорит, что тот проект, который обладает большей привлекательностью, является более выгодным.

Значение чистого денежного потока

Формула чистого денежного потока применяется при оценке эффективности вложений в определенные инвестиционные проекты следующими лицами:

  • Инвесторы,
  • Кредиторы,
  • Собственники компании.

Определение показателя чистого денежного потока также используют в процессе оценки стоимости самой компании. Поскольку почти все проекты для инвестирования имеют продолжительный срок реализации, их будущие денежные потоки необходимо привести к стоимости на настоящий момент(дисконтировать).

Для краткосрочных проектов можно пренебречь дисконтированием при расчете его стоимости.

Примеры решения задач

ru.solverbook.com

2.2. Расчет основных параметров потока.

Основными параметрами потока любого типа является:

  • такт-;

  • впуск изделий в смену — М;

  • количество рабочих- N;

  • Количество рабочих мест- ;

  • Длина поточной линии-;

  • Площадь потока-S;

Такт потока — это среднее время выполнение одной организационной операции, которое приходится на одного рабочего и является расчетным отрезком времени, а также средним промежутком времени между запуском двух следующих друг за другом изделий в потоке или выпуском двух следующих друг за другом изделий с потока.

Такт потока определяется по формуле:

= ,с.(1)

где: — трудоемкость изготовления изделия, с;R- продолжительность рабочей смены, с (28800с).

Выпуск изделий в смен у — и количество изделий, выпускаемое одним потоком за смену. Определяется по формуле:

М= , ед/смену.(2)

Количество рабочих — число рабочих потока. Определяется по формуле:

N==, чел. (3)

где: — санитарная норма площади на одного рабочего. Определяется в зависимости от вида изделия, типа транспортного средства и секции потока.

Количество рабочих мест – показатель, определяющий общее количество рабочих мест в потоке с учетом запасного оборудования и нестандартных рабочих мест. Рассчитывается по формуле

= NK, р.м. (4)

где: К — коэффициент, показывающий, сколько в среднем рабочих мест приходится на одного рабочего.

Длина поточной линии определяется по формуле:

L=N, м (5)

где: — шаг рабочего места — расстояние от начало одного рабочего места до начало следующего рабочего места, м.

Площадь потока определяется по формуле:

S=N (6)

Отчет по работе должен содержать все таблицы, эскизы и описания, расчеты и выводы. При выполнении лабораторной работы необходимо воспользоваться предложениями ниже литературными источниками.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

  1. Типовая техническая документация, нормативно — техническая документация по изготовлению швейных изделий.

  2. Мурыгин В.Е. и др. Основные функционирования технологических процессов швейного производства.

  3. Изместьева В.Я. и др. Проектирование предприятий швейной промышленности.

studfiles.net

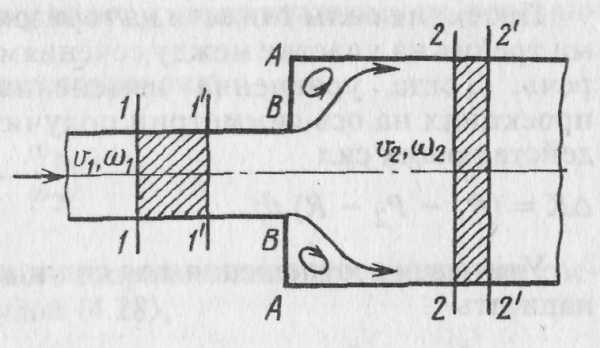
25. Внезапное расширение потока. Формула Борда-Хуи.

Выделим контроль­ный объем, ограниченный сечениями 1—1 и 2—2 и боковыми цилиндрическими поверхностями. Масса жидкости, заключенная в этом объеме, переместится за время dt и займет поло­жение между сечениями 1′-1’и 2′-2′.

Применим закон изме­нения количества движе­ния для выделенного объема жидкости за время dt. В силу установившего­ся движения количество движения массы жидкости в объеме между сечениями 1′-1’и 2′-2′ остается по­стоянным и изменение ко­личества движения массы

во всем контрольном объеме за время dt будет равняться разности значений количества движения в объеме между сечениями 2-2 — 2′-2′ ив объеме 1—1 и 1’—1’. Поэтому, обозначив изменение коли­чества движения 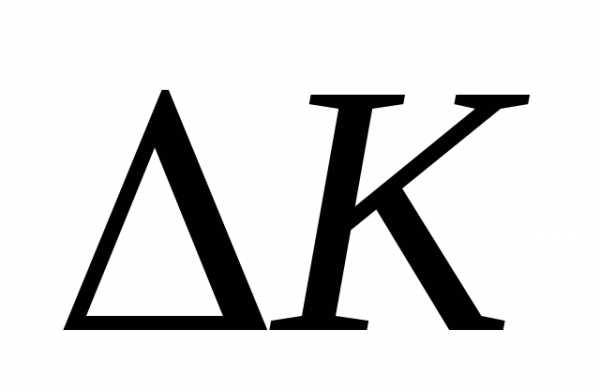, можно записать

(4.29)

считая, что распределение скоростей в соответствующих сечениях равномерное и равно средним значениям скорости. Значение масс т2 и 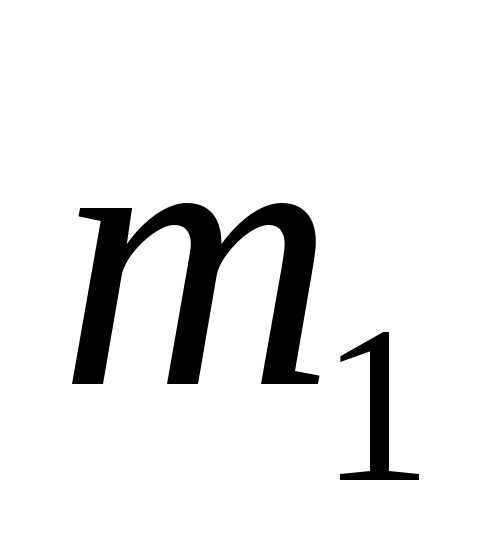можно записать в виде

Таким образом, равенство (4.29) запишем так

(4.30)

Составим сумму импульсов сил, действующих на выделенный объем жидкости в проекциях на ось симметрии трубопровода. Силы давления на торцовые поверхност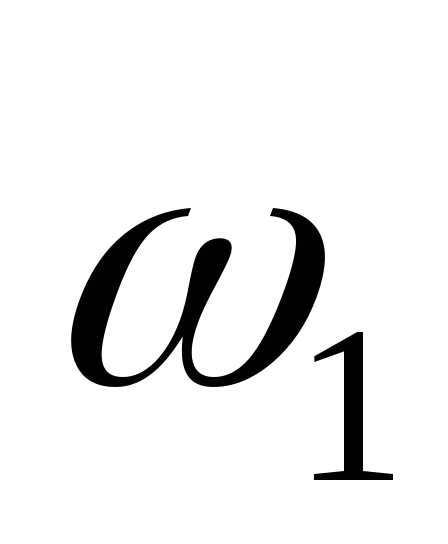и 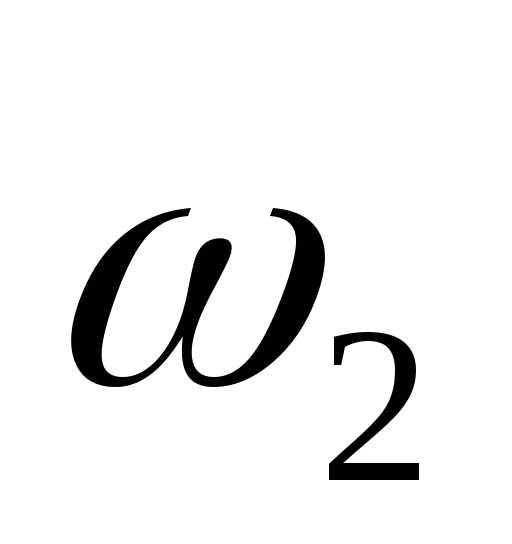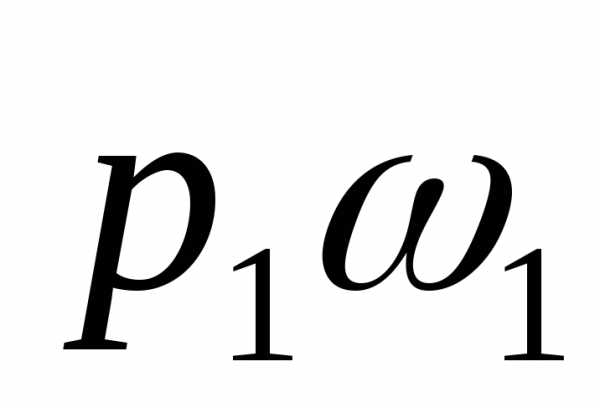и

=и

Проекции сил давления, действующих на боковую поверхность, равны нулю, а сила реакции стенки трубы в виде кольцевого сечения АВ—В А будет равна

Продолжение 25

если принять давление на кольцевую поверхность постоянным и рав­ным р1.

Проекция силы тяжести на горизонтальную равна нулю. Сила­ми трения на участке между сечениями 1—1 и 2—2 можно пренеб­речь. Тогда уравнение изменения количества движения в проекциях на ось симметрии получит вид с учетом направления действующих сил

Учитывая соотношения для сил и количества движения, можем написать

Раскрыв скобки и приведя подобные члены, получаем

Заметив, что из условия неразрывности , последнее ра­венство запишем так

(4.31)

Уравнение (4.31) позволяет определить разность давлений при внезапном расширении. Определим эту же разность давлений из уравнения Бернулли.

Напишем уравнение Бернулли для сечений 1—/ и 2—2:

Продолжение 25Отсюда, приняв а1=а2 = 1

При сопоставлении этого уравнения с уравнением (4.31) легко видеть, что потеря напора h1-2 на участке от первого сечения до вто­рого, т.е. местные потери напора на внезапном расширении hвр будут равны

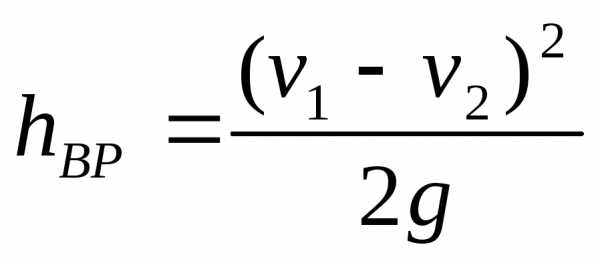
Полученная зависимость называется формулой Борда, которая словами формулируется так: потеря напора при внезапном расширении потока равна скоростному напору, подсчитанному по потерянной скорости.

26. Сложение потерь напора. Эквивалентная длина местного сопротивления.

Во многих случаях в трубопроводах существуют одновременно как потери напора на трение по длине, так местные; полная потеря напора в этих случаях равняется арифметической тех и других потерь. Например, полная потеря напора в трубопроводе длиной l, диаметром d, имеющим n местных сопротивлений, равна

или

Величину

называют коэффициентом сопротивления системы и обозначают через

Таким образом

При суммировании потерь на местных сопротивлениях удобно использовать понятие «эквивалентная длина»

Эквивалентной называется длина прямого участка трубопровода данного диаметра, на которой потеря напора на трение по длине 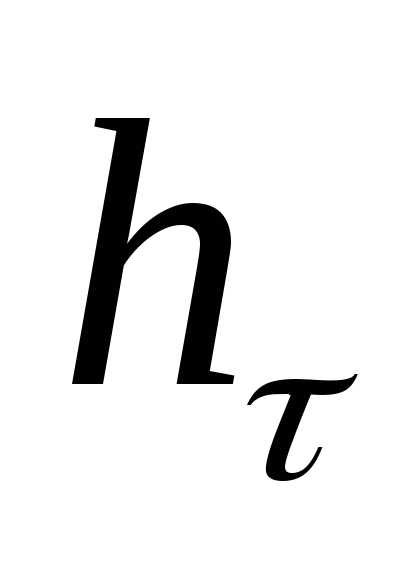равняется потере напора, вызываемой данным местным сопротивлением.

Продолжение 26 Выражение эквивалентной длины lэкв может быть установлено из сопоставления выражения для потерь напора по длине (формулы Дарси-Вейсбаха)

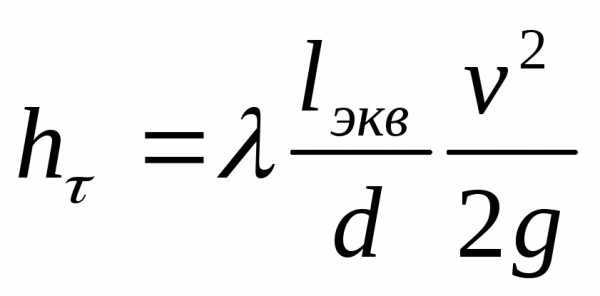
и выражения для местных потерь (Формула Вейсбаха)

Следовательно при условии 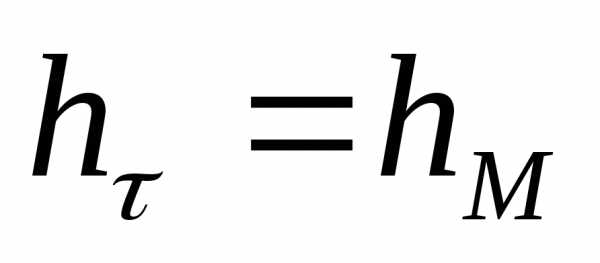должно быть

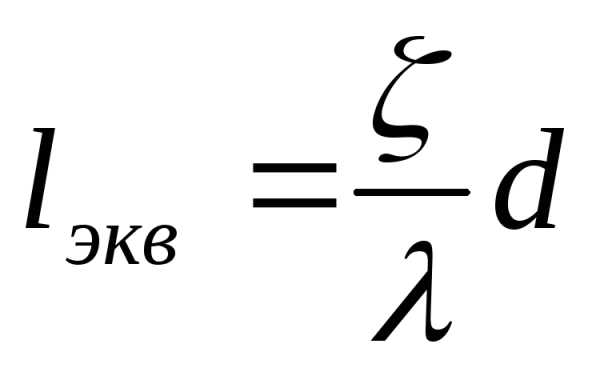
Если n учасков трубопровода, то

studfiles.net

РубрикаПолезно знать

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *