Последовательность математическая – Числовая последовательность — Википедия
ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ | Энциклопедия Кругосвет
Содержание статьиЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ – функция вида y = f(x), x О N, где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y1, y2,…, yn,…. Значения y1, y2, y3,… называют соответственно первым, вторым, третьим, … членами последовательности.
Например, для функции y = n2 можно записать:
y1 = 12 = 1;
y2 = 22 = 4;
y3 = 32 = 9;…yn = n2;…
Способы задания последовательностей. Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.
1. Последовательность задана аналитически, если задана формула ее n-го члена:
yn = f(n).
Пример. yn= 2n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …
2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.
Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….
Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.
3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. Название рекуррентный способ происходит от латинского слова recurrere – возвращаться. Чаще всего в таких случаях указывают формулу, позволяющую выразить n-й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.
Пример 1. y1
Здесь y1 = 3; y2 = 3 + 4 = 7; y3 = 7 + 4 = 11; ….
Можно видеть, что полученную в этом примере последовательность может быть задана и аналитически: yn = 4n – 1.
Пример 2. y1 = 1; y2 = 1; yn = yn–2 + yn–1 , если n = 3, 4,….
Здесь: y1 = 1; y2 = 1; y3 = 1 + 1 = 2; y4 = 1 + 2 = 3;
Последовательность, составленную в этом примере, специально изучают в математике, поскольку она обладает рядом интересных свойств и приложений. Ее называют последовательностью Фибоначчи – по имени итальянского математика 13 в. Задать последовательность Фибоначчи рекуррентно очень легко, а аналитически – очень трудно. n-е число Фибоначчи выражается через его порядковый номер следующей формулой .
На первый взгляд, формула для n-го числа Фибоначчи кажется неправдоподобной, так как в формуле, задающей последовательность одних только натуральных чисел, содержатся квадратные корни, но можно проверить «вручную» справедливость этой формулы для нескольких первых
Свойства числовых последовательностей.
Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.
Определение. Последовательность {yn} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:
y1y2y3ynyn+1
Определение. Последовательность {yn} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:
y1 > y2 > y
Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.
Пример 1. y1 = 1; yn = n2– возрастающая последовательность.
Пример 2. y1 = 1; – убывающая последовательность.
Пример 3. y1 = 1; – эта последовательность не является не возрастающей не убывающей.
Определение. Последовательность называется периодической, если существует такое натуральное число T, что начиная с некоторого n, выполняется равенство
Пример. Последовательность периодична с длиной периода T = 2.
Арифметическая прогрессия.
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.
Таким образом, арифметическая прогрессия – это числовая последовательность {an}, заданная рекуррентно соотношениями
a1 = a, an = an–1 + d (n = 2, 3, 4, …)
(a и d – заданные числа).
Пример. 1, 3, 5, 7, 9, 11, … – возрастающая арифметическая прогрессия, у которой a1 = 1, d = 2.
Пример. 20, 17, 14, 11, 8, 5, 2, –1, –4,… – убывающая арифметическая прогрессия, у которой a1 = 20, d = –3.
Нетрудно найти явное (формульное) выражение anчерез n. Величина очередного элемента возрастает на d по сравнению с предыдущим, таким образом, величина n элемента возрастет на величину (n – 1)d по сравнению с первым членом арифметической прогрессии, т.е.
an
Это формула n-го члена арифметической прогрессии.
Используя явное выражение anчерез n, можно доказать следующее свойство арифметической прогрессии: если натуральные числа i, j, k, l таковы, что i + j = k + l, то ai + aj= ak + al. Чтобы в этом убедиться, достаточно подставить i, j, k и l вместо n в формулу n-го члена арифметической прогрессии и сложить. Отсюда следует, что если рассматривать первые
a1 + an = a2 + an–1 = a3 + an–2 = … = 2a1 + (n – 1)d.
Последнее равенство позволяет вычислить сумму первых n членов арифметической прогрессии:
Sn = a1 + a2 + … + an–1 + an.
С этой целью берется еще одна такая же сумма, но слагаемые записывается в обратном порядке:
Sn = an + an–1 + … + a2 + a1.
Далее она складывается почленно с исходной суммой, причем слагаемые сразу попарно группируются. В результате
2Sn = (a1 + an) + (a2 + an–1) + … + (an + a1) = n(2a1 + (n – 1)d),
откуда . Это формула суммы n членов арифметической прогрессии.
Арифметической прогрессия названа потому, что в ней каждый член, кроме первого, равен среднему арифметическому двух соседних с ним – предыдущего и последующего. Действительно, так как
an = an–1 + d;
an = an+1 – d.
Сложение двух последних равенств дает .
Таким образом, верна следующая теорема (характеристическое свойство арифметической прогрессии). Числовая последовательность является арифметической тогда и только тогда, когда каждый ее член, кроме первого (и последнего в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов.
Пример. При каком значении x числа 3x + 2, 5x – 4 и 11
Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению
5x – 4 = ((3x + 2) + (11x + 12))/2.
Решение этого уравнения дает x = –5,5. При этом значении x заданные выражения 3x + 2, 5x – 4 и 11x + 12 принимают, соответственно, значения –14,5, –31,5, –48,5. Это – арифметическая прогрессия, ее разность равна –17.
Геометрическая прогрессия.
Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.
Таким образом, геометрическая прогрессия – это числовая последовательность {bn}, заданная рекуррентно соотношениями
b1 = b, bn = bn–1q (n = 2, 3, 4…).
(b и q – заданные числа, b ≠ 0, q ≠ 0).
Пример 1. 2, 6, 18, 54, … – возрастающая геометрическая прогрессия b = 2, q = 3.
Пример 2. 2, –2, 2, –2, … – геометрическая прогрессия b = 2, q = –1.
Пример 3. 8, 8, 8, 8, … – геометрическая прогрессия b = 8, q = 1.
Геометрическая прогрессия является возрастающей последовательностью, если b1 > 0, q > 1, и убывающей, если b1 > 0, 0 q
Одно из очевидных свойств геометрической прогрессии состоит в том, что если последовательность является геометрической прогрессией, то и последовательность квадратов, т.е.
b12, b22, b32, …, bn2,… является геометрической прогрессией, первый член которой равен b12, а знаменатель – q2.
Формула n-го члена геометрической прогрессии имеет вид
bn = b1qn–1.
Можно получить формулу суммы членов конечной геометрической прогрессии.
Пусть дана конечная геометрическая прогрессия
b1, b2, b3, …, bn
пусть Sn – сумма ее членов, т.е.
Sn= b1 + b2+ b3 + … + bn.
Принимается, что q № 1. Для определения Snприменяется искусственный прием: выполняются некоторые геометрические преобразования выражения Snq.
Тогда
Snq = (b1 + b2 + b3+ … + bn–1 + bn)q = b2 + b3 + b4 + …+ bn + bnq = Sn+ bnq – b1.
Таким образом, Snq = Sn + bnq – b1 и, следовательно,
.
Это формула суммы n членов геометрической прогрессии для случая, когда q ≠ 1.
При q = 1 формулу можно не выводить отдельно, очевидно, что в этом случае Sn = a1n.
Геометрической прогрессия названа потому, что в ней каждый член кроме первого, равен среднему геометрическому предыдущего и последующего членов. Действительно, так как
bn= bn-1q;
bn= bn+1/q,
следовательно, bn2= bn–1 bn+1 и верна следующая теорема (характеристическое свойство геометрической прогрессии):
числовая последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого ее члена, кроме первого (и последнего в случае конечной последовательности), равен произведению предыдущего и последующего членов.
Предел последовательности.
Пусть есть последовательность {cn} = {1/n}. Эту последовательность называют гармонической, поскольку каждый ее член, начиная со второго, есть среднее гармоническое между предыдущим и последующим членами. Среднее геометрическое чисел a и b есть число , или . С ростом n все члены геометрической прогрессии убывают и их значение приближается к нулю. В этом случае принято говорить, что при n, стремящемся к бесконечности, данная последовательность сходится и нуль есть ее предел. Записывается это так:
.
Строгое определение предела формулируется следующим образом:
Если существует такое число A, что для любого (сколь угодно малого) положительного числа ε найдется такое натуральное N (вообще говоря, зависящее от ε), что для всех n ≥ N будет выполнено неравенство |an – A| {an} сходится и A – ее предел.
Обозначается это так: .
В противном случае последовательность называется расходящейся.
Опираясь на это определение, можно, например, доказать наличие предела A = 0 у гармонической последовательности {cn} = {1/n}. Пусть ε – сколь угодно малое положительное число. Рассматривается разность
.
Существует ли такое N, что для всех n ≥ N выполняется неравенство 1/N ? Если взять в качестве N любое натуральное число, превышающее 1/ε, то для всех n ≥ N выполняется неравенство 1/n ≤ 1/N ε , что и требовалось доказать.
Доказать наличие предела у той или иной последовательности иногда бывает очень сложно. Наиболее часто встречающиеся последовательности хорошо изучены и приводятся в справочниках. Имеются важные теоремы, позволяющие сделать вывод о наличии предела у данной последовательности (и даже вычислить его), опираясь на уже изученные последовательности.
Теорема 1. Если последовательность имеет предел, то она ограничена.
Теорема 2. Если последовательность монотонна и ограничена, то она имеет предел.
Теорема 3. Если последовательность {an} имеет предел A, то последовательности {can}, {an + с} и {| an|} имеют пределы cA, A + c, |A| соответственно (здесь c – произвольное число).
Теорема 4. Если последовательности {an} и {bn} имеют пределы, равные A и B соответственно, то последовательность {pan + qbn} имеет предел pA + qB.
Теорема 5. Если последовательности {an} и {bn}имеют пределы, равные A и B соответственно, то последовательность {anbn} имеет предел AB.
Теорема 6. Если последовательности {an} и {bn} имеют пределы, равные A и B соответственно, и, кроме того, bn ≠ 0 и B ≠ 0, то последовательность {an / bn} имеет предел A/B.
Анна Чугайнова
www.krugosvet.ru
Математическая последовательность — это… Что такое Математическая последовательность?
- Математическая последовательность
Последовательность — функция одного натурального переменного, обладающая следующим свойством:
Областью значений функции может при этом быть произвольное множество X. Желая уточнить характер этой области, нередко говорят о «последовательности элементов множества X».
Значение обычно называют членом последовательности , имеющим номер .
Упорядоченные наборы первых членов последовательности (рассматриваемые в предположении о существовании члена ) называют начальными отрезками последовательности.
Символика
При записи членов последовательностей номер обычно пишут не в скобках после символа функции, а в качестве нижнего индекса при этом символе. Например, вместо записи x(n) для n-го члена последовательности x применяют запись xn.
Чаще всего рассматриваются последовательности, областью определения которых является весь натуральный ряд. С целью указать на такой характер области определения функции x используют обозначение . Аналогично, для последовательностей, областью определения которых является отрезок натурального ряда вида
- ,
используют обозначение .
Примеры
- Функция является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид .
- Функция является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид .
- Функция, сопоставляющая каждому натуральному числу одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида . В частности, пятым членом x5 этой последовательности является слово «май».
Типы последовательностей
- Бесконечно малая — последовательность, предел которой равен 0.
- Бесконечно большая — последовательность, предел которой равен бесконечности.
- Стационарная — последовательность, все члены которой, начиная с некоторого, равны.
Вариации и обобщения
См. также
Wikimedia Foundation. 2010.
- Математика Древнего Востока
- Математическая сингулярность
Смотреть что такое «Математическая последовательность» в других словарях:
ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ — ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ, математическая ПОСЛЕДОВАТЕЛЬНОСТЬ, каждый член которой является суммой двух предыдущих. Таким образом, если энный член последовательности обозначается хn, то для всей последовательности справедливым будет уравнение:… … Научно-технический энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА — математическая дисциплина, предметом к рой являются модели экономич. объектов и процессов и методы их исследования. Однако понятия, результаты, методы М. э. удобно и принято излагать в тесной связи с их экономич. происхождением, интерпретацией и… … Математическая энциклопедия
МАТЕМАТИЧЕСКАЯ (АНАЛИТИЧЕСКАЯ) ГЕОЛОГИЯ , — Вистелиус, 1944, 1969, научная дисциплина, занимающаяся математическим моделированием геол. процессов и примыкающими к этому вопросу задачами. Термин предложен в 1944 г. в русской лит., поддержан акад. В. И. Вернадским; в 1947 г. появился в англ … Геологическая энциклопедия
последовательность проверки кадра — Любая математическая формула, определяющая числовое значение на основе последовательности битов переданного блока информации и использующая это значение на приемном конце для обнаружения ошибок передачи. В сетях FDDI и Token Ring FCS использует… … Справочник технического переводчика
Математическая индукция — Математическая индукция один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала пров … Википедия
Математическая константа — У этого термина существуют и другие значения, см. Константа. Математическая константа величина, значение которой не меняется; в этом она противоположна переменной. В отличие от физических констант, математические константы определены… … Википедия
E (математическая константа) — e математическая константа, основание натурального логарифма, иррациональное и трансцендентное число. Иногда число e называют числом Эйлера (не путать с т. н. числами Эйлера I рода) или числом Непера. Обозначается строчной латинской буквой «e».… … Википедия
Е (математическая константа) — e математическая константа, основание натурального логарифма, иррациональное и трансцендентное число. Иногда число e называют числом Эйлера (не путать с т. н. числами Эйлера I рода) или числом Непера. Обозначается строчной латинской буквой «e».… … Википедия
Подпоследовательность — (математическая) последовательность x1, x2,…, xn,… с соблюдением порядка, т. е. при условии, что n1 … Большая советская энциклопедия
Теория волн Эллиотта — (Elliott Wave Theory) Теория волн Эллиотта это математическая теория об изменении поведения общества или финансовых рынков Все о волновой теории Эллиотта: видео, книги, статьи о теории волн, информация о советниках и индикаторах волн Эллиотта… … Энциклопедия инвестора
Книги
- Алгебра. 8 класс. Учебник + задачник. ФГОС (количество томов: 2), Мордкович А.Г.. Учебник написан в соответствии с ФГОС ООО, реализует авторскую концепцию, в которой приоритетной содержательно-методической основой является функционально-графическая линия, а идейным… Подробнее Купить за 969 руб
- Медицинская статистика. Гриф УМО по медицинскому образованию, Герасимов А. Н.. 480 стр. В книге, подготовленной заведующим кафедрой медицинской информатики и статистики ММА им. И. М. Сеченова, речь идет о статистической обработке медицинских данных с помощью пакетов… Подробнее Купить за 844 грн (только Украина)
- Медицинская статистика, А. Н. Герасимов. В книге, подготовленной заведующим кафедрой медицинской информатики и статистики ММА им. И. М. Сеченова, речь идет о статистической обработке медицинских данных с помощью пакетов… Подробнее Купить за 580 руб
dic.academic.ru
1. Введение в математический анализ. Числовая последовательность.
Числовая
последовательность – Функция вида 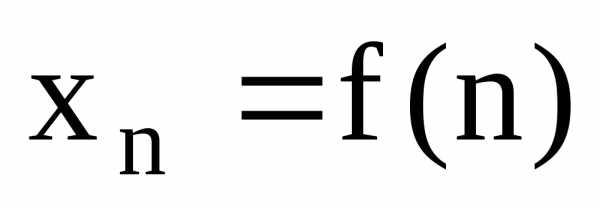 ,
заданная на множествеN
натуральных чисел.
Обозначается в
виде {xn},
,
заданная на множествеN
натуральных чисел.
Обозначается в
виде {xn}, 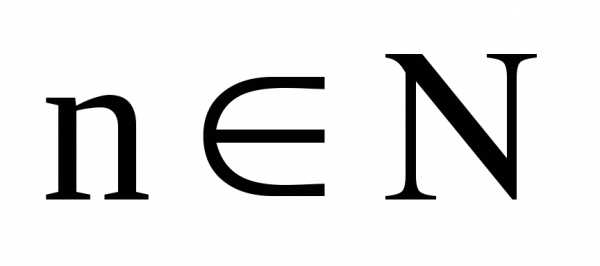 .
Число x1 называется первым членом (элементом)
последовательности, xn – общим или n-м
членом последовательности.
.
Число x1 называется первым членом (элементом)
последовательности, xn – общим или n-м
членом последовательности.
Задается либо формулой общего члена, либо рекуррентной формулой.
Формула
общего члена позволяет вычислить любой
член последовательности по номеру n
(при помощи этой формулы можно сразу
вычислить любой член последовательности). 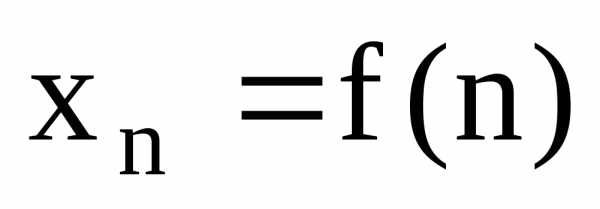
Пример: 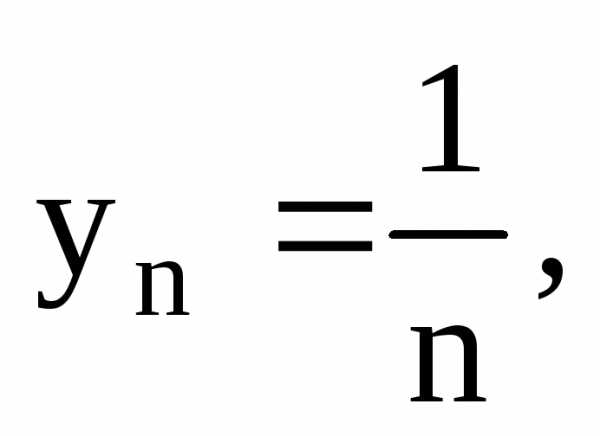
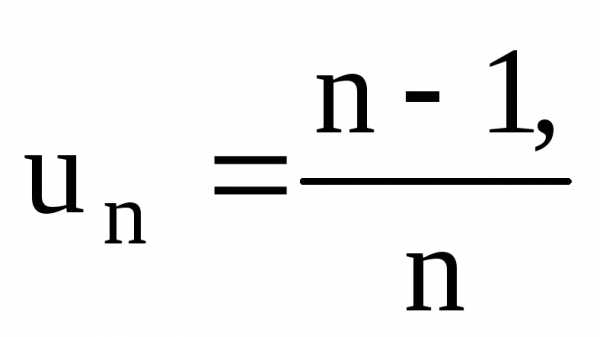
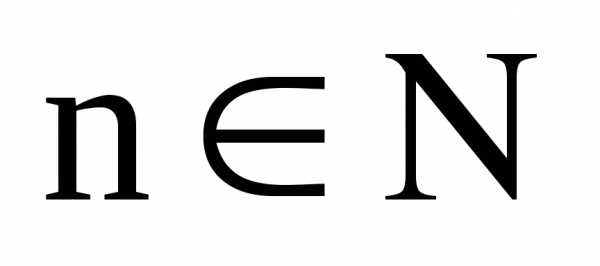
Рекуррентная формула определяет правило, по которому можно найти n-ый член последовательности, зная первый и (n-1)-ый члены (при таком способе для нахождения 100-го члена последовательности придётся сначала посчитать 99 предыдущих).
2. Ограниченные и неограниченные последовательности.
Числовая
последовательность – Функция вида 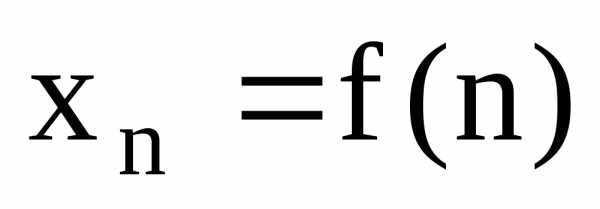 ,
заданная на множествеN
натуральных чисел.
Обозначается в
виде {xn},
,
заданная на множествеN
натуральных чисел.
Обозначается в
виде {xn}, 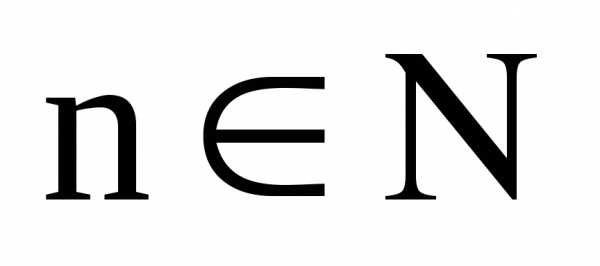 .
Число x1 называется первым членом (элементом)
последовательности, xn – общим или n-м
членом последовательности.
.
Число x1 называется первым членом (элементом)
последовательности, xn – общим или n-м
членом последовательности.
Последовательность
{xn}
называется ограниченной, если существует
такое число 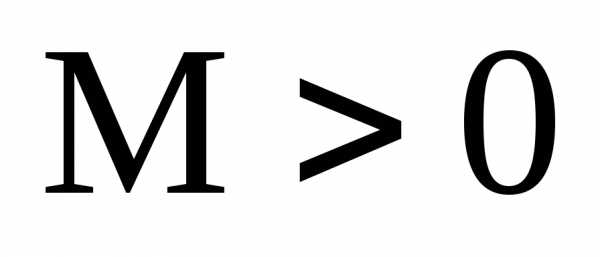 ,
что для любого
,
что для любого 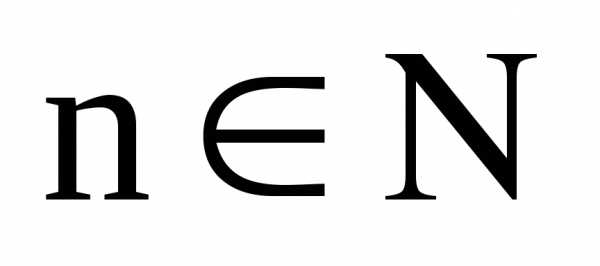 выполняется неравенство
выполняется неравенство 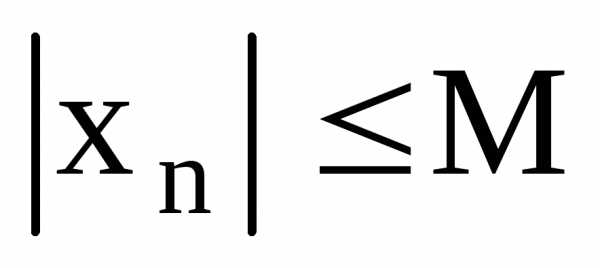 .
(если
.
(если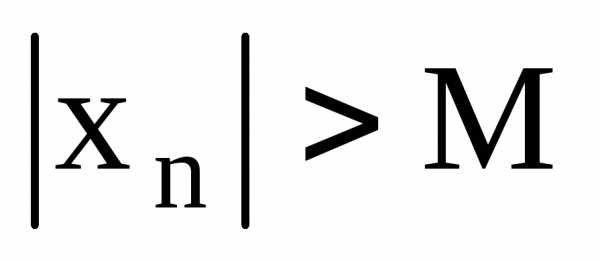 ,
то последовательность —неограниченная).
,
то последовательность —неограниченная).
3. Монотонные последовательности.
Числовая
последовательность – Функция вида 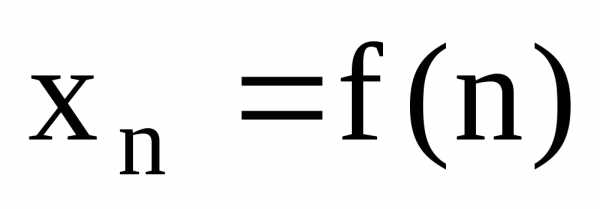 ,
заданная на множествеN
натуральных чисел.
Обозначается в
виде {xn},
,
заданная на множествеN
натуральных чисел.
Обозначается в
виде {xn}, 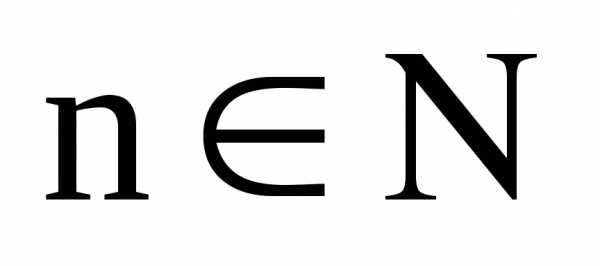 .
Число x1 называется первым членом (элементом)
последовательности, xn – общим или n-м
членом последовательности.
.
Число x1 называется первым членом (элементом)
последовательности, xn – общим или n-м
членом последовательности.
Последовательность
{xn}
называется возрастающей,
если для любого 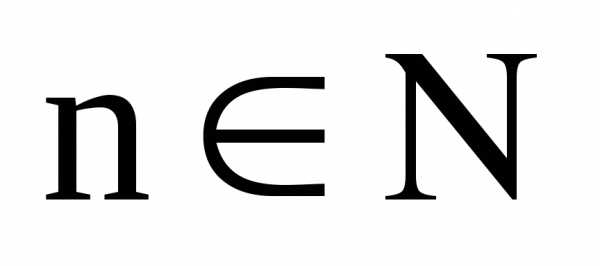 выполняется неравенство
выполняется неравенство 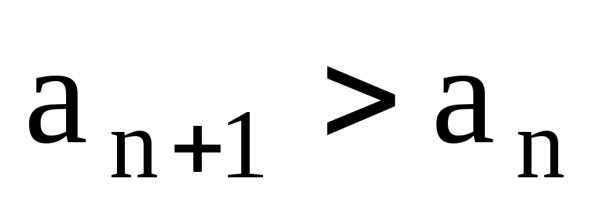 .
(если
.
(если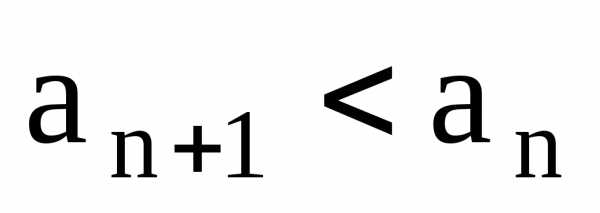 ,
то последовательность —убывающая).
Если все элементы последовательности
{xn}
равны одному и тому же числу с, то ее
называют постоянной.
,
то последовательность —убывающая).
Если все элементы последовательности
{xn}
равны одному и тому же числу с, то ее
называют постоянной.
Возрастающие, убывающие и постоянные последовательности – монотонные.
4. Число е.
Теорема Вейерштрасса. Всякая монотонная ограниченная последовательность имеет предел.
Рассмотрим
последовательность 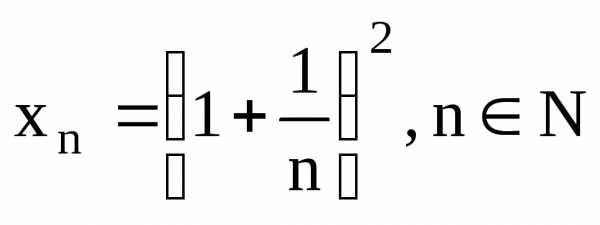 .
.
По формуле бинома Ньютона:
Пусть 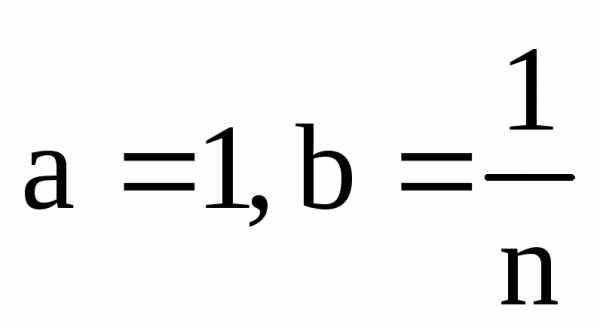 ,
тогда:
,
тогда:
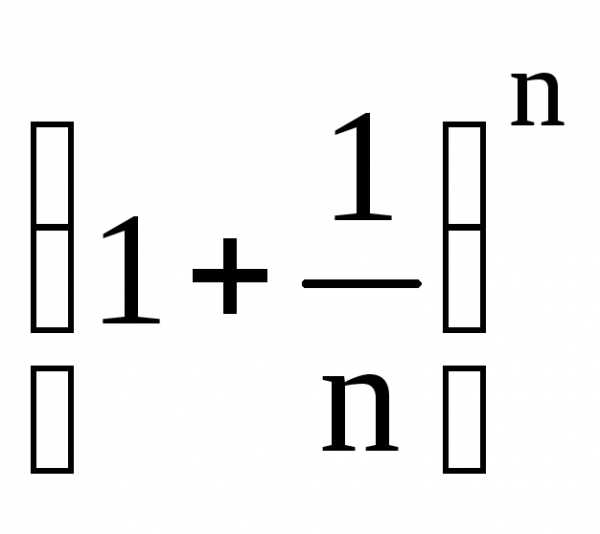 — возрастающая последовательность, причём
— возрастающая последовательность, причём 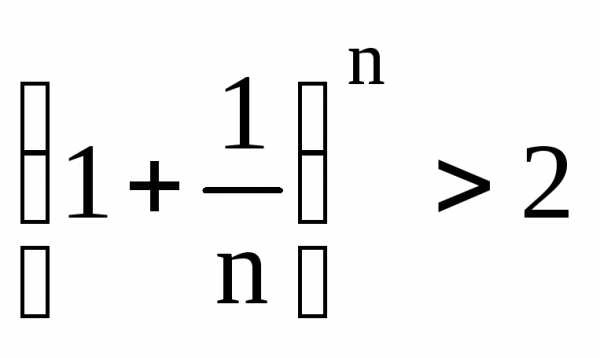 .
Заменим в правой части скобки на 1, а
факториалы на степени двойки. По формуле
суммы членов прогрессии найдём, что:
.
Заменим в правой части скобки на 1, а
факториалы на степени двойки. По формуле
суммы членов прогрессии найдём, что:
Последовательность ограничена,
при этом для 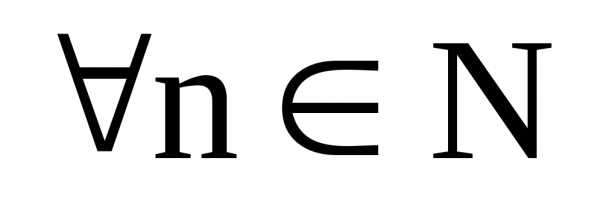 выполняется
неравенство:
выполняется
неравенство: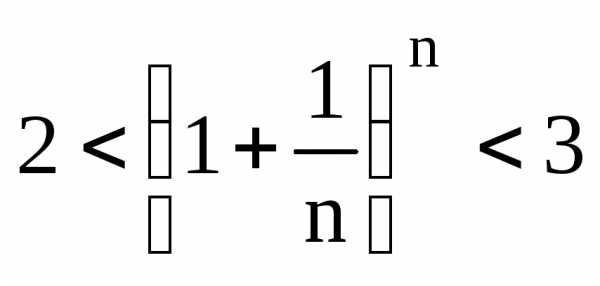 ,
следовательно на основаниитеоремы
Вейерштрасса последовательность
имеет предел, обозначаемей буквой е.
,
следовательно на основаниитеоремы
Вейерштрасса последовательность
имеет предел, обозначаемей буквой е.
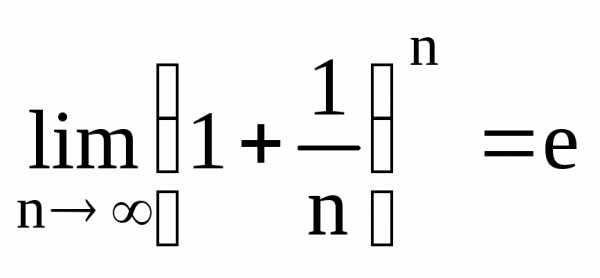 .
.
Число е называется неперовым числом. Число е иррациональное, его приближенное значение равно 2,72 (е = 2,718281828459045…). Число е принято за основание натуральных логарифмов ()
5. Связь натурального и десятичного логарифмов.
За основание натуральных логарифмов принято число е, десятичных – 10. (,)
По
определению логарифма имеем 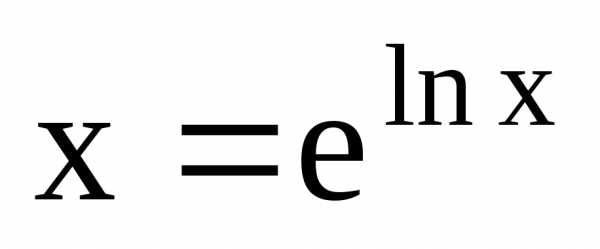 .
Прологарифмируем по основанию 10.
.
Прологарифмируем по основанию 10.
Пользуясь десятичными логарифмами, находим , значит, либо
6. Предел функции в точке.
Определение
1 (на “языке последовательностей”, или
по Гейне). Пусть
функция 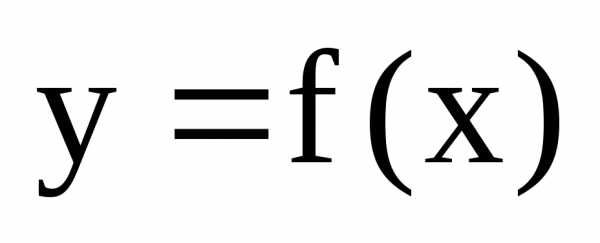 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки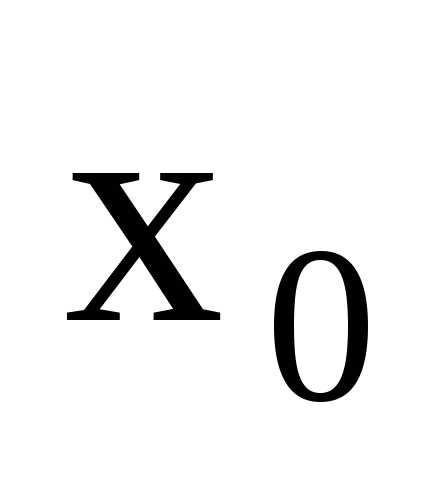 ,
кроме, быть может, самой точки.
Число А называется пределом функции
,
кроме, быть может, самой точки.
Число А называется пределом функции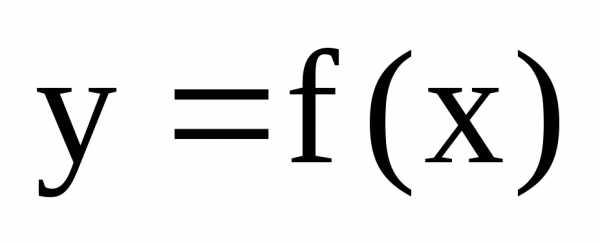 в точке
в точке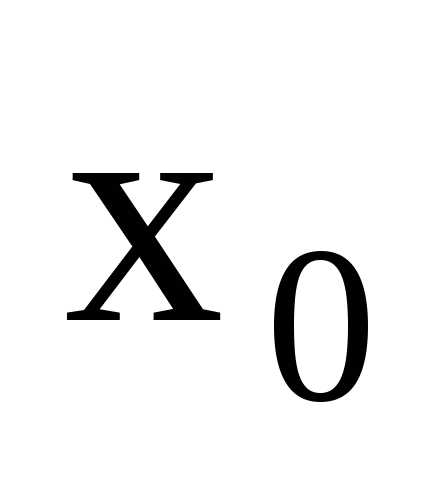 (или при
(или при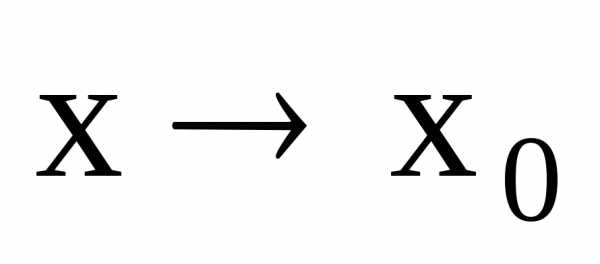 ),
если для любой последовательности
допустимых значений аргумента
),
если для любой последовательности
допустимых значений аргумента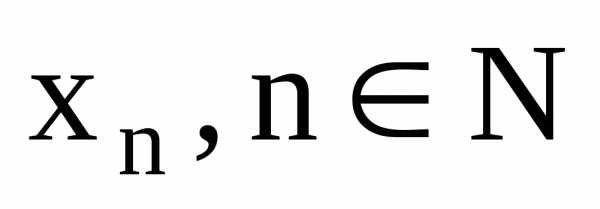
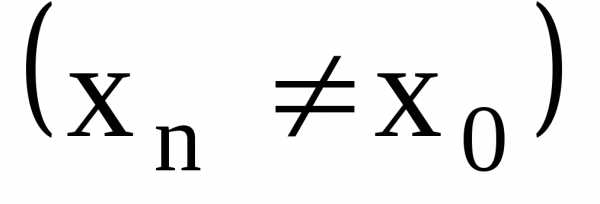 ,
сходящихся к числу
,
сходящихся к числу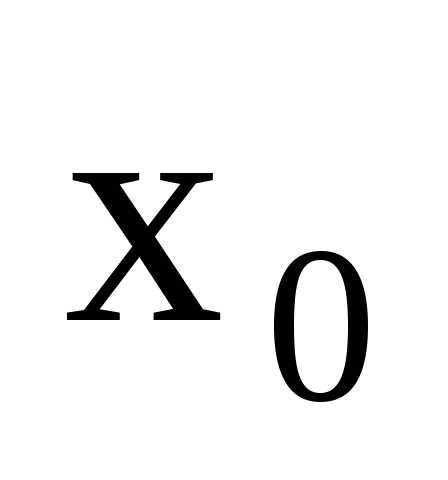 (т.е.
(т.е.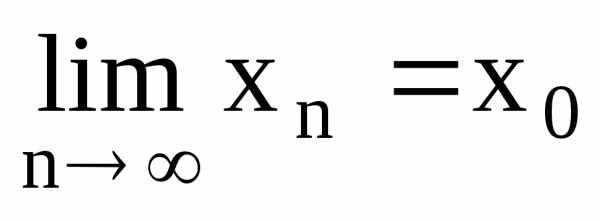 ),
последовательность соответствующих
значений,
сходится к числу А (т.е.).
),
последовательность соответствующих
значений,
сходится к числу А (т.е.).
Определение
2 (на “языке 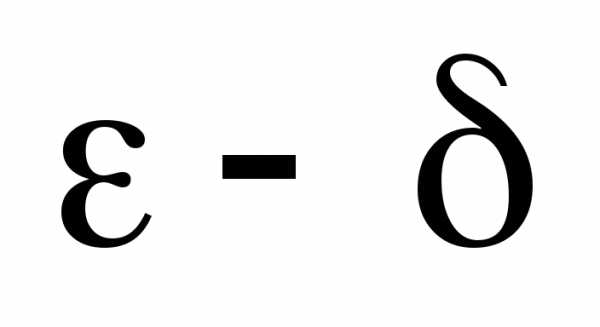 ”,
или по Коши). Пусть функция
”,
или по Коши). Пусть функция 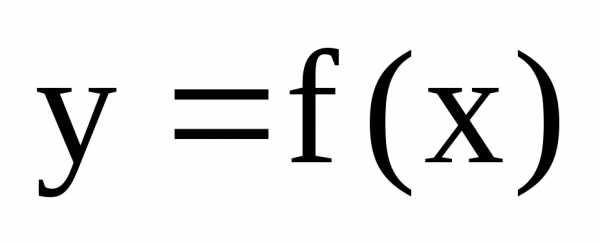 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки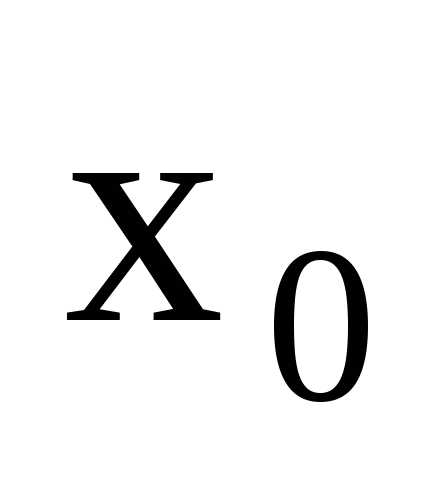 ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки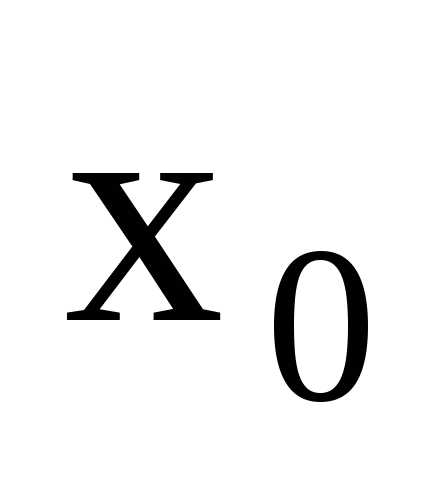 .
Число А называется пределом функции
.
Число А называется пределом функции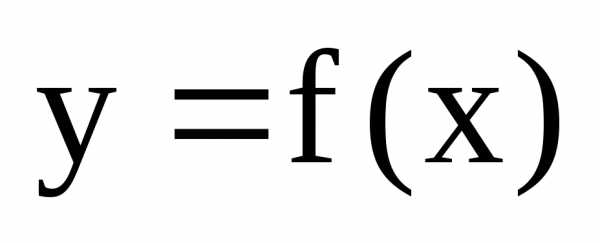 в точке
в точке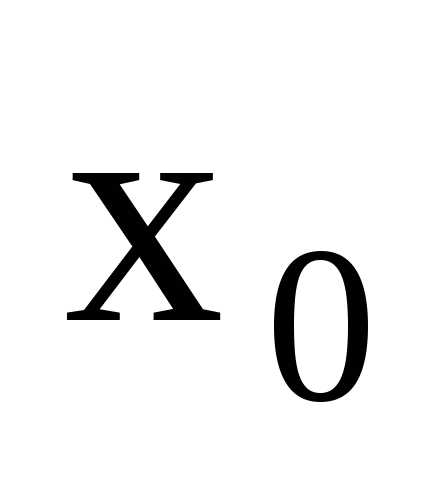 (или при
(или при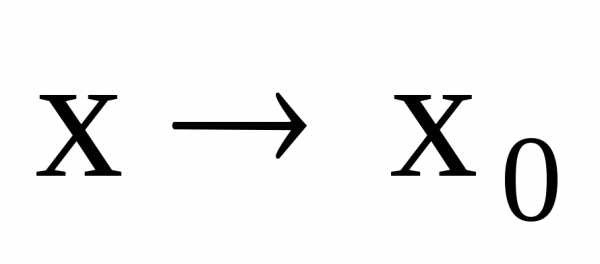 ),
если для любого положительного
),
если для любого положительного найдётся такое положительное число
найдётся такое положительное число ,
что при всехx,
удовлетворяющих неравенству
,
что при всехx,
удовлетворяющих неравенству 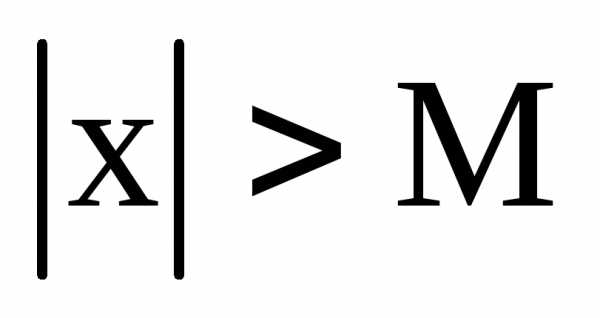 ,
выполнится неравенство.
,
выполнится неравенство.
studfiles.net
Математическая последовательность Википедия
Последовательность — это такой набор элементов некоторого множества, что:
- для каждого натурального числа можно указать элемент данного множества;
- это число является номером элемента и обозначает позицию данного элемента в последовательности;
- для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.
Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. Если любой конечный набор элементов называют выборкой конечного объёма, то последовательность оказывается выборкой бесконечного объёма.
Последовательность по своей природе — отображение, поэтому его не следует смешивать с множеством, которое «пробегает» последовательность.
В математике рассматривают различные типы последовательностей:
Целью изучения всевозможных последовательностей является поиск закономерностей, прогноз будущих состояний и генерация последовательностей.
Определение
Пусть задано некоторое множество X{\displaystyle X} элементов произвольной природы.
Всякое отображение f:N→X{\displaystyle f\colon \mathbb {N} \to X} множества натуральных чисел N{\displaystyle \mathbb {N} } в заданное множество X{\displaystyle X} называется последовательностью (элементов множества X{\displaystyle X}).
Образ натурального числа n{\displaystyle n}, а именно элемент xn=f(n){\displaystyle x_{n}=f(n)}, называется n{\displaystyle n}-ым членом или элементом последовательности, а порядковый номер члена последовательности — её индексом.
Связанные определения
- Подмножество f[N]{\displaystyle f\left[\mathbb {N} \right]} множества X{\displaystyle X}, которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.
- Если взять возрастающую последовательность натуральных чисел, то её можно рассматривать как последовательность индексов некоторой последовательности: если взять элементы исходной последовательности с соответствующими индексами (взятыми из возрастающей последовательности натуральных чисел), то можно снова получить последовательность, которая называется подпоследовательностью заданной последовательности.
Комментарии
- Не следует смешивать носитель последовательности и саму последовательность! Например, точка a∈X{\displaystyle a\in X} как одноточечное подмножество {a}⊂X{\displaystyle \{a\}\subset X} является носителем стационарной последовательности вида a,a,a,…{\displaystyle a,a,a,\dots }.
- Любое отображение множества N{\displaystyle \mathbb {N} } в себя также является последовательностью.
Обозначения
Последовательности вида
- x1,x2,x3,…{\displaystyle x_{1},\quad x_{2},\quad x_{3},\quad \dots }
принято компактно записывать при помощи круглых скобок:
- (xn){\displaystyle (x_{n})} или (xn)n=1∞{\displaystyle (x_{n})_{n=1}^{\infty }}
иногда используются фигурные скобки:
- {xn}n=1∞{\displaystyle \{x_{n}\}_{n=1}^{\infty }}
Допуская некоторую вольность речи, можно рассматривать и конечные последовательности вида
- (xn)n=1N{\displaystyle (x_{n})_{n=1}^{N}},
которые представляют собой образ начального отрезка последовательности натуральных чисел.
См. также
Примечания
Литература
wikiredia.ru
Математическая последовательность Википедия
Последовательность — это такой набор элементов некоторого множества, что:
- для каждого натурального числа можно указать элемент данного множества;
- это число является номером элемента и обозначает позицию данного элемента в последовательности;
- для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.
Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. Если любой конечный набор элементов называют выборкой конечного объёма, то последовательность оказывается выборкой бесконечного объёма.
Последовательность по своей природе — отображение, поэтому его не следует смешивать с множеством, которое «пробегает» последовательность.
В математике рассматривают различные типы последовательностей:
Целью изучения всевозможных последовательностей является поиск закономерностей, прогноз будущих состояний и генерация последовательностей.
Определение[ | ]
Пусть задано некоторое множество X{\displaystyle X} элементов произвольной природы.
Всякое отображение f:N→X{\displaystyle f\colon \mathbb {N} \to X} множества натуральных чисел N{\displaystyle \mathbb {N} } в заданное множество X{\displaystyle X} называется последовательностью (элементов множества X{\displaystyle X}).
Образ натурального числа n{\displaystyle n}, а именно элемент xn=f(n){\displaystyle x_{n}=f(n)}, называется n{\displaystyle n}-ым членом или элементом последовательности, а порядковый номер члена последовательности — её индексом.
Связанные определения[ | ]
ru-wiki.ru
Последовательность — это… Что такое Последовательность?
Последовательность — это набор элементов некоторого множества:
- для каждого натурального числа можно указать элемент данного множества;
- это число является номером элемента и обозначает позицию данного элемента в последовательности;
- для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.
Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. И, если любой набор элементов является конечным, и говорят о выборке конечного объёма, то последовательность оказывается выборкой бесконечного объёма.
Последовательность по своей природе — отображение, поэтому его не следует смешивать с множеством, которое «пробегает» последовательность.
В математике рассматривается множество различных последовательностей:
Целью изучения всевозможных последовательностей является поиск закономерностей, прогноз будущих состояний и генерация последовательностей.
Определение
Пусть задано некоторое множество элементов произвольной природы. | Всякое отображение множества натуральных чисел в заданное множество называется последовательностью (элементов множества ).
Образ натурального числа , а именно, элемент , называется —ым членом или элементом последовательности, а порядковый номер члена последовательности — её индексом.
Связанные определения
- Подмножество множества , которое образовано элементами последовательности, называется носителем последовательности: пока индекс пробегает множество натуральных чисел, точка, «изображающая» последовательность, «перемещается» по носителю.
- Если взять возрастающую последовательность натуральных чисел, то её можно рассматривать как последовательность индексов некоторой последовательности: если взять элементы исходной последовательности с соответствующими индексами (взятыми из возрастающей последовательности натуральных чисел), то можно снова получить последовательность, которая называется подпоследовательностью заданной последовательности.
Комментарии
- Не следует смешивать носитель последовательности и саму последовательность! Например, точка как одноточечное подмножество является носителем стационарной последовательности вида .
- Любое отображение множества в себя также является последовательностью.
Обозначения
Последовательности вида
принято компактно записывать при помощи круглых скобок:
- или
иногда используются фигурные скобки:
Допуская некоторую вольность речи, можно рассматривать и конечные последовательности вида
- ,
которые представляют собой образ начального отрезка последовательности натуральных чисел.
См. также
dic.academic.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Элементы математического анализа
Числовые последовательности. Способы задания числовых последовательностей
Если каждому натуральному числу n поставлено в соответствие некоторое действительное число xn , то говорят, что задана числовая последовательность
x1 , x2 , … xn , …
Число x1 называют членом последовательности с номером 1 или первым членом последовательности, число x2 — членом последовательности с номером 2 или вторым членом последовательности, и т.д. Число xn называют членом последовательности с номеромn .
Существуют два способа задания числовых последовательностей – с помощью формулы общего члена последовательности и с помощью рекуррентной формулы.
Задание последовательности с помощью формулы общего члена последовательности – это задание последовательности
x1 , x2 , … xn , …
с помощью формулы, выражающей зависимость члена xn от его номера n .
Пример 1. Числовая последовательность
1, 4, 9, … n2 , …
задана с помощью формулы общего члена
xn = n2, n = 1, 2, 3, …
Задание последовательности с помощью формулы, выражающей член последовательности xn через члены последовательности с предшествующими номерами, называют заданием последовательности с помощью рекуррентной формулы.
Пример 2 (Числа Фибоначчи). Числовая последовательность
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
может быть задана с помощью рекуррентной формулы
xn = xn – 1 + xn – 2 , n > 2 ,
с начальными условиями
x1 = 1, x2 = 1 .
Возрастающие и убывающие последовательности
Определение 1. Числовую последовательность
x1 , x2 , … xn , …
называют возрастающей последовательностью, если каждый член этой последовательности больше предшествующего члена.
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
xn + 1 > xn
Пример 3. Последовательность натуральных чисел
1, 2, 3, … n, …
является возрастающей последовательностью.
Определение 2. Числовую последовательность
x1 , x2 , … xn , …
называют убывающей последовательностью, если каждый член этой последовательности меньше предшествующего члена.
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
xn + 1 < xn
Пример 4. Последовательность
заданная формулой
является убывающей последовательностью.
Пример 5. Числовая последовательность
1, – 1, 1, – 1, …
заданная формулой
xn = (– 1)n, n = 1, 2, 3, …
не является ни возрастающей, ни убывающей последовательностью.
Определение 3. Возрастающие и убывающие числовые последовательности называют монотонными последовательностями.
Ограниченные и неограниченные последовательности
Определение 4. Числовую последовательность
x1 , x2 , … xn , …
называют ограниченной сверху, если существует такое число M, что каждый член этой последовательности меньше числа M.
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
xn < M
Определение 5. Числовую последовательность
x1 , x2 , … xn , …
называют ограниченной снизу, если существует такое число m, что каждый член этой последовательности больше числа m.
Другими словами, для всех n = 1, 2, 3, … выполнено неравенство
xn > m
Определение 6. Числовую последовательность
x1 , x2 , … xn , …
называют ограниченной, если она ограничена и сверху, и снизу.
Другими словами, существуют такие числа M и m, что для всех n = 1, 2, 3, … выполнено неравенство
m < xn < M
Определение 7. Числовые последовательности, которые не являются ограниченными, называют неограниченными последовательностями.
Пример 6. Числовая последовательность
1, 4, 9, … n2 , …
заданная формулой
xn = n2, n = 1, 2, 3, … ,
ограничена снизу, например, числом 0. Однако эта последовательность неограничена сверху.
Пример 7 . Последовательность
заданная формулой
является ограниченной последовательностью, поскольку для всех n = 1, 2, 3, … выполнено неравенство
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
