Почему косинус 0 равен 1 – Почему косинус 0 равен единице. Если он равен п/2. ))) Я чето голову сломал. Я не люблю математику. ПОМГОГИТТТЕЕ!
cos 0 равен
«cos 0 равен… »
Тригонометрическую функцию можно вычислить с помощью нескольких способов. Рассмотрим их.
Способ 1.
Является одним из самых применяемых, распространенных и простых. Чтобы с его помощью вычислить значение заданной функции необходимо использовать таблицу значений тригонометрических функций от основных углов.
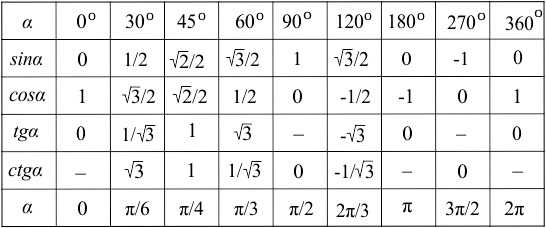
Таблица позволяет определить значение , которое равно единице:
Способ 2.
Если же таблицы значений функций нет, то можно использовать тригонометрический круг, который также называют тригонометрической окружностью. С его помощью можно вычислять значения основных тригонометрических функций (синус, косинус).
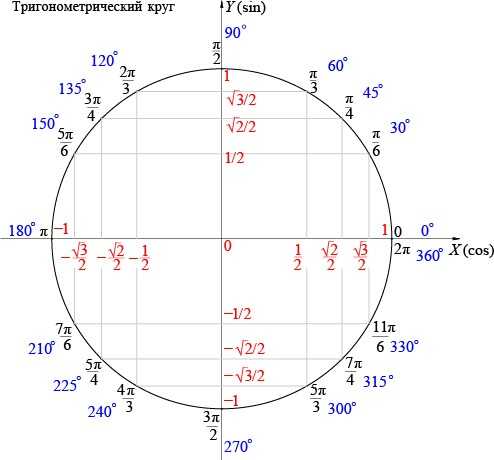
На тригонометрическом круге значения косинуса лежат на оси абсцисс (оси Ох). 0 градусов соответственно совпадает с числом 0. При проецировании этой точки на ось абсцисс получаем 1. Таким образом, косинус от 0 равен 1.
Способ 3.
Если запомнить как выглядит график косинуса (косинусоида), то нет необходимости запоминать или искать таблицу или учиться пользоваться тригонометрической окружностью.
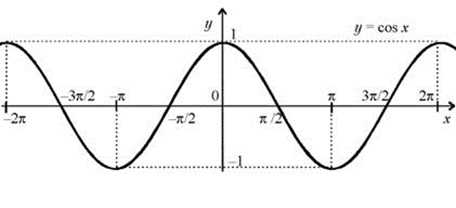
По графику возможно очень точное определение значения функции косинус при . Для этого найдем, в какой точке графика его аргумент равен 0 и проецируем эту точку на ось ординат. Получаем значение 1.
ru.solverbook.com
| Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. cos(0°)=cos(360°)=1; точная, но чуть более сложная таблица ( с точностью до 1″) здесь.
|
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций 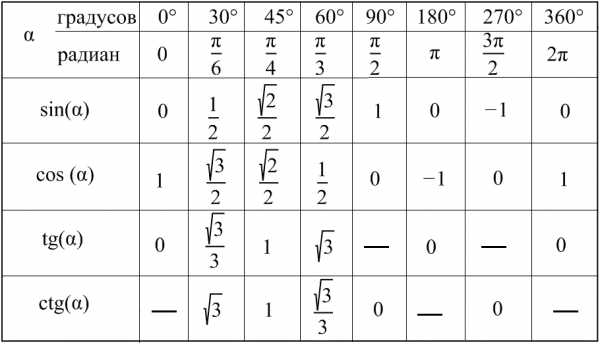 Доп. Инфо:
|
tehtab.ru
Разузнай! — Косинус — Косинус угла 30, 60, 45, 90, 0, 120, 135 и 150 градусов — Теорема косинусов
 |
В математике выделяют шесть тригонометрических функций, из которых четыре (синус, косинус, тангенс и котангенс) являются основными и еще две (секанс и косеканс) применяются довольно редко. Исходя из данного положения, косинус можно определить как одну из основных тригонометрических функций, выражающих отношение прилежащего катета в прямоугольном треугольнике к гипотенузе этого треугольника. Косинус угла x обозначается как cos x. Величина косинуса угла зависит от длины отрезков, образующих стороны прямоугольного треугольника и от его размера.
Чему равен косинус и синус 30 градусов
Косинус угла в 30 градусов получится, если корень из трех разделить на два. Вычисляя данное отношение, получаем значение косинуса равное 0,866. Синус угла в 30 градусов равен одной второй или 0,5.
Чему равен косинус и синус 60 градусов
Косинус угла в 60 градусов равен синусу угла 30 градусов, то есть одной второй (1111/2) или 0,5. Синус того же угла косинусу угла в 30 градусов, то есть корень из трех делим на 2 и получаем число 0,866.
Чему равен косинус и синус 45 градусов
Косинус 45 градусов получается путем деления корня из двух на два или единицы на корень из двух. Следовательно, косинус угла в 45 градусов равен 0,7071. Синус угла в 45 градусов равен косинусу угла в 45 градусов и также выражается как корень из двух, разделенный на два, или единица, разделенная на корень из двух. Числовое значение также 0,7071.
Чему равен косинус и синус 90 градусов
Косинус угла в 90 градусов равен нулю (0), а синус того же угла равен 1.
Чему равен косинус и синус 120 градусов
Косинус 120 градусов равен -0,5 (минус пять десятых), синус того же угла равен 0,866.
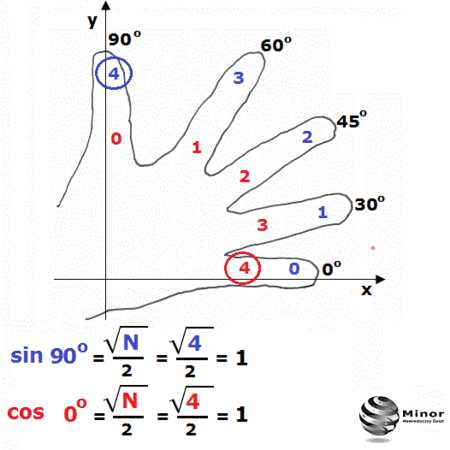
Чему равен косинус и синус 0 градусов
Косинус 0 градусов равен 1, а синус 0 градусов равен 0 (нулю).
Чему равен косинус и синус 135 градусов
Косинус 135 градусов равен -0,7071 (отрицательное значение), а синус того же угла равен 0,7071 (положительное значение).
Чему равен косинус и синус 150 градусов
Косинус угла в 150 градусов равен -0,866 (отрицательное значение), а синус того же угла равен 0,5 (пять десятых).
Теорема косинусов
Теорема косинусов для общего случая формулируется следующим образом: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника, минус удвоенное произведение этих сторон на косинус угла (х) между ними, что эквивалентно выражению: a2 = b2 + c2 х 2 b c cos х, где а, b, с – это стороны треугольника. Для вычисления стороны прямоугольного треугольника достаточно воспользоваться теоремой Пифагора, из которой вытекает теорема косинусов. Для гипотенузы прямоугольного треугольника теорема формулируется следующим образом: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Производная косинуса
Производная косинуса равна синусу с противоположным знаком (то есть производная cos x равна -sin x).
Читайте также:
- < Как сделать костюм на хэллоуин своими руками
- Как сделать дымовую шашку >
razuznai.ru
Таблица КОСИНУСОВ для углов от 0° до 360° градусов
КОСИНУС (COS α) острого угла в прямоугольном треугольнике равен отношению прилежащего катета к его гипотенузе…
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cos α (Косинус) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
…
| Угол в градусах | Cos (Косинус) |
|---|---|
| 0° | 1 |
| 1° | 0.9998 |
| 2° | 0.9994 |
| 3° | 0.9986 |
| 4° | 0.9976 |
| 5° | 0.9962 |
| 6° | 0.9945 |
| 7° | 0.9925 |
| 8° | 0.9903 |
| 9° | 0.9877 |
| 10° | 0.9848 |
| 11° | 0.9816 |
| 12° | 0.9781 |
| 13° | 0.9744 |
| 14° | 0.9703 |
| 15° | 0.9659 |
| 16° | 0.9613 |
| 17° | 0.9563 |
| 18° | 0.9511 |
| 19° | 0.9455 |
| 20° | 0.9397 |
| 21° | 0.9336 |
| 22° | 0.9272 |
| 23° | 0.9205 |
| 24° | 0.9135 |
| 25° | 0.9063 |
| 26° | 0.8988 |
| 27° | 0.891 |
| 28° | 0.8829 |
| 29° | 0.8746 |
| 30° | 0.866 |
| 31° | 0.8572 |
| 32° | 0.848 |
| 33° | 0.8387 |
| 34° | 0.829 |
| 35° | 0.8192 |
| 36° | 0.809 |
| 37° | 0.7986 |
| 38° | 0.788 |
| 39° | 0.7771 |
| 40° | 0.766 |
| 41° | 0.7547 |
| 42° | 0.7431 |
| 43° | 0.7314 |
| 44° | 0.7193 |
| 45° | 0.7071 |
| 46° | 0.6947 |
| 47° | 0.682 |
| 48° | 0.6691 |
| 49° | 0.6561 |
| 50° | 0.6428 |
| 51° | 0.6293 |
| 52° | 0.6157 |
| 53° | 0.6018 |
| 54° | 0.5878 |
| 55° | 0.5736 |
| 56° | 0.5592 |
| 57° | 0.5446 |
| 58° | 0.5299 |
| 59° | 0.515 |
| 60° | 0.5 |
| 61° | 0.4848 |
| 62° | 0.4695 |
| 63° | 0.454 |
| 64° | 0.4384 |
| 65° | 0.4226 |
| 66° | 0.4067 |
| 67° | 0.3907 |
| 68° | 0.3746 |
| 69° | 0.3584 |
| 70° | 0.342 |
| 71° | 0.3256 |
| 72° | 0.309 |
| 73° | 0.2924 |
| 74° | 0.2756 |
| 75° | 0.2588 |
| 76° | 0.2419 |
| 77° | 0.225 |
| 78° | 0.2079 |
| 79° | 0.1908 |
| 80° | 0.1736 |
| 81° | 0.1564 |
| 82° | 0.1392 |
| 83° | 0.1219 |
| 84° | 0.1045 |
| 85° | 0.0872 |
| 86° | 0.0698 |
| 87° | 0.0523 |
| 88° | 0.0349 |
| 89° | 0.0175 |
| 90° | 0 |
…
| Угол | cos (Косинус) |
|---|---|
| 91° | -0.0175 |
| 92° | -0.0349 |
| 93° | -0.0523 |
| 94° | -0.0698 |
| 95° | -0.0872 |
| 96° | -0.1045 |
| 97° | -0.1219 |
| 98° | -0.1392 |
| 99° | -0.1564 |
| 100° | -0.1736 |
| 101° | -0.1908 |
| 102° | -0.2079 |
| 103° | -0.225 |
| 104° | -0.2419 |
| 105° | -0.2588 |
| 106° | -0.2756 |
| 107° | -0.2924 |
| 108° | -0.309 |
| 109° | -0.3256 |
| 110° | -0.342 |
| 111° | -0.3584 |
| 112° | -0.3746 |
| 113° | -0.3907 |
| 114° | -0.4067 |
| 115° | -0.4226 |
| 116° | -0.4384 |
| 117° | -0.454 |
| 118° | -0.4695 |
| 119° | -0.4848 |
| 120° | -0.5 |
| 121° | -0.515 |
| 122° | -0.5299 |
| 123° | -0.5446 |
| 124° | -0.5592 |
| 125° | -0.5736 |
| 126° | -0.5878 |
| 127° | -0.6018 |
| 128° | -0.6157 |
| 129° | -0.6293 |
| 130° | -0.6428 |
| 131° | -0.6561 |
| 132° | -0.6691 |
| 133° | -0.682 |
| 134° | -0.6947 |
| 135° | -0.7071 |
| 136° | -0.7193 |
| 137° | -0.7314 |
| 138° | -0.7431 |
| 139° | -0.7547 |
| 140° | -0.766 |
| 141° | -0.7771 |
| 142° | -0.788 |
| 143° | -0.7986 |
| 144° | -0.809 |
| 145° | -0.8192 |
| 146° | -0.829 |
| 147° | -0.8387 |
| 148° | -0.848 |
| 149° | -0.8572 |
| 150° | -0.866 |
| 151° | -0.8746 |
| 152° | -0.8829 |
| 153° | -0.891 |
| 154° | -0.8988 |
| 155° | -0.9063 |
| 156° | -0.9135 |
| 157° | -0.9205 |
| 158° | -0.9272 |
| 159° | -0.9336 |
| 160° | -0.9397 |
| 161° | -0.9455 |
| 162° | -0.9511 |
| 163° | -0.9563 |
| 164° | -0.9613 |
| 165° | -0.9659 |
| 166° | -0.9703 |
| 167° | -0.9744 |
| 168° | -0.9781 |
| 169° | -0.9816 |
| 170° | -0.9848 |
| 171° | -0.9877 |
| 172° | -0.9903 |
| 173° | -0.9925 |
| 174° | -0.9945 |
| 175° | -0.9962 |
| 176° | -0.9976 |
| 177° | -0.9986 |
| 178° | -0.9994 |
| 179° | -0.9998 |
| 180° | -1 |
…
| Угол | cos (косинус) |
|---|---|
| 181° | -0.9998 |
| 182° | -0.9994 |
| 183° | -0.9986 |
| 184° | -0.9976 |
| 185° | -0.9962 |
| 186° | -0.9945 |
| 187° | -0.9925 |
| 188° | -0.9903 |
| 189° | -0.9877 |
| 190° | -0.9848 |
| 191° | -0.9816 |
| 192° | -0.9781 |
| 193° | -0.9744 |
| 194° | -0.9703 |
| 195° | -0.9659 |
| 196° | -0.9613 |
| 197° | -0.9563 |
| 198° | -0.9511 |
| 199° | -0.9455 |
| 200° | -0.9397 |
| 201° | -0.9336 |
| 202° | -0.9272 |
| 203° | -0.9205 |
| 204° | -0.9135 |
| 205° | -0.9063 |
| 206° | -0.8988 |
| 207° | -0.891 |
| 208° | -0.8829 |
| 209° | -0.8746 |
| 210° | -0.866 |
| 211° | -0.8572 |
| 212° | -0.848 |
| 213° | -0.8387 |
| 214° | -0.829 |
| 215° | -0.8192 |
| 216° | -0.809 |
| 217° | -0.7986 |
| 218° | -0.788 |
| 219° | -0.7771 |
| 220° | -0.766 |
| 221° | -0.7547 |
| 222° | -0.7431 |
| 223° | -0.7314 |
| 224° | -0.7193 |
| 225° | -0.7071 |
| 226° | -0.6947 |
| 227° | -0.682 |
| 228° | -0.6691 |
| 229° | -0.6561 |
| 230° | -0.6428 |
| 231° | -0.6293 |
| 232° | -0.6157 |
| 233° | -0.6018 |
| 234° | -0.5878 |
| 235° | -0.5736 |
| 236° | -0.5592 |
| 237° | -0.5446 |
| 238° | -0.5299 |
| 239° | -0.515 |
| 240° | -0.5 |
| 241° | -0.4848 |
| 242° | -0.4695 |
| 243° | -0.454 |
| 244° | -0.4384 |
| 245° | -0.4226 |
| 246° | -0.4067 |
| 247° | -0.3907 |
| 248° | -0.3746 |
| 249° | -0.3584 |
| 250° | -0.342 |
| 251° | -0.3256 |
| 252° | -0.309 |
| 253° | -0.2924 |
| 254° | -0.2756 |
| 255° | -0.2588 |
| 256° | -0.2419 |
| 257° | -0.225 |
| 258° | -0.2079 |
| 259° | -0.1908 |
| 260° | -0.1736 |
| 261° | -0.1564 |
| 262° | -0.1392 |
| 263° | -0.1219 |
| 264° | -0.1045 |
| 265° | -0.0872 |
| 266° | -0.0698 |
| 267° | -0.0523 |
| 268° | -0.0349 |
| 269° | -0.0175 |
| 270° | 0 |
…
| Угол | Cos (Косинус) |
|---|---|
| 271° | 0.0175 |
| 272° | 0.0349 |
| 273° | 0.0523 |
| 274° | 0.0698 |
| 275° | 0.0872 |
| 276° | 0.1045 |
| 277° | 0.1219 |
| 278° | 0.1392 |
| 279° | 0.1564 |
| 280° | 0.1736 |
| 281° | 0.1908 |
| 282° | 0.2079 |
| 283° | 0.225 |
| 284° | 0.2419 |
| 285° | 0.2588 |
| 286° | 0.2756 |
| 287° | 0.2924 |
| 288° | 0.309 |
| 289° | 0.3256 |
| 290° | 0.342 |
| 291° | 0.3584 |
| 292° | 0.3746 |
| 293° | 0.3907 |
| 294° | 0.4067 |
| 295° | 0.4226 |
| 296° | 0.4384 |
| 297° | 0.454 |
| 298° | 0.4695 |
| 299° | 0.4848 |
| 300° | 0.5 |
| 301° | 0.515 |
| 302° | 0.5299 |
| 303° | 0.5446 |
| 304° | 0.5592 |
| 305° | 0.5736 |
| 306° | 0.5878 |
| 307° | 0.6018 |
| 308° | 0.6157 |
| 309° | 0.6293 |
| 310° | 0.6428 |
| 311° | 0.6561 |
| 312° | 0.6691 |
| 313° | 0.682 |
| 314° | 0.6947 |
| 315° | 0.7071 |
| 316° | 0.7193 |
| 317° | 0.7314 |
| 318° | 0.7431 |
| 319° | 0.7547 |
| 320° | 0.766 |
| 321° | 0.7771 |
| 322° | 0.788 |
| 323° | 0.7986 |
| 324° | 0.809 |
| 325° | 0.8192 |
| 326° | 0.829 |
| 327° | 0.8387 |
| 328° | 0.848 |
| 329° | 0.8572 |
| 330° | 0.866 |
| 331° | 0.8746 |
| 332° | 0.8829 |
| 333° | 0.891 |
| 334° | 0.8988 |
| 335° | 0.9063 |
| 336° | 0.9135 |
| 337° | 0.9205 |
| 338° | 0.9272 |
| 339° | 0.9336 |
| 340° | 0.9397 |
| 341° | 0.9455 |
| 342° | 0.9511 |
| 343° | 0.9563 |
| 344° | 0.9613 |
| 345° | 0.9659 |
| 346° | 0.9703 |
| 347° | 0.9744 |
| 348° | 0.9781 |
| 349° | 0.9816 |
| 350° | 0.9848 |
| 351° | 0.9877 |
| 352° | 0.9903 |
| 353° | 0.9925 |
| 354° | 0.9945 |
| 355° | 0.9962 |
| 356° | 0.9976 |
| 357° | 0.9986 |
| 358° | 0.9994 |
| 359° | 0.9998 |
| 360° | 1 |
…
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите нужную часть таблицы, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Пример
Чему равен косинус 30? …
— Ищем в таблице соответствующее значение. Правильный ответ: 0.866
Автор: Bill4iam
kvn201.com.ua
Таблица синусов и косинусов
Таблица синусов и косинусов может пригодится учащимся, студентам и инженерам для произведения тригонометрических расчетов. Она позволяет найти синус и косинус любого целого угла от 0 до 360 градусов.
Пользоваться таблицей очень просто — найдите нужный угол и в той же строке увидите синус и косинус этого угла. Для примера возьмем угол, равный 30 градусам. Найдя его в таблице мы увидим, что Cos(30) = 0,866025404, а Sin(30) = 0,5.
| Угол (градусы) | Косинус (Cos) | Синус (Sin) |
|---|---|---|
| 0° | 1 | 0 |
| 1° | 0,999847695 | 0,017452406 |
| 2° | 0,999390827 | 0,034899497 |
| 3° | 0,998629535 | 0,052335956 |
| 4° | 0,99756405 | 0,069756474 |
| 5° | 0,996194698 | 0,087155743 |
| 6° | 0,994521895 | 0,104528463 |
| 7° | 0,992546152 | 0,121869343 |
| 8° | 0,990268069 | 0,139173101 |
| 9° | 0,987688341 | 0,156434465 |
| 10° | 0,984807753 | 0,173648178 |
| 11° | 0,981627183 | 0,190808995 |
| 12° | 0,978147601 | 0,207911691 |
| 13° | 0,974370065 | 0,224951054 |
| 14° | 0,970295726 | 0,241921896 |
| 15° | 0,965925826 | 0,258819045 |
| 16° | 0,961261696 | 0,275637356 |
| 17° | 0,956304756 | 0,292371705 |
| 18° | 0,951056516 | 0,309016994 |
| 19° | 0,945518576 | 0,325568154 |
| 20° | 0,939692621 | 0,342020143 |
| 21° | 0,933580426 | 0,35836795 |
| 22° | 0,927183855 | 0,374606593 |
| 23° | 0,920504853 | 0,390731128 |
| 24° | 0,913545458 | 0,406736643 |
| 25° | 0,906307787 | 0,422618262 |
| 26° | 0,898794046 | 0,438371147 |
| 27° | 0,891006524 | 0,4539905 |
| 28° | 0,882947593 | 0,469471563 |
| 29° | 0,874619707 | 0,48480962 |
| 30° | 0,866025404 | 0,5 |
| 31° | 0,857167301 | 0,515038075 |
| 32° | 0,848048096 | 0,529919264 |
| 33° | 0,838670568 | 0,544639035 |
| 34° | 0,829037573 | 0,559192903 |
| 35° | 0,819152044 | 0,573576436 |
| 36° | 0,809016994 | 0,587785252 |
| 37° | 0,79863551 | 0,601815023 |
| 38° | 0,788010754 | 0,615661475 |
| 39° | 0,777145961 | 0,629320391 |
| 40° | 0,766044443 | 0,64278761 |
| 41° | 0,75470958 | 0,656059029 |
| 42° | 0,743144825 | 0,669130606 |
| 43° | 0,731353702 | 0,68199836 |
| 44° | 0,7193398 | 0,69465837 |
| 45° | 0,707106781 | 0,707106781 |
| 46° | 0,69465837 | 0,7193398 |
| 47° | 0,68199836 | 0,731353702 |
| 48° | 0,669130606 | 0,743144825 |
| 49° | 0,656059029 | 0,75470958 |
| 50° | 0,64278761 | 0,766044443 |
| 51° | 0,629320391 | 0,777145961 |
| 52° | 0,615661475 | 0,788010754 |
| 53° | 0,601815023 | 0,79863551 |
| 54° | 0,587785252 | 0,809016994 |
| 55° | 0,573576436 | 0,819152044 |
| 56° | 0,559192903 | 0,829037573 |
| 57° | 0,544639035 | 0,838670568 |
| 58° | 0,529919264 | 0,848048096 |
| 59° | 0,515038075 | 0,857167301 |
| 60° | 0,5 | 0,866025404 |
| 61° | 0,48480962 | 0,874619707 |
| 62° | 0,469471563 | 0,882947593 |
| 63° | 0,4539905 | 0,891006524 |
| 64° | 0,438371147 | 0,898794046 |
| 65° | 0,422618262 | 0,906307787 |
| 66° | 0,406736643 | 0,913545458 |
| 67° | 0,390731128 | 0,920504853 |
| 68° | 0,374606593 | 0,927183855 |
| 69° | 0,35836795 | 0,933580426 |
| 70° | 0,342020143 | 0,939692621 |
| 71° | 0,325568154 | 0,945518576 |
| 72° | 0,309016994 | 0,951056516 |
| 73° | 0,292371705 | 0,956304756 |
| 74° | 0,275637356 | 0,961261696 |
| 75° | 0,258819045 | 0,965925826 |
| 76° | 0,241921896 | 0,970295726 |
| 77° | 0,224951054 | 0,974370065 |
| 78° | 0,207911691 | 0,978147601 |
| 79° | 0,190808995 | 0,981627183 |
| 80° | 0,173648178 | 0,984807753 |
| 81° | 0,156434465 | 0,987688341 |
| 82° | 0,139173101 | 0,990268069 |
| 83° | 0,121869343 | 0,992546152 |
| 84° | 0,104528463 | 0,994521895 |
| 85° | 0,087155743 | 0,996194698 |
| 86° | 0,069756474 | 0,99756405 |
| 87° | 0,052335956 | 0,998629535 |
| 88° | 0,034899497 | 0,999390827 |
| 89° | 0,017452406 | 0,999847695 |
| 90° | 0 | 1 |
| 91° | -0,017452406 | 0,999847695 |
| 92° | -0,034899497 | 0,999390827 |
| 93° | -0,052335956 | 0,998629535 |
| 94° | -0,069756474 | 0,99756405 |
| 95° | -0,087155743 | 0,996194698 |
| 96° | -0,104528463 | 0,994521895 |
| 97° | -0,121869343 | 0,992546152 |
| 98° | -0,139173101 | 0,990268069 |
| 99° | -0,156434465 | 0,987688341 |
| 100° | -0,173648178 | 0,984807753 |
| 101° | -0,190808995 | 0,981627183 |
| 102° | -0,207911691 | 0,978147601 |
| 103° | -0,224951054 | 0,974370065 |
| 104° | -0,241921896 | 0,970295726 |
| 105° | -0,258819045 | 0,965925826 |
| 106° | -0,275637356 | 0,961261696 |
| 107° | -0,292371705 | 0,956304756 |
| 108° | -0,309016994 | 0,951056516 |
| 109° | -0,325568154 | 0,945518576 |
| 110° | -0,342020143 | 0,939692621 |
| 111° | -0,35836795 | 0,933580426 |
| 112° | -0,374606593 | 0,927183855 |
| 113° | -0,390731128 | 0,920504853 |
| 114° | -0,406736643 | 0,913545458 |
| 115° | -0,422618262 | 0,906307787 |
| 116° | -0,438371147 | 0,898794046 |
| 117° | -0,4539905 | 0,891006524 |
| 118° | -0,469471563 | 0,882947593 |
| 119° | -0,48480962 | 0,874619707 |
| 120° | -0,5 | 0,866025404 |
| 121° | -0,515038075 | 0,857167301 |
| 122° | -0,529919264 | 0,848048096 |
| 123° | -0,544639035 | 0,838670568 |
| 124° | -0,559192903 | 0,829037573 |
| 125° | -0,573576436 | 0,819152044 |
| 126° | -0,587785252 | 0,809016994 |
| 127° | -0,601815023 | 0,79863551 |
| 128° | -0,615661475 | 0,788010754 |
| 129° | -0,629320391 | 0,777145961 |
| 130° | -0,64278761 | 0,766044443 |
| 131° | -0,656059029 | 0,75470958 |
| 132° | -0,669130606 | 0,743144825 |
| 133° | -0,68199836 | 0,731353702 |
| 134° | -0,69465837 | 0,7193398 |
| 135° | -0,707106781 | 0,707106781 |
| 136° | -0,7193398 | 0,69465837 |
| 137° | -0,731353702 | 0,68199836 |
| 138° | -0,743144825 | 0,669130606 |
| 139° | -0,75470958 | 0,656059029 |
| 140° | -0,766044443 | 0,64278761 |
| 141° | -0,777145961 | 0,629320391 |
| 142° | -0,788010754 | 0,615661475 |
| 143° | -0,79863551 | 0,601815023 |
| 144° | -0,809016994 | 0,587785252 |
| 145° | -0,819152044 | 0,573576436 |
| 146° | -0,829037573 | 0,559192903 |
| 147° | -0,838670568 | 0,544639035 |
| 148° | -0,848048096 | 0,529919264 |
| 149° | -0,857167301 | 0,515038075 |
| 150° | -0,866025404 | 0,5 |
| 151° | -0,874619707 | 0,48480962 |
| 152° | -0,882947593 | 0,469471563 |
| 153° | -0,891006524 | 0,4539905 |
| 154° | -0,898794046 | 0,438371147 |
| 155° | -0,906307787 | 0,422618262 |
| 156° | -0,913545458 | 0,406736643 |
| 157° | -0,920504853 | 0,390731128 |
| 158° | -0,927183855 | 0,374606593 |
| 159° | -0,933580426 | 0,35836795 |
| 160° | -0,939692621 | 0,342020143 |
| 161° | -0,945518576 | 0,325568154 |
| 162° | -0,951056516 | 0,309016994 |
| 163° | -0,956304756 | 0,292371705 |
| 164° | -0,961261696 | 0,275637356 |
| 165° | -0,965925826 | 0,258819045 |
| 166° | -0,970295726 | 0,241921896 |
| 167° | -0,974370065 | 0,224951054 |
| 168° | -0,978147601 | 0,207911691 |
| 169° | -0,981627183 | 0,190808995 |
| 170° | -0,984807753 | 0,173648178 |
| 171° | -0,987688341 | 0,156434465 |
| 172° | -0,990268069 | 0,139173101 |
| 173° | -0,992546152 | 0,121869343 |
| 174° | -0,994521895 | 0,104528463 |
| 175° | -0,996194698 | 0,087155743 |
| 176° | -0,99756405 | 0,069756474 |
| 177° | -0,998629535 | 0,052335956 |
| 178° | -0,999390827 | 0,034899497 |
| 179° | -0,999847695 | 0,017452406 |
| 180° | -1 | 1,22515E-16 |
| 181° | -0,999847695 | -0,017452406 |
| 182° | -0,999390827 | -0,034899497 |
| 183° | -0,998629535 | -0,052335956 |
| 184° | -0,99756405 | -0,069756474 |
| 185° | -0,996194698 | -0,087155743 |
| 186° | -0,994521895 | -0,104528463 |
| 187° | -0,992546152 | -0,121869343 |
| 188° | -0,990268069 | -0,139173101 |
| 189° | -0,987688341 | -0,156434465 |
| 190° | -0,984807753 | -0,173648178 |
| 191° | -0,981627183 | -0,190808995 |
| 192° | -0,978147601 | -0,207911691 |
| 193° | -0,974370065 | -0,224951054 |
| 194° | -0,970295726 | -0,241921896 |
| 195° | -0,965925826 | -0,258819045 |
| 196° | -0,961261696 | -0,275637356 |
| 197° | -0,956304756 | -0,292371705 |
| 198° | -0,951056516 | -0,309016994 |
| 199° | -0,945518576 | -0,325568154 |
| 200° | -0,939692621 | -0,342020143 |
| 201° | -0,933580426 | -0,35836795 |
| 202° | -0,927183855 | -0,374606593 |
| 203° | -0,920504853 | -0,390731128 |
| 204° | -0,913545458 | -0,406736643 |
| 205° | -0,906307787 | -0,422618262 |
| 206° | -0,898794046 | -0,438371147 |
| 207° | -0,891006524 | -0,4539905 |
| 208° | -0,882947593 | -0,469471563 |
| 209° | -0,874619707 | -0,48480962 |
| 210° | -0,866025404 | -0,5 |
| 211° | -0,857167301 | -0,515038075 |
| 212° | -0,848048096 | -0,529919264 |
| 213° | -0,838670568 | -0,544639035 |
| 214° | -0,829037573 | -0,559192903 |
| 215° | -0,819152044 | -0,573576436 |
| 216° | -0,809016994 | -0,587785252 |
| 217° | -0,79863551 | -0,601815023 |
| 218° | -0,788010754 | -0,615661475 |
| 219° | -0,777145961 | -0,629320391 |
| 220° | -0,766044443 | -0,64278761 |
| 221° | -0,75470958 | -0,656059029 |
| 222° | -0,743144825 | -0,669130606 |
| 223° | -0,731353702 | -0,68199836 |
| 224° | -0,7193398 | -0,69465837 |
| 225° | -0,707106781 | -0,707106781 |
| 226° | -0,69465837 | -0,7193398 |
| 227° | -0,68199836 | -0,731353702 |
| 228° | -0,669130606 | -0,743144825 |
| 229° | -0,656059029 | -0,75470958 |
| 230° | -0,64278761 | -0,766044443 |
| 231° | -0,629320391 | -0,777145961 |
| 232° | -0,615661475 | -0,788010754 |
| 233° | -0,601815023 | -0,79863551 |
| 234° | -0,587785252 | -0,809016994 |
| 235° | -0,573576436 | -0,819152044 |
| 236° | -0,559192903 | -0,829037573 |
| 237° | -0,544639035 | -0,838670568 |
| 238° | -0,529919264 | -0,848048096 |
| 239° | -0,515038075 | -0,857167301 |
| 240° | -0,5 | -0,866025404 |
| 241° | -0,48480962 | -0,874619707 |
| 242° | -0,469471563 | -0,882947593 |
| 243° | -0,4539905 | -0,891006524 |
| 244° | -0,438371147 | -0,898794046 |
| 245° | -0,422618262 | -0,906307787 |
| 246° | -0,406736643 | -0,913545458 |
| 247° | -0,390731128 | -0,920504853 |
| 248° | -0,374606593 | -0,927183855 |
| 249° | -0,35836795 | -0,933580426 |
| 250° | -0,342020143 | -0,939692621 |
| 251° | -0,325568154 | -0,945518576 |
| 252° | -0,309016994 | -0,951056516 |
| 253° | -0,292371705 | -0,956304756 |
| 254° | -0,275637356 | -0,961261696 |
| 255° | -0,258819045 | -0,965925826 |
| 256° | -0,241921896 | -0,970295726 |
| 257° | -0,224951054 | -0,974370065 |
| 258° | -0,207911691 | -0,978147601 |
| 259° | -0,190808995 | -0,981627183 |
| 260° | -0,173648178 | -0,984807753 |
| 261° | -0,156434465 | -0,987688341 |
| 262° | -0,139173101 | -0,990268069 |
| 263° | -0,121869343 | -0,992546152 |
| 264° | -0,104528463 | -0,994521895 |
| 265° | -0,087155743 | -0,996194698 |
| 266° | -0,069756474 | -0,99756405 |
| 267° | -0,052335956 | -0,998629535 |
| 268° | -0,034899497 | -0,999390827 |
| 269° | -0,017452406 | -0,999847695 |
| 270° | -1,83772E-16 | -1 |
| 271° | 0,017452406 | -0,999847695 |
| 272° | 0,034899497 | -0,999390827 |
| 273° | 0,052335956 | -0,998629535 |
| 274° | 0,069756474 | -0,99756405 |
| 275° | 0,087155743 | -0,996194698 |
| 276° | 0,104528463 | -0,994521895 |
| 277° | 0,121869343 | -0,992546152 |
| 278° | 0,139173101 | -0,990268069 |
| 279° | 0,156434465 | -0,987688341 |
| 280° | 0,173648178 | -0,984807753 |
| 281° | 0,190808995 | -0,981627183 |
| 282° | 0,207911691 | -0,978147601 |
| 283° | 0,224951054 | -0,974370065 |
| 284° | 0,241921896 | -0,970295726 |
| 285° | 0,258819045 | -0,965925826 |
| 286° | 0,275637356 | -0,961261696 |
| 287° | 0,292371705 | -0,956304756 |
| 288° | 0,309016994 | -0,951056516 |
| 289° | 0,325568154 | -0,945518576 |
| 290° | 0,342020143 | -0,939692621 |
| 291° | 0,35836795 | -0,933580426 |
| 292° | 0,374606593 | -0,927183855 |
| 293° | 0,390731128 | -0,920504853 |
| 294° | 0,406736643 | -0,913545458 |
| 295° | 0,422618262 | -0,906307787 |
| 296° | 0,438371147 | -0,898794046 |
| 297° | 0,4539905 | -0,891006524 |
| 298° | 0,469471563 | -0,882947593 |
| 299° | 0,48480962 | -0,874619707 |
| 300° | 0,5 | -0,866025404 |
| 301° | 0,515038075 | -0,857167301 |
| 302° | 0,529919264 | -0,848048096 |
| 303° | 0,544639035 | -0,838670568 |
| 304° | 0,559192903 | -0,829037573 |
| 305° | 0,573576436 | -0,819152044 |
| 306° | 0,587785252 | -0,809016994 |
| 307° | 0,601815023 | -0,79863551 |
| 308° | 0,615661475 | -0,788010754 |
| 309° | 0,629320391 | -0,777145961 |
| 310° | 0,64278761 | -0,766044443 |
| 311° | 0,656059029 | -0,75470958 |
| 312° | 0,669130606 | -0,743144825 |
| 313° | 0,68199836 | -0,731353702 |
| 314° | 0,69465837 | -0,7193398 |
| 315° | 0,707106781 | -0,707106781 |
| 316° | 0,7193398 | -0,69465837 |
| 317° | 0,731353702 | -0,68199836 |
| 318° | 0,743144825 | -0,669130606 |
| 319° | 0,75470958 | -0,656059029 |
| 320° | 0,766044443 | -0,64278761 |
| 321° | 0,777145961 | -0,629320391 |
| 322° | 0,788010754 | -0,615661475 |
| 323° | 0,79863551 | -0,601815023 |
| 324° | 0,809016994 | -0,587785252 |
| 325° | 0,819152044 | -0,573576436 |
| 326° | 0,829037573 | -0,559192903 |
| 327° | 0,838670568 | -0,544639035 |
| 328° | 0,848048096 | -0,529919264 |
| 329° | 0,857167301 | -0,515038075 |
| 330° | 0,866025404 | -0,5 |
| 331° | 0,874619707 | -0,48480962 |
| 332° | 0,882947593 | -0,469471563 |
| 333° | 0,891006524 | -0,4539905 |
| 334° | 0,898794046 | -0,438371147 |
| 335° | 0,906307787 | -0,422618262 |
| 336° | 0,913545458 | -0,406736643 |
| 337° | 0,920504853 | -0,390731128 |
| 338° | 0,927183855 | -0,374606593 |
| 339° | 0,933580426 | -0,35836795 |
| 340° | 0,939692621 | -0,342020143 |
| 341° | 0,945518576 | -0,325568154 |
| 342° | 0,951056516 | -0,309016994 |
| 343° | 0,956304756 | -0,292371705 |
| 344° | 0,961261696 | -0,275637356 |
| 345° | 0,965925826 | -0,258819045 |
| 346° | 0,970295726 | -0,241921896 |
| 347° | 0,974370065 | -0,224951054 |
| 348° | 0,978147601 | -0,207911691 |
| 349° | 0,981627183 | -0,190808995 |
| 350° | 0,984807753 | -0,173648178 |
| 351° | 0,987688341 | -0,156434465 |
| 352° | 0,990268069 | -0,139173101 |
| 353° | 0,992546152 | -0,121869343 |
| 354° | 0,994521895 | -0,104528463 |
| 355° | 0,996194698 | -0,087155743 |
| 356° | 0,99756405 | -0,069756474 |
| 357° | 0,998629535 | -0,052335956 |
| 358° | 0,999390827 | -0,034899497 |
| 359° | 0,999847695 | -0,017452406 |
| 360° | 1 | 0 |
Часто используемые значения косинуса
Косинус 0 градусов = 1
Косинус 30 градусов = 0,866025404 = {\frac {\sqrt{3}}{2}}
Косинус 45 градусов = 0,707106781 = {\frac {\sqrt{2}}{2}}
Косинус 60 градусов = 0,5 = {\frac {1}{2}}
Косинус 90 градусов = 0
Косинус 120 градусов = -0,5 = {-\frac {1}{2}}
Косинус 135 градусов = -0,707106781 = {-\frac {\sqrt{3}}{2}}
Косинус 180 градусов = -1
Ваша оценка
[Оценок: 72 Средняя: 4]Просмотров страницы: 54 543
mnogoformul.ru
Почему Косинус Равен 1-Sina (См.)?
Почему? Благодаря реформе образования! Этот самый «321-й апостол» есть продукт какой системы образования? Правильно, болонской. А для чего нам ея внедряли? А для того, чтобы (чуть не сказал — мозг…) моСК «жертв» этой самой системы низвести до уровня болонок. Которым ум нашего дворового Кабыздоха — даже и не снится. А на кой? Чтобы лизать ручки хозяев да выпрашивать подачки — ум не нужон… Впрочем, в сторону лирику — вернёмся к математике. Первое, что «дореформенные» школяры (причём даже не учили) понимали в тригонометрии — это то, что синус (как проекция единичного вектора на вертикальную ось) и косинус (как проекция ЕВ на горизонтальную) вместе с единичным вектором составляли тот самый пифагоров треугольник. У которого квадрат гипотенузы равен сумме квадратов катетов. И от понимания этого «танцует» вся тригонометрия. Любые сложнейшие тригонометрические преобразования можно «разобрать» на элементарные составляющие, если понимать, откуда «ноги растут» у синусов и косинусов. Если — ПОНИМАТЬ. А не зазубрить… А у нашего «пофигора» уже на старте — грубый ляп: сумма катетов равна гипотенузе. Пифагор в гробу пере… Впрочем, он сейчас уже даже не вентиллятор напоминает, скорее — турбину воздушного лайнера… Решение задачки: Синус А = 3/5, квадрат синуса = 9/25, отсюда квадрат косинуса А = 16/25, косинус А = 4/5… Числители в синусе и косинусе — ничего не напоминают? Ладно, «добьём» по тригонометрическим формулам… АС = 12, АВ = АС / косинус А = 12 / 4/5 = 15; ВС = АС х синус А = 15 / 3/5 = 9. А теперь выбросим из головы тригонометрию и вспомним «Пифагоровы штаны». Пифагор знаменитую теорему доказывал исходя из практики гарпедонаптов (египетских «натягивателей верёвок»), которые строили прямой угол с помощью верёвки, разделённой метками на 12 равных отрезков: если три отрезка идут по одной стороне угла, четыре — по другой, а пять — по диагонали, то угол прямой. И как раз треугольник со сторонами 3, 4 и 5 — самый маленький из пифагорейских. Величина синуса А (3/5) уже сама по себе показывает нам тот самый Пифагоров треугольник, так что косинус можно и не задумываясь найти из тех же «3, 4, 5»: косинус А = 4/5. Длина стороны АС кратна катетам Пифагорова треугольника (12 = 3 х 4), причём обоим. Но поскольку искомый катет ВС относится к диагонали АС как 3 к 5 (синус А = 3/5), то известный катет АС отностися к то же диагонали как 4 к 5. Елементарно делим длину АС на 4 и умножаем полученный результат на 3 — сторона ВС равна 9. ВСЁ!!!
otvet.expert
