Первичный план перевозок в транспортной задаче можно получить используя – Ветошкин А.А., Костякова А.И. Транспортная задача Методы задания базового плана перевозок. Вырожденность транспортной задачи и как с ней бороться
ТРАНСПОРТНАЯ ЗАДАЧА
| Напомним | сначала | метод северо-западного | угла. Заполнение | ||||||
|
|
|
|
|
|
|
| таблицы начинаем с левого | ||
|
| B1 | B2 | B3 | B4 | ai | верхнего (северо-западного) | |||
A1 |
| 1 | 40 | 11 | 3 | 13 | 140 | угла таблицы. Так как по- | ||
| 80 |
| 20 |
| ||||||
|
|
|
|
|
|
|
| требности первого потреби- | ||
A2 |
| 12 |
| 4 | 8 | 2 | 160 | |||
|
| теля В1 равны 80, а запасы | ||||||||
|
|
|
| 130 | 30 | |||||
A3 |
| 3 |
| 5 | 14 | 6 | 100 | первого поставщика A1 | рав- | |
|
|
|
|
| 100 | ны 140, то в клетку | A1B1 | |||
bj |
| 80 | 40 | 150 | 130 | 400 | ||||
| вписываем | максимально | ||||||||
|
|
| Таблица 2.3 |
|
| возможную перевозку | 80. | |||
|
|
|
|
|
|
|
| |||
Потребности В1 | полностью удовлетворены, поэтому первый столбец | |||||||||
исключаем из рассмотрения, а оставшиеся запасы первого поставщика, т.е. 60, переносим следующим потребителям. Мы можем 40 записать потребителю В2 (столбецВ2 исключается), а оставшиеся 20 –В3
и исключить первую строку из дальнейшего рассмотрения.
Далее, так как потребности В3 равны 150, а 20 единиц груза ему
уже доставлены, то оставшиеся 130 единиц доставляются от второго поставщика A2 (заполняем клеткуA2B3 ) . С толбецВ3 исключаем из
рассмотрения, а оставшиеся запасы второго поставщика (30 единиц) записываем потребителю В4 . Окончательно потребности последнего
удовлетворяются за счет поставщика A3 : вписываем в клеткуA3B4 пе-
ревозку 100. Заметим, что, так как исходная задача — с правильным балансом, то потребности последнего потребителя B4 равны запасам по-
ставщика A3 , т.е. 100. Получаем таблицу 2.3 с начальным опорным планом
| 80 | 40 | 20 | 0 |
|
| 0 | 0 | 130 | 30 |
|
X = | . | ||||
| 0 | 0 | 0 | 100 |
|
|
|
Суммарная стоимость перевозок равна
z(X )=1 80+11 40+3 20+8 130+ 2 30+6 100= 2280.
Из решения видно, что метод северо-западногоугла, с одной стороны, достаточно прост с точки зрения построения, а с другой стороны, не учитывает стоимость перевозок. Поэтому опорный план, построенный методомсеверо-западногоугла, как правило, далек от оптимального.
studfiles.net
Транспортная задача — решение методом потенциалов
Одна из самых распространенных и востребованных оптимизационных задач в логистике – транспортная задача. В классическом виде она предполагает нахождение оптимального (т.е. сопряженного с минимальными затратами) плана грузоперевозок.
Например, у нас есть сеть розничных магазинов, которым требуется определенное количество товаров. Также имеется ряд складов поставщиков, где требуемые товары хранятся. При этом на каждом складе различный объем запасов этих товаров. Кроме этого нам известны тарифы – затраты на перевозку 1 товара от каждого склада к каждому магазину.
Возникает необходимость разработать такой план перевозок, чтобы магазины получили требуемое количество товаров с наименьшими затратами на транспортировку. Вот именно в таких случаях (и во множестве других) приходится решать транспортную задачу.
Теоретический материал по транспортной задаче
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.
Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления (например, складов) в пункты потребления (например, магазины), с минимальными общими затратами на перевозки.
Математическая модель транспортной задачи имеет следующий вид:
где: Z — затраты на перевозку грузов;
X — объем груза;
C — стоимость (тариф) перевозки единицы груза;
A — запас поставщика;
B — запрос потребителя;
m — число поставщиков;n — число потребителей.
Общий план решения транспортной задачи методом потенциалов
Решить транспортную задачу можно различными методами, начиная от симплекс-метода и простого перебора, и заканчивая методом графов. Один из наиболее применяемых и подходящих для большинства случаев методов – итерационное улучшение плана перевозок.
Суть его в следующем: находим некий опорный план и проверяем его на оптимальность (Z → min). Если план оптимален – решение найдено. Если нет – улучшает план столько раз, сколько потребуется, пока не будет найден оптимальный план.
Ниже приведен алгоритм решения транспортной задачи в самом общем виде:
- Построение транспортной таблицы.
- Проверка задачи на закрытость.
- Составление опорного плана.
- Проверка опорного плана на вырожденность.
- Вычисление потенциалов для плана перевозки.
- Проверка опорного плана на оптимальность.
- Перераспределение поставок.
- Если оптимальное решение найдено, переходим к п. 9, если нет – к п. 5.
- Вычисление общих затрат на перевозку груза.
- Построение графа перевозок.
Подробная инструкция по решению транспортной задачи
1. Построение транспортной таблицы
Строим таблицу, где указываем запасы материалов, имеющиеся на складах поставщиков (Ai), и потребности заводов (Bj) в этих материалах.
В нижний правый угол ячеек таблицы заносим значение тарифов на перевозку груза (
Обозначим суммарный запас груза у всех поставщиков символом A, а суммарную потребность в грузе у всех потребителей – символом B.
Тогда:
Транспортная задача называется закрытой, если A = B . Если же A ≠ B , то транспортная задача называется открытой. В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.A = 10 + 20 + 30 = 60
B = 15 + 20 + 25 = 60
A = B, следовательно данная транспортная задача – закрытая.
3. Составление опорного плана
Составляет предварительный (опорный) план перевозок. Он не обязательно должен быть оптимальный. Это просто своеобразный «черновик», «набросок», улучшая который мы постепенно придем к плану оптимальному.
Есть разные методы нахождения опорного плана. Наиболее распространены следующие:
а) Метод Северо-Западного угла. Показать
Суть метода проста — ячейки транспортной таблицы последовательно заполняются максимально возможными объемами перевозок, в направлении
Подробное описание метода и пример можно посмотреть здесь.
б) Метод минимального элемента. Показать
Метод заключается в том, что для заполнения ячеек транспортной таблицы выбирается клетка с минимальным значением тарифа. Затем выбирается следующая клетка с наименьшим тарифом и так продолжается до тех пор, пока таблица не будет заполнена (все запасы и потребности при этом обнулятся).
Подробное описание метода и пример можно посмотреть здесь
в) Аппроксимация Фогеля. Показать
Основа метода в нахождении разности (по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем в строке или столбце с наибольшей разностью заполняется клетка с наименьшим тарифом. Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки.
Подробное описание аппроксимации Фогеля и пример можно посмотреть онлайн
г) Метод двойного предпочтения. Показать
Суть метода в том, что отмечаются клетки с наименьшим тарифом по строкам, а затем по столбцам. Затем ячейки заполняются в следующей очередности: сначала клетки с двумя отметками, потом с одной, наконец без отметок.Подробное описание метода и пример можно посмотреть здесь
4. Проверка опорного плана на вырожденность
Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свободными.
План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n -1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся). Однако проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим!
План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ниже приведен пример цикла:
Ломаная линия может иметь точки самопересечения, но не в клетках цикла.Кол-во базисных клеток = 5
m + n – 1 = 3 + 3 – 1 = 5
Следовательно, первоначальный план перевозок – невырожденный.
5. Вычисление потенциалов для плана перевозки
Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.
Этот метод улучшения плана перевозок называется методом потенциалов. Есть другие методы итерационного улучшения плана перевозок, но здесь мы их рассматривать не будем.
Итак, сопоставим каждому поставщику Ai и каждому потребителю Bj величины Ui и Vj соответственно так, чтобы для всех базисных клеток плана было выполнено соотношение:
Ui + Vj = Cij
Добавим к транспортной таблице дополнительную строку и столбец для Ui и Vj.
Предположим, что U1 = 0.
Тогда мы сможем найти V3 = C13 – U1 = 1 – 0 = 1.
Зная V3, мы теперь можем найти U3:
По аналогии вычисляем все оставшиеся потенциалы:
6. Проверка плана на оптимальность методом потенциалов
Для каждой свободной клетки плана вычислим разности
ΔCij = Cij – (Ui + Vj )
и запишем полученные значения в левых нижних углах соответствующих ячеек.
План является оптимальным, если все разности ΔCij ≥ 0.
В данном случае план – неоптимальный (ΔC22 < 0), и его следует улучшить путем перераспределения поставок.
7. Перераспределение поставок
Найдем ячейку с наибольшей по абсолютной величине отрицательной разностью ΔCij и построим цикл, в котором кроме этой клетки все остальные являются базисными. Такой цикл всегда существует и единственен.
Отметим ячейку с отрицательной разностью ΔCij знаком «+», следующую знаком «-», и так далее, поочередно.
Затем находим минимальной значение груза в ячейках цикла имеющих знак «-» (здесь это 5) и вписываем его в свободную ячейку со знаком «+». Затем последовательно обходим все ячейки цикла, поочередно вычитая и прибавляя к ним минимальное значение (в соответствии со знаками, которыми эти ячейки помечены: где минус — вычитаем, где плюс — прибавляем).
Получим новый опорный план перевозок:
Так как базисных клеток стало больше, чем m + n – 1, то базисную клетку с нулевым значением делаем свободной:
Снова вычисляем значения потенциалов и разности ΔCij:
На этот раз все разности ΔCij ячеек положительные, следовательно, найдено оптимальное решение.8. Если оптимальное решение найдено, переходим к п. 9, если нет – к п. 5.
У нас оптимальное решение найдено, поэтому переходим к пункту 9.
9. Вычисление общих затрат на перевозку груза
Вычислим общие затраты на перевозку груза (Z), соответствующие найденному нами оптимальному плану, по формуле:
Zmin = 10 ∙ 1 + 15 ∙ 3 + 5 ∙ 2 + 15 ∙ 1 + 15 ∙ 2 = 110 ден. ед.
Общие затраты на доставку всей продукции, для оптимального решения, составляют 110 ден. ед.
10. Построение графа перевозок
Найдя оптимальный план перевозок, построим граф. Вершинами графа будут «склады» и «магазины». В вершинах укажем соответствующие объемы запасов и потребностей. Дугам, соединяющим вершины графа, будут соответствовать ненулевые перевозки. Каждую такую дугу подпишем, указав объем перевозимого груза.
В результате получится граф, аналогичный изображенному ниже:
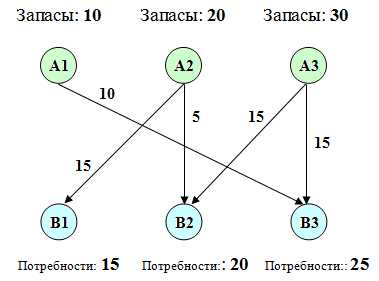
Все, транспортная задача решена. Поздравляю!
Практическое применение транспортной задачи
Транспортная задача применяется во многих случаях. Это оптимизация поставок сырья и материалов на производственные предприятия. Это оптимизация доставок товаров со складов в розничные магазины. Это оптимизация пассажирских перевозок, и много-многое другое.
Галяутдинов Р.Р.
© Копирование материала допустимо только при указании прямой гиперссылки на источник: Галяутдинов Р.Р.
galyautdinov.ru
6.2. Нахождение опорного плана транспортной задачи
Как и при решении ЗЛП по планированию симплексным методом, определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана. Рассмотрим несколько методов нахождения такого плана.
Метод северо-западного угла. На примере конкретной задачи продемонстрируем этот метод нахождения опорного плана.
З а д а ч а 12. На три базы А1, А2, А3 поступил однородный груз в количествах, соответственно равных 140, 180, 160 ед. Этот груз требуется перевезти в пять пунктов назначения В1, В2, В3, В4, В5 соответственно в количествах 60, 70, 120, 130, 100 ед. Тарифы перевозок единичного количества груза с каждого из складов в соответствующие пункты назначения указаны в табл.16. Найти план перевозок данной транспортной задачи методом северо-западного угла.
Таблица 16
Структурная запись задачи
Поставщик | Пункт назначения | Запасы | ||||
В1 | В2 | В3 | В4 | В5 | ||
А1 | 2 | 3 | 4 | 2 | 4 | 140 |
А2 | 8 | 4 | 1 | 4 | 1 | 180 |
А3 | 9 | 7 | 3 | 7 | 2 | 160 |
Потребность | 60 | 70 | 120 | 130 | 100 | 480 |
Р е ш е н и е. Введем понятие маршрута – наименование клетки АiBj, где i – порядковый номер поставщика, j – порядковый номер потребителя.
Задача является закрытой, так как количество имеющегося у поставщиков грузов равно объему грузов, запрашиваемых потребителями. Здесь число пунктов отправления m=3, а число пунктов назначения n=5. Следовательно, невырожденный опорный план задачи будет определяться числом заполненных маршрутов (ненулевых переменных) в количестве 5+3-1=7.
По рассматриваемому методу заполнение маршрутов начнем с клетки, стоящей в левом верхнем углу. Потребность в грузе пункта В1 составляет 60 ед и от поставщика А1 можно эту потребность полностью удовлетворить. Иначе, по маршруту А1В1 будет запланирована поставка в размере 60 ед. Следующий потребитель В2 нуждается в поставке 70 ед груза, что также можно выполнить, доставив требуемый объем груза от поставщика А1 , у которого после первой поставки осталось 140-60=80 ед. Таким образом, по маршруту А1В2 можно запланировать доставку груза в полном объеме. Оставшийся у поставщика А1 объем груза в 10 ед запланируем доставить потребителю В3,
т.е. по маршруту А1В3. Так как ресурсы поставщика А1 полностью израсходованы, потребителю В2 оставшиеся 110 ед груза запланируем доставить по маршруту А2В3 , т.е. от поставщика А2. Пользуясь подобным алгоритмом, по маршруту А2В4 запланируем доставку 70 ед, по маршруту А3В4 доставку 60 ед и по маршруту А3В5 оставшиеся 100 ед груза (табл.17).
Таблица 17
Результирующая таблица опорного плана задачи 12
Поставщик | Пункт назначения | Запасы | ||||
В1 | В2 | В3 | В4 | В5 | ||
А1 | 2 60 | 3 70 | 4 10 | 2 | 4 | 140 |
А2 | 8 | 4 | 1 110 | 4 70 | 1 | 180 |
А3 | 9 | 7 | 3 | 7 60 | 2 100 | 160 |
Потребность | 60 | 70 | 120 | 130 | 100 | 480 |
Теперь рассчитаем суммарные затраты на доставку всего объема грузов:
Остается только оценить полученный план. Он выглядит в матричной форме следующим образом:
 .
.
План имеет 7 заполненных маршрутов. Следовательно, полученный опорный план невырожденный, может быть проанализирован на оптимальность и при необходимости улучшен (см. ниже).
Метод минимального элемента. В методе северо-западного угла алгоритм заполнения маршрутов был построчный с учетом остатков груза у очередного поставщика, при этом полностью игнорировались размеры тарифных ставок на перевозки. Очевидно, что минимальная стоимость перевозок будет обеспечена в большей мере, если при заполнении соответствующих маршрутов (клеток) отдавать предпочтение маршрутам с минимальной тарифной ставкой на перевозку. В этом и заключается идея метода минимального элемента.
З а д а ч а 13. Повторим процедуру нахождения первичного опорного плана для сформулированной выше задачи, реализуя этот метод.
В общем наборе тарифов есть два маршрута со ставкой «1» и три маршрута со ставкой «2», два маршрута со ставкой «3», четыре маршрута со ставкой «4», два маршрута со ставкой «7», по одному маршруту со ставками «8» и «9». В такой же последовательности будем перераспределять груз. При равенстве тарифов маршрут выбирают произвольно.
Начнем с маршрута А2В5. Назначим объем перевозок по нему 100 ед, а по маршруту А2В3 оставшиеся у поставщика А2 80 ед груза. Естественно, маршруты А1В5 и А3В5 , а также А2В1, А2В2, А2В4 должны быть выключены из списка свободных (знак Х). Теперь заполним маршрут А1В1 , назначив по нему перевозку груза в объеме 60 ед (таков запрос потребителя В1) и выведем из состава свободных маршрут А3В1. Следующим заполняем маршрут А1В4 количеством груза в объеме 80 ед (оставшиеся у поставщика А1 после заполнения маршрута А1В1). Соответственно исключаем маршруты А1В2, А1В3. Оставшиеся маршруты закрываем безвариантно (табл.18).
Таблица 18
Заполнение таблицы при методе минимального элемента
Поставщик | Пункт назначения | Запасы | ||||
В1 | В2 | В3 | В4 | В5 | ||
А1 | 2 60 | 3 Х | 4 Х | 2 80 | 4 Х | 140 |
А2 | 8 Х | 4 Х | 1 80 | 4 Х | 1 100 | 180 |
А3 | 9 Х | 7 70 | 3 40 | 7 50 | 2 Х | 160 |
Потребность | 60 | 70 | 120 | 130 | 100 | 480 |
В результате получаем следующий опорный план:
 ,
,
для которого функция цели принимает значение
.
Полученный план имеет 7 заполненных маршрутов, поэтому план невырожденный и может быть в дальнейшем улучшен (если при первом шаге начать составление плана с маршрута А2В3, то получим план со значением функции цели F=1480).
Видим, что для данной задачи метод северо-западного угла дает более перспективный план.
Метод аппроксимации по Фогелю. В принципе этот метод является развитием идеи метода минимального элемента, т.е. заполнение маршрутов с учетом тарифных ставок.
З а д а ч а 14. Рассмотрим его на примере той же задачи. Правее столбцов и ниже строк записывают текущую разность между тарифными ставками незакрытых маршрутов как по строкам (справа), так и по столбцам (внизу). Разность определяется между двумя минимальными ставками. Из полученных разностей выбирается наибольшая по абсолютному значению и далее первым заполняется тот маршрут в данном столбце или строке, который имеет минимальную тарифную ставку. Если по какому-либо потребителю или поставщику полностью используются запасы или закрываются поставки, все остальные маршруты по данному направлению закрываются и прекращаются процедуры нахождения разностей по тарифам. В табл.19 представлены результаты поиска опорного плана по вышеописанной схеме.
Таблица 19
Нахождение опорного плана по Фогелю
Склад | Потребитель | Запас | Разность по строкам | ||||||||||
В1 | В2 | В3 | В4 | В5 | |||||||||
А1 | 2 60 | 3 Х | 4 Х | 2 80 | 4 Х | 140 | 1 | 1 | 1 | 1 | — | ||
А2 | 8 Х | 4 60 | 1 120 | 4 Х | 1 Х | 180 | 3 | 3 | 3 | 0 | 0 | ||
А3 | 9 Х | 7 10 | 3 Х | 7 50 | 2 100 | 160 | 1 | 1 | 5 | 0 | 0 | ||
Потреб- ность | 60 | 70 | 120 | 130 | 100 | 480 | |||||||
Разность по столбцам | 6 | 1 | 2 | 2 | 1 | ||||||||
— | 1 | 2 | 2 | 1 | |||||||||
— | 1 | — | 2 | 1 | |||||||||
— | 1 | — | 2 | — | |||||||||
— | 3 | — | 3 | — | |||||||||
В таблице соблюдался следующий порядок заполнения маршрутов: А1В1, А2В3, А3В5, А1В4, А2В2, А3В2, А3В4. Максимальные разности по столбцам и строкам выделены жирным шрифтом.
В результате получен следующий опорный план:
 ,
,
т.е. опорный план имеет 7 заполненных маршрутов, а, следовательно, он невырожденный. Функция цели принимает значение:
.
Очевидно, наилучший опорный план получен по методу Фогеля, но и он может быть в дальнейшем улучшен (см. ниже).
studfiles.net
Постановка транспортной задачи
Транспортная задача
Постановка транспортной задачи
Транспортная задача (Т-задача) является одной из наиболее распространенных специальных задач ЛП. Первая строгая постановка Т-задачи принадлежит Ф. Хичкоку, поэтому в зарубежной литературе ее часто называют проблемой Хичкока.
Первый точный метод решения Т-задачи разработан Л. В. Канторовичем и М. К. Гавуриным.
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления (заводы, склады, базы и т.д.) в n пунктов назначения (магазины). При этом, из каждого пункта отправления (производства) возможно транспортировка продукта в любой пункт назначения (потребления). В качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.
Пример.
Четыре предприятия данного экономического района для производства продукции используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 120, 50, 190 и 110 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 160, 140, 170 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей
Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.
Решение. Обозначим через количество единиц сырья, перевозимого из i–го пункта его получения на j–е предприятие. Тогда условия доставки и вывоза необходимого и имеющегося сырья обеспечиваются за счет выполнения следующих равенств:
(6)
При данном плане перевозок общая стоимость перевозок составит
(7)
Таким образом, математическая постановка данной транспортной задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений (6), при котором целевая функция (7) принимает минимальное значение.
Решение транспортной задачи
Основные шаги при решении транспортной задачи:
1. Найти начальный допустимый план.
2. Выбрать из небазисных переменных ту, которая будет вводиться в базис. Если все небазисные переменные удовлетворяют условиям оптимальности, то закончить решение, иначе к след. шагу.
3. Выбрать выводимую из базиса переменную, найти новое базисное решение. Вернуться к шагу 2.
Всякое неотрицательное решение систем линейных уравнений (2) и (3), определяемое матрицей , называется планом транспортной задачи. Опорным (базисным) планом Т-задачи называют любое ее допустимое, базисное решение.
Обычно исходные данные транспортной задачи записывают в виде таблицы.
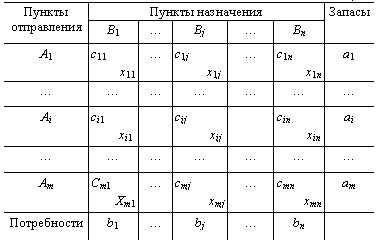
Матрицу С называют матрицей транспортных затрат, матрицу X, удовлетворяющую условиям Т-задачи (2) и (3) называют планом перевозок, а переменные — перевозками. План , при котором целевая функция минимальна, называется оптимальным.
Число переменных в транспортной задаче с m пунктами отправления и n пунктами назначения равно m*n, а число уравнений в системах (2) и (3) равно m+n. Так как мы предполагаем, что выполняется условие (5), то число линейно независимых уравнений равно m+n–1. Следовательно, опорный план транспортной задачи может иметь не более m+n–1отличных от нуля неизвестных.
Если в опорном плане число отличных от нуля компонент равно в точности m+n–1, то план является невырожденным, а если меньше – то вырожденным.
Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом.
Построение допустимого (опорного) плана в транспортной задаче
По аналогии с другими задачами линейного программирования решение транспортной задачи начинается с построения допустимого базисного плана. Существует несколько методов построения начальных опорных планов Т-задачи. Из них самый распространенный метод северо-западного угла и метод минимального элемента.
Наиболее простой способ его нахождения основывается на так называемом методе северо-западного угла. Суть метода состоит в последовательном распределении всех запасов, имеющихся в первом, втором и т. д. пунктах производства, по первому, второму и т. д. пунктам потребления. Каждый шаг распределения сводится к попытке полного исчерпания запасов в очередном пункте производства или к попытке полного удовлетворения потребностей в очередном пункте потребления. На каждом шаге q величины текущих нераспределенных запасов обозначаются аi(q), а текущих неудовлетворенных потребностей — bj(q). Построение допустимого начального плана, согласно методу северо-западного угла, начинается с левого верхнего угла транспортной таблицы, при этом полагаем аi(0)= аi, bj(0)= bj. Для очередной клетки, расположенной в строке i и столбце j, рассматриваются значения нераспределенного запаса в i-ом пункте производства и неудовлетворенной потребности j-ом пункте потребления, из них выбирается минимальное и назначается в качестве объема перевозки между данными пунктами: хi,j=min{аi(q), bj(q)}. После этого значения нераспределенного запаса и неудовлетворенной потребности в соответствующих пунктах уменьшаются на данную величину:
аi(q+1)= аi(q) — xi,j, bj(q+1)= bj(q) — xi,j
Очевидно, что на каждом шаге выполняется хотя бы одно из равенств: аi(q+1)= 0 или bj(q+1)= 0. Если справедливо первое, то это означает, что весь запас i-го пункта производства исчерпан и необходимо перейти к распределению запаса в пункте производства i+1, т. е. переместиться к следующей клетке вниз по столбцу. Если же bj(q+1) = 0, то значит, полностью удовлетворена потребность для j-го пункта, после чего следует переход на клетку, расположенную справа по строке. Вновь выбранная клетка становится текущей, и для нее повторяются все перечисленные операции.
Основываясь на условии баланса запасов и потребностей, нетрудно доказать, что за конечное число шагов мы получим допустимый план. В силу того же условия число шагов алгоритма не может быть больше, чем m+n-1, поэтому всегда останутся свободными (нулевыми) mn-(m+n-1) клеток. Следовательно, полученный план является базисным. Не исключено, что на некотором промежуточном шаге текущий нераспределенный запас оказывается равным текущей неудовлетворенной потребности (аi(q)=bj(q)). В этом случае переход к следующей клетке происходит в диагональном направлении (одновременно меняются текущие пункты производства и потребления), а это означает «потерю» одной ненулевой компоненты в плане или, другими словами, вырожденность построенного плана.
Особенностью допустимого плана, построенного методом северо-западного угла, является то, что целевая функция на нем принимает значение, как правило, далекое от оптимального. Это происходит потому, что при его построении никак не учитываются значения ci,j. В связи с этим на практике для получения исходного плана используется другой способ — метод минимального элемента, в котором при распределении объемов перевозок в первую очередь занимаются клетки с наименьшими ценами.
Пример нахождения опорного плана
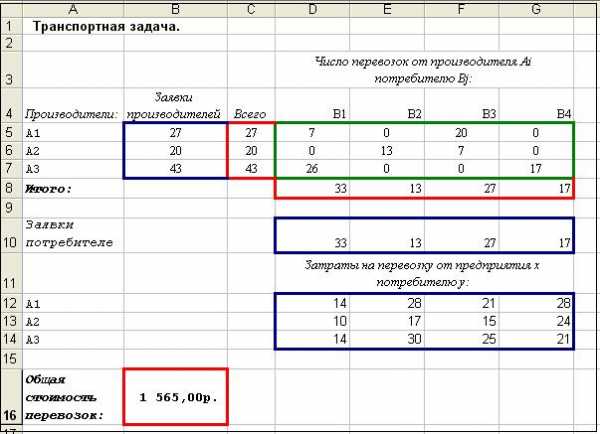
| Поставщики | Потребители и их спрос | Мощность поставщиков | |||
F=14 x11 + 28 x12 + 21 x13 + 28 x14 + 10 x21 + 17 x 22 + 15 x23 + 24 x24 + 14 x31 + 30 x32 +25 x33 + 21 x34
Первоначальный план получен по методу северо-западного угла. Задача сбалансированная (закрытая).
Таблица 1
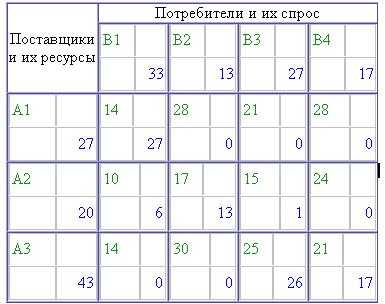
Стоимость перевозок по данному плану составляет: 1681:
F=14 *27 + 28* 0 + 21*0 + 28*0 + 10 *6 + 17 *13 + 15*1 + 24 *0 + 14 *0 + 30 *0 +25*26 + 21 *17 =1681
Решение задачи в Excel
Для решения задачи используется команда Сервис/Поиск решения.
Если такой команды в меню нет, то необходимо выполнить команду Сервис/Надстройки и установить Поиск решения.
После выполнения команды появится окно:
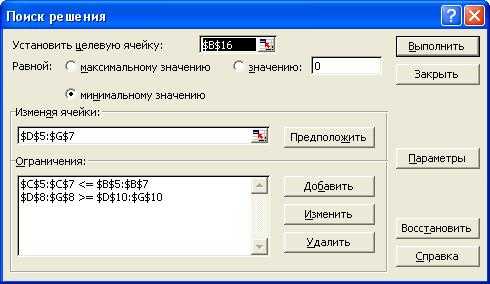
Задать ячейку с целевой функцией, изменяемые ячейки, ограничения.
Задать параметры «Линейная модель» и «Неотрицательные значения» (См. лекцию по ЛП).
Для нахождения решения нажать кнопку «Выполнить» в окне Поиска решения.
В появившемся окне «Результаты поиска решения» отображается информация о том, найдено или нет решение, в этом окне можно выбрать тип отчета.
Иногда сообщения о том, найдено или нет оптимальное решение свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Для выбора нужных отчетов необходимо выделить их названия. Отчет будет представлен на отдельном листе рабочей книги Excel.
Для получения более полной информации в отчете по устойчивости нужно в окне задания параметров установить флажок «Линейная модель«.
Для получения же ответа (значений переменных и ЦФ) прямо в экранной форме можно сразу нажать кнопку «OK». После этого в экранной форме появляется оптимальное решение задачи.
Замечания по решению ТЗ:
· Если запасы груза в пунктах отправления и потребности в пунктах назначения выражены целыми числами, то, исходя из алгоритма решения ТЗ будут получены целочисленные решения.
· Если задача не сбалансированная и при этом объемы предложения больше спроса, то ограничения не меняются.
· Если задача не сбалансированная и при этом объемы предложения меньше спроса, то в ограничениях на количество отправляемых грузов надо знак « <= » поменять на знак « = », а в ограничениях на количество доставляемых грузов поменять знак « >= » на знак « <= » (т.е. не все потребности будут удовлетворены).
· Если по каким-либо маршрутам нельзя перевозить продукцию, то стоимости перевозок по этим маршрутам задаются так, чтобы они превышали самые высокие стоимости возможных перевозок (для того, чтобы было невыгодно везти по недоступным маршрутам) – при решении задачи на минимум. На максимум – наоборот.
· Если нужно учесть, что между какими-то пунктами отправки и какими-то пунктами потребления заключены договора на фиксированные объемы поставки, то надо исключить объем гарантированной поставки из дальнейшего рассмотрения. Для этого объем гарантированной поставки вычитается из следующих величин:
§ из запаса соответствующего пункта отправки;
§ из потребности соответствующего пункта назначения.
Отчет по результатам
Отчет по результатам состоит из трех таблиц:
· таблица 1 содержит информацию о ЦФ;
· таблица 2 содержит информацию о значениях переменных, полученных в результате решения задачи;
· таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Отчет по устойчивости
Отчет по устойчивости состоит из двух таблиц.
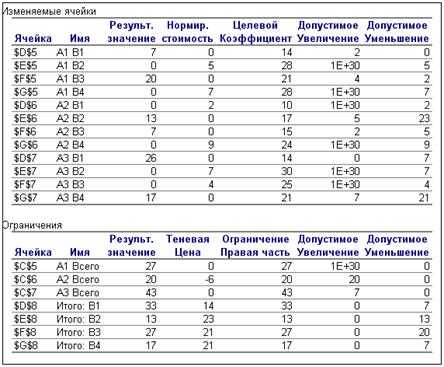
Таблица 1 содержит информацию, относящуюся к переменным:
· Результ. значение показывает результат решения задачи.
· Нормированная стоимостьпоказывает, на сколько изменится значение ЦФ в случае принудительного включения единицы соответствующей перевозки в оптимальное решение.
· Коэффициенты ЦФотображают исходные данные.
· Допустимое увеличение и уменьшениепоказывают предельные значения приращения целевых коэффициентов, при которых сохраняется первоначальное оптимальное решение. Другими словами: на сколько нужно снизить затраты на перевозку по неиспользуемым направлениям, чтобы по ним было выгодно везти продукцию. Например, если затраты на перевозку из А1 в В2 снизить более, чем на 5 единиц, т.е. они станут < 28-5, то везти груз по этому маршруту станет выгодно.
Таблица 2 содержит информацию, относящуюся к ограничениям.
· Результ. значение показывает сколько всего груза заберут у производителей и привезут потребителям.
· Теневая ценапоказывает, на сколько будет изменяться значение ЦФ (т.е. общие затраты на перевозки), если будут уменьшаться потребности в пунктах назначения или увеличиваться запасы в пунктах отправления (в другую сторону невозможно, т.к. данная задача будет неразрешима из-за превышения спроса над предложением).
· Ограничение правая частьпоказывает исходные данные из правых частей ограничений.
· Допустимое увеличение и уменьшение показывают предельные значения уменьшения потребностей или увеличения запасов.
Транспортная задача
Постановка транспортной задачи
Транспортная задача (Т-задача) является одной из наиболее распространенных специальных задач ЛП. Первая строгая постановка Т-задачи принадлежит Ф. Хичкоку, поэтому в зарубежной литературе ее часто называют проблемой Хичкока.
Первый точный метод решения Т-задачи разработан Л. В. Канторовичем и М. К. Гавуриным.
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления (заводы, склады, базы и т.д.) в n пунктов назначения (магазины). При этом, из каждого пункта отправления (производства) возможно транспортировка продукта в любой пункт назначения (потребления). В качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.
infopedia.su
Постановка транспортной задачи — Мегаобучалка
Существуют некоторые специальные классы задач линейного программирования, для решения которых можно использовать специальные методы, позволяющие ускорить процесс решения, учитывая специфику задачи. К таким задачам относятся, например, транспортные задачи (ТЗ).
Рассмотрим общую постановку транспортной задачи.
Постановка задачи. Пусть имеется пунктов производства некоторого товара, и пунктов потребления этого товара. Известны запасы товара ( ) на каждом пункте производства , потребности ( ) каждого пункта потребления , а также стоимости перевозок товара от каждого -того пункта производства к каждому -ому пункту потребления. Требуется составить наиболее экономичный план перевозок товара от пунктов производства к пунктам потребления.
Построим математическую модель задачи.
1). Искомые переменные задачи:
— объем перевозок от -ого пункта производства к -ому пункту потребления, где , .
План перевозок можно рассматривать, как вектор размерности .
2). Ограничения задачи.
а). Ограничения на возможности вывоза запасов из всех пунктов производства.
Суммарный объем перевозок из каждого пункта производства не может превышать объема, произведенного там товара:
, . (2.1)
b). Ограничения на потребности во всех пунктах потребления.
Суммарные перевозки в каждый пункт потребления должны полностью удовлетворять спрос на товар:
, . (2.2)
с). Ограничения на знак переменных.
Искомые переменные по условию не могут быть отрицательными:
, , . (2.3)
3). Целевая функция минимизирует общие затраты на перевозку.
Здесь — стоимость перевозок единицы товара от -ого пункта производства к -ому пункту потребления.
Математическая постановка транспортной задачи может быть записана в виде:
(2.4)
(2.5)
Отметим важное свойство транспортной задачи. Для разрешимости ТЗ необходимо и достаточно, чтобы выполнялось условие баланса, при котором суммарный объем производства равен суммарному объему потребления:
. (2.6)
Транспортная задача, для которой выполнено условие баланса (2.6), называется сбалансированной или закрытой. При невыполнении условия (2.6) соответствующая задача называется несбалансированной или открытой.
Заметим, что открытая ТЗ всегда может быть сведена к закрытой путем введения фиктивного пункта производства или фиктивного пункта потребления .
Сбалансированная задача, согласно свойству (2.6) всегда имеет решение.
Рассмотрим сбалансированную задачу. При этом неравенства (2.1) и (2.2) перейдут в равенства. Математическая постановка сбалансированной задачи можно записать в форме ЗЛП:
(2.7)
(2.8)
Таким образом, ТЗ является канонической задачей линейного программирования. Ее можно решать с помощью симплекс-метода, описанного в предыдущей главе. Однако на практике для решения ТЗ, в силу ее специфических свойств, можно использовать и другие методы, в частности метод потенциалов.
Решение ТЗ методом потенциалов состоит из двух шагов:
— Нахождение начального допустимого плана.
— Нахождение оптимального решения методом потенциалов.
2.2. Нахождение начального допустимого плана
Начальный допустимый план представляет собой любой план , удовлетворяющий всем ограничениям исходной задачи. Начальный допустимый план называют также базисным или опорным планом.
Желательно, найти базисный план, который обеспечит как можно меньшее значение целевой функции. Для этого пользуются специально разработанными методами:
1). Метод северо-западного угла.
2). Метод минимальной стоимости.
3). Метод Фогеля.
Методы отличаются алгоритмом выбора очередной клетки, в которую помещается объем очередной перевозки.
При заполнении транспортной таблицы значениями объемов перевозок , некоторые клетки могут остаться незаполненными, их называют свободными. Заполненные клетки, соответствующие ненулевым переменным называют занятыми, а сами переменными — базисными.
Если для сбалансированной задачи число ненулевых переменных в базисном плане равно , план называется невырожденным базисным планом.
План с меньшим, чем числом ненулевых компонент называется вырожденным планом. В этом случае необходимо ввести в базисный план нулевые переменные и считать их базисными.
Исходные данные ТЗ часто задаются в матричном виде:
При решении ТЗ используется транспортная таблица (рис.2.1). Строки таблицы отвечают пунктам производства. В последней клетке каждой строки указан соответствующий объем производства. Например, в первой строке, которая соответствует пункту производства , объем производства равен .
Столбцы соответствуют пунктам потребления. Последняя клетка каждого столбца содержит объем потребления для соответствующего пункта .
Каждая клетка транспортной таблицы содержит информацию о перевозке из -ого пункта в -ый. Здесь — объем перевозок, а — стоимость перевозки единицы товара.
Рис. 2.1. Транспортная таблица
Пример 1. Найти начальный допустимый план транспортной задачи, заданной в матричном виде:
.
a). Метод северо-западного угла.
Построим исходную транспортную таблицу.
Первой заполняем клетку в верхнем левом углу . Присвоим ей значение равное меньшему из объемов спроса и предложения , получим . Уменьшим потребности первого пункта потребления и запасы первого пункта производства на 2. Потребности первого пункта потребления исчерпаны, запретим перевозки в этот пункт, используя символ х:
Перейдем к следующей клетке и заполним ее аналогично . Уменьшим потребности второго пункта потребления и запасы первого пункта производства на 1. Запасы первого пункта производства при этом будут исчерпаны, запретим перевозки из этого пункта:
Перейдем к следующей клетке и заполним ее аналогично :
| Þ |
|
Уменьшим потребности второго пункта потребления и запасы второго пункта производства на 5. Запасы второго пункта производства исчерпаны, запретим перевозки из этого пункта.
Перейдем к следующей клетке, . Уменьшим потребности второго пункта потребления и запасы третьего пункта производства на 1. Потребности второго пункта потребления исчерпаны, запретим перевозки в этот пункт:
| Þ |
|
В последнюю клетку запишем . Уменьшим потребности третьего пункта потребления и запасы третьего пункта производства на 4. Получим допустимый базисный план:
| Þ |
|
Суммы перевозок по строкам и столбцам должны совпадать с исходной задачей. Необходимо выполнить проверку.
Найденный начальный план необходимо также проверить на вырожденность. Вычислим , количество ненулевых переменных в полученном плане тоже равно 5. Полученный базисный план (рис. 2.2) является невырожденным.
Рис. 2.2. Начальный базисный план, метод северо-западного угла
Найдем значение целевой функции для найденного плана:
b). Метод минимальной стоимости.
Алгоритм заполнения клеток такой же, как в методе северо-западного угла, изменяется последовательность заполнения клеток. Первой заполняется клетка с минимальной ценой перевозки. Если таких клеток несколько, выбираем любую из них.
Затем выбираем следующую из незаполненных клеток с минимальной ценой, пока не удовлетворим все потребности. При этом все запасы будут использованы полностью, так как рассматривается сбалансированная задача.
Применим метод минимальной стоимости к рассмотренной выше задаче.
Имеются две клетки с минимальной стоимостью перевозки единицы товара . Заполним сначала клетку .
Затем заполним клетку .
| Þ |
|
Следующее по величине значение стоимости равное 2 тоже соответствует двум клеткам . Заполним сначала клетку , а затем :
| Þ |
|
Осталось заполнить клетку =1 (рис. 2.3). Последовательность заполнения ячеек данным методом: , , , , .
| — | х | ||
| — | — | х | |
| — | х | ||
| х | х | х |
Рис. 2.3. Начальный базисный план, метод минимальной стоимости
Для данной исходной задачи планы, найденные двумя способами, совпали. Заметим, что обычно метод минимальной стоимости дает лучшее начальное решение.
Самым распространённым способом решения транспортной задачи является получение одного из допустимых планов «методом северо-западного угла», который требует меньшего объема вычислений, с последующим его улучшением «методом потенциалов».
megaobuchalka.ru
Тема 10. Транспортные задачи. Блокирование перевозок.
Если план транспортной задачи Х= является оптимальным, то ему соответствует система чисел, называемых потенциалами, для которых выполняются следующие условия
— для , для
— для , для
+ для , для
—
для , для
2Модель транспортной задачи закрытая, если
—
+
—
—
Цикл в транспортной задаче – это
—замкнутая прямоугольная ломаная линия, все вершины которой находятся в занятых клетках
— замкнутая прямоугольная ломаная линия, все вершины которых находятся свободных клетках
—замкнутая прямоугольная ломаная линия, одна вершина которой в занятой клетке, остальные в свободных клетках
+ замкнутая прямоугольная ломаная линия, одна вершина которой в свободной клетке, а остальные в занятых клетках
Если число занятых клеток меньше, чем (m+n-1), то одну свободную клетку делают занятой с нулевой перевозкой. Эта клетка
— должна образовывать цикл с вершинами только в занятых клетках
+ не должна образовывать цикл с вершинами только в занятых клетках
— должна образовывать цикл с вершинами только в свободных клетках
— может быть любой свободной клеткой
Модель транспортной задачи является открытой, если
+
—
— не зависит от и
—
Потенциалами транспортной задачи размерности (m×n) называются m+n чисел ui и vj, для которых выполняются условия
+ ui+vj=cij для занятых клеток
— ui+vj=cij для свободных клеток
— ui+vj=cij для первых двух столбцов распределительной таблицы
— ui+vj=cij для первых двух строк распределительной таблицы
Оценками транспортной задачи размерности (m+n) называются числа γij=cij-ui-vj, которые вычисляются
— для занятых клеток
+для свободных клеток
— для первых двух строк распределительной таблицы
— для первых двух столбцов распределительной таблицы
Целевая функция транспортной задачи имеет вид
—
—
—
+
При составлении первоначального плана транспортной задачи по методу минимальной стоимости в первую очередь заполняются клетки
— расположенные по главной диваглнали распределительной таблицы
— с максимальными тарифами
+ с минимальными тарифами
— расположенные в первых строках и столбцах распределительной таблицы
При решении транспортной задачи значение целевой функции должно от итерации к итерации
— увеличиваться
— увеличиваться или не меняться
— увеличиваться на γij
+уменьшаться или не меняться
В клетках распределительной таблицы располагаются
— только тарифы перевозок cij
— только планы перевозок xij
+планы перевозок xij и соответствующие тарифы cij
— значения поизведений cijxij
Если план транспортной задачи X=(xij)mxn является оптимальным, то оценки γij=cij-ui-vj удовлетворяют условиям
— γij 0 для всех клеток
— γij 0 для всех клеток
— γij <0 для свободных клеток
+ γij0 для свободных клеток
Открытая модель транспортной задачи
после приведения к закрытой должна иметь вид
—
+
Открытая модель транспортной задачи
после приведения к закрытой должна иметь вид
—
+
—
Чтобы произвести блокировку некоторой клетки транспортной задачи, в этой клетке тариф
— заменяют на нуль
— удваивают
+ заменяют на достаточно большое число М
— уменьшают в два раза
Число занятых клеток невырожденного плана транспортной задачи должно быть равно
— m+n
— m+n+2
+m+n-1
— m+n+1
Экономический смысл целевой функции транспортной задачи
—суммарный объем перевозок
+ суммарная стоимость перевозок
—суммарные поставки
— суммарные потребности
В целевой функции транспортной задачи коэффициенты cij – это
— коэффициенты прямых затрат
— коэффициенты полных затрат
+ стоимость перевозки одной тонны груза от i–ого поставщика к j–ому потребителю
— общая стоимость перевозки от i–ого поставщика к j–ому потребителю
В целевой функции транспортной задачи переменные xij – это
— тарифы перевозок
— коэффициенты полных затрат
— коэффициенты прямых затрат
+ объем перевозимого груза от i–ого поставщика к j–ому потребителю
В транспортной задаче сумма потенциалов ui+vj равна тарифу cij, , для
+ занятых клеток
— незанятых клеток
— для любых клеток
— для первого ряда клеток
В транспортной задаче оценки γij вы числяются для
—занятых клеток
— для всех клеток
+ для незанятых клеток
—для клеток первого столбца
В транспортной задаче
— максимизируется объем перевозок
+ минимизируется общая стоимость перевозок
— минимизируется общий объем перевозок
— минимизируется объем холостого пробега транспорта
Экономически отрицательная оценка показывает что, если в клетку перебросить 1т груза, то суммарная стоимость перевозки
—увеличится на
—не изменится
+уменьшится на
—уменьшится на 2
Оценки транспортной задачи, вычисляемые для свободных клеток, находятся по формуле
—
+
—
—
Блокирование перевозок применяется для клетки , в которой
—наибольший тариф
—перевозки разрешены
+перевозки запрещены
—наименьший тариф
План транспортной задачи называется невырожденным, если число загруженных клеток равно
— m+n-2
+ m+n-1
— m+n
— m+n+1
Если все оценки для свободных клеток , то план транспортной задачи будет
+оптимальным
—невырожденным
—неоптимальным
—вырожденным
Если число загруженных клеток в плане транспортной задачи меньше m+n-1, то план называется
—оптимальным
—неоптимальным
—невырожденным
+вырожденным
Блокирование перевозок применяется в транспортной задаче с открытой моделью. Если , то накладывается дополнительное условие, что груз i – го поставщика должен
+быть вывезен полностью
—частично остаться на складе
—не вывозиться совсем
—быть отправлен только j –му потребителю
Блокирование перевозок применяется в транспортной задаче с открытой моделью. Если , то вводится дополнительное условие, что потребности j – го потребителя должны
—не удовлетворяться
+удовлетворяться полностью
— удовлетворяться частично
—должны удовлетворятся полностью только i – м поставщиком
Если плану транспортной задачи соответствует система m+n чисел (потенциалов), для которых выполняются условия для и для , то план называется
—неоптимальным
—вырожденным
— невырожденным
+оптимальным
В транспортной задаче для плана, приведенного в таблице
неоптимальной клеткой будет
—(1,1)
+(1,2)
—(2,3)
—(1,3)
Если план транспортной задачи вырожденный, то число загруженных клеток
— больше, чем m+n-1
—равно m+n-1
+меньше, чем m+n-1
—равно m+n
В транспортной задаче для плана, приведенного в таблице
неоптимальной клеткой будет
—(1,1)
—(1,2)
—(1,3)
+(3,1)
Если модель транспортной задачи открытая и , то вводится
—дополнительный потребитель с тарифами, равными 1
+фиктивный потребитель с тарифами, равными 0
—фиктивный поставщик с тарифами, равными 0
— фиктивный поставщик с тарифами, равными 1
План транспортной задачи называется вырожденным, если число занятых клеток
— равно m+n
—равно m+n-1
—больше m+n-1
+меньше m+n-1
—
Дан план транспортной задачи и вычислены потенциалы:
Данный план является
+оптимальным
—вырожденным
—неоптимальным
— произвольным
Дана транспортная задача:
с открытой моделью. После приведения к закрытой модели она примет вид
—
+
Дана транспортная задача:
После приведения к закрытой модели она примет вид
—
+
Если в транспортной задачи , то для приведения к закрытой модели следует вводить
+фиктивного потребителя
—фиктивного поставщика
— фиктивных поставщика и потребителя
—нулевую поставку
Если в транспортной задачи , то для приведения к закрытой модели следует вводить
—фиктивного потребителя
+фиктивного поставщика
— фиктивных поставщика и потребителя
—нулевую поставку
infopedia.su
