Пересечение множеств калькулятор онлайн – Пересечение множеств | Онлайн калькулятор
Калькулятор расчета пересечения множеств онлайн
Пересечение двух множеств — это некое третье множество, которое содержит только элементы, общие для заданных математических объектов. Определить такое множество легко при помощи нашего онлайн-калькулятора.
Теория множеств
Говоря простым языком, множество — это элементарный математический объект, который содержит определенный набор данных, предметов или чисел. Это исходное математическое понятие, которое невозможно представить другими терминами. Именно поэтому множество описывается как набор разрозненных элементов, мыслимое как единое целое. Понятие множества ввел немецкий математик Георг Кантор, который развил собственную теорию трансфинитных чисел, позволяющую оперировать вполне упорядоченными бесконечными множествами.
Георг Кантор разработал уникальную программу стандартизации всех математических знаний, согласно которой любой математический объект является тем или иным множеством. К примеру, согласно канторовской теории, любое натуральное число — это одноэлементное множество, принадлежащее надмножеству натурального ряда. Натуральный ряд, в свою очередь, считается подмножеством целого ряда, а целое множество — подмножеством действительного или вещественного ряда.
Теория Георга Кантора вызвала широкий резонанс в математических кругах. Многие современники негативно отзывались о его работах, особенно его учитель Леопольд Кронекер, который не принимал канторовского определения натурального числа. Несмотря на это, теория множеств получила признание позже, когда группа французских математиков под псевдонимом Никола Бурбаки предприняла попытку перевести весь математический аппарат на теоретико-множественный язык.
Операции с множествами
Существует две основные операции над множествами: объединение и пересечение. Если X и Yпредставляют собой множества, то объект Z становится их объединением в случае, если он включает в себя элементы X, Y или их обоих. Математически операция объединения обозначается как X È Y. Объект Z = X Ç Y состоит из членов, которые одновременно входят как в X, так и в Y, и носит название «пересечения» двух множеств X и Y.
Если у нас есть X = {1, 2, 3, 4, 5} и Y = {1, 3, 5, 7, 13, 21} то объединение множеств Z будет выглядеть как X È Y = {1, 2, 3, 4, 5, 7, 13, 21}, а пересечение как X Ç Y = {1, 3, 5}. Операции объединения и пересечения соответствуют суммированию в алгебре. Вместе с разностью эти операции образуют оригинальную «алгебру множеств». Согласно аксиомам теории множеств, любые алгебраические операции с множествами в результате должны выдавать множество. Поэтому если операция над объектами приводит к нулевому результату, согласно теории, образуется пустое множество.
Пустое множество — это математический объект, не содержащий ни одного элемента. К примеру, если X = {1, 2, 3, 4, 5}, а Y = {10, 15}, то в результате пересечения X Ç Y получится пустое множество X Ç Y = Æ. Пустое множество обладает интересным свойством — оно является несобственным подмножеством для любого существующего множества элементов.
Наша программа позволяет выполнять алгебраическую операцию пересечения двух объектов с произвольным количеством элементов. Для работы с калькулятором вам потребуется ввести в ячейки программы элементы множества через запятую, после чего определить объект, равный пересечению заданных множеств. Вы можете задать целочисленные множества или математические объекты, содержащие элементы в виде десятичных дробей. Важно учесть, что десятичные дробный числа также перечисляются через запятую, поэтому для записи самой дроби необходимо использовать точку. Например, для перечисления дробей 1/2, 1/4 и 0,75 вам потребуется ввести в ячейку множество {0.5, 0.25, 0.75}.
Примеры из реальной жизни
Геометрические фигуры
Допустим, существует множество X, которое содержит прямоугольники с разными длинами сторон. Также существует множество Y, содержащее ромбы с разными углами. Из курса геометрии мы знаем, что ромб — это параллелограмм, у которого все стороны равны, а прямоугольник — это параллелограмм, у которого равны все углы. В множествах X и Y могут встретиться ромбы с углами по 90 градусов или прямоугольники с одинаковыми сторонами. Фигура, у которой все углы прямые, а все стороны равны — это квадрат. Соответственно, пересечением множеств ромбов X и прямоугольников Y является множество квадратов Z.
Отрезки
Пусть у нас есть два отрезка, которые задаются координатами X = [1, 3] и Y = [2, 4]. Пересечением данных множеств будет отрезок [2, 3], так как именно эти числа входят в диапазон значений обоих отрезков на числовой оси.
Еще пример
Давайте попробуем узнать пересечение пятиэлементных множеств простых и четных чисел. Простое число — это число, которое делится только на себя и на единицу. Четное число — число, которое делится на 2 без остатка. Итак, наши множества S = {2, 3, 5, 7, 11} и E = {2, 4, 6, 8, 10}. Введем эти данные в онлайн-калькулятор и получим результат в виде P = {2}.
Заключение
Теория множеств находит применение в различных прикладных задачах. Пользуйтесь нашими калькуляторами для решения учебных или реальных заданий по теории множеств.
bbf.ru
Онлайн-калькулятор по математике
Разность множеств
Под разностью двух множеств A и B понимают новое множество, состоящее из тех
Соответственно, разность B∖A – это множество, состоящее из тех элементов множества B, которые не принадлежат множеству A.
Пустое множество Ø применительно к разности множеств имеет свойства:
A∖A=Ø,Ø∖A=Ø,A∖Ø=A
Некоторые свойства разности множеств:
A∖B⊂A,
A∪(B∖A)=A∪B,
A∖B=A∖(A∩B),
A∩(B∖A)=Ø.
Пример
Для двух множеств {-1,7,8,11} и {-1,3,5,8,12} найдем разности:
A∖B= {7,11}
B∖A= {3,5,12}
Не следует путать разность множеств с симметрической разностью, которая обозначается как A∆B, и определяется как множество, состоящее из тех элементов множеств A и B, которые не являются общими:
A∆B=(A∪B)∖(A∩B)
В рассматриваемом примере A∆B={3,5,7,11,12}
Множество, не содержащее элементов, называется пустым множеством и обозначается $\emptyset$ или $\lbrace \rbrace$.
Отношения между множествами
Равенство множеств
Два множества $A$ и $B$ равны тогда и только тогда, когда они содержат одни и те же элементы, то есть если все элементы первого множества являются элементами второго множества, и наоборот.
$A=B \overset{def}{\Leftrightarrow} (\forall x)(x\in A \Leftrightarrow x\in B)$
Поскольку отношение равенства является транзитивным, рефлексивным и симметричным, его называют отношением эквивалентности.
Подмножество
Множество $A$ является подмножеством множества $B$ тогда и только тогда, когда любой элемент множества $A$ является также элементом множества $B$.
$A \subseteq B \overset{def}{\Leftrightarrow} (\forall x)(x \in A \Rightarrow x \in B)$
Множество $B$ в таком случае называется надмножеством множества $A$ и обозначается как $B \supseteq A$.
Если множество $A$ является подмножеством множества $B$ и если множество $B$ содержит хотя бы один элемент, не принадлежащий множеству $A$, то говорят, что множество $A$ является строгим подмножеством множества $B$.
Это обозначается как $A \subset B$, при этом множество $B$ называется строгим надмножеством множества $A$, что обозначается как $B \supset A$.
Отношение $\subset$ является транзитивным: $(A \subset B) \wedge (B \subset C) \Rightarrow A \subset C$.
Пустое множество является подмножеством любого множества.
Операции над множествами
Объединение двух множеств
Объединением двух множеств $A$ и $B$ называется множество, состоящее из всех элементов, принадлежащих множествам $A$ или $B$.
$A \cup B \overset{def}{=} \lbrace x \vert x \in A \vee x \in B \rbrace$
Операция объединения двух множеств является:
идемпотентной: $A\cup A=A$
2. коммутативной: $A \cup B = B \cup A$
3. ассоциативной: $(A \cup B) \cup C = A \cup (B \cup C)$
Пересечение множеств
Пересечением двух множеств $A$ и $B$ называется множество, которому принадлежат те и только те элементы, которые одновременно принадлежат множествам $A$ и $B$.
$A \cap B\overset{def}{=}\lbrace x \vert x\in A \wedge x\in B \rbrace$
Операция пересечения множеств является:
1.
Разность множеств
идемпотентной: $A\cap A=A$
2. коммутативной: $A \cap B = B \cap A$
3. ассоциативной: $(A \cap B) \cap C = A \cap (B \cap C)$
Разность двух множеств
Разностью двух множеств $A$ и $B$ является множество, содержащее все элементы множества $A$, не входящие в множество $B$.
$A \setminus B \overset{def}{=} \lbrace x \vert x \in A \wedge x \notin B \rbrace$
Симметрическая разность
Симметрическая разность двух множеств $A$ и $B$ — это множество, включающее все элементы исходных множеств, которые принадлежат только одному из множеств $A$ или $B$.
$A \bigtriangleup B \overset{def}{=} (A \setminus B) \cup (B \setminus A)$
Очевидно, что операция $\bigtriangleup$ коммутативна.
Дополнение множества
Пусть $A \subset B$. Дополнением множества $A$ относительно множества $B$ называется множество, состоящее из всех элементов множества $B$, которые не входят в множество $A$.
$C_B(A)\overset{def}{=}\lbrace x\vert x\in B \wedge x\notin A\rbrace$
Булеан
Булеан (степень множества) $A$ — это множество всех подмножеств множества $A$, включая пустое множество и само множество $A$.
$P(A) \overset{def}{=} \lbrace B \vert B \subset A \rbrace$
Например: Булеаном множества $A=\lbrace 1,2,3 \rbrace $ является множество $P(A)=\lbrace \emptyset ,\lbrace 1 \rbrace , \lbrace 2\rbrace, \lbrace 3 \rbrace , \lbrace 1,2 \rbrace , \lbrace 1,3 \rbrace , \lbrace 2,3 \rbrace , \lbrace 1,2,3 \rbrace \rbrace $
Декартово произведение
Декартовым произведением множеств $A$ и $B$ является множество, содержащее все возможные упорядоченные пары $(x,y)$ элементов исходных множеств ($x$ — элемент множества $A$, $y$ — элемент множества $B$).
$A \times B \overset{def}{=} \lbrace(x,y) \vert x \in A \wedge y \in B \rbrace $
Свойства операций над множествами
Дистрибутивный закон
$A \cup (B \cap C)=(A \cup B)\cap (A \cup B)$
$A \cap (B \cup C)=(A \cap B)\cup (A \cap B)$
Закон поглощения
$A\cup(A\cap B)=A$
$A\cap(A\cup B)=A$
Законы де Моргана
$C_U(A\cup B)=C_U(A)\cap C_U(B)$
$C_U(A\cap B)=C_U(A)\cup C_U(B)$
Отношения и функции
Отношения
Если множества $A$ и $B$ непустые, то любое подмножество $\rho$ множества $A\times B$ называется бинарным отношением между множествами $A$ и $B$.
Если $(a,b)\in \rho$, говорят, что $a$ и $b$ находятся в отношении, и это обозначается как $a\rho b$.
Отображения
Бинарное отношение $f\subset X\times Y$ называется отображением тогда и только тогда, когда для любого элемента $x\in X$ существует ровно один $y\in Y$, для которого выполняется $(x,y)\in f$ , то есть $(\forall x\in X)(\exists !y\in Y)(x,y)\in f$
В символьном обозначении: $f:X\longmapsto Y$ or $X\overset{f}{\longmapsto} Y$
Если $(x,y)\in f$, пишут $f(x)=y$.
Элемент $x$ называется прообразом, а $y$ образом.
Множество $X$ называется областью определения, а множество $Y$ — областью значений $f$.
Особое значение в математике придается трем специальным типам отображений – инъекции, сюръекции и биекции.
Инъекция
Отображение $f:X\longmapsto Y$ является инъекцией или однозначным отображением тогда и только тогда, когда для каждого элемента $x\in X$ существует ровно один элемент $y\in Y$, для которого выполняется $f(x)=y$.
$f:X\overset{1-1}{\longmapsto}Y\overset{def}{=}(\forall x_1,x_2\in X)(x_1\neq x_2\Rightarrow f(x_1)\neq f(x_2))$
Сюръекция
Отображение $f:X\longmapsto Y$ сюръективно тогда и только тогда, когда для каждого элемента $y\in Y$ существует хотя бы один элемент $x\in X$, для которого истинно $f(x)=y$.
$f:X\overset{onto}{\longmapsto}Y\overset{def}{=}(\forall y\in Y)(\exists x\in X)(f(x)=y)$
Биекция
Отображение $f:X\longmapsto Y$ называется биекцией, если оно является одновременно и сюръективным, и инъективным.
Очень часто в задачах дискретной математики, а именно в теории массы, необходимо доказать равенство масс. Предположим, что равенство множеств $ M = N $ влечет реализацию взаимного интегрирования, то есть $ M \ subseteq N $ и $ N \ subseteq M $.
Поэтому для доказательства равенства $ M = N $ множеств $ M, \ N $ необходимо показать выполнение этих включений. Вы можете сделать это по-разному:
- с определением теоретико-множественных операций;
- используя законы алгебры множества;
- построение диаграмм Эйлера-Венна;
- составление таблиц членства;
- используя функции индикатора.
Мы приводим каждый из этих методов к конкретному примеру.
Чтобы доказать равенство масс:
left $ (A \ cap B \ right) \ slash C = \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) $ $
1.
Равенство двух множеств $ M = N $ эквивалентно двум включениям $ M \ subseteq N, \ N \ subseteq M $.
Докажем, что $ \ left (A \ cap B \ right) \ slash C \ subseteq \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) $. Пусть $ x \ in \ left (A \ cap B \ right) \ slash C $, а затем по определению разность множеств $ x \ in \ left (A \ cap B \ right) $ и $ x \ notin C $. По определению пересечение множеств $ x \ in \ left (A \ cap B \ right) $ тогда и только тогда, когда $ x \ и A $ и $ x \ in B $.
Так как $ x \ и A $ и $ x \ notin C $, то $ x \ и A \ slash C $. Так как $ x \ и B $ и $ x \ notin C $, то $ x \ и B \ slash C $. В зависимости от соединения определения мы видим, что $ x \ v \ left (A \ backspace C \ right) \ cap \ left (B \ slash C \ right) $. Это доказывает, что $ \ left (A \ cap B \ right) \ C \ subseteq \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) $.
Докажем, что $ \ left (A \ backslash C \ right) \ cap \ left (B \ slash C \ right) \ subseteq \ left (A \ cap B \ right) \ slash C $.
Пусть $ x \ v \ left (A \ slash C \ right) \ Cap \ left (B \ slash C \ right) $, тогда трансверсальная HD устанавливает $ x \ v \ left (A \ slash C \ right) $ и $ x \ in \ left (B \ slash C \ right) $. Определив разность множеств $ x \ и A $, $ x \ notin C $ и $ x \ in B, \ x \ notin C $. Согласно узлу определения, мы видим, что $ x \ v \ left (A \ cap B \ right) \ in \ x \ notin C $, то есть $ x \ v \ left (A \ cap B \ right) \ backslash C $. Это доказывает, что $ \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) \ subseteq \ left (A \ cap B \ right) \ backslash C $.
Из доказанных включений следует, что $ A \ left (A \ cap B \ right) \ slash C = \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) $.
2. Докажем справедливость $ \ left (A \ cap B \ right) \ slash C = \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) $ с использованием основных законов алгебраических массивов.
Операцию $ X \ косой черты Y $ произвольных множеств $ X, \ Y $ можно записать в виде строки $ X \ линии Y = X \ cap \ overline {Y} $.
Тогда левая часть этого отношения $ \ left (A \ cap B \ right) \ backslash C = \ cap B \ cap \ overline {C} $. Справа: $ \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) = A \ cap \ overline {C} \ cap B \ cap \ overline {C} = A \ cap B \ cap \ overline {C} $. Мы видим, что левая и правая части, возникающие в результате изменений, совпадают с $ A \ cap B \ cap \ overline {C} = A \ cap B \ cap \ overline {C} $. Связь правильная.
3.
Решение проблем для математики
Мы видим, что граф множеств $ \ left (A \ cap B \ right) \ backslash C $ и $ \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) $ совпадают, равенство $ \ left (A \ cap B \ right) \ slash C = \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) $ истинно.
4. Создайте таблицу статей для левой и правой сторон данного равенства $ \ left (A \ cap B \ right) \ slash C = \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) $.
\ begin {array} {| c | c |} \ hline A & В & С & A \ cap B & left (A \ cap B \ right) \ Slash C cash & A \ черта линии C & B \ Slash C слэш & left (A \ slash строки C \ right) \ cap \ left (B \ slash C \ right) \\ \ hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \ hline 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ \ hline 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \\ \ hline 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ \ hline 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ \ hline 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ \ hline 1 & 1 & 0 & 1 & 1 & 1 & 1 & 1 \\ \ hline 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \ hline \ end {array}
Мы видим, что $ \ left (A \ cap B \ right) \ slash C = \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) = \ left (00.000.010 \ right ) $.
5.
Докажем справедливость отношения $ \ left (A \ cap B \ right) \ backslash C = \ left (A \ slash C \ right) \ cap \ left (B \ slash C \ right) $ с использованием функций индикатора. Функция индикатора для левой стороны соединения:
left (x \ right) \ left (x \ right) = {\ či} _ {a \ cap B} \ left (x \ right) {\ chi} _ {a \ cap B} \ left (x \ right) {\ chi} _C \ left (x \ right) = {\ či} _A \ left (x \ right) {\ či} _B \ left (x \ right) {\ chi} _A \ left (x \ right) {\ chi} _B \ left (x \ right) {\ chi} _C \ left (x \ right) = {\ či} _A \ left (x \ right) {\ chi} _B \ left (x \ right) \ cdot \ left (1 — {\ či} _C \ left (x \ wrong) \ неправильный) Индикатор $$ для правой стороны: $$ { \ left (A \ обратная косая черта C \ right) \ left (A \ обратная косая черта C \ справа) справа)} \ left (x \ right) {\ chi} _ {\ left (B \ slash C \ right)} left (x \ right) = \ left ({\ hi} _A \ left (x \ right) — {\ chi} _A \ left (x \ right) {\ chi} _C \ left (x \ right) \ left ({\ hi} _B \ left (x \ right) — {\ či} _B \ left (x \ right) {\ chi} _C \ left (x \ wrong) \ wrong) = {\ či} _A \ Left (x \ right) {\ chi} _B \ Criminal (x \ right) — {\ chi} _A \ left (x \ right) {\ chi} _B \ left (x \ right) {\ chi} _C \ left (x \ right) — {\ chi} _A \ left (x \ right) {\ chi} _B \ left (x \ right) {\ chi} _C \ left (x \ right) + {\ chi} _A \ left (x \ right) {\ chi} _B \ left (x \ right) {\ chi} _C \ left (x \ right) = {\ či} _A \ left (x \ right) {\ chi} _B \ left x \ right) {\ chi} _A \ left (x \ right) {\ chi} _B \ left (x \ right) {\ chi} _C \ left (x \ right) = {\ či} _A \ left x \ right) {\ chi} _B \ left (x \ right) \ left (1 — {\ chi} _C \ left (x \ right) \ right).
$$ Мы видим, что индексная функция обеих частей совпадает с $$ {\ či} _A \ left (x \ right) {\ chi} _B \ left (x \ right) \ cdot \ left (1 — {\ či} _C \ left (x \ right) \ right (x \ right) \ cdot \ left (1 \ {chi} _C \ left (x \ right) {\ chi} _B \ left right \ right). $$ Связь реальна.
Комментарии от HyperComments
vipstylelife.ru
Калькулятор расчета подмножеств в множестве онлайн
Множество — это набор элементов, которые обладают общим свойством. В каждом неупорядоченном множестве существует определенное количество подмножеств, которые можно рассчитать при помощи онлайн-калькулятора.
Множество
Множество представляет собой набор элементов, сгруппированных по определенному признаку. В математике это может быть множество натуральных, целых или рациональных чисел. В природе это множества яблок на дереве, песчинок в пустыне или звезд в космосе. На практике множество может представлять собой набор данных, массивы результатов измерений или входных воздействий. Множество — это простейший математический объект, поэтому с ним можно осуществлять простые арифметические действия, то есть складывать, вычитать или разбивать на составляющие — подмножества.
Несобственные подмножества
Каждое множественный объект имеет два несобственных подмножества: само множество и пустое. Согласно канторовской теории, любое множество считается подмножеством самого себя. Пустое множество — это своеобразный нуль теории множеств, и такой набор не содержит ни одного элемента. Потребность в пустом множестве обусловлена аксиомой, что любой результат операции между множествами также должен быть множеством. Пустой набор элементов также считается подмножеством для любого набора чисел.
Собственные подмножества
Помимо самого себя и пустого множества, набор чисел может иметь определенное количество собственных подмножеств. Их численность определяется мощностью множества, то есть количеством его элементов. Для объекта A, которое состоит из n-ного числа элементов, существует количество собственных подмножеств, которое определяется по формуле:
N = 2n — 2.
Из этого следует, что для набора из 3 элементов существует 23 — 2 = 6 собственных подмножеств, из 4 членов — 24 — 2 = 14 собственных подмножеств и так далее. К примеру, для множества {X, Y, Z} существуют следующие подмножества:
- {X};
- {Y};
- {Z};
- {XY};
- {XZ};
- {ZY}.
Если не разделять подмножества на собственные и несобственные, то для каждого множества существует подмножества, количеством:
N = 2n,
где n — количество элементов.
Это означает, что для того же набора {X, Y, Z} добавятся также пустое множество и оно само.
Подмножества и парадоксы
Канторовская теория множеств зашла в тупик, когда ее постулаты породили парадоксы. Наиболее известной проблемой наивной теории множеств считается парадокс Рассела. Известный британский философ и ученый Бертран Рассел рассмотрел бесконечные множества как абстрактные объекты. Если любое множество считается подмножеством самого себя, то верно выражение A Î A. Допустим, существует глобальное множество S, содержащее в себе все наборы объектов, которые не включают самих себя.
Далее возникает вопрос, верно ли, что S Î S? Если верно, то выходит, что S не содержит самого себя, так как изначально набор S содержит все множества, не содержащие себя, следовательно, S Î S. Если неверно, значит, набор S не соответствует первичному определению, следовательно, S Î S.
Данный парадокс так же известен как проблема цирюльника. Некий брадобрей заявляет, что будет брить только тех, кто не бреет сам себя. Тех, кто сами справляются с бритвой, цирюльник брить отказывается. Возникает парадокс: кто побреет цирюльника? Если он бреется сам, то он не должен себя брить, а если не бреется, то брить себя обязан. Для решения подобных парадоксов в теорию множеств была внесен раздел о типах объектов. Согласно теории типов, подмножества всегда должны быть низшего порядка по отношению к своему надмножеству.
Наша программа позволяет сгенерировать все возможные подмножества для любого заданного набора чисел. Для этого вам достаточно ввести числа через запятую в форму онлайн-калькулятора, после чего программа рассчитает все подмножества для выбранного набора, включая собственные и несобственные. Рассмотрим пример генерации подмножеств.
Пример работы калькулятора
Допустим, у нас есть множество последовательных натуральных чисел мощностью 4. Это означает, что наш объект выглядит как А = {1, 2, 3, 4,}. Согласно формуле, для A существует 24 = 16 подмножества: 14 собственных и 2 несобственных. При помощи калькулятора рассчитаем эти составляющие. Мы получим:
- пустое множество — {};
- одноэлементные наборы — {1}, {2}, {3}, {4};
- двухэлементные — {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4};
- трехэлементные — {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4};
- само множество — {1, 2, 3, 4}.
Точно также вы можете рассчитать количество подмножеств для множества произвольной мощности.
Заключение
Множество — это элементарный математический объект, с которым можно осуществлять разные арифметические операции. Используйте наши онлайн-калькуляторы для работы с множественными объектами.
bbf.ru
Калькулятор расчета разности двух множеств онлайн
Алгебра множеств — это математический аппарат, позволяющий выполнять над множественными объектами операции сложения и вычитания. Разность двух множеств — это алгебраическая операция, результатом которой является совокупность элементов, содержащее все элементы первого аргумента, не входящие во второй.
Теория множеств
Теорию множеств разработал немецкий математик Георг Кантор. Перевод математического аппарата на теоретико-множественный язык произвел переворот в современной науке. Ключевая мысль, на которой базируется канторовская теория, состоит в элементарном понятии пересчета предметов при помощи взаимно-однозначного соответствия.
Представьте себе античного пастуха, который не имеет представления о числах и счете. Как он может узнать, сколько у него овец и все ли они вернулись с выгула? Ответ элементарный и в тоже время исключительно математический. Выпуская стадо из загона, пастух постепенно откладывает столько камней, сколько овец вышло пастись. Вечером он загоняет стадо и возвращает камни на место. Если несколько животных потерялось, то он сразу это увидит по тому, сколько камней осталось не переложенными. Этот примитивный прием счета предметов лег в основу канторовской теории: взаимно-однозначное соответствие элементов множества камней и множества овец.
Понятие множества
Множество — элементарный математический объект, не сводимый к определению через другие термины. В классическом определении под множеством определяют совокупность неупорядоченных элементов, мыслимых как одно целое. Примерами реальных множеств выступают множества людей на планете, набор домов на улице или совокупность звезд на небе.
Каждое множество имеет подмножество, то есть набор элементов с общей характеристикой, которые принадлежат конкретной совокупности. В примере выше подмножествами множества людей будет совокупность жителей Европы, подмножеством для набора домов станут только кирпичные дома, а подмножеством всех существующих звезд выступят звезды галактики Млечный путь.
Георг Кантор пришел к выводу, что любой математический объект можно представить в виде определенного множества. Например, число 13 — это одноэлементное множество A = {13}, которое принадлежит надмножеству натуральных чисел. Как и с числами, с множествами легко выполнять алгебраические операции, то есть складывать и вычитать. Согласно аксиомам теории множеств, результат операции над совокупностями элементов должен также приводить к множеству. Пустое множество — нуль алгебры множеств, представляющий собой пустой набор элементов. Если из A вычесть A, то мы получим пустое множество.
Мощность множества
Мощность множества — это количество объектов, которое оно в себя включает. Число 13 как одноэлементное множество характеризуется мощностью, равной единице, а мощность пустого множества равна нулю. Множества можно сравнивать по мощности. Равномощными называются объекты, между элементами которых можно установить взаимно-однозначное отношение. Как и говорилось выше, множество камней и множество овец — это два равномощных математических объекта и именно с ними легко оперировать в прикладных задачах. Примером равномощных объектов в реальности можно привести базы данных. К примеру, множество студентов и множества их оценок по разным предметам в базе данных университета.
Разность множеств
Разность двух множеств A и B — это третьей множество C, каждый элемент которого принадлежит множеству A и не принадлежит множеству B. Математическим языком разность двух совокупностей записывается как A/B, а читается как «A без B». Такое прочтение позволяет интуитивно понять результат операции вычитания множеств.
Наша программа позволяет определить разность двух множеств разной мощности. Калькулятор работает с неупорядоченными объектами, поэтому порядковый номер элементов для него не важен. Для решения задач на разность множеств вам потребуется ввести в ячейку калькулятора совокупность чисел через запятую. Вы можете оперировать как целыми числами, так и десятичные дробями. Так как числа перечисляются через запятую, отделять целую часть от дробной требуется точкой. Например, множество рациональных чисел запишем как Q = {0,25; 0,75; 1,75}.
Пример работы калькулятора
Простая задача
В учебнике по теории множеств для чайников приведена простая задача. Есть множество X = {1, 2, 3, 4, 5, 6} и множество Y = {2, 4, 6, 7}. Требуется найти разность этих двух элементов. Вспомним, что разность X/Yчитается как X без Y, следовательно, решением данной задачи будет множество Z, содержащее элементы совокупности X за вычетом элементов Y. Общие для X и Y члены в данном случае — это 2, 4, 6. Объект X без этих элементов выглядит как {1, 3, 5}. Это и будет наше множество Z.
Заключение
Теория множеств находит широкое применение в прикладных науках. Используйте наш калькулятор для решения примеров по данной теме или для проверки результатов ваших вычислений.
bbf.ru
Калькулятор определения подмножества из множества онлайн
Подмножество множества A — это такой набор B, все члены которого принадлежат A. Существует знакомое всем с детства множество натуральных чисел N, а наборы четных E и нечетных O элементов являются подмножествами N.
Теория множеств
Проблема отображения бесконечности действительных чисел волновала математиков с самой древности. Натуральные числа люди использовали при счете, рациональные, то есть дроби – при операциях с частями целого, а действительные числа нашли свое применение в измерениях. Первым действительным и иррациональным числом, о котором узнали древние математики, было число, отображающее длину диагонали квадрата. Затем появилось Пи (отношение диаметра круга к его окружности), позднее и другие числа.
При измерении длины стороны фигуры или ее диагонали мы можем постоянно повышать точность измерений и получать все новые и новые числа. Например, диагональ единичного квадрата равна корню из двух. Мы можем выразить ее длину как 1,4 или 1,41 или 1,4142 или 1,41421356237. И это все разные действительные числа. Можно ли создать список всех действительных чисел от 0 до 1? Нет, так как каждый раз будет находиться еще одно число, отличное от всех, представленных в этом списке.
Именно с этой проблемой работал Георг Кантор, который создал наивную теорию множеств. Наивной его теория стала в результате образования нескольких логических парадоксов, которые были успешно решены при трансформации канторовской теории в аксиоматическую теорию множеств.
Подмножество
Давайте начнем с самого простого – множество натуральных чисел. Это бесконечная последовательность целых положительных чисел, которые мы используем при счете предметов. В отличие от измерений, мы не можем повышать точность счета. Если мы видим 5 яблок, то точнее мы выразить их количество никак не сможем. Кроме того, мы без проблем можем перечислить все натуральные числа в диапазоне от 1 до 10. Все натуральные числа могут быть как четными, так и нечетными, следовательно, натуральное множество содержит в себе четное и нечетное подмножества.
Целые числа – это продолжение натуральной последовательности в отрицательную область. К целым относится ноль, все натуральные числа, а также противоположные натуральным, то есть со знаком минус. Очевидно, что натуральное множество является подмножеством целых чисел.
Рациональное множество – это набор всех дробных чисел, которые возможно представить в виде обыкновенной дроби. В виде дроби мы можем выразить 0,25 – 1/4, 0,5 – 1/2, 1 – 1/1. В качестве дроби легко записать любое целое или натуральное число, например: 5/5 или 50/50. Таким образом, рациональное множество содержит два подмножества – наборы целых и натуральных чисел.
Действительное множество – это все числа на числовой оси. К ним относятся натуральные, целые, рациональные и иррациональные числа, которые формируют соответствующие подмножества во множестве действительных чисел. Множество действительных чисел – это самое мощное множество, которое стремится в бесконечность. Кроме того, пустое множество, которое не содержит ни одного элемента, является подмножеством любого выбранного набора чисел. Но и это еще не все. Каждое множество является подмножеством самого себя.
Мы перечислили глобальные примеры подмножеств, однако на практике нам может потребовать определить является ли один набор чисел подмножеством другого набора? К примеру, если у нас есть пара значений {3, 11}, то является ли она подмножеством набора {1, 3, 5, 7, 11, 13}? Очевидно, что ответ положительный, так как и 3, и 11 встречаются во множестве {1, 3, 5, 7, 11, 13}. Однако это верно только для множеств с неразличимыми элементами, то есть для обычного набора чисел. Если же важен порядковый номер элементов множества, то результат противоположный и {3, 11} не является подмножеством {1, 3, 5, 7, 11, 13}.
Наш калькулятор определения подмножеств позволяет выяснить, является набор чисел B подмножеством набора A. Программа использует алгоритм для надежно различимых элементов множества, для которых важен порядок расположения членов.
Пример определения подмножества
Выше мы выяснили, что четное множество – это подмножество натурального ряда. Для неразличимых элементов объект B = {2, 4, 6} является подмножеством набора A = {1, 2, 3, 4, 5, 6}. Однако представим, что это база данных, и n-ному элементу множества соответствует свое значение. Выходит, что первый член объекта B имеет значение 2, а первый элемент набора A равен 1. Второй элемент множества B равен 4, а второй элемент объекта A = 2. По такой логике это совершенно разные объекты, следовательно, множество B не является подмножеством набора A.
Заключение
Множество – это набор математических объектов, каждый из которых обладает определенным свойством. Каждое множество имеет минимум два подмножества: пустое и свое собственное. Для поиска других подмножеств используйте наш калькулятор, который позволяет определить принадлежность одного набора чисел к другому.
bbf.ru
Калькулятор объединения множеств онлайн
Множество – это набор объектов. Объединение двух множеств A и B — это набор математических объектов, которое содержит все элементы A и B. Объединение множеств соответствует арифметической операции сложения, а сумма двух наборов A и B обозначается как A Î B или A + B.
История теории множеств
История изучения множеств берет начало в 1872 году, когда Георг Кантор начал работать над созданием специальной теории множеств. Немецкий ученый стремился придать действительным числам осязаемый вид. Действительное число – это математический объект, возникший из потребности проводить измерения. При счете мы используем натуральные числа, при работе с долями целого – дроби, а при измерениях нам приходится оперировать действительными числами.
До 19-го века не существовало строгой теории действительных чисел, которая объясняла бы характер их бесконечности. Георг Кантор разработал арифметику трансфинитных чисел, придав осязаемость актуальной бесконечности. Именно он ввел в математику термин континуум действительных чисел, который обозначал мощность вещественного множества, то есть количество всех его элементов. Идеи Георга Кантора превосходили свое время, поэтому поначалу теорию множеств не принимало математическое сообщество, а самого ученого обвиняли в шарлатанстве и даже растлении молодежи.
Несмотря на стройность теории Кантора, позже в ней возникли логические парадоксы, наиболее известным из которых стал парадокс Рассела о существовании множества множеств, не включающих самих себя. Однако в 1930-х годах группа французских математиков, работавших под коллективным псевдонимом Никола Бурбаки, использовала идеи Кантора для аксиоматического описания всей математики на основе теории множеств. Выкладки Бурбаки и других математиков того времени (Цермело и Френкеля) позволили создать аксиоматическую теорию множеств, а канторовская теория получила название наивной. Аксиоматический подход произвел переворот в математических кругах, а теория множеств получила всеобщее признание.
Что такое множество
Множество – это набор неупорядоченных объектов. В математике в качестве элементов множества выступают числа, а в реальности мы можем говорить о множестве людей, звезд, песчинок или любых других объектов. Множество из 10 яблок и набор из 10 песчинок являются разными множествами. А вот множество из 10 яблок, уложенных в пирамиду и множество 10 яблок, собранных в корзину, остается одним и тем же неупорядоченным множеством.
Допустим, у нас есть множество 5 натуральных последовательных чисел, состоящее из 1, 2, 3, 4, 5. В математической записи такой объект будет записан как {1, 2, 3, 4, 5}. Обозначим его как A. Очевидно, что 1 принадлежит к множеству А, что записывается как 1 Î A. Числа 6 в данном множестве нет, что записывается как 6 Î A. Как и многие математические объекты, с множествами можно производить арифметические действия, например, складывать.
Объединение двух множеств
Опишем еще одно множество B = {5, 6, 7, 8, 9}. Объединенным множеством C будет набор чисел, который состоит из всех элементов слагаемых множеств. Таким образом, C = {1, 2, 3, 4, 5, 5, 6, 7, 8, 9}. В данном наборе у нас оказалось две пятерки. Если эти множества представляют собой комплекты чисел, то две пятерки неразличимы друг от друга, а согласно теории Кантора, множество не может содержать два неразличимых объекта. В результате объект C будет выглядеть как {1, 2, 3, 4, 5, 6, 7, 8, 9}
Если эти множества представляют собой различные данные, например, результаты замеров, и множество А содержит результаты замеров первого дня, а B — второго, то пятерки надежно различимы, так как имеют свой порядковый номер. Соответственно, результат сложения будет выглядеть как C = {1, 2, 3, 4, 5, 5, 6, 7, 8, 9}.
Наша программа позволяет объединить два набора элементов по принципу надежной различимости, следовательно, результирующее множество будет содержать все элементы слагаемых. Если множества содержат одинаковые элементы с одинаковыми порядковыми номерами, то программа считает такие элементы неразличимыми и не дублирует их. Следовательно, результаты этих операций будут следующими:
- {1, 2, 3} È {4, 2, 5} = {1, 2, 3, 4, 5}, так как в обоих наборах двойка занимает одно и то же место;
- {1, 2, 3} È {2, 1, 3} = {1, 2, 3, 2, 1, 3}, так как все числа имеют собственный порядковый номер.
Для объединения вам достаточно ввести в соответствующие ячейки элементы множеств через запятую, после чего нажать кнопку «Рассчитать». Программа мгновенно выдаст результат. Рассмотрим пример.
Примеры объединения
Пусть у нас есть два набора данных по 5 замеров, полученных в результате лабораторной работы:
- A = {6, 24, 60, 120, 210};
- B = {5, 25, 60, 117, 213}.
Оба набора содержат надежно различимые элементы, каждый из которых был получен в конкретных условиях. Для сохранения результатов объединим эти множества в одно. Для этого введем значения A и Bв соответствующие ячейки и получим результат:
{6, 24, 60, 120, 210, 5, 25, 117, 213}.
Наш калькулятор позволяет объединять множества с произвольным количеством элементов. При суммировании наборы могут содержать разное количество элементов, например, мы без проблем можем сложить наборы {1} и {3, 5, 8, 10, 7}, а в результате получить {1, 3, 5, 8, 10, 7}.
Заключение
Теория множеств внесла в развитие математики неоценимый вклад. Благодаря работам Кантора и Бурбаки в мир пришло новое понимание природы бесконечности, а современная теория множеств имеет глубокие связи с математической логикой. Используйте наш калькулятор для выполнения простых арифметических действий с различными множествами, что может потребоваться вам как в профессиональной деятельности, так и во время учебы.
bbf.ru
Круги Эйлера онлайн — 4 Июля 2016 — Примеры решений задач
Круги Эйлера, диаграммы Венна
Геометрическое моделирование множеств. Калькулятор.
Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна).
Универсальное множество изображают в виде прямоугольника, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга.
С помощью диаграмм Венна удобно иллюстрировать операции над множествами.
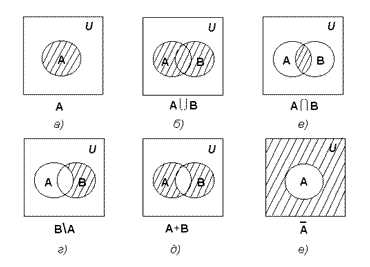
Калькулятор для построения кругов Эйлера.
Правила вввода основных обозначений операций над множествами:
| Операция | Обозначение | |
| математическое | в калькуляторе | |
| Дополнение | $\bar{A}$ | A’ |
| Пересечение | (A∩B) | (A intersection B) |
| Объединение | (А⋃B) | (A union B) |
| Симметрическая разность | (A∆B) | (symmetric difference of A and B) |
| Относительное дополнение | (A\B) | (A\B) |
Пример. Изобразить множество D с помощью кругов Эйлера (нарисовать диаграмму Эйлера-Венна):
№ | Множество D | Вводим в калькулятор |
1 | (А∩B’) ∪ C | (A intersection B’) union C |
2 | (А∩B) ∪C’ | (A intersection B’) union C’ |
3 | (А∪B) ∩ C | (A union B’) intersection C |
4 | (А∪B) ∩C’ | (A union B’) intersection C’ |
5 | (А∩B) ∪ C | (A intersection B) union C |
6 | (А∩B) ∪ (А∩C) | (A intersection B) union (A intersection C) |
В таблице показано: как правильно вводить в калькулятор выражения для операций над множествами.
www.reshim.su
