Параметры с модулем – «Графические методы решений уравнений с модулем и параметром Бойцов Михаил.». Скачать бесплатно и без регистрации.

Содержание

Задача с параметром и модулем

Задачи с параметром – наиболее сложные, но зато и самые интересные. Решение такой задачи – всегда исследование, всегда приключение. Тогда вперед, к приключениям!

Задача: Найти все значения параметра , при каждом из которых уравнение

Относительно переменной имеет ровно 4 решения.

Применим графическое решение. Запишем иначе:

Слева имеем параболу, график которой, вследствие наличия модуля, располагается только в верхней полуплоскости, вся его «подводная» часть отражена вверх:

Рисунок 1. Парабола “в модуле”

Справа имеем «галочку», вершина этой галочки будет перемещаться по прямой . То, что график выглядит, как «галка», понятно, но как была установлена траектория движения ее вершинки? А вот как:

Модуль может быть раскрыт как с плюсом, так и с минусом в зависимости от знака подмодульного выражения:

Тогда

Вычитаем уравнения:

Тогда

Теперь исследуем полученную систему двух графиков. Нас устраивают случаи, когда «галка» 4 раза пересекает параболу. Начинаем двигать нашу галочку слева направо:

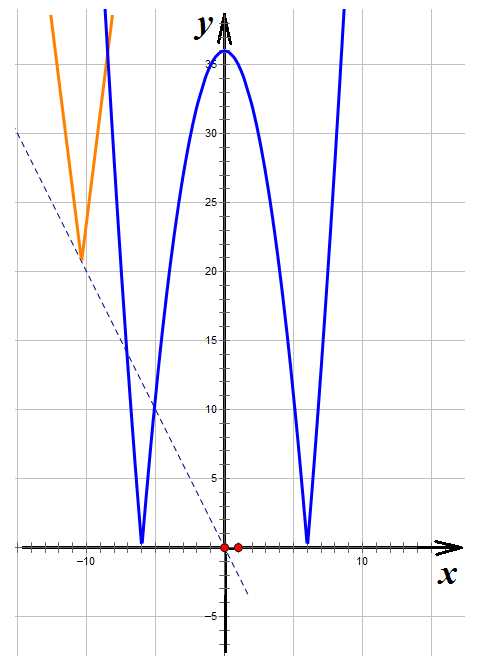
Рисунок 2. Галка спускается вниз. Два корня (два пересечения)

В указанном положении будем иметь два корня. Поэтому продолжаем двигать галку вниз:

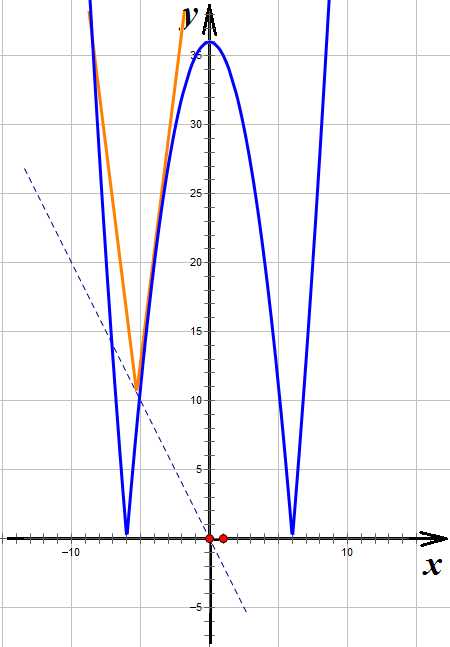
Рисунок 3. Галка спускается ниже. Три корня (два пересечения и касание)

Когда «галка» своим правым крылом коснется параболы, ее отраженного, внутреннего кусочка, у нас получится три решения. А чуть только мы сдвинемся еще чуть ниже – уже 4. Определим значение параметра при касании, это начальная точка того интервала, который нас интересует.

Определить значение параметра в этом случае просто. Правое крыло «галки» описывается уравнением: . При касании ордината точки, принадлежащей параболе, и ордината точки, принадлежащей прямой, одинаковы, поэтому приравняем ординаты. Та часть параболы, которой касается прямая, описывается уравнением:

Тогда, приравняв ординаты, получим:

Если общая точка одна, то дискриминант будет равен 0:

Сама эта точка нас еще не устраивает, но значения параметра, большие , уже подходят нам. Выясним, до какого момента будем иметь 4 пересечения:

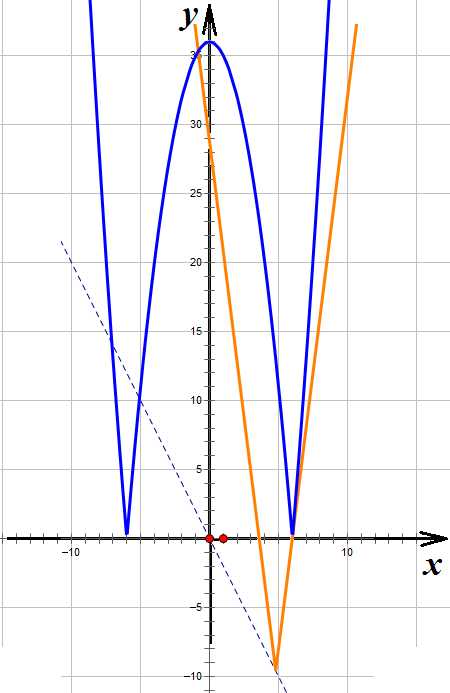
Рисунок 4. Три корня.

В показанном положении снова будем иметь три пересечения. В этот момент правое крыло «галки» проходит через точку , тогда

Итак, найден интервал решений: .

Однако, вдруг это еще не все решения? Сдвинем «галку» еще ниже:

Рисунок 5. Снова три корня.

Видим, что снова, при прохождении левого крыла «галки» через точку , появились три корня. Небольшой сдвиг еще чуть ниже даст четыре корня, и эта ситуация нас устраивает, следовательно, имеем еще один интервал решений. Определим значение параметра. Левое крыло «галки» описывается уравнением:

Подставляем координаты точки в уравнение:

Сдвигаем «галку» еще ниже, и получаем касание:

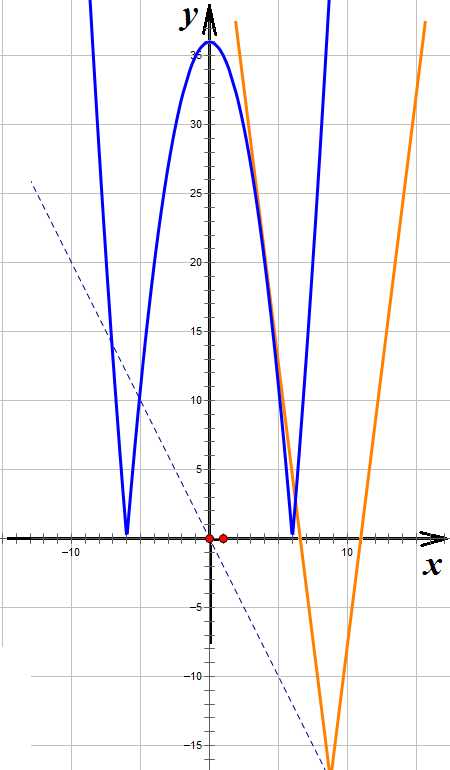
Рисунок 6. Два пересечения и касание

Приравниваем ординаты:

Если общая точка одна, то дискриминант будет равен 0:

Полученное значение параметра нас уже не устраивает: при таком снова имеем три решения.

Вот и второй интервал:

Ответ: .

easy-physic.ru

Уравнения с параметром, содержащие модуль — Мегаобучалка

Решить в зависимости от значений параметра а.

| x – 3 | = a

По свойству модуля при всех левая часть уравнения неотрицательна, следовательно, при a < 0 уравнение не имеет решений.

При a = 0 x = 3.

При a > 0 x – 3 = ± a, откуда x = 3 ± a.

Ответ: при a = 0 x = 3.

при a > 0 x = 3 + a. x

= 3 – a.

при a < 0 уравнение не имеет решений.

При каких значениях параметра a уравнение x = a · | x – 5 | имеет единственное решение, два решения, не имеет решения. Найдите их.

Для решения уравнения найдём нули модули x – 5 = 0 x = 5.

Раскроем модуль на двух промежутках: x ≥ 5 и x < 5.

1) x ≥ 5, 2) x < 5,

x = a ( x – 5 ) x = a ( – x + 5 )

x ≥ 5, x < 5,

– ax = – 5a;x + ax = 5a;

x ≥ 5, x < 5,

x ( 1– a )= – 5a;x ( 1+ a )= 5a ;

Исследуем линейное уравнение Исследуем линейное уравнение

в зависимости от параметра a. в зависимости от параметра a.

x ( 1– a )= – 5a ; x ( 1+ a )= 5a;

Если 1– a = 0, т.е. a = 1, то Если 1+ a = 0, т.е. a = – 1, то

x · 0 = – 5 Уравнение не имеет

x · 0 = – 5 Уравнение не имеет
решения. решений.
Если 1– a ≠ 0, т.е. a ≠ 1, то Если 1+ a ≠ 0, т.е. a ≠ – 1, то
— уравнение имеет — уравнение имеет
единственное решение. единственное решение.
x ≥ 5, x < 5,
, a ≠ 1; , a ≠ –1;
Учтем, что x ≥ 5, т.е. Учтем, что x < 5, т.е.
решим методом интервалов решим методом интервалов
неравенство. неравенство.
Получим a > 1. Т.е. при a > 1 Получим a
> – 1. Т.е. при a > –1
уравнение будет иметь уравнение будет иметь
единственное решение единственное решение
на промежутке x ≥ 5. на промежутке x < 5.

Ответим на поставленные вопросы. Наши решения покажем на координатных прямых.

одно решение
нет одно два
решения решение решения
При a > 1 уравнение имеет два корня ; ;
При a < – 1 уравнение не имеет решения.
При – 1< a ≤ 1 уравнение имеет одно решение, т.е. .
Ответ: a > 1, ; .

a < – 1, решений нет.
– 1< a ≤ 1, .
Решить самостоятельно:
При каком a уравнение имеет решения. Найдите их.

При каких значениях a уравнение | x + 3| · ( x – 3 ) + a = 0 имеет ровно 3 решения?

Найдем нули модуля: x + 3 =0; x = – 3.
Раскроем модуль на двух промежутках:
x ≥ – 3 x < – 3
x ≥ – 3, x < – 3
( x + 3) ( x – 3 ) + a = 0; (–
x – 3) ( x – 3 ) + a = 0;

Исследуем уравнение Исследуем уравнение
( x + 3) ( x – 3 ) + a = 0; (– x – 3) ( x – 3 ) + a = 0;
x² – 9 + a = 0; – ( x² – 9 ) = – a ;
x² = 9 – a ; x² – 9 = a ;
при 9 – a ≥ 0, т.е. a ≤ 9 x² = a + 9;
уравнение имеет два корня при a + 9 ≥ 0, т.е. a ≥ – 9

. уравнение имеет два корня

x ≥ – 3; a ≥ – 9
; a ≤ 9 x < – 3;

Учтем, что x ≥ – 3 Учтем, что x < – 3
при 9 – a ≥ 0
неравенство имеет решение, решения нет.
т.е. a ≤ 9.
a + 9 ≥ 0,
a + 9 > 9,
неравенство имеет решение Т.е. при a > 0
a ≤ 9; уравнение имеет один корень
a ≥ 0; т.е. 0 ≤ a ≤ 9;
Т.е. при 0 ≤ a ≤ 9 уравнение
имеет два различных корня.

, при a = 3
уравнение имеет два равных
корня .
Ответим на поставленный вопрос.
При 0 ≤ a < 9 уравнение имеет 3 корня.
нет три одно
решения решения решение
два два
решения решения
Ответ: при 0 ≤ a < 9 три корня.
При каких значениях a уравнение | x + 3| · ( x – 3 ) + a = 0 имеет ровно 3 решения? (Графический способ).
| x + 3| · ( x – 3 ) = – a
Построим графики, заданные в левой и правой частях:
1) y = | x + 3| · ( x – 3 )
Найдем нули модуля: x + 3 =0; x = – 3.
Раскроем модуль на двух промежутках: x < – 3; x ≥ – 3.
x ≥ – 3; x < – 3;
y = ( x + 3) ( x – 3 ) = x² – 9; y = – ( x + 3) ( x – 3 ) = 9 – x²;

2) y = – a – линейная функция, график прямая, параллельная оси OY.
Эскиз графиков. y

y = – a

Ответ: 0 < a < 9.
При каких значениях a уравнение имеет единственное решение?
ОДЗ: x²+ 8x + 12 ≠ 0; x ≠ – 6; x ≠ –2;
Найдем нули модуля: 2x + 6 = 0; x = –3;
Раскроем модуль на двух промежутках: x ≥ –3 и x < –3.
1) x ≥ –3; и 2) x < –3.
x ≥ –3; x < –3.
x ≥ –3; x < –3.
Исследуем уравнение: Исследуем уравнение
x ≠ – 6; x ≠ –2;
Если a = 0; 0 ∙ x = 3 Если a = 0; 0 ∙ x = – 1
решения нет. решения нет.
a ≠ 0; a ≠ 0;
единственное решение. единственное решение.
x ≥ –3; x < –3;
a ≠ 0; a ≠ 0;
Учтем, что x ≥ –3; т.е. Учтем, что x < –3; т.е.
Решим методом интервалов Решим методом интервалов
неравенство. неравенство
Получим 0 < a ≤ 1. Получим 0 < a < 1.
Т.е. при 0 < a ≤ 1 уравнение Т.е. при 0 < a < 1 уравнение
будет иметь единственное будет иметь единственное
решение решение

Ответим на поставленный вопрос. Наши решения покажем на координатных прямых.

нет два нет
решения решения решений
нет одно
решения решение
При a = 1 уравнение имеет одно решение.
Учтем ОДЗ x ≠ – 2; x ≠ –6;
x ≥ –3; x < –3;
x ≠ –6; x ≠ – 2; x ≠ –6; x ≠ – 2;
a ≠ 0;

С учетом ОДЗ

При и уравнение имеет одно решение.
Ответ: — единственное решение.
Решить самостоятельно:
При каких значениях a уравнение имеет единственное решение? Ответ:

При каких значениях параметра a уравнение имеет два различных корня?
Так как то сделав замену где получим новое квадратное уравнение
Для того чтобы исходное уравнение имело два различных корня, новое уравнение должно иметь только один положительный корень. Это будет в двух следующих случаях:
а) один из корней положителен, другой отрицателен. Для этого достаточно, чтобы дискриминант был положительным, а произведение корней было отрицательным;
б) оба равных корня положительны. Для этого достаточно, чтобы дискриминант был равен нулю, а сумма корней была положительной.
Таким образом, получим совокупность двух систем.
1) Д > 0, 2) Д = 0,
y₁ ∙ y₂ < 0; y₁ + y₂ > 0;
Так как
то системы будут иметь вид:
Откуда или
Ответ: ;
При каких значениях с уравнение x²– ( 3c – 2 ) ∙ | x | + 2c²– c = 0 имеет 4 различных корня?
Так как | x |² = x², то сделав замену | x | = y, где y ≥ 0, получим новое квадратное уравнение y²– ( 3c – 2 ) ∙ y + 2c²– c = 0.
Для того чтобы исходное уравнение могло иметь четыре различных корня новое уравнение должно иметь два положительных корня. Это будет в том случае, когда дискриминант, произведение и сумма корней будут положительны.
Таким образом, получим систему неравенств:
Д > 0;
Так как Д = ( 3c – 2 )² – 4∙ ( 2c²– c ) = 9c²– 12c + 4^{– 8c²+4c^{= c²– 8c +4}}
то система будет иметь вид:
c²– 8c +4 > 0;
3c – 2 > 0; Откуда имеем
2c²– c > 0;
Ответ:

СПИСОК ЛИТЕРАТУРЫ
1. М.Л. Галицкий, А.М. Гольдман, Л.И.Звавич. Сборник задач по алгебре 8-9.Москва, 2000
2. Г.А. Ястребинецкий. Задачи с параметрами. Москва, 1986
3. П.И.Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. Киев, 1992
4. В.В.Ткачук. Математика-абитуриенту,т1.Москва, 1994
5. С.Л.Попцов. Как решать задачи с параметром. Тверь, 1999
6. Сборник задач по математике для поступающих во втузы. Под редакцией М.И. Сканави, Москва, 2003
megaobuchalka.ru
Решение уравнений с модулями и параметрами
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (433,7 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения.

Задачи:
Образовательные: научить решать некоторые виды уравнений уравнений модулями и параметрами;

Развивающие: развивать культуру мысли, культуру речи и умение работать с тетрадью и доской.

Воспитательные: воспитывать самостоятельность и умение преодолевать трудности.

Оборудование: наглядный материал для устного счёта и объяснения новой темы. Интерактивная доска, мультимедийное оборудование урока.

Структура урока:
Повторение изученного материала (устный счёт).

Изучение нового материала.

Закрепление изученного материала.

Итог урока.

Домашнее задание.

ХОД УРОКА

1. Повторение важнейшего теоретического материала по темам: «Уравнения, содержащие модуль», «Решение уравнений с параметрами»

1) «Уравнения, содержащие модуль»

Абсолютной величиной или модулем числа a называется число a, если a > 0, число – a, если a < 0, нуль, если a = 0. Или

| a | ={ a, если a > 0
0, если a = 0
– a, если a < 0
Из определения следует, что | a | > 0 и | a | > a для всех a € R .
Неравенство | x | < a, (если a > 0) равносильно двойному неравенству – a < х < a.
Неравенство | x | < a, (если a < 0) не имеет смысла, так как | х | >0.
Неравенство | x | > a, (если a > 0) равносильно двум неравенствам
Неравенство | x | > a, (если a < 0) справедливо для любого х € R.

2) «Решение уравнений с параметрами»

Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.

а) определить множество допустимых значений неизвестного и параметров;

б) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнения.

2. Устные упражнения

1. Решить уравнение | x – 2 | = 5;  Ответ: 7; – 3

| x – 2 | = – 5; Ответ: решения нет

| x – 2 | = х + 5; Ответ: решения нет; 1,5

| x – 2 | = | x + 5 |; Ответ: решения нет; – 1,5; решения нет; – 1,5;

2. Решить уравнение: | x + 3 | + | y – 2 | = 4;

Расcмотрим четыре случая

1.

{ x + 3 > 0      { x > – 3
y – 2 > 0 y > 2
x + 3 + y – 2 = 4 y = – x + 3
2.

{ x + 3 > 0       { x > – 3
y – 2 < 0 y < 2
x + 3 – y + 2 = 4 y = x + 1
3.

{ x + 3 < 0      { x < – 3
y + 2 > 0 y > – 2
– x – 3 – y – 2 = 4 y = x + 9
4.

{ x + 3 < 0      { x < – 3
y + 2 < 0 y < – 2
– x – 3 – y – 2 = 4 y = – x – 9

В результате мы получаем квадрат, центр которого (–3; 2), а длина диагонали равна 8, причем диагонали параллельны осям координат.

Из наглядных соображений можно сделать вывод: что уравнение вида | х + a | + | у + b | = с; задает на плоскости квадрат с центром в точке (– а; – b), диагоналями параллельными осям OX и ОУ, и длина каждой диагонали равна 2с. Ответ: (– 3; 2).

2. Решить уравнение aх = 1

Ответ: если a = 0, то нет решения; если a = 0, то х = 1/ a

3. Решить уравнение (а² – 1) х = а + 1.

Решение.

Нетрудно сообразить, что при решении этого уравнения достаточно рассмотреть такие случаи:

1) а = 1; тогда уравнение принимает вид ОX = 2 и не имеет решения

2) а = – 1; получаем ОX = О , и очевидно х – любое.

                                       1
3) если а = + 1, то х = –––
                                    а – 1

Ответ:
если а = – 1, то х – любое;
если а = 1, то нет решения;

                                    1
если а = + 1 , то х = –––
                                 а – 1

3. Решения примеров (из вариантов С)

1. При каком значении параметра р уравнение | х² – 5х + 6 | + | х² – 5х + 4 | = р имеет четыре корня.

Решение.

Рассмотрим функцию у = | х² – 5х + 6 | + | х² – 5х + 4 |

Так как х² – 5х + 6 = (х – 2)(х – 3) и х² – 5х + 4 = (х – 1)(х – 4), то y = | (х – 2)(х – 3) | + | (х – 1)(х – 4) |, корни квадратных трехчленов отметим на числовой прямой

        1        2       3       4                           х

Числовая прямая при этом разбивает на 5 промежутков

1.

{ x < 1      { x < 1
y = x² – 5x + 6 + x² – 5x + 4 y = 2x² – 10x + 10
2.

{ 1 < x < 2      { 1 < x < 2
y = x² – 5x + 6 – x² + 5x – 4 y = 2
3.

{ 2 < x < 3      { 2 < x <3
y = – 2x² + 10x – 10 y = – x² + 5x – 6 – x² + 5x – 4
4.

{ 3 < x < 4      { 3 < x < 4
y = 2 y = x² – 5x + 6 – x² + 5x – 4
5.

{ x > 4      { x > 4
y = 2x² – 10x + 10 y= x² – 5x + 6 + x² –5x + 4
Для случая 3) х₀ = – b | 2a = 2, y₀ = 25 : 2 + 25 – 10 = 2,5

Итак, (2,5; 2,5) – координаты вершины параболы y = – 2x² + 10x – 10.

Построим график функции, заданной равенством

Как видно из рисунка, исходное уравнение имеет четыре корня, если 2 < а < 2,5

Ответ: при 2 < а < 2,5

4. Самостоятельная работа по уровням

1 уровень

1. Решить уравнение х² – | x | = 6
2. При каких целых значениях а имеет единственное решение уравнение ах² – (а + 1) + а² + а = 0?

2 уровень

1. Решить уравнение: | x – 5 | – | 2x + 3 | = 10
2. Найти все значениях параметра а, при которых уравнение (а –12) х² + 2 = 2(12 – а) имеет два различных корня?

3 уровень

1. Решить уравнение | x – 5 | – | 2x + 3| = 10
2. Найти все значениях параметра а, при которых уравнение (а – 12) х² + 2 = 2(12 – а) имеет два различных корня?

5. Итог урока

1. Определение модуля.
2. Что значит решить уравнение с параметром?

6. Задание на дом. C5 варианта №11 Ф.Ф. Лысенко. Математика, 2012
4.05.2012
xn--i1abbnckbmcl9fb.xn--p1ai
Уравнения с параметрами с модулем
Просмотр содержимого документа
«Уравнения с параметрами с модулем»

Уравнения с параметрами
Автор: Макарова Татьяна 11 а Руководитель: Польская Е. Н.

Математика – единственный совершенный метод, позволяющий провести самого себя за нос. Альберт Эйнштейн

№ 1 Найдите все значения a, при каждом из которых уравнение x² + (a + 5)² = |x + a + 5| + |x – a -5| имеет ровно три корня.
РЕШЕНИЕ Уравнение не изменится, если заменить x числом –x . Следовательно, уравнение имеет чётное число ненулевых решений. Значит, три решения уравнения имеет только тогда, когда одно из них 0. Поставим x = 0 .
Получим: (a + 5)² = 2|a + 5|
Откуда a + 5 = 0 или |a + 5| = 2.

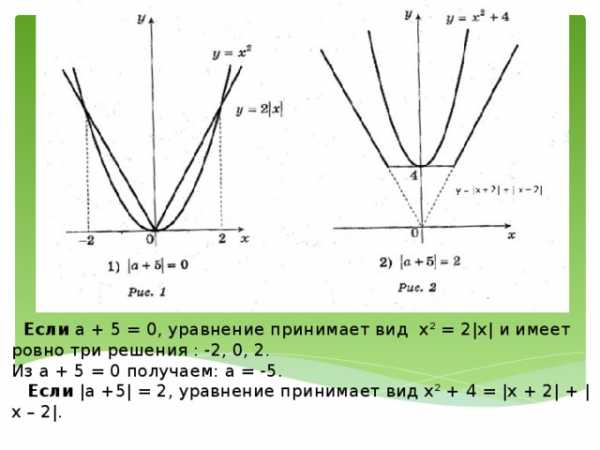
Если a + 5 = 0, уравнение принимает вид x² = 2|x| и имеет ровно три решения : -2, 0, 2. Из a + 5 = 0 получаем: a = -5. Если |a +5| = 2, уравнение принимает вид x² + 4 = |x + 2| + |x – 2|.
2 уравнение принимает вид x² — 2x + 4 = 0 и не имеет решений. Аналогично решений нет при x Ответ: a = -5. «
При -2 ≤ x ≤ 2 уравнение имеет единственное решение 0. При x 2 уравнение принимает вид x² — 2x + 4 = 0 и не имеет решений. Аналогично решений нет при x Ответ: a = -5.

№ 2
Найдите все значения параметра a, при котором уравнение f(x) = |2a + 5|x
имеет 6 решений, где f — чётная периодическая функция, с периодом Т = 2, определённая на всей числовой прямой, причём f(x) = ax², если 0≤x≤1 .
РЕШЕНИЕ Если а = 0, функция f(x) тождественно равна нулю, и её график имеет с прямой y = 5x единственную общую точку.
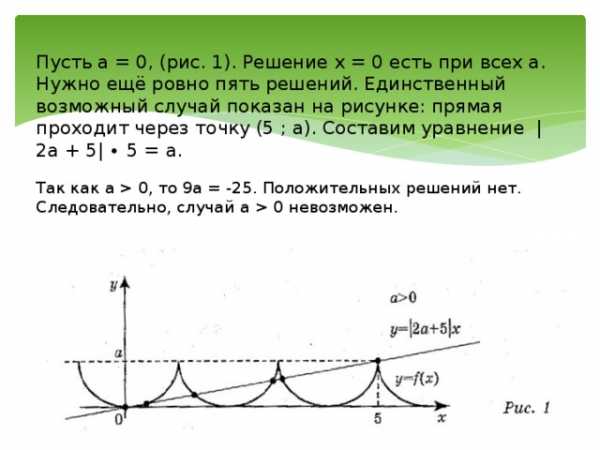0, то 9а = -25. Положительных решений нет. Следовательно, случай а 0 невозможен. «
Пусть а = 0, (рис. 1). Решение х = 0 есть при всех а. Нужно ещё ровно пять решений. Единственный возможный случай показан на рисунке: прямая проходит через точку (5 ; а). Составим уравнение |2a + 5| ∙ 5 = a. Так как а 0, то 9а = -25. Положительных решений нет. Следовательно, случай а 0 невозможен.

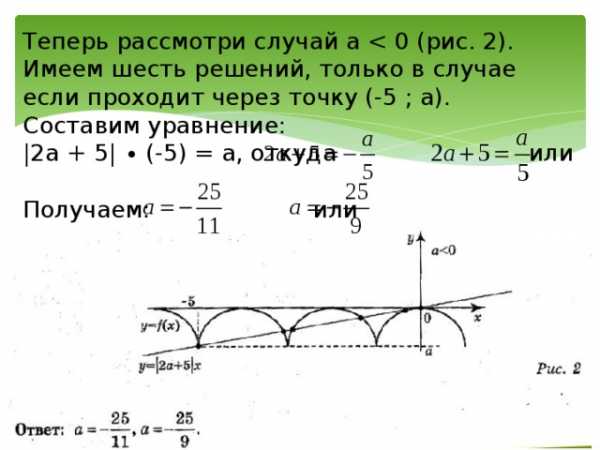
Теперь рассмотри случай а

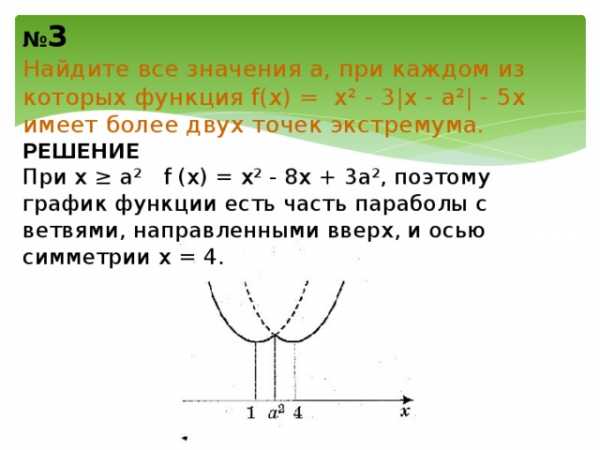
№ 3 Найдите все значения а, при каждом из которых функция f(x) = x² — 3|x — a²| — 5x имеет более двух точек экстремума. РЕШЕНИЕ При х ≥ а² f (x) = x² — 8x + 3a², поэтому график функции есть часть параболы с ветвями, направленными вверх, и осью симметрии х = 4.

При х ≤ а² f(x) = x² — 2x – 3a², поэтому график есть часть параболы с ветвями, направленными вверх, и осью симметрии х = 1.

Все возможные виды графика функции f(x) показаны на рисунке:

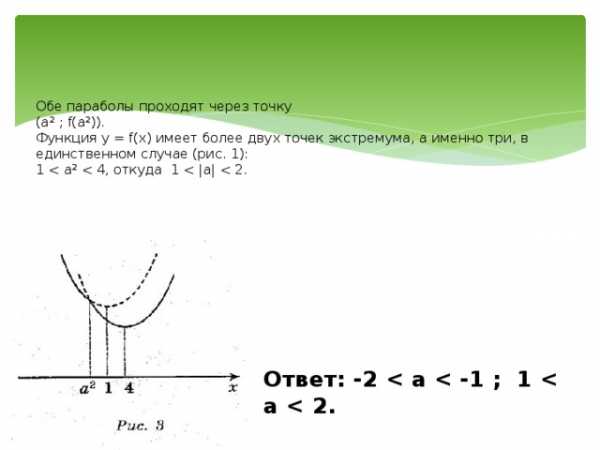
Обе параболы проходят через точку (а² ; f(a²)). Функция y = f(x) имеет более двух точек экстремума, а именно три, в единственном случае (рис. 1): 1
Ответ: -2

СПАСИБО ЗА ВНИМАНИЕ!
multiurok.ru
Задача с параметром, система с модулем
Задачи с параметром – одни из самых сложных в ЕГЭ, но зато и самые интересные. Решать их – одно удовольствие. Всем рекомендую подружиться с параметрами и не бояться сложных задач.
Задача. При каком значении параметра система имеет больше двух решений?

Раскроем модуль. Он будет сниматься с положительным знаком, если подмодульное выражение неотрицательно, и с отрицательным, если подмодульное выражение меньше 0:

Таким образом, выделив полный квадрат, получили две окружности (вернее, их части). Одна из окружностей существует выше прямой , а вторая – ниже. Части наших окружностей стыкуются в точках с координатами O(0;0) и C(-2;-4) – это легко проверяется подстановкой.
Рисунок 1
Окружности будет пересекать прямая, коэффициент наклона которой постоянен, а коэффициент – меняется:

Такая прямая будет скользить по оси вверх-вниз, нас интересуют случаи, когда эта прямая будет иметь более двух пересечений с «восьмеркой» из окружностей. Начнем исследование с положения прямой такого, когда она проходит через начало координат.
Рисунок 2
Это крайняя точка, в которой система имеет три решения. При более низком положении прямой она будет какое-то время только два раза пересекать окружности (пока на точку С не наткнется). А вот при сдвиге прямой вверх из начала координат видим, что пересечений четыре – и так будет, пока прямая не станет касательной к окружностям. Определим значение параметра в случае, если начало координат принадлежит прямой , просто подставив координаты точки O в уравнение:

Теперь сдвигаем нашу прямую вверх, пока она не станет касательной к окружностям. Если в этом положении прямой сможем определить координаты точки или точки – дело в шляпе.
Рисунок 3
Подумаем: если прямая касается окружности, то радиус, проведенный в точку касания, должен быть ей перпедикулярен. Заметим, что прямая , разграничивающая области существования окружностей, имеет коэффициент наклона 2, а прямая – коэффициент наклона , и произведение этих двух коэффициентов равно (-1), следовательно, прямые перпендикулярны. Таким образом, мы доказали, что прямая и прямая, которой принадлежит радиус , имеют одинаковый коэффициент наклона, равный 2, то есть параллельны. Зная, что прямая, содержащая радиус , проходит через точку , находим ее уравнение: .
Расстояние между точками и известно – оно равно радиусу окружности, они принадлежат одной прямой, координаты точки известны – ничего не стоит найти координаты .

Решим первое квадратное уравнение системы:

Два корня – это координаты по оси точек и противоположной ей точки – она нам понадобится чуть позже и мы к ней еще вернемся.
Найдем координату :

Теперь ищем параметр, подставляя координаты точки в уравнение прямой :

Откуда .
За нами маленькая победа: мы нашли один из диапазонов параметра, который бы нас устраивал:

Ноль войдет в этот интервал, так как там три пересечения, а вот вторая граница – не войдет, там всего две точки касания, а нужно больше.
Приступаем к отысканию второго интервала:
Аналогично, просто подставив в уравнение координаты точки С, определяем значение параметра в случае, когда прямая пройдет через эту точку:

Вот сейчас-то мы и вернемся ко второму решению квадратного уравнения: ведь это – координата по оси точки : .
Тогда ее координата по оси ординат:

Определяем значение параметра:

Откуда .
Тогда второй промежуток значений параметра равен: .
easy-physic.ru
уравнения и неравенства с параметром
Существует ровно три генеральных метода решения задач 18:
Метод перебора — классический перебор вариантов. Например, когда выражение под модулем больше нуля и когда меньше;

Графический метод — привлечение чертежа. Во многих задачах 18 достаточно начертить графики функций — и решение становится очевидным;

Метод следствий — нестандартный и, как правило, самый изощренный. Если в исходном условии удастся подметить что-нибудь полезное, в дальнейшем можно значительно упростить решение всей задачи.

Конечно, одну и ту же задачу зачастую можно решить разными способами. Но далеко не все они оптимальны: выбрав неправильный «путь», можно увязнуть в вычислениях, так и не дойдя до ответа.
Поэтому в данном разделе я рассмотрю все способы, а ваша задача — практиковаться и учиться правильно выбирать.:)
Глава 1.
Графический подход
§ 1.
Вебинар по задачам 18: модуль и окружности
§ 2.
Как решать задачу 18: графический подход
§ 3.
Задача 18: две окружности и модуль
§ 4.
Задача 18: пересечение графиков окружности и модуля
§ 5.
Новая задача 18 из пробного ЕГЭ — наглядный пример того, как эффективно работает графическое решение задач с параметром.
Глава 2.
Аналитический подход
§ 1.
Задачи 18: Аналитическое решение
§ 2.
Окружность и модуль: задачи 18 с двумя параметрами
§ 3.
Аналитическое решение задачи 18 с перебором различных вариантов
Глава 3.
Нестандартные приемы
§ 1.
Задача 18: метод симметричных корней
§ 2.
Как увидеть симметрию корней в задаче 18?
§ 3.
Метод мажорант в задаче 18
§ 4.
Графическое решение сложных задач 18 с модулем
§ 5.
Задание 18: Симметрия корней в системе уравнений
§ 6.
Анализ знаков квадратного трёхчлена в сложных задачах 18
§ 7.
Применение производной для отыскания точек пересечения графиков
§ 8.
Продвинутый метод симметричных корней
§ 9.
Новая задача 18 с графическим решением
Функции с параметром
1
2
3
4
5
6
7
8
9
10
11
12
Уравнения с параметром
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
Неравенства с параметром
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
Системы с параметром
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
www.berdov.com
Графическое решение неравенства с параметром и модулем
Здесь будет применен прием домножения на сопряженное выражение, и применен графический способ решения данного неравенства.
Задача. Найдите все значения параметра , при которых неравенство выполняется на отрезке :

Перепишем:

Применим прием «борьбы» с разностью двух положительных выражений: домножим на сопряженное выражение. Тогда неравенство будет записано:

Общий множитель в первой скобке выносим, а во второй – увидим и выделим полные квадраты:

Если теперь ввести систему координат , то в ней можно построить три объекта:

То есть две пересекающиеся прямые и окружность. Строим:

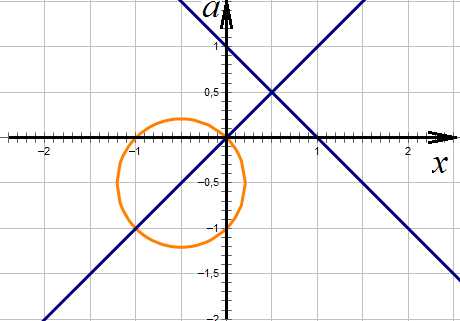
Рисунок 1. Построение линий
Теперь возьмем произвольную точку, например, с координатами и подставим ее координаты в неравенство. Видим, что все множители положительны и неравенство не выполняется. Оно не будет выполняться во всей области, но как только мы пересечем какую-либо ее границу, то попадем в область, где неравенство выполняется. Поэтому закрасим такие области в шахматном порядке:

Рисунок 2. Обозначение областей, где неравенство выполняется.
Теперь коричневыми вертикалями отграничим область , и посмотрим, при каких неравенство выполняется.

Рисунок 3. Ярким зеленым цветом и желтой полоской обозначаем решение неравенства на заданном отрезке
Очевидно, что это и промежуток от «верхушки» окружности до . А координату «верхушки» окружности найдем как разность радиуса и координаты центра:
.
Ответ: .
easy-physic.ru

РубрикаПолезно знать

\| a \| ={	a, если a > 0
	0, если a = 0
	– a, если a < 0

{	x + 3 > 0	{	x > – 3
	y – 2 > 0		y > 2
	x + 3 + y – 2 = 4		y = – x + 3

{	x + 3 > 0	{	x > – 3
	y – 2 < 0		y < 2
	x + 3 – y + 2 = 4		y = x + 1

{	x + 3 < 0	{	x < – 3
	y + 2 > 0		y > – 2
	– x – 3 – y – 2 = 4		y = x + 9

{	x + 3 < 0	{	x < – 3
	y + 2 < 0		y < – 2
	– x – 3 – y – 2 = 4		y = – x – 9

{	x < 1	{	x < 1
	y = x² – 5x + 6 + x² – 5x + 4		y = 2x² – 10x + 10

{	1 < x < 2	{	1 < x < 2
	y = x² – 5x + 6 – x² + 5x – 4		y = 2

{	2 < x < 3	{	2 < x <3
	y = – 2x² + 10x – 10		y = – x² + 5x – 6 – x² + 5x – 4

{	3 < x < 4	{	3 < x < 4
	y = 2		y = x² – 5x + 6 – x² + 5x – 4

{	x > 4	{	x > 4
	y = 2x² – 10x + 10		y= x² – 5x + 6 + x² –5x + 4

Параметры с модулем – «Графические методы решений уравнений с модулем и параметром Бойцов Михаил.». Скачать бесплатно и без регистрации.

Задача с параметром и модулем

Уравнения с параметром, содержащие модуль — Мегаобучалка

Решение уравнений с модулями и параметрами

Презентация к уроку

Уравнения с параметрами с модулем

Просмотр содержимого документа «Уравнения с параметрами с модулем»

Задача с параметром, система с модулем

уравнения и неравенства с параметром

Графическое решение неравенства с параметром и модулем

Добавить комментарий Отменить ответ

Просмотр содержимого документа
«Уравнения с параметрами с модулем»