Отрицательные числа в квадрате – Квадрат отрицательного числа | Математика
Квадрат отрицательного числа | Математика
Как найти квадрат отрицательного числа? Что можно сказать о значении квадрата любого числа?
Чтобы найти квадрат числа, надо это число взять множителем два раза.
Соответственно, чтобы возвести в квадрат отрицательное число, надо найти произведение двух множителей, каждый из которых равен этому отрицательному числу.
При умножении отрицательных чисел получаем положительное число. Значит, знак «минус» при возведении в квадрат отрицательного числа уходит:
Следовательно, квадрат отрицательного числа равен квадрату противоположному ему числа:
Таким образом, значение квадрата любого отрицательного числа равно положительному числу.
Квадрат положительного числа является числом положительным.
Квадрат нуля равен нулю.
Вывод: квадрат любого числа является неотрицательным числом:
Чтобы возвести в квадрат отрицательное число, можно возвести в квадрат противоположное ему число (знак «-» не писать).
Примеры.
Найти квадрат отрицательного числа:
Решение:
(При вычислении квадратов можно пользоваться готовыми значениями).
(Найти квадрат дроби можно одним из двух способов).
www.for6cl.uznateshe.ru
Что такое степень числа Возведение в степень отрицательного числа Порядок действий в примерах со степенями — Арифметика
Обращаем ваше внимание, что в данном разделе разбирается понятиестепени только с натуральным показателем
Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.
Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение. Так, вместо произведения шести одинаковых множителей 4 • 4 • 4 • 4 • 4 • 4 пишут 46 и произносят «четыре в шестой степени».
4 • 4 • 4 • 4 • 4 • 4 = 46Выражение 46 называют степенью числа, где:
- 4 — основание степени;
- 6 — показатель степени.
В общем виде степень с основанием «a» и показателем «n» записывается с помощью выражения:
Степенью числа «a» с натуральным показателем «n», бóльшим 1, называется произведение «n» одинаковых множителей, каждый из которых равен числу «a».
Запись an читается так: «а в степени n» или «n-ая степень числа a».
Исключение составляют записи:
- a2 — её можно произносить как «а в квадрате»;
- a3 — её можно произносить как «а в кубе».
Конечно, выражения выше можно читать и по определению степени:
- a2 — «а во второй степени»;
- a3 — «а в третьей степени».
Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0).
Степенью числа «а» с показателем n = 1 является само это число:
a1 = a
Любое число в нулевой степени равно единице.
a0 = 1
Ноль в любой натуральной степени равен нулю.
0n = 0
Единица в любой степени равна 1.
1n = 1
Выражение 00 (ноль в нулевой степени) считают лишённым смыслом.
- (-32)0 = 1
- 0253 = 0
- 14 = 1
При решении примеров нужно помнить, что возведением в степень называется нахождение значения степени.
Пример. Возвести в степень.
- 53 = 5 • 5 • 5 = 125
- 2.52 = 2.5 • 2.5 = 6.25
- (
)4 =
•
•
•
=
=3 • 3 • 3 • 3 4 • 4 • 4 • 4
Возведение в степень отрицательного числа
Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.
При возведении в степень положительного числа получается положительное число.
При возведении нуля в натуральную степень получается ноль.
При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.
Рассмотрим примеры возведения в степень отрицательных чисел.
Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.
Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.
Отрицательное число, возведённое в чётную степень, есть число положительное.
Отрицательное число, возведённое в нечётнуюстепень, — число отрицательное.
Квадрат любого числа есть положительное число или нуль, то есть:
a2 ≥ 0 при любом a.
- 2 • (- 3)2 = 2 • (- 3) • (- 3) = 2 • 9 = 18
- — 5 • (- 2)3 = — 5 • (- 8) = 40
Обратите внимание!
При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (- 5)4 и -54 это разные выражения. Результаты возведения в степень данных выражений будут разные.
Вычислить (- 5)4 означает найти значение четвёртой степени отрицательного числа.
(- 5)4 = (- 5) • (- 5) • (- 5) • (- 5) = 625В то время как найти -54 означает, что пример нужно решать в 2 действия:
- Возвести в четвёртую степень положительное число 5.
54 = 5 • 5 • 5 • 5 = 625 - Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание).
-54 = — 625
Пример. Вычислить: — 62 — (- 1)4
— 62 — (- 1)4 = — 37- 62 = 6 • 6 = 36
- -62 = — 36
- (- 1)4 = (- 1) • (- 1) • (- 1) • (- 1) = 1
- — (- 1)4 = — 1
- — 36 — 1 = — 37
Порядок действий в примерах со степенями
Вычисление значения называется действием возведения в степень. Это действие третьей ступени.
В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление, а в конце сложение и вычитание.
Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.
Пример. Вычислить:
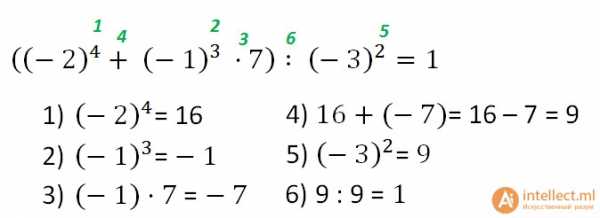
Для облегчения решения примеров полезно знать и пользоватьсятаблицей степеней, которую вы можете бесплатно скачать на нашем сайте.
Квадратные корниS-KUZ ‹ Сергей Кузнецов — репетитор по математике
Что такое квадратный корень?
Это понятие очень простое. Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня) в математике обозначается вот таким значком:
Сам значок называется красивым словом «радикал«.
Как извлечь корень? Это лучше рассмотреть на примерах.
Как извлечь (или посчитать — это всё едино) корень квадратный из 4? Нужно просто сообразить: какое число в квадрате даст нам 4? Да конечно же 2! Значит:
Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:
А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:
Уловили, что такое квадратный корень? Тогда считаем примеры:
Ответы (в беспорядке): 6; 1; 4; 9; 5.
Решили? Действительно, уж куда проще-то?!
Но… Что делает человек, когда видит какое-нибудь задание с корнями?
Тосковать начинает человек… Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает,
Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах…
Пунктик первый. Корни надо узнавать в лицо!
Сколько будет корень квадратный из 49? Семь? Верно! А как вы узнали, что семь? Возвели семёрку в квадрат и получили 49? Правильно! Обратите внимание, чтобы извлечь корень из 49 нам пришлось проделать обратную операцию — возвести 7 в квадрат! И убедиться, что мы не промахнулись. А могли и промахнуться…
В этом и есть сложность извлечения корней.
Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком — да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.
Этот сложный творческий процесс — подбор ответа — сильно упрощается, если вы
Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём тудаи обратно. Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый — выучить таблицу квадратов. Это здорово поможет решать примеры. Второй — решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.
И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно…
Итак, что такое квадратный корень и как извлекать корни — думаю, понятно. Теперь выясним ИЗ ЧЕГО можно их извлекать.
Пунктик второй. Корень, я тебя не знаю!
Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзяих извлекать.
Попробуем вычислить вот такой корень:
Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.
Что, не подбирается? 22 даёт +4. (-2)2 даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт — сами узнаете.
Такая же история будет с любым отрицательным числом. Отсюда вывод:
Выражение, в котором под знаком квадратного корня стоит отрицательное число — не имеет смысла! Это запретная операция. Такая же запретная, как и деление на ноль. Запомните этот факт железно!Или, другими словами:
Квадратные корни из отрицательных чисел извлечь нельзя!
Зато из всех остальных — можно. Например, вполне можно вычислить
или
На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить… Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов. Жизнь станет проще!
Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:
или
и т.д…
Ничего страшного. Всё то же самое. Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно:
Что интересно, эта дробь не кончается никогда… Такие числа называются иррациональными. В квадратных корнях это — самое обычное дело. Кстати, именно поэтому выражения с корнями называютиррациональными. Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют:
Если при решении примера у вас получилось что-то неизвлекаемое, типа:
то так и оставляем. Это и будет ответ.
Нужно чётко понимать, что под значками
, , ……
и так далее, скрываются просто числа! Неровные, лохматые, иррациональные, но числа!
Конечно, если корень из числа извлекается ровно, вы обязаны это сделать. Ответ задания в виде, например
никто не оценит… Надо корень посчитать и написать
х = 4.
А вот
вполне себе полноценный ответ.
И, конечно, надо знать на память приблизительные значения:
Это знание здорово помогает оценить ситуацию в сложных заданиях.
Идём дальше.
Пунктик третий. Самый хитрый.
Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах… Разберёмся с этим пунктиком как следует!
Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!
Какое число даст в квадрате 4? Ну два, два — слышу недовольные ответы…
Верно. Два. Но ведь и минус два даст в квадрате 4… А между тем, ответ
правильный, а ответ
грубейшая ошибка. Вот так.
Так в чём же дело?
Действительно, (-2)2 = 4. И под определение корня квадратного из четырёх минус два вполне подходит… Это тоже корень квадратный из четырёх.
Но! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа! Т.е ноль и все положительные. Даже термин специальный придуман: арифметический квадратный корень из числа а — это неотрицательное число, квадрат которого равен а. Отрицательные результаты при извлечении арифметического квадратного корня попросту отбрасываются. В школе все квадратные корни — арифметические. Хотя особо об этом не упоминается.
Ну ладно, это понятно. Это даже и лучше — не возиться с отрицательными результатами… Это ещё не путаница.
Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.
Уравнение простое, пишем ответ (как учили):
Такой ответ (совершенно правильный, кстати) — это просто сокращённая запись двух ответов:
и
Стоп-стоп! Чуть выше я написал, что квадратный корень — число всегда неотрицательное! А здесь один из ответов — отрицательный! Непорядок. Это первая ( но не последняя) проблемка, которая вызывает недоверие к корням… Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:
Скобки сути ответа не меняют. Просто я отделил скобками знаки от корня. Теперь наглядно видно, что сам корень (в скобках) — число всё равно неотрицательное! А знаки — это результат решения уравнения. Ведь при решении любого уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат. В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.
Если вы просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат. Например:
Потому, что это — арифметический квадратный корень.
Но если вы решаете какое-нибудь квадратное уравнение, типа:
то всегда получается два ответа (с плюсом и минусом):
Потому, что это — решение уравнения.
Надеюсь, что такое квадратный корень со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор… извините, камни!)
Формулы корней. Свойства квадратных корней.
В предыдущем уроке мы разобрались, что такое квадратный корень. Пришла пора разобраться, какие существуют формулы для корней, каковы свойства корней, и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Напоминаю: а и b — неотрицательные числа! Иначе формула смысла не имеет…
Это свойство корней, как видите простое, короткое и безобидное. Но с помощью этой формулы корней можно делать массу полезных вещей! Разберём на примерах все эти полезные вещи.
Полезная вещь первая. Эта формула позволяет нам умножать корни.
Как умножать корни?
Да очень просто. Прямо по формуле. Например:
Казалось бы, умножили, и что? Много ли радости?! Согласен, немного… А вот как вам такой пример?
Из множителей корни ровно не извлекаются. А из результата — отлично! Уже лучше, правда? На всякий случай сообщу, что множителей может быть сколько угодно. Формула умножения корней всё равно работает. Например:
Так, с умножением всё ясно, зачем нужно это свойство корней — тоже понятно.
Полезная вещь вторая. Внесение числа под знак корня.
Как внести число под корень?
Предположим, что у нас есть вот такое выражение:
Можно ли спрятать двойку внутрь корня? Легко! Если из двойки сделать корень, сработает формула умножения корней. А как из двойки корень сделать? Да тоже не вопрос! Двойка — это корень квадратный из четырёх!
Вот и пишем:
Корень, между прочим, можно сделать из любого неотрицательного числа! Это будет корень квадратный из квадрата этого числа. 3 — корень из 9. 8 — корень из 64. 11 — корень из 121. Ну, и так далее.
Конечно, расписывать так подробно нужды нет. Разве что, для начала… Достаточно сообразить, что любое неотрицательное число, умноженное на корень, можно внести под корень. Но — не забывайте! — под корнем это число станет квадратом самого себя. Это действие — внесение числа под корень — можно ещё назвать умножением числа на корень. В общем виде можно записать:
Процедура простая, как видите. А зачем она нужна?
Как и любое преобразование, эта процедура расширяет наши возможности. Возможности превратить жестокое и неудобное выражение в мягкое и пушистое). Вот вам простенький пример:
Как видите, свойство корней, позволяющее вносить множитель под знак корня, вполне годится для упрощения.
Кроме того, внесение множителя под корень позволяет легко и просто сравнивать значения различных корней. Безо всякого их вычисления и калькулятора! Третья полезная вещь.
Как сравнивать корни?
Это умение очень важно в солидных заданиях, при раскрытии модулей и прочих крутых вещах.
Сравните вот эти выражения. Какое из них больше? Без калькулятора! С калькулятором каждый… э-э-э… короче, каждый справится!)
Так сразу и не скажешь… А если внести числа под знак корня?
и
Запомним (вдруг, не знали?): если число под знаком корня больше, то и сам корень — больше! Отсюда сразу правильный ответ, безо всяких сложных вычислений и расчётов:
и, следовательно:
Здорово, да? Но и это ещё не всё! Вспомним, что все формулы работают как слева направо, так и справа налево. Мы пока формулу умножения корней слева направо употребляли. Давайте запустим это свойство корней наоборот, справа налево. Вот так:
И какая разница? Разве это что-то даёт!? Конечно! Сейчас сами увидите.
Предположим, нам нужно извлечь (без калькулятора!) корень квадратный из числа 6561. Кое-кто на этом этапе и падёт в неравной борьбе с задачей… Но мы упорные, мы не сдаёмся! Полезная вещь четвёртая.
Как извлекать корни из больших чисел?
Вспоминаем формулу извлечения корней из произведения. Ту, что я чуть выше написал. Но где у нас произведение!? У нас огромное число 6561 и всё… Да, произведения здесь нет. Но если нам надо — мы егосделаем! Разложим это число на множители. Имеем право.
Для начала сообразим, на что делится это число ровно? Что, не знаете!? Признаки делимости забыли!? Зря.На 3 и на 9 делится это число. Потому, что сумма цифр (6+5+6+1=18) делится на эти числа. Это один из признаков делимости. На три нам делить ни к чему (сейчас поймёте, почему), а вот на 9 поделим. Хотя бы и уголком. Получим 729. Вот мы и нашли два множителя! Первый — девятка (это мы сами выбрали), а второй — 729 (такой уж получился). Уже можно записать:
Улавливаете идею? С числом 729 поступим аналогично. Оно тоже делится на 3 и 9. На 3 опять не делим, делим на 9. Получаем 81. А это число мы знаем! Записываем:
Всё получилось легко и элегантно! Корень пришлось по кусочкам извлекать, ну и ладно. Так можно поступать с любыми большими числами. Раскладывать их на множители, и — вперёд!
Кстати, а почему на 3 делить не надо было, догадались? Да потому, что корень из трёх ровно не извлекается! Имеет смысл раскладывать на такие множители, чтобы хотя бы из одного корень хорошо извлекался. Это 4, 9, 16 ну, и так далее. Делите своё громадное число на эти числа поочерёдно, глядишь, и повезёт!
Но не обязательно. Может и не повезти. Скажем, число 432 при разложении на множители и использовании формулы корней для произведения даст такой результат:
Ну и ладно. Всё равно мы упростили выражение. В математике принято оставлять под корнем самое маленькое число из возможных. В процессе решения все зависит от примера (может и без упрощения всё посокращается), а вот в ответе надо дать результат, который уже дальнейшему упрощению не поддаётся.
Кстати, знаете, что мы с вами сейчас с корнем из 432 сделали?
Мы вынесли множители из-под знака корня! Вот так называется эта операция. А то попадётся задание — «вынести множитель из-под знака корня» а мужики-то и не знают…) Вот вам ещё одно применение свойства корней. Полезная вещь пятая.
Как вынести множитель из-под корня?
Легко. Разложить подкоренное выражение на множители и извлечь корни, которые извлекаются. Смотрим:
Ничего сверхъестественного. Важно правильно выбрать множители. Здесь мы разложили 72 как 36·2. И всё получилось удачно. А могли разложить иначе: 72 = 6·12. И что!? Ни из 6, ни из 12 корень не извлекается… Что делать?!
Ничего страшного. Или поискать другие варианты разложения, или продолжать раскладывать всё до упора! Вот так:
Как видим, всё получилось. Это, кстати, не самый быстрый, но самый надёжный способ. Раскладывать число на самые маленькие множители, а затем собирать в кучки одинаковые. Способ успешно применяется и при перемножении неудобных корней. Например, надо вычислить:
Перемножать всё — сумасшедшее число получится! И как потом из него корень извлекать?! Опять на множители раскладывать? Не, лишняя работа нам ни к чему. Сразу раскладываем на множители и собираем одинаковые по кучкам:
Вот и всё. Конечно, раскладывать до упора не обязательно. Всё определяется вашими личными способностями. Довели пример до состояния, когда вам всё ясно, значит, можно уже считать. Главное — не ошибаться. Не человек для математики, а математика для человека!)
Применим знания к практике? Начнём с простенького:
1. Вычислить:
2. Вычислить (без калькулятора!):
3. Вычислить:
Слегка усложним:
4. Вычислить:
Чуть ближе к ГИА:
5. Выполнить действия:
Ну и, самое крутое, прямо как в ГИА:
6. Укажите наибольшее из следующих чисел:
Ответы для заданий 1 — 4, в беспорядке: 2; 1; 9, 96.
Ответы на задания 5 — 6 здесь не дам). В этих примерах главное не ответ, а принцип решения. Если знаете как делать подобные задания, ответ сам получится. Если не знаете, ответ особого смысла не имеет).
Подведём итоги.
Обратите внимание. Всего одно свойство корней, одна небольшая формула умножения корней — и какие разнообразные возможности для практического применения!
Формула умножения корней позволяет:
— умножать корни,
— вносить число под корень,
— сравнивать корни,
— извлекать корни из больших чисел,
— выносить множитель из-под корня.
И все эти возможности вытекают из одной небольшого свойства корней. Мощное свойство, но… одно. Это — как табурет на одной ножке…) Сидеть можно, но с изрядными усилиями.
В нашем арсенале есть ещё два свойства корней. Одно — простое, второе — не очень. Но разобраться с ними можно и нужно. Оба этих свойства — в следующем уроке. Там же — примеры для тренировки. Там же описана одна тупая, но очень популярная ошибка в корнях, после которой люди бьют себя по голове и страшно ругаются…
Как делить корни?
Продолжаем развлечение? В предыдущих уроках мы осознали, что такое квадратный корень. И разобрались как умножать корни. Формулу умножения корней мы разобрали по винтикам. Очень уж она полезная в решении примеров! Осталось ещё две. Переходим к следующей формуле. Это будет деление корней.
Формула столь же проста, как и умножение. Вот она:
Напоминаю: здесь а — неотрицательное число (больше или равно нулю), b — положительное (больше нуля)! Иначе формула смысла не имеет… Об этих тонкостях мы ниже поговорим.
У формулы деления корней возможности не так обширны, как у умножения. Что можно делать прямо по формуле? Очевидно, делить корни.
Элементарно. Вот вам примерчик:
В этом примере деление корней помогло нам получить хороший ответ. Бывают более хитрые преобразования. Например:
Здесь мы превратили двойку в корень квадратный из четырёх. Исключительно для того, чтобы формулуделения корней в дело употребить. Как видите, ничего здесь сложного нет.
Рассмотрим формулу деления корней в обратном направлении. Справа налево. Вот так:
Какие возможности раскрывает нам такая запись? Ничего нового, думаете? Ошибаетесь! Забавно, но простая запись формулы в другом направлении частенько высвечивает дополнительные возможности!
В нашем случае такая формулировка деления корней здорово помогает извлекать корни из дробей! Например, пусть нам надо извлечь квадратный корень из дроби 25/144. Спокойно пишем себе:
Вот и все дела! От работы с дробью целиком, мы переходим к работе отдельно с числителем, отдельно со знаменателем. Что гораздо проще. А если дробь десятичная? Не вопрос! Если сразу корень не можете извлечь — переводите десятичную дробь в обыкновенную, и — вперёд! По формуле деления корней. Например:
Бывает ещё круче, когда корень из смешанного числа надо извлечь! Как поступаем? Правильно! Переводим смешанное число в неправильную дробь — и по знакомой формуле деления корней! К примеру, вот так:
Что, забыли, как переводить дроби? Срочно прокрутите страницу выше и вспоминайте. А то ни дробь преобразовать, ни сократить её… И зачем вам тогда квадратные корни?
Надеюсь, что деление корней проблем не составляет. Простая и безобидная формула, простое употребление. Теперь в нашем арсенале уже две формулы. Умножение и деление корней. Табурет на двух ножках. Сидеть можно, но… некомфортно.)
Займёмся последним свойством квадратных корней. Здесь уже будут некоторые тонкости и подводные камни. Это свойство кратко называют корень из квадрата. Или корень в квадрате. Или корень из степени. Корень в степени. Всяко называют. Но суть одна. Это возведение в степень подкоренного выражения или самого корня.
Можно ли корень возвести в квадрат? А почему нет? Умножить корень сам на себя — да все дела! И не только в квадрат можно. В любую степень. А извлечь корень из квадрата? Да тоже не проблема! Мы же умеем корень из произведения извлекать. Так что можно извлечь корень не только из квадрата, но и из любой степени.
Но именно эти действия вызывают массу проблем… С этим надо разобраться основательно. Что мы сейчас и сделаем. Начнём с безобидного действия. С корня в квадрате.
Как возвести корень в квадрат?
Так как посчитать корень в квадрате? Очень просто. Прямо по смыслу корня. Что такое корень квадратный из двух, например? Это число, которое при возведении в квадрат должно дать двойку. Так вот, если мы число, которое при возведении в квадрат должно дать двойку, возведём-таки в этот самый квадрат? Что получим? Двойку, конечно! Т.е. подкоренное выражение. Или, в общем виде:
Вот и всё! Никаких подводных камней, всё строго по формуле! Возведение в квадрат корня квадратного из любого выражения даст нам это самое выражение. Понятно, что а — число неотрицательное. Иначе формула смысла не имеет.
А если корень не в квадрате, а в другой степени? Не вопрос! Если, конечно, знаете действия со степенями… По правилам этих действий сами приведём исходное выражение к корням в квадрате и всё посчитаем. Например, вот так (расписываю подробно):
Как видим, корень исчезает, Степень результата в два раза меньше исходной степени.
Если степень нечётная — разложим исходное выражение на множители, и все дела:
Так поступаем с любой степенью корня из любого выражения, и всё у нас посчитается, упростится и получится. Корень в квадрате — штука бесхитростная. Разберёмся теперь с корнем из квадрата.
Как извлечь корень из квадрата?
Пусть у нас есть хорошее число 2. Возведём его в квадрат.
22 = 4
Кто бы спорил? А теперь давайте обратно, извлечём из результата квадратный корень:
Опять всё чудесно, правда? С чего начали, к тому и вернулись! Стало быть, можно записать:
Оно и естественно, правда? Возведение в квадрат компенсируется обратной операцией — извлечением квадратного корня. В общем виде формула выглядит вот так:
Стоп! Внимание! Во всех учебниках, справочниках и пособиях рядом с такой формулой всегда пишут:»где а — больше, либо равно нулю». В этих словах, которые многие просто пропускают, и кроются главные сложности корней. Потому, что в примерах а частенько бывает отрицательным! Пока и мы будем считать, что а — неотрицательное. Для простоты.
Продолжаем. Корень из квадрата извлекается просто. А если у нас подкоренное выражение не в квадрате, а в другой степени? Допустим, в четвёртой? Да нет проблем. Приведём нашу степень к квадрату. Вот так:
24=(22)2
Для таких преобразований надо опять-таки знать действия со степенями, но тут уж ничего не поделаешь…
Теперь по формуле корня из квадрата:
Вот и всё. Корень из любой чётной степени даст в результате подкоренное выражение в степени, в два раза меньше исходной. Корень из 310 ? Легко! Это будет 35. Корень из 518 ? Запросто! Это будет 59. Ну, и так далее.
А если степень нечётная? Подумаешь! Раскладываем подкоренное выражение на множители — и вперёд! Используем вынесение множителя из-под корня. Например:
Всё просто. Но до сего момента мы работали только с неотрицательными числами и выражениями. Как только в игру вступают отрицательные величины, простота куда-то пропадает начисто… Вернём эту простоту и ясное понимание.
Вот тут и будет мрачный заяц. Для лучшего запоминания.) Концентрируем внимание и собираем весь интеллект в кулак!)
Итак, откуда в корнях могут появиться отрицательные числа и выражения?
Пунктик первый. Отрицательные значения даны прямо в задании. Вспоминаем пример корня из квадрата двойки:
Здесь всё понятно и просто.
А теперь попробуем вычислить:
Берём, и просто считаем, безо всяких формул:
(-2)2 = 4
Извлекаем корень из четырёх и получаем 2. Так как арифметический квадратный корень (а в школе мы работаем только с такими!) — всегда число неотрицательное! То есть:
А если бы мы использовали формулу:
получили бы не два, а минус два! Что является ошибкой.
Не работает эта формула для отрицательных значений.
Для того, чтобы формула корня из квадрата работала для всех значений а, она записывается вот так:
Это и есть последнее, третье свойство корней. Корень из квадрата. Третья ножка для табурета.)
Здесь появляется страшный значок для старшеклассников. Модуль. Если вы пока не сильны в раскрытии модулей, не волнуйтесь. Здесь он означает лишь то, что при любом знаке а, результат извлечения корня из квадрата будет всегда неотрицательный. Формула стала полноценной. Модуль просто отсекает минусы:
Пунктик второй. Отрицательные значения спрятаны в буквах и дополнительных условиях. Например, требуется упростить выражение:
где х<0.
Казалось бы, ответ прост. Получится просто х. Но зачем тогда дополнительная информация?! Приходится соображать. Если х<0, это отрицательное число. Минус два, или минус тридцать, там… Но корень квадратный отрицательным быть не может! Это будет точно х, но он должен быть с плюсом! Где взять плюс? А мы его сделаем! Если перед заведомо отрицательным числом, поставить минус, это число станет, число станет… положительным! И верное решение выглядит так.
Собственно, это и есть главная трудность в работе с корнями. В отличие от более простых разделов математики, здесь правильный ответ частенько не вытекает автоматически из формул. Необходимо подумать и лично принять верное решение.)
И как справляться со всем разнообразием заданий с корнями? А есть ещё иррациональные уравнения и неравенства, где эти пунктики играют главную роль…
Спокойно! Вникайте и запоминайте.
Главный практический совет по работе с квадратными корнями.
В любом задании с квадратными корнями лично контролируйте знаки подкоренного выражения и результата извлечения корня.
Прикидывайте, и оценивайте ситуацию, исходя из внешнего вида примера и всех дополнительных условий задания. Если под знаком корня — минус, дальше можно не решать. Выражение не имеет смысла. Что нам делать нечего, бессмысленные выражения решать?!
Если под корнем всё нормально, плюс, а в результате извлечения получается заведомый минус — сделайте из него плюс! Этого требуют правила действий с квадратными корнями.
Ну вот, основные тонкости корней мы разобрали. Теперь об одной ошибке, рассказать про которую я обещал в предыдущем уроке. Эта ошибка ничего общего с тонкостями не имеет! Это абсолютно тупой косяк, о котором и говорить-то неловко. Но надо. Слишком часто он встречается…
Обратите внимание! Все свойства корней связаны с умножением-делением. И ни одного — со сложением-вычитанием! На сложение-вычитание корней — не существует специальных формул!
Однако народ складывает… И не самый трудный народ… Поэтому громко напоминаю:
или:
Хотя одинаковые корни можно, конечно, складывать-вычитать. Как приводить подобные с буквами. Например:
или:
Но эти действия к специфическим свойствам корней не имеют никакого отношения.
А теперь попрактикуемся в корнях. От примитивных заданий до продвинутых. Все ответы даны в беспорядке.
Вычислить:
Ответы: 1, 9, 2.
Примитив? Тогда решаем дальше.
Упростить:
Ответы: 3а4 b, -4а4 b5 , 3а.
Получилось? Неплохо. А как вам эти примерчики?
Вычислить (все буквы — неотрицательные):
Ответы (в беспорядке): выражение не имеет смысла; 5; 4; 1; -3; 0,5
Всё нормально!? Отлично. Корни — не ваша проблема.
Материал позаимствован с замечательного сайта: http://egesdam.ru/page260.php . Спасибо автору за понятное изложение материала!
s-kuz.ru
Квадрат — действительное число — Большая Энциклопедия Нефти и Газа, статья, страница 1
Квадрат — действительное число
Cтраница 1
Квадрат действительного числа может быть равен любому неотрицательному числу. [1]
Квадрат действительного числа всегда больше нуля или равен нулю. [2]
Квадрат действительного числа может быть равен любому неотрицательному числу. [3]
А так как квадрат действительного числа не может быть отрицательным, то, значит, в этом случае уравнение ( 2) не имеет действительных корней. Как мы знаем, существует два комплексных числа, квадрат каждого из которых равен отрицательному числу D ( см. стр. Эти числа являются чисто мнимыми и притом сопряженными. [4]
Может ли быть отрицательным числом квадрат действительного числа. [5]
Показать, что положительное число, как квадрат действительного числа, переходит в положительное. Затем, пользуясь тем, что между двумя различными действительными числами лежит рациональное, и сохранением рациональных чисел, доказать неизменность любого действительного числа. [6]
Показать, что положительное число, как квадрат действительного числа, переходит в положительное. Затем, пользуясь тем, что между двумя различными действительными числами лежит рациональное, и сохранением рациональных чисел, доказать неизменность любого действительного числа. [7]
А 0, у 0; 3) сумма квадратов действительных чисел не может быть отрицательным числом; ни при каких действительных хну это уравнение не удовлетворяется. [8]
Уравнение ( 7) при D 0 не имеет корней, потому что квадрат действительного числа не может быть отрицательным числом. Следовательно, при / 3 0 уравнение ( 1) не имеет корней. [9]
В этом случае преобразованное, а значит, и исходное уравнение решений не имеет, так как квадрат действительного числа не может быть отрицательным. [10]
Из уравнения ( 3) следует, что если D 0, то квадратное уравнение не имеет решений, так как квадрат действительного числа не может быть отрицательным. [11]
Страницы: 1
www.ngpedia.ru
