Основные свойства степени – Свойства степеней с натуральными показателями. Натуральная степень. Степени чисел. Свойства показателей степеней
Свойства степеней
Свойства степеней. Разъяснения
\begin{align} & 1-3.\ x^1=x,\ x^0=1,\ x^{-1}=\frac{1}{x}\ \end{align}
Рассмотрим первые 3 свойства на примере числа 5.
| Пример | ||
|---|---|---|
\begin{align} & 5^2\\ \end{align} |
\begin{align} & 1×5×5\\ \end{align} |
\begin{align} & 25\\ \end{align} |
\begin{align} & 5^1\\ \end{align} |
\begin{align} & 1×5\\ \end{align} |
\begin{align} & 5\\ \end{align} |
\begin{align} & 5^0\\ \end{align} |
\begin{align} & 1\\ \end{align} |
\begin{align} & 1\\ \end{align} |
\begin{align} & 5^{-1}\\ \end{align} |
\begin{align} & 1÷5\\ \end{align} |
\begin{align} & \frac{1}{5}\\ \end{align} |
\begin{align} & 5^{-2}\\ \end{align} |
\begin{align} & 1÷5÷5\\ \end{align} |
\begin{align} & \frac{1}{25}\\ \end{align} |
\begin{align} & 4.\ x^m x^n=x^{m+n}\ \end{align}
xmxn сколько раз мы должны умножить x? Ответ: вначале m-раз, потом n-раз, итого m+n раз
\begin{align} & x^2 x^3=(xx)(xxx)=xxxxx=x^5\ \end{align}
\begin{align} & 5.\ \frac{x^m}{x^n}=x^{m-n}\ \end{align}
xm/xn сколько раз мы должны умножить x? Ответ: вначале m-раз умножить, затем n-раз поделить, итого m-n раз умножить
\begin{align} & \frac{x^5}{x^2}=\frac{xxxxx}{xx}=xxx=x^3\ \end{align}
\begin{align} & 6.\ (x^m)^n=x^{mn}\ \end{align}
xmxn сколько раз мы должны умножить x? Ответ: вначале m-раз, потом полученный результат n-раз, итого m×n раз
\begin{align} & (x^3)^4=(xxx)^4=(xxx)(xxx)(xxx)(xxx)=xxxxxxxxxxxx=x^12\ \end{align}
\begin{align} & 7.\ (xy)^n=x^n y^n\ \end{align}
Рассмотрим свойство на примере:
\begin{align} & (xy)^3=(xy)(xy)(xy)=xyxyxy=xxxyyy=(xxx)(yyy)=x^3 y^3\ \end{align}
\begin{align} & 8.\ \left ( \frac{x}{y} \right )^n=\frac{x^n}{y^n}\ \end{align}
Рассмотрим свойство на примере:
\begin{align} & \left ( \frac{x}{y} \right )^3=\left ( \frac{x}{y} \right )\left ( \frac{x}{y} \right )\left ( \frac{x}{y} \right )=\frac{(xxx)}{(yyy)}=\frac{x^3}{y^3}\ \end{align}
calcs.su
Свойства степени
I. Произведение степеней с одинаковыми основаниями.
Произведение двух степеней с одинаковыми основаниями всегда можно представить в виде степени с основанием х.
По определению степени х7 есть произведение семи множителей, каждый из которых равен х, а х9 – произведение девяти таких же множителей. Следовательно, х7 · х9 равно произведению 7 + 9 множителей. Каждый из которых равен х, то есть
х7 · х9 = х7+9 = х16
Получается, если основание степени а – произвольное число, а m и n – любые натуральные числа, то верно равенство:
am · an = am+n
Это равенство выражает одно из свойств степени.
Произведение двух степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, равным сумме показателей этих степеней.
Это свойство имеет место и в случаях, когда число множителей больше двух.
Например, в случае трёх множителей имеем:
am · an · ak = (am · an)ak = am+n · ak = am+n+k
При выполнении преобразований удобно пользоваться правилом: при умножении степеней с одинаковыми основаниями основания оставляют прежним, а показатели степеней складывают.
Рассмотрим примеры.
Пример 1.
х6
Пример 2.
а7 · а-8 = а-1
Пример 3.
61.7 · 6— 0.9 = 61.7+( — 0.9) = 61.7 — 0.9 = 60.8
II. Частное степеней с одинаковыми основаниями.
Частное двух степеней с одинаковыми показателями всегда можно представить в виде степени с тем же основанием.
Рассмотрим примеры.
Пример 1. Частное х17 : х5 можно представить виде степени с основанием х:
х17 : х5 = х12,
так как по определению частного и на основании свойства степени х
х17 : х5 = х17-5
Пример 2.
8 16 : 8 12 = 816-12 = 84
Пример 3.
а-8 : а6 = а -8-6 = а-14
Пример 4.
b5 : b-4 = b5-(-4) = b9
Пример 5.
91.5 : 9— 0.5 = 91.5 — (- 0.5)
При выполнении преобразований удобно пользоваться правилом: при делении степеней с одинаковыми основаниями основания оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Пример 6.
а4 : а4 = а4-4 = а0
Значение выражения а0 при всяком а ≠ 0 равно 1.
III. Возведение степени в степень.
Пусть требуется седьмую степень выражения а2 представить в виде степени с основанием а.
По определению степени (а2)7 есть произведение семи множителей, каждый из которых равен а
(а2)7 = а2 · а2 · а2 × а2 · а2 · а2 · а2.
Применяя свойство степени, получим:
а2 · а2 · а2 · а2 · а2 · а2 · а2 = а2+2+2+2+2+2+2 = a2·7.
 Получается, (а2)7 = а2·7 = а14.
Получается, (а2)7 = а2·7 = а14.
При возведении степени в степень основание оставляют тем же, а показатели перемножают:
(аm)n = аmn.
Рассмотрим примеры.
Пример 1.
(43)4 = 43·4 = 412
Пример 2.
((-2)2)5 = (-2)10 = 1024
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Свойства степени с натуральным показателем
Свойства степени с натуральным показателем 7 класс
Свойство 1, формулаЕсли степени умножать ( при одинаковый основания), то показатели
степени сложить, основание остается неизменным.
42 • 43 = 45 = 1 024;
y3 • y5 = y8.
Свойство 2, формулаПример (- 2)10 : (- 2)7 = (- 2)3 = 8;
(0,1)101 : (0,1)101 = 1;
57 : 59 = 152 =
Если основание не равно нулю, то любое основание в степени нуль,
равно единице.
a0 = 1
Пример 30 = 0;(? 5)0 = 1;
(- 2,5)0 = 1.
Свойство 4, формулаЕсли степень возвести в степень, то показатели — перемножить.
(am)n = amn
Пример (32)3 = 36 = 729.
Свойство 5, формулаЕсли произведение требуется возвести в степень, то каждый
(ab)n = anbn
ПримерПример (0,9 • 2)2 = 0,92 • 22 = 0,81 • 4 = 1,62;
(3z)3 = 33z3=27z3.
Свойство 6, формулаЕсли требуется возвести в степень дробь, то возводят в степень
числитель и знаменатель. Свойство 7, формула
При возведении отрицательного числа в степень, все зависит от
четности степени. Если степень четная, то и число получится четное,
(- x)2 = x2;
(- z)3 = -z3;
(- 2ab)2 = (2ab)2 = 22a2b2 = 4a2b2.
formula-xyz.ru
Основные свойства степеней
Основные свойства степеней
Скачать шпаргалку «Свойства степеней» (формат .pdf)
Свойства
a0=1, если a≠0
a1=a
(−a)n=an, если n — четное
(−a)n=−an, если n — нечетное
(a⋅b)n=an⋅bn
(ab)n=anbn
a−n=1an
(ab)−n=(ba)n
an⋅am=an+m
anam=an−m
(an)m=an⋅m
Свойства степеней (с примерами)
1-е свойство степениЛюбое число отличное от нуля в нулевой степени равно единице.a0=1, если a≠0Например: 1120=1, (−4)0=1, (0,15)0=1
2-е свойство степениЛюбое число в первой степени равно самому числу.a1=aНапример: 231=23, (−9,3)1=−9,3
3-е свойство степениЛюбое число в четной степени положительно.an=an, если n — четное (делящееся на 2) целое число(−a)n=an, если n — четное (делящееся на 2) целое числоНапример: 24=16, (−3)2=32=9, (−1)10=110=1
4-е свойство степениЛюбое число в нечетной степени сохраняет свой знак.an=an, если n — нечетное (не делящееся на 2) целое число(−a)n=−an, если n — нечетное (не делящееся на 2) целое числоНапример: 53=125, (−3)3=33=27, (−1)11=−111=−1
5-е свойство степениПроизведение чисел, возведенное в степень, можно представить как произведение чисел возведенных в эту степень (и наоборот).(a⋅b)n=an⋅bn, при этом a, b, n — любые допустимые (не обязательно целые) числаНапример: (2,1⋅0,3)4,5=2,14,5⋅0,34,5
6-е свойство степениЧастное (деление) чисел, возведенное в степень, можно представить как частное чисел возведенных в эту степень (и наоборот).(ab)n=anbn, при этом a, b, n — любые допустимые (не обязательно целые) числаНапример: (1,75)0,1=(1,7)0,150,1
7-е свойство степениЛюбое число в отрицательной степени равно обратному числу в этой степени. (Обратное число это число на которое нужно умножить данное число, чтобы получить единицу.)a−n=1an, при этом a и n — любые допустимые (не обязательно целые) числаНапример: 7−2=172=149
8-е свойство степениЛюбая дробь в отрицательной степени равна обратной дроби в этой степени.(ab)−n=(ba)n, при этом a, b, n — любые допустимые (не обязательно целые) числаНапример: (23)−2=(32)2, (14)−3=(41)3=43=64
9-е свойство степениПри умножении степеней с одинаковым основанием показатели степени складываются, а основание остается прежним.an⋅am=an+m, при этом a, n, m — любые допустимые (не обязательно целые) числаНапример: 23⋅25=23+5=28, обратите внимание, что это свойство степени сохраняется и для отрицательных значений степеней 3−2⋅36=3−2+6=34, 47⋅4−3=47+(−3)=47−3=44
10-е свойство степениПри делении степеней с одинаковым основанием показатели степени вычитаются, а основание остается прежним.anam=an−m, при этом a, n, m — любые допустимые (не обязательно целые) числаНапример: (1,4)2(1,4)3=1,42+3=1,45, обратите внимание, как применяется это свойство степени к отрицательным значения степеней3−236=3−2−6=3−8, 474−3=47−(−3)=47+3=410
11-е свойство степениПри возведении степени в степень степени перемножаются.(an)m=an⋅mНапример: (23)2=23⋅2=26=64
Таблица степеней до 10
Мало кому удается запомнить всю таблицу степеней, да и кому это нужно когда ее так легко найти? Наша таблица степеней включает в себя как популярные таблицы квадратов и кубов (от 1 до 10), так и таблицы других степеней, которые встречаются реже. В столбцах таблицы степеней указываются основания степени (число, которое нужно возвести в степень), в строках – показатели степени (степень, в которую нужно возвести число), на пересечении нужного столбца и нужной строки находится результат возведения нужного числа в заданную степень. Существуют несколько типов задач, решаемых с помощью таблицы степеней. Прямая задача – это вычислить n-ю степень числа. Обратная задача, которая так же может быть решена с помощью таблицы степеней, может звучать так: «в какую степень нужно возвести число a, чтобы получить число b?» или «Какое число в степени n дает число b?».
Таблица степеней до 10
1n | 2n | 3n | 4n | 5n | 6n | 7n | 8n | 9n | 10n | |
1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
3 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
4 | 1 | 16 | 81 | 256 | 625 | 1296 | 2401 | 4096 | 6561 | 10000 |
5 | 1 | 32 | 243 | 1024 | 3125 | 7776 | 16807 | 32768 | 59049 | 100000 |
6 | 1 | 64 | 729 | 4096 | 15625 | 46656 | 117649 | 262144 | 531441 | 1000000 |
7 | 1 | 128 | 2187 | 16384 | 78125 | 279936 | 823543 | 2097152 | 4782969 | 10000000 |
8 | 1 | 256 | 6561 | 65536 | 390625 | 1679616 | 5764801 | 16777216 | 43046721 | 100000000 |
9 | 1 | 512 | 19683 | 262144 | 1953125 | 10077696 | 40353607 | 134217728 | 387420489 | 1000000000 |
10 | 1 | 1024 | 59049 | 1048576 | 9765625 | 60466176 | 282475249 | 1073741824 | 3486784401 | 10000000000 |
Как пользоваться таблицей степеней
Рассмотрим несколько примеров использования таблицы степеней.
Пример 1. Какое число получится в результате возведения числа 6 в 8 степень?В таблице степеней ищем столбец 6n, так как по условию задачи число 6 возводится в степень. Затем в таблице степеней ищем строку 8, так как заданное число необходимо возвести в степень 8. На пересечении смотрим ответ: 1679616.
Пример 2. В какую степень нужно возвести число 9, чтобы получить 729?В таблице степеней ищем колонку 9n и спускаемся по ней вниз до числа 729 (третья строчка нашей таблицы степеней). Номер строчки и есть искомая степень, то есть ответ: 3.
Пример 3. Какое число нужно возвести в степень 7, чтобы получить 2187?В таблице степеней ищем строку 7, затем двигаемся по ней вправо до числа 2187. От найденного числа поднимаемся вверх и узнаем, что заголовок этого столбца 3n, что означает, что ответ: 3.
Пример 4. В какую степень нужно возвести число 2, чтобы получить 63?В таблице степеней находим столбец 2n и спускаемся по нему до тех пор, пока не встретим 63… Но этого не произойдет. Число 63 мы никогда не встретим ни в этом столбце, ни в любом другом столбце таблицы степеней, а это означает, что никакое целое число от 1 до 10 не дает число 63 при возведении в целую степень от 1 до 10. Таким образом, ответа нет.
sundekor.ru
Свойства степени с одинаковыми основаниями.
Понятие степени в математике вводится еще в 7 классе на уроке алгебры. И в дальнейшем на протяжении всего курса изучения математики это понятие активно используется в различных своих видах. Степени — достаточно трудная тема, требующая запоминания значений и умения правильно и быстро сосчитать. Для более быстрой и качественной работы со степенями математики придумали свойства степени. Они помогают сократить большие вычисления, преобразовать огромный пример в одно число в какой-либо степени. Свойств не так уж и много, и все они легко запоминаются и применяются на практике. Поэтому в статье рассмотрены основные свойства степени, а также то, где они применяются.

Свойства степени
Мы рассмотрим 12 свойств степени, в том числе и свойства степеней с одинаковыми основаниями, и к каждому свойству приведем пример. Каждое из этих свойств поможет вам быстрее решать задания со степенями, а так же спасет вас от многочисленных вычислительных ошибок.
1-е свойство.
а0 = 1
Про это свойство многие очень часто забывают, делают ошибки, представляя число в нулевой степени как ноль.
2-е свойство.
а1 = а
3-е свойство.
аn * am = a(n+m)
Нужно помнить, что это свойство можно применять только при произведении чисел, при сумме оно не работает! И нельзя забывать, что это, и следующее, свойства применяются только к степеням с одинаковыми основаниями.
4-е свойство.
an/am = a(n-m)
Если в знаменателе число возведено в отрицательную степень, то при вычитании степень знаменателя берется в скобки для правильной замены знака при дальнейших вычислениях.
Свойство работает только при делении, при вычитании не применяется!
5-е свойство.
(an)m = a(n*m)
6-е свойство.
a-n = 1/an
Это свойство можно применить и в обратную сторону. Единица деленная на число в какой-то степени есть это число в минусовой степени.
7-е свойство.
(a*b)m = am * bm
Это свойство нельзя применять к сумме и разности! При возведении в степень суммы или разности используются формулы сокращенного умножения, а не свойства степени.
8-е свойство.
(a/b)n = an/bn
9-е свойство.
а½ = √а
Это свойство работает для любой дробной степени с числителем, равным единице, формула будет та же, только степень корня будет меняться в зависимости от знаменателя степени.
Также это свойство часто используют в обратном порядке. Корень любой степени из числа можно представить, как это число в степени единица деленная на степень корня. Это свойство очень полезно в случаях, если корень из числа не извлекается.
10-е свойство.
(√а)2 = а
Это свойство работает не только с квадратным корнем и второй степенью. Если степень корня и степень, в которую возводят этот корень, совпадают, то ответом будет подкоренное выражение.
11-е свойство.
n √an = a
Это свойство нужно уметь вовремя увидеть при решении, чтобы избавить себя от огромных вычислений.
12-е свойство.
am/n = n √am
Каждое из этих свойств не раз встретится вам в заданиях, оно может быть дано в чистом виде, а может требовать некоторых преобразований и применения других формул. Поэтому для правильного решения мало знать только свойства, нужно практиковаться и подключать остальные математические знания.
Применение степеней и их свойств
Они активно применяются в алгебре и геометрии. Степени в математике имеют отдельное, важное место. С их помощью решаются показательные уравнения и неравенства, а так же степенями часто усложняют уравнения и примеры, относящиеся к другим разделам математики. Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять. Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.
Особую роль понятие степени играет в логарифмах. Так как логарифм, по сути своей, и есть степень числа.
Формулы сокращенного умножения — еще один пример использования степеней. В них нельзя применять свойства степеней, они раскладываются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.
Так же степени активно используются в физике и информатике. Все переводы в систему СИ производятся с помощью степеней, а в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие расчеты по переводам единиц измерения или же расчеты задач, так же, как и в физике, происходят с использованием свойств степени.
Еще степени очень полезны в астрономии, там редко можно встретить применение свойств степени, но сами степени активно используются для сокращения записи различных величин и расстояний.
Степени применяют и в обычной жизни, при расчетах площадей, объемов, расстояний.
С помощью степеней записывают очень большие и очень маленькие величины в любых сферах науки.
Показательные уравнения и неравенства
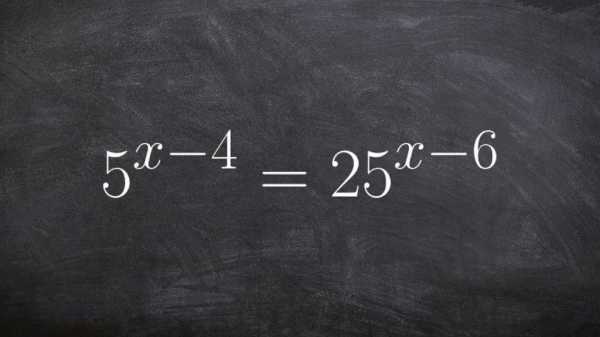
Особое место свойства степени занимают именно в показательных уравнениях и неравенствах. Эти задания очень часто встречаются, как в школьном курсе, так и на экзаменах. Все они решаются за счет применения свойств степени. Неизвестное всегда находится в самой степени, поэтому зная все свойства, решить такое уравнение или неравенство не составит труда.
fb.ru
Свойства степени
Возведение числа в натуральную степень означает его непосредственное повторение собственным сомножителем в натуральное число раз. Число, повторяющееся в качестве сомножителя – это основание степени, а число, указывающее на количество одинаковых множителей, называют показателем степени. Полученный результат выполненных действий и есть степень. Например, три в шестой степени означает повторение числа три в виде множителя шесть раз.
Основанием степени может выступать любое число, отличное от нуля.
Вторая и третья степени числа имеют специальные названия. Это, соответственно, квадрат и куб.
За первую степень числа принимают само же это число.
Для положительных чисел также определена степень, имеющая рациональный показатель. Как всем известно, любое рациональное число записывается в виде дроби, числитель которой является целым, знаменатель же – натуральным, то есть целым положительным, отличным от единицы.
Степень с рациональным показателем представляет из себя корень степени, равной знаменателю показателя степени, а подкоренное выражение – это основание степени, возведенное в степень, равную числителю. Например: три в 4/5 равно корню пятой степени из трех в четвертой.
Отметим некоторые свойства, вытекающие непосредственно из рассматриваемого определения:
- любое положительное число в рациональной степени – положительно;
- значение степени с рациональным показателем не зависит от формы его записи;
- если основание отрицательное, то рациональная степень этого числа не определена.
При положительном основании свойства степени верны независимо от показателя.
Свойства степени с натуральным показателем:
1. Умножая степени, имеющие одинаковые основания, основание оставляют без изменения и складывают показатели. Например: при умножении трех в пятой степени на три в седьмой получают три в двенадцатой степени (5+7=12) .
2. При делении степеней, имеющих одинаковые основания, их оставляют без изменения, а показатели вычитывают. Например: при делении трех в восьмой на три в пятой степени получают три в квадрате (8-5=3).
3. Когда степень возводят в степень, основание оставляют без изменения, а показатели перемножают. Например: при возведении 3 в пятой в седьмую получают 3 в тридцать пятой (5х7=35).
4. Чтобы возвести произведение в степень, в ту же возводится каждый из множителей. Например: при возведении произведения 2х3 в пятую получают произведение два в пятой на три в пятой.
5. Чтобы возвести дробь в степень, в ту же степень возводят числитель и знаменатель. Например: при возведении 2/5 в пятую получают дробь, в числителе которой – два в пятой, в знаменателе – пять в пятой.
Отмеченные свойства степени справедливы и для дробных показателей.
Свойства степени с рациональным показателем
Введем некоторые определения. Любое отличное от 0 действительное число, возведенное в нулевую, равно единице.
Любое отличное от 0 действительное число, возведенное в степень с отрицательным целым показателем – это дробь с числителем единица и знаменателем, равным степени того же числа, но имеющего противоположный показатель.
Дополним свойства степени несколькими новыми, которые касаются рациональных показателей.
Степень с рациональным показателем не меняется при умножении или делении числителя и знаменателя его показателя на неравное нулю одно и то же число.
При основании больше единицы:
- если показатель положительный, то степень больше 1;
- при отрицательном – меньше единицы.
При основании меньше единицы, наоборот:
- если показатель положительный, то степень меньше единицы;
- при отрицательном – больше 1.
Когда показатель степени растет, то:
- растет сама степень, если основание больше единицы;
- убывает, если основание меньше единицы.
fb.ru
Свойства степеней с натуральными показателями. Натуральная степень. Степени чисел. Свойства показателей степеней
Свойства степеней с натуральными показателями
Говоря про свойства степеней, считаем, что числа a и b действительные, а числа m и n натуральные.
Свойства степеней с натуральными показателями:
Свойство 1.
1. При умножении степеней с одинаковыми основаниями, показатели степеней складываются:
aman = am + n
Пример умножения степеней с одинаковыми основаниями:
52 * 53 =
52 + 3 =
55
Обратите внимание на то, что основания степеней одинаковые, оба равны 5-ти.
Свойство 2.
2. Если степень возводится в степень, то показатели перемножаются:
(am)n = am * n
Пример возведения степени в степень:
(52)4 =
52 * 4 =
58
То есть при возведении степени в степень показатели перемножаются.
Свойство 3.
3. Если основания степеней разные, а показатели одинаковые, то произведение степеней равно степени произведения:
ambm = (ab)m
Пример произведения степеней:
42 * 32 =
(4 * 3)2
То есть произведение степеней равно степени произведения.
Свойство 4.
4. Частное степеней с одинаковыми основаниями, m > n:
am : an = am — n
Пример частного степеней с одинаковыми основаниями:
106 : 104 =
106 — 4 = 102 = 100
То есть основание остается, а показатели степеней вычитаются.
Свойство 5.
5. Если основания степеней разные, а показатели одинаковые, то частное степеней равно степени частного:
an : bn = (a/b)n
Пример частного степеней с разными основаниями и одинаковыми показателями:
52 : 62 =
(5/6)2
То есть частное степеней с одинаковыми показателями равно степени частного.
www.sbp-program.ru
