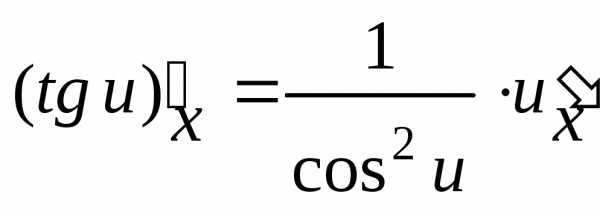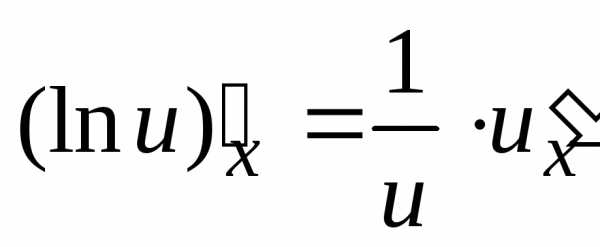Основные производные – Таблица производных (основных)
1.3. Основные правила дифференцирования
Теорема 1.
Если функции  и
и дифференцируемы в данной точке, то в
той же точке дифференцируема и их сумма,
причем производная суммы равна сумме
производных слагаемых:
дифференцируемы в данной точке, то в
той же точке дифференцируема и их сумма,
причем производная суммы равна сумме
производных слагаемых:
.
Формула обобщается на случай любого конечного числа слагаемых.
Теорема 2.
Если функции  и
и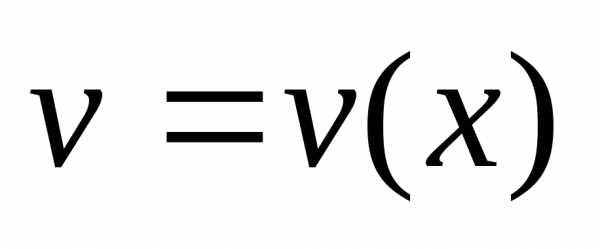 дифференцируемы в данной точкех,
то в этой же точке дифференцируемо и их
произведение, при этом:
дифференцируемы в данной точкех,
то в этой же точке дифференцируемо и их
произведение, при этом:
.
Следствие. Постоянный множитель можно выносить за знак производной:
, где .
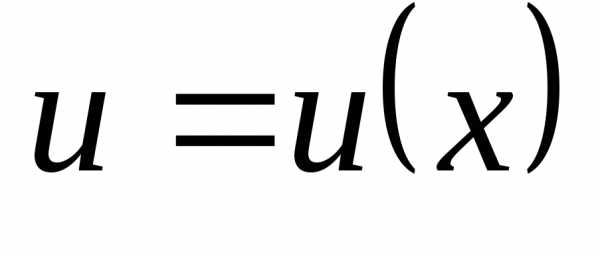 и
и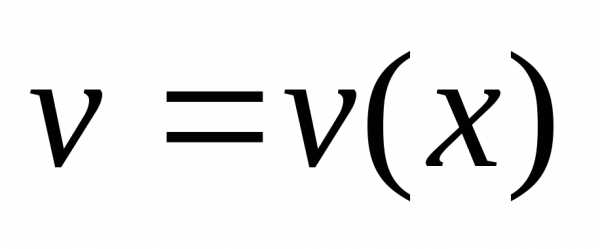 дифференцируемы и
дифференцируемы и ,
то в той же точке дифференцируемо и их
частное, причем
,
то в той же точке дифференцируемо и их
частное, причем .
.
1.4. Обратная функция и ее производная
Рассмотрим функцию y = f (x) с областью определения (a, b) и множеством значений (c, d). Пусть эта функция такова, что всякая прямая, проходящая через точку интервала (c, d) параллельно оси Ох, пересекает ее график только в одной точке, т.е. уравнение
 (c, d)
определяет единственное значение x
(c, d)
определяет единственное значение x (a, b).
В этом случае каждому значению y
(a, b).
В этом случае каждому значению y (c, d)
соответствует единственное значение x
(c, d)
соответствует единственное значение x (a, b),
т.е. на интервале (c, d)
задана функция, множество значений
которой есть интервал (a, b).
Эта функция называется обратной по
отношению к функции y
(a, b),
т.е. на интервале (c, d)
задана функция, множество значений
которой есть интервал (a, b).
Эта функция называется обратной по
отношению к функции y .
Очевидно, что для функции
.
Очевидно, что для функции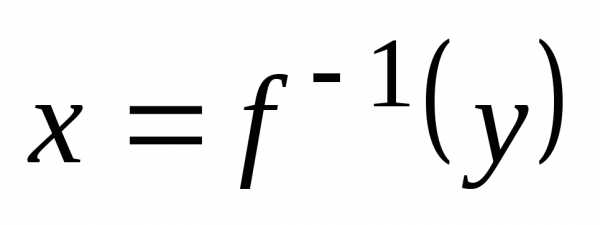 обратной является функция
обратной является функция .
Поэтому обе эти функции называютсявзаимно
обратными.
.
Поэтому обе эти функции называютсявзаимно
обратными. Теорема. Если функция y = f (x)
монотонна и дифференцируема в некотором
интервале и имеет в точке x этого интервала производную 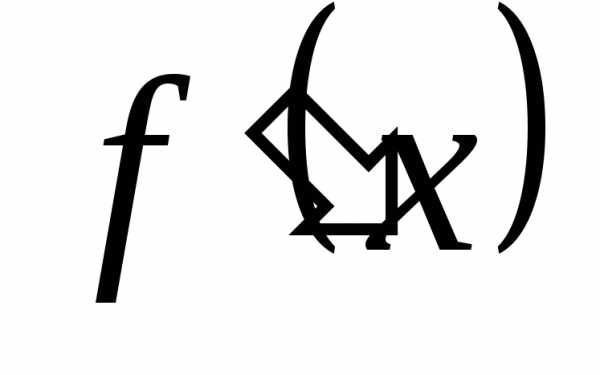 ,
не равную нулю, то обратная функция
,
не равную нулю, то обратная функция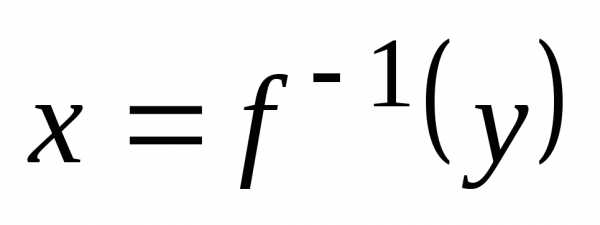
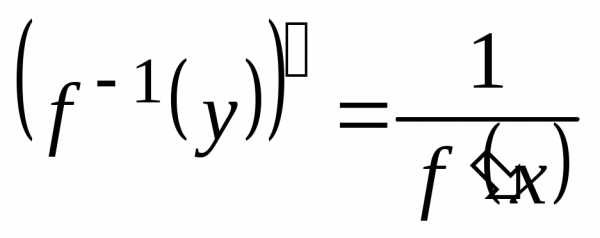 или иначе
или иначе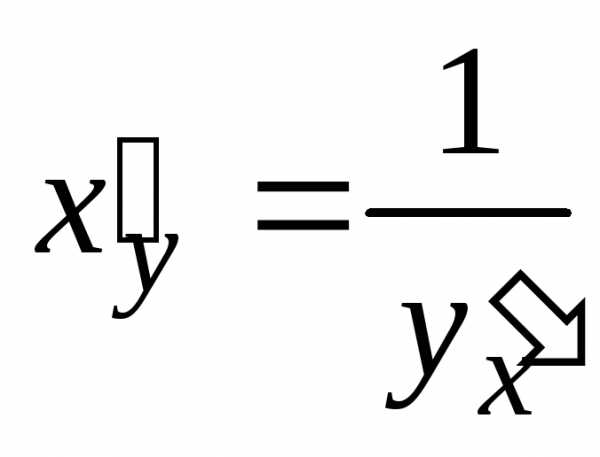 .
.1.5. Производная сложной функции
Если 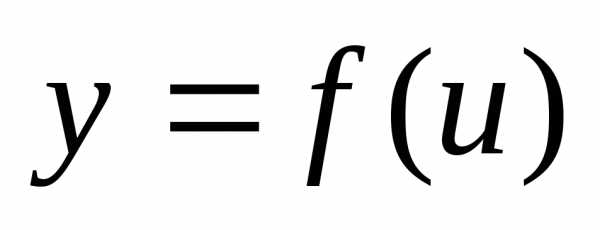 и
и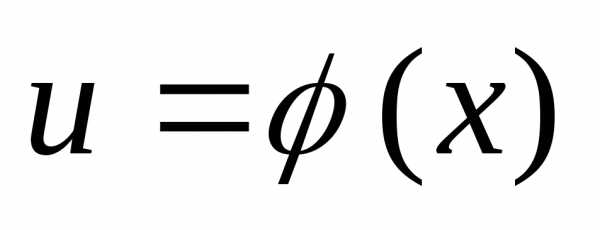 ,
тоестьсложная
функция независимого аргумента x с промежуточным аргументом u.
,
тоестьсложная
функция независимого аргумента x с промежуточным аргументом u.
Теорема.
Если 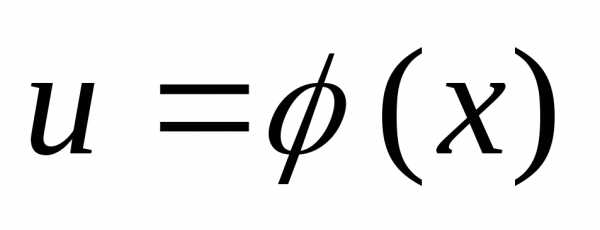 имеет производную
имеет производную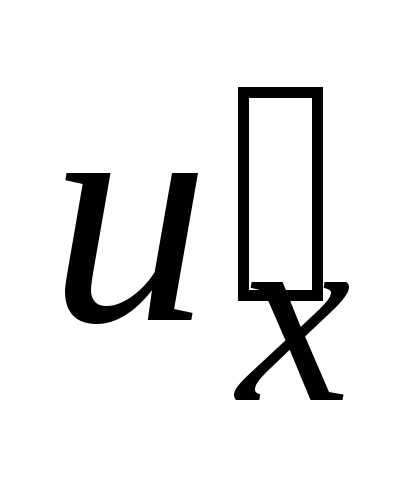 в точкеx,
а функция
в точкеx,
а функция 
 в соответствующей точкеu,
то сложная функция
в данной точкеx имеет производную
в соответствующей точкеu,
то сложная функция
в данной точкеx имеет производную  ,
которая находится по следующей формуле.
,
которая находится по следующей формуле.Часто пользуются следующей формулировкой этой теоремы: производная сложной функции равна произведению производной внешней функции по промежуточному аргументу на производную внутренней функции по независимому аргументу.
Сложная функция может быть составлена не из двух функций, а из большого их числа. В таких случаях теорема применяется последовательно несколько раз.
В частности, если
функция 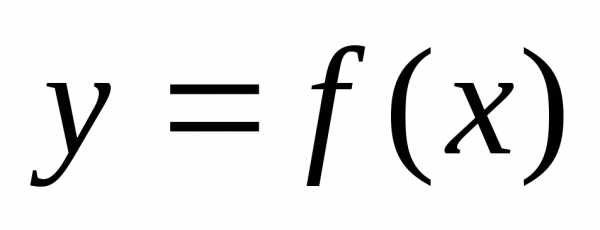
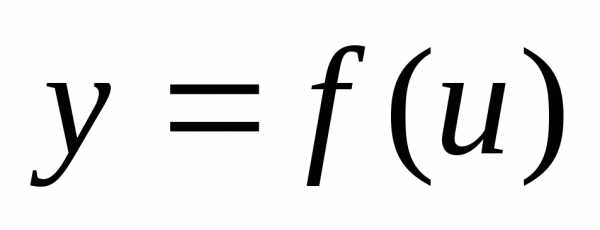 ,
,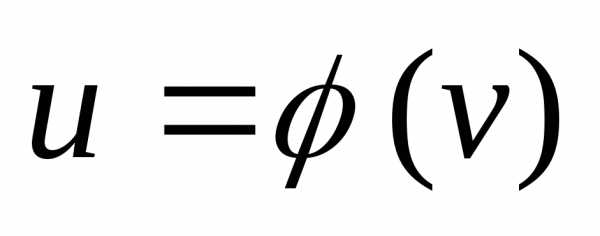 ,
,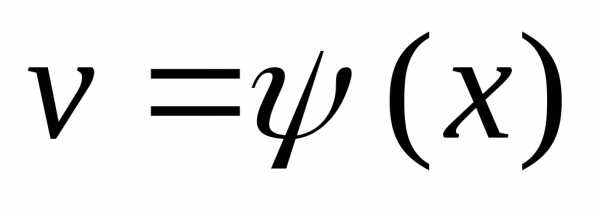 ,
то производная
,
то производная находится по формуле.
находится по формуле.1.6. Производные основных элементарных функций.
Таблица производных
Используя определение производной, можно найти производные основных элементарных функций.
1. Производная степенной функции .
2. Производная показательной функции .
В
частности, 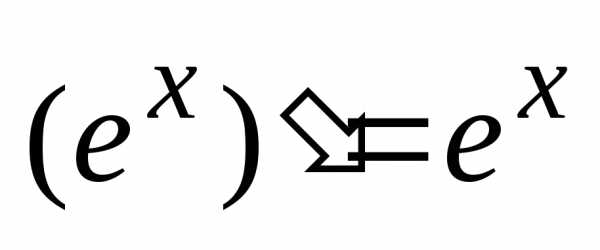
3. Производная логарифмической
функции ,  ,
,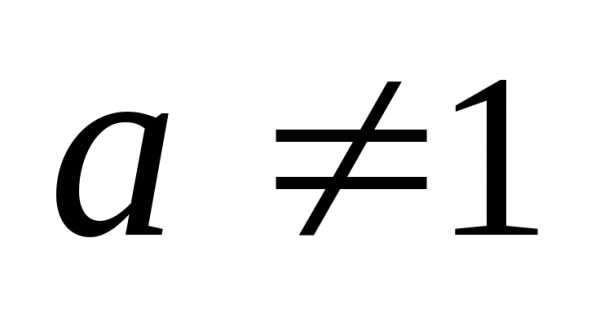 .
В частности,
.
В частности,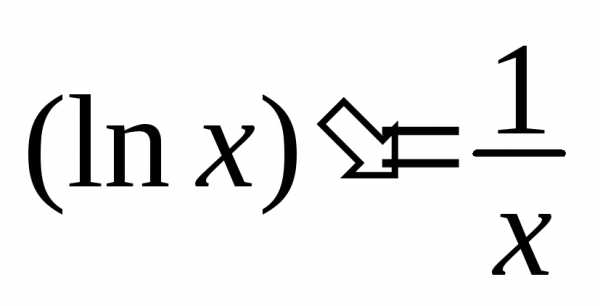 .
.
4. Производные тригонометрических
функций ,,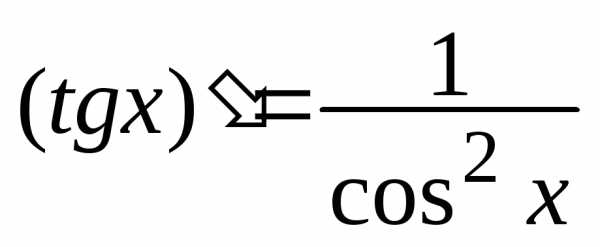 ,
,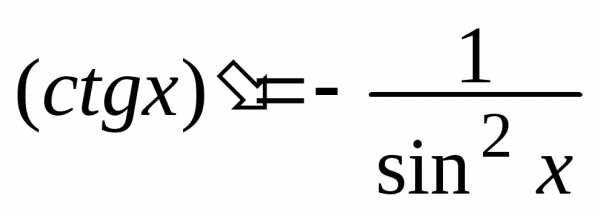 .
.
Найдем, например,
производную функции  .
По определению производной имеем:
.
По определению производной имеем:
.
 можно найти по правилу дифференцирования
частного двух функций:
можно найти по правилу дифференцирования
частного двух функций:.
5. Производные обратных тригонометрических функций ,.
Найдем, например,
производную функции
.
Функция,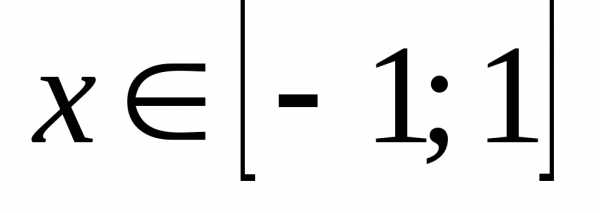 обратная к функции
обратная к функции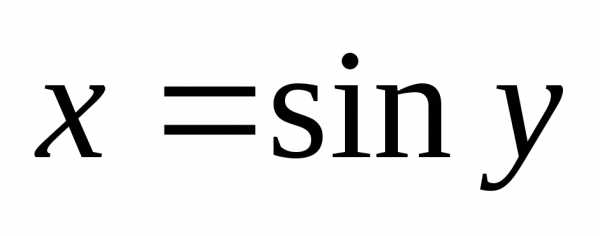 ,
,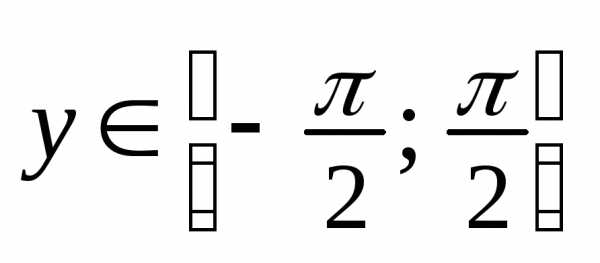 .
По правилу дифференцирования обратной
функции
.
По правилу дифференцирования обратной
функции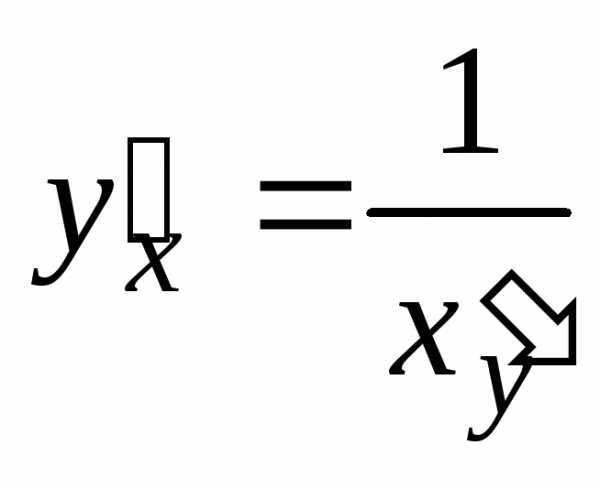 .
На интервале
.
На интервале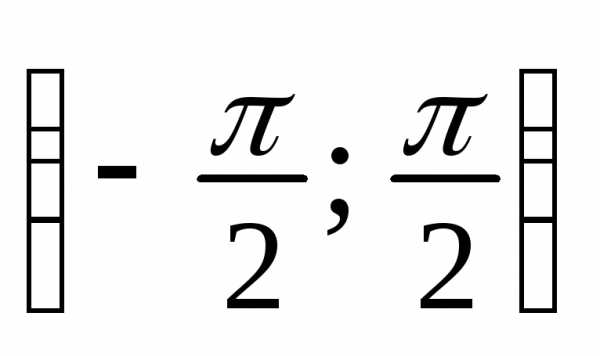
Запишем таблицу
производных для 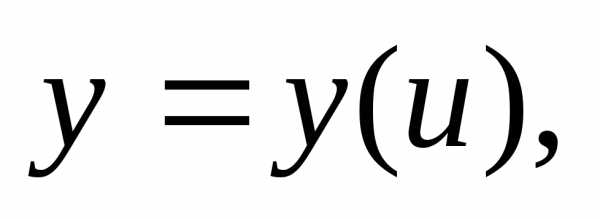 где
где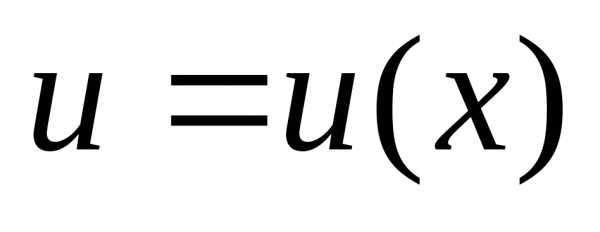 .
.
1. | 8. |
2. | 9. |
3. | 10. |
4. | 11. |
5. | 12. |
6. | 13. |
7. | 14. |
Применяя формулы и правила дифференцирования, найдем производные следующих функций:
1) .
Применим правило дифференцирования произведения двух функций:
.
2) 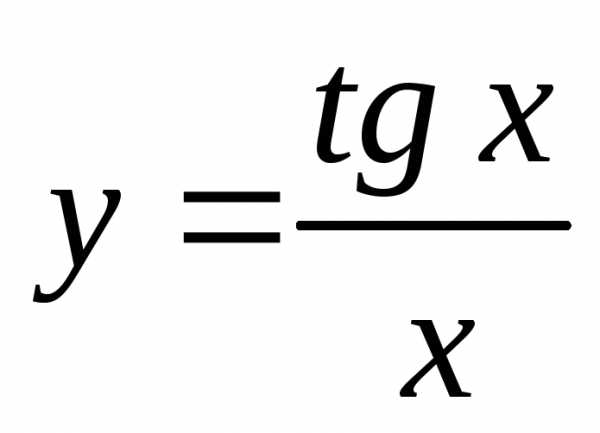 .
.
Применим правило дифференцирования частного двух функций:
.
3) 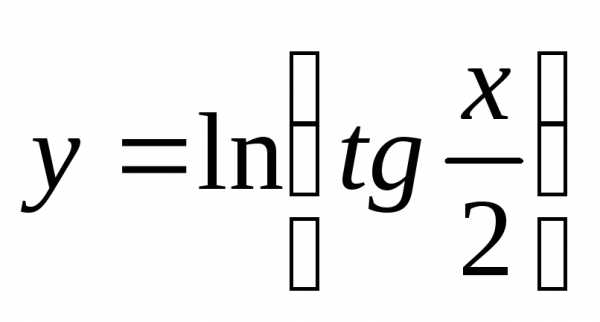 .
.
Применим правило дифференцирования сложной функции:
.
studfiles.net
Производные некоторых основных элементарных функций (Лекция №5)
- y = xn.
Если n – целое положительное
число, то, используя формулу бинома Ньютона:
(a + b)n = an+n·an-1·b + 1/2∙n(n – 1)an-2∙b2+ 1/(2∙3)∙n(n – 1)(n – 2)an-3b3+…+ bn,
можно доказать, что
Итак, если x получает приращение Δx, то f(x+Δx) = (x + Δx)n, и, следовательно,
Δy=(x+Δx)n – xn =n·xn-1·Δx + 1/2·n·(n–1)·xn-2·Δx2 +…+Δxn.
Заметим, что в каждом из пропущенных слагаемых есть множитель Δx в степени выше 3.
Найдем предел
Мы доказали эту формулу для n Î N. Далее увидим, что она справедлива и при любом
- y= sin x. Вновь воспользуемся определением производной.
Так как, f(x+Δx)=sin(x+Δx), то
Таким образом,
- Аналогично можно показать, что
- Рассмотрим функцию y= ln x.
Имеем f(x+Δx)=ln(x+Δx). Поэтому
Итак,
- Используя свойства логарифма можно показать, что
Формулы 3 и 5 докажите самостоятельно.
ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x.
- .
- (справедлива для любого конечного числа слагаемых).
- .
- .
а) .
б) .
Формулы 1 и 2 докажите самостоятельно.
Доказательство формулы 3.
Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx).
Тогда
Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv.
Следовательно,
.
Доказательство формулы 4.
Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому
Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x).
Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0.
Поэтому можем записать
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.
Пусть, например, y=u·v·w. Тогда,
y ‘ = u ‘·(v·w) + u·(v ·w) ‘ = u ‘·v·w + u·(v ‘·w +v·w ‘) = u ‘·v·w + u·v ‘·w + u·v·w ‘.
Доказательство формулы 5.
Пусть . Тогда

При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0.
Примеры.
- Если , то
- y = x3 – 3x2 + 5x + 2.
Найдем y ‘(–1).
y ‘ = 3x2 – 6x+ 5. Следовательно, y ‘(–1) = 14.
- y = ln x · cos x, то y ‘ = (ln x) ‘ cos x + ln x (cos x) ‘ =1/x∙cos x – ln x · sin x.
Таким образом,
- Аналогично для y= ctgx,
ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Областью определения функции y = f(u(x)) является либо вся область определения функции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области определения функции y= f(u).
Операция «функция от функции» может проводиться не один раз, а любое число раз.
Установим правило дифференцирования сложной функции.
Теорема. Если функция u= u(x) имеет в некоторой точке x0 производную и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0 производную y ‘u= f ‘(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y ‘x= f ‘(u0)·u ‘(x0), где вместо u должно быть подставлено выражение u= u(x).
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.
Доказательство. При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx:
Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0).
Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0.
По условию . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)
,
где α→0 при Δu→0, а, следовательно, и при Δx→0.
Перепишем это равенство в виде:
Δy= y ‘uΔu+α·Δu.
Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx
.
По условию . Поэтому, переходя к пределу при Δx→0, получим y ‘x= y ‘u·u ‘x . Теорема доказана.
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от «внешней» функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от «внутренней» функции по независимой переменной.
Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y ‘x осуществляется последовательным применением предыдущей теоремы.
По доказанному правилу имеем y ‘x= y ‘u·u ‘x . Применяя эту же теорему для u ‘x получаем , т.е.
y ‘x = y ‘x· u ‘v· v ‘x = f ‘u (u)·u ‘v (v)·v ‘x (x).
Примеры.
- y = sin x2. Тогда .
ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ
Начнем с примера. Рассмотрим функцию y= x3. Будем рассматривать равенство y= x3 как уравнение относительно x. Это уравнение для каждого значения у определяет единственное значение x: . Геометрически это значит, что всякая прямая параллельная оси Oxпересекает график функции y= x3 только в одной точке. Поэтому мы можем рассматривать x как функцию от y. Функция называется обратной по отношению к функции y= x3.

Прежде чем перейти к общему случаю, введем определения.
Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x2>x1, то f(x2) > f(x1).
Аналогично функция называется убывающей, если меньшему значению аргумента соответствует большее значение функции, т.е. еслих2 < х1 , то f(x2) > f(х1).
Итак, пусть дана возрастающая или убывающая функция y= f(x), определенная на некотором отрезке [a; b]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично).
Рассмотрим два различных значения х1 и х2. Пусть y1=f(x1), y2=f(x2). Из определения возрастающей функции следует, что если x1<x2, то у1<у2. Следовательно, двум различным значениям х1 и х2 соответствуют два различных значения функции у1 и у2. Справедливо и обратное, т.е. если у1<у2, то из определения возрастающей функции следует, чтоx1<x2. Т.е. вновь двум различным значениям у1 и у2 соответствуют два различных значенияx1 и x2. Т.о., между значениями x и соответствующими им значениями y устанавливается взаимно однозначное соответствие, т.е. уравнение y=f(x) для каждого y (взятого из области значений функции y=f(x)) определяет единственное значение x, и можно сказать, что x есть некоторая функция аргумента y: x= g(у).
Эта функция называется обратной для функции y=f(x). Очевидно, что и функция y=f(x) является обратной для функции x=g(у).
Заметим, что обратная функция x=g(y) находится путем решения уравнения y=f(x) относительно х.
Пример. Пусть дана функция y = ex. Эта функция возрастает при –∞ < x <+∞. Она имеет обратную функцию x = lny. Область определения обратной функции 0 < y < + ∞.
Сделаем несколько замечаний.
Замечание 1. Если возрастающая (или убывающая) функция y=f(x) непрерывна на отрезке [a; b], причем f(a)=c, f(b)=d, то обратная функция определена и непрерывна на отрезке [c; d].
Замечание 2. Если функция y=f(x) не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций.
Пример. Функция y=x2 определена при –∞<x<+∞. Она не является ни возрастающей, ни убывающей и не имеет обратной функции. Однако, если мы рассмотриминтервал 0≤x<+∞, то здесь функция является возрастающей и обратной для нее будет . На интервале – ∞ <x≤ 0 функция – убывает и обратная для нее .
Замечание 3. Если функции y=f(x) и x=g(y) являются взаимно обратными, то они выражают одну и ту же связь между переменными x и y. Поэтому графикомих является одна и та же кривая. Но если аргумент обратной функции мы обозначим снова через x, а функцию через y и построим их в одной системе координат, то получим уже два различных графика. Легко заметить, что графики будут симметричны относительно биссектрисы 1-го координатного угла.
ТЕОРЕМА О ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ
Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции.
Теорема. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у0 имеет производную g ‘(v0), отличную от нуля, то в соответствующей точке x0=g(x0) функция y=f(x) имеет производную f ‘(x0), равную , т.е. справедлива формула.
Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0.
Покажем, что .
Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. .
Следовательно,
,
что и требовалось доказать.
Эту формулу можно записать в виде .
Рассмотрим применение этой теоремы на примерах.
Примеры.
- y = ex. Обратной для этой функции
является функция x= ln y. Мы уже доказали, что .
Поэтому согласно сформулированной выше теореме
Итак, (ex) ‘ = ex
- Аналогично можно показать, что (ax) ‘ = ax·lna. Докажите самостоятельно.
- y = arcsin x.
Рассмотрим обратную функцию x = sin y. Эта функция в интервале – π/2<y<π/2 монотонна. Ее производная
x ‘ = cos y не
обращается в этом интервале в нуль. Следовательно, по теореме о производной
обратной функции
.
Но на (–π/2; π/2) .
Поэтому
- Аналогично
Докажите самостоятельно.
- y = arctg x.
Эта функция по определению удовлетворяет условию существования обратной функции
на интервале –π/2< y < π/2. При этом обратная функция x = tg y монотонна.
По ранее доказанному .
Следовательно, y ‘ = cos2y . Но .
Поэтому
- Используя эти формулы, найти производные следующих функций:
www.toehelp.ru
Свойства производных с примерами
Пусть функции и являются дифференцируемыми, и – произвольные константы. Тогда имеют место следующие соотношения:
1. Линейность:
ПРИМЕР
2. Производная произведения:
ПРИМЕР
3. Производная частного:
ПРИМЕР
4. Постоянный множитель можно выносить за знак производной:
ПРИМЕР
5. Производная сложной функции: если задана функция , у которой аргумент есть в свою очередь функцией от то производная равна:
ПРИМЕР
6. Производная обратной функции: если функция , является обратной к функции то их производные связаны соотношением:
ПРИМЕР
| Рассмотрим функцию , обратной к ней есть функция Найдем производные:
то есть
|
ru.solverbook.com
Производные основных элементарных функций
Теорема 1. Пусть функция , непрерывна, строго монотонна на отрезке и дифференцируема во внутренней точке этого отрезка, причем . Тогда обратная функция дифференцируема в точке , причем .
Доказательство. Заметим, что в условиях теоремы обратная функция существует, непрерывна и строго монотонна на отрезке в силу теоремы из § 19 главы 1.
Придадим значению приращение . Тогда получит приращение
(так как функция строго монотонна). Поэтому можно записать . Поскольку при в силу непрерывности обратной функции и и, по условию, существует , имеем . Отсюда следует существование и равенство . Теорема доказана.
Пример 1. Найдем производные функций arcsin x, arccos x, arctg x, arcctg x/
Решение. По теореме 1 имеем (поскольку , имеем и корень берем со знаком плюс).
Аналогично,
,
, .
Теорема 2. Если функции и имеют производные в точке , то в точке имеют производные и функции (если ) и справедливы формулы
а) ; б) ; в) .
Доказательство. а) Пусть . Дадим приращение . Тогда функции u, v, y получат приращения , причем
. Отсюда и и равенство а) доказано.
б) Пусть . Аналогично пункту а) имеем
, , , т.е. имеет место формула б).
в) Пусть . Имеем , , , т.е. имеет место формула в).
Теорема доказана.
Следствия. 1) Если , то .
2) Формула а) имеет место для любого конечного числа слагаемых.
3) .
Доказательство. 1) Поскольку , имеем .
2) Например, имеем .
3) Например, имеем .
В общем случае следствия 2) и 3) доказываются методом математической индукции.
Рассмотрим показательно-степенную функцию , где u и v – некоторые функции от х. Найдем производную функции у в точке, в которой дифференцируемы функции u и v .Для этого представим функцию у в виде .По правилу дифференцирования сложной функции, в силу теоремы 2 и примера 1 § 1 имеем
.
Таким образом,
.
Заметим, что в полученной формуле первое слагаемое есть результат дифференцирования как показательной функции, а второе – как степенной функции. Примененный прием дифференцирования называется логарифмическим дифференцированием. Им бывает удобно пользоваться и тогда, когда дифференцируемая функция является произведением нескольких сомножителей.
Перейдем теперь к параметрическому заданию функций. Если зависимость функции у от аргумента х устанавливается не непосредственно, а с помощью некоторой третьей переменной t, называемой параметром, формулами
, (3.1)
то говорят, что функция у от х задана параметрически.
Если х и у рассматривать как прямоугольные координаты точки на плоскости, то уравнения (3.1) ставят в соответствие каждому значению точку на плоскости. С изменением t точка опишет некоторую кривую на плоскости. Уравнения (3.1) называются параметрическими уравнениями этой кривой. Например, уравнения
(3.2)
являются параметрическими уравнениями эллипса с полуосями а и b.
Если в (3.1) уравнение разрешается относительно t, , то параметрическое задание функции можно свести к явному:
.
Найдем производную функции, заданной параметрически. Для этого предположим, что функции и дифференцируемы, причем на некотором промежутке, а для функции существует обратная функция , имеющая конечную производную . Тогда по правилу дифференцирования сложной и обратной функций находим: . Таким образом,
. (3.3)
Например, производная функции, определяемой уравнениями (3.2) имеет вид
.
Уравнение касательной к кривой, заданной параметрически, в точке , соответствующей значению параметра , получается из уравнения (1.4), если вместо подставить :
,
отсюда при имеем
. (3.4)
Аналогично из уравнения (1.5) получаем уравнение нормали:
или . (3.5)
Запишем теперь сводные таблицы производных основных элементарных функций и правил дифференцирования, полученных ранее.
Правила дифференцирования
1. . 2. . 3. . 4. .
5. Если , то . 6. Если то .
7. Если – обратная функция, то . 8. .
Таблица производных основных элементарных функций
1. , где . 2. , в частности,
3. . 4. . .
5. . 6. .
7. . 8. .
9. . 10. .
11. , в частности, . 12. , в частности, .
Похожие статьи:
poznayka.org
2. Основные и производные физические величины
ГОСТустанавливает единицы физических величин, а также наименования, обозначения и правила применения этих единиц. В соответствии с ним подлежат обязательному применению единицы Международной системы единиц (а также десятичные кратные и дольные от них), представляющие собой основу для унификации единиц физических величин во всем мире [4].
Стандарт не распространяется на единицы величин, оцениваемых в условных шкалах, например, шкалам твердости Роквелла, Виккерса и др.
2.1. Единицы международной системы
Международная система единиц (международное сокращенное наименование – SI, в русской транскрипции —СИ) принята в в1960 г.
Сокращенное наименование Международной системы единиц следует произносить и писать «единицы СИ», а не «единицы системыСИ», так как слово «система» уже входит в наименование в виде буквы «С».
Наименования и обозначения основных и дополнительных единиц приведены в таблице 1.
В качестве основныхединиц измерения выбраносемь(наименование, размерность, величина, обозначение: международное и русское):
1. метр —L(длина)m, м;
2. килограмм —M(масса)kg, кг;
3.секунда –T(время)s, с;
4. ампер —I(сила тока)A, А;
5. кельвин –θ(температура)K, К;
6. моль –N(количество вещества)mol, моль;
7. кандела –J(сила света)cd, кд.
Система включает также две дополнительныеединицы:радиан для плоского истерадиандля телесного угла.
Таблица 1
Основные и дополнительныеединицы
Международной системы единиц

Кроме температуры по шкале Кельвина(обозначаемойT) допускается применять температуру по шкалеЦельсия(обозначаемуюt):t = T – T0, где T0 = 273,15 К по определению. Градусы Цельсия имеют обозначение (международное и русское)0С. По размеру градус Цельсия равен градусу Кельвина.
Производные единицы СИ образуются с помощью простейших уравнений связи из основных и дополнительных единиц по правилам образования когерентных* производных единиц.
(* Когерентность –«лат. сцепление, связь» — физ. согласованное протекание во времени нескольких колебательных процессов, разность фаз которых постоянна; когерентные волны при сложении либо усиливают, либо ослабляют друг друга).
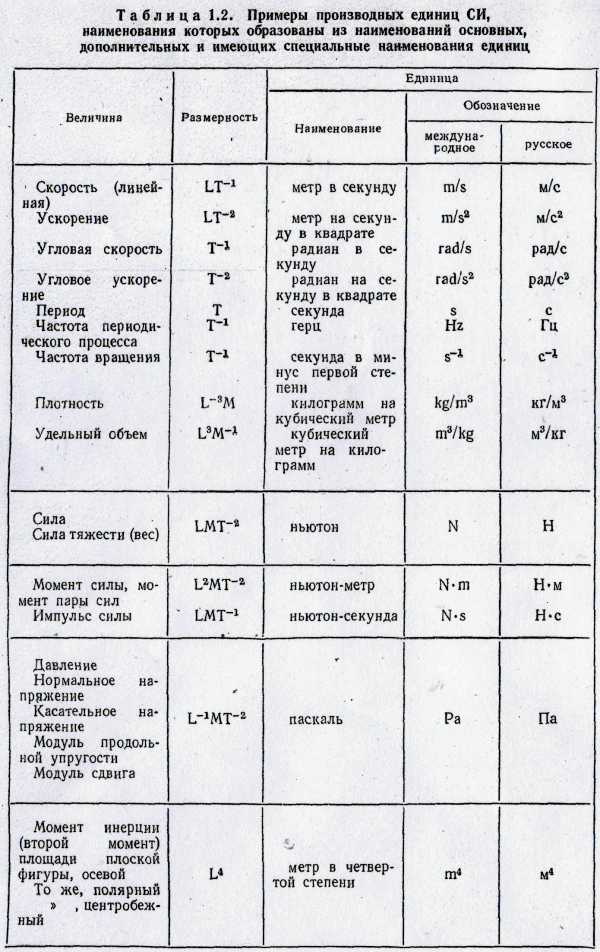
В таблице 2приведеныпроизводные единицыСИ, образованные из наименований единиц основных, дополнительных и имеющих специальные наименования единиц (величина, размерность, наименование, обозначение: международное и русское):
Таблица 2
Примеры производныхединиц СИ, наименования которых
образованы из наименований основных, дополнительных
и имеющих специальные наименования единиц
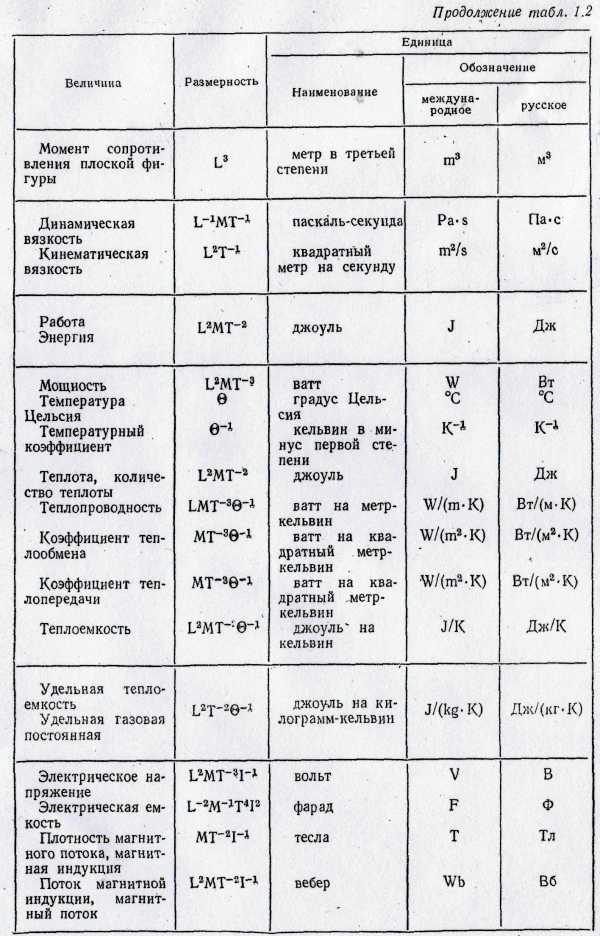
Продолжение таблицы 2
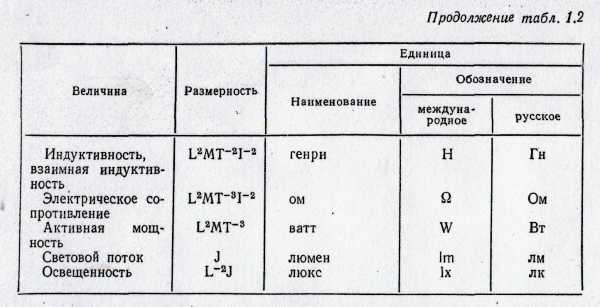
Продолжение таблицы 2
2.2. Единицы, не входящие в си
Существует ограниченная группа единиц, которые не во всех случаях можно заменить единицами СИ. В таблице 3 помещен перечень единиц, допускаемых к применению наравне с единицами СИ без ограничения срока. Однако стандарт допускает их применение лишь в обоснованных случаях, т. е. тогда, когда замена их единицами СИ при современном состоянии соответствующих областей техники и народного хозяйства вызвала бы неоправданные затруднения.
В стандарт включены единицы: массы (тонна), объема и вместимости (литр), времени (минута, час, сутки), плоского угла (градус, минута, секунда).
Без ограничения срока разрешается применять относительные и логарифмические единицы. Эти единицы не связаны с какой-либо системой единиц, так как не зависят от выбора основных единиц и во всех системах остаются неизменными. К относительным величинам (безразмерное отношение физической величины к одноименной физической величине, принимаемой за исходную) относятся: КПД, относительное удлинение, относительная плотность, относительные диэлектрическая и магнитная проницаемости и др.
Таблица 3
Внесистемныеединицы, допускаемые к применению
наравне с единицами СИ
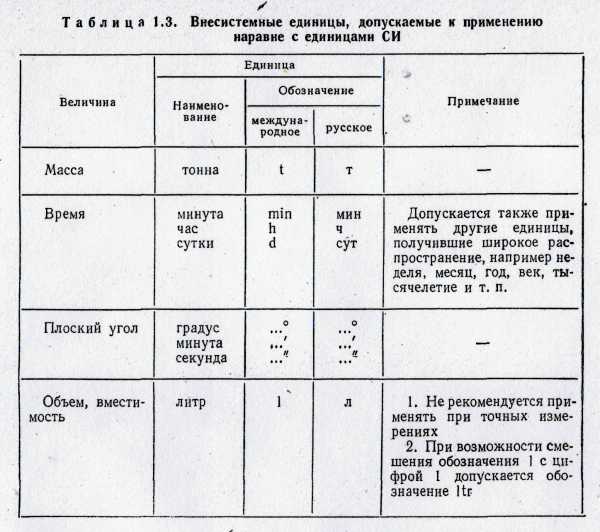
Все единицы других систем, которые допускались к применению до 1 января 1980 г., заменены единицами СИ, за исключением восьми единиц: карат, оборот в секунду, оборот в минуту, бар, текс, непер, морская миля, узел.
studfiles.net