Окружность с координатами – Как найти координаты центра окружности, описанной около треугольника, знаякоординаты его вершин. Построение этой окружности

Окружность, круг, сегмент, сектор. Формулы и свойства

Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.

Определение. Единичная окружность — окружность, радиус которой равна единице.

Определение. Круг — часть плоскости, ограничена окружностью.

Определение. Радиус окружности R — расстояние от центра окружности О до любой точки окружности.

Определение. Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.

Основные свойства окружности

1. Диаметр окружности равен двум радиусам.

D = 2r

2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.

3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.

4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.

5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.

Формулы длины окружности и площади круга

Формулы длины окружности

1. Формула длины окружности через диаметр:

L = πD

2. Формула длины окружности через радиус:

L = 2πr

Формулы площади круга

1. Формула площади круга через радиус:

S = πr²

2. Формула площади круга через диаметр:

S = πD²4

Уравнение окружности

1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:

r² = x² + y²

2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

r

2 = (x — a)² + (y — b)²

3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:

{	x = a + r cos t
	y = b + r sin t

Касательная окружности и ее свойства

Определение. Касательная окружности — прямая, которая касается окружности только в одной точке.

Основные свойства касательных к окружности

1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.

2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

AB = AC

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

∠ОAС = ∠OAB

Секущая окружности и ее свойства

Определение. Секущая окружности — прямая, которая проходит через две точки окружности.

Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:

AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:

AQ ∙ BQ = CQ²

Хорда окружности ее длина и свойства

Определение. Хорда окружности — отрезок, который соединяет две точки окружности.

Длина хорды

1. Длина хорды через центральный угол и радиус:

AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:

AB = 2r sin α

Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:

если хорды AB = CD, то

дуги ◡ AB = ◡ CD

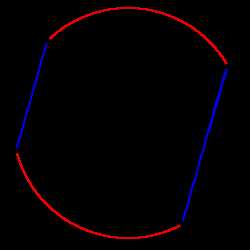2. Если хорды параллельные, то дуги между ними будут одинаковые:

если хорды AB ∣∣ CD, то

◡ AD = ◡ BC

3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:

если OD ┴ AB, то

AC = BC

4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:

AQ ∙ BQ = DQ ∙ QC

5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.

если хорды AB = CD, то

ON = OK

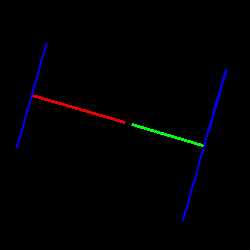6. Чем больше хорда тем ближе она к центру.

если CD > AB, то

ON < OK

Центральный угол, вписанный угол и их свойства

Определение. Центральный угол окружности — угол, вершиной которого есть центр окружности.

Определение. Угол вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.

Основные свойства углов

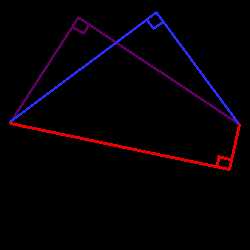1. Все вписанные углы, которые опираются на одну дугу — равны. 2. Вписанний угол, который опирается на диаметр будет прямым (90°). 3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу

β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.

α + β = 180°

Определение. Дуга окружности (◡) — часть окружности, которая соединяет две точки на окружности.

Определение. Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.

Формула длины дуги через центральный угол (в градусах):

l = πr180°∙ α

Определение. Полуокружность — дуга в которой концы соединены диаметром окружности.

Определение. Полукруг (◓) — часть круга, которая ограничена полуокружностью и диаметром.

Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)

S = πr²360°∙ α

Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.

Определение. Концентрические окружности — окружности с различными радиусами, которые имеют общий центр.

Определение. Кольцо — часть плоскости ограниченная двумя концентрическими окружностями.

ru.onlinemschool.com

Уравнение окружности и прямой

Уравнение линии на плоскости

Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).

Рисунок 1. Произвольная линия в системе координат

Определение 1

Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$

Уравнение окружности

Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).

Рисунок 2. Окружность в декартовой системе координат

Расстояние от центра окружности до точки $M$ вычисляется следующим образом

Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее

Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.

В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид

Уравнение прямой.

Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $\left\{x_1,\ y_1\right\}$ и $\{x_2,\ y_2\}$ соответственно, причем точки $A$ и $B$ выбраны так, что прямая $l$ — серединный перпендикуляр к отрезку $AB$. Выберем произвольную точку $M=\{x,y\}$, принадлежащую прямой $l$ (рис. 3).

Рисунок 3. Прямая в декартовой системе координат

Так как прямая $l$ — серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.

Найдем длины данных сторон по формуле расстояния между точками:

Следовательно

Обозначим через $a=2\left(x_1-x_2\right),\ b=2\left(y_1-y_2\right),\ c={x_2}^2+{y_2}^2-{x_1}^2-{y_1}^2$, Получаем, что уравнение прямой в декартовой системе координат имеет следующий вид:

Замечание 1

Здесь можно выделить два частных случая для уравнения прямой. Пусть прямая $l$ проходит через точку $M=\{x_0,y_0\}$, тогда

1. Если прямая $l$ параллельна оси $Ox$, то она имеет вид

   \[y=y_0\]

2. Если прямая $l$ параллельна оси $Oy$, то она имеет вид

   \[x=x_0\]

Пример задачи на нахождение уравнений линий в декартовой системе координат

Пример 1

Найти уравнение окружности с центром в точке $(2,\ 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.

Решение.

Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2,\ 4)$, получим

\[{(x-2)}^2+{(y-4)}^2=r^2\]

Найдем радиус окружности как расстояние от точки $(2,\ 4)$ до точки $(0,0)$

\[r=\sqrt{{(2-0)}^2+{(4-0)}^2}=\sqrt{20}=2\sqrt{5}\]

Получаем, уравнение окружности имеет вид:

\[{(x-2)}^2+{(y-4)}^2=20\]

Найдем теперь уравнение окружности, используя частный случай 1. Получим

\[y=4\]

spravochnick.ru

Окружность. Как построить окружность? Формула окружности.

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а)² + (у – b)² = R ²

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
(х – 1)² + (у – 2)² = 4²

Найдем центр окружности:
х – 1=0
x=1

у – 2=0
y=2

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R ²=4
R ²=2²
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.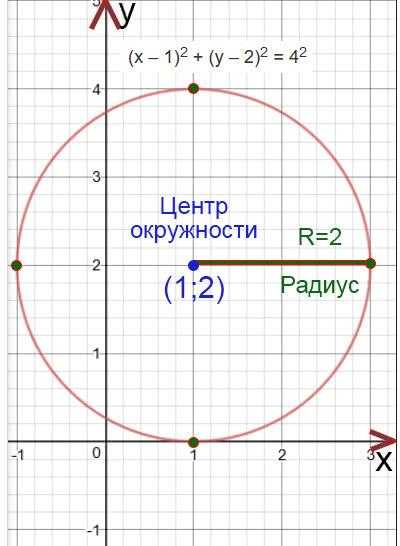

Пример №2:
х² + (у + 1)² =1

Можно представить уравнение окружности ввиде:
(х-0)² + (у + 1)² =1²

Найдем центр окружности:
х=0

у + 1=0
y=–1

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R ²=1
R ²=1²
R=1

Построим окружность.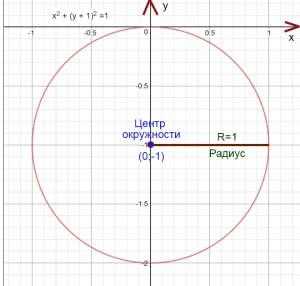

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

tutomath.ru

Единичная окружность | Треугольники

Что такое единичная окружность и как с ее помощью вводятся определения синуса, косинуса, тангенса и котангенса?

Рассмотрим в прямоугольной декартовой системе координат окружность с центром в начале координат — точке O.

 

Отметим на окружности точку P, лежащую на оси абсцисс справа от точки O.

Осуществим поворот радиуса OP около точки O на угол α в верхнюю полуплоскость.

При этом радиус OP займет положение OA. Говорят, что при повороте на угол альфа радиус OP переходит в радиус OA, а точка P переходит в точку точку A(x;y).

 

Опустив перпендикуляр AB из точки A на ось Оx, получим прямоугольный треугольник OAB, в котором гипотенуза OA равна радиусу окружности, катеты AB и OB — ординате и абсциссе точки A: OA=R, AB=y, OB=x.

Катет AB — противолежащий углу AOB, равному α, катет OB — прилежащий.

По определению косинуса острого угла в прямоугольном треугольнике,

   

Таким образом, на окружности косинус угла α — это отношение абсциссы точки A окружности к радиусу этой окружности.

Аналогично, по определению синуса острого угла в прямоугольном треугольнике,

   

Значит,  синус угла α — это отношение ординаты точки A окружности к радиусу этой окружности.

Для окружности любого радиуса отношения x/R и y/R не зависят от величины радиуса, а зависят только от  угла альфа. Поэтому удобно взять R=1. Для окружности единичного радиуса определение синуса и косинуса упрощаются:

   

   

Определение.

Окружность с центром в начале координат и радиусом, равным единице, называется единичной окружностью.

Отсюда получаем определения синуса и косинуса на единичной окружности.

Определение.

Синусом угла α называется ордината точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.

Косинусом угла α называется абсцисса точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.

Применив определения тангенса и котангенса острого угла в прямоугольном треугольнике в ∆AOB,  получаем:

   

откуда

   

   

Приходим к определению тангенса и котангенса на единичной окружности.

Определение.

Тангенсом угла α называется отношение ординаты точки A единичной окружности к абсциссе этой точки.

Котангенсом угла α называется отношение абсциссы точки A единичной окружности к ординате этой точки.

www.treugolniki.ru

Внеклассный урок — Числовая окружность

Числовая окружность

Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.

Единичной окружностью называют окружность радиуса 1.

 

Общий вид числовой окружности.

1) Ее радиус принимается за единицу измерения.

2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.

3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:

первая четверть – это дуга AB

вторая четверть – дуга BC

третья четверть – дуга CD

четвертая четверть – дуга DA

4) Начальная точка числовой окружности – точка А.

Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.

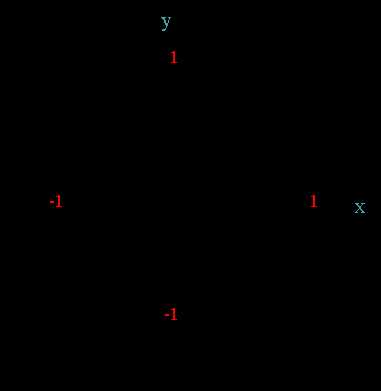 Числовая окружность на координатной плоскости.

Центр радиуса числовой окружности соответствует началу координат (числу 0).

Горизонтальный диаметр соответствует оси x, вертикальный – оси y.

Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).

 

Значения x и y в четвертях числовой окружности:

1-я четверть	2-я четверть	3-я четверть	4-я четверть
x > 0, y > 0	x < 0, y > 0	x < 0, y < 0	x > 0, y < 0

 

Значение любой точки числовой окружности:

Любая точка числовой окружности с координатами (x; y) не может быть меньше -1, но не может быть больше 1: –1 ≤ x ≤ 1;   –1 ≤ y ≤ 1

 

Основные величины числовой окружности:

	Величина в радианах	Величина в радиусах
Окружность	2π	360º
Полуокружность	π	180º
Четверть окружности	π — 2	90º

 

Имена и местонахождение основных точек числовой окружности:

  
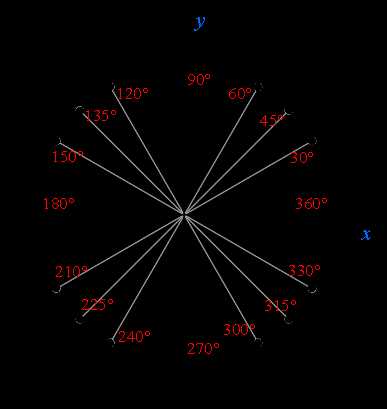
Как запомнить имена числовой окружности.

Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.

Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.

1) Начнем с крайних точек на осях координат.

Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).

Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.

Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.

Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.

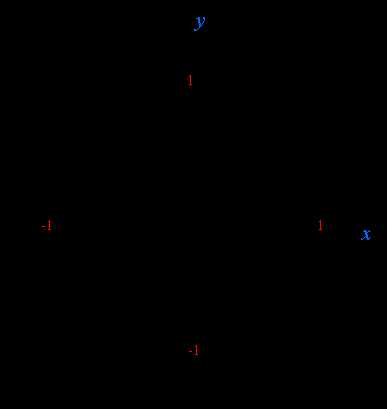
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.

Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:

— Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.

  — Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.

Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.

— Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.

Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.

3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.

 

Особенности числовой окружности. Сравнение с числовой прямой.

Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.

На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:

Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.

Отсюда формула:

Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число: M(t) = M(t + 2πk), где k ∈ Z. Число k называется параметром.

 

Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):

 

raal100.narod.ru

Окружность на координатной плоскости — Науколандия

Если расположить единичную числовую окружность на координатной плоскости, то для ее точек можно найти координаты. Числовую окружность располагают так, чтобы ее центр совпал с точкой начала координат плоскости, т. е. точкой O (0; 0).

Обычно на единичной числовой окружности отмечают точки соответствующие от начала отсчета на окружности

• четвертям — 0 или 2π, π/2, π, (2π)/3,
• серединам четвертей — π/4, (3π)/4, (5π)/4, (7π)/4,
• третям четвертей — π/6, π/3, (2π)/3, (5π)/6, (7π)/6, (4π)/3, (5π)/3, (11π)/6.

На координатной плоскости при указанном выше расположении на ней единичной окружности можно найти координаты, соответствующие этим точкам окружности.

Координаты концов четвертей найти очень легко. У точки 0 окружности координата x равна 1, а y равен 0. Можно обозначить так A (0) = A (1; 0).

Конец первой четверти будет располагаться на положительной полуоси ординат. Следовательно, B (π/2) = B (0; 1).

Конец второй четверти находится на отрицательной полуоси абсцисс: C (π) = C (-1; 0).

Конец третьей четверти: D ((2π)/3) = D (0; -1).

Но как найти координаты середин четвертей? Для этого строят прямоугольный треугольник. Его гипотенузой является отрезок от центра окружности (или начала координат) к точке середины четверти окружности. Это радиус окружности. Поскольку окружность единичная, то гипотенуза равна 1. Далее проводят перпендикуляр из точки окружности к любой оси. Пусть будет к оси x. Получается прямоугольный треугольник, длины катетов которого — это и есть координаты x и y точки окружности.

Четверть окружности составляет 90º. А половина четверти составляет 45º. Поскольку гипотенуза проведена к точке середины четверти, то угол между гипотенузой и катетом, выходящим из начала координат, равен 45º. Но сумма углов любого треугольника равна 180º. Следовательно, на угол между гипотенузой и другим катетом остается также 45º. Получается равнобедренный прямоугольный треугольник.

Из теоремы Пифагора получаем уравнение x² + y² = 1². Поскольку x = y, а 1² = 1, то уравнение упрощается до x² + x² = 1. Решив его, получаем x = √½ = 1/√2 = √2/2.

Таким образом, координаты точки M₁ (π/4) = M₁ (√2/2; √2/2).

В координатах точек середин других четвертей будут меняться только знаки, а модули значений оставаться такими же, так как прямоугольный треугольник будет только переворачиваться. Получим:
M₂ ((3π)/4) = M₂ (-√2/2; √2/2)
M₃ ((5π)/4) = M₃ (-√2/2; -√2/2)
M₄ ((7π)/4) = M₄ (√2/2; -√2/2)

При определении координат третьих частей четвертей окружности также строят прямоугольный треугольник. Если брать точку π/6 и проводить перпендикуляр к оси x, то угол между гипотенузой и катетом, лежащим на оси x, составит 30º. Известно, что катет, лежащий против угла в 30º, равен половине гипотенузы. Значит, мы нашли координату y, она равна ½.

Зная длины гипотенузы и одного из катетов, по теореме Пифагора находим другой катет:
x² + (½)² = 1²
x² = 1 — ¼ = ¾
x = √3/2

Таким образом T₁ (π/6) = T₁ (√3/2; ½).

Для точки второй трети первой четверти (π/3) перпендикуляр на ось лучше провести к оси y. Тогда угол при начале координат также будет 30º. Здесь уже координата x будет равна ½, а y соответственно √3/2: T₂ (π/3) = T₂ (½; √3/2).

Для других точек третей четвертей будут меняться знаки и порядок значений координат. Все точки, которые ближе расположены к оси x будут иметь по модулю значение координаты x, равное √3/2. Те точки, которые ближе к оси y, будут иметь по модулю значение y, равное √3/2.
T₃ ((2π)/3) = T₃ (-½; √3/2)
T₄ ((5π)/6) = T₄ (-√3/2; ½)
T₅ ((7π)/6) = T₅ (-√3/2; -½)
T₆ ((4π)/3) = T₆ (-½; -√3/2)
T₇ ((5π)/3) = T₇ (½; -√3/2)
T₈ ((11π)/6) = T₈ (√3/2; -½)

scienceland.info

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра

Числовая ось

      Определение 1. Числовой осью (числовой прямой, координатной прямой)   Ox   называют прямую линию, на которой точка   O   выбрана началом отсчёта (началом координат) (рис.1), направление

O → x

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Рис.1

      Определение 2. Отрезок, длина которого принята за единицу длины, называют масштабом.

      Каждая точка числовой оси имеет координату, являющуюся вещественным числом. Координата точки   O   равна нулю. Координата произвольной точки   A ,   лежащей на луче   Ox ,   равна длине отрезка   OA .   Координата произвольной точки   A   числовой оси, не лежащей на луче   Ox ,   отрицательна, а по абсолютной величине равна длине отрезка   OA .

Прямоугольная декартова система координат на плоскости

      Определение 3. Прямоугольной декартовой системой координат   Oxy   на плоскости называют две взаимно перпендикулярных числовых оси   Ox   и   Oy   с одинаковыми масштабами и общим началом отсчёта в точке   O ,   причём таких, что поворот от луча   Ox   на угол   90°   до луча   Oy   осуществляется в направлении против хода часовой стрелки (рис.2).

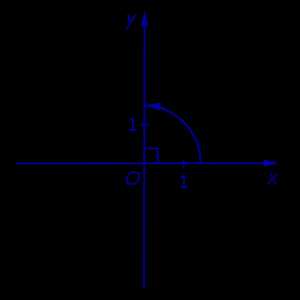
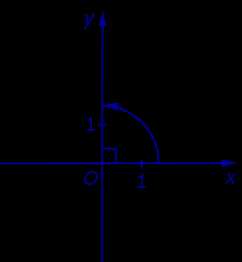
Рис.2

      Замечание. Прямоугольную декартову систему координат   Oxy ,   изображённую на рисунке 2, называют правой системой координат, в отличие от левых систем координат, в которых поворот луча   Ox   на угол   90°   до луча   Oy   осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

      Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат   Oxy ,   то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть   A   – произвольная точка плоскости. Опустим из точки   A   перпендикуляры   AA₁   и   AA₂   на прямые   Ox   и   Oy   соответственно (рис.3).

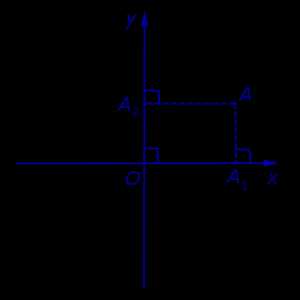
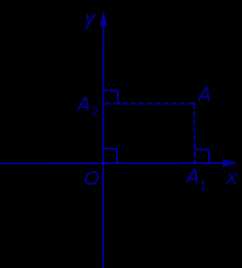
Рис.3

      Определение 4. Абсциссой точки   A   называют координату точки   A₁   на числовой оси   Ox ,   ординатой точки   A   называют координату точки   A₂   на числовой оси   Oy .

      Обозначение. Координаты (абсциссу и ординату) точки   A   в прямоугольной декартовой системе координат   Oxy   (рис.4) принято обозначать   A (x ; y)   или   A = (x ; y).

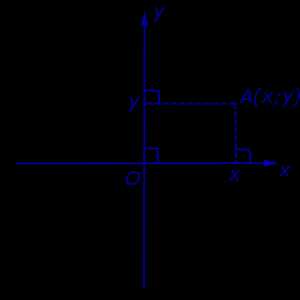
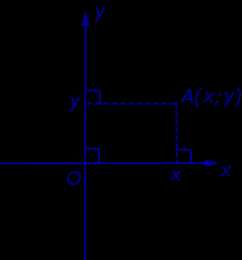
Рис.4

      Замечание. Точка   O ,   называемая началом координат, имеет координаты   O (0 ; 0) .

      Определение 5 . В прямоугольной декартовой системе координат   Oxy   числовую ось   Ox   называют осью абсцисс, а числовую ось   Oy   называют осью ординат (рис. 5).

      Определение 6. Каждая прямоугольная декартова система координат делит плоскость на   4   четверти (квадранта), нумерация которых показана на рисунке 5.

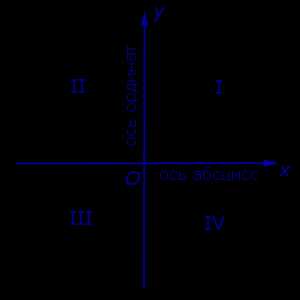
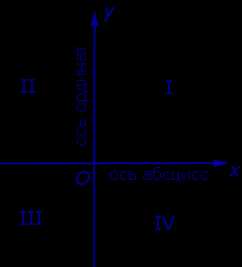
Рис.5

      Определение 7. Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью.

      Замечание. Ось абсцисс задаётся на координатной плоскости уравнением   y = 0 ,   ось ординат задаётся на координатной плоскости уравнением   x = 0.

Формула для расстояния между двумя точками координатной плоскости

      Утверждение 1. Расстояние между двумя точками координатной плоскости

A₁ (x₁ ; y₁)   и   A₂ (x₂ ; y₂)

вычисляется по формуле

      Доказательство. Рассмотрим рисунок 6.

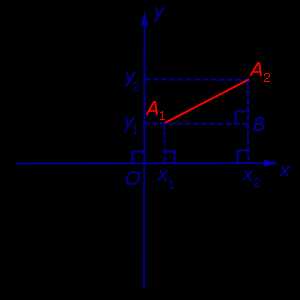
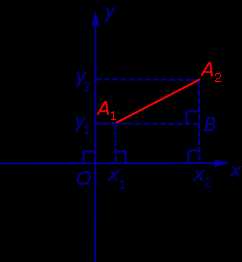
Рис.6

      Поскольку в прямоугольном треугольнике   A₁A₂B   длина катета   A₁B   равна   | x₂ – x₁|    а длина катета   A₂B   равна   | y₂ – y₁| ,   то по теореме Пифагора

| A1A2|2 = = ( x2 – x1)2 + ( y2 – y1)2 .

(1)

     Следовательно,

что и требовалось доказать.

Уравнение окружности на координатной плоскости

      Рассмотрим на координатной плоскости   Oxy   (рис. 7) окружность радиуса   R   с центром в точке   A₀ (x₀ ; y₀) .

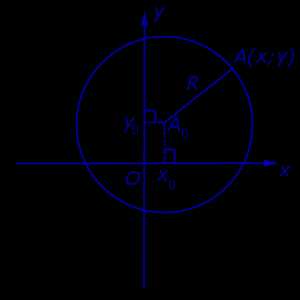
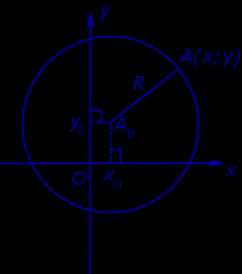
Рис.7

      Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

( x – x₀)² + ( y – y₀)² = R².

Уравнение (2) и есть искомое уравнение окружности радиуса   R   с центром в точке   A₀ (x₀ ; y₀) .

      Следствие. Уравнение окружности радиуса   R   с центром в начале координат имеет вид

x² + y² = R².

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru