Обозначение производной – Что такое производная 🚩 для чего нужна производная 🚩 Математика

Производная

График функции, обозначены черным цветом, и касательная к нему (красный цвет). Значение тангенса угла наклона касательной является значением производной в указанной точке.

Производная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как граница отношения приращения функции к приращению ее аргумента когда прирост аргумента направляется к нулю (если такая граница существует). Функцию, имеет конечную производную, называют дифференцируемой.

1. Определение

Пусть в некотором окрестности точки x ₀ определена функция f. Если мы возьмем произвольное число x в этом округе, то прирост аргумента (обозначается Δx) в этом случае определяется как x-x _0, а прирост функции (Δy) — как f (x)-f (x _0). Тогда, если существует предел , То она называется производной функции f в точке x _0.

Производной функцией данной функции называется функция, в любой точке области определения равна производной данной функции в этой точке.

2. Дифференцировки и производная

Дифференцирование — это метод вычисления соотношения прироста зависимой переменной y по отношению к приросту независимой переменной x. Это соотношение приростов называется производной функции y по переменной x. Если говорить более точно, зависимость y от x означает, что y функция от x. Эта функциональная зависимость часто обозначается y = ? (x), где ? обозначает функцию. Если x и y действительные числа, и если график функции y изображен относительно x, производная равна наклона касательной к этому графику в каждой точке.

Простейший случай когда y — линейная функция от x, значит график функции y относительно x прямая линия. В таком случае, y = ? (x) = m x + b, для вещественных чисел m и b, и наклон m определяется так

где символ Δ (греческая буква в верхнем регистре дельта) — это сокращение для «изменения в». Эта формула справедлива том, что

y + Δ y = ? (x + Δ x) = m (x + Δ x) + b = m x + b + m Δ x = y + m Δ x.

Из этого следует, что Δ y = m Δ x.

Получили точное значение наклона прямой линии. Если функция ? не линейная (т.е. график функции не прямая линия), тогда прирост y разделен на прирост x меняется: дифференцирование это способ вычисления точного значения видношенння приростов для любого значения x.

Соотношение приростов как предельная величина

Рисунок 2. Секущая линия к кривой y = ? (x) задается точками (x, ? (x)) and (x + h, ? (x + h))

Рисунок 3. Касательная как предел секущих линий

Идея состоит в том, см.. рисунки 1-3, чтобы вычислить отношение приращений как предельную величину Δ y / Δ x когда Δ x становится бесконечно малым.

Если использовать обозначения Лейбница, тогда бесконечно малый прирост x обозначается как dx, а производная функции y по переменной x записывается:

выглядит как отношение двух бесконечно малых величин. (Это выражение читается так: «производная функции y по переменной x» или «dy по dx»)

2.1. Объяснение определения

Пусть ? — функция действительных чисел. В классической геометрии, касательная к графику функции ? для действительного числа a была единственная линия через точку (a, ? (a)), не пересекающийся с графиком функции ? трансверсально, значит эта линия не проходит через график. Производная функции y по переменной x в точке a, с геометрической точки зрения, это наклон касательной линии к графику функции ? в точке a. Наклон касательной очень близок к наклону линии, проходящей через точку (a, ? (a)) и другую близкую точку на графике, например (A + h, ? (a + h)) . Такие линии называются секущими. Значение h близкое к нулю дает хорошее приближение для наклона касательной, а чем меньше значение h, в общем случае, тем лучше будет приближение. Наклон m секущей линии равна разности значений y для этих точек разделить на разность значений x, т.е.

Это выражение — это отношение приростов Исаака Ньютона. Производная — это значение отношения приростов в случае когда январе линии приближаются к касательной. Строго говоря, производная функции ? в точке a это граница :

отношение приростов когда h стремится к нулю, если такая граница существует. Если граница существует тогда ? — дифференцированная в точке a. Здесь ? ‘(a) одно из нескольких возможных обозначений производной ( см..ниже)

Запишем эквивалентный выражение, для производной справедливо равенство

также подвергается интуитивном пониманию (см. рис.1), где касательная линия ? в точке a дает наилучшее линейное приближение

для ? у точки a (например, для малых h). Если подставить 0 вместо h в отношений приростов то получим деление на ноль, значит наклон касательной линии нельзя вычислить таким способом. Зато запишем Q (h), отношение приростов как функцию от h:

Q (h) — это наклон секущей линии между точками (a, ? (a)) and (a + h, ? (a + h)). Если ? — непрерывная функция, т.е. если график функции нет разрывов, тогда Q также непервна функция начиная с точки h = 0. Если существует предел , Т.е. если существует способ вычислить значение для Q (0), значит график функции Q непрерывный, тогда функция ? дифференцирована в точке a, и ее производная в точке a равна Q (0).

На практике, существование непервного продолжение отношения приростов Q (h) в точке h = 0 показывают по-другому: меняют числитель таким образом, чтобы сократить h в знаменателе. Этот прроцес может быть длинным и скучным для сложных функций, поэтому в таких случаях используют много упрощений.

2.2. Пример

Квадратная функция ? (x) = x ? — дифференцированная в точке x = 3 и ее производная в этой точке равна 6. Этого результата можно достичь, если вычислить границу отношения приростов ? (3) при h стремится к нулю:

Теперь можем вычислить границу, если подставим вместо h ноль:

Следовательно, наклон графика квадратной функции в точке (3, 9) равен 6, а ее производная в точке x = 3 равна ? ‘(3) = 6. Обобщая, если провести похожие вычисления то получим, что квадратная функция в точке x = a равно ? ‘(a) = 2 a.

2.3. Непрерывность и дифференцируемость

Эта функция не имеет производной в указанной точке, поскольку функция не является непрерывной в этой точке.

Если y = ? (x) — дифференцированная в точке a, тогда ? также быть непрерывная в точке a. Например, выберем точку a и пусть ? будет шаговой функцией, равной 1, для всех x меньших чем a и равен другому значению, скажем 10, для всех x, которые больше или равны a. Ƒ не имеет производной в точке a. Если h — отрицательное, тогда a + h находится на нижней ступеньке функции, тогда секущая линия от a до a + h очень круто поднимается вверх и если h стремится к нулю тогда наклон линии стремится к бесконечности. Если h положительное, тогда a + h на верхней ступеньке и секущая линия от a до a + h имеет наклон, равный нулю. Согласно январе линии не образуют единый наклон, следовательно пределом отношения приростов не существует.

Функция абсолютной величины является непрерывная, но от нее нельзя получить производную в точке x = 0, так наклон касательной приближается к различным значениям по разные стороны от данной точки.

Однако функция непрерывна в точке, она не обязательно дифференцирована в этой точке. Например, функция абсолютной величины y = | x | является неперрервною в точке x = 0, но не дифференцируема в этой точке. Если h положительное, тогда наклон секущей линии от 0 до h равен единице, если h отрицательное, тогда наклон секущей линии от 0 до h равна -1. На графике эту точку видно как «зубец» в точке x = 0. Также функции графику без «зубцов» не является дифференцированы в точке где касательная линия является вертикальная: например функция y = ³ √ x не является дифференцированная в точке x = 0.

Подведем итоги: чтобы получить производную от функции ? необходимое условие чтобы функция ? была непрерывной, но только этого недостаточно.

Большинство функций, встречающихся на практике имеют производные во всех точках, или почти во всех точках. Ранее в начале изучения математического анализа, многие математики предполагали, что непрерывная функция дифференцируема в большинстве точек. Для мягких условиях, например если есть монотонную функцию или Липщицову функцию эта формулировка справедливо. Однако в 1872 Вейерштрасс нашел первый пример функции, непрерывной всюду, но не дифференцированной в одной точке. Эта функция известна как Вейерштрасова. В 1931 году Стефан Банах доказал, что множество функций, имеющих производную хотя бы в какой-то точке есть множество первой категории в пространстве всех непрерывных функций. ^[1]

3. Обозначение

Производная обозначается как , Что произносится «эф-штрих от икс».

Функция, имеющая конечное производную в точке x, называется дифференцированной в точке x.

Производная также сказывается, как отношение дифференциалов . В физике для обозначения производных по времени используют точку над переменной, например .

3.1. Обозначение Лейбница

Обозначение производной предложенное Лейбницем было одним из первых. Оно широко используется до сих пор. Если выражение y = ? (x) рассматривается как функциональная зависимость между зависимой и независимой переменными. Тогда первая производная обозначается как:

производные высшего порядка обозначаются следующим образом

для производной n-го порядка y = ? (x) (по переменной x). Це является сокращение для многократного применения оператора производной. Например,

Через обозначение Лейбница мы можем записать производную функции y в точке x = a двумя различными способами:

Обозначение Лейбница позволяет указывать переменную дифференцирования (в знаменику). Это особенно важно для частичного дифференцировки. В таком обозначении также легче запомнить цепное правило :

3.2. Обозначение Лагранжа

Обозначение Лагранжа одно из самых распространенных современных обозначений для дифференцировки, впервые использовал Жозеф-Луи Лагранж. Для обозначения производной используют знак штрих, таким образом производная функции ? (x) обозначается ? ‘(x) или просто ?’ подобным образом вторая и третья производная обозначаются

and

Начиная отсюда некоторые авторы применяют римские цифры:

для четвертой производной, тогда как другие авторы ставят цифру порядка производной в скобки:

Последняя запись обобщает обозначения ? ⁽ⁿ⁾ для производной функции ? n-го порядка — такое обозначение особенно удобно когда мы говорим о производную как о функции, в этом случае применение обозначения Лейбница может быть слишком громоздким.

3.3. Обозначение Ньютона

Обозначение Ньютона для дифференцировки, также называется точечное обозначение, ставят точку над названием функции для обозначения производной. Если y = ? (t), тогда

и

означает соответственно первую и вторую производную функции y по переменной t. Такое обозначение применяется почти исключительно для производных по времени, т.е. независимая переменная функции является время. Оно очень распространено в физике и математическим дисциплинам связанных с физикой, например дифференциальные уравнения. Хотя такое обозначение становится проблематичным в использовании для производных высокого порядка, на практике нужны только несколько первых производных.

4. Вычисление производной

Производную функции можно, теоретически, вычислять используя границу отношения приростов. На практике, достаточно знать производные ограниченного количества простых функций, тогда можно вычислить сложные случаи с помощью правил дифернециювання.

4.1. Производные простых функций

В большинстве случаев для того чтобы вычислить производную нужно знать производные определенных распространенных функций. Ниже приведен неполный перечень из производных некоторых важнейших функций одной действительной переменной.

,

где r — любое действительное число, тогда

,

для любых случаев, когда определенная функция. Например, если r = 1/2, тогда

.

здесь функция определена только для положительных x. Если r = 0, это правило повторяет правило константы.

5. Пример нахождения производной по определению

Пусть имеется функция y = c, где c — некоторая константа. Тогда при любом x ₀ и при любом Δx изменение (прирост) функции равна нулю, следовательно и производная такой функции равен нулю.

6. Производные высших (старших) порядков

Понятие производной произвольного порядка задается рекуррентным:

• производная нулевого порядка — сама функция
• производная n-го порядка для натурального n, что больше 0, — производная производной (n-1)-го порядка

Иногда вместо «производная n-го порядка» говорят «n-я производная».

Производная n-го порядка функции f обычно обозначается как f ⁽ⁿ⁾ (x)

• если n малое (1, 2, 3) — то используется соответствующее рисков, f ‘(x), f» (x), f»’ (x), произносится как «эф-штрих от икс»; о второй — «эф-два-штрихи от икс».
• Можно встретить историческое обозначение производной с помощью римской системы счисления (первая производная: f ‘(x), вторая: f ^II (x), шестнадцатая: f ^XVI (x)).
• В физике также встречается обозначение производной второго порядка по времени в виде двух точек над переменной: .

7. Геометрический смысл производной

Значение производной функции в точке равно значению углового кофициента касательной к кривой в точке с абсциссой .

Уравнение касательной к кривой в точке M ( ) Имеет вид:

y = f (x) = tga

8. Физический смысл производной

Производная от пути по времени равна мгновенной скорости движения материальной точки.

См.. также

Примечания

1. Banach, S. (1931), «Uber die Baire’sche Kategorie gewisser Funktionenmengen», Studia. Math. (3): 174-179. . Cited by Hewitt, E and Stromberg, K (1963), Real and abstract analysis, Springer-Verlag, Theorem 17.8

nado.znate.ru

Обозначения производной в физике

Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.

Во-первых,меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами:

x(t) = 1 + 12t 3t2;	(1.13)
v(t) = 12 6t:	(1.14)

Таким образом, аргументом функции теперь является время t, а буква x отныне обозначает функцию координату точки.

Во-вторых,меняется обозначение производной. Штрих в физике зарезервирован для других целей, и вместо него мы используем точку над буквой:

производная функции x(t) обозначаетсяx(t)

(1.15)

(читается ¾икс с точкой¿).

Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:

dx		(1.16)
производная функции x(t) обозначается
	dt

(читается ¾дэ икс по дэ тэ¿).

Остановимся подробнее на смысле обозначения (1.16). Математик понимает его двояко либо как предел:

	dx	= lim	x	= lim	x(t + t) x(t)	;	(1.17)
	dt		t		t
		t!0		t!0

либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.

Физик, не скованный требованиями математической строгости, понимает обозначение (1.16) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (1.17) с устраивающей нас точностью.

И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло.

Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.

Производная x(t) физической величины x(t) снова является функцией времени, и эту функцию снова можно продифференцировать найти производную производной, или вторую производную функции x(t). Вот одно обозначение второй производной:

вторая производная функции x(t) обозначаетсяx•(t)

(читается ¾икс с двумя точками¿), а вот другое:

d2x

вторая производная функции x(t) обозначаетсяdt2

(читается ¾дэ два икс по дэ тэ квадрат¿ или ¾дэ два икс по дэ тэ дважды¿).

studfiles.net

Производная функции — это… Что такое Производная функции?

У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.

История

В классическом дифференциальном исчислении производная чаще всего определяется через понятия теории пределов, однако исторически теория пределов появилась позже дифференциального исчисления.

Русский термин «производная функции» впервые употребил В. И. Висковатов.^[1]

Определение

Пусть в некоторой окрестности точки определена функция Производной функции называется такое число , что функцию в окрестности можно представить в виде

если существует.

Определение производной функции через предел

Пусть в некоторой окрестности точки определена функция Производной функции в точке называется предел, если он существует,

Общепринятые обозначения производной функции в точке

Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).

Дифференцируемость

Производная функции в точке , будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция является дифференцируемой в точке тогда и только тогда, когда её производная в этой точке существует и конечна:

Для дифференцируемой в функции в окрестности справедливо представление

при

Замечания

Геометрический и физический смысл производной

Тангенс угла наклона касательной прямой

Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Если функция имеет конечную производную в точке то в окрестности её можно приблизить линейной функцией

Функция называется касательной к в точке Число является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть  — закон прямолинейного движения. Тогда выражает мгновенную скорость движения в момент времени Вторая производная выражает мгновенное ускорение в момент времени

Вообще производная функции в точке выражает скорость изменения функции в точке , то есть скорость протекания процесса, описанного зависимостью

Производные высших порядков

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

Если функция дифференцируема в , то производная первого порядка определяется соотношением

Пусть теперь производная -го порядка определена в некоторой окрестности точки и дифференцируема. Тогда

Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от   может иметь в некоторой точке частные производные по той же или по любой другой переменной. Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).

  или  

  или  

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

Способы записи производных

В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:

• Лагранжа , при этом для малых n часто используют штрихи и римские цифры:

и т. д.

Такая запись удобна своей краткостью и широко распространена; однако штрихами разрешается обозначать не выше третьей производной.

• Лейбница, удобная наглядной записью отношения бесконечно малых (только в случае, если  — независимая переменная; в противном случае обозначение верно лишь для производной первого порядка):

• Ньютона, которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например:

 — производная первого порядка по при , или  — вторая производная по в точке и т. д.

, или иногда .

• В вариационном исчислении и математической физике часто применяется обозначение , ; для значения производной в точке — . Для частных производных обозначение то же, поэтому смысл обозначения определяют из контекста.

Конечно, при этом необходимо не забывать, что служат все они для обозначения одних и тех же объектов:

Примеры

• Пусть . Тогда

• Пусть . Тогда если то

где обозначает функцию знака. Если то а следовательно не существует.

Правила дифференцирования

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x)

 — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

, то

• Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):

где  — биномиальные коэффициенты.

Следующие свойства производной служат дополнением к правилам дифференцирования:

Доказательство  

Таблица производных некоторых функций

Производная вектор-функции по параметру

Определим производную вектор-функции по параметру:

.

Если производная в точке существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут .

Свойства производной вектор-функции (всюду предполагается, что производные существуют):

См. также

Примечания

Литература

• В. Г. Болтянский, Что такое дифференцирование?, «Популярные лекции по математике», Выпуск 17, Гостехиздат 1955 г., 64 стр.
• В. А. Гусев, А. Г. Мордкович «Математика»
• Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
• В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1

dic.academic.ru

Обозначения производной в физике

Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.

Во-первых,меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами:

x(t) = 1 + 12t 3t2;	(1.13)
v(t) = 12 6t:	(1.14)

Таким образом, аргументом функции теперь является время t, а буква x отныне обозначает функцию координату точки.

Во-вторых,меняется обозначение производной. Штрих в физике зарезервирован для других целей, и вместо него мы используем точку над буквой:

производная функции x(t) обозначаетсяx(t)

(1.15)

(читается ¾икс с точкой¿).

Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:

dx		(1.16)
производная функции x(t) обозначается
	dt

(читается ¾дэ икс по дэ тэ¿).

Остановимся подробнее на смысле обозначения (1.16). Математик понимает его двояко либо как предел:

	dx	= lim	x	= lim	x(t + t) x(t)	;	(1.17)
	dt		t		t
		t!0		t!0

либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.

Физик, не скованный требованиями математической строгости, понимает обозначение (1.16) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (1.17) с устраивающей нас точностью.

И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло.

Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.

Производная x(t) физической величины x(t) снова является функцией времени, и эту функцию снова можно продифференцировать найти производную производной, или вторую производную функции x(t). Вот одно обозначение второй производной:

вторая производная функции x(t) обозначаетсяx•(t)

(читается ¾икс с двумя точками¿), а вот другое:

d2x

вторая производная функции x(t) обозначаетсяdt2

(читается ¾дэ два икс по дэ тэ квадрат¿ или ¾дэ два икс по дэ тэ дважды¿).

studfiles.net

Производная функции. Геометрический и физический смысл

Категория: Справочные материалы

Елена Репина 2013-08-06 2014-01-11

Определение производной

 

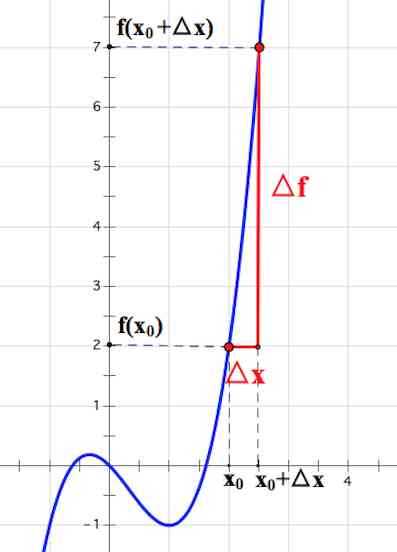
Производной функции в точке называется предел отношения приращения функции к приращению аргумента при , если этот предел существует.

 

 

 

 

Пример: 

Но нет необходимости каждый раз пользоваться этим определением для нахождения производной…

Работу нам упростит таблица производных и правила дифференцирования.

 

Геометрический смысл производной

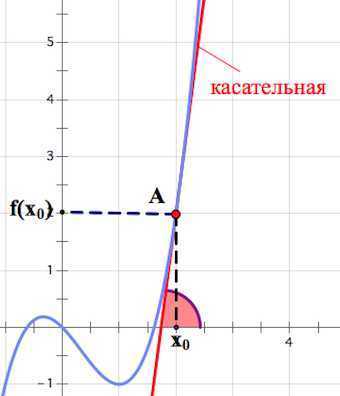
Если мы рассмотрим прямоугольный треугольник , то заметим, что есть .

А при стремлении к нулю, точка будет приближаться к точке и секущая «превратится» в касательную к графику функции в точке .

 

Поэтому геометрический смысл производной таков:

Производная  в точке  () равна тангенсу угла   наклона   касательной к графику функции в этой точке:

,

где – угол наклона касательной (проведенной  к в т. )

 

Физический смысл производной

 

Если точка движется вдоль оси и ее координаты изменяются по закону , то мгновенная скорость точки:

,

а ускорение:

Пример:

Материальная точка движется прямолинейно по закону , где  — расстояние от точки отсчета в метрах,  — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени .

Решение:

м/с

Ответ: 60.

Уравнение касательной

 

Уравнение касательной к графику в точке :

Пример:

Составить уравнение касательной к графику функции  в точке .

Решение:

1.

2.

3.

Ответ:

Смотрите также  «Производная функции в точке. Знак производной и монотонность функции»

Автор: egeMax | Нет комментариев

egemaximum.ru

Что такое производная?

Производной функции называется базовый элемент в дифференциальном исчислении. Этот элемент и является определенным результатом применения какой-то определенной операции дифференцирования по отношению к исходной функции.

Определение производной

Для того, чтобы понять, что такое производная, необходимо знать, что название функции происходит непосредственно от слова «произведенная», то есть образовавшаяся от другой какой-либо величины. При этом сам процесс определения производной какой-то определенной функции имеет название — «дифференцирование». 

Наиболее распространенный метод представления и определения, при использовании теории пределов, несмотря на то, что она появилась гораздо позже дифференциальных исчислений. По определению данной теории, производной называется предел в отношении приращения функций к приращению аргумента, в случае если таковой предел имеется, и при условии, что данный аргумент стремится к нулевому значению. 

Принято считать, что, впервые, термин и понятие «производная» употребил в своих трудах известный русский математик по имени В.И.Висковатов.

Рассмотренный ниже небольшой пример поможет наглядно понять, что такое производная.

1. Для поиска производной функции f в точке х, нам нужно определить значения данной функции непосредственно в точке х, а так же в точке х+Δх. Причем Δx – это приращения аргумента х.
2. Найти приращение для функции у приравненное к f(х+Δх) – f(х).
3. Записать производную при помощи предела отношения f’ = lim(f(x+Δх) – f(x))/Δх, исчислить при Δх → 0.

Обычно производная обозначается знаком апострофа — «’» непосредственно над дифференцируемой функцией. Обозначение в виде одного апострофа обозначает первую производную, в виде двух – вторую. Производную наивысшего порядка принято задавать соответствующей цифрой, к примеру f^(n) – что означает производную n-го порядка, где буква «n» – целое число , которое ? 0. Производная нулевого порядка — это и есть сама дифференцируемая функция.

С целью облегчения дифференцирования усложненных функций, были разработаны и приняты определенные правила дифференцирования функций:

elhow.ru

Обозначения производной в физике

Переходя к физическим приложениям производной, мы будем использовать несколько иные обозначения те, которые приняты в физике.

Во-первых,меняется обозначение функций. В самом деле, какие функции мы собираемся дифференцировать? Этими функциями служат физические величины, зависящие от времени. Например, координата тела x(t) и его скорость v(t) могут быть заданы формулами:

x(t) = 1 + 12t 3t2;	(13)
v(t) = 12 6t:	(14)

Таким образом, аргументом функции теперь является время t, а буква x отныне обозначает функцию координату точки.

Во-вторых,меняется обозначение производной. Штрих в физике зарезервирован для других целей, и вместо него мы используем точку над буквой:

производная функции x(t) обозначаетсяx(t)

(15)

(читается ¾икс с точкой¿).

Имеется ещё одно обозначение производной, очень распространённое как в математике, так и в физике:

dx		(16)
производная функции x(t) обозначается
	dt

(читается ¾дэ икс по дэ тэ¿).

Остановимся подробнее на смысле обозначения (16). Математик понимает его двояко либо как предел:

	dx	= lim	x	= lim	x(t + t) x(t)	;	(17)
	dt		t		t
		t!0		t!0

либо как дробь, в знаменателе которой стоит приращение времени dt, а в числителе так называемый дифференциал dx функции x(t). Понятие дифференциала не сложно, но мы не будем его сейчас обсуждать; оно ждёт вас на первом курсе.

Физик, не скованный требованиями математической строгости, понимает обозначение (16) более неформально. Пусть dx есть изменение координаты за время dt. Возьмём интервал dt настолько маленьким, что отношение dx=dt близко к своему пределу (17) с устраивающей нас точностью.

И тогда, скажет физик, производная координаты по времени есть попросту дробь, в числителе которой стоит достаточно малое изменение координаты dx, а в знаменателе достаточно малый промежуток времени dt, в течение которого это изменение координаты произошло.

Такое нестрогое понимание производной характерно для рассуждений в физике. Далее мы будем придерживаться именно этого физического уровня строгости.

Производная x(t) физической величины x(t) снова является функцией времени, и эту функцию снова можно продифференцировать найти производную производной, или вторую производную функции x(t). Вот одно обозначение второй производной:

вторая производная функции x(t) обозначаетсяx•(t)

(читается ¾икс с двумя точками¿), а вот другое:

d2x

вторая производная функции x(t) обозначаетсяdt2

(читается ¾дэ два икс по дэ тэ квадрат¿ или ¾дэ два икс по дэ тэ дважды¿).

studfiles.net