Область определения с модулем – Графики функций, содержащих модуль — ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ — РАЦИОНАЛЬНЫЕ ДРОБИ — ПОУРОЧНЫЕ РАЗРАБОТКИ ПО АЛГЕБРЕ 8 КЛАСС — Поурочные планы — разработки уроков — авторские уроки — план-конспект урока

Область определения и множество значений

$ |x| = \begin{cases} x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0 \\ -x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x А графиком является

Свойства:

1) $|x| \geq 0$
2) $|x|=0 \longleftrightarrow x=0$
3) $|xy|=|x||y|$
4) $|x+y| \leq |x|+|y|$
5) $||x||=|x|$
6) $|-x|=|x|$
7) $|x-y|=0 \longleftrightarrow x=y$
8) $|x-y| \leq |x-z|+|z-y|$
9) $|\dfrac{x}{y}|=\dfrac{|x|}{|y|} \,\,\,\,\, y \neq 0$
10) $ ||x|-|y|| \leq |x-y|$

Для того, чтобы найти область определения и множество значений функции, состоящей из абсолютных значений, необходимо учитывать вышеуказанные свойства.
Пример:
Найти область определения и множество значений $f(x)=\dfrac{x+2}{|x|-2}$
Решение:

$|x|-2=0 \rightarrow |x|=2 \rightarrow x=\pm 2$

Таким образом

$D_f=\mathbb{R} — \lbrace \pm 2 \rbrace$

С другой стороны $f(x)=\dfrac{x+2}{|x|-2}= \begin{cases} \dfrac{x+2}{x-2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x \geq 0 \\ \\ \dfrac{x+2}{-x-2}=-1 \,\,\,\,\,\,\,\,\, x So

$x \geq 0 \rightarrow y=\dfrac{x+2}{x-2} \rightarrow x=\dfrac{2(y+1)}{y-1} \geq 0$

Следовательно $\begin{cases} x \geq 0 \,\,\,\,\,\,\,\, y\in (-\infty,-1] \cup (1,+\infty) \\ \\ x

$\rightarrow R_f=(-\infty,-1] \cup (1,+\infty)$

Вот график $f$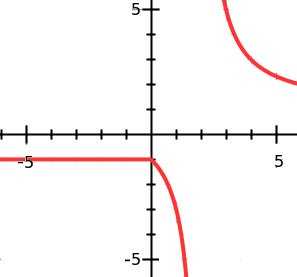
Пример:
Найти область определения и множество значений $f(x)=\dfrac{1}{\sqrt{|x+1|-4}}$.
Решение:
$|x+1|-4 >0 \,\, \rightarrow|x+1|>4 \rightarrow$ $\begin{cases} x+1>4 \rightarrow x>3 \\ x+1

$D_f=(-\infty,-5) \cup (3,+\infty)$

Отметим, что

$y=\dfrac{1}{\sqrt{|x+1|-4}}>0$

С другой стороны

$y^2=\dfrac{1}{|x+1|-4} \rightarrow |x+1|=\dfrac{1}{y^2}+4>4 \rightarrow \dfrac{1}{y^2}>0 \rightarrow y \in (-\infty,0)\cup(0,+\infty)$

Следовательно

$y \in (\mathbb{R}-\lbrace 0 \rbrace ) \cap ( \mathbb{R} ^+ )$

Значит

$R_f=(0,+\infty)=\mathbb{R}^+$

Вот график $f$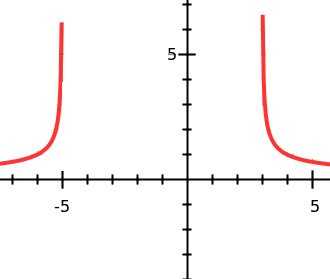

Упражнения

Найти область определения и множество значений.

1) $y=\dfrac{x}{|x-1|}$
2) $y=\dfrac{x-4}{|x|-4}$
3) $y=\dfrac{\sqrt{\sqrt{(x+1)^2}-1}}{\sqrt{|x+1|-1}}$
4) $y=\dfrac{\sqrt{(x-1)^2}}{x-1}$
5) $y=\sqrt{-|x+1|}$
6) $y=\dfrac{\sqrt{(x^2-3x+2)^2}}{\sqrt{(x-2)^2}}$
7) $y=|x-1|+|x|+|x+1|$

Общий вид показательной функции $y=a^{u(x)}$, где $a>0$, а $u(x)$ — функция. Нахождение области определения и множества значений показательной функции зависит от $u(x)$.
В специальном виде, если $a=e \simeq 2.71828\cdots$, то $y=e^{u(x)}$. Для лучшего понимания $y=a^{u(x)}$ его можно переписать как $y=e^{u(x)\log_e a}$. Отметим, что $\log_e a$ обозначается как $\ln a$. Следовательно,

$y=e^{u(x)\ln a}$

Согласно этому определению $a>0$ является достаточным условием для определения показательной функции, если $u(x)$ вещественная функция.

Совет:

$y=e^x=\lim_{n \rightarrow \infty} (1+\dfrac{1}{n})^nx=1+\dfrac{x}{1!}+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\cdots\,\,\,\,\, (n \in \mathbb{N})$

Пример:
Найти область определения и множество значений $f(x)=2^{-x^{-2}}$.
Решение:
Отметим, что если $x=0$, то знаменатель дроби неопределен. Следовательно,

$D_f=\mathbb{R}-\lbrace 0 \rbrace$

Определим множество значений:
Для начала отметим, что $y>0$. С другой стороны

$\log y=-\dfrac{1}{x^2}\log 2 \rightarrow x^2=-\dfrac{\log 2}{\log y} \rightarrow x=\pm \sqrt{-\dfrac{\log 2}{\log y}} \rightarrow \dfrac{\log 2}{-\log y}>0 \rightarrow$

$ \log y 0 \rightarrow 0 Значит

$R_f=(0,1)$

График этой функции

Пример:
Найти область определения и множество значений $f(x)=3^{-x}$.
Решение:
Очевидно, что $D_f=\mathbb{R}$. С другой стороны

$y=\dfrac{1}{3^x} \rightarrow 3^x=\dfrac{1}{y} \rightarrow x=\log_3 \dfrac{1}{y}$

$R_f= \lbrace y| y \in \mathbb{R},\dfrac{1}{y}>0 \rbrace = \lbrace y \in \mathbb{R} | y>0 \rbrace =(0,+\infty)$

$R_f=\mathbb{R^+}$

График $f$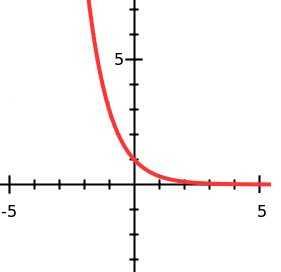

Упражнения

Найти область определения и множество значений.

1) $y=e^{-\dfrac{1}{\sqrt{x-\lfloor x \rfloor}}}$
2) $y=3^{\dfrac{\sqrt{8}}{2}}$
3) $y=5^{-x^2}$
4) $y=5^{\lfloor x \rfloor + \l

www.math10.com

Уравнения с модулем: учет области значений

23 мая 2014

Очень часто в уравнениях под знаком модуля стоят довольно сложные конструкции, которые было бы крайне затруднительно раскрывать, а затем решать «напролом». Для таких случаев существует множество приемов и замечаний, позволяющих значительно ускорить вычисления.

Одним из таких приемов является учет области значений модуля (учителя называют это решение методом следствий). Суть его можно описать одним простым предложением: «Сумма неотрицательных чисел равна нулю тогда и только тогда, когда каждое из этих чисел равно нулю».

Сегодня мы продолжаем изучать конструкции, содержащие знак модуля функции и переходим уже к более сложным конструкциям, когда ихдва, либо само уравнение содержит нестандартную функцию.

Немного теории

Для начала вспомним определение модуля: модулем числа $x$ называется либо само это число (при условии, что оно неотрицательное), либо минус это число, если оно отрицательно:

\[\left| x \right|=\left\{ \begin{align}& x,x\ge 0 \\& -x,x<0 \\\end{align} \right.\]

Данная запись является алгебраическим определением, потому что здесь используется только алгебраическая терминология и никак не привлекается геометрия. И именно это определение позволяет нам заключить следующий факт: модуль числа всегда неотрицателен:

\[\left| x \right|\ge 0\]

Именно поэтому его иногда еще называют абсолютным значением, т.е. расстоянием от 0 до этого числа на числовой прямой. И именно тот факт, что модуль функции всегда является неотрицательным числом, позволяет решить целый класс задач, которые иначе решались бы весьма проблематично.

Решаем реальные задачи

Пример № 1

\[\left| x-{{x}^{3}} \right|+\left| {{x}^{2}}+x-2 \right|=0\]

Чтобы решить такое выражение, давайте для начала вспомним, как решается простейшая конструкция с модулем, т.е уравнение вида $\left| f \right|=g$.

Решаются она довольно просто. Рассматривается два случая: в первом случае $f$ неотрицательно — в этом случае модуль функции снимается без всяких изменений и получается, что $f$ равно $g$. А во втором случае $f$ отрицательно — в этом случае модуль раскрывается со знаком «минус», как мы уже знаем из определения. Запишем совокупность систем:

\[\left| f \right|=g=>\left[ \begin{align}& \left\{ \begin{align}& f\ge 0 \\& f=g \\\end{align} \right. \\& \left\{ \begin{align}& f<0 \\& -f=g \\\end{align} \right. \\\end{align} \right.\]

Но все это работает только при условии, что модуль функции в выражении один, а у нас сегодня сразу два. Что делать в такой ситуации?

Давайте заметим, что при сложении двух модулей возникает выражение, значение которого 0. Но, с другой стороны, мы можем записать следующее:

\[\left| x-{{x}^{3}} \right|\ge 0\]

\[\left| {{x}^{2}}+x-2 \right|\ge 0\]

В этом случае сумма вышеописанных двух элементов также будет давать некое число (назовем его $k$), которое больше или равняется 0. При этом от нас требуется, чтобы оно строго равнялось 0. А это значит, что нас устроит только тот вариант, когда каждый из модулей равен 0, т.е. мы можем записать:

\[\left| x-{{x}^{3}} \right|=0\]

\[\left| {{x}^{2}}+x-2 \right|=0\]

Другими словами, сумма двух чисел, каждое из которых не меньше 0, дает в сумме ноль только в том случае, когда каждое из них равняется 0, т.е. требования должны выполняться одновременно. Поэтому запишем систему:

\[\left\{ \begin{align}& \left| x-{{x}^{3}} \right|=0 \\& \left| {{x}^{2}}+x-2 \right|=0 \\\end{align} \right.\]

Модуль функции равен 0, когда подмодульное выражение равно 0, т.е:

\[\left\{ \begin{align}& x-{{x}^{3}}=0 \\& {{x}^{2}}+x-2=0 \\\end{align} \right.\]

Давайте решим каждое из полученных выражений отдельно. Решаем первое:

\[x\left( {{1}^{2}}-{{x}^{2}} \right)=0\]

\[x\left( 1-x \right)\left( 1+x \right)=0\]

\[{{x}_{1}}=0\]

\[{{x}_{2}}=1\]

\[{{x}_{3}}=-1\]

При трех таких значениях тождество обнуляется.

Теперь разберемся со вторым выражением. Будем решать его при помощи формулы Виета:

\[{{x}^{2}}+x-2=0\]

\[\left( x+2 \right)\left( x-1 \right)=0\]

\[{{x}_{1}}=-2\]

\[x=1\]

А теперь вспоминаем, что мы решаем систему уравнений, т.е. нужно из первого и из второго наборов выбрать корни, которые принадлежат каждому из этих наборов. Очевидно, что такой корень только один — $x=1$.

Итого решением первого выражения является единственный корень $x=1$.

Как видите, такое решение оказалось существенно проще стандартного подхода. Здесь достаточно просто заметить,что сумма двух неотрицательных чисел равняется 0 только тогда, когда каждое из этих чисел имеет значение 0.

Пример № 2

Переходим ко второй конструкции:

\[\left| x-2 \right|=-{{x}^{6}}\]

На первый взгляд, можно сказать, что данная конструкция является простейшим уравнением. И, строго говоря, оно хорошо решается по выше записанной формуле, т.е. переходом от выражения с модулем функции к совокупности двух систем. Однако нас смущает степенная функция — степень слишком большая. Поэтому давайте заметим, что функция $f\left( x \right)={{x}^{6}}$ является не просто четной, но и еще неотрицательной на всей числовой оси. А это значит, что $-{{x}^{6}}$ всегда будет либо отрицательной, либо равняться 0. Однако с другой стороны от знака равенства у нас стоит модуль функции — а он всегда неотрицателен. Это значит что, слева значение больше или равно нулю, а справа — меньше или равно. И от нас требуется узнать, когда эти значения друг другу тождественны. Очевидно, что такими они могут быть только тогда, когда каждое из них равняется 0, потому что в противном случае они будут лежать по разные стороны от разделяющего 0, т.е. $\left| x-2 \right|$ будет постоянно отклоняться вправо, а $-{{x}^{6}}$ — влево. Поэтому наше выражением может быть переписано следующим образом:

\[\left\{ \begin{align}& \left| x-2 \right|=0 \\& -{{x}^{6}}=0 \\\end{align} \right.\]

Давайте решим эти конструкции:

\[\left\{ \begin{align}& x-2=0 \\& {{x}^{6}}=0 \\\end{align} \right.\]

Решаем каждое из этих выражений:

\[\left\{ \begin{align}& x=2 \\& x=0 \\\end{align} \right.\]

Мы получаем, что корень должен быть одновременно равен и 2 и 0. Это невозможно, поэтому решением данного выражения является пустое множество. Пусть вас не смущают подобные ответы при решении задач с модулями. Как и при работе с любыми другими функциями, накладывающими ограничения на область определения или значения в рамках задачи, в процессе решения сложных выражений с модулями функции вполне может оказаться, что этих решений просто не существует.

Ключевые моменты

1. Сумма двух неотрицательных чисел равна нулю тогда, когда каждое из этих чисел равно нулю. В результате уравнение, которое само по себе далеко не тривиальное, разбивается на систему из двух отдельных уравнений, каждое из которых решается существенно проще.
2. Тот факт, что модуль сам по себе является неотрицательным значением, можно использовать и иначе, например, когда с одной стороны стоит модуль функции (эта сторона неотрицательна), а с другой стороны — функция, которая меньше нуля или равна нулю. В этом случае все уравнение сводится к системе из двух уравнений, каждое из которых легко решается.

Как пример, второе вырадением может быть сведено к равенству первого вида следующим образом:

\[\left| x-2 \right|+{{x}^{6}}=0\]

Мы снова видим сумму двух функций, каждая из которых неотрицательна. Запомните этот прием, он очень эффективен при работе со всевозможными функциями, о которых точно известно, что они принимают лишнее отрицательное значение.

Смотрите также:

1. Нестандартные уравнения с модулем
2. Дробно-рациональные уравнения с модулем
3. Как решать квадратные уравнения
4. Пробный ЕГЭ 2012. Вариант 9 (без логарифмов)
5. Тригонометрические функции
6. Тест по задачам B14: средний уровень, 2 вариант

www.berdov.com

Область определения функции, теория и примеры

1) Функцию можно представить в виде разности двух функций

   

Функция является многочленом и её областью определения есть множество всех действительных чисел .

Функция является дробно-рациональной. Найдем значения , которые обнуляют знаменатель

   

Таким образом, область определения функции находится из системы

   

2) Для нахождения области определения решим неравенство

   

Разложим на множители левую часть этого неравенства. Для этого решим уравнение . По теореме Виета: , отсюда . Таким образом, неравенство примет вид

   

Обозначим найденные корни на числовой оси и определим знак неравенства на полученных интервалах.

Таким образом, .

3) Функция представляет собой дробно-рациональную функцию, в числителе которой многочлен. Область определения многочлена есть множество действительных чисел . В знаменателе корень, область его определения находим из системы

   

Таким образом, .

ru.solverbook.com

Область определения функции

Сегодня потренируемся в отыскании области определения выражения и функции.

Когда отыскивают область определения функции, то часто она совпадает с областью определения выражения, задающего функцию: такая область определения называется естественной. Но бывает и так, что условия задачи накладывают особые ограничения: например, естественная область определения функции от (-8) до 8, но аргумент этой функции – время (или вес). Понятно тогда, что время (как и вес) не может быть отрицательной величиной и тогда естественная область определения  такой функции сужается до промежутка (0; 8).
При отыскании области определения функции надо помнить о следующих ограничениях:
1. При извлечении корня четной степени подкоренное выражение обязано быть неотрицательным (что не запрещает ему быть равным нулю). 2. Знаменатель дроби не может быть равным нулю. 3. Выражение, стоящее под знаком логарифма, не может быть отрицательным или равняться нулю. 4. Выражение, стоящее под знаком арксинуса или арккосинуса, не может превышать 1 по модулю

Также надо помнить, что область определения всегда нужно искать для исходной функции, до каких-либо преобразований.
Например, функции  и  имеют разные области определения: для первой это – вся числовая ось, а вторая не определена в точке 0. То же относится к функциям  и  –  у первой область определения – также вся числовая ось, а у второй – [)

1. Найдите область определения выражения:

Перепишем выражение:

Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:

Дробь положительна, если числитель и знаменатель ее одновременно положительны или отрицательны. У нас в числителе положительное число, поэтому знаменатель неотрицателен. Кроме того, знаменатель не может быть равен нулю, поэтому неравенство становится таким:

Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:




Наносим полученные точки на координатную прямую и расставляем знаки. Так как  (старший член) – со знаком «плюс», то ветви параболы направлены вверх, на самом правом отрезке ставим знак «плюс», а далее знаки меняются. Точки выкалываем, поскольку неравенство строгое:

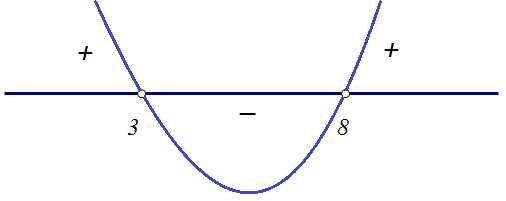
Ответ: – круглые скобки показывают, что концы интервалов не входят в ответ.

2. Найдите область определения выражения:

Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:

Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:

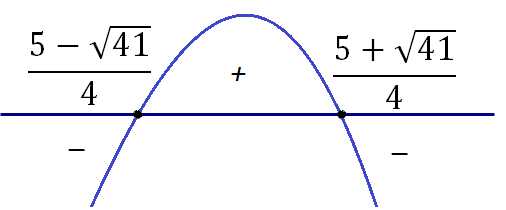
Наносим полученные точки на координатную прямую и расставляем знаки. Так как  (старший член) в исходном неравенстве – со знаком «минус», то ветви параболы направлены вниз, на самом правом отрезке ставим знак «минус», а далее знаки меняются. Точки закрашиваем, поскольку неравенство нестрогое.
Ответ: – квадратные скобки показывают, что концы отрезка  входят в ответ.

3. Найдите область определения функции:

Очевидно, что область определения функции будет совпадать с областью определения выражения  – ищем естественную  область определения функции.  Данное выражение имеет смысл только при – задача сводится к решению этого неравенства. Определяем точки перемены знака:


Изображаем полученные точки на числовой оси, ставим знаки:

Точки закрашены, концы интервалов входят в решение. Тогда область определения функции: (] [)
4. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения  – ищем естественную  область определения функции.  Данное выражение имеет смысл только при ; – задача сводится к решению системы неравенств. Определяем точки перемены знака:

Изображаем полученные точки на числовой оси:

Решение системы неравенств:  
Область определения функции: [ )
5. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения
– ищем естественную  область определения функции.  Данное выражение имеет смысл только при – задача сводится к решению неравенства.
Рассмотрим два случая:


Решение:
Или


Решение:
Область определения функции: [)

6. Найти область определения функции:

Решение:



Ответ:

7. Найти область определения функции:
Решение:






Ответ:
8. Найти область определения функции:

Решение:


Ответ:

easy-physic.ru

Тема 2. Область определения функции. Предел функции.

Тема 1. Значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы. Основные математические методы решения прикладных задач в области профессиональной деятельности.

Для продуктивной деятельности в современном ин­формационном мире требуется достаточно прочная базо­вая математическая подготовка.

Математика, давно став языком науки и техники, в настоящее время все шире проникает в повседневную жизнь и обиходный язык, все более внедряется в тради­ционно далекие от нее области. Интенсивная математи­зация различных областей человеческой деятельности осо­бенно усилилась с появлением и развитием ЭВМ. Ком­пьютеризация общества, внедрение современных инфор­мационных технологий требуют математической грамот­ности человека буквально на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый мате­матикой.

Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количествен­ные отношения — от простейших, усваиваемых в непосредственном опыте людей до достаточно сложных, необ­ходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современ­ней техники ,восприятие научных знаний, восприятие и интерпретации разнообразной социальной, экономической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, пользоваться вычислительной техникой, находить в справочниках и использовать нужные формулы, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.

Без базовой математической подготовки невозможна постановка образования современного человека. И, наконец, все больше профессий, тре­бующих высокого уровня образования, связано с непо­средственным применением математики (экономика, биз­нес, финансы, физика, химия, техника, информатика, биология, психология и многое другое).

Важным для жизни в современном обществе также является формирование математического стиля мышле­ния, проявляющегося в определенных умственных навы­ках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естествен­ным образом включаются индукция и дедукция, обобще­ние и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты ма­тематических умозаключений и правила их конструирова­ния вскрывают механизм логических построений, выраба­тывают умения формулировать, обосновывать и доказы­вать суждения, тем самым развивают логическое мышле­ние. Ведущая роль принадлежит математике в формиро­вании алгоритмического мышления, воспитании умений действовать по заданному алгоритму и конструировать новые.

Использование в математике, наряду с естественным, нескольких математических языков дает возможность раз­вивать у учащихся чувство точности, экономности, инфор­мативности речи, формировать умение точно выразить мысль, отобрав для этого наиболее подходящие языковые (в частности, символические, графические) средства.

Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии. Изучение математики развивает воображение, пространственные представления. Математическое образование вносит свой вклад в формирование общей культуры человека.

 

 

Тема 2. Область определения функции. Предел функции.

Область определения функции с одной независимой переменной

Пусть переменная хпринимает числовые значения из множе­ства Е.

Определение. Функция —это правило, которое каждому числу хиз Есопоставляет одно определенное число у.

При этом хназывают независимойпеременной или аргументомфункции, а у -зависимойпеременной; множество Е — областьюопределенияили областью заданияфункции. Множество значений, принимаемых переменной у,называется множеством значенийили областью измененияфункции.

Запись y=f(x)или у(х)означает, что узависит от х.Бук­ва fсимволизирует правило, по которому получается значение у,соответствующее данному значению хиз множества Е.

Вместо букв х, Е, у,f(x)используются и любые другие бук­вы и обозначения.

Задать функцию y=f(x)на множестве Е— это значит указать правило, по которому для каждого хиз Еполучается соответ­ствующее ему значение у.

Предел переменной величины

Пусть переменная величина хв процессе своего изменения неограниченно приближается к числу 5, принимая при этом сле­дующие значения: 4,9; 4,99; 4,999; … или 5,1; 5,01; 5,001; …. В этих случаях модуль разности | х— 5| стремится к нулю: |х — 5|= 0,1; 0,01; 0,001;….

Число 5 в приведенном примере называют пределомпере­менной величины хи пишут lim x = 5.

Определение. Постоянная величина а называется пределомпеременной х,если модуль разности | х – а|при изменении хстановится и остается меньше любого как угодно малого положительного числа ԑ.

Итак, lim x=a(предел хравен а) или х→а ( хстремится к а).

Замечания.1. Предел постоянной величины равен самой постоянной: lim a = a, так как | а—a|< ԑ.

2. Переменная величина может иметь только один предел.

3. Предел положительной переменной величины не отрицателен, пре­дел отрицательной переменной величины не положителен.

Пример. Показать, что при t → ∞ предел переменной величины равен 3.

Решение. Находим разность между переменной величиной хи число 3: x– 3 =

Если t → ∞ , то →0. Значит, выполняется условие | x—3|< ԑ и, следовательно, .

 

Основные свойства пределов

1. Предел алгебраической суммы конечного числа переменныхвеличин равен алгебраической сумме пределов слагаемых: lim ( x+y+…+t)= lim x+ lim y+ … + lim t

2.Предел произведения конечного числа переменных величин равен произведению их пределов: lim ( x∙y∙…∙t)= lim x∙ lim y∙ … ∙ lim t

3. Постоянный множитель можно выносить за знак предела: lim (c x)= lim c ∙lim x= c lim x

4. Предел отношения двух переменных величин равен отношению пределов, если предел знаменателя не равен нулю: , если lim y≠ 0

5. Предел целой положительной степени переменной величины равен той же степени предела этой же переменной: lim xⁿ = (lim x) ⁿ

^{6. Если переменные х, у, z удовлетворяют неравенствамx≤y≤z иx→a,z→a, тоy→a.}

Предел функции в точке

Выше мы рассматривали независимые переменные величины, каждая из которых стремится к своему пределу независимо от другой.

Пусть теперь даны две переменные величины хи у,связанные функциональной зависимостью y=f(x).Рассмотрим вопрос о пре­деле функции при условии, что задан предел ее аргумента.

Если при х,стремящемся к а, функция f(x)стремится к b ,то говорят, что предел функции f(x)в точкех=аравен b и пишут .

Отметим, что во всем дальнейшем изложении, где говорится о пределе функции в точке а,будем предполагать, что функция определена в некоторой окрестности точки а.В самой же точке афункция может быть не определена.

Замечание.За окрестность точки а принимается любой интервал, содержащий точку а.

Определение .Число bназывается пределомфункции f(x)в точке а, если для всех значений х,достаточно близ­ких к аи отличных от а, значения функции f(x)сколь угод­но мало отличаются от числаb.

Пример. Найти .

Решение. Используя последовательно свойства 1, 3 и 5 предела, получим

 

3∙2 ² — 2∙2=8

 

 

Два замечательных предела

 

 

 

 

Производная функции

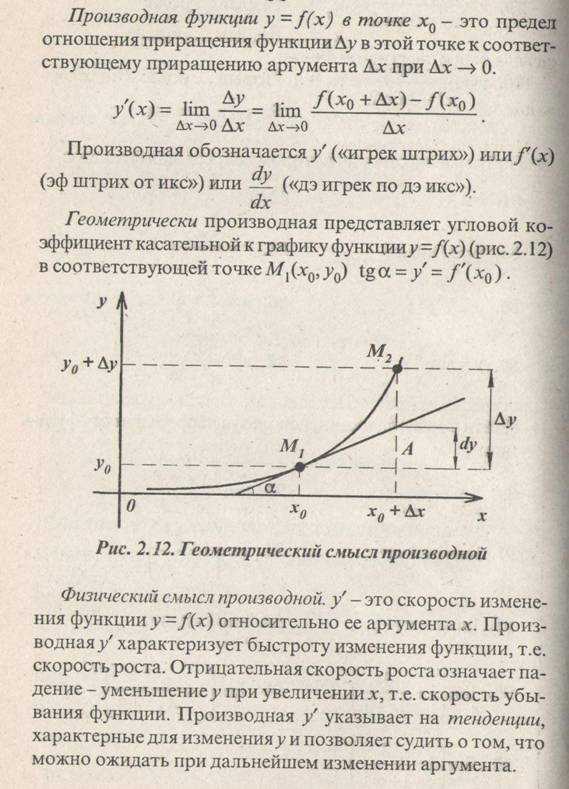
Уравнение касательной к кривой в точке М ₁ ( x₀,y₀) (рис. 2.12) и имеющий угловой коэффициент k= f'(x₀), т.е. y–f(x₀)=f‘(x₀)(x–x₀)

Пример. Составить уравнение касательной к кривой y=x²– 2x+3в ее точке с абсциссой x₀= 2.

Решение. Находим: f(x₀)=y(2)=3,f‘(x₀)=y‘ (2) = (2x-2)_x=2=2

Подставив найденные значения f(x₀)и f‘(x₀)в формулу , найдем искомое уравнение касательной y – 3=2(x — 2)или 2x-y-1=0.

Производная функции

Уравнение касательной к кривой в точке М ₁ ( x₀,y₀) (рис. 2.12) и имеющий угловой коэффициент k= f'(x₀), т.е. y–f(x₀)=f‘(x₀)(x–x₀)

Пример. Составить уравнение касательной к кривой y=x²– 2x+3в ее точке с абсциссой x₀= 2.

Решение. Находим: f(x₀)=y(2)=3,f‘(x₀)=y‘ (2) = (2x-2)_x=2=2

Подставив найденные значения f(x₀)и f‘(x₀)в формулу , найдем искомое уравнение касательной y – 3=2(x — 2)или 2x-y-1=0.

Построение графика функции

 

 

Задание к модулю

Задание 1. Найти область определения функций:

a) ;

b)

 

Задание 2 . Вычислить пределы :

a) ;

b) ;

c) ;

d) .

 

Задание 3 . Найти производную функций :

a) y = ;

b) y = sin³2x;

c) y =arccos ;

d) y = ln cos x.

Задание 4. Найти интервалы монотонности функции :

y=x²-4x+1

Задание 5. Исследовать на экстремум с помощью второй производной функцию :

y= 4x+x²

 

Задание 6.Найти наибольшее и наименьшее значения функции :

y=x³-6 на отрезке [-3; 4]

 

 

Тема 1. Значение математики в профессиональной деятельности и при освоении основной профессиональной образовательной программы. Основные математические методы решения прикладных задач в области профессиональной деятельности.

Для продуктивной деятельности в современном ин­формационном мире требуется достаточно прочная базо­вая математическая подготовка.

Математика, давно став языком науки и техники, в настоящее время все шире проникает в повседневную жизнь и обиходный язык, все более внедряется в тради­ционно далекие от нее области. Интенсивная математи­зация различных областей человеческой деятельности осо­бенно усилилась с появлением и развитием ЭВМ. Ком­пьютеризация общества, внедрение современных инфор­мационных технологий требуют математической грамот­ности человека буквально на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый мате­матикой.

Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количествен­ные отношения — от простейших, усваиваемых в непосредственном опыте людей до достаточно сложных, необ­ходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современ­ней техники ,восприятие научных знаний, восприятие и интерпретации разнообразной социальной, экономической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, пользоваться вычислительной техникой, находить в справочниках и использовать нужные формулы, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.

Без базовой математической подготовки невозможна постановка образования современного человека. И, наконец, все больше профессий, тре­бующих высокого уровня образования, связано с непо­средственным применением математики (экономика, биз­нес, финансы, физика, химия, техника, информатика, биология, психология и многое другое).

Важным для жизни в современном обществе также является формирование математического стиля мышле­ния, проявляющегося в определенных умственных навы­ках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естествен­ным образом включаются индукция и дедукция, обобще­ние и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты ма­тематических умозаключений и правила их конструирова­ния вскрывают механизм логических построений, выраба­тывают умения формулировать, обосновывать и доказы­вать суждения, тем самым развивают логическое мышле­ние. Ведущая роль принадлежит математике в формиро­вании алгоритмического мышления, воспитании умений действовать по заданному алгоритму и конструировать новые.

Использование в математике, наряду с естественным, нескольких математических языков дает возможность раз­вивать у учащихся чувство точности, экономности, инфор­мативности речи, формировать умение точно выразить мысль, отобрав для этого наиболее подходящие языковые (в частности, символические, графические) средства.

Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии. Изучение математики развивает воображение, пространственные представления. Математическое образование вносит свой вклад в формирование общей культуры человека.

 

 

Тема 2. Область определения функции. Предел функции.

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Область определения функции | Онлайн калькулятор

Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.
Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма. Областью определения показательной функции, также как и у постоянной функции, является множество всех действительных чисел.

Областью определения сложных функций y=f1(f2(x)) является пересечение двух множеств: x∈D(f2) и множества всех x, для которых f2(x) ∈ D(f1). Следовательно, для того чтобы найти область определения сложной функции, необходимо решить систему неравенства.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать и понимать, как находить область определения функции. Чтобы получить ответ, укажите функцию, для которой Вы хотите найти область определения. Основные примеры ввода функций для данного калькулятора указаны ниже.

Вам помог этот калькулятор?
Предложения и пожелания пишите на [email protected]

Поделитесь этим калькулятором на форуме или в сети!

Это помогает делать новые калькуляторы.

НЕТ

Смотрите также

allcalc.ru

Область определения и множество значений

Автор: Sepehr Hassannejad

Часть 2

Определение:
Множество первых элементов пары $f$ называется областью определения, а множество вторых элементов называется множеством значений. Область определения и множество значений функции обозначаются как $D_f$ и $R_f$ соответственно.
Математическим языком

$D_f=\lbrace x |(x,y) \in f \rbrace$
$R_f= \lbrace y | (x,y) \in f \rbrace $

Пример:
Пусть $f=\lbrace (1,-1),(3,3),(7,-1),(5,3) \rbrace$. Определить $D_f$ и $R_f$.
Решение:

$D_f=\lbrace 1,3,5,7 \rbrace$
$R_f= \lbrace -1,3 \rbrace$

Пример:
Если $D_f=R_f=\lbrace 1,2,3 \rbrace$, то сколько разных функций можно составить с данной областью определений и множеством значений?
Решение:

$f=\lbrace (1, \bigcirc ),(2 , \bigcirc),(3,\bigcirc) \rbrace$

Первую позицию можно заполнить 1, либо 2 или 3, следовательно существует три способа заполнения первой позиции. Вторую позицию можно также заполнить тремя разными способами. Значит существует $ 3 \times 3 \times 3=27$ способов. Это означает, что есть 27 разных функций, у который будут данные $D_f$ и $R_f$. Некоторые из них указаны ниже. Можно также доказать ответ, написав все возможные решения.

$f_1 = \lbrace (1,1),(2,2),(3,3) \rbrace$
$f_2 = \lbrace (1,1),(2,1),(3,1) \rbrace$
$f_3 = \lbrace (1,1),(2,3),(3,2) \rbrace$

Если $f$ определена множеством пар или таблицей, тогда область определения и множество значений четко определены.

Пример:
Найти область определения и множество значений у $f=\lbrace (1,4),(2,5),(3,6) \rbrace$.
Решение:

$D_f=\lbrace 1,2,3 \rbrace \,\,,\,\, R_f= \lbrace 4,5,6 \rbrace$

Математически

$D_f= \lbrace x | x \in \mathbb{N} , 1 \leq x \leq 3 \rbrace$

$R_f= \lbrace x | x \in \mathbb{N} , 4 \leq x \leq 6 \rbrace$

Пример:
Найти область определения и множество значений у
$f=\lbrace (1,1),(2,3),(3,5),(4,7),(5,9),(6,11),(7,1),(8,7),(9,8),(10,9),(11,10) \rbrace$.
Затем определить функцию.
Решение:

$D_f=\lbrace 1,2,3 , \cdots ,11 \rbrace = \lbrace x| x \in \mathbb{N} , x \leq 11 \rbrace$

$R_f= \lbrace 1,3,5,7,8,9,10,11 \rbrace$

$f(x)= \begin{cases} 2x-1 \,\,\,\,\,\,\,\,\,\,\,\, x \leq 6 \,\,\,\, x \in \mathbb{N}\\ 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=7\\ x-1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, 1 \leq x \leq 8 \,\,\,\, x \in \mathbb{N} \end{cases}$

Пример:
Найти область определения и множество значений указаной ниже кусочно-заданной функции. Затем задать ее множеством пар и начертить ее график. $f(x)= \begin{cases} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0\\ 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=0\\ -1 \,\,\,\,\,\,\,\,\,\,\,\, x
Решение:
Очевидно, что

$D_f= \mathbb{R} \,\,,\,\, R_f= \lbrace -1,0,1 \rbrace $

$f(x)=f_1 \cup f_2 \cup f_3= \begin{cases} f_1 = \lbrace (x,y) | x \in \mathbb{R^+} \,\,,\,\, y=1 \rbrace \\ f_2 = \lbrace (0,0) \rbrace \\ f_3 = \lbrace (x,y) | x \in \mathbb{R^-} \,\,,\,\, y=-1 \rbrace \end{cases}$

Совет:
Эта функция также называется кусочно-постоянная функция и обозначается как $\textit{Sgn(x)}$. $Sgn(x)= \begin{cases} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0 \\ 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=0 \\ -1 \,\,\,\,\,\,\,\,\,\,\,\, x

Упражнения

Найти область определения и множество значений функций.
1) $f(x)= \begin{cases} 3 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>1 \\ 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=1 \\ -3 \,\,\,\,\,\,\,\,\,\,\,\, x

2) $g(x)= \begin{cases} -1 \,\,\,\,\,\,\,\,\,\,\, x0 \end{cases} $

3) $h(x)= \begin{cases} -2 \,\,\,\,\,\,\,\,\,\,\,\,-2 4 \end{cases} $

4)$k(x)= \begin{cases} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x\geq 2 \\ 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x Полиномиальная функция Определение:
$f$ называется полиномиальной функцией тогда и только тогда, если для каждого действительного значения $x$ ($x \in \mathbb{R}$)

$f(x)=a_n x^n+a_{n-1} x^{x-1}+\cdots+a_1 x+a_0 \,\,\,\,\,\,\,\, n \in \mathbb{N} \cup \lbrace 0 \rbrace$

$a_0,a_1,\cdots,a_n$, принимающие действительные значения, называют коэффициентом полинома, а неотрицательные целые значения $n$ если $a_n \neq 0$ называют степенью полинома.
Область определения полиномиальной функции $\mathbb{R}$. Для определения множества значений полиномиал

www.math10.com