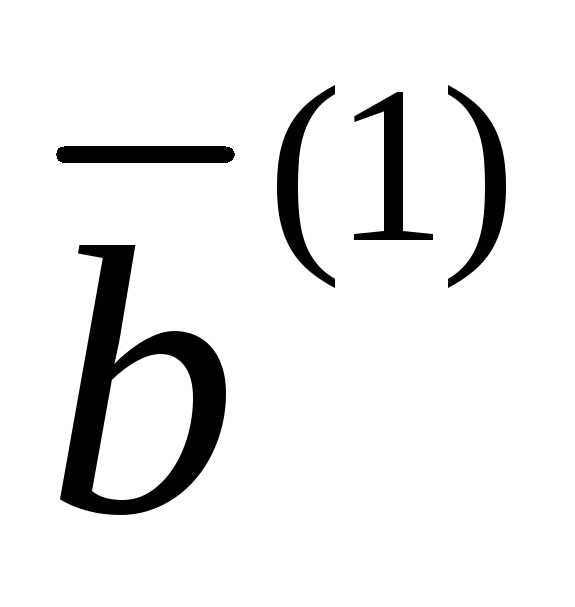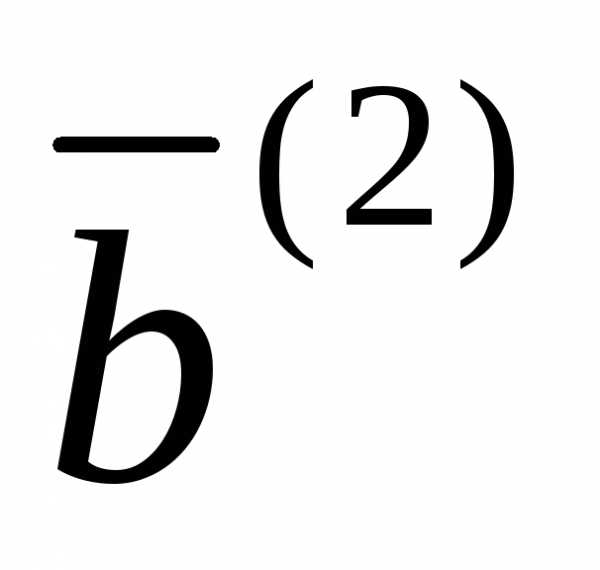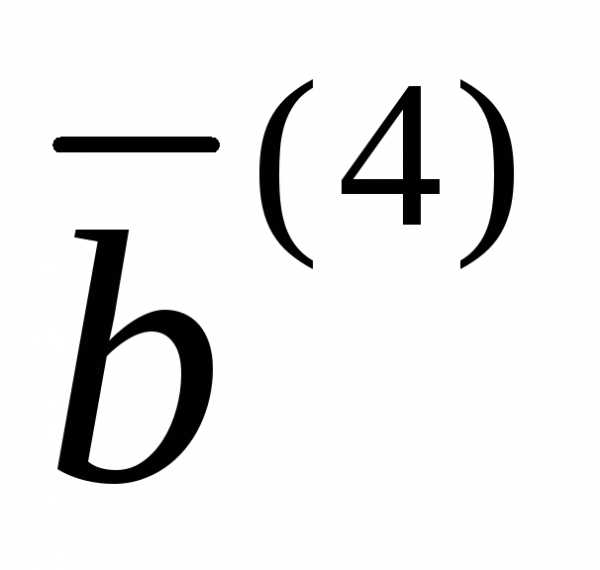Область допустимых решений – Найти область решений и область допустимых решений системы неравенств — 22 Апреля 2015 — Примеры решений задач
Область допустимых решений — Википедия
 Задача с пятью линейными ограничениями (выделено синим цветом, включая условие неотрицательности). При отсутствии требований целочисленности решения область допустимых решений ограничена синими отрезками, а при наличии требований целочисленности область является множеством красных точек.
Задача с пятью линейными ограничениями (выделено синим цветом, включая условие неотрицательности). При отсутствии требований целочисленности решения область допустимых решений ограничена синими отрезками, а при наличии требований целочисленности область является множеством красных точек. 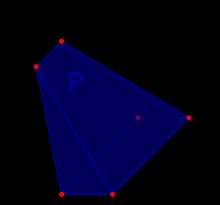 Замкнутая область допустимых решений задачи линейного программирования с тремя переменными является выпуклым многогранником.
Замкнутая область допустимых решений задачи линейного программирования с тремя переменными является выпуклым многогранником.В теории оптимизации допустимая область, допустимое множество, пространство поиска или пространство решений — это множество всех возможных точек (значений переменных) задачи оптимизации, которые удовлетворяют ограничениям[en] задачи. Эти ограничения могут включать неравенства, равенства и требование целочисленности решения [1][2]. Область допустимых решений является начальной областью поиска кандидатов в решение задачи, и эта область во время поиска может сужаться.
Например, возьмём задачу
- Минимизировать x12+x24{\displaystyle x_{1}^{2}+x_{2}^{4}}
с ограничениями на переменные x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}}
ru.wikipedia.org
Область допустимых решений Википедия
 Задача с пятью линейными ограничениями (выделено синим цветом, включая условие неотрицательности). При отсутствии требований целочисленности решения область допустимых решений ограничена синими отрезками, а при наличии требований целочисленности область является множеством красных точек.
Задача с пятью линейными ограничениями (выделено синим цветом, включая условие неотрицательности). При отсутствии требований целочисленности решения область допустимых решений ограничена синими отрезками, а при наличии требований целочисленности область является множеством красных точек. 
В теории оптимизации допустимая область, допустимое множество, пространство поиска или пространство решений — это множество всех возможных точек (значений переменных) задачи оптимизации, которые удовлетворяют ограничениям[en] задачи. Эти ограничения могут включать неравенства, равенства и требование целочисленности решения [1][2]. Область допустимых решений является начальной областью поиска кандидатов в решение задачи, и эта область во время поиска может сужаться.
Например, возьмём задачу
- Минимизировать x12+x24{\displaystyle x_{1}^{2}+x_{2}^{4}}
с ограничениями на переменные x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}}
- 1≤x1≤10{\displaystyle 1\leq x_{1}\leq 10}
и
- 5≤x2≤12.{\displaystyle 5\leq x_{2}\leq 12.}
В этом случае область допустимых решений представляет собой множество пар (x1, x2), для которых значение x1 не меньше 1 и не больше 10, а значение x2 не меньше 5 и не больше 12. Заметим, что множество допустимых решений рассматривается отдельно от целевой функции, которая определяет критерий оптимизации и которая в вышеприведённом примере равна x12+x24.{\displaystyle x_{1}^{2}+x_{2}^{4}.}
Во многих задачах допустимая область решений включает ограничение, по которому одна и более переменных должны быть неотрицательными. В задачах чисто целочисленного программирования множество допустимых решений состоит из целых чисел (или некоторого подмножества). В задачах линейного программирования область допустимых решений является выпуклым политопом — областью в многомерном пространстве, границы которого образованы гиперплоскостями[1].
Удовлетворение ограничений — это процесс поиска точки в области допустимых решений.
Связанные определения
При ограничениях в виде неравенств точка может быть либо внутренней точкой (допустимой точкой), либо граничной точкой (допустимой точкой), либо внешней точкой (недопустимой точкой). Активным, или связывающим, ограничением называется такое, которое в данной точке превращается в равенство[1]. Некоторые алгоритмы могут использовать понятие активного ограничения для построения более эффективного алгоритма (см. метод переменного базиса.
Если для задачи не существует допустимой точки, задача называется недопустимой.
Условный оптимум представляет собой локальный оптимум, лежащий на границе допустимой области[1].
Выпуклая область допустимых решений
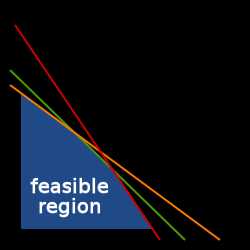 В задаче линейного программирования набор линейных ограничений образует выпуклую область допустимых решений. Для двух переменных эта область имеет форму выпуклого многоугольника.
В задаче линейного программирования набор линейных ограничений образует выпуклую область допустимых решений. Для двух переменных эта область имеет форму выпуклого многоугольника.Выпуклая область допустимых решений — это множество решений, в котором отрезок, соединяющий два допустимых решения, содержит только допустимые точки и не проходит через какую-либо недопустимую точку. Выпуклое множество допустимых решений возникает во многих типах задач, включая задачи линейного программирования, и представляют определённый интерес, поскольку, если задача заключается в оптимизации выпуклой целевой функции, в общем случае такую задачу проще решить на выпуклом множестве решений, и любой локальный оптимум
Отсутствие допустимых решений
Если ограничения задачи оптимизации совместно противоречивы, не существует точки, которая бы удовлетворяла всем ограничениям, а тогда область допустимых решений пуста. В этом случае задача не имеет решений и говорят, что она недопустима[1].
Ограниченные и неограниченные области допустимых решений
 Ограниченная область допустимых решений (сверху) и неограниченная (снизу). Нижняя область распространяется направо неограниченно.
Ограниченная область допустимых решений (сверху) и неограниченная (снизу). Нижняя область распространяется направо неограниченно.Множество допустимых решений может быть ограниченным или неограниченным. Например, множество допустимых решений, определяемое ограничениями {
Если множество допустимых решений является неограниченной, оптимальное решение может как существовать, так и не существовать, в зависимости от поведения целевой функции. Например, если множество определено ограничениями {
- ↑ 1 2 3 4 5 Д. Химмельблау. Прикладное нелинейное программирование. — Москва: «Мир», 1975. — С. 36.
- ↑ Л.Р. Форд, Д.Р. Фалкерсон. Потоки в сетях. — Москва: «Мир», 1966. — С. 48.
wikiredia.ru
Область допустимых решений — Энциклопедия по экономике
В рассмотренных моделях нелинейный характер зависимости экономических показателей от технологических учитывался на основе фиксации технологических параметров, которые в действительности являются искомыми. Так, например, в модели должен определяться фонд ежегодно буримых скважин. При этом, например, эксплуатационные затраты и некоторые нормативы на обслуживание вводимых скважин нелинейно зависят от фонда действующих скважин (включая и буримые в данном году). Фиксация этого и аналогичных ему нормативов приводит к сужению области допустимых решений и при незначительных размерах технологических матриц не позволяет учесть эффект экономичности масштаба , определяемого нелинейным характером нормативов. [c.205]График на рис. 8.4 показывает область, которая удовлетворяет всем ограничениям. Эта область называется областью допустимых решений, так как она содержит все допустимые решения задачи линейного программирования. [c.268]
Т Определение. Область допустимых решений — это область, полученная путем графического отображения ограничений конкретной задачи и включающая все возможные решения оптимизации. А [c.268]
Любая точка в области допустимых решений может быть решением задачи максимизации прибыли, Нам только остается найти ту точку, которая максимизирует эту функцию. Так называемая объективная функция имеет следующий вид [c.268]
Мы можем взять любую точку в области допустимых решений и вычислить соответствующую прибыль. Так, область допустимых решений содержит точку х = =500 и у — 500. Эти значения дают прибыль в сумме 70 х 500 + 60 х 500 = 65 000 долл. США. [c.269]
Это прямолинейное уравнение можно нанести на график с областью допустимых решений, как это показано на рис. 8.5. Любая точка на этой линии даст прибыль в 30 000 долл. А теперь рассмотрим большее значение прибыли, например 50 000 долл. Получаем уравнение [c.269]
Альтернативный метод можно использовать для получения оптимального значения объективной функции исходя из знания области допустимых решений. Известно, что оптимальное значение лежит на границе области допустимых решений. Фактически оптимальное значение всегда находится в угловой точке области допустимых решений. (Хотя и другие пограничные точки также могут показать аналогичное оптимальное значение. Такой пример мы рассмотрим позднее.) [c.271]
Так, рассмотрим область допустимых решений на рис. 8.4. Эта область показана на рис. 8.9. Давайте вычислим значения функции прибыли прибыль составляет 70х + 60у для всех угловых точек этой области. [c.271]
| Рис. 8.9. Угловые точки области допустимых решений | 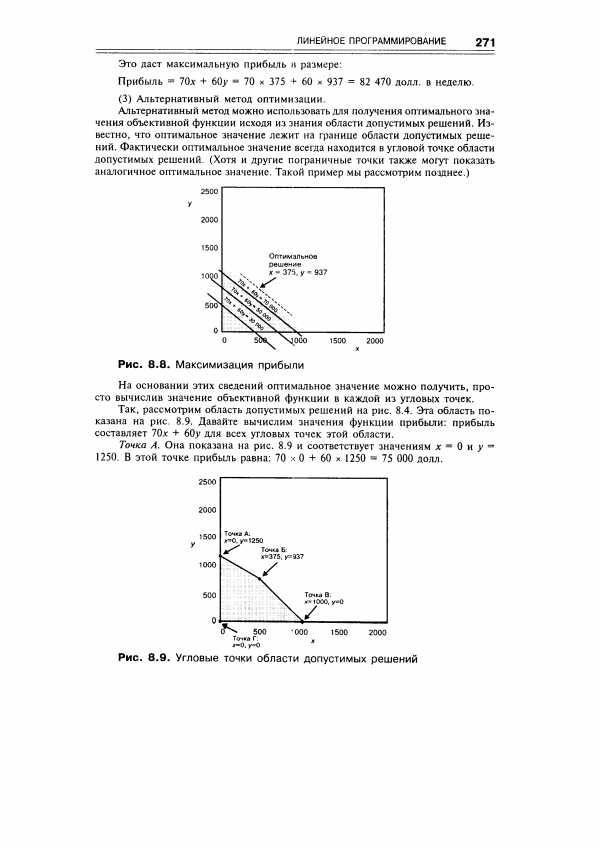 |
Найдите область допустимых решений Мы должны определить область, которая отвечает всем необходимым условиям. [c.273]
| Рис. 8.10. Область допустимых решений. | 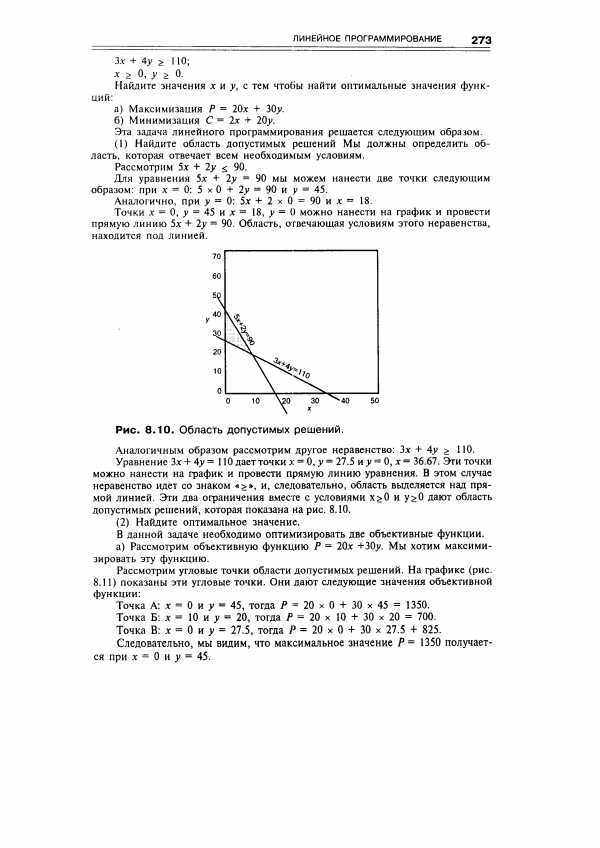 |
Рассмотрим угловые точки области допустимых решений. На графике (рис. 8.11) показаны эти угловые точки. Они дают следующие значения объективной функции [c.273]
Область допустимых решений показана на рис. 8.12. Обратите внимание, что три основные условия даны со знаком > , и поэтому выделенная область поднимается над линией. Условие х [c.274]
Таким образом, минимальное значение С = 1840 получается при х = 12 и у = 4. Можно заметить, что иногда метод вычисления значений объективной функции по всем угловым точкам области допустимых решений может оказать- [c.274]
В этой ситуации мы имеем дело с ограничениями, которые не позволяют определить область допустимых решений. Нет таких точек, которые могли бы удовлетворить всем условиям. Например, рассмотрим следующие ограничения [c.276]График, представленный на рис. 8.15, показывает область допустимых решений с учетом этих ограничений. На графике также проведена линия Р = 8х + Юу = 40. Эту линию можно сдвигать в направлении к краю области допустимых решений. Видно, что эта линия параллельна одной из линий по границе области. Поэтому максимальное значение Р находится в любой точке по этой линии. [c.276]
График, представленный на рис. 8.16, показывает область допустимых решений, которые удовлетворяют всем условиям. Видно, что эта область не имеет границы в правом верхнем углу, и, следовательно, отсутствует предел максимальных значений х и у. Таким образом, решение таково, что х и у должны быть бесконечны. На практике такая ситуация может возникнуть, если при постановке задачи упущено из вида одно или несколько условий. Так, если х и у — количества двух производимых изделий, то, в качестве верхней границы, следует ввести ограничение по вероятному покупательскому спросу на эти товары или по наличию людских, материальных или финансовых ресурсов. [c.277]
Е) Отобразите на графике области допустимых решений исходя из следующих условий [c.277]
| Рис. 8.16. Безграничная область допустимых решений |  |
Модели с переменными параметрами и диапазонные модели при одних и тех же нагрузках имеют расширенные по отношению к моделям с фиксированными параметрами области допустимых решений. [c.28]
Существует множество критериев (/,, /,,…, /j) — F, с помощью которых оценивается качество альтернативы ае/4 или качество исходов х из области допустимых решений D. Необходимо найти оптимальное решение а 0 или ха, удовлетворяющее условиям [c.191]
Область допустимых решений в задачах принятия плановых решений задается, в зависимости от информированности ЛПР о состоянии среды, системой линейных детерминированных неравенств [c.191]
Специфика этой задачи такова, что для ее решения удобно использовать метод динамического программирования. Не останавливаясь на изложении математических методов, укажем, что в рассматриваемой задаче между отдельными средствами регулирования распределяются две величины — годовой ресурс природного газа и интенсивность газопотребления (условия а, б). Оптимальное распределение этих двух величин (QM. ч, V) методом динамического программирования возможно лишь вследствие условия ( ), позволившего условие (в) свести к относи тельно простой проверке принадлежности точки (Х , г/г-) к области допустимых решений. [c.347]
Правовые ограничения нас интересуют с двух точек зрения 1) определения области допустимых решений, не противоречащих правовым положениям 2) возможности, условия, процедуры и последствий расширения области допустимых решений за счет выхода за правовые ограничения. [c.52]
Один из видов координирующих воздействий — задание каждому нижележащему органу управления области допустимых решений, другой — задание нижележащему органу соответствующего критерия, следование которому поощряется. [c.66]
Месячный план, декадные или ежедневные графики отгрузок каждым видом транспорта по определенным адресам, пятидневные графики приема нефтепродуктов от НПЗ, необходимость вывоза определенных нефтепродуктов для освобождения соответствующих емкостей, требования транспортных организаций. Это определяет область допустимых решений территориального управления. Кроме того, существует общий системный принцип равномерности отгрузок, в соответствии с которым при отсутствии специальных конкретных команд верхнего уровня относительно большое отклонение от среднедневных норм отгрузки каждого нефтепродукта по запланированным направлениям и тем более суммарной отгрузки нефтепродукта с данного пункта по всем адресам оценивается как плохое. [c.67]
Значит, на втором этапе решения в областях 3 и 4 действует та же стратегия, что и в области 2, но область допустимых решений уже расширена за счет ресурсов, дополнительно привлеченных на первом этапе решения. Поэтому можно считать, что алгоритм работы системы области 2 составляет некоторое ядро, используемое для работы системы в других областях состояния. — . [c.104]
При анализе рынка и принятии решений возможно применение такого парадоксального метода, как принцип противоположного мнения. Суть его состоит в том, что если подавляющее большинство людей согласны с одним и тем же мнением, то они не правы. Источник этого принципа можно попробовать искать в признании идеального механизма поиска истины, аналогичного борьбе спроса и предложения. Последние могут найти равновесную и оптимальную цену лишь в условиях массового рынка и свободной конкуренции. Также и истина обычно может появиться только в условиях борьбы различных мнений, потому что, как мы видели (см. 2.6), не существует истины самой по себе, а существует область допустимых решений. [c.171]
Область допустимых решений задачи на рис. 3.1 — многоугольник [c.41]
Области допустимых решений, представленные на рисунке 2, [c.56]
Все реформаторские действия в основном соответствовали ряду канонов теории и мировой практики. Но игнорировалась необходимость обязательных ограничений предлагаемой модели развития, которые определяются конкретными социально-экономическими и общественно-политическими реальностями и в своей совокупности детерминируют область допустимых решений. Не учитывались ограничения, налагаемые, во-первых, новыми федеративными отношениями и стоящими за ними интересами региональных элит, во-вторых, наиболее вероятным сценарием криминализации хозяйственной жизни (об этом речь пойдет далее), в-третьих, вполне предсказуемыми социальными и бюджетно-налоговыми последствиями реформ, в-четвертых, искаженными представлениями основной массы населения об условиях социальной жизни в новорыночной стране, в-пятых, неизбежным соединением вопросов реформирования с вопросами персонификации власти. [c.39]
Необходимо отметить, что в этой области допустимых решений имеется еще одна угловая точка. Она показана на рис. 8.9 буквой Г, где х = 0и>> = 0. В этой точке прибыль равна 70×0 + 60×0 = 0 долл. [c.272]
Влияние 7/ на область допустимых решений при нормальном законе распределения случайных величин может оыть в определенной мере оценено на основании приведенных в табл. 3.1 значений обратной функции нормального распределения. [c.93]
economy-ru.info
Область допустимых решений — WiKi
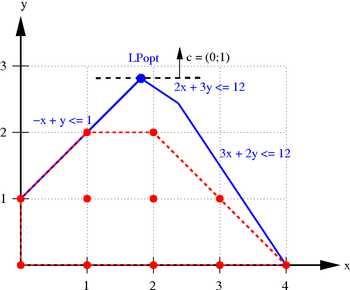 Задача с пятью линейными ограничениями (выделено синим цветом, включая условие неотрицательности). При отсутствии требований целочисленности решения область допустимых решений ограничена синими отрезками, а при наличии требований целочисленности область является множеством красных точек.
Задача с пятью линейными ограничениями (выделено синим цветом, включая условие неотрицательности). При отсутствии требований целочисленности решения область допустимых решений ограничена синими отрезками, а при наличии требований целочисленности область является множеством красных точек. 
В теории оптимизации допустимая область, допустимое множество, пространство поиска или пространство решений — это множество всех возможных точек (значений переменных) задачи оптимизации, которые удовлетворяют ограничениям[en] задачи. Эти ограничения могут включать неравенства, равенства и требование целочисленности решения [1][2]. Область допустимых решений является начальной областью поиска кандидатов в решение задачи, и эта область во время поиска может сужаться.
Например, возьмём задачу
- Минимизировать x12+x24{\displaystyle x_{1}^{2}+x_{2}^{4}}
с ограничениями на переменные x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}}
- 1≤x1≤10{\displaystyle 1\leq x_{1}\leq 10}
и
- 5≤x2≤12.{\displaystyle 5\leq x_{2}\leq 12.}
В этом случае область допустимых решений представляет собой множество пар (x1, x2), для которых значение x1 не меньше 1 и не больше 10, а значение x2 не меньше 5 и не больше 12. Заметим, что множество допустимых решений рассматривается отдельно от целевой функции, которая определяет критерий оптимизации и которая в вышеприведённом примере равна x12+x24.{\displaystyle x_{1}^{2}+x_{2}^{4}.}
Во многих задачах допустимая область решений включает ограничение, по которому одна и более переменных должны быть неотрицательными. В задачах чисто целочисленного программирования множество допустимых решений состоит из целых чисел (или некоторого подмножества). В задачах линейного программирования область допустимых решений является выпуклым политопом — областью в многомерном пространстве, границы которого образованы гиперплоскостями[1].
Удовлетворение ограничений — это процесс поиска точки в области допустимых решений.
Связанные определения
При ограничениях в виде неравенств точка может быть либо внутренней точкой (допустимой точкой), либо граничной точкой (допустимой точкой), либо внешней точкой (недопустимой точкой). Активным, или связывающим, ограничением называется такое, которое в данной точке превращается в равенство[1]. Некоторые алгоритмы могут использовать понятие активного ограничения для построения более эффективного алгоритма (см. метод переменного базиса.
Если для задачи не существует допустимой точки, задача называется недопустимой.
Условный оптимум представляет собой локальный оптимум, лежащий на границе допустимой области[1].
Выпуклая область допустимых решений
См. также: Выпуклое программирование
 В задаче линейного программирования набор линейных ограничений образует выпуклую область допустимых решений. Для двух переменных эта область имеет форму выпуклого многоугольника.
В задаче линейного программирования набор линейных ограничений образует выпуклую область допустимых решений. Для двух переменных эта область имеет форму выпуклого многоугольника.Выпуклая область допустимых решений — это множество решений, в котором отрезок, соединяющий два допустимых решения, содержит только допустимые точки и не проходит через какую-либо недопустимую точку. Выпуклое множество допустимых решений возникает во многих типах задач, включая задачи линейного программирования, и представляют определённый интерес, поскольку, если задача заключается в оптимизации выпуклой целевой функции, в общем случае такую задачу проще решить на выпуклом множестве решений, и любой локальный оптимум[en] будет также глобальным оптимумом[en].
Отсутствие допустимых решений
Если ограничения задачи оптимизации совместно противоречивы, не существует точки, которая бы удовлетворяла всем ограничениям, а тогда область допустимых решений пуста. В этом случае задача не имеет решений и говорят, что она недопустима[1].
Ограниченные и неограниченные области допустимых решений
 Ограниченная область допустимых решений (сверху) и неограниченная (снизу). Нижняя область распространяется направо неограниченно.
Ограниченная область допустимых решений (сверху) и неограниченная (снизу). Нижняя область распространяется направо неограниченно.Множество допустимых решений может быть ограниченным или неограниченным. Например, множество допустимых решений, определяемое ограничениями {x ≥ 0, y ≥ 0}, является неограниченным, поскольку в некоторых направлениях можно идти бесконечно, оставаясь в области допустимых решений. Для контраста множество допустимых решений, образованное ограничениями {x ≥ 0, y ≥ 0, x + 2y ≤ 4}, является ограниченным, поскольку движение в любом направлении ограничено. В задачах линейного программирования с n переменными необходимым, но не достаточным условием ограниченности области допустимых решений является наличие как минимум n + 1 ограничений.
Если множество допустимых решений является неограниченной, оптимальное решение может как существовать, так и не существовать, в зависимости от поведения целевой функции. Например, если множество определено ограничениями {x ≥ 0, y ≥ 0}, то задача оптимизации x + y не имеет решений, поскольку любой кандидат может быть улучшен путём увеличения x или y, а вот задача минимизировать x + y имеет оптимальное решение (а именно, в точке (x, y) = (0, 0)).
- ↑ 1 2 3 4 5 Д. Химмельблау. Прикладное нелинейное программирование. — Москва: «Мир», 1975. — С. 36.
- ↑ Л.Р. Форд, Д.Р. Фалкерсон. Потоки в сетях. — Москва: «Мир», 1966. — С. 48.
ru-wiki.org
Область допустимых решений — Википедия
 Задача с пятью линейными ограничениями (выделено синим цветом, включая условие неотрицательности). При отсутствии требований целочисленности решения область допустимых решений ограничена синими отрезками, а при наличии требований целочисленности область является множеством красных точек.
Задача с пятью линейными ограничениями (выделено синим цветом, включая условие неотрицательности). При отсутствии требований целочисленности решения область допустимых решений ограничена синими отрезками, а при наличии требований целочисленности область является множеством красных точек. 
В теории оптимизации допустимая область, допустимое множество, пространство поиска или пространство решений — это множество всех возможных точек (значений переменных) задачи оптимизации, которые удовлетворяют ограничениям[en] задачи. Эти ограничения могут включать неравенства, равенства и требование целочисленности решения [1][2]. Область допустимых решений является начальной областью поиска кандидатов в решение задачи, и эта область во время поиска может сужаться.
Например, возьмём задачу
- Минимизировать x12+x24{\displaystyle x_{1}^{2}+x_{2}^{4}}
с ограничениями на переменные x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}}
- 1≤x1≤10{\displaystyle 1\leq x_{1}\leq 10}
и
- 5≤x2≤12.{\displaystyle 5\leq x_{2}\leq 12.}
В этом случае область допустимых решений представляет собой множество пар (x1, x2), для которых значение x1 не меньше 1 и не больше 10, а значение x2 не меньше 5 и не больше 12. Заметим, что множество допустимых решений рассматривается отдельно от целевой функции, которая определяет критерий оптимизации и которая в вышеприведённом примере равна x12+x24.{\displaystyle x_{1}^{2}+x_{2}^{4}.}
Во многих задачах допустимая область решений включает ограничение, по которому одна и более переменных должны быть неотрицательными. В задачах чисто целочисленного программирования множество допустимых решений состоит из целых чисел (или некоторого подмножества). В задачах линейного программирования область допустимых решений является выпуклым политопом — областью в многомерном пространстве, границы которого образованы гиперплоскостями[1].
Удовлетворение ограничений — это процесс поиска точки в области допустимых решений.
При ограничениях в виде неравенств точка может быть либо внутренней точкой (допустимой точкой), либо граничной точкой (допустимой точкой), либо внешней точкой (недопустимой точкой). Активным, или связывающим, ограничением называется такое, которое в данной точке превращается в равенство[1]. Некоторые алгоритмы могут использовать понятие активного ограничения для построения более эффективного алгоритма (см. метод переменного базиса.
Если для задачи не существует допустимой точки, задача называется недопустимой.
Условный оптимум представляет собой локальный оптимум, лежащий на границе допустимой области[1].
Выпуклая область допустимых решений[править | править код]
 В задаче линейного программирования набор линейных ограничений образует выпуклую область допустимых решений. Для двух переменных эта область имеет форму выпуклого многоугольника.
В задаче линейного программирования набор линейных ограничений образует выпуклую область допустимых решений. Для двух переменных эта область имеет форму выпуклого многоугольника.Выпуклая область допустимых решений — это множество решений, в котором отрезок, соединяющий два допустимых решения, содержит только допустимые точки и не проходит через какую-либо недопустимую точку. Выпуклое множество допустимых решений возникает во многих типах задач, включая задачи линейного программирования, и представляют определённый интерес, поскольку, если задача заключается в оптимизации выпуклой целевой функции, в общем случае такую задачу проще решить на выпуклом множестве решений, и любой локальный оптимум[en] будет также глобальным оптимумом[en].
Если ограничения задачи оптимизации совместно противоречивы, не существует точки, которая бы удовлетворяла всем ограничениям, а тогда область допустимых решений пуста. В этом случае задача не имеет решений и говорят, что она недопустима[1].
Ограниченные и неограниченные области допустимых решений[править | править код]
 Ограниченная область допустимых решений (сверху) и неограниченная (снизу). Нижняя область распространяется направо неограниченно.
Ограниченная область допустимых решений (сверху) и неограниченная (снизу). Нижняя область распространяется направо неограниченно.Множество допустимых решений может быть ограниченным или неограниченным. Например, множество допустимых решений, определяемое ограничениями {x ≥ 0, y ≥ 0}, является неограниченным, поскольку в некоторых направлениях можно идти бесконечно, оставаясь в области допустимых решений. Для контраста множество допустимых решений, образованное ограничениями {x ≥ 0, y ≥ 0, x + 2y ≤ 4}, является ограниченным, поскольку движение в любом направлении ограничено. В задачах линейного программирования с n переменными необходимым, но не достаточным условием ограниченности области допустимых решений является наличие как минимум n + 1 ограничений.
Если множество допустимых решений является неограниченной, оптимальное решение может как существовать, так и не существовать, в зависимости от поведения целевой функции. Например, если множество определено ограничениями {x ≥ 0, y ≥ 0}, то задача оптимизации x + y не имеет решений, поскольку любой кандидат может быть улучшен путём увеличения x или y, а вот задача минимизировать x + y имеет оптимальное решение (а именно, в точке (x, y) = (0, 0)).
- ↑ 1 2 3 4 5 Д. Химмельблау. Прикладное нелинейное программирование. — Москва: «Мир», 1975. — С. 36.
- ↑ Л.Р. Форд, Д.Р. Фалкерсон. Потоки в сетях. — Москва: «Мир», 1966. — С. 48.
ru.wikiyy.com
Свойства области допустимых решений
Область допустимых решений выпуклая.
Это всегда многоугольник (многогранник в пространстве более двух переменных).
Оптимальное решение достигается в угловой точке. Если оптимальное решение достигается в двух угловых точках, то оно достигается и на отрезке, соединяющем эти точки.
Глава 2. Математические свойства задачи линейного программирования
2.1. Свойства области допустимых решений
Пусть дана задача в канонической форме:
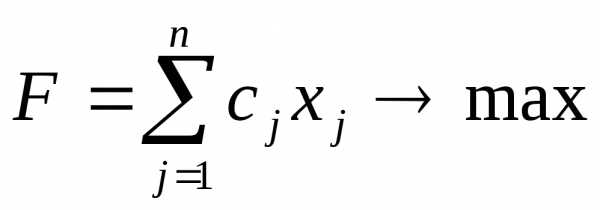
(1)
(2)
(3)
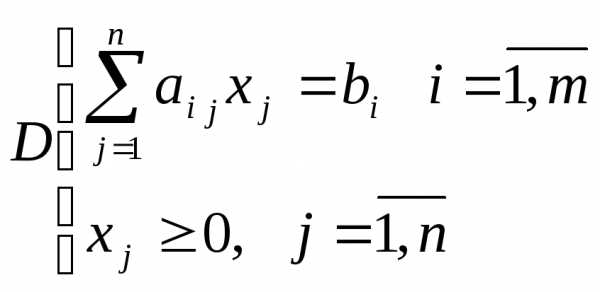
Пусть все уравнения линейно-независимые.
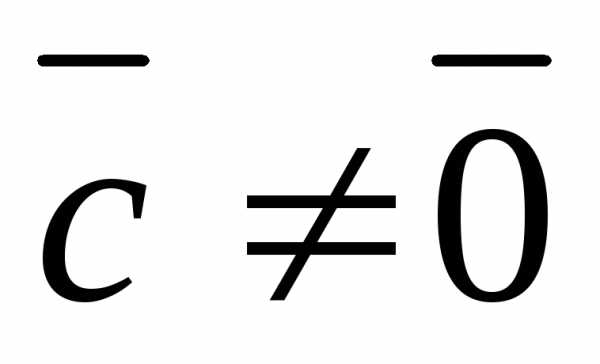
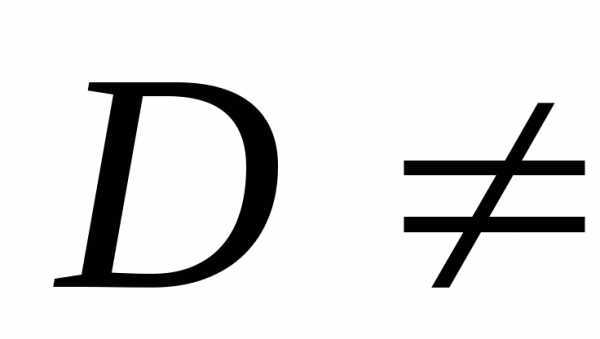 ø
ø
И пусть есть
несколько 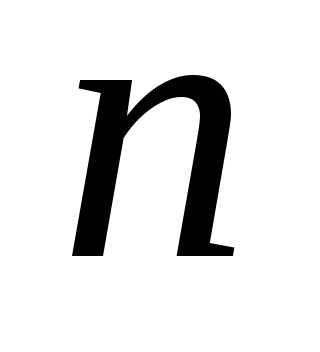 —
мерных векторов.
—
мерных векторов.
Выпуклая оболочка 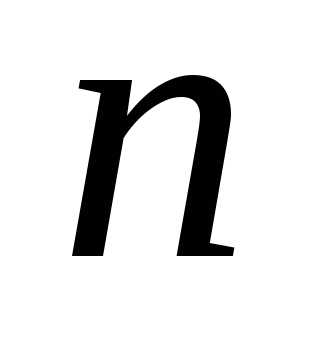 —
мерных векторов – множество точек вида:
—
мерных векторов – множество точек вида:
(4)
(5)
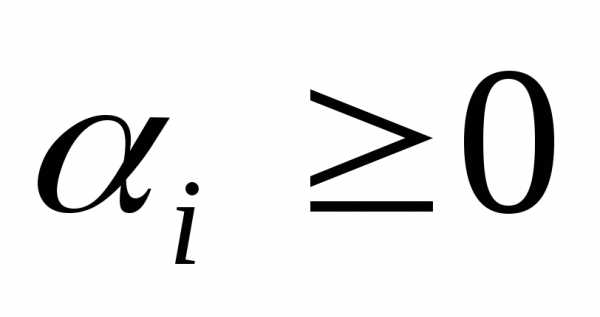 ,
, 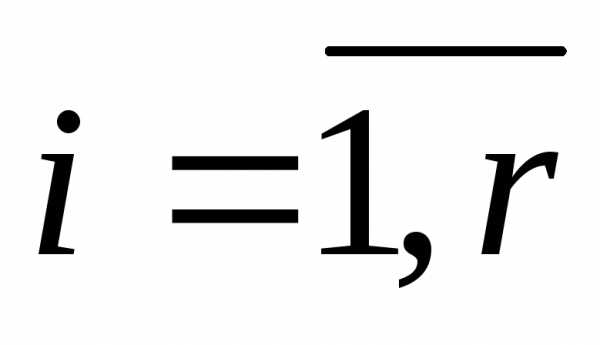 ,
,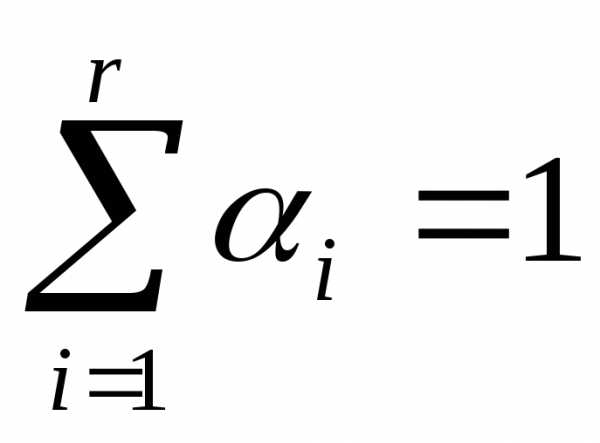
Выпуклая линейная комбинация двух векторов называется отрезком.

(6)
, Область 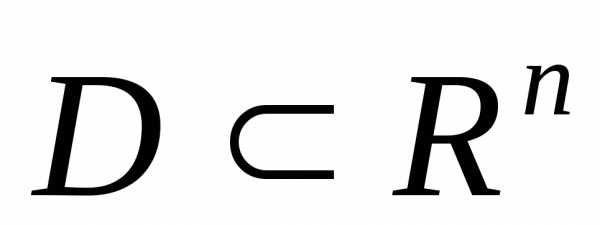 называетсявыпуклой,
если вместе с любыми двумя своими точками
она содержит отрезок, соединяющий их.
называетсявыпуклой,
если вместе с любыми двумя своими точками
она содержит отрезок, соединяющий их.
Теорема
1: Область
допустимых решений 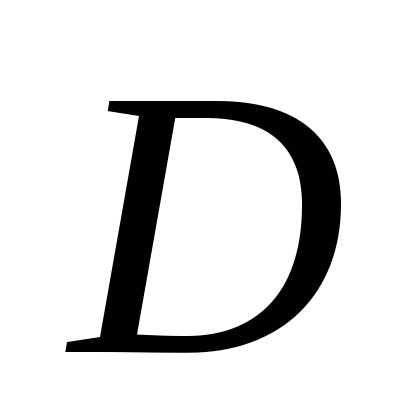 задачи ЛП выпуклая.
задачи ЛП выпуклая.
Доказательство:
Пусть, т.е. для них выполняются (2) и (3).
таким образом, условие (3)выполняется.
таким образом и условие (2) выполняется, произвольная точка отрезка принадлежит области D, то есть эта область выпукла.
Теорема доказана.
Точка называетсяугловой (крайней), если не существует двух других точек области, на отрезке между которыми лежит эта точка.
не 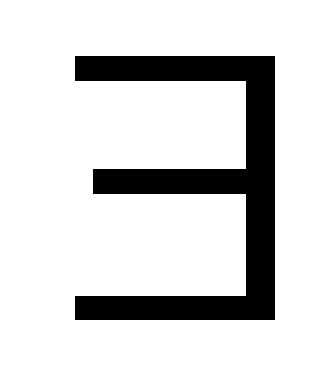
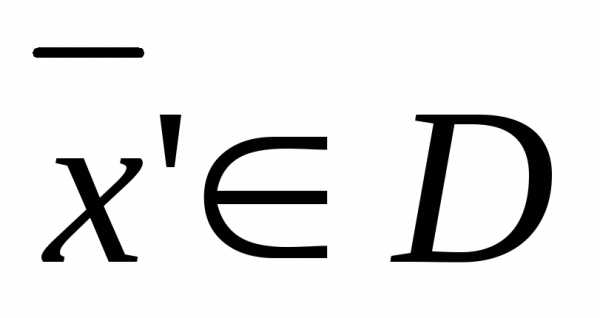 ,
,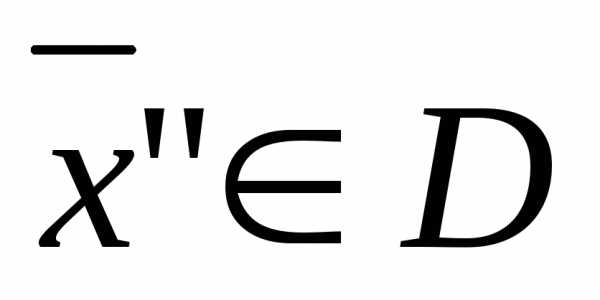 ,
,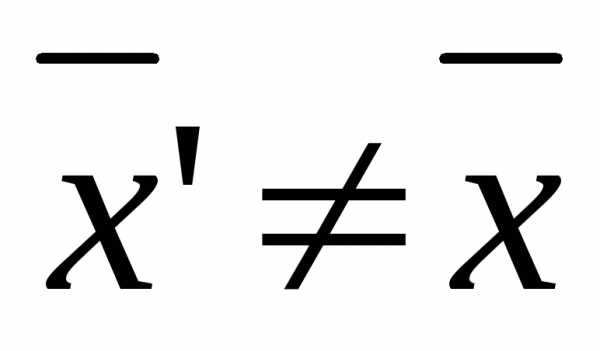
(7)
, ,
таких, что
,
,
таких, что
, Лемма
1: Область
допустимых решений 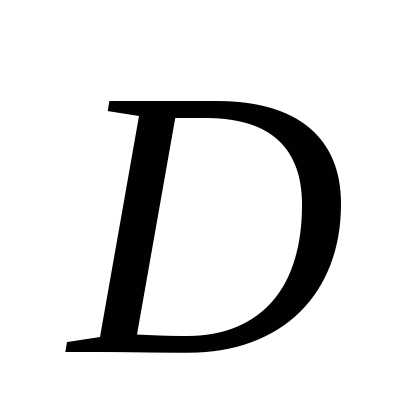 задачи ЛП является выпуклой линейной
комбинацией своих угловых точек.
задачи ЛП является выпуклой линейной
комбинацией своих угловых точек.
Таким образом, если найти все угловые точки, то любая точка внутри области записывается через уравнение (4).
Теорема
2: Оптимальное
решение задачи ЛП достигается в одной
из угловых точек области допустимых
решений 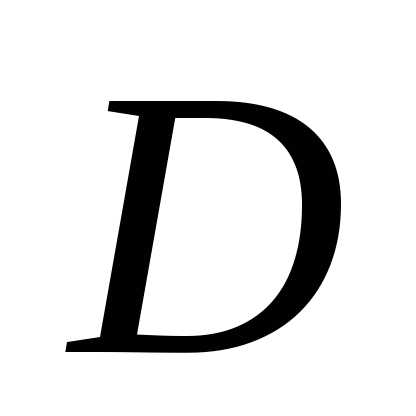 .
.
Покажем, что оптимальное решение не может быть внутри области.
Пусть – внутренняя точка области. Тогда функция дифференцируема в этой точке:
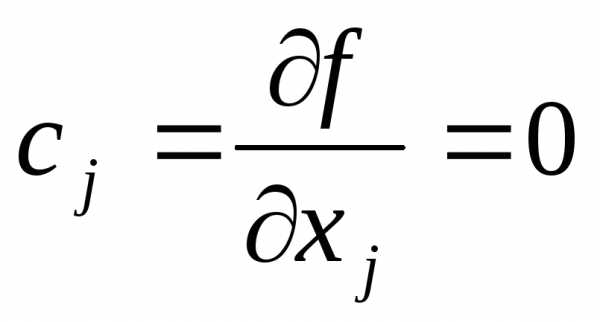
Так как в этой точке достигается максимум, то и производная здесь обратится в ноль.

Но это противоречит
условию, которое мы накладывали ранее,
а именно 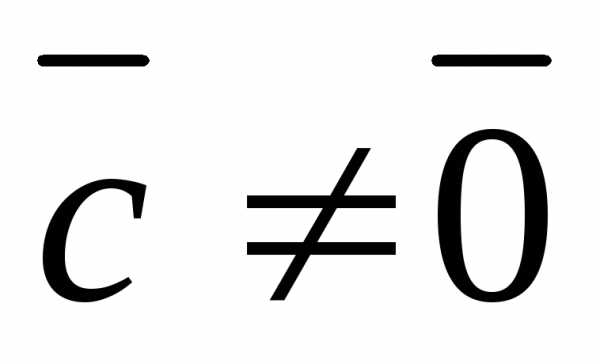 .
Значит точка, в которой достигается
оптимальное решение, лежит на границе
области. Можно показать [8], что хотя бы
одно оптимальное решение достигается
в угловой точке.
.
Значит точка, в которой достигается
оптимальное решение, лежит на границе
области. Можно показать [8], что хотя бы
одно оптимальное решение достигается
в угловой точке.
2.2. Базисные и опорные решения
Напомним, что
допустимое решение задачи линейного
программирования называется планом
(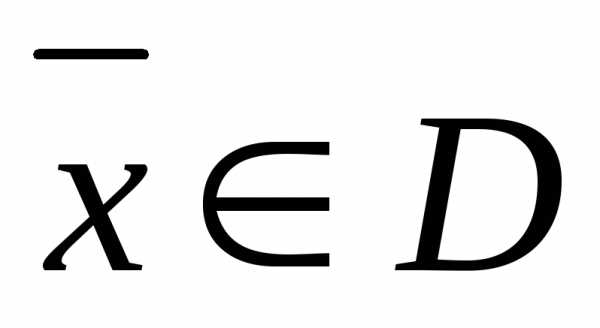 ).
В силу условия (3) компоненты плана
неотрицательны. Выделим отдельно
положительные и отрицательные компоненты.
Пусть первыеk компонент положительны.
Будем рассматривать вектора условий
при положительных и отрицательных
компонентах плана.
).
В силу условия (3) компоненты плана
неотрицательны. Выделим отдельно
положительные и отрицательные компоненты.
Пусть первыеk компонент положительны.
Будем рассматривать вектора условий
при положительных и отрицательных
компонентах плана.
Допустимое решение называетсяопорным, если вектора условий при его положительных компонентах решения линейно-независимы.
Вектора линейно-зависимые, если (для трех векторов)такие, что выполняется равенство; либо если определитель из этих векторов равен нулю.
Пример:




8
10
5
12
10
18
7
15
19
22
9
23
Проверим, опорное это решение или нет:
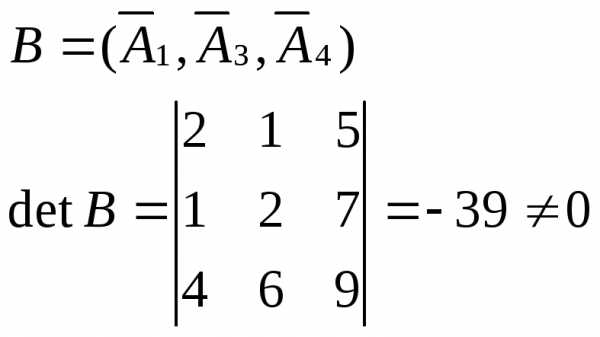

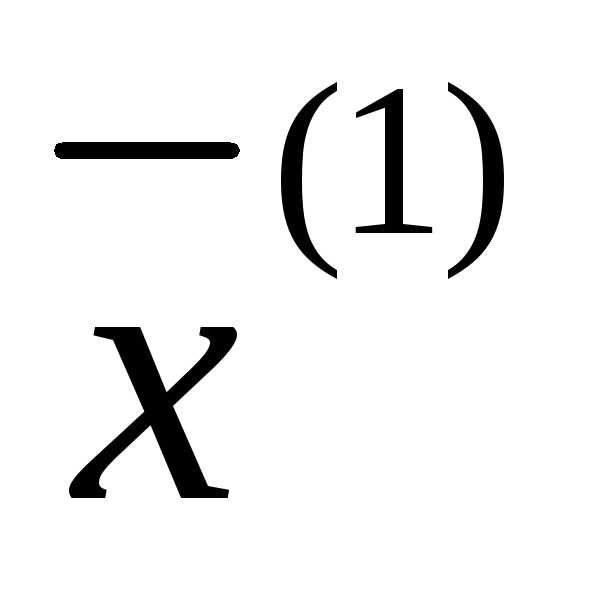 –опорное решение
(невырожденное).
–опорное решение
(невырожденное).
В трехмерном пространстве максимум только 3 вектора могут быть независимыми.

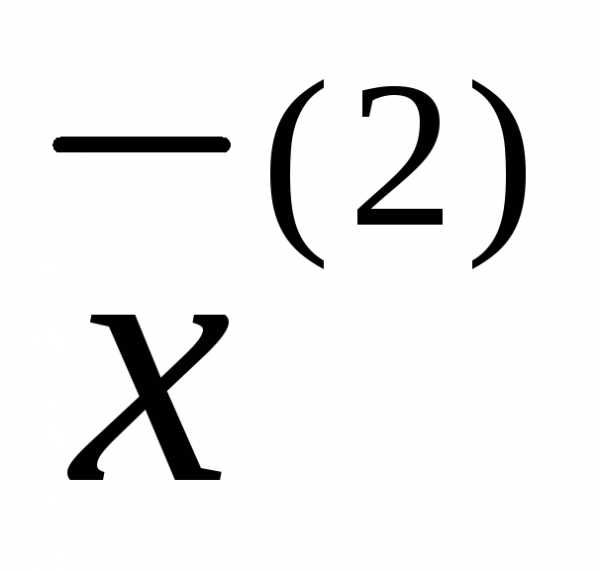 –не является опорным
решением, так как векторы
линейно-зависимые. Значит, эта точка
будет внутренней точкой области.
–не является опорным
решением, так как векторы
линейно-зависимые. Значит, эта точка
будет внутренней точкой области.
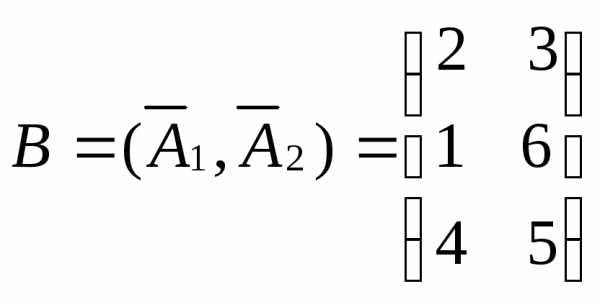

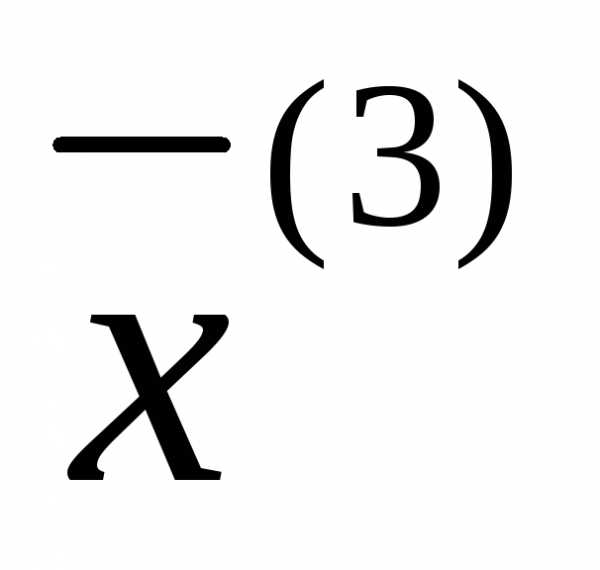 –опорное решение
(вырожденное).
–опорное решение
(вырожденное).
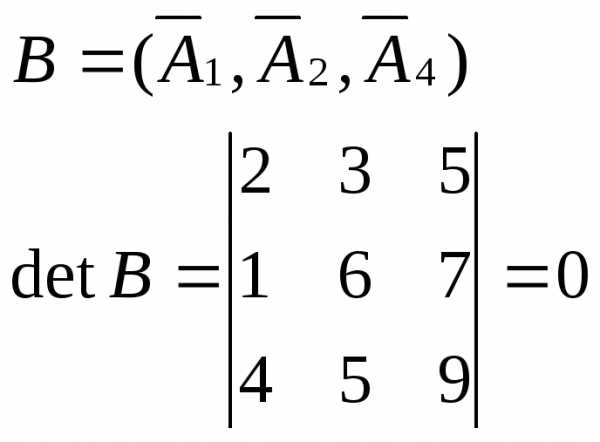
Так как определитель равен нулю, вектора линейно-зависимые.

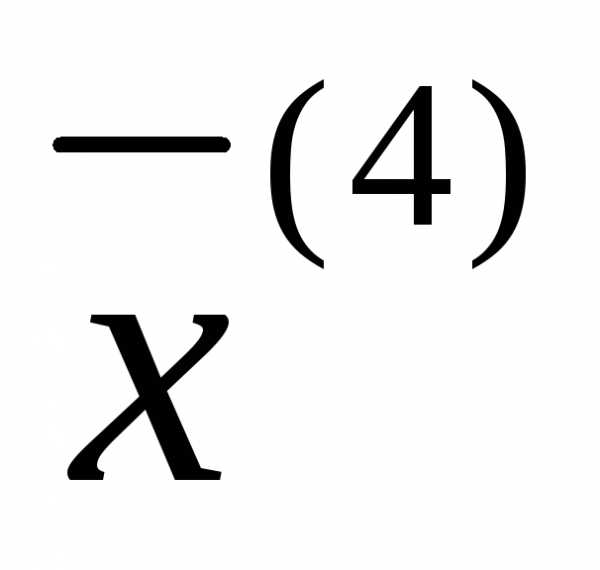 –не является опорным
решением.
–не является опорным
решением.
Положительные компоненты опорного решения называются базисными.
Вектора условий линейных компонентов могут быть базисом в пространстве.
Базис 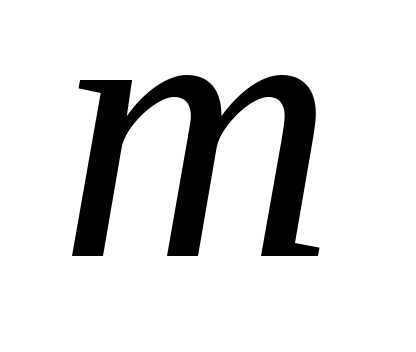 —
мерного пространства – совокупность любых
—
мерного пространства – совокупность любых 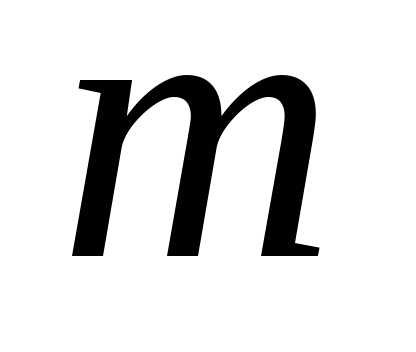 линейно-независимых векторов
линейно-независимых векторов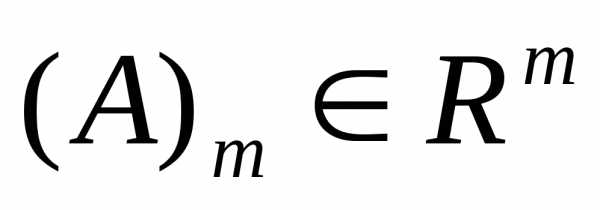 .
.
Опорное решение называется невырожденным, если количество положительных компонент равно числу линейно-независимых ограничений (k=m).
Опорное решение называется вырожденным, если количество положительных компонент меньше числа линейно-независимых ограничений (k<m).
Нулевые переменные невырожденного опорного решения называются свободными.
Матрица, состоящая из векторов при положительных компонентах невырожденного опорного плана, называется базисной.
Базисное решение – решение системы уравнений (2) , если вектора условий при егоненулевых компонентах линейно-независимые.
Базисная матрица – матрица из 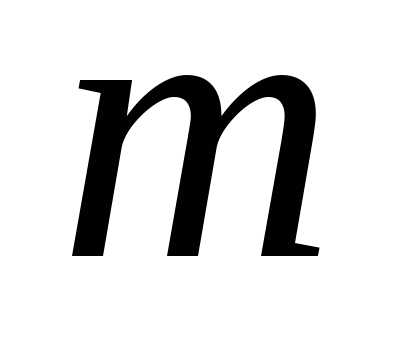 линейно-независимых векторов условий,
содержащая все вектора условий при
ненулевых компонентах. Она всегда
квадратная.
линейно-независимых векторов условий,
содержащая все вектора условий при
ненулевых компонентах. Она всегда
квадратная.
Базисная матрица невырожденного решения определяется однозначно, а базисная матрица вырожденного – неоднозначно.
Для определения
базисного решения нужно выбрать
произвольные 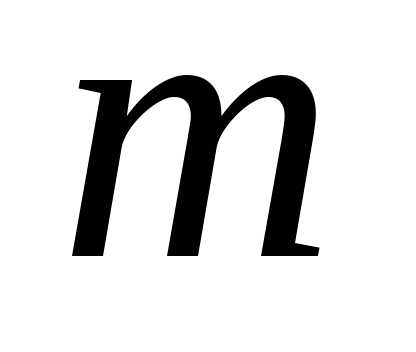 переменных
переменных ,
вычислить определительB из векторов условий этих переменных.
Если
,
то занулить остальные переменные. Тогда
для базисных переменных получим систему
уравнений:
,
вычислить определительB из векторов условий этих переменных.
Если
,
то занулить остальные переменные. Тогда
для базисных переменных получим систему
уравнений:
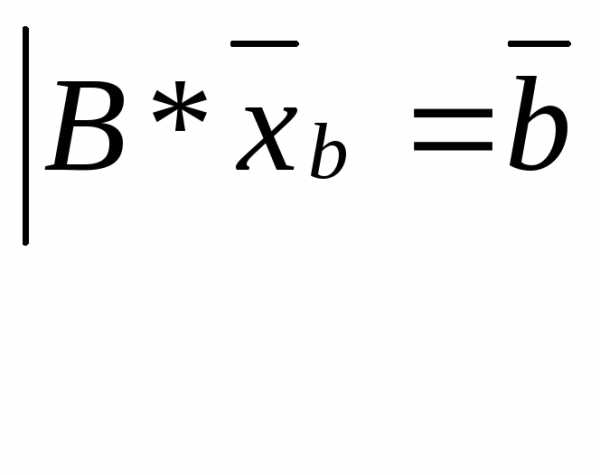
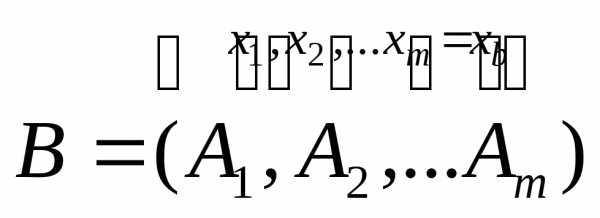
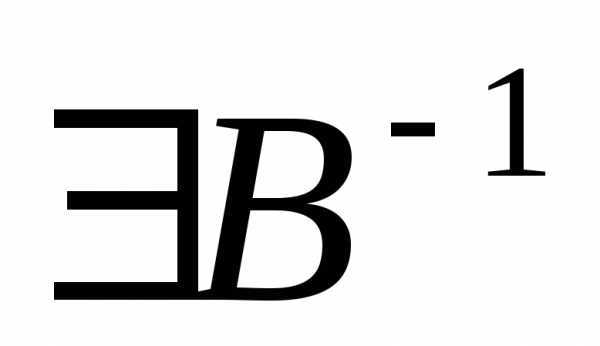
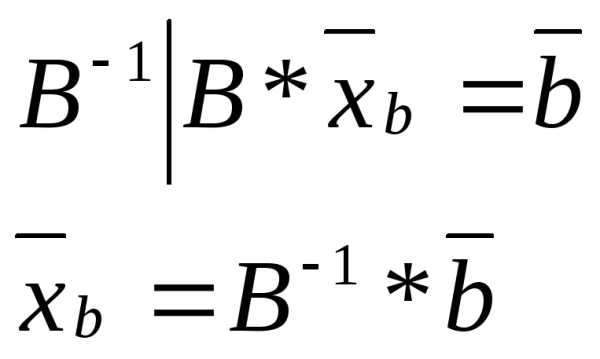
(8)
Максимальное
количество базисных решений равно 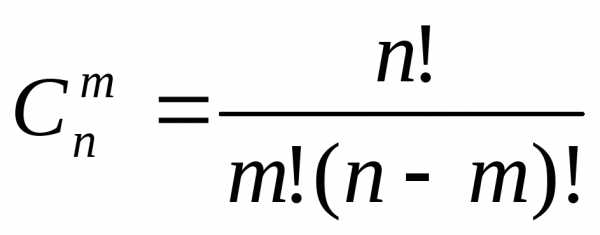 .
.
Опорное решение – допустимое базисное решение. Для поиска опорных решений можно перебрать все базисные решения и выбрать из них допустимые (с неотрицательными компонентами).
Теорема 3: опорные решения задачи ЛП совпадают с угловыми точками области допустимых решений.
Доказательство теоремы смотри в [8].
studfiles.net
Область допустимых решений — Википедия
 Задача с пятью линейными ограничениями (выделено синим цветом, включая условие неотрицательности). При отсутствии требований целочисленности решения область допустимых решений ограничена синими отрезками, а при наличии требований целочисленности область является множеством красных точек.
Задача с пятью линейными ограничениями (выделено синим цветом, включая условие неотрицательности). При отсутствии требований целочисленности решения область допустимых решений ограничена синими отрезками, а при наличии требований целочисленности область является множеством красных точек. 
В теории оптимизации допустимая область, допустимое множество, пространство поиска или пространство решений — это множество всех возможных точек (значений переменных) задачи оптимизации, которые удовлетворяют ограничениям[en] задачи. Эти ограничения могут включать неравенства, равенства и требование целочисленности решения [1][2]. Область допустимых решений является начальной областью поиска кандидатов в решение задачи, и эта область во время поиска может сужаться.
Например, возьмём задачу
- Минимизировать x12+x24{\displaystyle x_{1}^{2}+x_{2}^{4}}
с ограничениями на переменные x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}}
- 1≤x1≤10{\displaystyle 1\leq x_{1}\leq 10}
и
- 5≤x2≤12.{\displaystyle 5\leq x_{2}\leq 12.}
В этом случае область допустимых решений представляет собой множество пар (x1, x2), для которых значение x1 не меньше 1 и не больше 10, а значение x2 не меньше 5 и не больше 12. Заметим, что множество допустимых решений рассматривается отдельно от целевой функции, которая определяет критерий оптимизации и которая в вышеприведённом примере равна x12+x24.{\displaystyle x_{1}^{2}+x_{2}^{4}.}
Во многих задачах допустимая область решений включает ограничение, по которому одна и более переменных должны быть неотрицательными. В задачах чисто целочисленного программирования множество допустимых решений состоит из целых чисел (или некоторого подмножества). В задачах линейного программирования область допустимых решений является выпуклым политопом — областью в многомерном пространстве, границы которого образованы гиперплоскостями[1].
Удовлетворение ограничений — это процесс поиска точки в области допустимых решений.
Связанные определения
При ограничениях в виде неравенств точка может быть либо внутренней точкой (допустимой точкой), либо граничной точкой (допустимой точкой), либо внешней точкой (недопустимой точкой). Активным, или связывающим, ограничением называется такое, которое в данной точке превращается в равенство[1]. Некоторые алгоритмы могут использовать понятие активного ограничения для построения более эффективного алгоритма (см. метод переменного базиса.
Если для задачи не существует допустимой точки, задача называется недопустимой.
Условный оптимум представляет собой локальный оптимум, лежащий на границе допустимой области[1].
Видео по теме
Выпуклая область допустимых решений
 В задаче линейного программирования набор линейных ограничений образует выпуклую область допустимых решений. Для двух переменных эта область имеет форму выпуклого многоугольника.
В задаче линейного программирования набор линейных ограничений образует выпуклую область допустимых решений. Для двух переменных эта область имеет форму выпуклого многоугольника.Выпуклая область допустимых решений — это множество решений, в котором отрезок, соединяющий два допустимых решения, содержит только допустимые точки и не проходит через какую-либо недопустимую точку. Выпуклое множество допустимых решений возникает во многих типах задач, включая задачи линейного программирования, и представляют определённый интерес, поскольку, если задача заключается в оптимизации выпуклой целевой функции, в общем случае такую задачу проще решить на выпуклом множестве решений, и любой локальный оптимум[en] будет также глобальным оптимумом[en].
Отсутствие допустимых решений
Если ограничения задачи оптимизации совместно противоречивы, не существует точки, которая бы удовлетворяла всем ограничениям, а тогда область допустимых решений пуста. В этом случае задача не имеет решений и говорят, что она недопустима[1].
Ограниченные и неограниченные области допустимых решений
 Ограниченная область допустимых решений (сверху) и неограниченная (снизу). Нижняя область распространяется направо неограниченно.
Ограниченная область допустимых решений (сверху) и неограниченная (снизу). Нижняя область распространяется направо неограниченно.Множество допустимых решений может быть ограниченным или неограниченным. Например, множество допустимых решений, определяемое ограничениями {x ≥ 0, y ≥ 0}, является неограниченным, поскольку в некоторых направлениях можно идти бесконечно, оставаясь в области допустимых решений. Для контраста множество допустимых решений, образованное ограничениями {x ≥ 0, y ≥ 0, x + 2y ≤ 4}, является ограниченным, поскольку движение в любом направлении ограничено. В задачах линейного программирования с n переменными необходимым, но не достаточным условием ограниченности области допустимых решений является наличие как минимум n + 1 ограничений.
Если множество допустимых решений является неограниченной, оптимальное решение может как существовать, так и не существовать, в зависимости от поведения целевой функции. Например, если множество определено ограничениями {x ≥ 0, y ≥ 0}, то задача оптимизации x + y не имеет решений, поскольку любой кандидат может быть улучшен путём увеличения x или y, а вот задача минимизировать x + y имеет оптимальное решение (а именно, в точке (x, y) = (0, 0)).
- ↑ 1 2 3 4 5 Д. Химмельблау. Прикладное нелинейное программирование. — Москва: «Мир», 1975. — С. 36.
- ↑ Л.Р. Форд, Д.Р. Фалкерсон. Потоки в сетях. — Москва: «Мир», 1966. — С. 48.
wiki2.red