Независимая вероятность – Теория вероятности. Вероятность события, случайные события (теория вероятности). Независимые и несовместные события в теории вероятности

Зависимые и независимые случайные события

Понятия зависимости и независимости случайных событий. Условная вероятность. Формулы сложения и умножения вероятностей для зависимых и независимых случайных событий. Формула полной вероятности и формула Байеса.

Теоремы сложения вероятностей

Найдем вероятность суммы событий [cbm]A[/cbm] и [cbm]B[/cbm] (в предположении их совместности либо несовместности).

Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:

[cbm]P\{A+B+\ldots+N\}=P\{A\}+P\{B\}+\ldots+P\{N\}.[/cbm]

Пример 1. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го — 0,04; 46-го и большего — 0,01. Найти вероятность того, что будет продана пара мужской обуви не меньше 44-го размера.

Решение. Искомое событие [cbm]D[/cbm] произойдет, если будет продана пара обуви 44-го размера (событие [cbm]A[/cbm] ) или 45-го (событие [cbm]B[/cbm] ), или не меньше 46-го (событие [cbm]C[/cbm] ), т. е. событие [cbm]D[/cbm] есть сумма событий [cbm]A,B,C[/cbm] . События [cbm]A[/cbm] , [cbm]B[/cbm] и [cbm]C[/cbm] несовместны. Поэтому согласно теореме о сумме вероятностей получаем

[cbm]P\{D\}=P\{A+B+C\}=P\{A\}+P\{B\}+P\{C\}=0,\!12+0,\!04+0,\!01[/cbm] [cbm]=0,\!17.[/cbm]

Пример 2. При условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше 44-го размера.

Решение. События «очередной будет продана пара обуви меньше 44-го размера» и «будет продана пара обуви размера не меньше 44-го» противоположные. Поэтому по формуле (1.2) вероятность наступления искомого события

[cbm]P\{\overline{D}\}=1-P\{D\}=1-0,\!17=0,\!83.[/cbm]

поскольку [cbm]P\{D\}=0,\!17[/cbm] , как это было найдено в примере 1.

Теорема 2.1 сложения вероятностей справедлива только для несовместных событий. Использование ее для нахождения вероятности совместных событий может привести к неправильным, а иногда и абсурдным выводам, что наглядно видно на следующем примере. Пусть выполнение заказа в срок фирмой «Electra Ltd» оценивается вероятностью 0,7. Какова вероятность того, что из трех заказов фирма выполнит в срок хотя бы какой-нибудь один? События, состоящие в том, что фирма выполнит в срок первый, второй, третий заказы обозначим соответственно [cbm]A,B,C[/cbm] . Если для отыскания искомой вероятности применить теорему 2.1 сложения вероятностей, то получим [cbm]P\{A+B+C\}=0,\!7+0,\!7+0,\!7=2,\!1[/cbm] . Вероятность события оказалась больше единицы, что невозможно. Это объясняется тем, что события [cbm]A,B,C[/cbm] являются совместными. Действительно, выполнение в срок первого заказа не исключает выполнения в срок двух других.

Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).

Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:

[cbm]P\{A+B\}=P\{A\}+P\{B\}-P\{AB\}.[/cbm]

---

Зависимые и независимые события. Условная вероятность

Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.

Пример 3. Монета брошена два раза. Вероятность появления «герба» в первом испытании (событие [cbm]A[/cbm] ) не зависит от появления или не появления «герба» во втором испытании (событие [cbm]B[/cbm] ). В свою очередь, вероятность появления «герба» во втором испытании не зависит от результата первого испытания. Таким образом, события [cbm]A[/cbm] и [cbm]B[/cbm] независимые.

Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.

События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события [cbm]B[/cbm] , вычисленная в предположении осуществления другого события [cbm]A[/cbm] , называется условной вероятностью события [cbm]B[/cbm] и обозначается [cbm]P\{B|A\}[/cbm] .

Условие независимости события [cbm]B[/cbm] от события [cbm]A[/cbm] записывают в виде [cbm]P\{B|A\}=P\{B\}[/cbm] , а условие его зависимости — в виде [cbm]P\{B|A\}\ne{P\{B\}}[/cbm] . Рассмотрим пример вычисления условной вероятности события.

---

Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.

Решение. Обозначим [cbm]A[/cbm] извлечение изношенного резца в первом случае, а [cbm]\overline{A}[/cbm] — извлечение нового. Тогда [cbm]P\{A\}=\frac{2}{5},~P\{\overline{A}\}=1-\frac{2}{5}=\frac{3}{5}[/cbm] . Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.

Обозначим [cbm]B[/cbm] событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:

[cbm]P\{B|A\}=\frac{1}{4},~~~P\{B|\overline{A}\}=\frac{2}{4}=\frac{1}{2}.[/cbm]

Следовательно, вероятность события [cbm]B[/cbm] зависит от того, произошло или нет событие [cbm]A[/cbm] .

---

Формулы умножения вероятностей

Пусть события [cbm]A[/cbm] и [cbm]B[/cbm] независимые, причем вероятности этих событий известны. Найдем вероятность совмещения событий [cbm]A[/cbm] и [cbm]B[/cbm] .

Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

[cbm]P\{AB\}=P\{A\}\cdot P\{B\}.[/cbm]

Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

[cbm]P\{A_1A_2\ldots{A_n}\}=P\{A_1\}P\{A_2\}\ldots{P\{A_n\}}.[/cbm]

---

Пример 5. Три ящика содержат по 10 деталей. В первом ящике — 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.

Решение. Вероятность того, что из первого ящика взята стандартная деталь (событие [cbm]A[/cbm] ), [cbm]P\{A\}=\frac{8}{10}=\frac{4}{5}[/cbm] . Вероятность того, что из второго ящика взята стандартная деталь (событие [cbm]B[/cbm] ), [cbm]P\{B\}=\frac{7}{10}[/cbm] . Вероятность того, что из третьего ящика взята стандартная деталь (событие [cbm]C[/cbm] ), [cbm]P\{C\}=\frac{9}{10}[/cbm] . Так как события [cbm]A[/cbm] , [cbm]B[/cbm] и [cbm]C[/cbm] независимые в совокупности, то искомая вероятность (по теореме умножения)

[cbm]P\{ABC\}=P\{A\}P\{B\}P\{C\}=\frac{4}{5}\frac{7}{10}\frac{9}{10}=0,\!504.[/cbm]

Пусть события [cbm]A[/cbm] и [cbm]B[/cbm] зависимые, причем вероятности [cbm]P\{A\}[/cbm] и [cbm]P\{B|A\}[/cbm] известны. Найдем вероятность произведения этих событий, т. е. вероятность того, что появится и событие [cbm]A[/cbm] , и событие [cbm]B[/cbm] .

Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

[cbm]P\{AB\}=P\{A\}\cdot P\{B|A\};\qquad P\{AB\}=P\{B\}\cdot P\{A|B\}[/cbm]

Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.

---

Пример 6. В урне находятся 5 белых шаров, 4 черных и 3 синих. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие [cbm]A[/cbm] ), при втором — черный (событие [cbm]B[/cbm] ) и при третьем — синий (событие [cbm]C[/cbm] ).

Решение. Вероятность появления белого шара при первом испытании [cbm]P\{A\}=\frac{5}{12}[/cbm] . Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, т. е. условная вероятность [cbm]P\{B|A\}=\frac{4}{11}[/cbm] . Вероятность появления синего шара при третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором — черный, [cbm]P\{C|AB\}=\frac{3}{10}[/cbm] . Искомая вероятность

[cbm]P\{ABC\}=P\{A\}P\{B|A\}P\{C|AB\}=\frac{5}{12}\frac{4}{11}\frac{3}{10}.[/cbm]

---

Формула полной вероятности

Теорема 2.5. Если событие [cbm]A[/cbm] наступает только при условии появления одного из событий [cbm]B_1,B_2,\ldots{B_n}[/cbm] , образующих полную группу несовместных событий, то вероятность события [cbm]A[/cbm] равна сумме произведений вероятностей каждого из событий [cbm]B_1,B_2,\ldots{B_n}[/cbm] на соответствующую условную вероятность события [cbm]B_1,B_2,\ldots{B_n}[/cbm] :

[cbm]P\{A\}=\sum\limits_{i=1}^{n}P\{B_i\}P\{A|B_i\}.[/cbm]

(2.1)

При этом события [cbm]B_i,~i=1,\ldots,n[/cbm] называются гипотезами, а вероятности [cbm]P\{B_i\}[/cbm] — априорными. Эта формула называется формулой полной вероятности.

Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.

Решение. Обозначим [cbm]A[/cbm] событие, означающее годность собранного узла; [cbm]B_1[/cbm] , [cbm]B_2[/cbm] и [cbm]B_3[/cbm] — события, означающие, что детали сделаны соответственно на первом, втором и третьем станке. Тогда

[cbm]P\{B_1\}=0,\!5;~~~~~P\{B_2\}=0,\!3;~~~~~P\{B_3\}=0,\!2;[/cbm]
[cbm]P\{A|B_1\}=0,\!98;~~~P\{A|B_2\}=0,\!95;~~~P\{A|B_3\}=0,\!8.[/cbm]

Искомая вероятность

[cbm]\begin{gathered}P\{A\}=P\{B_1\}P\{A|B_1\}+P\{B_2\}P\{A|B_2\}+P\{B_3\}P\{A|B_3\}=\hfill\\=0,\!5\cdot0,\!98+0,\!3\cdot0,\!95+0,\!2\cdot0,\!8=0,\!935.\end{gathered}[/cbm]

---

Формула Байеса

Эта формула применяется при решении практических задач, когда событие [cbm]A[/cbm] , появляющееся совместно с каким-либо из событий [cbm]B_1,B_2,\ldots{B_n}[/cbm] , образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез [cbm]B_1,B_2,\ldots{B_n}[/cbm] . Априорные (до опыта) вероятности [cbm]P\{B_1\},P\{B_2\},\ldots{P\{B_n\}}[/cbm] известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности [cbm]P\{B_1|A\},P\{B_2|A\},\ldots{P\{B_n|A\}}[/cbm] . Для гипотезы [cbm]B_j[/cbm] формула Байеса выглядит так:

[cbm]P\{B_j|A\}=\frac{P\{B_j\} P\{A|B_j\}}{P\{A\}}.[/cbm]

Раскрывая в этом равенстве [cbm]P\{A\}[/cbm] по формуле полной вероятности (2.1), получаем

[cbm]P\{B_j|A\}=\dfrac{P\{B_j\}P\{A|B_j\}}{\sum\limits_{i=1}^{n}P\{B_i\}P\{A|B_i\}}.[/cbm]

---

Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.

Решение. Рассчитаем условные вероятности по формуле Байеса:

для первого станка

[cbm]P\{B_1|A\}=\dfrac{P\{B_1\}P\{A|B_1\}}{P\{A\}}=\frac{0,\!5\cdot0,\!98}{0,\!935}\approx0,\!525;[/cbm]

для второго станка

[cbm]P\{B_2|A\}=\dfrac{P\{B_2\}P\{A|B_2\}}{P\{A\}}=\frac{0,\!3\cdot0,\!95}{0,\!935}\approx0,\!304;[/cbm]

для третьего станка

[cbm]P\{B_3|A\}=\dfrac{P\{B_3\}P\{A|B_3\}}{P\{A\}}=\frac{0,\!2\cdot0,\!8}{0,\!935}\approx0,\!171.[/cbm]

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Источник

calcsbox.com

Зависимые и независимые события. Условная вероятность

Определения вероятности

Классическое определение

Классическое «определение» вероятности исходит из понятия равновозможности как объективного свойства изучаемых явлений. Равновозможность является неопределяемым понятием и устанавливается из общих соображений симметрии изучаемых явлений. Например, при подбрасывании монетки исходят из того, что в силу предполагаемой симметрии монетки, однородности материала и случайности (непредвзятости) подбрасывания нет никаких оснований для предпочтения «решки» перед «орлом» или наоборот, то есть выпадение этих сторон можно считать равновозможными (равновероятными).

Наряду с понятием равновозможности в общем случае для классического определения необходимо также понятие элементарного события (исхода), благоприятствующего или нет изучаемому событию A. Речь идет об исходах, наступление которых исключает возможность наступления иных исходов. Это несовместимые элементарные события. К примеру при бросании игральной кости выпадение конкретного числа исключает выпадение остальных чисел.

Классическое определение вероятности можно сформулировать следующим образом:

Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N:

Например, пусть подбрасываются две кости. Общее количество равновозможных исходов (элементарных событий) равно очевидно 36 (6 возможностей на каждой кости). Оценим вероятность выпадения 7 очков. Получение 7 очков возможно следующими способами: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. То есть всего 6 равновозможных исходов, благоприятствующих событию A — получению 7 очков. Следовательно, вероятность будет равна 6/36=1/6. Для сравнения вероятность получения 12 очков или 2 очков равна всего 1/36 — в 6 раз меньше.

Геометрическое определение

Несмотря на то, что классическое определение является интуитивно понятным и выведенным из практики, оно, как минимум не может быть непосредственно применено в случае, если количество равновозможных исходов бесконечно. Ярким примером бесконечного числа возможных исходов является ограниченная геометрическая область G, например, на плоскости, с площадью S. Случайно «подброшенная» «точка» с равной вероятностью может оказаться в любой точке этой области. Задача заключается в определении вероятности попадания точки в некоторую подобласть g с площадью s. В таком случая обобщая классическое определение можно прийти к геометрическому определению вероятности попадания в подобласть :

В виду равновозможности вероятность эта не зависит от формы области g, она зависит только от ее площади. Данное определение естественно можно обобщить и на пространство любой размерности, где вместо площади использовать понятие «объема». Более того, именно такое определение приводит к современному аксиоматическому определению вероятности. Понятие объема обобщается до понятия «меры» некоторого абстрактного множества, к которой предъявляются требования, которыми обладает и «объем» в геометрической интерпретации — в первую очередь, это неотрицательность и аддитивность.

Частотное (статистическое) определение

Классическое определение при рассмотрении сложных проблем наталкивается на трудности непреодолимого характера. В частности, в некоторых случаях выявить равновозможные случаи может быть невозможно. Даже в случае с монеткой, как известно существует явно не равновероятная возможность выпадения «ребра», которую из теоретических соображений оценить невозможно (можно только сказать, что оно маловероятно и то это соображение скорее практическое). Поэтому еще на заре становления теории вероятностей было предложено альтернативное «частотное» определение вероятности. А именно, формально вероятность можно определить как предел частоты наблюдений события A, предполагая однородность наблюдений (то есть одинаковость всех условий наблюдения) и их независимость друг от друга:

где — количество наблюдений, а — количество наступлений события .

Несмотря на то, что данное определение скорее указывает на способ оценки неизвестной вероятности — путем большого количества однородных и независимых наблюдений — тем не менее в таком определении отражено содержание понятия вероятности. А именно, если событию приписывается некоторая вероятность, как объективная мера его возможности, то это означает, что при фиксированных условиях и многократном повторении мы должны получить частоту его появления, близкую к (тем более близкую, чем больше наблюдений). Собственно, в этом заключается исходный смысл понятия вероятности. В основе лежит объективистский взгляд на явления природы. Ниже будут рассмотрены так называемые законы больших чисел, которые дают теоретическую основу (в рамках излагаемого ниже современного аксиоматического подхода) в том числе для частотной оценки вероятности.

Аксиоматическое определение

В современном математическом подходе вероятность задаётся аксиоматикой Колмогорова. Предполагается, что задано некоторое пространство элементарных событий . Подмножества этого пространства интерпретируются как случайные события. Объединение (сумма) некоторых подмножеств (событий) интерпретируется как событие, заключающееся в наступлении хотя бы одного из этих событий. Пересечение (произведение) подмножеств (событий) интерпретируется как событие, заключающееся в наступлении всех этих событий. Непересекающиеся множества интерпретируются как несовместные события (их совместное наступление невозможно). Соответственно, пустое множество означает невозможноесобытие.

Вероятностью (вероятностной мерой) называется мера (числовая функция) , заданная на множестве событий, обладющая следующими свойствами:

• Аддитивность: вероятность наступления хотя бы одного (то есть суммы) из попарно несовместных событий равна сумме вероятностей этих событий, то есть формально если т.е. при , то .

В случае если пространство элементарных событий X конечно, то достаточно указанного условия аддитивности для произвольных двух несовместных событий, из которого будет следовать аддитивность для любого конечного количества несовместных событий. Однако, в случае бесконечного (счетного или несчетного) пространства элементарных событий этого условия оказывается недостаточно. Требуется так называемая счетная или сигма- аддитивность, то есть выполнение свойства аддитивности для любого не более чем счетногосемейства попарно несовместных событий. Это необходимо для обеспечения «непрерывности» вероятностной меры.

Вероятностная мера может быть определена не для всех подмножеств множества . Предполагается, что она определена на некоторой сигма-алгебре подмножеств ^[6]. Эти подмножества называются измеримыми по данной вероятностной мере и именно они являются случайными событиями. Совокупность  — то есть множество элементарных событий, сигма-алгебра его подмножеств и вероятностная мера — называется вероятностным пространством.

   Непрерывные случайные величины.     Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины:   

   Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х.     Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины.     Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x равенству

(22)

   Функция называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x₁<x₂, то на основании формул (20) и (22) имеем

(23)

   Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств равна площади криволинейной трапеции с основанием[x₁,x₂], ограниченной сверху кривой (рис. 6).

   Так как , а на основании формулы (22)   

   , то

(24)

   Пользуясь формулой (22), найдем как производную интеграла по переменной верхней границе, считая плотность распределения непрерывной**:

(25)

   Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция непрерывна. Это следует из того, что F(х) в этих точках дифференцируема.     На основании формулы (23), полагая x₁=x, , имеем   

   В силу непрерывности функции F(х) получим, что   

   Следовательно   

   Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю.     Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств   

 , , , 

   Имеют одинаковую вероятность, т.е.   

   В самом деле, например,   

   так как     Замечание. Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытания конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания. В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение x₁ как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение x₁. Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение.     Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска.     Пример. Плотность распределения непрерывной случайной величины задана следующим образом:   

   График функции представлен па рис. 7. Определить вероятность того, что случайная величина примет значение, удовлетворяющее неравенствам .Найти функцию распределения заданной случайной величины. (Решение)

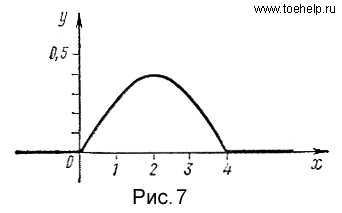
   Следующие два пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин — равномерному и нормальному распределениям. 

Дальше…

   * Функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода.     ** Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле,   

   Так как интеграл

   есть величина постоянная.

Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.

Пример 3. Монета брошена два раза. Вероятность появления «герба» в первом испытании (событие ) не зависит от появления или не появления «герба» во втором испытании (событие ). В свою очередь, вероятность появления «герба» во втором испытании не зависит от результата первого испытания. Таким образом, события и независимые.

Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.

События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события , называется условной вероятностью события и обозначается .

Условие независимости события от события записывают в виде , а условие его зависимости — в виде . Рассмотрим пример вычисления условной вероятности события.

Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.

Решение. Обозначим извлечение изношенного резца в первом случае, а — извлечение нового. Тогда . Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.

Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:

Следовательно, вероятность события зависит от того, произошло или нет событие .

Пло́тность вероя́тности — один из способов задания вероятностной меры на евклидовом пространстве . В случае, когда вероятностная мера является распределением случайной величины, говорят о плотности случайной величины.

Плотность вероятности Пусть является вероятностной мерой на , то есть определено вероятностное пространство , где обозначает борелевскую σ-алгебру на . Пусть обозначает меру Лебега на .

Определение 1. Вероятность называется абсолютно непрерывной (относительно меры Лебега) (), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

Если вероятность абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция такая, что

,

где использовано общепринятое сокращение , и интеграл понимается в смысле Лебега.

Определение 2. В более общем виде, пусть — произвольное измеримое пространство, а и — две меры на этом пространстве. Если найдется неотрицательная , позволяющая выразить меру через меру в виде

то такую функцию называют плотностью меры по мере , или производной Радона-Никодима меры относительно меры , и обозначают

.

studfiles.net

Независимость (теория вероятностей) | Математика

В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если значение одной из них не влияет на вероятность значений другой.

Независимые событияПравить

Будем считать, что дано фиксированное вероятностное пространство $ (\Omega, \mathcal{F}, \mathbb{P}) $.

Определение 1. Два события $ A,B\in \mathcal{F} $ независимы, если

$ \mathbb{P}(A \cap B) = \mathbb{P}(A) \cdot \mathbb{P}(B) $.

Замечание 1. В том случае, если вероятность одного события, скажем $ B $ ненулевая, то есть $ \mathbb{P}(B)>0 $, определение независимости эквивалентно:

$ \mathbb{P}(A \mid B ) = \mathbb{P}(A) $,

то есть условная вероятность события $ A $ при условии $ B $ равна безусловной вероятности события $ A $.

Определение 2. Пусть есть семейство (конечное или бесконечное) случайных событий $ \{A_{i}\}_{i\in I}\subset \mathcal{F} $, где $ I $ — произвольное индексное множество. Тогда эти события попарно независимы, если любые два события из этого семества независимы, то есть

$ \mathbb{P}(A_i \cap A_j) = \mathbb{P}(A_i) \cdot \mathbb{P}(A_j),\; \forall i \not= j $.

Определение 3. Пусть есть семейство (конечное или бесконечное) случайных событий $ \{A_{i}\}_{i\in I}\subset \mathcal{F} $. Тогда эти события совместно независимы, если для любого конечного набора этих событий $ \{A_{i_k}\}_{k=1}^N $ верно:

$ \mathbb{P}(A_{i_1} \cap \ldots \cap A_{i_N}) = \mathbb{P}( A_{i_1} ) \ldots \mathbb{P}(A_{i_N}) $.

Замечание 2. Cовместная независимость, очевидно, влечет попарную независимость. Обратное, вообще говоря, неверно.

Пример 1. Пусть брошены три уравновешенные монеты. Определим события следующим образом:

• $ A_1 $: монеты 1 и 2 упали одной и той же стороной;
• $ A_2 $: монеты 2 и 3 упали одной и той же стороной;
• $ A_3 $: монеты 1 и 3 упали одной и той же стороной;

Легко проверить, что любые два события из этого набора независимы. Все же три в совокупности зависимы, ибо зная, например, что события $ A_1,A_2 $ произошли, мы знаем точно, что $ A_3 $ также произошло.

Независимые сигма-алгебрыПравить

Определение 4. Пусть $ \mathcal{A}_1,\mathcal{A}_2 \subset \mathcal{F} $ две сигма-алгебры на одном и том же вероятностном пространстве. Они называются независимыми, если любые их представители независимы между собой, то есть:

$ \mathbb{P}(A_1 \cap A_2) = \mathbb{P}(A_1) \cdot \mathbb{P}(A_2),\; \forall A_1 \in \mathcal{A}_1,\, A_2\in \mathcal{A}_2 $.

Если вместо двух имеется целое семейство (возможно бесконечное) сигма-алгебр, то для него определяется попарная и совместная независимость очевидным образом.

Независимые случайные величиныПравить

ОпределенияПравить

Определение 5. Пусть дано семейство случайных величин $ (X_i)_{i\in I} $, так что $ X_i:\Omega \to \mathbb{R},\; \forall i\in I $. Тогда эти случайные величины попарно независимы, если попарно независимы порождённые ими сигма-алгебры $ \{\sigma(X_i)\}_{i\in I} $. Случайные величины независимы в совокупности, если таковы порождённые ими сигма-алгебры.

Определение, данное выше, эквивалентно любому другому из нижеперечисленных. Две случайные величины $ X,Y $ независимы тогда и только тогда, когда:

• Для любых $ A, B\in \mathcal{B}(\mathbb{R}) $,

$ \mathbb{P}(X \in A, Y \in B) = \mathbb{P}(X\in A) \cdot \mathbb{P}(Y \in B) $;

• Для любых борелевских функций $ f, g:\mathbb{R} \to \mathbb{R} $ случайные величины $ f(X), g(Y) $ независимы;
• Для любых ограниченных борелевских функций $ f,g:\mathbb{R} \to \mathbb{R} $

$ \mathbb{E}\left[f(X) g(Y)\right] = \mathbb{E}\left[f(X)\right] \cdot \mathbb{E}\left[g(Y)\right] $;

Свойства независимых случайных величинПравить

• Пусть $ \mathbb{P}^{X,Y} $ — распределение случайного вектора $ (X,Y) $, $ \mathbb{P}^X $ — распределение $ X $ и $ \mathbb{P}^Y $ — распределение $ Y $. Тогда $ X,Y $ независимы тогда и только тогда, когда

$ \mathbb{P}^{X,Y} = \mathbb{P}^X \otimes \mathbb{P}^Y $,

где $ \otimes $ обозначает (прямое) произведение мер;

$ F_{X,Y}(x,y) = F_X(x) \cdot F_Y(y) $;

• Пусть случайные величины $ X,Y $ дискретны. Тогда они независимы тогда и только тогда, когда

$ \mathbb{P}(X = i, Y = j) = \mathbb{P}(X=i) \cdot \mathbb{P}(Y = j) $.

• Пусть случайные величины $ X,Y $ совместно абсолютно непрерывны, то есть их совместное распределение имеет плотность $ f_{X,Y}(x,y) $. Тогда они независимы тогда и только тогда, когда

$ f_{X,Y}(x,y) = f_X(x) \cdot f_Y(y),\; \forall (x,y)\in \mathbb{R}^2 $,

где $ f_X(x), f_Y(y) $ — плотности случайных величин $ X $ и $ Y $ соответственно.


Эта статья содержит материал из статьи Независимость (теория вероятностей) русской Википедии.

ru.math.wikia.com

Теория вероятностей, действия над вероятностями

Необходимость в действиях над вероятностями наступает тогда, когда известны вероятности некоторых событий, а вычислить нужно вероятности других событий, которые связаны с данными событиями.

Сложение вероятностей используется тогда, когда нужно вычислить вероятность объединения или логической суммы случайных событий.

Сумму событий A и B обозначают A + B или A ∪ B. Суммой двух событий называется событие, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий. Это означает, что A + B – событие, которое наступает тогда и только тогда, когда при наблюдении произошло событие A или событие B, или одновременно A и B.

Если события A и B взаимно несовместны и их вероятности даны, то вероятность того, что в результате одного испытания произойдёт одно из этих событий, рассчитывают, используя сложение вероятностей.

---

Теорема сложения вероятностей. Вероятность того, что произойдёт одно из двух взаимно несовместных событий, равна сумме вероятностей этих событий:

       (3)

---

Например, на охоте произведены два выстрела. Событие А – попадание в утку с первого выстрела, событие В – попадание со второго выстрела, событие (А + В) – попадание с первого или второго выстрела или с двух выстрелов. Итак, если два события А и В – несовместные события, то А + В – наступление хотя бы одного из этих событий или двух событий.

Можно рассчитать как классические, так и статистические вероятности.

---

Пример 1. В ящике 30 мячиков одинаковых размеров: 10 красных, 5 синих и 15 белых. Вычислить вероятность того, что не глядя будет взят цветной (не белый) мячик.

Решение. Примем, что событие А – «взят красный мячик», а событие В – «взят синий мячик». Тогда событие — «взят цветной (не белый) мячик». Найдём вероятность события А:

и события В:

События А и В – взаимно несовместные, так как если взят один мячик, то нельзя взять мячики разных цветов. Поэтому используем сложение вероятностей:

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей — на странице «Различные задачи на сложение и умножение вероятностей».

---

Теорема сложения вероятностей для нескольких несовместных событий. Если события составляют полное множество событий, то сумма их вероятностей равна 1:

Сумма вероятностей противоположных событий также равна 1:

Противоположные события образуют полное множество событий, а вероятность полного множества событий равна 1.

Вероятности противоположных событий обычно обозначают малыми буквами p и q. В частности,

из чего следуют следующие формулы вероятности противоположных событий:

и .

---

Пример 2. Цель в тире разделена на 3 зоны. Вероятность того что некий стрелок выстрелит в цель в первой зоне равна 0,15, во второй зоне – 0,23, в третьей зоне – 0,17. Найти вероятность того, что стрелок попадет в цель и вероятность того, что стрелок попадёт мимо цели.

Решение: Найдём вероятность того, что стрелок попадёт в цель:

Найдём вероятность того, что стрелок попадёт мимо цели:

 

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей — на странице «Различные задачи на сложение и умножение вероятностей».

---

Два случайных события называются совместными, если наступление одного события не исключает наступления второго события в том же самом наблюдении. Например, при бросании игральной кости событием А считается выпадение числа 4, а событием В – выпадение чётного числа. Поскольку число 4 является чётным числом, эти два события совместимы. В практике встречаются задачи по расчёту вероятностей наступления одного из взаимно совместных событий.

---

Теорема сложения вероятностей для совместных событий. Вероятность того, что наступит одно из совместных событий, равна сумме вероятностей этих событий, из которой вычтена вероятность общего наступления обоих событий, то есть произведение вероятностей. Формула вероятностей совместных событий имеет следующий вид:

           

---

Поскольку события А и В совместимы, событие А + В наступает, если наступает одно из трёх возможных событий: или АВ. Согласно теореме сложения несовместных событий, вычисляем так:

         (5)

Событие А наступит, если наступит одно из двух несовместных событий:  или АВ. Однако вероятность наступления одного события из нескольких несовместных событий равна сумме вероятностей всех этих событий:

Поэтому

                              (6)

Аналогично:

Поэтому

                             (7)

Подставляя выражения (6) и (7) в выражение (5), получаем формулу вероятности для совместных событий:

             (8)

При использовании формулы (8) следует учитывать, что события А и В могут быть:

• взаимно независимыми;
• взаимно зависимыми.

Формула вероятности для взаимно независимых событий:

Формула вероятности для взаимно зависимых событий:

Если события А и В несовместны, то их совпадение является невозможным случаем и, таким образом, P(AB) = 0. Четвёртая формула вероятности для несовместных событий такова:

---

Пример 3. На автогонках при заезде на первой автомашине вероятность победить , при заезде на второй автомашине . Найти:

• вероятность того, что победят обе автомашины;
• вероятность того, что победит хотя бы одна автомашина;

 

Решение.

1) Вероятность того, что победит первая автомашина, не зависит от результата второй автомашины, поэтому события А (победит первая автомашина) и В (победит вторая автомашина) – независимые события. Найдём вероятность  того, что победят обе машины:

2) Найдём вероятность того, что победит одна из двух автомашин:

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей — на странице «Различные задачи на сложение и умножение вероятностей».

---

Решить задачу на сложение вероятностей самостоятельно, а затем посмотреть решение

Пример 4. Бросаются две монеты. Событие A — выпадение герба на первой монете. Событие B — выпадение герба на второй монете. Найти вероятность события C = A + B.

Посмотреть правильное решение и ответ.

Умножение вероятностей используют, когда следует вычислить вероятность логического произведения событий.

При этом случайные события должны быть независимыми. Два события называются взаимно независимыми, если наступление одного события не влияет на вероятность наступления второго события.

Логическим произведением двух событий А и В, обозначаемым А ∩ В, называют событие, которое понимают как одновременное наступление событий А и В. Больше о сути логического произведения можно узнать в соответствующем месте статьи «Булева алгебра (алгебра логики)».

---

Теорема умножения вероятностей для независимых событий. Вероятность одновременного наступления двух независимых событий А и В равна произведению вероятностей этих событий и вычисляется по формуле:

                   (4)

---

Пример 5. Монету бросают три раза подряд. Найти вероятность того, что все три раза выпадет герб.

Решение. Вероятность того, что при первом бросании монеты выпадет герб , во второй раз , в третий раз . Найдём вероятность того, что все три раза выпадет герб:

Решить задачи на умножение вероятностей самостоятельно, а затем посмотреть решение

Пример 6. Имеется коробка с девятью новыми теннисными мячами. Для игры берут три мяча, после игры их кладут обратно. При выборе мячей игранные от неигранных не отличают. Какова вероятность того, что после трёх игр в коробке не останется неигранных мячей?

Посмотреть правильное решение и ответ.

Пример 7. 32 буквы русского алфавита написаны на карточках разрезной азбуки. Пять карточек вынимаются наугад одна за другой и укладываются на стол в порядке появления. Найти вероятность того, что из букв получится слово «конец».

Посмотреть правильное решение и ответ.

---

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей, а также вычислять произведение нескольких событий — на странице «Различные задачи на сложение и умножение вероятностей».

---

Вероятность того, что произойдёт хотя бы одно из взаимно независимых событий , можно вычислить путём вычитания из 1 произведения вероятностей противоположных событий , то есть по формуле:

---

Пример 10. Грузы доставляют тремя видами транспорта: речным, железнодорожным и автотранспортом. Вероятность того, что груз будет доставлен речным транспортом, составляет 0,82, железнодорожным транспортом 0,87, автотранспортом 0,90. Найти вероятность того, что груз будет доставлен хотя бы одним из трёх видов транспорта.

Решение. Найдём вероятности противоположных событий – того, что груз не будет доставлен одним из видов транспорта:

Теперь у нас есть всё, чтобы найти требуемую в условии задачи вероятность того, что груз будет доставлен хотя бы одним из трёх видов транспорта:

Решить задачу на умножение вероятностей самостоятельно, а затем посмотреть решение

Пример 11. Из полной колоды карт (52 карты) вынимают одновременно четыре карты. Событие А — среди вынутых карт будет хотя бы одна бубновая. Событие B — среди вынутых карт будет хотя бы одна червонная. Найти вероятность события C = A + B.

Посмотреть правильное решение и ответ.

---

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей, а также вычислять произведение нескольких событий — на странице «Различные задачи на сложение и умножение вероятностей».

---

Если наступление одного события влияет на вероятность наступления второго события, то события называют взаимно зависимыми.

Если события А и В взаимно зависимы, то условной вероятностью называют вероятность события В, принимая, что событие А уже наступило.

---

Теорема умножения вероятностей взаимно зависимых событий. Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого, то есть вычисляется по формуле:

или

---

Пример 12. В ящике 26 лотерейных билетов, из которых 3 с выигрышем. Найти вероятности того, что первый билет будет с выигрышем, вероятность того, что второй билет будет с выигрышем при условии, что первого билета уже нет в ящике и вероятность того, что два взятые подряд билета будут с выигрышем.

Решение. Найдём вероятность того, что первый взятый билет будет с выигрышем:

Найдём вероятность того, что второй взятый билет будет с выигрышем при условии, что первого билета уже нет в ящике:

Найдём теперь вероятность того, что оба взятые подряд билеты будут с выигрышем, т.е. вероятность общего наступления двух зависимых событий, которая является произведением вероятности первого события и условной вероятности второго события:

  

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей, а также вычислять произведение нескольких событий — на странице «Различные задачи на сложение и умножение вероятностей».

---

function-x.ru

8. Зависимые и независимые событий. Вероятность безотказной работы сети.



Вероятность безотказной работы сети





9. Формула полной вероятности. Формула Байеса.

Следствием обеих теорем вероятности: теоремы сложения и теоремы

умножения – является формула полной вероятности.

Пусть проводится опыт, об условиях которого можно сделать n

исключающих друг друга предположений (гипотез), образующих полную

группу:

Каждая из гипотез осуществляется случайным образом и представляет

собой случайное событие. Вероятности гипотез известны и равны:

Требуется определить полную (безусловную) p(А) вероятности события А.

Представим событие А как сумму из n несовместимых вариантов:

A = A⋅Ω = A(h2 + h3 + … + Hn) = A⋅h2 + A/h3 + … + A/Hn.

На основании второй аксиомы

С учетом теоремы умножения вероятностей p(HiA) = p(Hi)p(A/Hi), тогда

(3.1)

Формула Байеса

Базируется на формуле полной вероятности и теореме умножения

вероятностей.

Пусть до проведения некоторого опыта об его условиях n можно сделать n

исключающих друг друга предположений (гипотез), образующих полную

группу:

Вероятности гипотез до опыта (априорные вероятности) известны:

Раскроем p(A) по формуле полной вероятности (3.1) и получим формулу Байеса

Формула Байеса позволяет пересчитать априорные вероятности гипотез с

учетом того, что опыт завершился событием А.

10. Схема испытаний Бернулли. Теорема о повторении опытов.

Схема Бернулли состоит в следующем: производится последовательность испытаний, в каждом из которых вероятность наступления определенного события А одна и та же и равна р. Испытания предполагаются независимыми (т.е. считается, что вероятность появления события А в каждом из испытаний не зависит от того, появилось или не появилось это событие в других испытаниях). Наступление события А обычно называют успехом, а ненаступление — неудачей. Обозначим вероятность неудачи q=1-P(A)=(1-p). Вероятность того, что в n независимых испытаниях успех наступит ровно m раз, выражается формулой Бернулли:

Вероятность Рn(m) при данном n сначала увеличивается при увеличении m от 0 до некоторого значения m0, а затем уменьшается при изменении m от m0 до n. Поэтому m0, называют наивероятнейшим числом наступлений успеха в опытах. Это число m0, заключено между числами np-q и np+p (или, что то же самое, между числами n(p+1)-1 и n(p+1)) .Если число np-q — целое число, то наивероятнейших чисел два: np-q и np+p.

Важное замечание. Если np-q< 0, то наивероятнейшее число выигрышей равно нулю.

11. Предельные теоремы в схеме испытаний Бернулли

Предельными теоремами в схеме испытаний Бернули являются теорема Пуассона и Муавра-Лапласа.

Теорема Пуассона

Если n велико, а np не велико, следует пользоваться пуассоновским приближением;

Муавра-Лапласа.



Если n велико и np(1 − p) велико, то можно применять нормальное приближение.

12. Случайные величины. Типы величин. Закон распределения дискретной случайной величины.

Под случайной величиной (СВ) понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение, причем заранее, до опыта, неизвестно, какое именно.

Типы: Случайная величина (СВ) Х называется дискретной, если множество ΩX – счетное, т.е. его элементы можно расположить в определенном порядке и пронумеровать. Случайная величина Х называется непрерывной (недискретной), если множество ΩX – несчетное. ΩX – множество возможных значений величины X.

Законом распределения случайной величины Х называется любая функция (правило, таблица и т.п.), устанавливающая соответствие между значениями случайной величины и вероятностями их наступления и позволяющая находить вероятности всевозможных событий связанных со случайной величиной.

studfiles.net

25. Условная вероятность

Определение.Пусть при проведениииспытаний число наступлений события(то есть событиявместе с событием) равно, причемнаступилораз.Условной относительной частотой события при условии наступления событияназывается отношение.

Обозначение условной относительной частоты: . Таким образом,.

Теорема.Для условной относительной частоты справедлива формула:

. (10)

Определение.Пусть. Условной вероятностью событияпри условии наступления событияназывается отношение:

. (11)

26. Теорема умножения

Теорема (умножения).Если (так что существует условная вероятность ), то для вероятности произведения событий справедлива формула:

. (12)

Доказательство.Достаточно в формуле (11) обе части равенства умножить на. ▄

27. Независимость событий

I. Независимость двух событий.

Определение.Событияиназываютсянезависимыми, если вероятность произведения этих событий равна произведению их вероятностей:

. (14)

Таким образом, имеются две формы теоремы умножения:

1. Для произвольных событий:

.

2. Для независимыхсобытий:

.

Теорема (критерий независимости двух событий).Пусть . Для того, чтобы событияибыли независимы, необходимо и достаточно, чтобы условная вероятность событиясовпадала с его безусловной вероятностью:.

28.Теорема (независимость для противоположных событий).Если события инезависимы, то независимы также пары событий

и ,и,и.

Теорема (о независимости от и).Любое событиене зависит от достоверного события и от невозможного события.

Доказательство.1., так чтоинезависимы.

2. , так чтои независимы. ▄

II. Независимость событий в совокупности.

Для трех и более событий их взаимная независимость («независимость в совокупности») означает не только то, что любые два из них не влияют друг на друга (попарная независимость):

, (), (15)

но и что для любого подмножества из трех, четырех и т.д. событий этой совокупности вероятность произведения событий равна произведению их вероятностей:

, (), (16)

, (), (17)

и т. д. вплоть до условия

. (18)

Недостаточность попарных соотношений (15) для справедливости совокупности равенств (16)–(18) показывает

Пример С.Н.Бернштейна. Испытание: наугад бросается игральная кость, имеющая форму правильного тетраэдра, четыре грани которого имеют, соответственно, белую, синюю, красную и тройную бело-сине-красную (полосатую) окраску.

Рассмотрим события: — на выпавшей грани присутствует белый цвет,— на выпавшей грани присутствует синий цвет,— на выпавшей грани присутствует красный цвет. По схеме равновозможных исходов легко убедиться, что. Далее, произведение любых двух из них означает выпадение полосатой грани, так что. Значит, условие (15) выполняется. В то же время, и условие (16) не выполняется.

30. Формула полной вероятности

Определение.Событияобразуютполную группу, если выполняются два условия: 1)в результате испытания одно из них обязательно наступает, то есть их сумма есть достоверное событие:; 2) события попарно несовместны, то естьпри.

Теорема.Пусть выполняются два условия:

1. События («гипотезы») образуют полную группу.

2. События имеют ненулевые вероятности:.

Тогда для всякого события справедлива формула:

,

или в краткой записи:

. (19)

31. Формулы Бейеса

Теорема.Пусть для событий («гипотез») и событиявыполняются три условия:

1. Гипотезы образуют полную группу.

2. Гипотезы имеют ненулевые вероятности:

.

3. .

Тогда при справедливы формулы:

или в краткой записи:

. (20)

32. Схема независимых испытаний Бернулли

Определение.Испытанияобразуют относительно исходапоследовательность независимых испытаний по схеме Бернулли, если выполняются два условия:

1. Исходы испытаний независимы в совокупности.

2. Вероятность исхода во всех испытаниях одинакова и равна.

Терминология: — успех,— вероятность успеха,— неудача,— вероятность неудачи.

Теорема (о вероятности числа успехов).Справедлива формула:

. (21)

(Здесь – число сочетаний изпо; см. п. 1.5).

33. Локальная теорема Лапласа

I. Дифференциальная функция Лапласа.

Определение. Дифференциальной функцией Лапласаназывается функция.

График дифференциальной функции Лапласа («колокол») приведен на рис. 10.

Рис. 10.

Свойства функции .

1.при всех.

2. —чётная функция, то есть. График функции симметричен относительно оси ординат.

3..

Стремление к нулю в последнем пределе достаточно быстрое. Так, с точностью до четырех знаков после запятой .

Для отыскания значений функции имеются таблицы и стандартные компьютерные программы.

II. Предельное равенство.

Введём для испытаний по схеме Бернулли с вероятностью успехаобозначения:

, где – количество успехов (),.

Теорема. Пусть вероятность успеха в серии независимых испытаний по схеме Бернулли удовлетворяет условию. Тогда

. (24)

3.13. Интегральная теорема Лапласа

I. Интегральная функция Лапласа.

Определение. Интегральной функцией Лапласаназывается интеграл с переменным верхним пределом:

.

Для отыскания значений функции имеются таблицы и стандартные компьютерные программы.

График интегральной функции Лапласа приведен на рис. 11. Геометрически выражает площадь заштрихованной части криволинейной трапеции на рис. 12.

Рис. 11.

x

t

(x)

Рис. 12.

Свойства функции .

1.при всех .

2. – нечётная функция, то есть. График

функции симметричен относительно начала координат.

3. ; .

4. является производной для :.

5.Функция строго возрастает.

II. Предельное равенство.

Введём обозначение: — вероятность того, что в серии изиспытаний по схеме Бернулли число успеховлежит в пределах:.

Пусть, как и в п. 3.12: — количество испытаний по схеме Бернулли,— вероятность успеха,.

Теорема. Пусть для вероятности успеха в серии независимых испытаний по схеме Бернулли выполняется условие. Тогда для вероятности:

, (25)

или, учитывая определение функции:

. (26)

studfiles.net

Теоремы сложения и умножения вероятностей. Примеры решения задач

Теоремы сложения и умножения вероятностей

Основные понятия
События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. В противном случае они называются совместными.
Полной группой называют совокупность событий, объединение которых есть событие достоверное.
Противоположными называют два единственно возможных события, образующих полную группу.
События называются зависимыми, если вероятность появления одного из них зависит от наступления или ненаступления других событий.
События называются независимыми, если вероятность одного из них не зависит от наступления или ненаступления других.
Теорема сложения вероятностей несовместных событий
Р(A+B)=Р(A)+Р(B),
где А, В — несовместные события.

Теорема сложения вероятностей совместных событий
Р(A+B)=Р(A)+Р(B)-P(AB), где А и В — совместные события.


Теорема умножения вероятностей независимых событий
,
где А и В независимые события.
Теорема умножения вероятностей зависимых событий
Р(АВ)=Р(А)Р_A(B),
где Р_A(B) — вероятность наступления события В при условии, что произошло событие А; А и В- зависимые события.


Задача 1.
Стрелок производит два выстрела по мишени. Вероятность попадания при каждом выстреле 0,8. Составить полную группу событий и найти их вероятности. Решение.
Испытание — Производится два выстрела по мишени.
Событие А — оба раза промахнулся.
Событие В — попал один раз.
Событие С — оба раза попал.
.

Контроль: P(A) + P(B) + P(C) = 1.
Задача 2.
Согласно прогнозу метеорологов Р(дождь)=0,4; Р(ветер)=0,7; Р(дождь и ветер)=0,2. Какова вероятность того, что будет дождь или ветер? Решение. По теореме сложения вероятностей и в силу совместности предложенных событий имеем:
Р(дождь или ветер или то и другое)=Р(дождь) +Р(ветер) –Р(дождь и ветер)=0,4+0,7-0,2=0,9.
Задача 3.
На станции отправления имеется 8 заказов на отправку товара: пять – внутри страны, а три – на экспорт. Какова вероятность того, что два выбранных наугад заказа окажутся предназначенными для потребления внутри страны? Решение. Событие А – первый взятый наугад заказ – внутри страны. Событие В – второй тоже предназначен для внутреннего потребления. Нам необходимо найти вероятность  Тогда по теореме об умножении вероятностей зависимых событий имеем

Задача 4.
Из партии изделий товаровед наудачу отбирает изделия высшего сорта. Вероятность того, что выбранная вещь окажется высшего сорта равна, 0,8; первого сорта – 0,7; второго сорта – 0,5. Найти вероятность того, что из трех наудачу отобранных изделий будут:
а) только два высшего сорта;
б) все разные. Решение. Пусть событие  — изделие высшего сорта; событие — изделие первого сорта; событие — изделие второго сорта.
По условию задачи ; ;  События — независимы.
а) Событие А – только два изделия высшего сорта будет выглядеть так тогда

б) Событие В – все три изделия различны — выразим так:, тогда .
Задача 5.
Вероятности  попадания в цель при стрельбе из трех орудий таковы: p1=0,8;  p2=0,7;  p3=0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события  (попадание первого орудия),  (попадание второго орудия) и  (попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям  (т.е. вероятности промахов), соответственно равны:

Искомая вероятность
Задача 6.
В типографии имеется 4 печатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А). Решение. События «машина работает» и «машина не работает» (в данный момент) – противоположные, поэтому сумма их вероятностей равна единице:
Отсюда вероятность того, что машина в данный момент не работает, равна
Искомая вероятность . Задача 7. В читальном зале имеется 6 учебников по теории вероятностей , из которых три в переплете . Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.

Решение. Рассмотрим следующие события:
А1- первый взятый учебник в переплете;
A2- второй взятый учебник в переплете.
Событие, состоящее в том, что оба взятых учебника в переплете . События А1 и А2 являются зависимыми, так как вероятность наступления события А2 зависит от наступления события А1. Для решения указанной задачи воспользуемся теоремой умножения вероятностей зависимых событий: .
Вероятность наступления события А1  p(A1) в соответствии с классическим определением вероятности:
P(A1)=m/n=3/6=0,5.
Вероятность наступления события А2 определяется условной вероятностью наступления события А2 при условии наступления события А1 , т.е. (A2)==0,4.
Тогда искомая вероятность наступления события:
P(A)=0,5*0,4=0,2.

www.matem96.ru