Модель экономического роста харрода – Модель Харрода — Домара — Википедия

Экономический рост: модель Харрода

Негативные факторы экономического роста

Неразвитая торговая политика на мировых рынках. На сегодняшний день наиболее эффективная экономика у тех стран, которые наладили партнерские, торговые, политические связи с другими странами на предмет экономического взаимодействия. Импорт и экспорт, важная составляющая экономики любого государства, поэтому внешняя политика формирует тот уровень экспортируемого и импортируемого товара, который необходим для достижения экономического роста.

Неразвитые экономические отношения на внутреннем рынке страны. Неграмотная управляемость процессами экономического характера, приводит к тому, что вся экономика государства теряет свои позиции по всем направлениям, включая производство, торговлю, образование и др. Управление в экономике играет большую роль, а также опыт и степень профессионализма. Немаловажен и слаженный процесс работы в экономической команде. Все это способно либо тормозить, либо ускорять рост экономики.

Недостаток экономических ресурсов.

Достаточно сложно наладить экономику, не имея для этого необходимых ресурсов. Многие страны ограничены в необходимых ресурсах для налаживания производства и промышленности.

Данные негативные факторы, снижающие темпы экономического роста, имеют место быть в любом государстве, однако, надо отметить, что есть такие страны, которые, несмотря на имеющиеся проблемы, смогли сформировать эффективную экономическую систему, способную развиваться и расти.

Тенденции экономического роста

Экономический рост – это нестабильное экономическое явление, которое может продолжаться либо долгий период времени, либо короткий, в зависимости от условий внешнего и внутреннего воздействия на экономическую систему страны.

Замечание 1

Тенденции экономического роста могут давать как положительную динамику, так и отрицательную.

Положительная динамика выражается в росте основных экономических показателей, в снижении уровня безработицы, повышении качества образования, в развитии инновационной деятельности и т.д.

Отрицательная динамика проявляется по средствам снижения качества и уровня жизни населения, снижению темпов производства, повышение объемов импорта в страну и т.д.

Замечание 2

Экономику можно назвать развивающейся, если экономический рост имеет положительную тенденцию, причем длительное время, даже, если имеется в какие — то года отрицательная динамика, но отклонение не критичное, все равно, можно определить, что такая экономика находится в стадии роста.

На тенденции в экономике и ее росте можно влиять посредством:

1. Заранее спланированной и спрогнозированной программы экономического роста. Такая программа может позволить заранее избежать насущных и «предвиденных» проблем;
2. Грамотного аппарата экономического управления. В экономике не достаточно иметь опыт правления, основанный только на одной или нескольких экономических теориях, необходимо рассматривать экономические процессы под разными углами, то есть всестороннее;
3. Стабильного финансирования на инновационные проекты и деятельность. Развитие и рост экономики, прежде всего, можно обеспечить за счет инновационных направлений, которые могут максимально ускорить все экономические возможности страны.

Итак, тенденциями экономического роста можно вполне себе управлять, их можно направлять в нужное русло, контролировать и снижать риск наступления негативных последствий, для этого необходимо сформировать грамотный аппарат управления, иметь стабильное финансирование и выделять достаточно средств и внимания на инновационные идеи.

Модель экономического роста Харрода

Тенденции экономического роста, а особенно стабильного, сбалансированного и уравновешенного роста, волновали ведущих экономистов всех времен. Так, еще достаточно давно ученые и исследователи пытались выявить основные положения и постулаты того, как обеспечить такого рода экономический рост.

В 1939 году экономист и ученый Харрод разработал модель экономического роста, в основе этой модели всего два основных элемента:

• Первый – она опирается на поведение предпринимателей в тех или иных рыночных условиях, где поведение анализируется с точки зрения психологии;
• Второй – это уравнения, которые отражают экономические функциональные связи в экономике.

Замечание 3

Отличительной особенностью модели Харрода от других моделей экономического роста, является то, что он включил в свою модель эндогенную функцию инвестиций, которая в целом основана на определенных психологических ожиданиях бизнесмена на рынке.

Помимо этого модель Харрода делает акцент на темпы роста национального дохода страны, что вполне совпадает с суждениями кейсианской экономической теорией.

Суть модели Харрода

Модель Харрода рассматривает экономический рост с разных сторон, изучая ее более тщательно и подробно, в основе идет выявление проблематики, сдерживающий темпы экономического роста.

Всю модель ученый описал с помощью уравнения, в котором говорится о том, что искомый темп экономического роста равен соотношению доли сбережений в национальном доходе к коэффициенту капиталоемкости.

Так, если показатель доли сбережений растет, что и экономический рост увеличивается, а вот чем, ниже коэффициент капиталоемкости, тем хуже условия роста экономики.

Идеальная ситуация экономическая ситуация в стране может сложиться только в том случае, если уравнение Харрода будет равное, но такого быть практически не может. В связи с этим ученый и экономист Харрод выдвинул идею о том, что государство и экономика – неделимое целое, причем правительство страны должно постоянно вмешиваться в экономические процессы, для того чтобы наладить экономические отношения, и по возможности, балансировать данные показатели уравнения с целью максимизации баланса.

Таким образом, модель экономического роста Харрода вполне обоснованная и имеет особое место в экономических учениях. Она показывает прямую зависимость одних действий от других, поэтому, если учитывать это уравнение в рамках экономического управления, то можно добиться стабильного экономического роста.

spravochnick.ru

Модель экономического роста Харрода — Мегаобучалка

В конце 1930-х гг. английский экономист Рой Ф. Харрод, которого Дж. М. Кейнс провозгласил продолжателем своих научных идей, создал динамическую модель экономического роста. Он исследо­вал, каким образом в процессе роста происходит взаимодействие капи­тала, рабочей силы и величины дохода на душу населения, как должен изменяться объем капитала, чтобы соответствовать росту рабочей силы и дохода при постоянной процентной ставке.

По Харроду, в условиях роста населения в геометрической прогрес­сии, при фиксированных темпах технического прогресса и неизменной процентной ставке спрос на капитал будет расти в одинаковой пропор­ции с ростом населения. Тогда норма сбережения, поддерживающая экономический рост, должна быть равна

произведению капиталоемкос­ти и прироста населения в текущем периоде. Однако для обеспече­ния экономического роста при изменяющихся темпах технического про­гресса и, наоборот, при зафиксированных темпах роста населения по­требуется такая норма сбережения, величину которой Харрод измеря­ет посредством следующего равенства:

G ■ С = s, (8)

где G (growth) = ДУ/У₍₁— рост выпуска продукции за период

t, изме­ряемый в темпах прироста; С = ДК/АУ₍— предельная капиталоемкость, рассчитанная по количеству фактически произведенных капитальных

 

 

благ; s = S/V — предполагаемая норма сбережения, т. е. сберегаемая часть совокупного дохода.1 Если мы вспомним, что предельная капита­лоемкость и предельная капиталоотдача являются обратными величи­нами, то величину С можно представить как 1/<х Тогда можно записать G -(1/a)=s или G = o-s (9) Сопоставив равенства (7) и (9), мы видим, что и Домар, и Харрод приходят к одному и тому же выводу.2 Для того, чтобы достичь равновесного экономического роста, т. е. экономического роста в условиях динамического равновесия, норма сбережения, как полагает Харрод (при нейтральности технического про­гресса3 и неизменности процентной ставки), должна удовлетворять сле­дующему равенству:

G_w-C_r = s, (10)

где G_w— темп роста, гарантирующий полную занятость растущего капитала, который и обеспечивает равновесное по­ложение производителей. Таким спосо­бом Харрод вводит понятие гарантиро­ванного (warranted) темпа роста. С_г -это требуемая (required) капиталоем­кость, выражающая потребность в доба­вочном капитале для выпуска дополни­тельной продукции.

4

По Харроду, фактический темп роста складывается в результате проб и оши­бок множества людей и лишь случайно может совпадать с уровнем гарантиро­ванного темпа роста. Последний показа­тель, т. е. G_wотражает линию «предпри­нимательского равновесия» и совместим с вынужденной безработицей.

Однако рост экономики имеет свои естественные ограничения в виде темпов роста населения и темпа технического прогресса. Для обозначения верхней и нижней границ подъема или падения объемов производства Харрод вводит по­нятие естественного темпа роста G_N, определяемого ростом населения и тех­нологией производства (или техническим прогрессом). В отличие от гарантирован-

¹ Харрод Р. К теории экономи­
ческой динамики. Классики кейн-
сианства.Т.1.М., 1997.0.112,113.

² Сходство выводов и допуще­
ний в моделях Харрода и Домара,
созданных в разное время и неза­
висимо друг от друга, позволило
дать им общее название: «модель
Харрода-Домара». Мы еще не раз
столкнемся со случаем объедине­
ния независимых моделей на ос­
нове общности их основных прин­
ципов.

³ Под нейтральным техничес­
ким прогрессом Харрод понимает
«поток изобретений, оставляющих
без изменения ту пропорцию, в
которой совокупный продукт рас­
пределяется между трудом и капи­
талом при постоянной процентной
ставке». Это возможно потому, что
эффекты от изобретений, требую­
щих увеличения капитальных зат­
рат, уравновешиваются с эффек­
тами от изобретений, снижающих
затраты капитала.

⁴ Харрод трактует С как «пре­
дельную величину, выражающую
потребность в новом капитале для
сохранения такого выпуска про­
дукции, который должен удовлет­
ворить потребительский спрос,
возникающий из предельного до­
бавочного дохода потребителей»
(Харрод Р. К теории экономичес­
кой динамики. Классики кейнсиан-
ства. Т. 1. М. 1997. С. 117).

кономическии рост

ного темпа роста, совместимого, как отмечалось выше, с безработицей, естественный темп роста предполагает полное использование растуще­го предложения на рынке труда, обеспечивая его равновесие. Если фак­тический темп роста G равен G_N, то экономика развивается в условиях полной занятости.

Идеальные условия для поддержания стабильных равновесных тем-ов экономического роста в долгосрочном плане в модели Харрода вы­ражаются следующим равенством:

G.C_r^s = G_NC_r(11)

Однако, основная проблема заключается в отклонении от равнове-ия (когда G_N C_r ф s), которое ведет к расхождению между G_wи G_N, по­рождая хроническую безработицу. Другая важная проблема — отклоне­ние фактического темпа роста от гарантированного (G от G_w), что лежит, по мнению Харрода, в основе циклических колебаний.

Действительно, если G_w< G_N, то появится хроническая нехватка сбе­режений. Спрос на инвестиции будет превышать их предложение, а от­сюда вытекает тенденция к буму. При этом может оказаться, что гаран­тированный темп роста меньше фактического темпа (G_w< G ) и в таком случае экономика сталкивается с описанной выше повышательной вол­ной делового цикла. Следует отметить, что фактический темп роста может оказаться и равным гарантированному. В таком случае, развитие экономики будет характеризоваться динамическим равновесием, но со­путствующим феноменом будет циклическая безработица.

Если G_w > G_N, то экономика столкнется с депрессивными явления­ми. Естественный темп роста не сможет обеспечить такой рост инвес­тиций, который полностью использовал бы сбережения. Следствием этого станут неполное использование производственных мощностей, накопление товарно-материальных запасов, банкротства и вынужденная безработица. При этом гарантированный темп роста окажется выше фактического: G^>G. Это означает, что предприниматели будут разоча­ровываться в своих ожиданиях относительно предполагаемого роста выпуска, снизят объемы производства и капиталовложения.

Таким образом, Харрод обосновывает крайнюю неустойчивость рас­сматриваемой им системы, получившую в экономической науке назва­ние «балансирование на лезвии ножа» (knife edge). Отклонение от ра­венства G — G_wприводит к нарастанию из периода в период центробеж­ных сил, углубляющих этот дисбаланс и приводящих все к большему расхождению между совокупным спросом и совокупным предложением.

Интересно заметить, что, исследуя функцию сбережений в экономи­ке, Харрод по-своему разрешает основное противоречие между кейнси-анской и классической школами, отраженное в известном «парадоксе бережливости». Он показал, что сбережения могут играть как положи-

 

Глава 25

тельную, так и отрицательную роль в зависимости от соотношения меж­ду G_Nи G_w. В условиях избытка рабочей силы, когда G_w< G_N, сбереже­ния «добродетельны». Когда же, наоборот, наблюдается дефицит рабо­чей силы и избыток капитала, т. е. G_w> G_N, рост сбережений приобрета­ет деструктивный характер.

Какие же рецепты для экономической политики следуют из модели Харрода? Во-первых, государство должно опираться на корректирую­щую инвестиционную политику, регулирующую баланс между сбереже­ниями и инвестициями. Во-вторых, стараться минимизировать отклоне­ния гарантированного от естественного темпа роста. В-третьих, Р. Хар-род утверждал, что для поддержания равновесного темпа роста при сохра­нении полной занятости необходимо поступательное снижение процентной ставки, а не снижение уровня заработной платы, как предполагали клас­сики. В рыночной системе процентная ставка подвержена колебаниям и поэтому поддержание ее на стабильном низком уровне, по мнению кей-нсианцев, — долгосрочная задача экономической политики.

§ 4. Неоклассические модели

экономического роста

Неоклассические модели экономического роста строятся на базе производственной функции и основаны на предпосылках пол­ной занятости, гибкости цен на всех рынках, а также полной взаимоза­меняемости факторов производства. Попытки исследовать, в какой сте­пени качество факторов производства и различные пропорции в их со­четании воздействуют на экономический рост, привели к созданию мо­дели производственной функции Кобба-Дугласа. Рассмотрим эту модель подробнее.

Производственная функция Кобба-Дугласа и ее свойства

Функция Кобба-Дугласа получена в результате математи­ческого преобразования простейшей производственной функции У = F(L, К) в модель, которая показывает, какой долей совокупного про­дукта вознаграждается участвующий в его создании фактор производ­ства. Она имеет следующий вид:

Y = AK^aL>³, (12)

где а изменяется в пределах от 0 до 1, а р = 1 — а. Функция Кобба-Дугласа содержит два переменных фактора произ-

Экономический рост

водства — труд (L) и капитал (К). Параметр А — коэффициент, отражаю­щий уровень технологической производительности, и в краткосрочном периоде он не изменяется. Показатели а и р- коэффициенты эластич­ности объема выпуска (У) по фактору производства: а — по капиталу, а р — по труду. Заметим, что, если каждый из факторов оплачивается в соответствии со своим предельным продуктом, то а и р показывают доли капитала и труда в совокупном доходе. Иными словами, если цена капитала равна предельному продукту капитала, а цена труда рав­на предельному продукту труда (вспомним условие оптимального со­четания факторов производства из гл. 10, § 5), то параметры а и р определяют пропорцию, в которой труд и капитал получают свое воз­награждение за созданный продукт. Доля капитала в доходе составит величину аУ, а доля труда в доходе — величину р Y. Так как р = 1 — а, то а + р — 1, из чего следует, что мы имеем дело с постоянной отда­чей от масштаба.

Интересно рассмотреть эмпирические значения параметров функ­ции Кобба-Дугласа: А = 1,1; а= 1/4; р — 3/4, т. е. доля капитала в наци­ональном доходе составляет 25%, а доля труда — 75%.

В поисках путей наибольшей эффективности производства нас все­гда должна интересовать предельная производительность участвующих в нем факторов¹, с помощью которой определяется оптимальный объем используемых ресурсов. Предельный продукт капитала МР_Кпропорцио­нален отношению доли капитала в доходе к объему использованного капитала: МР_К= а У/ К. Аналогично определяется и предельная произ­водительность труда: MP_L= P У/ L.

Рассмотрим свойства производственной функции Кобба-Дугласа.

Первое свойство — постоянство отдачи от масштаба— описывает­ся формулой F (nK, nL) = n А К» /Л которая показывает, что если коли­чество капитала и труда увеличить в п раз, то объем совокупного вы­пуска, или объем дохода, возрастет в такое же количество раз.

1 Предельная производи­тельность капитала и труда пред­ставляют собой производные функции Кобба-Дугласа: МРК= а А К»-‘ L»\ MPL=/3A К» L»-‘. В фун­кции Кобба-Дугласа МРКпропор­циональна средней производи­тельности капитала У/К , a MPLпропорциональна средней про­изводительности труда Y/L.

Второе важное свойство функции Кобба-Дугласа связано с измене­нием предельной производительности факторов. Например, если при­влечь в производство дополнительное количество капитала К, а труд L использовать в прежнем объеме, то, при прочих равных условиях, предельная производительность труда MP_Lувеличит­ся, а предельная производительность возросшего объема капитала МР_К снизится. Если же увеличить количество труда, при прочих равных условиях, то его предельная производительность сни­зится, а предельная производительность капитала возрастет. Вывод: нарушение

 

Глава 25

Экономический рост

 

пропорции между трудом и капиталом при заданной технологии приво­дит к отклонению от оптимального объема совокупного выпуска, т. е. к неэффективности производства.

Однако, если увеличивается параметр А, например, при внедрении более производительной технологии, то будет наблюдаться одновре­менное повышение MP_Kv\ MP_L, что является условием интенсивного эко­номического роста.

Третье свойство производственной функции Кобба-Дугласа — посто­янство отношения дохода от труда к доходу от капитала(ft/a), т. е. постоянство соотношения долей капитала и труда в национальном про­дукте.

Исследования американского сенатора и экономиста Пола Дугласа¹ показали, что в Соединенных Штатах за сорок лет (с 1948 по 1989 гг.) соотношение ji/a колебалось в пределах между 2 и 3, в результате чего оплата труда в 2-3 раза превышала вознаграждение капитала.² Можно предположить, что постоянные рамки колебания соотношения р/сс зада­ны технологически. Колебания ji/a внутри этих рамок могут быть объяс­нены отклонением в соотношении / и S, так как вряд ли заработная пла­та, шкала налогообложения и норма амортизации почти ежегодно мог­ли претерпевать значительные изменения.

Макроэкономическое равенство / = S является условием равновес­ного роста еще одной неоклассической модели, которая строится на осно­ве производственной функции Кобба-Дугласа. Речь пойдет о модели эко­номического роста, автор которой — известный американский экономист, лауреат Нобелевской премии Роберт Солоу. Данная модель объясняет ме­ханизм роста экономики в устойчивом состоянии и показывает, как осу­ществляется экономический рост в условиях технического прогресса.

Модель роста Солоу

1 Мэнкью Г. Макроэкономика. М. 1994. С. 113. 2 В понятие вознаграждение капитала, или дохода на капи­ тал, включается совокупная не­ распределенная прибыль корпо­ раций (т. е. прибыль за вычетом налогов, амортизационных от­ числений и рентных платежей). Под вознаграждением труда, или доходом на труд, подразумевает­ ся лишь заработная плата. Во избежание искажений из данной модели исключен доход соб­ ственников, будучи доходом сме­ шанного типа.

Цель данной модели — от­ветить на очень важные вопросы эконо­мической теории и экономической поли­тики: каковы факторы сбалансированного экономического роста; какой темп роста может позволить себе экономика при за­данных параметрах экономической систе­мы и как при этом максимизировать до­ход на душу населения и объем потреб­ления; какое влияние на темпы роста экономики оказывают рост населения, накопление капитала и технический про-

гресс. Модель Солоу показывает не только возможность равновесного экономического роста при полной занятости и полном использовании производственных мощностей. Особенностью этой неоклассической мо­дели является и то, что она демонстрирует устойчивость экономическо­го роста, т. е. способность экономической системы возвращаться к тра­ектории сбалансированного развития при помощи внутренних рыночных механизмов саморегулирования.

Предпосылки модели

В отличие от неокейнсианских моделей, факторы производства в модели Солоу, основанной на производственной функции Кобба-Дугла­са, являются взаимозаменяемыми. А это позволяет построить модель, альтернативную «балансированию на лезвии ножа» Р. Харрода, когда равновесный рост оказывается крайне нестабильным.

Капиталовооруженность (K/L) является не постоянным соотноше­нием, как в моделях Харрода и Домара, а меняющимся в зависимости от макроэкономической конъюнктуры.

Цены в модели Солоу являются гибкими, т.е присутствует пред­посылка о совершенной конкуренции на рынках факторов производства, что и позволяет отнести рассматриваемую модель к неоклассической.

Предполагается, что темп роста трудовых ресурсов (предложения труда, L) равен темпу роста населения п, т. е. мы встречаемся с извес­тным нам из модели Харрода естественным темпом роста.

Первоначально при построении модели предполагается, что темпы роста населения не изменяются, а технический прогресс отсутствует.

Такие переменные, как норма сбережения, норма амортизации, рост населения, технический прогресс являются экзогенно заданными.

Построение модели

Разделив двухфакторную производственную функцию У = F(K,L) на количество труда L, мы получим производственную функцию для одно­го работника: у = f(k), где к — K/L — уровень капиталовооруженности еди­ницы труда, или одного работника. Доход (у = Y/L) предстает как функ­ция только одного фактора — капиталовооруженности {к). Такая единич­ная производственная функция, отражающая средний уровень произво­дительности труда показана на рис. 25.2.

Заметим, что крутизна ее наклона, определяемая величиной пре­дельной производительности капитала МР_К, изменяется. По мере уве­личения количества капитала на одного работника, предельная произ­водительность этого фактора уменьшается (в соответствии с известной нам из гл. 10 теорией предельной производительности факторов), что и вызывает замедление роста функции дохода.

 

Глава 25

Экономический рост

 

 

Выпуск на У одного работника (производи­тельность)

Капиталовооруженность К

Рис. 25.2. Производственная функция у = f (k)

Данная функция построена из расчета на одного работника и характеризуется понижающейся пре­дельной производительностью капитала МР_К.

Как мы помним, часть дохода используется на потребление, а дру­гая часть сберегается. В модели Солоу, где все макроэкономические показатели рассчитываются на одного работника, сбережения тоже бу­дут представлять собой часть единичного дохода sy, или sf(k), где s — норма сбережения, определяющая, какая часть дохода сберегается.

Нам известно, что условием макроэкономического равновесия явля­ется равенство совокупного спроса и совокупного предложения, что ав­томатически приводит нас к макроэкономическому равенству / = S. Все сбережения в экономике полностью инвестируются, и это позволяет приравнять функцию фактических инвестиций на одного работника (/) к единичной функции сбережений / = sy = sf(k).

Помня о макроэкономическом равенстве Y = С + I, выпуск в расче­те на одного занятого можно записать в виде у = с + i, где у = Y/L, с = C/L, i = I/L, а функцию потребления представить как с = у — i = f (k) — sf(k).

Графически размер потребления и инвестиций при каждом уровне капиталовооруженности изображены на рис. 25.2. Кривой sf(k) обозна­чен график фактически осуществленных инвестиций, которые по усло­вию модели равны сбережениям. Поскольку сбережения составляют некую определенную долю от выпуска, то и фактически осуществленные инвестиции на душу населения представлены графиком, лежащим ниже графика производственной функции на рис. 25.2. Расстояние между гра­фиками функций f(k) и sf(k) определяет объем потребления. Таким об­разом, функция потребления описывается формулой

c = f(k)-sf(k) (13)

По условию модели, экономика изначально находится в состоянии

устойчивого равновесия. Это значит, что планируемые, или требуемые инвестиции / равны фактически осуществленным инвестициям, т. е. сбе­режениям S. Данное условие макроэкономического равновесия извест­но нам из гл.18, § 4. В модели Солоу оно описывается, как устойчивое,или стационарное(steady-state) состояние экономики, при котором объем капитала на одного работника постоянен. Для определения ста­ционарного состояния экономики в модели Солоу необходимо рассмот­реть и проблему накопления капитала. Очевидно, для того, чтобы капи­таловооруженность оставалась неизменной при условии роста населе­ния, необходимо, чтобы капитал К увеличивался тем же темпом п, что и рост населения L. Таким образом, требуемые инвестиции в расчете на одного работника с (верхний индекс г у символа инвестиций / — от анг­лийского слова required — требуемый) можно записать в виде следую­щего равенства:

i^r=nk (14)

При этом, если темп роста населения и темп накопления капитала равны, то выпуск на душу населения у остается неизменным.

Но не будем забывать, что для описания чистого прироста капи­тала нужно учесть выбытие капитала, или амортизацию. Растущего капитала должно быть достаточно не только для оснащения новыми капитальными благами дополнительной рабочей силы, но и для попол­нения выбывающего капитала. Обозначим норму выбытия (норму амор­тизации) символом 8. Таким образом, требуемые инвестиции в расчете на одного работника будут записаны в виде равенства

i^r=(n + b)k (15)

С учетом постоянного темпа роста населения и постоянной нормы выбытия можно в формализованном виде записать условия накопления капитала:

Лк = sf(k)-(n + Ь)к (16)

Итак, мы имеем все необходимые данные, для того, чтобы объяс­нить механизм установления стационарного состояния в модели Солоу.

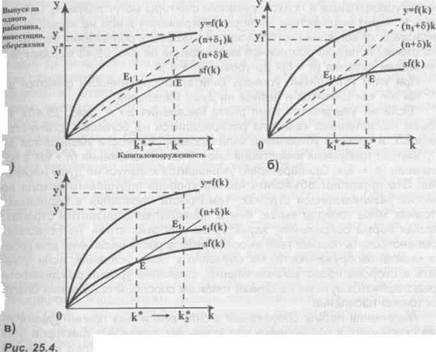
В ходе производства ежегодно пополняются капитальные запасы, независимо от того, с каким объемом капитала экономика начинает раз­виваться. Однако прирост фактических инвестиций, отображаемый гра­фиком sf(k), идет затухающими темпами (см. рис. 25.3).

Это объясняется уже рассмотренным выше снижением предельной производительности капитала МР_К, происходящим по мере увеличения капиталовооруженности одного работника. Но наращивание капиталово­оруженности увеличивает и объем требуемых инвестиций, представлен­ных на рис. 25.3 прямой линией (п + о)к. Наклон этой линии определя-

 

Глава 25

Экономический рост

 

 

Выпуск на

одного

работника,

инвестиции,

сбережения

— k_2k

Капиталовооруженность

Рис. 25.3.

Определение устойчивого уровня капиталовооруженности к*

Величину к* можно найти, опустив перпендикуляр на ось абсцисс из точки пересечения графика сбережений с графиком требуемых инвестиций, чему соответствует равенство sf(k)= (n + &)к. При этом устойчивый уровень выпуска на душу населения у* соответствует уровню устойчивой капиталовооруженности к*.

ется величиной (п + 8). С ростом производства разница между сбереже­ниями (фактически осуществленными инвестициями) sf(k) и требуемы­ми инвестициями (п + Ъ)к будет уменьшаться до тех пор, пока эти вели­чины не выровняются между собой. Когда Ак = О, тогда производство, сбережения и требуемые инвестиции достигают определенного устойчи­вого уровня, т. е. экономика достигает состояния равновесия. Уровень капиталовооруженности, при котором Ак — 0, называется устойчивым уровнем капиталовооруженности (к*) и характеризует состояние рав­новесия экономики. В равновесном состоянии объем выпуска не изме­няется, а сбережения и требуемые инвестиции равны:

(17)

sf(k*) — (п + 8)к*

sf(k*) = (n + Ь)к* (18)

Таким образом, на рис. 25.3 пересечение графика сбережений sf(k) и графика требуемых инвестиций (п + Ь)к будет показывать состояние равновесия, определяя величину устойчивого уровня капиталовоору­женности к*.

Каков же в модели Солоу механизм, который обеспечивает равно­весный рост? Для этого обратимся вновь к рис. 25.3. В точке к₁сбере­жения превышают уровень требуемых инвестиций. Предложение капи­тала превышает спрос на него, т. е. объем капитала в точке к₁является избыточным. В условиях гибких цен начнется процесс удешевления это­го фактора производства по сравнению с трудом и таким образом нач-

megaobuchalka.ru

Модель экономического роста Харрода-Домара

История создания модели

В 1939 году вышла первая работа Р. Харрода по экономической динамике «Очерк теории динамики», а после войны были изданы лекции Харрода, которые читались в 1946-1947 годах в университете Лондона. В 1973 году была опубликована книга «Теория экономической динамики», которая содержала наиболее полное изложение теории Харрода в области экономической динамики и более четкие определения модели в ряде понятий.

В 1941-1942 годах Е. Домар, основываясь на схеме из книги Э. Хансена «Бюджетная политика и деловые циклы», отражающей воздействие постоянного инвестиционного потока на национальный доход, сделал вывод, что такой поток положительно влияет на рост дохода, в результате чего написал статью «Долговое бремя и национальный доход». Данная статья послужила началом других его известных статей, в которых Домар применял темп роста в качестве аналитического инструмента для исследования специфических проблем экономики. В 1957 году Домар сформировал собственную модель.

В 1956 году Р. Слоу первый объединил два подхода воедино, обозначив это как модель Харрода-Домара. Данная модель пользуется популярностью и в современном мире во многих исследованиях международных организаций.

Сущность модели Харрода-Домара

Динамикой Р. Харрод считает такое экономическое состояние, при котором объем выпуска продукции изменяется не циклически или эпизодически, а в течение длительного временного периода. Харрод ввел такие понятия как гарантированный темп роста и естественный темп роста. Под гарантированным темпом роста он понимал такой темп выпуска товаров, который позволяет получать максимальную прибыль, т.е. это является динамическим равновесием.

Проблема, которой Харрод в своей теории уделяет основное внимание – это проблема темпа роста доходов, необходимых для полного использования постоянно возрастающего объема капитала. Харрод попытался определить, насколько постоянны темпы роста, перечень корректирующих факторов, при отклонении естественного темпа роста от гарантированного.

Замечание 1

Теории Харрода и Домара объединяет общий вывод о целесообразности устойчивого темпа роста экономики в качестве решающего фактора динамического равновесия, при котором достигается полное использование мощностей производства и трудовых ресурсов.

Отличительные черты в моделях Харрода и Домара обусловлены только лишь некоторыми различиями в исходном положении при построении модели. Так, основу модели Харрода составляет идея равенства сбережений и инвестиций, а модели Домара – равенство денежных доходов (спроса) и мощностей производства (предложения).

Оба ученых сходятся во мнении, что повышение национального дохода находится в зависимости от его капиталоемкости и нормы накопления. В их модели капитал рассматривается в качестве единственного фактора роста экономики. Данный фактор объединяет в себе все функции остальных факторов. Подразумевается, что все факторы задействованы, а прирост спроса равняется приросту предложения.

Модель Харрода-Домара – это вспомогательный инструмент при рассмотрении проблем роста экономики в долгосрочном периоде. Она выражается формулой:

$G = S / C$, где:

• $G$ – это искомый темп роста экономики,
• $C$– коэффициент капиталоемкости, т.е. соотношение «капитал-выпуск»,
• $S$ – это доля всех сбережений в структуре национального дохода.

Чем больше объем чистых сбережений, тем больше объемы инвестиций, а, следовательно, и темпы роста. Чем больше капиталоемкость, тем темпы экономического роста ниже.

Используя данные основных экономических параметров, можно составить прогноз ожидаемых темпов роста экономики на перспективу. Фактические значения темпа роста будут незначительно отличаться от расчетных, если в прогнозируемом периоде будет сохраняться постоянная доля сбережений в структуре национального дохода $S$ и коэффициент капиталоемкости $C$ останется неизменным. В условиях высоких темпов роста экономики коэффициент капиталоемкости будет стимулом этого роста. При депрессии будет недоставать снижающихся темпов роста, чтобы поддерживать желаемые темпы инвестиций.

При помощи модели Харрода-Домара можно представить вид кривой экономического роста не в коротком, а в длительном периоде. Модель показывает необходимые условия для поддержания как постоянного, так и относительно равномерного экономического роста.

Рассматриваемая модель имеет ряд допущений:

• Капиталоемкость – это постоянная величина;
• Темпы расширения предложения трудовых ресурсов и темпы повышения трудовой производительности постоянны и экзогенны;
• Постоянна склонность к сбережениям, т.е. при увеличении доходов объемы сбережений увеличатся;
• Сбережения равны инвестициям, т.е. увеличение сбережений при росте доходов приводит к большему инвестированию, что является причиной увеличения капитала, используемого для производства ВВП;
• Выпуск зависит от капитала;
• Инвестиционный лаг равняется нулю.

Недостатки модели Харрода-Домара

Модель позволяет объяснить высокие темпы роста регионов, в которых изначально имелись незначительные сбережения и соотношения капитала и выпуска, а также отрицательный торговый баланс, связанный с импортом капитала. Между тем, модель Харрода-Домара имеет некоторые недостатки:

• Закрытая экономика, т.е. модель не дает объяснение возникновению потоков рабочей силы и капиталов между регионами при нарушениях в равновесии;
• Модель не показывает возможность конвергенции-дивергенции;
• Модель не показывает привлекательность для инвестиций бедных регионов, являющихся чистыми экспортерами капиталов;
• Наращивание инвестиций и сбережений – это необходимое, но недостаточное условие ускоренного роста;
• Для работы модели необходимы структурные, институциональные и культурные предпосылки;
• Нестабильная траектория сбалансированного роста – в экономике нет стабилизаторов, позволяющих снижать внешние воздействия;
• Не учитывается роль правительства, внешних торговых связей, неэкономических факторов.

spravochnick.ru

4.2. Модель экономического роста Харрода.

Базилинська. Макроэкономика (2005)

К аналогичным выводам на несколько лет раньше Е. Домара пришел Р. Харрод. В отличие от Домара Харрод особое внимание уделяет занятости рабочей силы при экономическом зростанни.
Если в модели Домара объем инвестиций задается экзогенно, то Харрод включает в своей модели эндогенную функцию инвестиций, основанную на принципе акселерации и ожиданиях предпринимателей относительно совокупного попиту.
Харрод назвал «гарантированным» темпом роста, поскольку он гарантирует полное использование производственных мощностей (капитала).
Наряду с гарантированным темпом роста Харрод ввел понятие «естественного» темпа роста, под которым понимал такой темп роста капитала и национального дохода, который обеспечивает полную занятость растущего предложения труда. Если в исходном периоде существует полная занятость и капиталовооруженность труда постоянна, как это предусматривается в посткейнсианських моделях, то естественный темп роста экономики равен темпу роста трудовых ресурсив.
Соотношение между значениями гарантированного и природного темпов роста определяет состояние экономической конъюнктуры.
Если темп роста трудовых ресурсов («естественный» темп роста национального дохода) отстает от темпа роста капитала («гарантированного» темпа роста национального дохода), то вследствие недостатка трудовых ресурсов ожидаемый предпринимателями темп роста не будет достигнут. В результате объем инвестиций сократится и возникнет депресия.
Соответственно при обратном соотношении, когда естественный темп роста превышает гарантированный, фактический темп роста может быть равным гарантированному, и экономика окажется в состоянии динамического равновесия при наличии конъюнктурного безработицы. В случае превышения естественного темпа роста над гарантированным фактический темп роста также может оказаться выше гарантирован, поскольку избыток трудовых ресурсов позволяет увеличить инвестиции. Тогда фактический объем производства превысит ожидаемый, стимулируя дальнейший рост инвестиций и вызывая бум.
Таким образом, в модели Харрода, как и в модели Домара, динамическое равновесие в условиях экономического роста неустойчива.

econbooks.ru

Модель экономического роста Харрода  Домара

Исходя из кейнсианской модели макроэкономического равновесия, в краткосрочном периоде сбережения равны инвестициям, в долгосрочном же периоде они не совпадают. Экономисты  англичанин Р. Ф. Харрод и американец Е. Д. Домар  одновременно предложили модель для анализа экономического роста в долгосрочном периоде в рамках кейнсианских воззрений (в настоящее время она известна как модель Харрода  Домара):

G  s  c,

где G  темпы экономического роста;

s  доля сбережений в совокупном доходе;

c  коэффициент капиталоемкости (отношение капитала к выпуску продукции).

Из данной модели можно вывести, что темпы роста находятся в прямой зависимости от s, так как чем больше чистые сбережения, тем больше могут быть инвестиции; темпы роста находятся в обратной зависимости от c  коэффициента капиталоемкости: чем он выше, тем ниже темпы экономического роста.

Можно рассчитать s и c из данных статистики, следовательно, используя модель Харрода  Домара, можно с известной долей вероятности прогнозировать будущие темпы экономического роста. Однако при этом она имеет слишком высокую степень агрегирования показателей, чтобы служить точным инструментом. Это, скорее, полезный инструмент теоретического анализа для разработки экономической политики.

Исследователи подметили и другой недостаток данной модели. Согласно допущениям темп роста, обеспечивающий полную загрузку мощностей, определяется одной группой факторов, а темп роста, обеспечивающий полную занятость,  другими. Их совпадение  редкий случай, и модель его не предусматривает. Замещение факторов «труд» и «капитал» не предполагается. Экономика в модели Харрода  Домара балансирует на лезвии ножа. Задача создания устойчивых темпов роста лежит вне этой модели.

Неоклассическая модель экономического роста Солоу

Свое дальнейшее развитие и совершенствование рассмотренная теория получила в неоклассической факторной модели экономического роста Роберта Солоу, которая уже предполагает замещение факторов производства, так как изменяются относительные цены на них. По Солоу, инвестиции и сбережения определяют не темпы экономического роста, а соотношение между факторами капитал  труд и объемом производства на душу населения.

За основу своей модели Солоу взял простую производственную функцию, введя в нее уровень развития технологий (Т):

Y  f(K, L, Т).

Далее он предположил, что Т в равной мере воздействует и на труд, и на капитал. Функция в этом случае получила следующий вид:

Y  Тf(K, L).

На основании своего подхода и данных о развитии американской экономики за 19091949 гг. Солоу определил, что более 80% роста показателя выпуска продукции на отработанный человеко-час объясняется научно-техническим прогрессом.

Таким образом, если в модели Харрода  Домара НТП выступает как фактор, внешний по отношению к экономическому росту (экзогенный), то в модели Солоу он рассматривается уже как внутренний (эндогенный) фактор, органически присущий современному экономическому развитию. Это соответствует тому, что именно НТП выступает главным фактором экономического роста в долгосрочном периоде.

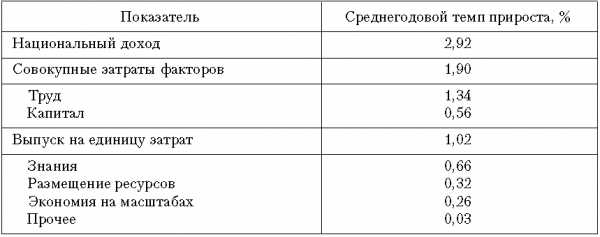
Последователь Солоу  американский экономист Э. Денисон, используя данные за 19291982 гг., сделал детальную разбивку НТП по отдельным компонентам и определил составляющие экономического роста. Э. Денисон указал на важность процесса накопления знаний, обеспечивающих почти 2/3 вклада технического прогресса в производство. Оставшаяся 1/3 этого вклада связана с более эффективным размещением ресурсов и, кроме того, с экономией факторов производства на единицу продукции. Такую экономию при увеличении масштабов производства обеспечивает также НТП (табл. 6.1).

Таблица 6.1 Факторы роста национального дохода США (19291982 гг.)

Выводы, сделанные на основе эмпирических исследований, позволяют определить наиболее эффективный фактор производства. Понятия роста и прогресса связаны не только с необходимостью пополнения материально-вещественной основы производства, но все в большей мере с накоплением знаний, повышением квалификации работников, без чего невозможно внедрение НТП.

studfiles.net

Модель экономического роста Харрода

Количество просмотров публикации Модель экономического роста Харрода — 529

В конце 30-х гᴦ. нашего века английский экономист Рой Ф. Харрод, ко­торого Кейнс провозгласил продолжателœем своих научных идей, создает динамическую модель¹ экономического роста. Он исследует, каким образом в процессе роста происходит взаимодействие капитала, рабочей силы и ве­личины дохода на душу населœения. Первый вопрос, который ставит Хар­род, сводится к следующему: как должен изменяться объём капитала, что­бы соответствовать росту остальных названных элементов при постоянной процентной ставке.

При условии, что населœение растет в геометрической прогрессии, а уро­вень технического развития и процентной ставки остается неизменным, спрос на капитал, по утверждению Харрода, будет расти в той же пропор­ции, что и населœение. Достижение равновесного объёма производства воз­можно, в случае если норма сбережения s и отношение величины используемого капитала к объёму дохода K/Y (коэффициент капитала, или капиталоем­кость) постоянны. Харрод полагает, что при соблюдении этих условий для обеспечения экономического роста крайне важно , чтобы норма сбережения была равна произведению капиталоемкости и прироста населœения в теку­щем периоде. В случае если изменить условия, зафиксировав движение населœения и учитывать непрерывное развитие технического прогресса, то для обеспече­ния экономического роста потребуется такая же норма сбережения (так как технический прогресс выражается в сбережении труда или капитала).

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, увеличение численности населœения и поступательное движение технического прогресса являются естественными условиями эко­номического роста.

Методом исследования и систематизации факторов экономического ро­ста в модели Харрода является основное уравнение:

GxC = s, (10)

где G = AY_t/Y_tл— рост (growth) выпуска продукции за единичный пери­од, измеряемый в темпах прироста; С =AK/AY, — предельная капиталоем­кость, выражающая количество капитальных благ, фактически произведенных ex-post за каждый период, делœенное на прирост продукции за тот же период¹; s = S/Y — предполагавшаяся норма сбережения (Харрод считает, что ʼʼвероятную величину сбереженияʼʼ ex-ante лучше всœего выразить как сбе­регаемую часть совокупного дохода)². Основное уравнение определяет, какой должна быть норма сбережения для достижения экономического роста.

Следует отметить, что AK_t =I_tlи в связи с этим величину С можно выразить как1_ы,/ДУ₍(т. е. как акселœератор). Подставив в формулу (] 0) значения ее ве­личин, получим AY_t/Y_tl X I _tl/AY= S_t/Y_tlпри условии, что сбережения осу­ществляются и расходуются на капиталовложения (инвестиции) в рамках одного временного периода. Сократив левую часть равенства на AY_t, полу­чим IJY⁼S_t_,/Y_t_,т. e. I = S: инвестиции ex-post равны сбережениям ex-ante (инвестиции, фактически осуществленные в данный период, совпали с ранее планировавшимися на данный период сбережениями), что является важным условием динамического равновесия.

Основное уравнение (10) выражает фактический темп роста͵ наблюда­ющийся как при подъеме, так и при рецессии.

Для характеристики условий стабильного поступательного экономичес­кого роста (при нейтральности³ технического прогресса и при неизменной процентной ставке) Харрод использует формулу:

G.xC=_S,

где C_w— темп роста͵ гарантирующий полную занятость растущего ка­питала, при котором производители из периода в период остаются в поло­жении равновесия (т. е. G — линия предпринимательского равновесия). Так Харрод вводит понятие гарантированного (warranted) темпа роста.

С.— это требуемая (required) предельная капиталоемкость, выражаю­щая, в отличие от фактического показателя предельной капиталоемкости С, потребность в добавочном капитале для выпуска добавочной продукции.⁴

Итак, для поддержания стабильного и равновесного роста необходима такая норма сбережений, величина которой равна произведению показателя гарантированного темпа роста и требуемой для его обеспечения пре­дельной капиталоемкости.

Между уравнениями (10) и (11) существует определœенная связь, осно­ванная на том, что, в случае если растет G, то уменьшается значение С (разумеется, при условии, что норма сбережения s постоянна). Следовательно, в случае если фак­тический темп роста превышает гарантированный (G > G_w), то значение показателя фактической предельной капиталоемкости становится ниже тре­буемой (С < С_r). Это говорит о том, что фактических товарно-материаль­ных запасов и оборудования становится недостаточно и предприниматели увеличивают свои заказы. В случае если же фактический рост меньше гарантирован­ного (G < G_w) то С > С_r, и предприниматели будут сокращать инвестиции, что приведет к дальнейшему снижению совокупного спроса и увеличению избыточных производственных мощностей. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, Харрод обо­сновывает крайнюю неустойчивость рассматриваемой им системы, полу­чившую в экономической науке название ʼʼбалансирование на лезвии ножаʼʼ (knife edge). Отклонение от равенства G = G_wприводит к нарастанию из периода в период центробежных сил, углубляющих данный дисбаланс и при­водящих всœе к большему расхождению между совокупным спросом и со­вокупным предложением.

При этом рост G имеет естественные ограничители в виде темпов роста населœения и темпа технического прогресса. Харрод вводит понятие есте­ственного темпа роста G_Nучитывающий эти естественные условия эко­номического роста. G_N— это темп роста͵ при котором полностью использу­ется растущее предложение труда. Он характеризует такую линию разви­тия, которая обеспечивает равновесие на рынке труда. В случае если фактический темп роста G равен G_Nто экономика развивается в условиях полной занятости. Та­ким образом, G_N— это верхний предел фактического темпа роста G.

Харрод исследует связь между G, G_wи G_Nс помощью уравнений:

G_NC_r= s или G_NC_r <>S (12)

Иными словами, идеальные условия для поддержания стабильных рав­новесных темпов экономического роста выражаются в равенстве:

G_wC_r = s = G_NC_r¹(13)

При этом основная проблема состоит в отклонении от равновесия (когда G_NC_r <> s), порождающем расхождение между G_wи G_Nчто обуслов­ливает хроническую безработицу. Другая важная проблема, которая рас­сматривалась выше — отклонение фактического темпа роста от гарантированного (G от G_n ), что лежит, по мнению Харрода, в базе промышленно­го цикла.

Соотношение G_N G и G_W имеет решающее значение для определœения тенденций экономической конъюнктуры. Харрод считает, что тенденции бума или кризиса определяются не величиной G_w, а степенью отклонения от нее. Подведем итоги рассматриваемой проблемы:

1) В случае если G > G_w или G_N > G_w, то возникает тенденция к развитию бума. Действительно, недостаточность в капитале вызывает повышение спроса на капитал и способствует росту инвестиций.

2) В случае если G_N < G_w, то и G, ограниченный уровнем G_Nв среднем должен быть ниже G , что подталкивает экономику к депрессии. Это обстоятель­ство Харрод считает парадоксальным. Ведь на первый взгляд может пока­заться, что более быстрое развитие экономики, превышающее темпы, за­данные естественными условиями, должно привести к буму.

Интересно заметить, что, по мнению Харрода, данный ʼʼпарадоксʼʼ касает­ся основного противоречия между кейнсианской и классической школами. Сбережения в экономике могут играть как положительную, так и отрица­тельную роль исходя из соотношения между G_Nи G_w. До тех пор, пока G_N > G_W, сбережения ʼʼдобродетельныʼʼ. Когда же G_N <G_w, то сбереже­ния приобретают деструктивный характер.
Размещено на реф.рф
Ведь данное неравенство сви­детельствует об избытке капитала и дефиците рабочей силы в экономике. В такой ситуации, как известно, инвестиционные процессы затухают.

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, политика государства, стимулирующая экономический рост, должна опираться на корректирующую (сдерживающую или стиму­лирующую) инвестиционную политику, на регулирование баланса между сбережениями и инвестициями. Государственное регулирование также дол­жно стремиться к минимизации отклонения между гарантированным и ес­тественным темпом роста. При этом для поддержания равновесного темпа роста и сохранения уровня полной занятости крайне важно поступательное снижение процентной ставки (а не снижение уровня заработной платы, как считают классики). В рыночной системе процентная ставка неизбежно ко­леблется, и поддержание ее на стабильно низком уровне, по мнению кеЙн-сианцев, — долгосрочная задача экономической политики.

referatwork.ru

Модель экономического роста Харрода — КиберПедия

В конце 30-х гг. нашего века английский экономист Рой Ф. Харрод, ко­торого Кейнс провозгласил продолжателем своих научных идей, создает динамическую модель¹ экономического роста. Он исследует, каким образом в процессе роста происходит взаимодействие капитала, рабочей силы и ве­личины дохода на душу населения. Первый вопрос, который ставит Хар­род, сводится к следующему: как должен изменяться объем капитала, что­бы соответствовать росту остальных названных элементов при постоянной процентной ставке.

При условии, что население растет в геометрической прогрессии, а уро­вень технического развития и процентной ставки остается неизменным, спрос на капитал, по утверждению Харрода, будет расти в той же пропор­ции, что и население. Достижение равновесного объема производства воз­можно, если норма сбережения s и отношение величины используемого капитала к объему дохода K/Y (коэффициент капитала, или капиталоем­кость) постоянны. Харрод полагает, что при соблюдении этих условий для обеспечения экономического роста необходимо, чтобы норма сбережения была равна произведению капиталоемкости и прироста населения в теку­щем периоде. Если изменить условия, зафиксировав движение населения и учитывать непрерывное развитие технического прогресса, то для обеспече­ния экономического роста потребуется такая же норма сбережения (так как технический прогресс выражается в сбережении труда или капитала).

Таким образом, увеличение численности населения и поступательное движение технического прогресса являются естественными условиями эко­номического роста.

Методом исследования и систематизации факторов экономического ро­ста в модели Харрода является основное уравнение:

GxC = s, (10)

где G = AY_t/Y_tл— рост (growth) выпуска продукции за единичный пери­од, измеряемый в темпах прироста; С =AK/AY, — предельная капиталоем­кость, выражающая количество капитальных благ, фактически произведен-

¹ Модель Харрода была создана им раньше модели Домара. Сходство выводов и допущений этих двух независимых моделей позволило дать им общее название: модель Харрода-Домара.

Глава 25

ных ex-post за каждый период, деленное на прирост продукции за тот же период¹; s = S/Y — предполагавшаяся норма сбережения (Харрод считает, что «вероятную величину сбережения» ex-ante лучше всего выразить как сбе­регаемую часть совокупного дохода)². Основное уравнение определяет, какой должна быть норма сбережения для достижения экономического роста.

Следует отметить, что AK_t =I_tlи поэтому величину С можно выразить как1_ы,/ДУ₍(т. е. как акселератор). Подставив в формулу (] 0) значения ее ве­личин, получим AY_t/Y_tl X I _tl/AY= S_t/Y_tlпри условии, что сбережения осу­ществляются и расходуются на капиталовложения (инвестиции) в рамках одного временного периода. Сократив левую часть равенства на AY_t, полу­чим IJY⁼S_t_,/Y_t_,т. e. I = S: инвестиции ex-post равны сбережениям ex-ante (инвестиции, фактически осуществленные в данный период, совпали с ранее планировавшимися на этот период сбережениями), что является важным условием динамического равновесия.

Основное уравнение (10) выражает фактический темп роста, наблюда­ющийся как при подъеме, так и при рецессии.

Для характеристики условий стабильного поступательного экономичес­кого роста (при нейтральности³ технического прогресса и при неизменной процентной ставке) Харрод использует формулу:

G.xC=_S, (И)

где C_w— темп роста, гарантирующий полную занятость растущего ка­питала, при котором производители из периода в период остаются в поло­жении равновесия (т. е. G — линия предпринимательского равновесия). Так Харрод вводит понятие гарантированного (warranted) темпа роста.

С.— это требуемая (required) предельная капиталоемкость, выражаю­щая, в отличие от фактического показателя предельной капиталоемкости С, потребность в добавочном капитале для выпуска добавочной продукции.⁴

Итак, для поддержания стабильного и равновесного роста необходима такая норма сбережений, величина которой равна произведению показате-

¹ Харрод Р. К теории экономической динамики. Классики кейнсианства. T.I. M., 1997.
С. 112.

² Харрод Р. К теории экономической динамики. Классики кейнсианства. T.I. M.. 1997.
С. 113.

s Нейтральным Харрод считает технический прогресс, т. е. «поток ичобретении, оставля­ющих без изменения ту пропорцию, в которой совокупный продукт распределяется между трудом и капиталом при постоянной процентной ставке». Это объясняется тем, что эффекты от изобретений, требующих увеличения капитальных затрат, и от изобретений, снижающих затраты капитала, уравновешиваются.

⁴ Харрод трактует С, как «предельную величину, выражающую потребность в новом капи­тале для сохранения такого выпуска продукции, который должен удовлетворить потребитель­ский спрос, возникающий из предельного добавочного дохода потребителей» {Харрод Р. К теории экономической динамики. Классики кейнсианства. Т. 1. М. 1997. С. 117).

Экономический рост

ля гарантированного темпа роста и требуемой для его обеспечения пре­дельной капиталоемкости.

Между уравнениями (10) и (11) существует определенная связь, осно­ванная на том, что, если растет G, то уменьшается значение С (разумеется, при условии, что норма сбережения s постоянна). Следовательно, если фак­тический темп роста превышает гарантированный (G > G_w), то значение показателя фактической предельной капиталоемкости становится ниже тре­буемой (С < С_r). Это говорит о том, что фактических товарно-материаль­ных запасов и оборудования становится недостаточно и предприниматели увеличивают свои заказы. Если же фактический рост меньше гарантирован­ного (G < G_w) то С > С_r, и предприниматели будут сокращать инвестиции, что приведет к дальнейшему снижению совокупного спроса и увеличению избыточных производственных мощностей. Таким образом, Харрод обо­сновывает крайнюю неустойчивость рассматриваемой им системы, полу­чившую в экономической науке название «балансирование на лезвии ножа» (knife edge). Отклонение от равенства G = G_wприводит к нарастанию из периода в период центробежных сил, углубляющих этот дисбаланс и при­водящих все к большему расхождению между совокупным спросом и со­вокупным предложением.

Однако рост G имеет естественные ограничители в виде темпов роста населения и темпа технического прогресса. Харрод вводит понятие есте­ственного темпа роста G_Nучитывающий эти естественные условия эко­номического роста. G_N— это темп роста, при котором полностью использу­ется растущее предложение труда. Он характеризует такую линию разви­тия, которая обеспечивает равновесие на рынке труда. Если фактический темп роста G равен G_Nто экономика развивается в условиях полной занятости. Та­ким образом, G_N— это верхний предел фактического темпа роста G.

Харрод исследует связь между G, G_wи G_Nс помощью уравнений:

G_NC_r= s или G_NC_r <>S (12)

Иными словами, идеальные условия для поддержания стабильных рав­новесных темпов экономического роста выражаются в равенстве:

G_wC_r = s = G_NC_r¹(13)

Однако основная проблема заключается в отклонении от равновесия (когда G_NC_r <> s), порождающем расхождение между G_wи G_Nчто обуслов­ливает хроническую безработицу. Другая важная проблема, которая рас­сматривалась выше — отклонение фактического темпа роста от гарантиро-¹ Такое равенство допустимо при больших величинах С_r и выполняется в долгосрочном плане.

37*

Глава 25

ванного (G от G_n ), что лежит, по мнению Харрода, в основе промышленно­го цикла.

Соотношение G_N G и G_W имеет решающее значение для определения тенденций экономической конъюнктуры. Харрод считает, что тенденции бума или кризиса определяются не величиной G_w, а степенью отклонения от нее. Подведем итоги рассматриваемой проблемы:

1) Если G > G_w или G_N > G_w, то возникает тенденция к развитию бума. Действительно, недостаточность в капитале вызывает повышение спроса на капитал и способствует росту инвестиций.

2) Если G_N < G_w, то и G, ограниченный уровнем G_Nв среднем должен быть ниже G , что подталкивает экономику к депрессии. Это обстоятель­ство Харрод считает парадоксальным. Ведь на первый взгляд может пока­заться, что более быстрое развитие экономики, превышающее темпы, за­данные естественными условиями, должно привести к буму.

Интересно заметить, что, по мнению Харрода, этот «парадокс» касает­ся основного противоречия между кейнсианской и классической школами. Сбережения в экономике могут играть как положительную, так и отрица­тельную роль в зависимости от соотношения между G_Nи G_w. До тех пор, пока G_N > G_W, сбережения «добродетельны». Когда же G_N <G_w, то сбереже­ния приобретают деструктивный характер. Ведь данное неравенство сви­детельствует об избытке капитала и дефиците рабочей силы в экономике. В такой ситуации, как известно, инвестиционные процессы затухают.

Таким образом, политика государства, стимулирующая экономический рост, должна опираться на корректирующую (сдерживающую или стиму­лирующую) инвестиционную политику, на регулирование баланса между сбережениями и инвестициями. Государственное регулирование также дол­жно стремиться к минимизации отклонения между гарантированным и ес­тественным темпом роста. Однако для поддержания равновесного темпа роста и сохранения уровня полной занятости необходимо поступательное снижение процентной ставки (а не снижение уровня заработной платы, как считают классики). В рыночной системе процентная ставка неизбежно ко­леблется, и поддержание ее на стабильно низком уровне, по мнению кеЙн-сианцев, — долгосрочная задача экономической политики.

cyberpedia.su