Метод гаусса решение систем линейных уравнений – Метод Гаусса для решения матриц. Решение системы линейных уравнений методом Гаусса :: SYL.ru

Решение матриц методом Гаусса, с примерами

Метод Гаусса используется для решения систем линейных уравнений и для нахождения обратной матрицы. Начнем с нахождения обратной матрицы.

Алгоритм нахождения обратной матрицы методом Гаусса

1. Пусть задана квадратная матрица

   

припишем к столбцам матрицы справа столбцы единичной матрицы того же порядка. Получим матрицу

   

2. С помощью элементарных преобразований строк приведем матрицу к матрице, в левой части которой будет стоять единичная матрица:

   

3. Полученная таким образом матрица, стоящая в правой части матрицы , и будет обратной матрицей к матрице

   

Алгоритм применения метода Гаусса для решения СЛУ

Пусть задана система линейных уравнений

   

Записывается матрица – расширенная матрица этой системы:

   

Над строками матрицы производятся элементарные преобразования: разрешается изменять порядок строк, умножать строки на любые отличные от нуля числа и прибавлять к любой строке матрицы любую другую её строку, умноженное на произвольное число. В результате таких элементарных преобразований основная матрица системы должна быть приведена к нижнему треугольному виду

   

Эта матрица эквивалентна системе линейных уравнений

   

Из этой системы последовательно снизу вверх выражаются все неизвестные переменные.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Метод Гаусса (последовательного исключения неизвестных). Примеры решений для чайников

Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Как решить систему линейных уравнений? Далее полезно изучить урок Правило Крамера. Матричный метод.

Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». 

А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной).

Метод  Гаусса – наиболее мощный и универсальный инструмент для нахождения решениялюбой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных 

в любом случаеприведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статьяНесовместные системы и системы с общим решением. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений? и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы: . По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями

.

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: 

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить

. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и 

ко второй строке прибавляем первую строку умноженную на –2: . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.

На практике так подробно, конечно, не расписывают, а пишут короче: Еще раз: ко второй строке прибавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Элементарные преобразования не меняют решение системы уравнений

! ВНИМАНИЕ: рассмотренные манипуляции нельзя использовать, если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя! Вернемся к нашей системе . Она практически разобрана по косточкам.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид. 

 В результате элементарных преобразований получена эквивалентная исходной система уравнений:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.

В нижнем уравнении у нас уже готовый результат: .

Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

Ответ: 

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Пример 1

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число:  Почти всегда здесь должна находиться единица. Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения. Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2:

Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3:

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО: А мысленный ход самих расчётов я уже рассмотрел выше.

Далее нужно получить единицу на следующей «ступеньке»:

В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2: Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: Круто.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат: 

Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:

И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:

Ответ: 

Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.

Пример 2

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса. Но вот ответы обязательно должны получиться одинаковыми!

Пример 3

Решить систему линейных уравнений методом Гаусса

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:  (1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).

Дальше алгоритм работает уже по накатанной колее:

(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:

Ответ: .

Пример 4

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения. 

В последней части рассмотрим некоторые особенности алгоритма Гаусса. Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например: Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод. В расширенной матрице системы на месте отсутствующих переменных ставим нули: Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .

Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.

Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:

Пример 5

Решить методом Гаусса систему 4-х линейных уравнений с четырьмя неизвестными.

Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением. Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Желаю успехов!

Решения и ответы:

Пример 2: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду. Выполненные элементарные преобразования: (1) Ко второй строке прибавили первую строку, умноженную на –2.  К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем! (2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание, что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее. (3) К третьей строке прибавили вторую строку, умноженную на 5. (4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход: 

Ответ: .

Пример 4: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования: (1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке». (2) Ко второй строке прибавили первую строку, умноженную на 7.  К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже, «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы (3) К третьей строке прибавили вторую, умноженную на –1. (4) Ко второй строке прибавили третью, умноженную на –3. Нужная вещь на второй ступеньке получена. (5) К третьей строке прибавили вторую, умноженную на 6. (6) Вторую строку умножили на –1, третью строку разделили на -83.

Обратный ход: 

Ответ: 

Пример 5: Решение: Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования: (1) Первую и вторую строки поменяли местами. (2) Ко второй строке прибавили первую строку, умноженную на –2.  К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3. (3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1. (4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки. (5) К четвертой строке прибавили третью строку, умноженную на  –5.

Обратный ход:

Ответ: 

\

studfiles.net

2.3 Решение систем линейных уравнений методом Гаусса

Одним из универсальных и эффективных методов реше­ния линейных алгебраических систем является метод Гаусса, состо­ящий в последовательном исключении неизвестных.

Напомним, две системы называются эквивалентными (равносильными), если множества их решений совпадают. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой и наоборот. Эквивалентные системы получаются приэлементарных преобразованияхуравнений системы:

1. умножение обеих частей уравнения на число отличное от нуля;

2. прибавление к некоторому уравнению соответствующих частей другого уравнения, умноженных на число отличное от нуля;

3. перестановка двух уравнений.

Пусть дана система уравнений

Процесс решения этой системы по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система с помощью элементарных преобразований приводится к ступен­чатому, илитреугольному виду, а на втором этапе (обратный ход) идет последовательное, начиная с последнего по номеру переменного, определение неизвестных из полученной ступенчатой системы.

Предположим, что коэффициент данной системы , в против­ном случае в системе первую строку можно поменять местами с любой другой строкой так, чтобы коэффициент прибыл отличен от нуля.

Преобразуем систему, исключив неизвестное во всех уравне­ниях, кроме первого. Для этого умножим обе части первого уравнения наи сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения наи сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалент­ную систему

Здесь – новые значения коэффициентов и свободных членов, которые получаются после первого шага.

Аналогичным образом, считая главным элементом , исклю­чим неизвестноеиз всех уравнений системы, кроме первого и второго. Продолжим этот процесс, пока это возможно, в результате получим ступенчатую систему

,

где ,,…,– главные элементы системы.

Если в процессе приведения системы к ступенчатому виду появятся уравнения , т. е. равенства вида, их отбрасывают, так как им удовлетворяют любые наборы чисел. Если же припоявится уравнение вида, которое не имеет решений, то это свидетельствует о несовместности системы.

При обратном ходе из последнего уравнения преобразованной сту­пенчатой системы выражается первое неизвестное через все остальные неизвестные, которые называютсвободными.Затем выражение переменнойиз последнего уравнения системы подставляется в предпоследнее уравнение и из него выражается переменная. Аналогичным образом последовательно определяются переменные. Переменные, выраженные через свободные переменные, называютсябазисными(зависимыми). В результате получается общее решение системы линейных уравнений.

Чтобы найти частное решениесистемы, свободным неизвестнымв общем решении придаются произвольные значения и вычисляются значения переменных.

Технически удобнее подвергать элементарным преобразованиям не сами уравнения системы, а расширенную матрицу системы

.

Метод Гаусса — универсальный метод, который позволяет решать не только квадратные, но и прямоугольные системы, в которых число неизвестных не равно числу уравнений.

Достоинство этого метода состоит также в том, что в процессе решения мы одновременно исследуем систему на совместность, так как, приведя расширенную матрицу к ступенчатому виду, легко определить ранги матрицыи расширенной матрицыи применитьтеорему Кронекера — Капелли.

Пример 2.1 Методом Гаусса решить систему

Решение. Число уравненийи число неизвестных.

Составим расширенную матрицу системы, приписав справа от матрицы коэффициентов столбец свободных членов.

Приведём матрицу к треугольному виду; для этого будем получать «0» ниже элементов, стоящих на главной диагонали с помощью элементарных преобразований.

Чтобы получить «0» во второй позиции первого столбца, умножим первую строку на (-1) и прибавим ко второй строке.

Это преобразование запишем числом (-1) против первой строки и обозначим стрелкой, идущей от первой строки ко второй строке.

Для получения «0» в третьей позиции первого столбца, умножим первую строку на (-3) и прибавим к третьей строке; покажем это действие с помощью стрелки, идущей от первой строки к третьей.

.

В полученной матрице, записанной второй в цепочке матриц, получим «0» во втором столбце в третьей позиции. Для этого умножили вторую строку на (-4) и прибавили к третьей. В полученной матрице вторую строку умножим на (-1), а третью — разделим на (-8). Все элементы этой матрицы, лежащие ниже диагональных элементов — нули.

Так как ,система является совместной и определенной.

Соответствующая последней матрице система уравнений имеет треугольный вид:

Из последнего (третьего) уравнения . Подставим во второе уравнение и получим.

Подставим ив первое уравнение, найдём.

Итак

Пример 2.2. Исследовать систему на совместность и в случае совместности найти решение:

Решение. Применим к данной системе метод Гаусса.

Запишем расширенную матрицу системы, предварительно для удобства вычислений поменяв местами вторую и первую строку. Приведем ее к ступенчатому виду.

̴̴.

Найдем ранги матриц: . Так как ,то система является несовместной, т.е. не имеет решений.

Иначе говоря, система содержит противоречивое уравнение вида:

или, поэтому является несовместной.

studfiles.net

Метод Гаусса

Метод Гаусса: описание алгоритма решения системы линейных уравнений, примеры, решения.

Метод Гаусса прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с другими методами:

• во-первых, нет необходимости предварительно исследовать систему уравнений на совместность;

• во-вторых, методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю;

• в-третьих, метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.

Краткий обзор статьи.

Сначала дадим необходимые определения и введем обозначения.

Далее опишем алгоритм метода Гаусса для простейшего случая, то есть, для систем линейных алгебраических уравнений, количество уравнений в которых совпадает с количеством неизвестных переменных и определитель основной матрицы системы не равен нулю. При решении таких систем уравнений наиболее отчетливо видна суть метода Гаусса, которая заключается в последовательном исключении неизвестных переменных. Поэтому метод Гаусса также называют методом последовательного исключения неизвестных. Покажем подробные решения нескольких примеров.

В заключении рассмотрим решение методом Гаусса систем линейных алгебраических уравнений, основная матрица которых либо прямоугольная, либо вырожденная. Решение таких систем имеет некоторые особенности, которые мы подробно разберем на примерах.

Навигация по странице.

• Основные определения и обозначения.

• Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса.

• Решение систем линейных алгебраических уравнений, в которых число уравнений не совпадает с числом неизвестных или основная матрица системы вырожденная, методом Гаусса.

Основные определения и обозначения.

Рассмотрим систему из p линейных уравнений с n неизвестными (p может быть равно n): где- неизвестные переменные,- числа (действительные или комплексные),- свободные члены.

Если , то система линейных алгебраических уравнений называетсяоднородной, в противном случае – неоднородной.

Совокупность значения неизвестных переменных , при которых все уравнения системы обращаются в тождества, называетсярешением СЛАУ.

Если существует хотя бы одно решение системы линейных алгебраических уравнений, то она называется совместной, в противном случае – несовместной.

Если СЛАУ имеет единственное решение, то она называется определенной. Если решений больше одного, то система называется неопределенной.

Говорят, что система записана в координатной форме, если она имеет вид .

Эта система в матричной форме записи имеет вид , где- основная матрица СЛАУ,- матрица столбец неизвестных переменных,- матрица свободных членов.

Если к матрице А добавить в качестве (n+1)-ого столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу системы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т, а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,

Квадратная матрица А называется вырожденной, если ее определитель равен нулю. Если , то матрицаА называется невырожденной.

Следует оговорить следующий момент.

Если с системой линейных алгебраических уравнений произвести следующие действия

• поменять местами два уравнения,

• умножить обе части какого-либо уравнения на произвольное и отличное от нуля действительное (или комплексное) число k,

• к обеим частям какого-либо уравнения прибавить соответствующие части другого уравнения, умноженные на произвольное число k,

то получится эквивалентная система, которая имеет такие же решения (или также как и исходная не имеет решений).

Для расширенной матрицы системы линейных алгебраических уравнений эти действия будут означать проведение элементарных преобразований со строками:

• перестановку двух строк местами,

• умножение всех элементов какой-либо строки матрицы T на отличное от нуля число k,

• прибавление к элементам какой-либо строки матрицы соответствующих элементов другой строки, умноженных на произвольное число k.

Теперь можно переходить к описанию метода Гаусса.

К началу страницы

Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса.

Как бы мы поступили в школе, если бы получили задание найти решение системы уравнений .

Некоторые сделали бы так.

Заметим, что прибавив к левой части второго уравнения левую часть первого, а к правой части — правую, можно избавиться от неизвестных переменных x₂ и x₃ и сразу найти x₁:

Подставляем найденное значение x₁=1 в первое и третье уравнение системы:

Если умножить обе части третьего уравнения системы на -1 и прибавить их к соответствующим частям первого уравнения, то мы избавимся от неизвестной переменной x₃ и сможем найти x₂:

Подставляем полученное значение x₂=2 в третье уравнение и находим оставшуюся неизвестную переменную x₃:

Другие поступили бы иначе.

Разрешим первое уравнение системы относительно неизвестной переменной x₁ и подставим полученное выражение во второе и третье уравнение системы, чтобы исключить из них эту переменную:

Теперь разрешим второе уравнение системы относительно x₂ и подставим полученный результат в третье уравнение, чтобы исключить из него неизвестную переменную x₂: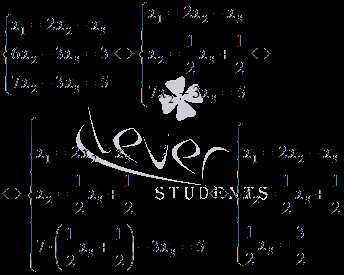

Из третьего уравнения системы видно, что x₃=3. Из второго уравнения находим , а из первого уравнения получаем.

Знакомые способы решения, не правда ли?

Самое интересное здесь то, что второй способ решения по сути и есть метод последовательного исключения неизвестных, то есть, метод Гаусса. Когда мы выражали неизвестные переменные (сначала x₁, на следующем этапе x₂) и подставляли их в остальные уравнения системы, мы тем самым исключали их. Исключение мы проводили до того момента, пока в последнем уравнении не осталась одна единственная неизвестная переменная. Процесс последовательного исключения неизвестных называется прямым ходом метода Гаусса. После завершения прямого хода у нас появляется возможность вычислить неизвестную переменную, находящуюся в последнем уравнении. С ее помощью из предпоследнего уравнения находим следующую неизвестную переменную и так далее. Процесс последовательного нахождения неизвестных переменных при движении от последнего уравнения к первому называется обратным ходом метода Гаусса.

Следует заметить, что когда мы выражаем x₁ через x₂ и x₃ в первом уравнении, а затем подставляем полученное выражение во второе и третье уравнения, то к такому же результату приводят следующие действия:

• к левой и правой частям второго уравнения прибавляем соответствующие части первого уравнения, умноженные на ,

• к левой и правой частям третьего уравнения прибавляем соответствующие части первого уравнения, умноженные на .

Действительно, такая процедура также позволяет исключить неизвестную переменную x₁ из второго и третьего уравнений системы:

Нюансы с исключением неизвестных переменных по методу Гаусса возникают тогда, когда уравнения системы не содержат некоторых переменных.

Например, в СЛАУ в первом уравнении отсутствует неизвестная переменнаяx₁ (иными словами, коэффициент перед ней равен нулю). Поэтому мы не можем разрешить первое уравнение системы относительно x₁, чтобы исключить эту неизвестную переменную из остальных уравнений. Выходом из этой ситуации является перестановка местами уравнений системы. Так как мы рассматриваем системы линейных уравнений, определители основных матриц которых отличны от нуля, то всегда существует уравнение, в котором присутствует нужная нам переменная, и мы это уравнение можем переставить на нужную нам позицию. Для нашего примера достаточно поменять местами первое и второе уравнения системы , дальше можно разрешить первое уравнение относительноx₁ и исключить ее из остальных уравнений системы (хотя во втором уравнении x₁ уже отсутствует).

Надеемся, что суть Вы уловили.

Опишем алгоритм метода Гаусса.

Пусть нам требуется решить систему из n линейных алгебраических уравнений с nнеизвестными переменными вида , и пусть определитель ее основной матрицы отличен от нуля.

Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменнуюx₁ из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на, и так далее, кn-омууравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет видгде, а.

К такому же результату мы бы пришли, если бы выразили x₁ через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x₁ исключена из всех уравнений, начиная со второго.

Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке

Будем считать, что (в противном случае мы переставим местами вторую строку сk-ой, где ). Приступаем к исключению неизвестной переменнойx₂ из всех уравнений, начиная с третьего.

Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на, и так далее, кn-омууравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет видгде, а. Таким образом, переменнаяx₂ исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x₃, при этом действуем аналогично с отмеченной на рисунке частью системы

Так продолжаем прямой ход метода Гаусса пока система не примет вид

С этого момента начинаем обратный ход метода Гаусса: вычисляем x_n из последнего уравнения как , с помощью полученного значенияx_n находим x_n-1 из предпоследнего уравнения, и так далее, находим x₁ из первого уравнения.

Разберем алгоритм на примере.

Пример.

Найдите решение системы уравнений методом Гаусса.

Решение.

Коэффициент a₁₁ отличен от нуля, так что приступим к прямому ходу метода Гаусса, то есть, к исключению неизвестной переменной x₁ из всех уравнений системы, кроме первого. Для этого к левой и правой частям второго, третьего и четвертого уравнения прибавим левую и правую части первого уравнения, умноженные соответственно на ,и: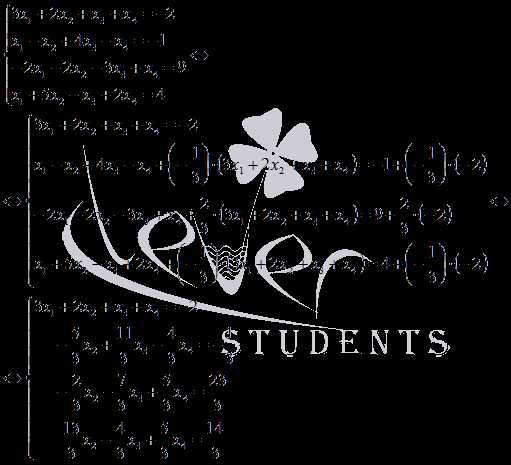

Неизвестную переменную x₁ исключили, переходим к исключению x₂. К левым и правым частям третьего и четвертого уравнений системы прибавляем левую и правую части второго уравнения, умноженные соответственно на и:

Для завершения прямого хода метода Гаусса нам осталось исключить неизвестную переменную x₃ из последнего уравнения системы. Прибавим к левой и правой частям четвертого уравнения соответственно левую и правую часть третьего уравнения, умноженную на :

Можно начинать обратный ход метода Гаусса.

Из последнего уравнения имеем , из третьего уравнения получаем, из второго, из первого.

Для проверки можно подставить полученные значения неизвестных переменных в исходную систему уравнений. Все уравнения обращаются в тождества, что говорит о том, что решение по методу Гаусса найдено верно.

Ответ:

.

А сейчас приведем решение этого же примера методом Гаусса в матричной форме записи.

Пример.

Найдите решение системы уравнений методом Гаусса.

Решение.

Расширенная матрица системы имеет вид . Сверху над каждым столбцом записаны неизвестные переменные, которым соответствуют элементы матрицы.

Прямой ход метода Гаусса здесь предполагает приведение расширенной матрицы системы к трапецеидальному виду с помощью элементарных преобразований. Этот процесс схож с исключением неизвестных переменных, которое мы проводили с системой в координатной форме. Сейчас Вы в этом убедитесь.

Преобразуем матрицу так, чтобы все элементы в первом столбце, начиная со второго, стали нулевыми. Для этого к элементам второй, третьей и четвертой строк прибавим соответствующие элементы первой строки умноженные на ,и насоответственно:

Далее полученную матрицу преобразуем так, чтобы во втором столбце все элементы, начиная с третьего стали нулевыми. Это будет соответствовать исключению неизвестной переменной x₂. Для этого к элементам третьей и четвертой строк прибавим соответствующие элементы первой строки матрицы, умноженные соответственно на и:

Осталось исключить неизвестную переменную x₃ из последнего уравнения системы. Для этого к элементам последней строки полученной матрицы прибавим соответствующие элементы предпоследней строки, умноженные на :

Следует отметить, что эта матрица соответствует системе линейных уравнений которая была получена ранее после прямого хода.

Пришло время обратного хода. В матричной форме записи обратный ход метода Гаусса предполагает такое преобразование полученной матрицы, чтобы матрица, отмеченная на рисунке  стала диагональной, то есть, приняла видгде- некоторые числа.

Эти преобразования аналогичны преобразованиям прямого хода метода Гаусса, но выполняются не от первой строки к последней, а от последней к первой.

Прибавим к элементам третьей, второй и первой строк соответствующие элементы последней строки, умноженные на , наи насоответственно:

Теперь прибавим к элементам второй и первой строк соответствующие элементы третьей строки, умноженные на и насоответственно:

На последнем шаге обратного хода метода Гаусса к элементам первой строки прибавляем соответствующие элементы второй строки, умноженные на :

Полученная матрица соответствует системе уравнений , откуда находим неизвестные переменные.

Ответ:

.

ОБРАТИТЕ ВНИМАНИЕ.

При использовании метода Гаусса для решения систем линейных алгебраических уравнений следует избегать приближенных вычислений, так как это может привести к абсолютно неверным результатам. Рекомендуем не округлять десятичные дроби. Лучше от десятичных дробей переходить к обыкновенным дробям.

Пример.

Решите систему из трех уравнений методом Гаусса .

Решение.

Отметим, что в этом примере неизвестные переменные имеют другое обозначение (неx₁, x₂, x₃, а x, y, z). Перейдем к обыкновенным дробям:

Исключим неизвестную x из второго и третьего уравнений системы:

В полученной системе во втором уравнении отсутствует неизвестная переменная y, а в третьем уравнении y присутствует, поэтому, переставим местами второе и третье уравнения:

На этом прямой ход метода Гаусса закончен (из третьего уравнения не нужно исключать y, так как этой неизвестной переменной уже нет).

Приступаем к обратному ходу.

Из последнего уравнения находим ,  из предпоследнегоиз первого уравнения имеем

Ответ:

x = 10, y = 5, z = -20.

К началу страницы

Решение систем линейных алгебраических уравнений, в которых число уравнений не совпадает с числом неизвестных или основная матрица системы вырожденная, методом Гаусса.

Системы уравнений, основная матрица которых прямоугольная или квадратная вырожденная, могут не иметь решений, могут иметь единственное решение, а могут иметь бесконечное множество решений.

Сейчас мы разберемся, как метод Гаусса позволяет установить совместность или несовместность системы линейных уравнений, а в случае ее совместности определить все решения (или одно единственное решение).

В принципе процесс исключения неизвестных переменных в случае таких СЛАУ остается таким же. Однако следует подробно остановиться на некоторых ситуациях, которые могут возникнуть.

1. На определенном этапе исключения неизвестных переменных некоторые уравнения системы могут обратиться в тождества . Это говорит о том, что такие уравнения излишни, то есть, их можно смело убрать из системы уравнений и продолжить прямой ход метода Гаусса.

К примеру, при исключении x₁ из второго и третьего уравнений системы мы имеем такую ситуацию:

Следовательно, второе уравнение можно удалить из системы и продолжить решение.

2. При проведении прямого хода метода Гаусса одно (или несколько) уравнений системы могут принять вид , где- некоторое число, отличное от нуля. Это говорит о том, что уравнение, которое обратилось в равенство, не может обратиться в тождество ни при каких значениях неизвестных переменных. Другими словами, система линейных алгебраических уравнений в этом случае несовместна (не имеет решения). Наиболее часто такие ситуации встречаются, когда число уравнений в системе больше числа неизвестных переменных.

Пример.

Найдите решение системы линейных уравнений методом Гаусса.

Решение.

Исключим неизвестную переменную x₁ из всех уравнений системы, начиная со второго. Для этого прибавим к левой и правой частям второго, третьего и четвертого уравнения левую и правую части первого уравнения, умноженные на (-1), (-2) и (-3) соответственно: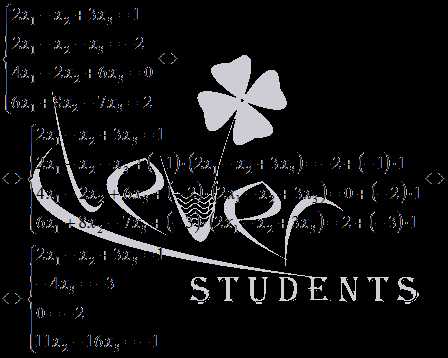

Равенство 0=-2, которое получилось в третьем уравнении системы, не достижимо ни для каких значений неизвестных переменных x₁, x₂ и x₃, поэтому, исходная система уравнений решений не имеет.

Ответ:

система несовместна.

3. Предположим, что мы выполняем прямой ход метода Гаусса, и мы подошли к моменту исключения неизвестной переменной x_k, а на каком-то предыдущем i-омшаге (i < k) эта переменная уже исключилась вместе с x_i. Как поступать в данном случае? В этом случае следует перейти к исключению неизвестной переменнойx_k+1. Если x_k+1 также уже исключилась, то переходим к x_k+2 и так далее.

К примеру, после исключения неизвестной переменной x₁ система уравнений принимает вид.

Вместе с x₁ исключились x₂ и x₃. Так что прямой ход метода Гаусса продолжаем исключением переменной x₄ из всех уравнений, начиная с третьего:

studfiles.net

Решение системы линейных уравнений (метод Гаусса)

Этот онлайн калькулятор позволит вам очень просто решить систему линейных уравнений (СЛУ) методом Гаусса.

Для того чтобы решить систему линейных уравнений методом Гаусса, выберите количество неизвестных величин: 2345

Заполните систему линейных уравнений

Для изменения в уравнении знаков с «+» на «-» вводите отрицательные числа. Если в вашем уравнение отсутствует какой-то коэффициент, то на его месте в калькуляторе введите ноль. Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.

Решить систему

Воспользуйтесь также:
Решение системы линейных уравнений (метод подстановки)
Решение системы линейных уравнений (метод Крамера)
Решение системы линейных уравнений (матричный метод)

Решение системы линейных уравнений методом Гаусса

Метод Гаусса

Это классический метод решения системы линейных уравнений, в основе которого лежат элементарные преобразования системы (сложение, вычитание уравнений, умножение на коэффмцменты) для приведения к равносильной системе уравнений треугольного типа, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные неизвестные. Решение системы линейных уравнений методом Гаусса осуществляется в два этапа.

На нашем сайте решение происходит в режиме онлайн, каждый шаг решения имеет подробное описание, поэтому вы с легкость сможете освоить метод Гаусса решения систем линейных уравнений. Также мы применяем наиболее полную форму метода Гаусса, когда матрица приводится не к диагональному виду, а к единичной форме. В этом случае правая колонка и будет представлять значения неизвестных переменных. При этом нет необходимости вычислять новые неизвестные через ранее рассчитанные.

matematikam.ru

Метод Гаусса для решения матриц. Решение системы линейных уравнений методом Гаусса :: SYL.ru

Еще с начала XVI-XVIII веков математики усиленно начали изучать функции, благодаря которым так много в нашей жизни изменилось. Компьютерная техника без этих знаний просто не существовала бы. Для решения сложных задач, линейных уравнений и функций были созданы различные концепции, теоремы и методики решения. Одним из таких универсальных и рациональных способов и методик решения линейных уравнений и их систем стал и метод Гаусса. Матрицы, их ранг, детерминант — все можно посчитать, не используя сложных операций.

Что представляет собой СЛАУ

В математике существует понятие СЛАУ — система линейных алгебраических уравнений. Что же она собой представляет? Это набор из m уравнений с искомыми n неизвестными величинами, обычно обозначающимися как x, y, z, или x₁, x₂… x_n, или другими символами. Решить методом Гаусса данную систему — означает найти все искомые неизвестные. Если система имеет одинаковое число неизвестных и уравнений, тогда она называется системой n-го порядка.

Наиболее популярные методы решения СЛАУ

В учебных заведениях среднего образования изучают различные методики решения таких систем. Чаще всего это простые уравнения, состоящие из двух неизвестных, поэтому любой существующий метод для поиска ответа на них не займет много времени. Это может быть как метод подстановки, когда из одного уравнения выводится другое и подставляется в изначальное. Или метод почленного вычитания и сложения. Но наиболее легким и универсальным считается метод Гаусса. Он дает возможность решать уравнения с любым количеством неизвестных. Почему именно эта методика считается рациональной? Все просто. Матричный способ хорош тем, что здесь не требуется по несколько раз переписывать ненужные символы в виде неизвестных, достаточно проделать арифметические операции над коэффициентами — и получится достоверный результат.

Где используются СЛАУ на практике

Решением СЛАУ являются точки пересечения прямых на графиках функций. В наш высокотехнологический компьютерный век людям, которые тесно связаны с разработкой игр и прочих программ, необходимо знать, как решать такие системы, что они представляют и как проверить правильность получившегося результата. Наиболее часто программисты разрабатывают специальные программы-вычислители линейной алгебры, сюда входит и система линейных уравнений. Метод Гаусса позволяет высчитать все существующие решения. Также используются и другие упрощенные формулы и методики.

Критерий совместимости СЛАУ

Такую систему можно решить только в том случае, если она совместима. Для понятности представим СЛАУ в виде Ax=b. Она имеет решение, если rang(A) равняется rang(A,b). В этом случае (A,b) – это матрица расширенного вида, которую можно получить из матрицы А, переписав ее со свободными членами. Выходит, что решить линейные уравнения методом Гаусса достаточно легко.

Возможно, некоторые обозначения не совсем понятны, поэтому необходимо рассмотреть все на примере. Допустим, есть система: x+y=1; 2x-3y=6. Она состоит всего из двух уравнений, в которых 2 неизвестные. Система будет иметь решение только в том случае, если ранг ее матрицы будет равняться рангу расширенной матрицы. Что такое ранг? Это число независимых строк системы. В нашем случае ранг матрицы 2. Матрица А будет состоять из коэффициентов, находящихся возле неизвестных, а в расширенную матрицу вписываются и коэффициенты, находящиеся за знаком «=».

Почему СЛАУ можно представить в матричном виде

Исходя из критерия совместимости по доказанной теореме Кронекера-Капелли, систему линейных алгебраических уравнений можно представить в матричном виде. Применяя каскадный метод Гаусса, можно решить матрицу и получить единственный достоверный ответ на всю систему. Если ранг обычной матрицы равняется рангу ее расширенной матрицы, но при этом меньше количества неизвестных, тогда система имеет бесконечное количество ответов.

Преобразования матриц

Прежде чем переходить к решению матриц, необходимо знать, какие действия можно проводить над их элементами. Существует несколько элементарных преобразований:

• Переписывая систему в матричный вид и осуществляя ее решение, можно умножать все элементы ряда на один и тот же коэффициент.
• Для того чтобы преобразовать матрицу в канонический вид, можно менять местами два параллельных ряда. Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся — нулями.
• Соответствующие элементы параллельных рядов матрицы можно прибавлять один к другому.

Метод Жордана-Гаусса

Суть решения систем линейных однородных и неоднородных уравнений методом Гаусса в том, чтобы постепенно исключить неизвестные. Допустим, у нас есть система из двух уравнений, в которых две неизвестные. Чтобы их найти, необходимо проверить систему на совместимость. Уравнение методом Гаусса решается очень просто. Необходимо выписать коэффициенты, находящиеся возле каждого неизвестного в матричный вид. Для решения системы понадобится выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, тогда на место пропущенного элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, прибавление соответствующих элементов рядов друг к другу и другие. Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.

Простой пример решения системы 2х2

Для начала возьмем простенькую систему алгебраических уравнений, в которой будет 2 неизвестных.

Перепишем ее в расширенную матрицу.

Чтобы решить данную систему линейных уравнений, требуется проделать всего две операции. Нам необходимо привести матрицу к каноническому виду, чтобы по главной диагонали стояли единицы. Так, переводя с матричного вида обратно в систему, мы получим уравнения: 1x+0y=b1 и 0x+1y=b2, где b1 и b2 — получившиеся ответы в процессе решения.

1. Первое действие при решении расширенной матрицы будет таким: первый ряд необходимо умножить на -7 и прибавить соответственно отвечающие элементы ко второй строке, чтобы избавиться от одного неизвестного во втором уравнении.
2. Так как решение уравнений методом Гаусса подразумевает приведение матрицы к каноническому виду, тогда необходимо и с первым уравнением проделать те же операции и убрать вторую переменную. Для этого вторую строку отнимаем от первой и получаем необходимый ответ — решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же.

Как видим, наша система решена методом Жордана-Гаусса. Переписываем ее в необходимую форму: x=-5, y=7.

Пример решения СЛАУ 3х3

Предположим, что у нас есть более сложная система линейных уравнений. Метод Гаусса дает возможность высчитать ответ даже для самой, казалось бы, запутанной системы. Поэтому, чтобы более глубоко вникнуть в методику расчета, можно переходить к более сложному примеру с тремя неизвестными.

Как и в прежнем примере, переписываем систему в вид расширенной матрицы и начинаем приводить ее к каноническому виду.

Для решения этой системы понадобится произвести гораздо больше действий, чем в предыдущем примере.

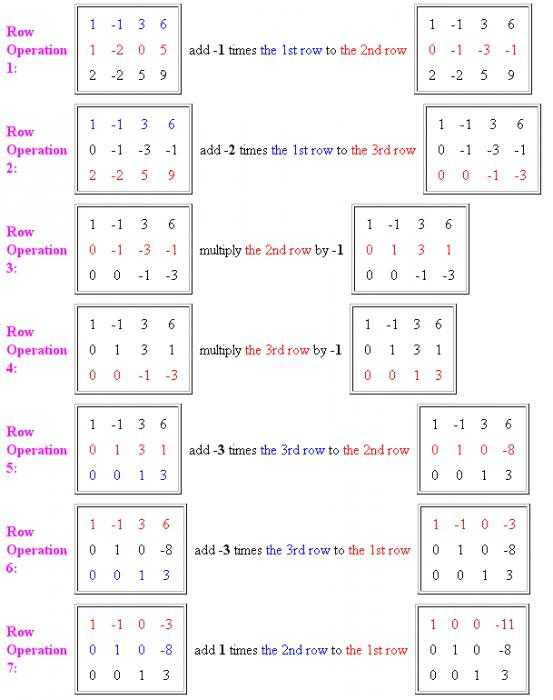
1. Сначала необходимо сделать в первом столбце один единичный элемент и остальные нули. Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую — уже в измененном.
2. Далее убираем эту же первую неизвестную из третьего уравнения. Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья — уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.
3. Теперь необходимо проделать операции и над другими элементами рядов. Третье и четвертое действие можно объединить в одно. Нужно разделить вторую и третью строку на -1, чтобы избавиться от минусовых единиц по диагонали. Третью строку мы уже привели к необходимому виду.
4. Дальше приведем к каноническому виду вторую строку. Для этого элементы третьего ряда умножаем на -3 и прибавляем их ко второй строчке матрицы. Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки.
5. Чтобы из второго элемента строки сделать 0, необходимо умножить третью строку на -3 и прибавить ее к первому ряду.
6. Следующим решающим этапом будет прибавление к первой строке необходимые элементы второго ряда. Так мы получаем канонический вид матрицы, а, соответственно, и ответ.

Как видно, решение уравнений методом Гаусса довольно простое.

Пример решения системы уравнений 4х4

Некоторые более сложные системы уравнений можно решить методом Гаусса посредством компьютерных программ. Необходимо вбить в существующие пустые ячейки коэффициенты при неизвестных, и программа сама пошагово рассчитает необходимый результат, подробно описывая каждое действие.

Ниже описана пошаговая инструкция решения такого примера.

• В первом действии в пустые ячейки вписываются свободные коэффициенты и числа при неизвестных. Таким образом, получается такая же расширенная матрица, которую мы пишем вручную.

• Далее меняются все строки местами, чтобы можно было выразить по главной диагонали единичные элементы.

• И производятся все необходимые арифметические операции, чтобы привести расширенную матрицу к каноническому виду. Необходимо понимать, что не всегда ответ на систему уравнений — это целые числа. Иногда решение может быть из дробных чисел.

Проверка правильности решения

Метод Жордана-Гаусса предусматривает проверку правильности результата. Для того чтобы узнать, правильно ли посчитаны коэффициенты, необходимо всего-навсего подставить результат в изначальную систему уравнений. Левая сторона уравнения должна соответствовать правой стороне, находящейся за знаком «равно». Если ответы не совпадают, тогда необходимо пересчитывать заново систему или попробовать применить к ней другой известный вам метод решения СЛАУ, такой как подстановка или почленное вычитание и сложение. Ведь математика – это наука, которая имеет огромное количество различных методик решения. Но помните: результат должен быть всегда один и тот же, независимо от того, какой метод решения вы использовали.

Метод Гаусса: наиболее часто встречающиеся ошибки при решении СЛАУ

Во время решения линейных систем уравнений чаще всего возникают такие ошибки, как неправильный перенос коэффициентов в матричный вид. Бывают системы, в которых отсутствуют в одном из уравнений некоторые неизвестные, тогда, перенося данные в расширенную матрицу, их можно потерять. В результате при решении данной системы результат может не соответствовать действительному.

Еще одной из главных ошибок может быть неправильное выписывание конечного результата. Нужно четко понимать, что первый коэффициент будет соответствовать первому неизвестному из системы, второй — второму, и так далее.

Метод Гаусса подробно описывает решение линейных уравнений. Благодаря ему легко произвести необходимые операции и найти верный результат. Кроме того, это универсальное средство для поиска достоверного ответа на уравнения любой сложности. Может быть, поэтому его так часто используют при решении СЛАУ.

www.syl.ru

Метод Гаусса для решения систем линейных уравнений

1. Система линейных алгебраических уравнений

1.1 Понятие системы линейных алгебраических уравнений

Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких переменных. Системой линейных алгебраических уравнений (далее – СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:

где числа a_ij называются коэффициентами системы, числа b_i – свободными членами, a_ij и b_i (i=1,…, m; b=1,…, n) представляют собой некоторые известные числа, а x₁ ,…, x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент. Подлежат нахождению числа x_n . Такую систему удобно записывать в компактной матричной форме: AX=B. Здесь А – матрица коэффициентов системы, называемая основной матрицей;

– вектор-столбец из неизвестных xj.
– вектор-столбец из свободных членов bi.

Произведение матриц А*Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).

Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов

1.2 Решение системы линейных алгебраических уравнений

Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений системы обращается в верное равенство.

Решением системы называется n значений неизвестных х1=c1, x2=c2,…, xn=cn, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: перестановка местами двух уравнений системы, перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений, умножение обеих частей какого-либо уравнения системы на отличное от нуля число.

Система линейных уравнений называется однородной, если все свободные члены равны нулю:

Однородная система всегда совместна, так как x1=x2=x3=…=xn=0 является решением системы. Это решение называется нулевым или тривиальным.

2. Метод исключения Гаусса

2.1 Сущность метода исключения Гаусса

Классическим методом решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных – метод Гаусса (его еще называют методом гауссовых исключений). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Процесс решения по методу Гаусса состоит из двух этапов: прямой и обратный ходы.

1. Прямой ход.

На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним.

После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.

Приведенная ниже система имеет ступенчатый вид:

,

где

Коэффициенты aii называются главными (ведущими) элементами системы.

1-й шаг.

Будем считать, что элемент

(если a11=0, переставим строки матрицы так, чтобы a ₁₁ не был равен 0. Это всегда возможно, т. к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна).

Преобразуем систему, исключив неизвестное х1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на

и сложим почленно со вторым уравнением системы (или из второго уравнения почленно вычтем первое, умноженное на ). Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы (или из третьего почленно вычтем первое, помноженное на ). Таким образом, последовательно умножаем первую строку на число и прибавляем к i -й строке, для i= 2, 3, …, n.

Продолжая этот процесс, получим эквивалентную систему:

Здесь

– новые значения коэффициентов при неизвестных и свободные члены в последних m-1 уравнениях системы, которые определяются формулами:

Таким образом, на первом шаге уничтожаются все коэффициенты, лежащие под первым ведущим элементом a₁₁

0, на втором шаге уничтожаются элементы, лежащие под вторым ведущим элементом а₂₂⁽¹⁾ (если a₂₂⁽¹⁾0) и т.д. Продолжая этот процесс и дальше, мы, наконец, на (m-1) шаге приведем исходную систему к треугольной системе.

Если в процессе приведения системы к ступенчатому виду появятся нулевые уравнения, т.е. равенства вида 0=0, их отбрасывают. Если же появится уравнение вида

то это свидетельствует о несовместности системы.

На этом прямой ход метода Гаусса заканчивается.

2. Обратный ход.

На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений.

Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (она в нем всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх.

Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Примечание: на практике удобнее работать не с системой, а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент a11 был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на a11).

2.2 Примеры решения СЛАУ методом Гаусса

В данном разделе на трех различных примерах покажем, как методом Гаусса можно решить СЛАУ.

Пример 1. Решить СЛАУ 3-го порядка.

Обнулим коэффициенты при

во второй и третьей строчках. Для этого домножим их на 2/3 и 1 соответственно и сложим с первой строкой:

mirznanii.com