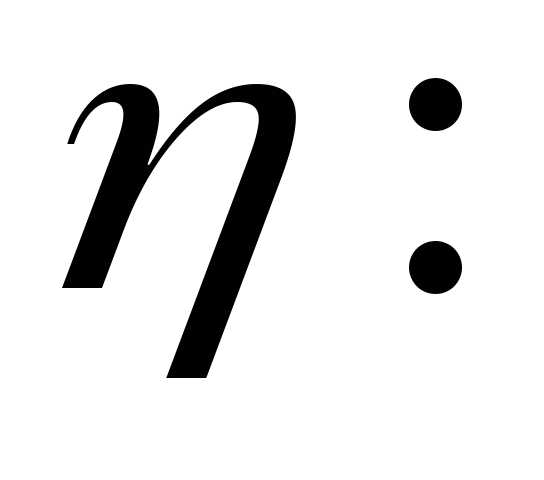Медиана и мода в теории вероятности – Начальные и центральные моменты непрерывной случайной величины, асимметрия и эксцесс. Мода и медиана
Мода и медиана. Примеры
Для нахождения моды и медианы случайной величины необходимы хорошие умения интегрировать и знания следующего теоретического материала. Модой дискретной случайной величины называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины , которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей
В зависимости от вида функции случайная величина может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой случайной величины называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)
Графически мода и медиана изображенные на рисунке
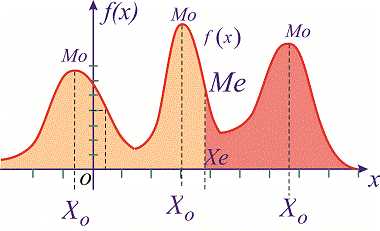
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин то медиана равна средней величине
в случае четного количества полусумме средних величин
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины — количество дорожек, которые требуют уборки. Найти моду .
Решение. Случайной величина может принимать значения
Вероятности появления значений определяем по образующей функцией
Для заданной задачи входные величины принимают значения
Искомые вероятности входят множителями при степенях аргумента
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду , как значение при максимальной вероятности. Получили одномодальное распределение
Пример 2. По заданной плотностью вероятностей
найти параметр , плотность вероятностей , моду .
Решение. Применяя условие нормирования выполняем интегрирование
после того определяем параметр
Плотность вероятностей, учитывая найденное значение будет иметь вид
а ее график изображен на рисунке ниже
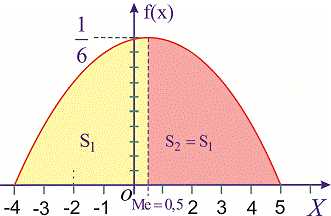
Из графика плотности вероятностей видим, что мода принимает значение . Определим медиану с помощью функции распределения вероятностей. Ее значение на промежутке находим интегрированием
Функция распределения иметь следующий вид
а ее график будет иметь вид
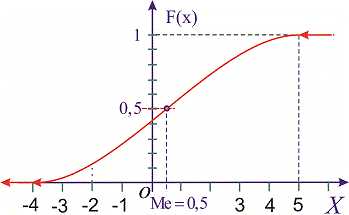
Для определения медианы случайной величины применяем формулу
Медиану можно найти с помощью плотности вероятностей
для дискретной случайной величины из промежутка
Таким образом медиану — возможное значение случайной величины , при котором прямая, проведенная перпендикулярно соответствующей точки на плоскости , делит площадь фигуры, ограниченной функцией плотности вероятностей на две равные части.
——————————-
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.
yukhym.com
3.5. Мода и медиана дискретной случайной величины
Значение случайной
величины  ,
принимаемое с наибольшей вероятностью,
называетсямодойи обозначается
,
принимаемое с наибольшей вероятностью,
называетсямодойи обозначается
Мода называется еще наивероятнейшим значениемслучайной величины.
Если эксперимент описывается случайной величиной, то в результате проведенной серии этого эксперимента чаще всего встречается мода случайной величины.
Медиана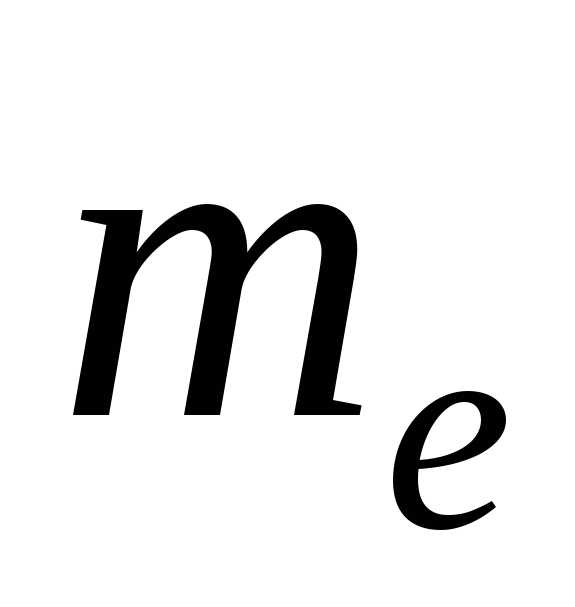 является значением случайной величины
является значением случайной величины .
Вероятность того, что случайная величина
принимает значение меньше медианы,
равна 0,5:
.
Вероятность того, что случайная величина
принимает значение меньше медианы,
равна 0,5:
Не все дискретные случайные величины имеют медиану.
Пример 1. Задан закон распределения случайной величины
|
| 3 | 5 | 6 |
0,2 | 0,3 | 0,4 | 0,1 |
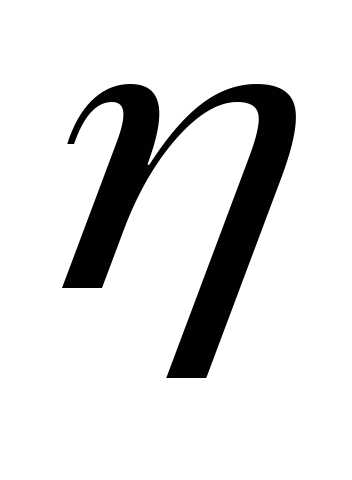 .
.Найдем моду:
.
Тогда 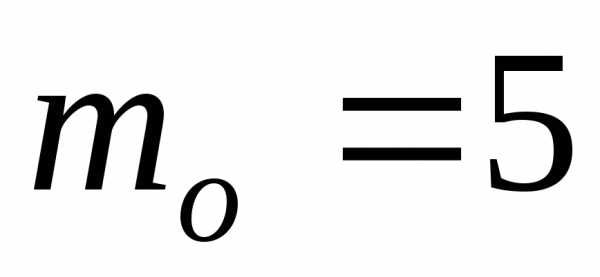 .
.
Для нахождения
медианы нужно рассмотреть 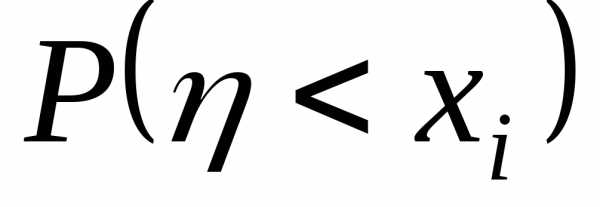 ,
где
,
где значения
случайной величины
значения
случайной величины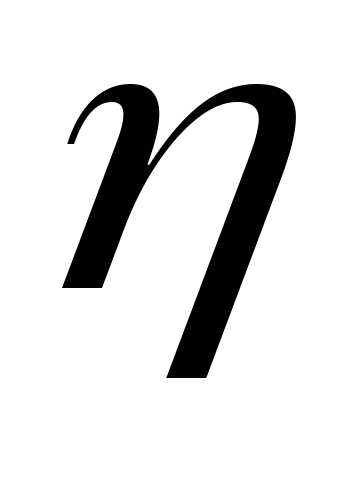 .
.
.
Заметим, что .

.
Тогда  .
Нет необходимости находить
.
Нет необходимости находить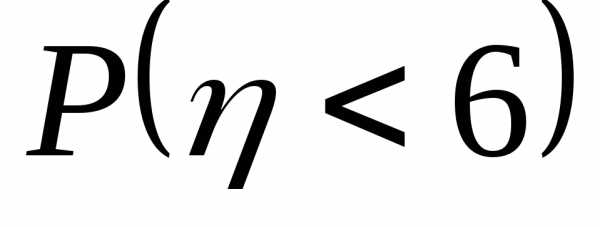 .
.
Пример 2. Задан закон распределения случайной величины
| 0 | 1 |
0,9 | 0,1 |
Найти моду и медиану
случайной величины  .
Значение 0 принимается с наибольшей
вероятностью
.
Значение 0 принимается с наибольшей
вероятностью
.
Тогда 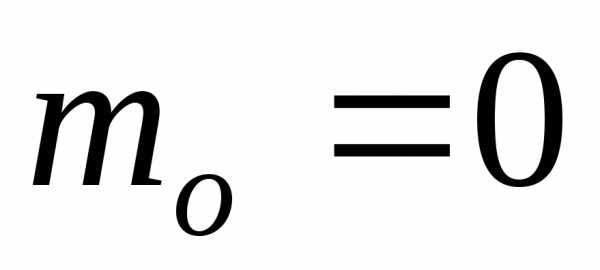 .
.
Найдем медиану
.
Нет значения 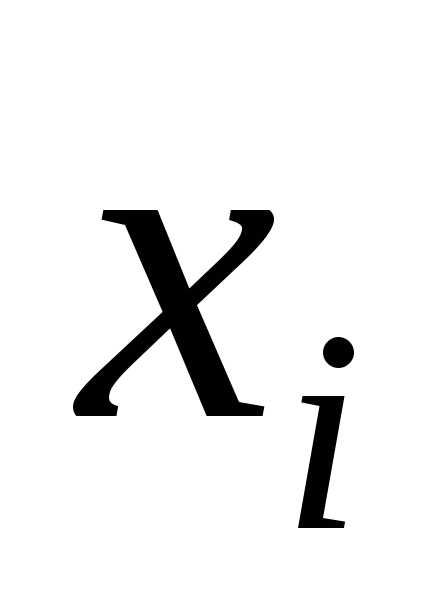
 ,
при котором.
Поэтому случайная величина
,
при котором.
Поэтому случайная величина медианы не имеет.
медианы не имеет.3.6. Корреляционный момент. Коэффициент корреляции
Вводится величина,
характеризующая зависимость между
двумя случайными величинами. Задано
совместное распределение случайных
величин  и
и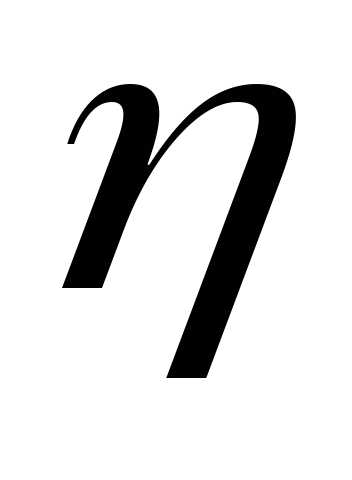
.
Корреляционным
моментомслучайных величин
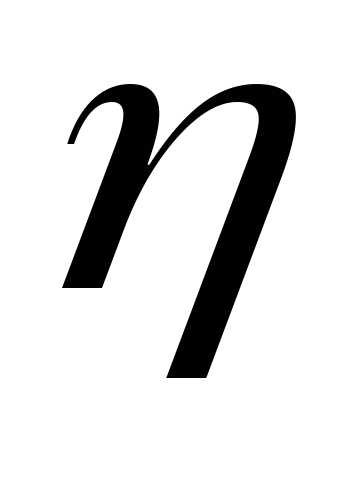 (иликовариациеймежду
(иликовариациеймежду и
и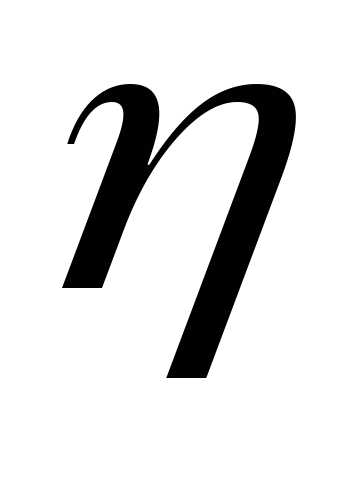 )
называется число
)
называется число Для дискретных
случайных величин  и
и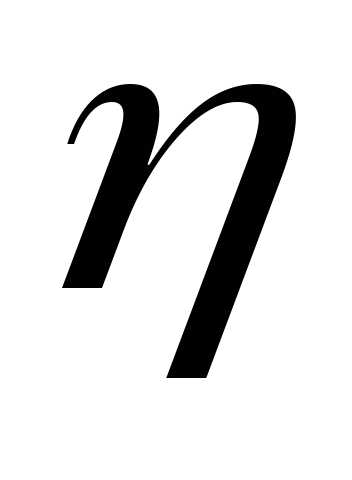 имеем
имеем
.
Непосредственно из свойств математического ожидания вытекают свойства ковариации:
;
;
;
;
Если случайные величины независимы, то их ковариация равна нулю.
Обратное не верно.
Если
,
то случайные величины и
и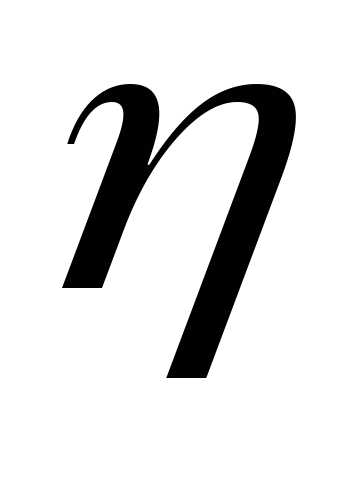 могут быть как зависимыми, так и
независимыми.
могут быть как зависимыми, так и
независимыми.
Коэффициентом
корреляциимежду случайными величинами и
и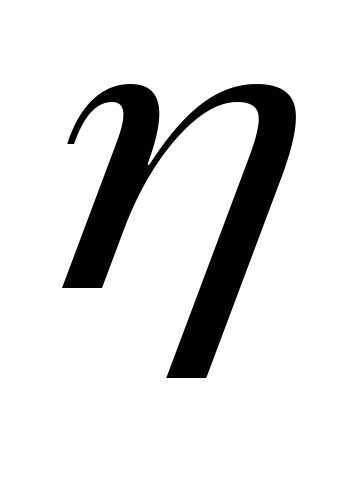
.
Приведем некоторые свойства коэффициента корреляции.
Пусть  и введем случайную величину
и введем случайную величину
.
Знакоположительная
случайная величина  имеет не отрицательное математическое
ожидание:
имеет не отрицательное математическое
ожидание:
при любом  .
.
Распишем 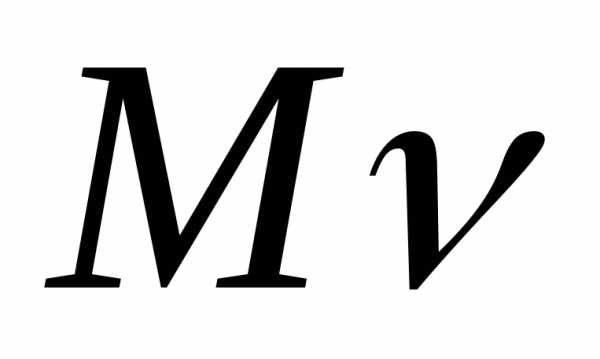
.
Получаем квадратичное неравенство
,
где
, .
.
Неравенство
выполняется при любом  ,
если дискриминант неположительный.
Тогда
,
если дискриминант неположительный.
Тогда
, откуда
.
Таким образом, .
Если
 и
и
Коэффициент корреляции равен
 тогда и только тогда, когда случайные
величины линейно зависимы
тогда и только тогда, когда случайные
величины линейно зависимы
Пусть . Тогдаи,
.
Тогда .
Пусть .
Рассмотрим случайную величину
.
Найдем
,
.
Из свойства математического ожидания
.
и
.
Получим линейное
выражение 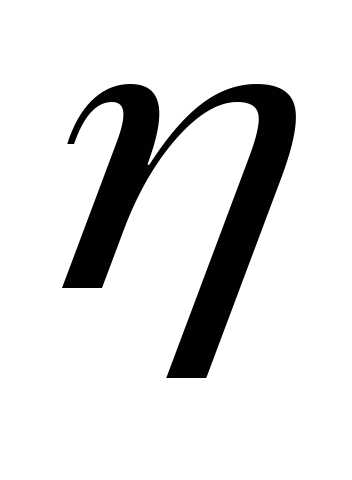 через
через .
.
Случай разбирается аналогично. Вводится случайная величина.
Пример 1. Задано
совместное распределение случайных
величин и
и
Найти 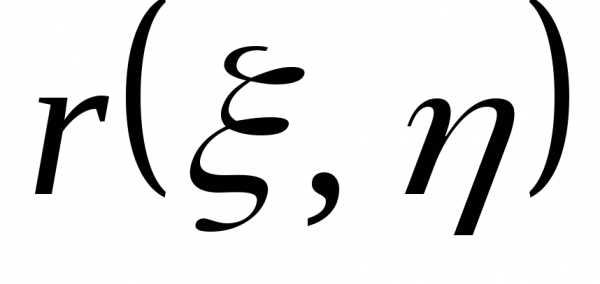 .
.
Запишем распределения
случайных величин 
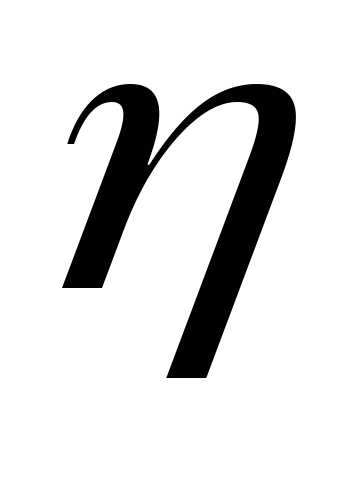

0
1
;
0,4

2
4
.
0,3
0,7
Найдем основные
характеристики случайных величин  и
и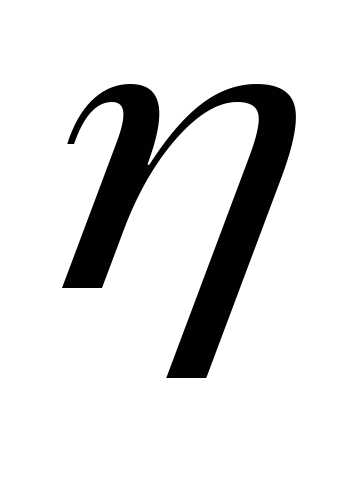 :
:
;
;
.
Используем формулу .
Найдем :
.
Тогда и
.
studfiles.net
5.2. Мода и медиана | Решение задач по математике и другим предметам!!! |
Кроме математического ожидания и дисперсии в теории вероятностей применяется еще ряд числовых характеристик, в частности, мода и медиана случайной величины.
Модой Дискретной случайной величины X называется ее наиболее вероятное значение.
Модой непрерывной случайной величины X называется такое ее значение , при котором плотность распределения Имеет максимум, т. е. .
На рис. 3 и 4 показана мода для дискретной и непрерывной случайной величины.
Рис. 3 Рис. 4
Если многоугольник распределения (кривая распределения) имеет два или несколько максимумов, то распределение называется Двухмодальным или многомодальным.
Иногда встречаются распределения, которые имеют минимум, но не имеют максимум. Такие распределения называются Антимодальными.
Медианой непрерывной случайной величины X (обозначение:) называется такое ее значение , для которого одинаково вероятно, окажется ли случайная величина Меньше или больше, т. е.
. (9)
Геометрически вертикальная прямая , Проходящая через точку с абсциссой, равной , делит площадь фигуры под кривой распределения на две равные части (рис. 5). Каждая из этих площадей равна , т. к. площадь, ограниченная кривой распределения, равна единице. Поэтому функция распределения в точке равна , т. е. .
Рис. 5
Для дискретной случайной величины медиана обычно не определяется.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Найти моду, медиану, дисперсию может каждый!
Найти моду, медиану, дисперсию и другие характеристики учат в курсе теории вероятностей для анализа статистического распределения выборки. Если Вы имеете заготовленные формулы или методичку, то само по себе вычисления числовых характеристик статистических выборок не является сложным. Однако на контрольных, индивидуальных заданиях, а еще для заочников все всегда выглядит сложнее, чем есть на самом деле. Ниже приведены решения которые многие вещи из вероятности сделают для Вас простыми и понятными. Главное не спешите и в подобных примерах поступайте по аналогии.
Индивидуальное задание 1
Вариант 8
Задача 1. Составить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моде;
- квантильное отклонения;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Выборка задана следующими значениями
4, 9, 7, 4, 7, 5, 6, 3, 4, 5, 7, 2, 3, 8, 5, 6, 7, 4, 3, 4.
Решение: Записываем выборку в виде вариационного ряда (в порядке возрастания):
2; 3; 3; 3; 4; 4; 4; 4; 4; 5; 5; 5; 6; 6; 7; 7; 7; 7; 8; 9.
Запишем статистическое распределение выборки в виде дискретного статистического распределения частот:
Значение эмпирической функции распределения определяем по формуле
где nx количество элементов выборки меньше х. Используя таблицу, а также учитывая, что объем выборки n=1+3+5+3+2+4+1+1=20, запишем эмпирическую функцию распределения:
Далее вычислим числовые характеристики статистического распределения выборки.
1. Выборочное среднее вычисляем по формуле
2. Выборочную дисперсию вычисляем по формуле
3. Подправленную дисперсию находим по формуле
4. Выборочное среднее квадратичное отклонение вычисляем по формуле
5. Подправленное среднее квадратичное отклонение находим по формуле
6. Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:
7. Медиану вычисляют по формулам:
если число n — четное;
если число n — нечетное.
Здесь берем индексы в x[i] согласно нумерации вариант в вариационном ряду.
В нашем случае п=20, поэтому
8. Мода — это варианта которая в вариационном ряду случается чаще всего, то есть
9. Квантильное отклонение найдем по формуле
половины разницы – третьего и – первого квантилей.
Сами же квантили получаем искусственной разбивкой вариационного ряда на 4 равные части. В нашем случае
10. Коэффициент вариации вычисляем по формуле
11. Коэффициент асимметрии находим по формуле
Здесь m3 центральный эмпирический момент 3-го порядка,
Отсюда коэффициент асимметрии равен 0,3
12. Эксцессом статистического распределения выборки называется число которое находят по формуле:
В числителе имеем центральный эмпирический момент 4-го порядка
Момент и среднее квадратичное отклонение подставляем в формулу и определяем эксцесс
По тому как все доступно и понятно на практике выглядит делаем вывод, что найти моду, медиану и дисперсию должен уметь каждый студент, который изучает теорию вероятностей.
Готовые решения по теории вероятностей
yukhym.com
5.4. Мода и медиана случайной величины
Наряду с математическим ожиданием, дисперсией и моментами для описания распределения случайной величины применяют также моду и медиану.
Модой Mo случайной величины X называется наиболее вероятное значение случайной величины.
Термин «наиболее вероятное значение», строго говоря, применим только к ДСВ, в случае НСВ мода совпадает с таким значением случайной величины, при котором плотность распределения имеет максимум. Различают унимодальные (имеющие одну моду), бимодальные (имеющие две моды) и мультимодальные (имеющие несколько мод) распределения. Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом. Такие распределения называются антимодальными.
Мода, например, часто используется при экономических расчетах, когда нужно дать ответ на вопрос, каковы преобладающие в данный момент уровни производительности труда, себестоимость, какой товар имеет наибольший спрос и т.д. В связи с этим вводятся понятия модальная производительность, модальная себестоимость и т.д.
Медианой Me случайной величины X называется такое ее значение, для которой справедливо равенство
P(X<Me) = P(X>Me)
т.е. равновероятно, что случайная величина окажется меньше или больше медианы.
С геометрической точки зрения, медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам. Так как вся площадь должна равняться единице, то функция распределения в этой точке равна 0,5:
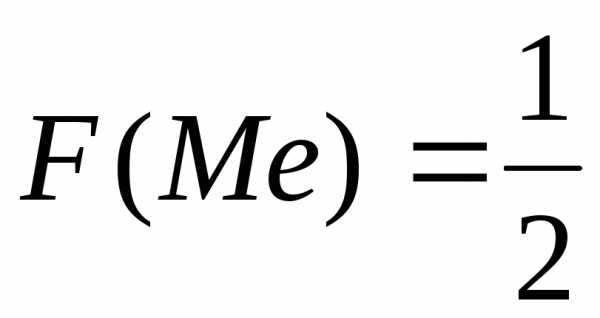 .
.
Отметим оптимальное свойство медианы: сумма абсолютных величин отклонений возможных значений случайной величины от медианы, умноженных на соответствующие вероятности, меньше, чем от любой другой величин, т.е. медианы удовлетворяют условию:
Это свойство медианы, в частности, используется в теории оптимального проектирования. Например, при проектировании остановок, при условии, чтобы общий путь пассажиров был минимальным.
Следует отметить, что если распределение симметрично и унимодально, то математическое ожидание, медиана и мода совпадают.
Кроме моды и медианы иногда используются и другие числовые характеристики. Например,
—квантилью Q (0<<1) случайной величины X называется число, удовлетворяющее неравенствам
.
Квантили находят самое широкое применение в математической статистике при построении доверительных интервалов и проверке статистических гипотез. Отметим, ½-квантиль совпадает с медианой.
Энтропия H=H(X) дискретной случайной величины X определяется по формуле
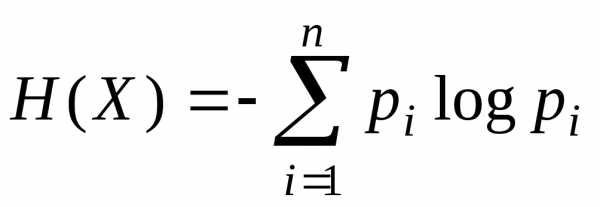 .
.
Отметим, что энтропия не зависит от значений xi от случайной величины X, а зависит только от вероятностей pi, с которыми эти значения принимаются. Энтропия является мерой априорной неопределенности случайной величины. Максимального значения Hmax=logn энтропия ДСВ достигает тогда, когда все n возможных значений случайная величина принимает с одной и той же вероятностью pi=1/n, минимальное Hmin=0 – когда случайная величина принимает единственное значение с вероятностью, равной единице.
Энтропия играет важную роль в теории информации, она в некотором смысле представляет собой минимальный объем памяти, необходимый для записи информации, содержащейся в случайной величине. Поскольку информация записывается обычно в двоичной системе, то основание логарифма берется число 2.
Энтропия H=H(X) непрерывной случайной величины X определяется по формуле
.
Заметим, что в отличие, например, от математического ожидания энтропию НСВ нельзя получить предельным переходом от дискретного случая. Отметим также, что при заданной дисперсии 2 максимальную энтропию имеет нормально распределенная случайная величина.
studfiles.net
Мода (в теории вероятностей) | Наука
Мода (от лат. modus — мера, способ, правило) — одна из числовых характеристик распределения вероятностей случайной величины; для случайной величины, имеющей плотность вероятностей $ f(x) $ определяется как любая точка максимума $ f(x) $; определяется и для распределений, не имеющих плотности: например мода дискретной случайной величины — любое её значение, имеющее вероятность, равную максимальной вероятности; иногда под модой случайной величины $ \xi $ понимают точку, где достигается абсолютный максимум её плотности вероятности или вероятностей её значений — главное значение моды, обозначаемое $ {\rm Mod}\xi $; менее употребительная характеристика распределения, чем математическое ожидание и медиана.
Распределения с одной, двумя или большим числом мод называются соответственно унимодальными (одновершинными), бимодальными или мультимодальными.
Унимодальные распределенияПравить
В теории вероятностей и математической статистике наиболее используемыми являются унимодальные распределения. Для унимодальных распределений, симметричных относительно некоторой точки $ a $, мода равна $ a $ и совпадает с медианой и математическим ожиданием, если последнее существует. Если распределение случайной величины $ \xi $ унимодально и непрерывно, то для любого $ \varepsilon > 0 $
- $ \mathbf{P} \Big( |\xi-{\rm Mod}\xi| \geq \varepsilon \tau \Big) \leq \frac{4}{9 \varepsilon^2}, $
где $ {\rm Mod}\xi $ — мода случайной величины $ \xi $, а $ \tau^2 = {\rm E}|\xi-{\rm Mod}\xi|. $
Экстремальные свойстваПравить
Мода $ {\rm Mod}\xi $ случайной величины $ \xi $ минимизирует её среднее отклонение в дискретной метрике:
- $ {\rm E} d(\xi,{\rm Mod}\xi) = \min_a {\rm E}d(\xi,a), $
где $ d(a,b) = 0 $, если $ a = b $, и $ d(a,b) = 1 $, если $ a \not= b. $
- Frechet, M. (1948) Les elements aleatories de nature quelconque dans un espace distancie. Ann.Inst.H.Poincare 10, 215—310.
См.такжеПравить
У этого термина существуют и другие значения, см. Мода.Статья основана на материалах Большой советской энциклопедии.
ru.science.wikia.com
Мода, медиана. Моменты случайных величин. Асимметрия, эксцесс. Квантили —
Модой дискретной случайной величины называется значение этой величины, принимаемое с наибольшей вероятностью в сравнении с двумя соседними значениями. Мода обозначается через . Для непрерывной случайной величины мода — точка максимума (локального) плотности .
Если мода единственна, то распределение случайной величины называется унимодальным, в противном случае — полимодальным (рисунок 3.13).
Рис 3.13
Медианой непрерывной случайной величины называется такое ее значение , для которого
,
т. е. одинаково вероятно, окажется ли случайная величина меньше или больше (рис. 3.13).
С помощью функции распределения равенство для медианы можно записать в виде . Отсюда .
Для дискретной случайной величины медиана обычно не определяется.
Математическое ожидание и дисперсия являются частными случаями следующих более общих понятий – моментов случайной величины .
Начальным моментом порядка случайной величины называется математическое ожидание -й степени этой величины, и обозначается через . Таким образом, по определению .
Для дискретной случайной величины начальный момент выражается суммой: , а для непрерывной случайной величины – интегра-лом: . В частности, , т.е. начальный момент 1-го порядка есть математическое ожидание.
Центральным моментом порядка случайной величины называется математическое ожидание величины обозначается через
Таким образом, по определению В частности, т.е. центральный момент 2-го порядка есть дисперсия; (по свойству 4 математического ожидания).
Для дискретной случайной величины имеем а для непрерывной случайной величины : .
Центральные моменты могут быть выражены через начальные моменты. Например, Действительно:
;
и т.д.
Среди моментов высших порядков особое значение имеют центральные моменты 3-го и 4-го порядков, называемых соответственно коэффициентами асимметрии и эксцесса.
Коэффициентом асимметрии («скошенности») случайной величины называется величина
.
Если , то кривая распределения более полога справа от (рисунок 3.14).
Рис. 3.14
Если , то кривая распределения более полога слева от (рисунок 3.15).
Рис. 3.15
Коэффициентом эксцесса («островершинности») случайной величины называется величина
.
Величина характеризует островершинность или плосковершинность распределения. Для нормального закона распределения и ; остальные распределения сравниваются с нормальным: если — более островершинные, а распределения «плосковершинные» имеют (рисунок 3.16).
Рис. 3.16
Кроме рассмотренных выше числовых характеристик случайной величины в приложениях используются так называемые квантили.
Квантилью уровня случайной величины называется решение уравнения
,
где — некоторое число, .
Квантили , и имеют свои названия: нижняя квантиль, медиана (), верхняя квантиль соответственно. Они делят числовую прямую на 4 части, вероятности попадания в которые равны 0,25 (рисунок 3.17).
Рис. 3.17
einsteins.ru




 и
и
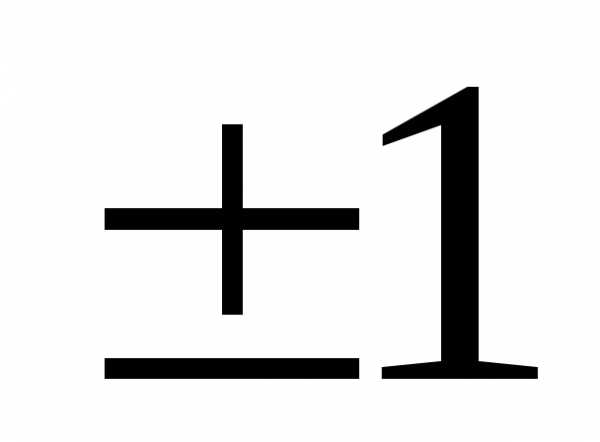 тогда и только тогда, когда случайные
величины линейно зависимы
тогда и только тогда, когда случайные
величины линейно зависимы